Optimal Control of Drug Therapy in a Hepatitis B Model
Abstract
:1. Introduction
2. Mathematical Model and Analysis
2.1. Model of Hepatitis B Virus (HBV) Drug Therapy
2.2. Model Analysis
2.3. Numerical Results
3. Optimal Control Problem
3.1. Analysis of the Optimal Control Problem
3.2. Implementation of the Optimal Control Problem
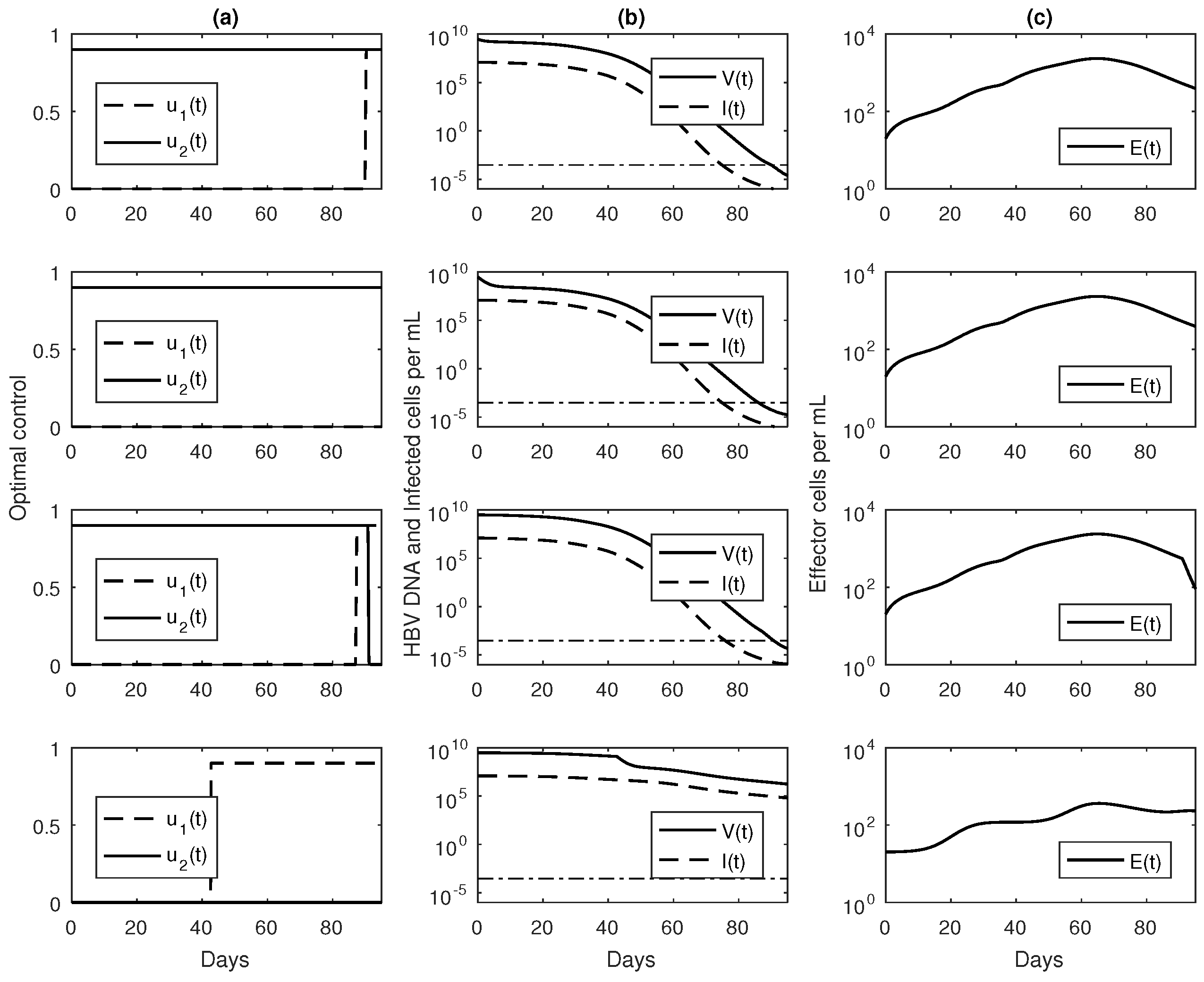
3.3. Numerical Results with Optimal Controls
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Manzoor, S.; Saalim, M.; Imran, M.; Resham, S.; Ashraf, J. Hepatitis B virus therapy: What’s the future holding for us? World J. Gastroenterol. 2015, 21, 12558–12575. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.S. Hepatitis B vaccination: The key towards elimination and eradication of hepatitis B. J. Hepatol. 2009, 50, 805–816. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, S.T.; Zhou, F.; Hadler, S.C.; Bell, B.P.; Mast, E.E.; Margolis, H.S. A mathematical model to estimate global hepatitis B disease burden and vaccination impact. Int. J. Epidemiol. 2005, 34, 1329–1339. [Google Scholar] [CrossRef] [PubMed]
- Ott, J.J.; Stevens, G.A.; Groeger, J.; Wiersma, S.T. Global epidemiology of hepatitis B virus infection: New estimates of age-specific HBsAg seroprevalence and endemicity. Vaccine 2012, 30, 2212–2219. [Google Scholar] [CrossRef] [PubMed]
- Lok, A.S.; McMahon, B.J. Chronic hepatitis B. Hepatology 2007, 45, 507–539. [Google Scholar] [CrossRef] [PubMed]
- Bhat, M.; Ghali, P.; Deschenes, M.; Wong, P. Prevention and management of chronic hepatitis B. Int. J. Prev. Med. 2014, 5, S200–S207. [Google Scholar] [PubMed]
- Lok, A.S.F.; McMahon, B.J.; Brown, R.S.; Wong, J.B.; Ahmed, A.T.; Farah, W.; Almasri, J.; Alahdab, F.; Benkhadra, K.; Mouchli, M.A.; et al. Antiviral therapy for chronic hepatitis B viral infection in adults: A systematic review and meta-analysis. Hepatology 2016, 63, 284–306. [Google Scholar] [CrossRef] [PubMed]
- Lampertico, P.; Aghemo, A.; Viganò, M.; Colombo, M. HBV and HCV therapy. Viruses 2009, 1, 484–509. [Google Scholar] [CrossRef] [PubMed]
- Sonneveld, M.J.; Wong, V.; Woltman, A.M.; Wong, G.L.H.; Cakaloglu, Y.; Zeuzem, S.; Buster, E.; Uitterlinden, A.G.; Hansen, B.E.; Chan, H.; et al. Polymorphisms near IL28B and serologic response to peginterferon in HBeAg-positive patients with chronic hepatitis B. Gastroenterology 2012, 142, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Hadziyannis, S.J.; Tassopoulos, N.C.; Heathcote, E.J.; Chang, T.-T.; Kitis, G.; Rizzetto, M.; Marcellin, P.; Lim, S.G.; Goodman, Z.; Wulfsohn, M.S.; et al. Adefovir dipivoxil for the treatment of hepatitis B e antigen—Negative chronic hepatitis B. N. Eng. J. Med. 2003, 348, 800–807. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.L.; Wang, H.; Niu, J.; Chim, A.M.; Sung, J.J. Two-year lamivudine treatment for hepatitis B e antigen-negative chronic hepatitis B: A double-blind, placebo-controlled trial. Antivir. Ther. 2007, 12, 345–353. [Google Scholar] [PubMed]
- Locarnini, S.; Hatzakis, A.; Chen, D.S.; Lok, A. Strategies to control hepatitis B: Public policy, epidemiology, vaccine and drugs. J. Hepatol. 2015, 62, S76–S86. [Google Scholar] [CrossRef] [PubMed]
- Ciupe, S.M.; Catlla, A.; Forde, J.; Schaeffer, D.G. Dynamics of hepatitis B virus infection: What causes viral clearance? Math. Popul. Stud. 2011, 18, 87–105. [Google Scholar] [CrossRef]
- Ciupe, S.M.; Ribeiro, R.M.; Nelson, P.W.; Dusheiko, G.; Perelson, A.S. The role of cells refractory to productive infection in acute hepatitis B viral dynamics. Proc. Natl. Acad. Sci. USA 2007, 104, 5050–5055. [Google Scholar] [CrossRef] [PubMed]
- Ciupe, S.M.; Ribeiro, R.M.; Nelson, P.W.; Perelson, A.S. Modeling the mechanisms of acute hepatitis B virus infection. J. Theor. Biol. 2007, 247, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Ciupe, S.M.; Ribeiro, R.M.; Perelson, A.S. Antibody responses during Hepatitis B viral infection. PLoS Comput. Biol. 2014, 10, e1003730. [Google Scholar] [CrossRef] [PubMed]
- Dahari, H.; Shudo, R.M.; Ribeiro, E.; Perelson, A.S. Modeling complex decay profiles of Hepatitis B virus during antiviral therapy. Hepatology 2009, 49, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Lewin, S.R.; Ribeiro, R.M.; Walters, T.; Lau, G.K.; Bowden, S.; Locarnini, S.; Perelson, A.S. Analysis of hepatitis B viral load decline under potent therapy: Complex decay profiles observed. Hepatology 2001, 34, 1012–1020. [Google Scholar] [CrossRef] [PubMed]
- Tsiang, M.; Rooney, J.F.; Toole, J.J.; Gibbs, C.S. Biphasic clearance kinetics of hepatitis B virus from patients during adefovir dipivoxil therapy. Hepatology 1999, 29, 1863–1869. [Google Scholar] [CrossRef] [PubMed]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelize, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Fister, K.R.; Lenhart, S.; McNally, S. Optimizing chemotherapy in an HIV model. Electron. J. Differ. Eq. 1998, 32, 1–12. [Google Scholar]
- Fister, K.R.; Panetta, J.C. Optimal control applied to competing chemotherapeutic cell-kill strategies. SIAM J. Appl. Math. 2003, 63, 1954–1971. [Google Scholar]
- Joshi, H.R. Optimal control of an HIV immunology model. Opt. Control Appl. Methods 2003, 23, 199–213. [Google Scholar] [CrossRef]
- Ledzewicz, U.; Brown, T.; Schattler, H. A comparison of optimal controls for a model in cancer chemotherapy with L1- and L2-type objectives. Opt. Methods Softw. 2004, 19, 351–359. [Google Scholar]
- Lenhart, S.L.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Gollman, L.; Mauer, H. Theory and applications of optimal control problems with multiple time-delays. J. Ind. Manag. Opt. 2014, 10, 413–441. [Google Scholar]
- Kharatishvili, G.L. Maximum principle in the theory of optimal time-delay processes. Dokl. Akad. Nauk USSR 1961, 136, 39–42. [Google Scholar]
- Banks, H.T. Approximation of nonlinear functional differential equations control systems. J. Opt. Theory Appl. 1979, 29, 383–408. [Google Scholar] [CrossRef]
- Banks, H.T.; Burns, J.A. Hereditary control problems: Numerical methods based on averaging approximations. SIAM J. Control Opt. 1978, 16, 169–208. [Google Scholar] [CrossRef]
- Eliaw, A.M.; Alghamdi, M.A.; Aly, S. Hepatitis B virus dynamics: Modeling, analysis and optimal treatment scheduling. Discret. Dyn. Nat. Soc. 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Hattaf, K.; Rachik, M.; Saadi, S.; Yousfi, N. Optimal control in a basic virus infection model. Appl. Math. Sci. 2009, 3, 949–958. [Google Scholar]
- Mouofo, P.T.; Tewa, J.J.; Mewoli, B.; Bowong, S. Optimal control of a delayed system subject to mixed control-state constraints with application to a within-host model of hepatitis virus B. Ann. Rev. Control 2013, 37, 246–259. [Google Scholar] [CrossRef]
- Su, Y.; Sun, D. Optimal control of anti-HBV treatment based on combination of Traditional Chinese Medicine and Western Medicine. Biomed. Signal Proc. Control 2015, 15, 41–48. [Google Scholar] [CrossRef]
- Guo, J.-T.; Zhou, H.; Liu, C.; Aldrich, C.; Saputelli, J.; Whitaker, T.; Barrasa, M.I.; Mason, M.S.; Seeger, C. Apoptosis and regeneration of hepatocytes during recovery from transient hepadnavirus infections. J. Virol. 2000, 74, 1495–1505. [Google Scholar] [CrossRef] [PubMed]
- Guidotti, L.G.; Rochford, R.; Chung, J.; Shapiro, M.; Purcell, R.; Chisari, F.V. Viral clearance without destruction of infected cells during acute HBV infection. Science 1999, 284, 825–829. [Google Scholar] [CrossRef] [PubMed]
- Marrack, P.; Kappler, J.; Mitchell, T. Type I interferons keep activated T cells alive. J. Exp. Med. 1999, 189, 521–529. [Google Scholar] [CrossRef] [PubMed]
- Rehermann, B.; Bertoletti, A. Immunological aspects of antiviral therapy of chronic hepatitis B virus and hepatitis C virus infections. Hepatology 2015, 61, 712–721. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Ribeiro, R.M. Hepatitis B virus kinetics and mathematical modeling. Sem. Liv. Dis. 2004, 24, 11–16. [Google Scholar] [CrossRef] [PubMed]
- Banks, H.T.; Dediu, S.; Ernstberger, S.E. Sensitivity functions and their uses in inverse problems. J. Inverse Ill-posed Probl. 2007, 15, 683–708. [Google Scholar] [CrossRef]
- Hackbush, W. A numerical method for solving parabolic equations with opposite orientations. Computing 1978, 20, 229–240. [Google Scholar] [CrossRef]
- Chisari, F.V.; Isogawa, M.; Wieland, S.F. Pathogenesis of hepatitis B virus infection. Pathol. Biol. 2010, 58, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Li, G.T.; Yu, Y.-Q.; Chen, S.L.; Fan, P.; Shao, L.-Y.; Chen, J.-Z.; Li, C.-S.; Yi, B.; Chen, W.-C.; Xie, S.-Y.; et al. Sequential combination therapy with pegylated interferon leads to loss of hepatitis B surface antigen and hepatitis B e antigen (HBeAg) seroconversion in HBeAg-positive chronic hepatitis B patients receiving long-term entecavir treatment. Antimicrob. Agents Chemother. 2015, 59, 4121–4128. [Google Scholar] [CrossRef] [PubMed]
- Alaluf, M.B.; Shlomai, A. New therapies for chronic hepatitis B. Liver Int. 2016, 36, 775–782. [Google Scholar] [CrossRef] [PubMed]
- Gollman, L.; Kern, D.; Maurer, H. Optimal control problems with delays in state and control variables subject to mixed control-state constraints. Optim. Control Appl. Meth. 2009, 30, 341–365. [Google Scholar] [CrossRef]
- Micco, L.; Peppa, D.; Loggi, E.; Schurich, A.; Jefferson, L.; Cursaro, C.; Panno, A.M.; Bernardi, M.; Brander, C.; Bihl, F.; et al. Differential boosting of innate and adaptive antiviral responses during pegylated-interferon-alpha therapy of chronic hepatitis B. J. Hepatol. 2013, 58, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Dunn, C.; Peppa, D.; Khanna, P.; Nebbia, G.; Jones, M.; Brendish, N.; Lascar, R.M.; Brown, D.; Gilson, R.J.; Tedder, R.J.; et al. Temporal analysis of early immune responses in patients with acute hepatitis B virus infection. Gastroenterology 2009, 137, 1289–1300. [Google Scholar] [CrossRef] [PubMed]
- Lucifora, J.; Xia, Y.; Reisinger, F.; Zhang, K.; Stadler, D.; Cheng, X.; Sprinzl, M.F.; Koppensteiner, H.; Makowska, Z.; Volz, T.; et al. Specific and nonhepatotoxic degradation of nuclear hepatitis B virus cccDNA. Science 2014, 343, 12221–12228. [Google Scholar] [CrossRef] [PubMed]






| Variables | ||||
|---|---|---|---|---|
| T | Target cells | per mL | ||
| I | Infected cells | per mL | ||
| V | Free virus | per mL | ||
| E | Effector cells | per mL | ||
| R | Refractory cells | per mL | ||
| Parameters | ||||
| r | Hepatocyte maximum proliferation rate | 1 day | ||
| β | Infectivity rate constant | mL (virion × day) | ||
| K | Hepatocyte carrying capacity | cells per mL | ||
| μ | Infected cell killing rate | mL (cell × day) | ||
| ν | Refractory cell killing rate | mL (cell × day) | ||
| ρ | Cure rate | mL (cell × day) | ||
| α | Effector cell expansion rate | mL (cell × day) | ||
| τ | Delay | days | ||
| π | Virus production rate | 164 virion (cell × day) | ||
| c | Virus clearance rate | day | ||
| s | Effector cell production | 10 day | ||
| d | Effector cell clearance rate | day | ||
| q | Waning of refractory cell immunity | day | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forde, J.E.; Ciupe, S.M.; Cintron-Arias, A.; Lenhart, S. Optimal Control of Drug Therapy in a Hepatitis B Model. Appl. Sci. 2016, 6, 219. https://doi.org/10.3390/app6080219
Forde JE, Ciupe SM, Cintron-Arias A, Lenhart S. Optimal Control of Drug Therapy in a Hepatitis B Model. Applied Sciences. 2016; 6(8):219. https://doi.org/10.3390/app6080219
Chicago/Turabian StyleForde, Jonathan E., Stanca M. Ciupe, Ariel Cintron-Arias, and Suzanne Lenhart. 2016. "Optimal Control of Drug Therapy in a Hepatitis B Model" Applied Sciences 6, no. 8: 219. https://doi.org/10.3390/app6080219
APA StyleForde, J. E., Ciupe, S. M., Cintron-Arias, A., & Lenhart, S. (2016). Optimal Control of Drug Therapy in a Hepatitis B Model. Applied Sciences, 6(8), 219. https://doi.org/10.3390/app6080219





