Laterally Loaded Single Pile Response Considering the Influence of Suction and Non-Linear Behaviour of Reinforced Concrete Sections
Abstract
:Featured Application
Abstract
1. Introduction
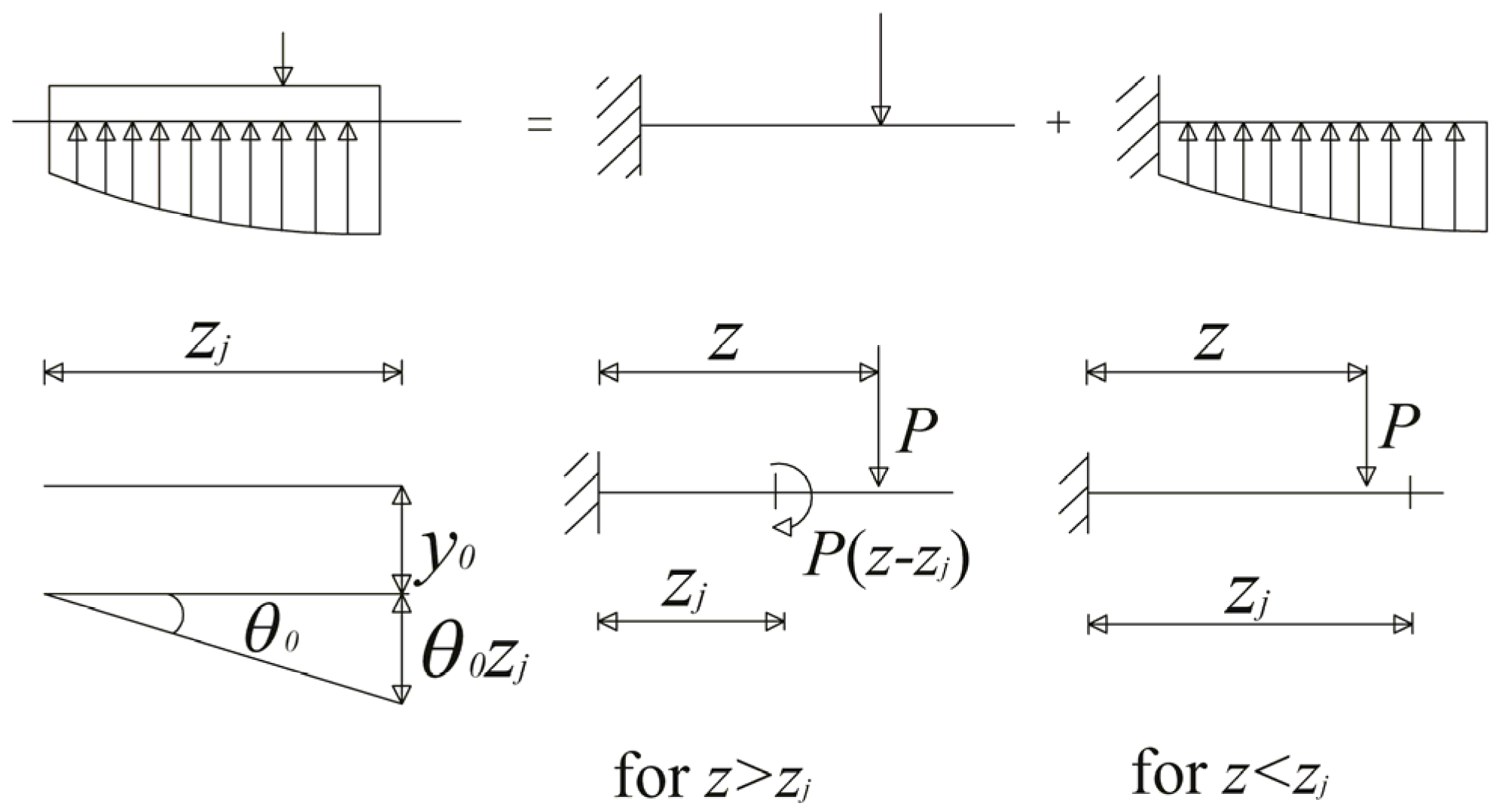
2. Proposed “Hybrid BEM-p-y Curve” Method
2.1. Pile Modelling
- 20 blocks with a thickness ∆ = D/8, starting from the ground level up to a depth of 2.5D;
- 10 blocks with a thickness ∆ = D/4, starting from a depth of 2.5D up to a depth of 5D;
- 10 blocks with a thickness ∆ = D/2, starting from a depth of 5D up to a depth of 10D;
- 10 blocks with a thickness ∆ = D, starting from a depth of 10D up to a depth of 20D;
- 10 blocks with a thickness ∆ = (L − 20D)/10, starting from a depth of 20D up to the pile base depth.
- the conservation of planar sections;
- concrete tension strength equal to zero for cracked sections;
- perfect bonding between steel bars and the surrounding concrete;
- the constitutive model proposed by Mander et al. [24] for confined concrete in compression;
- the constitutive model proposed by Popovics [25] for unconfined concrete in compression;
- the constitutive model proposed by CEB-FIP [26] for concrete in tension;
- a simple strain-hardening model or a bilinear model for steel reinforcement;
- a bond-slip law as suggested by Sigrist [27];
- the tension stiffening is considered using a variable elastic modulus for the concrete in tension along a pile-block between two consecutive cracks;
- the crack spacing can be estimated using the expression suggested by the CEB-FIP;
- no other secondary cracks develop between two consecutive cracks.
2.2. Soil Modelling
2.3. Non-Linear Solution Procedure
2.4. Influence of Suction on Pile Lateral Response
3. Validation of the Proposed Method
3.1. Analysis Results of a Specific Case Study
3.1.1. Soil Conditions and Pile Properties
3.1.2. Single Bored Pile B7: Analysis Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mokwa, R.L.; Duncan, J.M. Experimental evaluation of lateral-load resistance of pile caps. J. Geotech. Geoenviron. Eng. 2001, 127, 185–192. [Google Scholar] [CrossRef]
- Katzenbach, R.; Turek, J. Combined pile-raft foundation subjected to lateral loads. In Proceedings of the International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; AA Balkema Publishers: Rotterdam, The Netherlands; Volume 16. No. 4. [Google Scholar]
- Reese, L.C.; Wang, S.T.; Isenhower, W.M.; Arrellaga, J.A. Computer Program Lpile Plus; Version 5.0 Technical Manual; Ensoft: Austin, TX, USA, 2004. [Google Scholar]
- Khari, M.; Kassim, K.A.; Adnan, A. Development of Curves of Laterally Loaded Piles in Cohesionless Soil. Sci. World J. 2014, 2014, 917174. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.Y.; Cai, F.; Wang, G.X.; Chen, G.X.; Li, Y.Y. Nonlinear analysis of single reinforced concrete piles subjected to lateral loading. KSCE J. Civ. Eng. 2017, 1–12. [Google Scholar] [CrossRef]
- Mardfekri, M.; Gardoni, P.; Roesset, J.M. Modeling laterally loaded single piles accounting for nonlinear soil-pile interactions. J. Eng. 2013, 2013, 243179. [Google Scholar] [CrossRef]
- Yang, Z.; Jeremić, B. Numerical analysis of pile behaviour under lateral loads in layered elastic–plastic soils. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 1385–1406. [Google Scholar] [CrossRef]
- Yang, Z.; Jeremić, B. Numerical study of group effects for pile groups in sands. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 1255–1276. [Google Scholar] [CrossRef]
- Fatahi, B.; Basack, S.; Ryan, P.; Zhou, W.H.; Khabbaz, H. Performance of laterally loaded piles considering soil and interface parameters. Geomech. Eng. 2014, 7, 495–524. [Google Scholar] [CrossRef]
- Poulos, H.G. User’s Guide to Program DEFPIG 3/4 Deformation Analysis of Pile Groups; Revision 6; School of Civil Engineering, University of Sidney: Sidney, Australia, 1990. [Google Scholar]
- Randolph, M.F. PIGLET, A Computer Program for the Analysis and Design of Pile Groups; Report Geo, 86033; Department of Engineering, University of Cambridge: Cambridge, UK, 1980. [Google Scholar]
- Basile, F. A practical method for the non-linear analysis of piled rafts. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–5 September 2013. [Google Scholar]
- Mindlin, R.D. Force at a point in the interior of a semi-infinite solid. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Spillers, W.R.; Stoll, R.D. Lateral response of piles. J. Soil Mech. Found. Division 1964, 90, 1–10. [Google Scholar]
- Poulos, H.G.; Davis, E.H. Pile Foundation Analysis and Design; Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Davies, T.G.; Banerjee, P.K. The displacement field due to a point load at the interface of a two layer elastic half-space. Geotechnique 1978, 28, 43–56. [Google Scholar] [CrossRef]
- Sharnouby, B.E.; Novak, M. Flexibility coefficients and interaction factors for pile group analysis. Can. Geotech. J. 1986, 23, 441–450. [Google Scholar] [CrossRef]
- Budhu, M.; Davies, T.G. Nonlinear analysis of laterality loaded piles in cohesionless soils. Can. Geotech. J. 1987, 24, 289–296. [Google Scholar] [CrossRef]
- Brown, D.; Morrison, C.; Reese, L. Lateral load behavior of pile group in sand. J. Geotech. Eng. 1988, 114, 1261–1276. [Google Scholar] [CrossRef]
- Ashour, M.; Norris, G.; Pilling, P. Lateral Loading of a Pile in Layered Soil Using the Strain Wedge Model. J. Geotech. Geoenviron. Eng. 1998, 124, 303–315. [Google Scholar] [CrossRef]
- Ashour, M.; Pilling, P.; Norris, G. Lateral Behavior of Pile Groups in Layered Soils. J. Geotech. Geoenviron. Eng. 2004, 130, 580–592. [Google Scholar] [CrossRef]
- Landi, G. Pali Soggetti a Carichi Orizzontali: Indagini Sperimentali ed Analisi. Ph.D Thesis, University of Naples Federico II, Napoli, Italy, 2006. (In Italian). [Google Scholar]
- Morelli, F.; Amico, C.; Salvatore, W.; Squeglia, N.; Stacul, S. Influence of Tension Stiffening on the Flexural Stiffness of Reinforced Concrete Circular Sections. Materials 2017, 10. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Comité Euro-International du Béton. CEB-FIP Model Code 1990; Bulletin d’Information: Telford, UK, 1993. [Google Scholar]
- Sigrist, V. Zum Verformungsvermögen von Stahlbetonträgern. PhD Thesis, Institut für Baustatik und Konstruktion, ETH Zürich, Zurich, Switzerland, 1995. [Google Scholar]
- Salvatore, W.; Buratti, G.; Maffei, B.; Valentini, R. Dual-phase steel re-bars for high-ductile rc structures, Part 2: Rotational capacity of beams. Eng. Struct. 2007, 29, 3333–3341. [Google Scholar] [CrossRef]
- Hetényi, M. Beams on Elastic Foundation: Theory with Applications in the Fields of Civil and Mechanical Engineery; University of Michigan Press: Ann Arbor, MI, USA, 1946. [Google Scholar]
- Reese, L.C.; Van Impe, W.F. Single Piles and Pile Groups under Lateral Loading; AA Balkema: Rotterdam, The Netherlands, 2001. [Google Scholar]
- Matlock, H. Correlations for design of laterally loaded piles in soft clay. In Proceedings of the 2nd Annual Offshore Technology Conference, Houston, TX, USA, 22–24 April 1970; Volume 1, pp. 577–588. [Google Scholar]
- Reese, L.C.; Cox, W.R.; Koop, F.D. Analysis of laterally loaded piles in sand. In Offshore Technology in Civil Engineering Hall of Fame Papers from the Early Years; American Society of Civil Engineers: Reston, VA, USA, 1974; pp. 95–105. [Google Scholar]
- Welch, R.C.; Reese, L.C. Lateral Load Behavior of Drilled Shafts. (No. Interim); University of Texas at Austin: Austin, TX, USA, 1972. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C++. The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 2002; pp. 714–718. [Google Scholar]
- Aubertin, M.; Mbonimpa, M.; Bussière, B.; Chapuis, R.P. A model to predict the water retention curve from basic geotechnical properties. Can. Geotech. J. 2003, 40, 1104–1122. [Google Scholar] [CrossRef]
- Bishop, A.W. The principle of effective stress. Teknisk Ukeblad 1959, 39, 859–863. [Google Scholar]
- Jennings, J.E.B.; Burland, J.B. Limitations to the use of effective stresses in partly saturated soils. Géotechnique 1962, 12, 125–144. [Google Scholar] [CrossRef]
- Bishop, A.W.; Donald, I.B. The experimental study of partly saturated soil in the triaxial apparatus. In Proceedings of the 5th International Conference on soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961; Volume 1, pp. 13–21. [Google Scholar]
- Bishop, A.W.; Alpan, I.; Blight, G.E.; Donald, I.B. Factors Controlling the Strength of Partly Saturated Cohesive Soils. In Proceedings of the Research Conference on Shear Strength of Cohesive Soils, ASCE, Boulder, CO, USA, 13–17 June 1960; pp. 503–532. [Google Scholar]
- Brown, D.; Reese, L.; O’Neill, M. Cyclic lateral loading of a large-scale pile group. J. Geotech. Eng. 1987, 113, 1326–1343. [Google Scholar] [CrossRef]
- Cox, W.R.; Reese, L.C.; Grubbs, B.R. Field testing of laterally loaded piles in sand. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–8 May 1974. [Google Scholar]
- Dunnavant, T.W.; O’Neill, M.W. Experimental p-y Model for Submerged, Stiff Clay. J. Geotech. Eng. 1989, 115, 95–114. [Google Scholar] [CrossRef]
- Huang, A.B.; Hsueh, C.K.; O’Neill, M.W.; Chern, S.; Chen, C. Effects of construction on laterally loaded pile groups. J. Geotech. Geoenviron. Eng. 2001, 127, 385–397. [Google Scholar] [CrossRef]
- Khalili-Tehrani, P.; Ahlberg, E.R.; Rha, C.; Lemnitzer, A.; Stewart, J.P.; Taciroglu, E.; Wallace, J.W. Nonlinear load-deflection behavior of reinforced concrete drilled piles in stiff clay. J. Geotech. Geoenviron. Eng. 2013, 140. Available online: https://ascelibrary.org/doi/abs/10.1061/(ASCE)GT.1943-5606.0000957 (accessed on 17 December 2017). [CrossRef]
- Mandolini, A.; Viggiani, C. Terreni ed opere di fondazione di un viadotto sul fiume Garigliano. Rivista Italiana di Geotecnica 1992, 26, 95–113, (In Italian, summary in English). [Google Scholar]
- McVay, M.; Casper, R.; Shang, T.I. Lateral response of three-row groups in loose to dense sands at 3D and 5D pile spacing. J. Geotech. Eng. 1995, 121, 436–441. [Google Scholar] [CrossRef]
- Ng, C.W.; Zhang, L.; Nip, D.C. Response of laterally loaded large-diameter bored pile groups. J. Geotech. Geoenviron. Eng. 2001, 127, 658–669. [Google Scholar] [CrossRef]
- Portugal, J.C.; Sêco e Pinto, P.S. Analysis and design of piles under lateral loads. In Proceedings of the 2nd International Geotechnical Seminar on Deep Foundations on Bored and Auger Piles, Ghent, Belgium, 1–4 June 1993; pp. 309–312. [Google Scholar]
- Price, G.; Wardle, I.F. Horizontal load tests on steel piles in London clay. In Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering, Stockholm, Sweden, 15–19 June 1981; Volume 2, pp. 803–808. [Google Scholar]
- Price, G.; Wardle, I.F. Lateral Load Tests on Large Diameter Bored Piles; Contractor Report 46; Transport and Road Research Laboratory, Department of Transport: Crowthorne, UK, 1987. [Google Scholar]
- Remaud, D.; Garnier, J.; Frank, R. Laterally loaded piles in dense sand: Group effects. In Proceedings of the Conference Centrifuge 98, Tokyo, Japan, 23–25 September 1998; pp. 533–538. [Google Scholar]
- Reese, L.; Cox, W.; Koop, F. Field testing and analysis of laterally loaded piles in stiff clay. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 1975; pp. 671–690. [Google Scholar]
- Reese, L.C.; Welch, R.C. Lateral loading of deep foundations in stiff clay. J. Geotech. Geoenviron. Eng. 1975, 101, 633–649. [Google Scholar]
- Rollins, K.M.; Peterson, K.T.; Weaver, T.J. Lateral load behavior of full-scale pile group in clay. J. Geotech. Geoenviron. Eng. 1998, 124, 468–478. [Google Scholar] [CrossRef]
- Rollins, K.M.; Gerber, T.M.; Lane, J.D.; Ashford, S.A. Lateral resistance of a full-scale pile group in liquefied sand. J. Geotech. Geoenviron. Eng. 2005, 131, 115–125. [Google Scholar] [CrossRef]
- Rollins, K.M.; Olsen, K.G.; Jensen, D.H.; Garrett, B.H.; Olsen, R.J.; Egbert, J.J. Pile spacing effects on lateral pile group behavior: Analysis. J. Geotech. Geoenviron. Eng. 2006, 132, 1272–1283. [Google Scholar] [CrossRef]
- Mayne, P.W. In-situ test calibrations for evaluating soil parameters. In Characterisation and Engineering Properties of Natural Soils. In Proceedings of the Second International Workshop on Characterisation and Engineering Properties of Natural Soils, Singapore, 29 November–1 December 2006; Taylor & Francis: New York, NY, USA; pp. 1601–1652. [Google Scholar]
- Wu, G.; Finn, W.L.; Dowling, J. Quasi-3D analysis: Validation by full 3D analysis and field tests on single piles and pile groups. Soil Dyn. Earthq. Eng. 2015, 78, 61–70. [Google Scholar] [CrossRef]
- Reese, L.C.; Wang, S.T. LPILE 4.0, Ensoft, Inc.: Austin, TX, USA, 1993.
- Wu, G. VERSAT-P3D: A Computer Program for Dynamic 3-Dimensional Finite Element Analysis of Single Piles and Pile Groups; Wutec Geotechnical International: Vancouver, BC, Canada, 2006. [Google Scholar]












| Case | Pile Material | Pile Diameter D (m) | Pile Length L (m) | Soil Type | H Max (kN) | y/D (%) at H Max |
|---|---|---|---|---|---|---|
| [40] | Steel with Grout-fill | 0.273 | 13.11 | OC Clay | 92.7 | 11.2 |
| [19] | Steel with Grout-fill | 0.273 | 13.11 | Sand | 133.5 | 13.8 |
| [41] | Steel-pipe | 0.61 | 21 | Sand | 263.4 | 4.9 |
| [42] | Steel | 0.273 | 11.8 | Clay | 116.8 | 31.4 |
| [42] | Steel | 1.22 | 11.4 | Clay | 1074.7 | 4.79 |
| [43] | Bored RC | 1.5 | 34.9 | Silty Sand | 2945.7 | 8.5 |
| [44] | Bored RC (Flagpole) | 0.60 | 11.68 | OC Clay | 104.7 | 24.9 |
| [45] | Multiton | 0.457 | 17.5 | Clay | 119.8 | 8.9 |
| [45] | Multiton | 0.406 | 17.5 | Clay | 119.9 | 11.7 |
| [31] | Steel-pipe | 0.319 | 12.8 | Clay | 105.0 | 17.6 |
| [46] | Aluminum | 0.43 | 13.3 | Sand | 109.5 | 18.6 |
| [46] | Aluminum | 0.43 | 13.3 | Sand | 134.1 | 18.6 |
| [47] | Bored RC | 1.50 | 30 | Sand | 2950.4 | 8.4 |
| [48] | Bored RC | 1.20 | 40 | Clay | 300.74 | 0.7 |
| [49] | Steel-pipe | 0.406 | 16.5 | Clay | 100.0 | 8.0 |
| [50] | Bored RC | 1.50 | 12.5 | Sand | 2394.1 | 3.4 |
| [51] | Aluminum | 0.72 | 12 | Sand | 804.7 | 15.4 |
| [52] | Steel-pipe | 0.641 | 15.2 | Clay | 596.7 | 3.3 |
| [53] | Bored RC | 0.762 | 12.8 | Clay | 443.5 | 3.8 |
| [54] | Steel with Grout-fill | 0.305 | 8.7 | Clay | 178.3 | 22.0 |
| [55] | Steel pipe | 0.324 | 11.5 | Sand | 112.3 | 13.3 |
| [56] | Steel pipe | 0.324 | 11.9 | Clay | 210.8 | 27.6 |
| Pile Diameter D (mm) | 1500 |
|---|---|
| Pile Length (m) | 34.9 |
| Cross Sectional area (cm2) | 17,672 |
| Concrete compressive strength f’c (MPa) | 27.5 |
| Reinforcement Yield Stress fy (MPa) | 471 |
| Steel Ratio ρs | 0.025 |
| Intact flexural rigidity EI (GNm2) | 6.86 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stacul, S.; Squeglia, N.; Morelli, F. Laterally Loaded Single Pile Response Considering the Influence of Suction and Non-Linear Behaviour of Reinforced Concrete Sections. Appl. Sci. 2017, 7, 1310. https://doi.org/10.3390/app7121310
Stacul S, Squeglia N, Morelli F. Laterally Loaded Single Pile Response Considering the Influence of Suction and Non-Linear Behaviour of Reinforced Concrete Sections. Applied Sciences. 2017; 7(12):1310. https://doi.org/10.3390/app7121310
Chicago/Turabian StyleStacul, Stefano, Nunziante Squeglia, and Francesco Morelli. 2017. "Laterally Loaded Single Pile Response Considering the Influence of Suction and Non-Linear Behaviour of Reinforced Concrete Sections" Applied Sciences 7, no. 12: 1310. https://doi.org/10.3390/app7121310
APA StyleStacul, S., Squeglia, N., & Morelli, F. (2017). Laterally Loaded Single Pile Response Considering the Influence of Suction and Non-Linear Behaviour of Reinforced Concrete Sections. Applied Sciences, 7(12), 1310. https://doi.org/10.3390/app7121310







