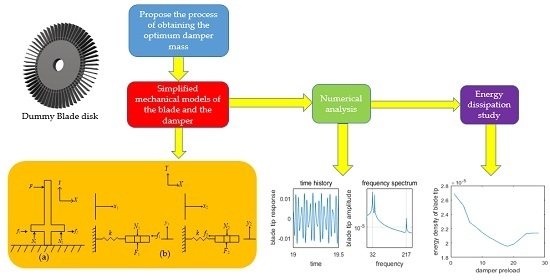
Dynamic Response of a Simplified Turbine Blade Model with Under-Platform Dry Friction Dampers Considering Normal Load Variation

Abstract

Dry friction dampers are widely used to reduce vibration. The forced vibration response of a simplified turbine blade with a new kind of under-platform dry friction dampers is studied in this paper. The model consists of a clamped blade as two rigidly connected beams and two dampers in the form of masses which are allowed to slide along the blade platform in the horizontal direction and vibrate with the blade platform in the vertical direction. The horizontal and vertical vibrations of the two dampers, and the horizontal and transverse platform vibrations are coupled by friction at the contact interfaces which is assumed to follow the classical discontinuous Coulomb’s law of friction. The vertical motion of the dampers leads to time-varying contact forces and can cause horizontal stick-slip motion between the contact surfaces. Due to the relative horizontal motion between the dampers and the blade platform, the vertical contact forces and the resultant friction forces act as moving loads. The Finite Element (FE) method and Modal Superposition (MS) method are applied to solve the dynamic response, together with an algorithm that can capture nonsmooth transitions from stick to slip and slip to stick. Quasi-periodic vibration is found even under harmonic excitation.

1. Introduction

Blades are a major component in aero-engines. High-cycle fatigue (HCF) failure due to high dynamic stresses caused by blade vibration is one of the main causes of aero-engine incidents [1]. A dry friction damper dissipates energy in the form of heat as a result of the relative rubbing motion at the contact surfaces, which has many advantages, for instance, having a simple structure, and being insensitive to temperature variation and easy to manufacture and install. Thus, dry friction dampers are widely used as a means of vibration suppression for turbine blades. A common damper configuration is the so-called under-platform dry friction damper in the form of a small piece of metal device located underneath the blade platform and actuated by centrifugal force against the platform due to engine shaft rotation. Figure 1 shows a Dummy bladed disk for vibration analysis. A damper could be installed between two adjacent blades under their platforms.

Extensive research on under-platform dry friction dampers has been carried out. A macroslip model to investigate the resonant stresses of a blade with a dry friction damper was presented by Griffin [2]. Menq et al. [3] developed a microslip model for analyzing the dynamic response of frictionally damped structures in which the friction interface was subjected to high normal loads, the microslip model derived by Menq et al. [3] was improved by Csaba [4]. A new two-dimensional model for point friction contacts was introduced by Sanliturk and Ewins [5]. Xia [6] proposed a model for investigating the stick–slip motion caused by dry friction of a two-dimensional oscillator under arbitrary excitations. A friction contact model was proposed to characterize the contact kinematics that imposed both friction nonlinearity and intermittent separation nonlinearity on structures having three-dimensional frictional constraint by Yang et al. [7]. Cigeroglu et al. [8] adopted a one-dimensional dynamic microslip friction model, including the damper inertia. This microslip friction model was further developed for a two-dimensional distributed parameter model with normal load variation induced by normal motion [9], in which they explored the use of this new model with harmonic balance method in frictionally constrained structures with a varying normal load. Further on, Cigeroglu et al. [10] implemented this model on wedge-shaped under-platform dampers in a bladed disc assembly. They allowed the wedge dampers to undergo three-dimensional translation and rotation along with elastic deformation while the damper was constrained only by friction contacts. Allara [11] proposed a model to characterize friction contact of non-spherical contact geometries obeying the Coulomb’s law of friction with a constant friction coefficient and constant normal load. From this model, the effect of the main contact parameters (contact geometry, material properties, and loads) on the contact behavior could be effectively estimated.

In [3,5] the dampers were always in full contact with the blade platform. In [9,12] the dampers could partially detach from the blade platforms during vibration. In [13,14] the dampers were modeled with the finite elements. A carefully designed and constructed rotating test rig was used to make precise measurements of the forced vibration response of a bladed disk with fitted under-platform “cottage-roof” friction dampers, the corresponding numerical predictions were carried out too, and then a comparison between the measured and predicted response curves was made and the degree of correlation was discussed [15]. To what extent microslip due to the combined nonlinearities along the normal and the tangent of non-conforming contact surfaces influenced the damper behavior was investigated [16]. Ostachowicz [17] established a harmonic balance method (HBM) for forced vibration analysis of dynamic systems damped by dry friction forces. Guillen and Pierre [18] introduced a Hybrid Frequency-Time (HFT) method for analyzing the steady-state response of the large-scale dry-friction damped structural systems. The correlation of the static/dynamic coupling of the under-platform dampers was investigated by Firrone, Zucca [19]. Mathematical relationships of dry friction force versus relative velocity in friction contact of two bodies were studied by Půst et al. [20]. Schwingshackl et al. [21] focused their research on contact interface parameters in a nonlinear dynamic analysis of assembled structures.

Gola et al. [22] studied the design and the calibration of a test rig specially developed to measure the in-plane forces transferred between the blade platforms through the under-platform damper and their relative displacement. A nonlinear analysis based on an updated explicit damper model having different levels of details was performed [23], and the results were evaluated against a newly-developed under-platform damper test rig. A standard Scanning Laser Doppler Vibrometer (SLDV) technology to measure the mistuned bladed disk vibration was put forward by Di Maio [24]. Then Zucca et al. [25] used a rotating laser Doppler Vibrometer to measure the performance of under-platform dampers for turbine blades. Nikhamkin et al. [26] developed an experimental technique for damping efficiency estimation of gas-turbine blades. The experimental investigation into the dynamic response of the blades of a gas turbine for power generation carrying asymmetric under-platform dampers was presented [27]. Quot et al. [28] proposed a novel approach which could directly measure the forces transmitted between the two platforms through the dampers. Rastogi et al. [29] utilized the Bond graph model of dry friction dampers in structural analysis of turbine blades. An FE modal analysis was described and a simplified method to evaluate the under-platform damper effects was also presented by Bessone and Traversone [30]. Based on a set of newly introduced non-dimensional parameters that ensured a similar dynamic behavior of the test rig to a real turbine blade-damper system, a new experimental damper rig was developed [31].

Friction dampers are widely used in machines and structures, including under-platform dampers studied as a particular example in this paper, shrouds in steam engines [32], those used in buildings [33], washing machines [34] and train suspensions [35]. They share the same features of stick-slip vibration and are worth studying. Stick-slip vibration is a kind of nonsmooth nonlinearity and requires special mathematical treatment. Popp et al. [36] made a comparison and classification of different contact models with friction that had been commonly used. In [37], the sticking and non-sticking orbits of a two-degree-of-freedom oscillator subjected to dry friction and a harmonic load were obtained in a closed form. Li et al. [38] developed a model of an elastic disc in sliding frictional contact with a rotating oscillator. Separation of the moving slider form the disc and its subsequent reattachment to the disc were considered, and various dynamic behaviors were discovered.

One aim of this study is to propose a more accurate model to study the motion of a friction damper. Another aim is to study the general dynamic behaviour of friction dampers in various applications (using aero engine under-platform dampers as a particular example). A third aim is to establish an effective algorithm for dealing with stick-slip vibration. In this paper, the normal contact force and the resultant friction force at the contact interface is modeled as moving loads, which is what really happens in many friction dampers but has not been modeled as such in the past. A numerical approach for solving the steady-state vibration of a simplified blade-damper system with nonsmooth friction contact is put forward and three distinct types of vibration, including stick-slip vibration between the two dampers and the blade platform surface, are studied. Each damper is partially constrained by a short cantilever beam and thus is different from those dampers reported in all of the above-mentioned papers about friction dampers.

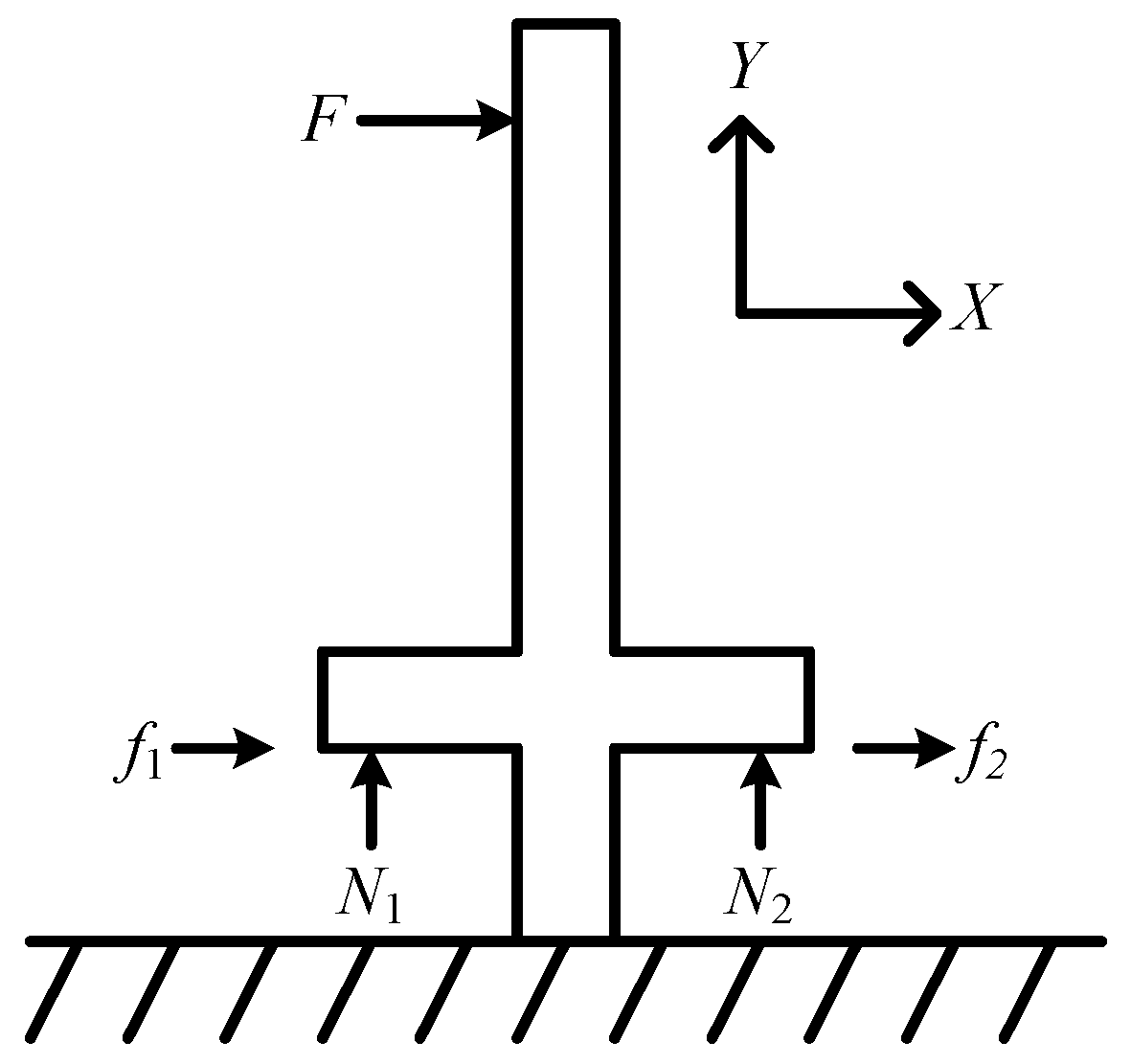
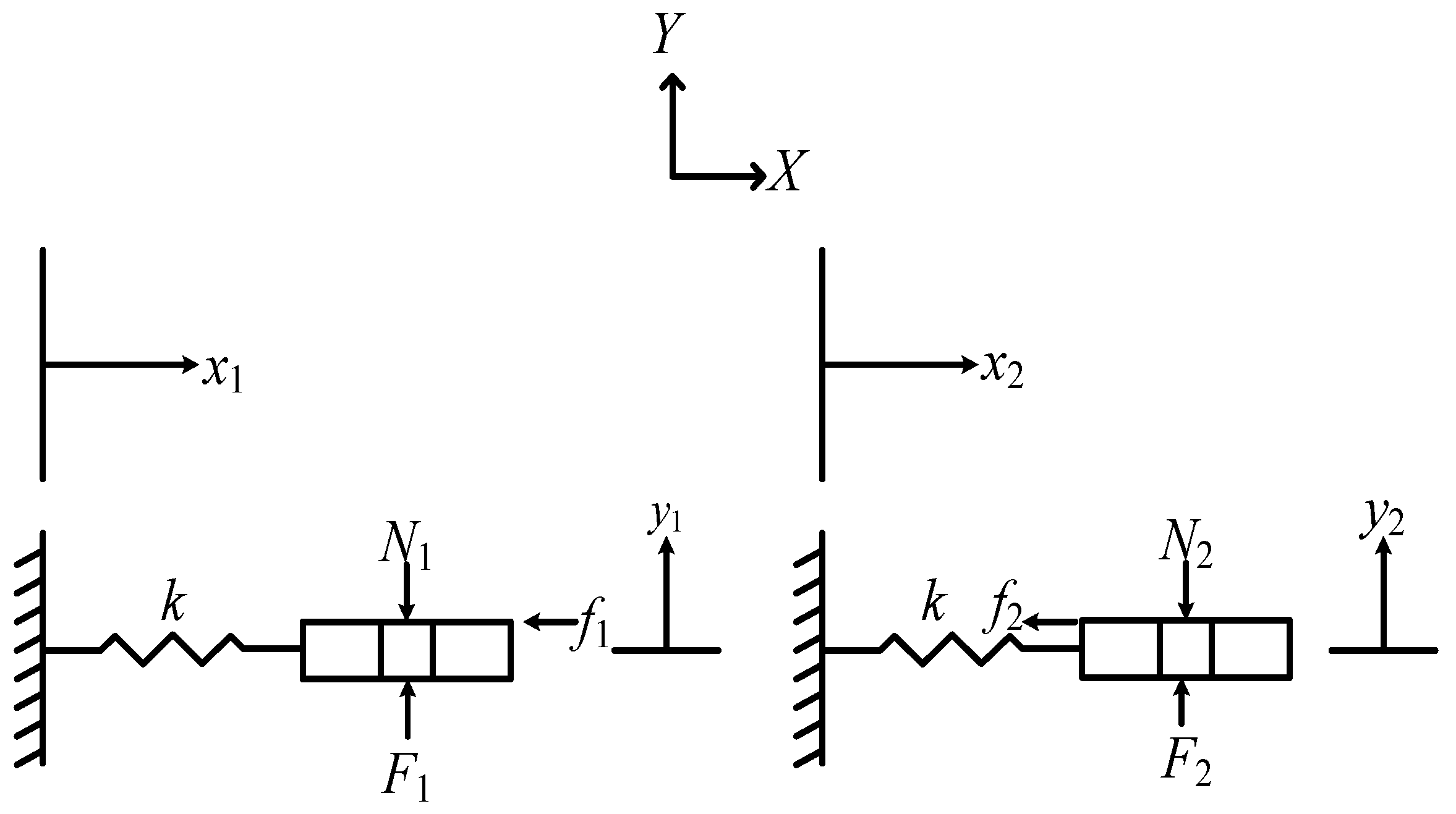
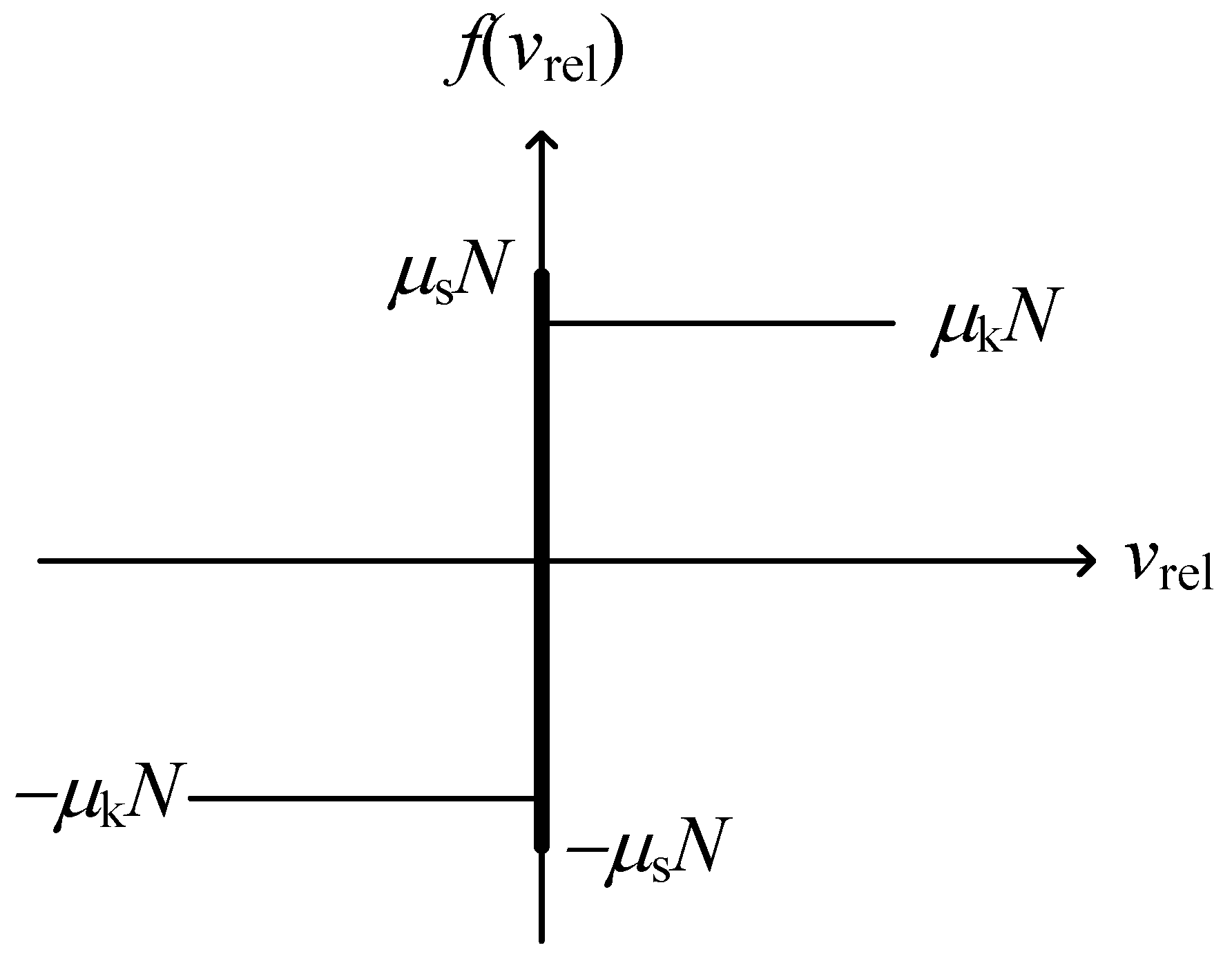
2. Blade-Damper Model and Theoretical Development

The structural model of the blades with under-platform dry friction dampers is shown in Figure 2: the X-Y-Z coordinate system (the global cylindrical coordinate system) is defined in accordance with the convention of tangential (X), radial (Y), and axial (Z) directions; the x₁-y₁ coordinate system which is a plane Cartesian coordinate frame (called the left damper coordinate system) is defined with the local coordinate origin being at the left initial contact point, the x₂-y₂ coordinate system which is a plane Cartesian coordinate frame (called the right damper coordinate system) is defined similarly. In this paper, the blade-platform structure is simplified and regarded as two rigidly connected Euler–Bernoulli beams, as illustrated in Figure 3. Unlike a conventional under-platform damper which is a floating mass actuated by centrifugal force, the under-platform damper studied here is mounted on the free end of a small vertical cantilever beam. The mechanical models of the blades and under-platform dampers are shown in Figure 3 and Figure 4. In Figure 3 and Figure 4, $F$ is the external excitation force acting on a blade, $N_1$ and $N_2$ are the normal contact forces acting on the blade platform from the dampers, $f_1$ and $f_2$ are the friction forces at the contact interface, $F_1$ and $F_2$ are the centrifugal forces of the under-platform dampers, and $k$ is a spring constant (the equivalent lateral stiffness of the tip of the small vertical cantilever beam). $F_1=m_{1}r{\Omega }^2$, $F_2=m_{2}r{\Omega }^2$, where $m_1$ and $m_2$ are the mass of the dampers, $r$ is the distance between the platform and the centre of the disk, and $\Omega$ is the rotating speed of the disk. The weights of the dampers are very small in comparison with the centrifugal forces and thus can be ignored.

In this investigation, the normal contact forces and the tangential friction forces at the contact interface are modeled as moving loads (which are a distinct feature of this paper and have not been modeled as such in previous research of blade under-platform friction dampers), and the two dampers are assumed to undergo horizontal and vertical vibrations, but no rotation. They are in point contact with the platform and do not separate with the platform during vibration excited by excitation force $F$. Therefore, displacements $y_1$ and $y_2$ of the dampers are equal to the local transverse deflections of the platform; but they can slide along the underside of the platform in the global X direction. The horizontal vibration and the vertical vibration of the two dampers, and the horizontal and transverse platform vibrations are coupled by friction at the contact interface.

A classical Coulomb friction model [39] is adopted in this paper: before sliding occurs, the friction force equals the shear force at the contact interface due to the applied external force and acts to resist the initiation of sliding; during sliding the friction force is proportional to the normal force at the contact interface and acts in the direction opposite to sliding. A further assumption is that the static coefficient of friction ${\mu }_{\mathrm{s}}$ is greater than the kinetic coefficient of friction ${\mu }_{\mathrm{k}}$ (so that stick-slip vibration of the damper is possible) and both are constant. Figure 5 describes the Coulomb friction model.

Accordingly, the relationship between the friction force $f\left(v_{\mathrm{rel}}\right)$ and the relative velocity $v_{\mathrm{rel}}$ and the local normal force N is

$$\{\begin{array}{c}f\left(v_{\mathrm{rel}}\right)={\mu }_{\mathrm{k}}N\left(v_{\mathrm{rel}}>0\right)\\ f\left(v_{\mathrm{rel}}\right)=-{\mu }_{\mathrm{k}}N\left(v_{\mathrm{rel}}<0\right)\\ -{\mu }_{\mathrm{s}}N\le f\left(v_{\mathrm{rel}}\right)\le {\mu }_{\mathrm{s}}N\left(v_{\mathrm{rel}}=0\right)\end{array}$$

(1)

The equations of free vibration in the local transverse and longitudinal directions of the component of the blade modeled as an Euler–Bernoulli beam [40] (denoted by 1) in its local coordinate $\epsilon$ are

$$\{\begin{array}{c}{\rho }_1{A}_1\frac{{\partial }^2{w}_1}{\partial t^2}\left(\epsilon ,t\right)+E_1{I}_1\frac{{\partial }^4{w}_1}{\partial {\epsilon }^4}\left(\epsilon ,t\right)=0\\ {\rho }_1{A}_1\frac{{\partial }^2{u}_1}{\partial t^2}\left(\epsilon ,t\right)-E_1{A}_1\frac{{\partial }^2{u}_1}{\partial {\epsilon }^2}\left(\epsilon ,t\right)=0\end{array}$$

(2)

In the same approach, the equations of free vibration of the platform component modeled as an Euler–Bernoulli beam (denoted by 2) are

$$\{\begin{array}{c}{\rho }_2{A}_2\frac{{\partial }^2{w}_2}{\partial t^2}\left(\epsilon ,t\right)+E_2{I}_2\frac{{\partial }^4{w}_2}{\partial {\epsilon }^4}\left(\epsilon ,t\right)=0\\ {\rho }_2{A}_2\frac{{\partial }^2{u}_2}{\partial t^2}\left(\epsilon ,t\right)-E_2{A}_2\frac{{\partial }^2{u}_2}{\partial {\epsilon }^2}\left(\epsilon ,t\right)=0\end{array}$$

(3)

where $w_1$ and $w_2$ are the transverse displacements, and $u_1$ and $u_2$ are the longitudinal displacements, all in their local coordinates; $E_1$ and $E_2$ are Young’s moduli of these two components; ${\rho }_1$ and ${\rho }_2$ are the mass densities; $A_1$ and $A_2$ are the cross-sectional areas; and $I_1$ and $I_2$ are the second moment of the areas. The $w$-component and $u$-component of the k-th beam’s n-th analytical mode can be denoted as ${\psi }_{wkn}\left(\epsilon \right)$ and ${\psi }_{ukn}\left(\epsilon \right)$, $\left(k=1,2\right)$ in its local coordinate $\epsilon$, which consist of base functions of sine, cosine, hyperbolic sine and hyperbolic cosine functions when expressed exactly [41]. Equations (2) and (3) are solved to get the natural frequencies and modes of the cross structure, which will be used in the mode superposition method for subsequent analysis. However, when the configuration of the beam structure is complex, analytical modes are difficult to obtain accurately. In general, the FE method provides a simple and effective approach to obtain the frequencies and modes of a structure of arbitrary configuration and hence is used.

The blade-platform system is discretized with a number of two-node Euler–Bernoulli Beam elements. Each node has three degrees-of-freedom: one translation along the longitudinal axis of the beam element, denoted by $u$; one translation lateral to the beam axis, denoted by $w$; and a rotation around the axis normal to this plane, denoted by $\theta$ [42]. Denote the k-th beam’s n-th numerical mode as ${\mathsf{\psi }}_{kn}^{\mathrm{FE}}$

$${\mathsf{\psi }}_{kn}^{\mathrm{FE}}=\{u_{k1},w_{k1},{\theta }_{k1},u_{k2},w_{k2},{\theta }_{k2},\dots u_{ki},w_{ki},{\theta }_{ki},u_{k\left(i+1\right)},w_{k\left(i+1\right)},{\theta }_{k\left(i+1\right)},{\dots \}}_n^{\mathrm{T}}$$

$${\mathsf{\psi }}_{ukn}^{\mathrm{FE}}={\left\{u_{k1},u_{k2},\dots u_{ki},u_{k\left(i+1\right)},\dots \right\}}_n^{\mathrm{T}},{\mathsf{\psi }}_{wkn}^{\mathrm{FE}}={\left\{w_{k1},w_{k2},\dots w_{ki},w_{k\left(i+1\right)},\dots \right\}}_n^{\mathrm{T}},$$

$${\mathsf{\psi }}_{\theta kn}^{\mathrm{FE}}={\left\{{\theta }_{k1},{\theta }_{k2},\dots {\theta }_{ki},{\theta }_{k\left(i+1\right)},\dots \right\}}_n^{\mathrm{T}}$$

$k=1,2$, where subscript $i$ is the left node of the i-th beam element and the right node of the $\left(i-1\right)$-th beam element, and superscript $\mathrm{T}$ stands for matrix transpose. When the number of beam elements is sufficient, the numerical modes and frequencies will be very close to the analytical modes and frequencies of the whole structure. Denote the $i$-th element shape function matrix of the k-th beam for $w$-displacement and $u$-displacement by $N_{wki}\left(\epsilon \right)$ and $N_{uki}\left(\epsilon \right)\left(k=1,2\right)$. Then, one acquires an approximate expression of the $n$-th analytical mode of the blade-platform structure as

$${\psi }_{w1n}\left(\epsilon \right)=\{\begin{array}{c}{N}_{w11}\left({\epsilon }_1\right)\{u_{11},{\theta }_{11},u_{12},{{\theta }_{12}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_1\\ N_{w12}\left({\epsilon }_2\right)\{u_{12},{\theta }_{12},u_{13},{{\theta }_{13}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_2\\ .\\ .\\ .\\ N_{w1i}\left({\epsilon }_i\right){\left\{u_{1i},{\theta }_{1i},u_{1\left(i+1\right)},{\theta }_{1\left(i+1\right)}\right\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_i\\ .\\ .\\ .\end{array}$$

(4)

$${\psi }_{u1n}\left(\epsilon \right)=\{\begin{array}{c}{N}_{u11}\left({\epsilon }_1\right)\{w_{11},{w_{12}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_1\\ N_{u12}\left({\epsilon }_2\right)\{w_{12},{w_{13}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_2\\ .\\ .\\ .\\ N_{u1i}\left({\epsilon }_i\right){\left\{w_{1i},w_{1\left(i+1\right)}\right\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_i\\ .\\ .\\ .\end{array}$$

(5)

where ${\epsilon }_i$ is the local longitudinal coordinate within the i-th element of the blade. ${\mathsf{\psi }}_{u1n}^{\mathrm{FE}}$ and ${\mathsf{\psi }}_{w1n}^{\mathrm{FE}}$ are the numerical modes of the blade of the global coordinate axes $X$ and $Y$, respectively. Because the local coordinate axes of the blade are perpendicular to the global coordinate axes, ${\mathsf{\psi }}_{u1n}^{\mathrm{FE}}$ corresponds to the numerical modes of the blade in the lateral direction, while ${\mathsf{\psi }}_{w1n}^{\mathrm{FE}}$ corresponds to the numerical modes of the blade in the axial direction.

$${\psi }_{w2n}\left(\epsilon \right)=\{\begin{array}{c}{N}_{w21}\left({\epsilon }_1\right)\{w_{21},{\theta }_{21},w_{22},{{\theta }_{22}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_1\\ N_{w22}\left({\epsilon }_2\right)\{w_{22},{\theta }_{22},w_{23},{{\theta }_{23}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_2\\ .\\ .\\ .\\ N_{w2i}\left({\epsilon }_i\right){\left\{w_{2i},{\theta }_{2i},w_{2\left(i+1\right)},{\theta }_{2\left(i+1\right)}\right\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_i\\ .\\ .\\ .\end{array}$$

(6)

$${\psi }_{u2n}\left(\epsilon \right)=\{\begin{array}{c}{N}_{u21}\left({\epsilon }_1\right)\{u_{21},{u_{22}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_1\\ N_{u22}\left({\epsilon }_2\right)\{u_{22},{u_{23}\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_2\\ .\\ .\\ .\\ N_{u2i}\left({\epsilon }_i\right){\left\{u_{2i},u_{2\left(i+1\right)}\right\}}_n^{\mathrm{T}}\epsilon \subset {\epsilon }_i\\ .\\ .\\ .\end{array}$$

(7)

where ${\epsilon }_i$ is the local longitudinal coordinate within the i-th element of the platform; $N_{wki}({\epsilon }_i)=\frac{1}{{L_{ki}}^3}[({L_{ki}}^3-3L_{ki}{\epsilon }_i^2+2{\epsilon }_i^3),({L_{ki}}^2{\epsilon }_i-2L_{ki}{\epsilon }_i^2+{\epsilon }_i^3),(3L_{ki}{\epsilon }_i^2-2{\epsilon }_i^3),({\epsilon }_i^3-L_{ki}{\epsilon }_i^2)]$; and $N_{uki}\left({\epsilon }_i\right)=\left[1-\frac{{\epsilon }_i}{L_{ki}},\frac{{\epsilon }_i}{L_{ki}}\right]$; $\left(k=1,2\right)$; and $L_{ki}$ is the length of the $i$-th element of the k-th beam. The reason for converting the FE modes to approximate analytical modes is to accommodate the tracking of horizontal positions of the friction dampers relative to the platform, which is a common formulation of moving-load problems [43]. Such a numerical-analytical combined formulation allows dynamic responses of complicated structures excited by moving loads to be determined conveniently [44].

The combined equations of motion of the blade-platform structure under external excitation can be written as

$$M\left\{\begin{array}{c}\begin{array}{c}{\ddot{u}}_1\\ {\ddot{u}}_2\end{array}\\ \begin{array}{c}{\ddot{w}}_1\\ {\ddot{w}}_2\end{array}\end{array}\right\}+K\left\{\begin{array}{c}\begin{array}{c}{u}_1\\ u_2\end{array}\\ \begin{array}{c}{w}_1\\ w_2\end{array}\end{array}\right\}=f$$

(8)

$$M=\left[\begin{array}{cccc}{\rho }_1{A}_1& 0& 0& 0\\ 0& {\rho }_2{A}_2& 0& 0\\ 0& 0& {\rho }_1{A}_1& 0\\ 0& 0& 0& {\rho }_2{A}_2\end{array}\right]K=\left[\begin{array}{cccc}-E_1{A}_1\frac{{\partial }^2}{\partial {\epsilon }^2}& 0& 0& 0\\ 0& -E_2{A}_2\frac{{\partial }^2}{\partial {\epsilon }^2}& 0& 0\\ 0& 0& E_1{I}_1\frac{{\partial }^4}{\partial {\epsilon }^4}& 0\\ 0& 0& 0& E_2{I}_2\frac{{\partial }^4}{\partial {\epsilon }^4}\end{array}\right]$$

$$f=\left\{\begin{array}{c}\begin{array}{c}0\\ f_1\delta \left(\epsilon -X_1\right)+f_2\delta \left(\epsilon -X_2\right)\end{array}\\ \begin{array}{c}F\delta \left(\epsilon -Y_0\right)\\ N_1\delta \left(\epsilon -X_1\right)+N_2\delta \left(\epsilon -X_2\right)\end{array}\end{array}\right\}$$

where $M$ and $K$ are the “mass” and “stiffness” operator matrices of the blade-platform structure; and ${\left\{u_1,u_2,w_1,w_2\right\}}^{\mathrm{T}}$ and $f$ are, respectively, the nodal displacement vector and force vector of the structure. The dot over a symbol represents differentiation with respect to time t, $Y_0$ is the location of the external excitation force $F$, $X_1$ and $X_2$ are the location of the contact points which are unknown a priori and vary with time. Please note that the first element of f is zero because there is no external force acting in the u₁ direction for beam 1 (the blade) while the second element denotes the friction forces at the two damper-platform interfaces.

The nodal displacement vector of the whole structure can be expressed as

$$\left\{\begin{array}{c}\begin{array}{c}{u}_1\left(t\right)\\ u_2\left(t\right)\\ w_1\left(t\right)\end{array}\\ \begin{array}{c}{w}_2\left(t\right)\\ {\mathsf{\theta }}_1\left(t\right)\\ {\mathsf{\theta }}_2\left(t\right)\end{array}\end{array}\right\}={\displaystyle \sum }_{i=1}^n\left\{\begin{array}{c}\begin{array}{c}{\mathsf{\psi }}_{u1i}^{\mathrm{FE}}\\ {\mathsf{\psi }}_{u2i}^{\mathrm{FE}}\\ {\mathsf{\psi }}_{w1i}^{\mathrm{FE}}\end{array}\\ \begin{array}{c}{\mathsf{\psi }}_{w2i}^{\mathrm{FE}}\\ {\mathsf{\psi }}_{\theta 1i}^{\mathrm{FE}}\\ {\mathsf{\psi }}_{\theta 2i}^{\mathrm{FE}}\end{array}\end{array}\right\}{q}_i\left(t\right)=\left\{\begin{array}{c}\begin{array}{c}{\mathsf{\Psi }}_{u1}^{\mathrm{FE}}\\ {\mathsf{\Psi }}_{u2}^{\mathrm{FE}}\\ {\mathsf{\Psi }}_{w1}^{\mathrm{FE}}\end{array}\\ \begin{array}{c}{\mathsf{\Psi }}_{w2}^{\mathrm{FE}}\\ {\mathsf{\Psi }}_{\theta 1}^{\mathrm{FE}}\\ {\mathsf{\Psi }}_{\theta 2}^{\mathrm{FE}}\end{array}\end{array}\right\}q\left(t\right)$$

(9)

where $q_i\left(t\right)$ is the i-th modal coordinate of the blade-platform structure.

$$q\left(t\right)=\{q_1\left(t\right),q_2\left(t\right),q_3\left(t\right),\dots {q_n\left(t\right)\}}^{\mathrm{T}}$$

$${\mathsf{\Psi }}_{u1}^{\mathrm{FE}}=[{\mathsf{\psi }}_{u11}^{\mathrm{FE}},{\mathsf{\psi }}_{u12}^{\mathrm{FE}},{\mathsf{\psi }}_{u13}^{\mathrm{FE}},\dots {\mathsf{\psi }}_{u1n}^{\mathrm{FE}}],{\mathsf{\Psi }}_{u2}^{\mathrm{FE}}=[{\mathsf{\psi }}_{u21}^{\mathrm{FE}},{\mathsf{\psi }}_{u22}^{\mathrm{FE}},{\mathsf{\psi }}_{u23}^{\mathrm{FE}},\dots \left[{\mathsf{\psi }}_{u2n}^{\mathrm{FE}}\right]$$

$${\mathsf{\Psi }}_{w1}^{\mathrm{FE}}=[{\mathsf{\psi }}_{w11}^{\mathrm{FE}},{\mathsf{\psi }}_{w12}^{\mathrm{FE}},{\mathsf{\psi }}_{w13}^{\mathrm{FE}},\dots {\mathsf{\psi }}_{w1n}^{\mathrm{FE}}],{\mathsf{\Psi }}_{w2}^{\mathrm{FE}}=[{\mathsf{\psi }}_{w21}^{\mathrm{FE}},{\mathsf{\psi }}_{w22}^{\mathrm{FE}},{\mathsf{\psi }}_{w23}^{\mathrm{FE}},\dots {\mathsf{\psi }}_{w2n}^{\mathrm{FE}}]$$

$${\mathsf{\Psi }}_{\theta 1}^{\mathrm{FE}}=[{\mathsf{\psi }}_{\theta 11}^{\mathrm{FE}},{\mathsf{\psi }}_{\theta 12}^{\mathrm{FE}},{\mathsf{\psi }}_{\theta 13}^{\mathrm{FE}},\dots {\mathsf{\psi }}_{\theta 1n}^{\mathrm{FE}}],{\mathsf{\Psi }}_{\theta 2}^{\mathrm{FE}}=[{\mathsf{\psi }}_{\theta 21}^{\mathrm{FE}},{\mathsf{\psi }}_{\theta 22}^{\mathrm{FE}},{\mathsf{\psi }}_{\theta 23}^{\mathrm{FE}},\dots {\mathsf{\psi }}_{\theta 2n}^{\mathrm{FE}}]$$

${\mathsf{\psi }}_{uki}^{\mathrm{FE}}$, ${\mathsf{\psi }}_{wki}^{\mathrm{FE}}$ and ${\mathsf{\psi }}_{\theta ki}^{\mathrm{FE}}$ ($k=1,2$) form the i-th mass-normalized FE mode of the k-th beam (in the order of ascending frequencies).

It follows from Equation (9) that the horizontal and the vertical displacements of the platform can be expressed as

$$\left[u_2\left(\epsilon ,t\right),w_2\left(\epsilon ,t\right)\right]=q^{\mathrm{T}}\left(t\right)\left[{\mathsf{\psi }}_{u2}\left(\epsilon \right),{\mathsf{\psi }}_{w2}\left(\epsilon \right)\right]$$

(10)

where ${\mathsf{\psi }}_{u2}\left(\epsilon \right)$ and ${\mathsf{\psi }}_{w2}\left(\epsilon \right)$ are approximate analytical $u$-component and $w$-component mode vectors converted from ${\mathsf{\Psi }}_{u2}^{\mathrm{FE}}$, ${\mathsf{\Psi }}_{w2}^{\mathrm{FE}}$ and ${\mathsf{\Psi }}_{\theta 2}^{\mathrm{FE}}$ through element shape functions. Very similarly, the two displacements of the blade can also be expressed like Equation (10). Analytical modes (even though approximate), instead of numerical modes, are particular useful in dealing with moving loads [44].

Regardless of relative sticking or slipping of the dampers to the platform, friction forces $f_1$ and $f_2$ and normal forces $N_1$ and $N_2$ at the contact points always satisfy

$$\frac{1}{2}{m}_1{\ddot{x}}_1+\frac{1}{2}k{x}_1=f_1$$

(11)

$$\frac{1}{2}{m}_2{\ddot{x}}_2+\frac{1}{2}k{x}_2=f_2$$

(12)

$$\frac{1}{2}{F}_1-\frac{1}{2}{m}_1{\ddot{y}}_1=N_1$$

(13)

$$\frac{1}{2}{F}_2-\frac{1}{2}{m}_2{\ddot{y}}_2=N_2$$

(14)

where $x_1$ and $x_2$, and $y_1$ and $y_2$ are the local horizontal displacements and the vertical displacements of the two dampers, respectively; and the $\frac{1}{2}$ in the above equations is due to the equal share of a damper by two adjacent blades (see Figure 2). Platform horizontal displacements $u_2$ at the contact points can be found from Equation (10).

Denote $X_1=u_2-x_1+x_{10}$, $X_2=u_2-x_2+x_{20}$, $\frac{1}{2}{F}_1=\frac{1}{2}{F}_2=N_0$. $N_0$ is the preload, $x_{10}$ is the coordinate of the $X$ direction of the left damper coordinate system origin in the global coordinate system and $x_{20}$ is the coordinate of the $X$ direction of the right damper coordinate system origin in the global coordinate system. Figure 6 shows the un-deformed and deformed configuration of the blade-damper system.

If the left damper slips relatively to the platform, the friction force is known as

$$f_1={\mu }_{\mathrm{k}}{N}_1\mathrm{sgn}\left({\dot{u}}_2-{\dot{x}}_1\right)={\mu }_{\mathrm{k}}{N}_1\mathrm{sgn}({\dot{X}}_1)$$

(15)

Similarly, if the right damper slips relatively to the platform, the friction force could be also written as

$$f_2={\mu }_{\mathrm{k}}{N}_2\mathrm{sgn}\left({\dot{u}}_2-{\dot{x}}_2\right)={\mu }_{\mathrm{k}}{N}_2\mathrm{sgn}({\dot{X}}_2)$$

(16)

If there is contact between the left damper and the platform, the relationship between the transverse displacement $w_1$ of the contact point of the platform and the vertical displacement $y_1$ of the damper is:

$$y_1\left(t\right)=w_2\left(X_1\left(t\right),t\right)=q^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_1\right)$$

(17)

Therefore,

$${\dot{y}}_1\left(t\right)={\dot{q}}^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_1\right)+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\dot{X}}_1$$

(18)

$${\ddot{y}}_1\left(t\right)={\ddot{q}}^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_1\right)+2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\dot{X}}_1+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_1\right){\dot{X}}_1^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\ddot{X}}_1$$

(19)

where a dash denotes the differentiation with respect to the local spatial coordinate $\epsilon$.

In the same way, if there is contact between the right damper and the platform, the relationship between the transverse displacement $w_2$ of the contact point of the platform and the vertical displacement $y_2$ of the damper is:

$$y_2\left(t\right)=w_2\left(X_2\left(t\right),t\right)=q^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_2\right)$$

(20)

and

$${\dot{y}}_2\left(t\right)={\dot{q}}^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_2\right)+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\dot{X}}_2$$

(21)

$${\ddot{y}}_2\left(t\right)={\ddot{q}}^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_2\right)+2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\dot{X}}_2+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_2\right){\dot{X}}_2^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\ddot{X}}_2$$

(22)

By substituting Equations (19) and (22) into Equations (13) and (14), assuming $m_1=m_2=m$, normal contact forces $N_1$ and $N_2$ can be expressed as

$$N_1=N_0-\frac{1}{2}m[{\ddot{q}}^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_1\right)+2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\dot{X}}_1+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_1\right){\dot{X}}_1^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\ddot{X}}_1]$$

(23)

$$N_2=N_0-\frac{1}{2}m[{\ddot{q}}^{\mathrm{T}}{\mathsf{\psi }}_{w2}\left(X_2\right)+2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\dot{X}}_2+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_2\right){\dot{X}}_2^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\ddot{X}}_2]$$

(24)

Due to the orthogonality between modes of beam structures, the left-hand side of the equation of motion for the blade-platform structure, Equation (8), can be decoupled using the approximate analytical modes described in Equations (4)–(7) in the modal coordinator vector as

$$\ddot{q}\left(t\right)+\mathrm{diag}[{\omega }^2]q\left(t\right)=F{\mathsf{\psi }}_{w1}\left(Y_0\right)-f_1{\mathsf{\psi }}_{u2}\left(X_1\right)-f_2{\mathsf{\psi }}_{u2}\left(X_2\right)+N_1{\mathsf{\psi }}_{w2}\left(X_1\right)+N_2{\mathsf{\psi }}_{w2}\left(X_2\right)$$

(25)

If the two dampers are all in slip phase, by substituting Equations (15), (16), (23) and (24) into Equation (25), denoting $\left(X_1\right)={\mathsf{\psi }}_{w2}\left(X_1\right)-{\mu }_{\mathrm{k}}\mathrm{sgn}({\dot{X}}_1){\mathsf{\psi }}_{u2}\left(X_1\right)$, $g\left(X_2\right)={\mathsf{\psi }}_{w2}\left(X_2\right)-{\mu }_{\mathrm{k}}\mathrm{sgn}({\dot{X}}_2){\mathsf{\psi }}_{u2}\left(X_2\right)$, one gets

$$\begin{array}{l}\left[I+\frac{1}{2}mg\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_1\right)+\frac{1}{2}mg\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_2\right)\right]\ddot{q}\\ =F{\mathsf{\psi }}_{w1}\left(Y_0\right)+N_0\left[g\left(X_1\right)+g\left(X_2\right)\right]-\mathrm{diag}[{\omega }^2]q\\ -\frac{1}{2}mg\left(X_1\right)[2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\dot{X}}_1+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_1\right){\dot{X}}_1^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\ddot{X}}_1]\\ -\frac{1}{2}mg\left(X_2\right)[2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\dot{X}}_2+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_2\right){\dot{X}}_2^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\ddot{X}}_2]\end{array}$$

(26)

If the two dampers are all in stick phase, the blade platform and the two dampers vibrate together and form one new system; $u_2=q^{\mathrm{T}}\left(t\right){\mathsf{\psi }}_{u2}\left(X_1\right)$; $u_2-x_1=c_1$; $u_2-x_2=c_2$; ${\dot{X}}_1=0$; ${\ddot{X}}_1=0$; ${\dot{X}}_2=0$; ${\ddot{X}}_2=0$; $c_1$ is the horizontal displacement difference between the left initial contact point and the left damper at the end of the previous slip phase and $c_2$ is the horizontal displacement difference between the right initial contact point and the right damper at the end of the previous slip phase. By substituting Equations (11), (12), (23) and (24) into Equation (25), then the equation of motion of the new system in the modal coordinator vector can be derived as

$$\begin{array}{l}[I+\frac{1}{2}m{\mathsf{\psi }}_{u2}\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_1\right)+\frac{1}{2}m{\mathsf{\psi }}_{u2}\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_2\right)+\frac{1}{2}m{\mathsf{\psi }}_{w2}\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_1\right)\\ +\frac{1}{2}m{\mathsf{\psi }}_{w2}\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_2\right)]\ddot{q}\\ =F{\mathsf{\psi }}_{w1}\left(Y_0\right)+N_0\left[{\mathsf{\psi }}_{w2}\left(X_1\right)+{\mathsf{\psi }}_{w2}\left(X_2\right)\right]\\ -\frac{1}{2}k[{\mathsf{\psi }}_{u2}\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_1\right)+{\mathsf{\psi }}_{u2}\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_2\right)]q-\mathrm{diag}[{\omega }^2]q\\ +\frac{1}{2}k\left[c_1{\mathsf{\psi }}_{u2}\left(X_1\right)+c_2{\mathsf{\psi }}_{u2}\left(X_2\right)\right]\end{array}$$

(27)

If the left damper is in slip phase, and the right damper is in stick phase, one can get the equation of the new system in the modal coordinator as

$$\begin{array}{l}\left[I+\frac{1}{2}mg\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_1\right)+\frac{1}{2}m{\mathsf{\psi }}_{u2}\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_2\right)+\frac{1}{2}m{\mathsf{\psi }}_{w2}\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_2\right)\right]\ddot{q}\\ =F{\mathsf{\psi }}_{w1}\left(Y_0\right)+N_0\left[g\left(X_1\right)+{\mathsf{\psi }}_{w2}\left(X_2\right)\right]\\ -\frac{1}{2}mg\left(X_1\right)[2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\dot{X}}_1+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_1\right){\dot{X}}_1^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_1\right){\ddot{X}}_1]\\ -\frac{1}{2}k{\mathsf{\psi }}_{u2}\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_2\right)q-\mathrm{diag}[{\omega }^2]q+\frac{1}{2}k{c}_2{\mathsf{\psi }}_{u2}\left(X_2\right)\end{array}$$

(28)

Similarly, if the left damper is in stick phase, and the right damper is in slip phase, one can get the equation of the new system in the modal coordinator as

$$\begin{array}{l}\left[I+\frac{1}{2}mg\left(X_2\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_2\right)+\frac{1}{2}m{\mathsf{\psi }}_{u2}\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_1\right)+\frac{1}{2}m{\mathsf{\psi }}_{w2}\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{w2}\left(X_1\right)\right]\ddot{q}\\ =F{\mathsf{\psi }}_{w1}\left(Y_0\right)+N_0\left[g\left(X_2\right)+{\mathsf{\psi }}_{w2}\left(X_1\right)\right]\\ -\frac{1}{2}mg\left(X_2\right)[2{\dot{q}}^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\dot{X}}_2+q^{\mathrm{T}}{{\mathsf{\psi }}^{″}}_{w2}\left(X_2\right){\dot{X}}_2^2+q^{\mathrm{T}}{{\mathsf{\psi }}^{\prime }}_{w2}\left(X_2\right){\ddot{X}}_2]\\ -\frac{1}{2}k{\mathsf{\psi }}_{u2}\left(X_1\right){{\mathsf{\psi }}^{\mathrm{T}}}_{u2}\left(X_1\right)q-\mathrm{diag}[{\omega }^2]q+\frac{1}{2}k{c}_1{\mathsf{\psi }}_{u2}\left(X_1\right)\end{array}$$

(29)

where $I$ is identity matrix of appropriate dimension. Equations (11)–(14) and (26)–(29) must be solved simultaneously to obtain the dynamic responses of the two dampers and the blade-platform structure.

Please note that in Equations (26)–(29), $X_1$ and $X_2$ are unknown and vary with time t, so they represent a time-varying system. Additionally, $X_1$ and $X_2$ are nonsmooth because of the discontinuous Coulomb’s law of friction used, and the dynamic system is highly nonlinear. As a result, small time steps must be used. The precise time instants when stick regime switches to slip regime must be captured, and vice versa. These make numerical solutions of the system quite challenging.

A computational scheme for the numerical implementation in Matlab is shown in Figure 7.

3. Numerical Simulation

As the state of the system switches between stick and slip phases, and the motions of the blade-platform structure and the two dampers are coupled, the dynamic behavior of the blade-damper system needs to be obtained by solving four different sets of governing equations of the blade-platform structure together with four governing equations of the two dampers at the same time, which brings about some difficulties in the numerical computations. A numerical integration scheme implementing Runge–Kutta algorithm appropriate for the second-order differential equations coded in MATLAB and capable of dealing with nonsmooth friction and contact behavior is developed to solve them in this paper. The states of the blade-platform structure and the two dampers during vibration, including values of the contact normal forces and tangential friction forces, and the forces on the spring and the two dampers, are monitored at each time step. If the results at the end of a time step do not satisfy the conditions for the system to stay in the same motion phase as at the start of the time step, then the bisection method is used to find the critical point where the dynamics switches from one phase to another phase. After getting the critical point, the current set of equations of motion changes to another set.

In this numerical example, the external excitation frequency is fixed as 200 rad/s and the amplitude is fixed at 20 N. The time step used in the numerical integrations is 0.0001 s. The simulation results have been visualized by means of time histories, frequency spectra and phase-plane plots. Due to the limited space, only some distinct and interesting results are presented. The basic parameter values used are: $k=1.0\times {10}^4\mathrm{N}/\mathrm{m}$; $\Omega =50\mathrm{rad}/\mathrm{s}$; $r=0.46$; $E_1=E_2=2.06\times {10}^{11}\mathrm{Pa}$; ${\mu }_{\mathrm{s}}=0.35$; ${\mu }_{\mathrm{k}}=0.3$; ${\rho }_1={\rho }_2=7800\mathrm{kg}/{\mathrm{m}}^3$; $A_1=6\times {10}^{-5}{\mathrm{m}}^2$; $A_2=6\times {10}^{-5}{\mathrm{m}}^2$; $I_1=2\times {10}^{-11}{\mathrm{m}}^4$; $I_2=2\times {10}^{-11}{\mathrm{m}}^4$; $L_1=0.2\mathrm{m}$; $L_2=0.04\mathrm{m}$; $L_1$ and $L_2$ are the length of the blade and the platform, respectively. The first natural frequency of the blade-platform structure alone is 32 Hz, while the first natural frequency of the blade platform structure and the two dampers with their cantilevers together as one system is 45.7 Hz.

3.1. Gross Slip Regime

Figure 8, Figure 9, Figure 10 and Figure 11 show the results when the preload $N_0$ is 1 N. The steady-state response and frequency spectrum of the blade tip are illustrated in Figure 8, and the normal contact forces and friction forces versus time $t$ curves and frequency spectrums of the normal contact forces and friction forces are given in Figure 9, and the results for the motion and frequency spectrums of the dampers with dry friction are given in Figure 10. Phase plane plots of the relative velocity of the contact points and displacements of the two dampers are shown in Figure 11. It can be seen that the forced vibration of the blade tip is periodic and has the same frequency as the excitation force (Figure 8). This is not unexpected since during gross sliding, the amplitudes of the normal contact forces and the friction forces are fairly small in comparison with the amplitude of excitation, and therefore their effect on blade tip vibration is small so that the blade tip vibration only contains one frequency component (the driving frequency). Figure 9a,b demonstrates that the normal contact forces fluctuate around the preload, and the first-order and higher-order harmonics of the driving frequency appear (Figure 9c,d), so the normal contact forces are periodic. Figure 9e,f shows that friction force amplitudes $f_1$ and $f_2$ are equal to ${\mu }_k{N}_1$ and ${\mu }_k{N}_2$, respectively, and they are also periodic (Figure 9g,h). Figure 10 shows that the motions of the two dampers are not harmonic. Effectively, the friction forces and the normal contact forces act as excitations of horizontal and vertical directions to the two dampers, respectively. Equations (11)–(14) suggest that the horizontal and vertical motions of the dampers should contain the same frequency components as the friction forces and the normal contact forces. Thus it can be concluded that the vibrations of the dampers are periodic whose period are the period of the excitation. From Figure 11, it is clear that the phase plane maps of the dampers are smooth closed curves.

3.2. Stick-Slip Regime

Figure 12, Figure 13, Figure 14 and Figure 15 show the results when the preload $N_0$ is 12 N. Figure 12 shows the steady-state response and frequency spectrum of the blade tip, and the normal contact forces and friction forces versus time $t$ curves and frequency spectrums of the normal contact forces are provided in Figure 13, and the results for the motion and frequency spectrums of the dampers with dry friction are given in Figure 14. Phase plane plots of the relative velocity of the contact points and displacements of the two dampers are shown in Figure 15. As Figure 12 shows, the forced vibration of the blade tip remains periodic but is no longer harmonic, and it has the same frequency as the excitation force as in the gross slip regime, but the difference here is the appearance of the higher order harmonics of the driving frequency. This is because the increase of the normal contact forces leads to horizontal stick-slip vibration of the dampers. As a result, an increase in friction forces brings about a greater contribution of its influence on blade tip vibration. As illustrated in Figure 13a,b, the normal contact forces continue to fluctuate around the preload and are periodic, and the first-order and higher-order harmonics of the driving frequency appear (see Figure 13c,d). However, the friction forces are now very interesting. Friction forces $f_1$ and $f_2$ fluctuate between $\pm {\mu }_s{N}_1$ and $\pm {\mu }_s{N}_2$, respectively, and are periodic. At times, $f_1$ equals $\pm {\mu }_k{N}_1$ and $f_2$ equals $\pm {\mu }_k{N}_2$, which is when the dampers slip to the platform. At any other time, the dampers stick relatively to the platform. Therefore, the dampers are sometimes slipping and sometimes sticking relatively to the blade platform. When the dampers stick to the platform, the relative velocity between the dampers and the blade platform is zero; on the other hand, while the dampers slip relatively to the platform, the relative velocity between the dampers and the blade platform is non-zero. These lead to the phase plane plots of Figure 15. The motions of the dampers in stick-slip regime are similar to the motions of the dampers in gross slip regime, as shown in Figure 14.

3.3. Complete Stick Regime

Figure 16, Figure 17, Figure 18 and Figure 19 show the results when the preload $N_0$ is 26 N. Figure 16 displays the steady-state response and frequency spectrum of the blade tip, the normal contact forces and friction forces versus time $t$ curves and frequency spectrums of the normal contact forces are given in Figure 17, and the results for the motion and frequency spectrums of the dampers with dry friction are illustrated in Figure 18. Phase plane plots of the relative velocity of the contact points and displacements of the two dampers are presented in Figure 19. Figure 16 shows that the forced vibration of the blade tip is now quasi-periodic and it has three kinds of harmonic components (excitation frequency and the first-order and fifth-order bending frequency of the blade-platform structure with the two dampers and the short cantilever beams as a whole). Figure 17 indicates that the normal contact forces and the friction forces exhibit a quasi-periodic variation. Figure 19 shows that the relative velocity of the contact points of the dampers and the blade platform is always zero, hence, the dampers are always sticking to the horizontal beam. As a result, the blade-platform structure and the dampers form one new system. As shown in Figure 18, the motions of the dampers are non-periodic. There are three peaks in the frequency spectrum plots: the frequency of the first peak is the same as the excitation frequency, but the frequencies of the second peak and the third peak are now the first-order bending frequency and the fifth-order bending frequency of the whole new system.

3.4. The Effect of the Preload $N_0$ for Vibration Reduction

In order to predict the effect of the preload $N_0$ on the blade tip vibration reduction, a normalized energy density ($E_{\rho }$) is defined below as a measure of vibration response so that the vibration reduction effect of the damper in various conditions can be assessed. The smallest $E_{\rho }$ is considered to indicate the best vibration reduction. $E_{\rho }=({{\displaystyle \int }}_{t_1}^{t_2}{x}_{\mathrm{tip}}{\left(t\right)}^2\mathrm{d}t)/\left(t_2-t_1\right)(t_1=19\mathrm{s}$; $t_2=19.5\mathrm{s})$.

As illustrated in Figure 20, with the increase of the pre-load ($N_0$), the normalised energy density ($E_{\rho }$) decreases continuously at first, then increases and finally stays the same. It is found that there is an optimal pre-load which can make the biggest vibration reduction. Hence, the damper mass can be optimized in order to reduce the vibration and thus dynamic stresses of a blade to the maximum extent. This could provide a useful guideline for the design of the damper. Other parameters can also affect vibration reduction but are not reported here.

3.5. Further Discussion

As shown in the previous sub-sections, depending on the values of the preload, the dry friction dampers can display distinct dynamic behavior, and a suitable value of the preload can be determined that would allow best energy dissipation of the dynamic system so that blade vibration can be contained.

The difference between ${\mu }_{\mathrm{s}}$ and ${\mu }_{\mathrm{k}}$ influences the degree of nonsmoothness of the dynamic process and is also worth studying. In this paper, a simple classical friction law is used. In reality, friction is often more complicated than what the Coulomb’s law of friction can cover. More sophisticated friction laws, even state-dependent dynamic friction laws, may be needed. A comprehensive review of friction, in particular in dynamic context, can be found in [45].

Spring constant k obviously affects the horizontal motion of the damper. If it is too big, the damper would slide most time; on the other hand, if it is too small, the damper would stick most time. Thus, its value regulates the time durations of stick and slip and thus can be used as another design parameter.

The study of the last two aspects (the friction laws and the stiffness of the short vertical beams) is beyond the scope of this paper and will be conducted in near future.

4. Conclusions

This paper presents a study on the forced vibration response of a simplified turbine blade model with a new kind of under-platform dry friction dampers. It establishes a numerical approach which uses numerical modes of the structure and is capable of accommodating the discontinuous classical Coulomb’s law of friction and dealing with moving loads efficiently.

In this study, both the normal contact forces and the resultant friction forces at the damper-platform interfaces are modeled as moving loads, and the normal contact force variation as a result of platform vibration is also considered. Parametric analysis demonstrates that the dampers will experience three motion regimes: gross slip regime, stick-slip regime, and pure stick regime, as the preloads at the contact points between the dampers and blade platform increase. The following conclusions can be drawn:

(1)

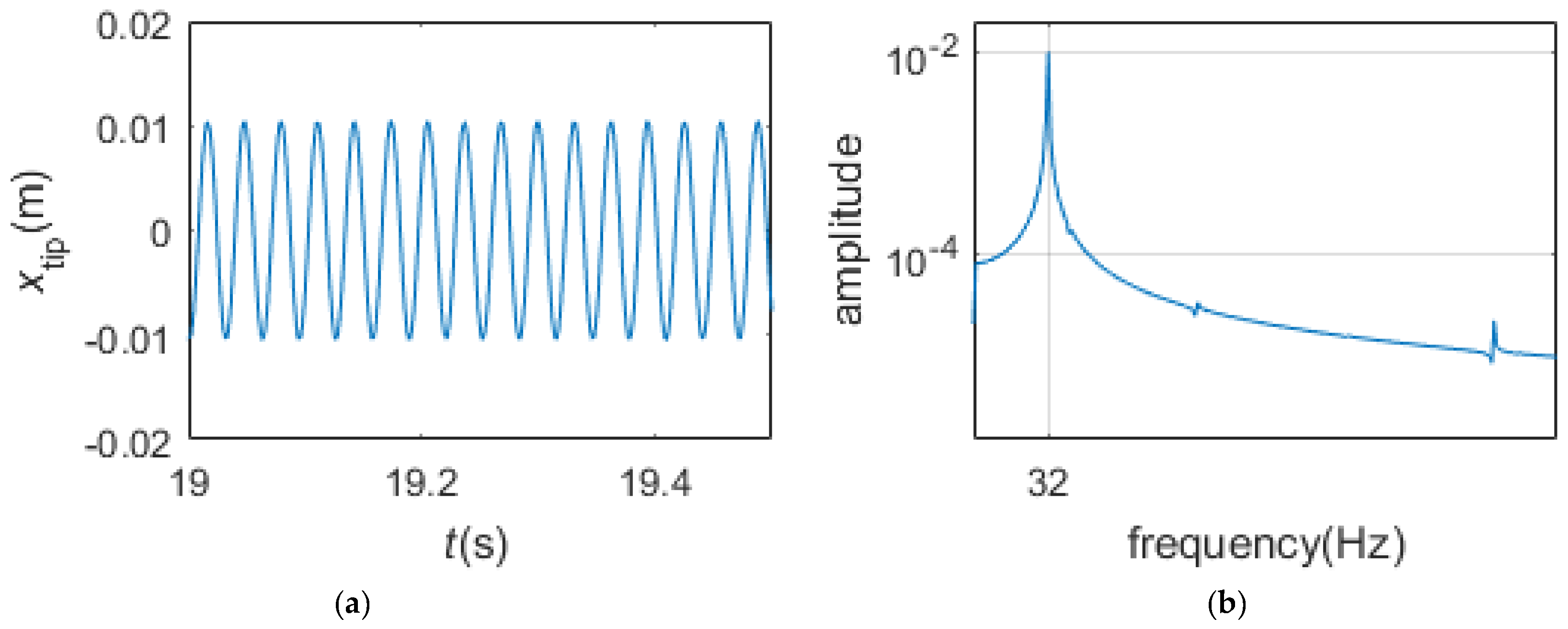
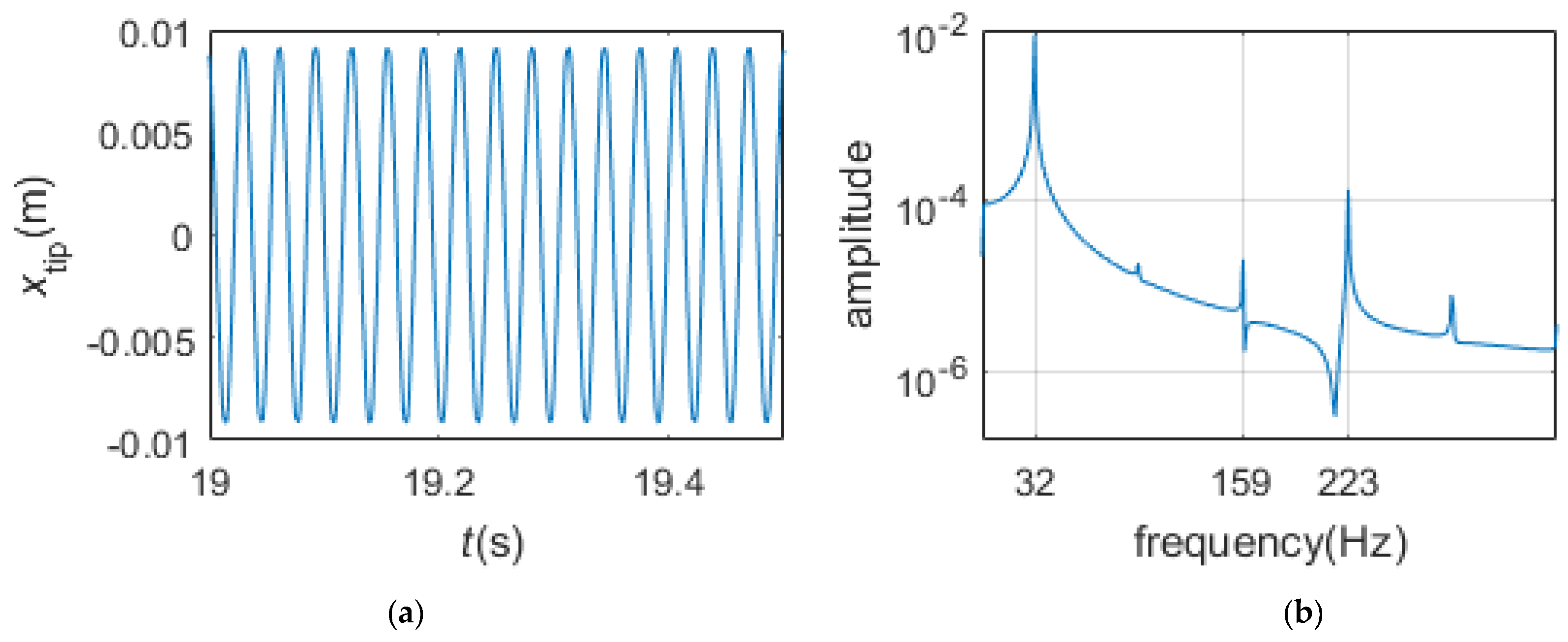
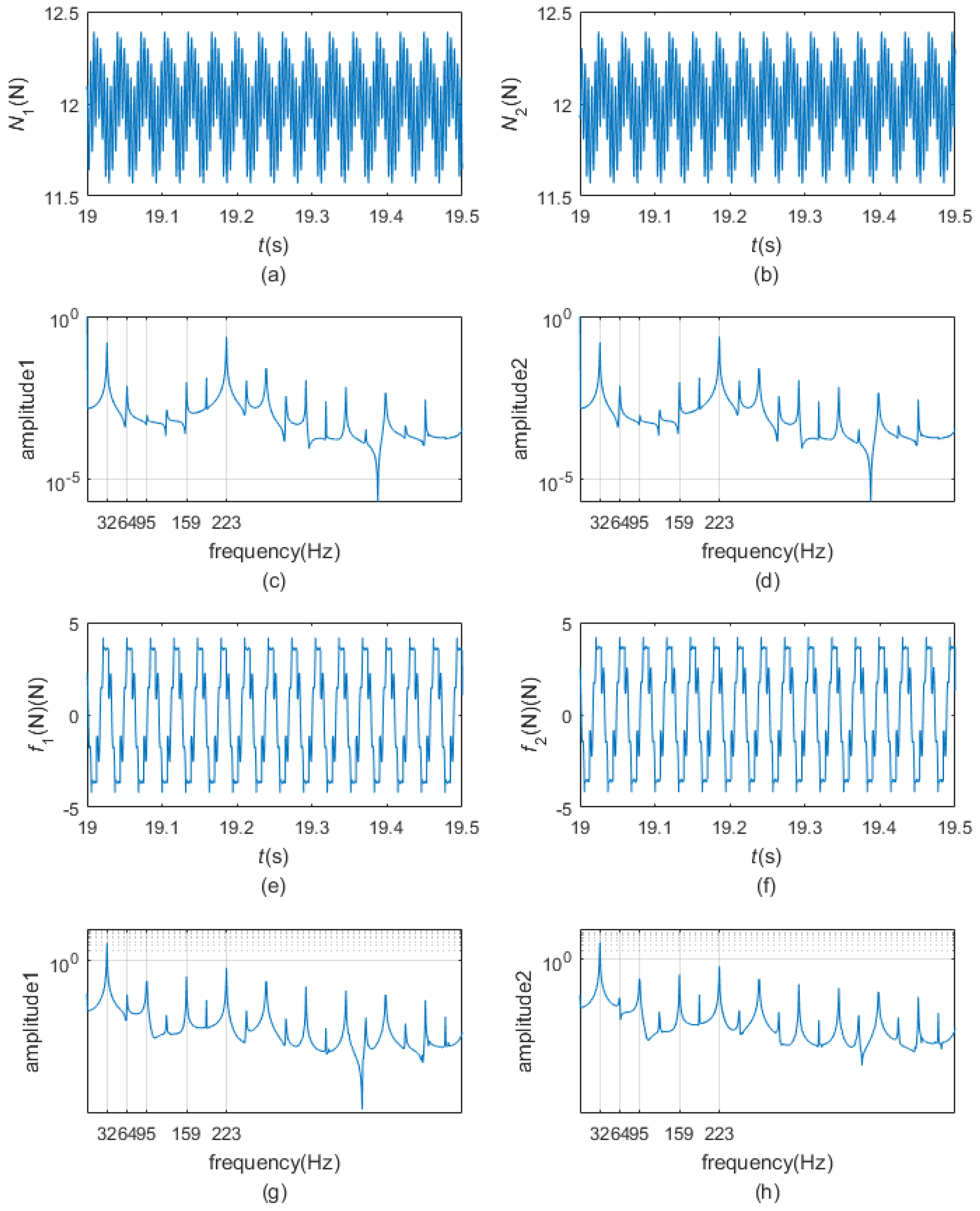
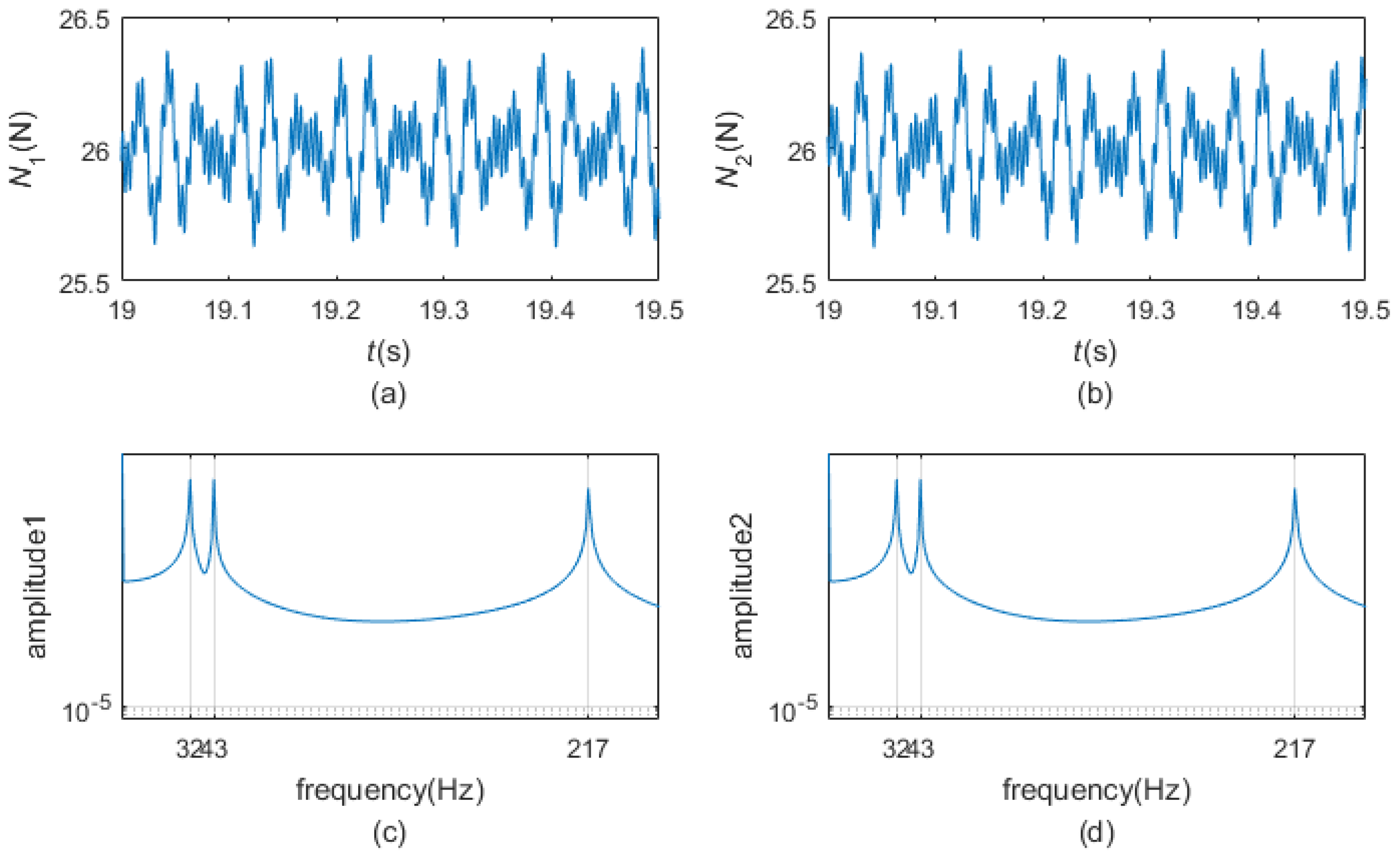
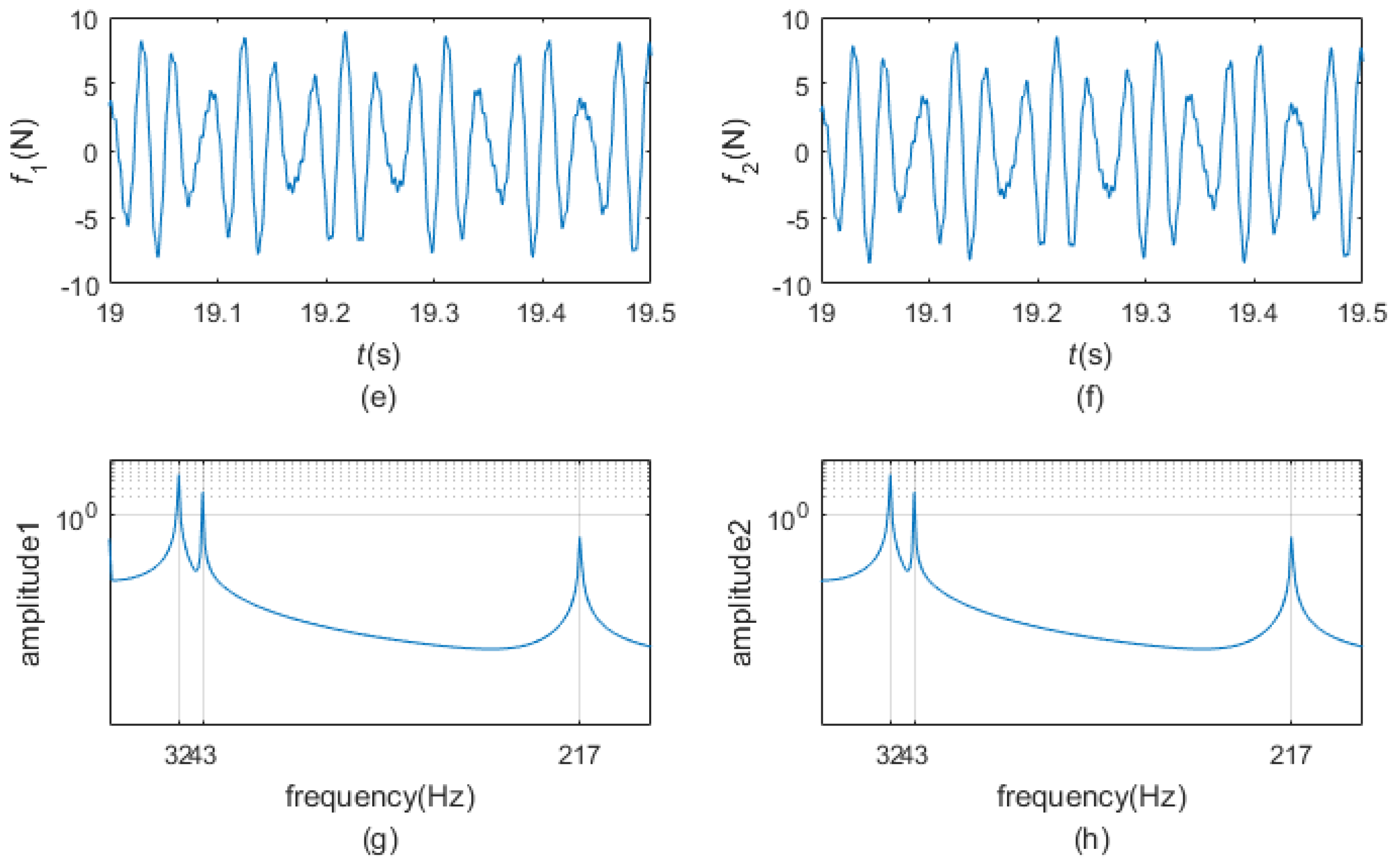
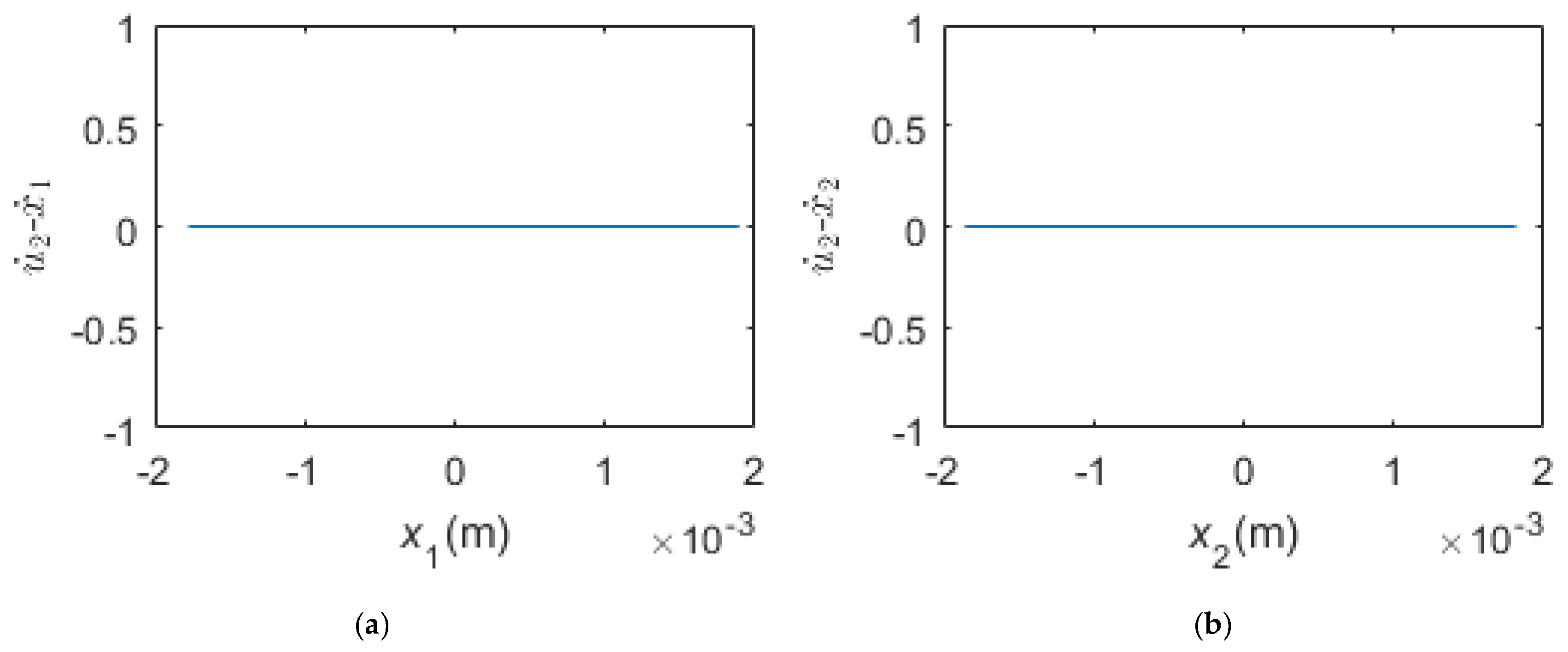
When the pre-load $N_0$ is very small, the two dampers are all in gross slip regime in the steady state. The motion of the blade tip is harmonic. The normal contact forces fluctuate around the preload and are periodic, the friction forces $f_1$ and $f_2$ undulate between $\pm {\mu }_k{N}_1$ and $\pm {\mu }_k{N}_2$, respectively, and are also periodic. The motions of the two dampers are not harmonic but periodic whose periods are the period of the excitation. The phase plane maps of the dampers are smooth closed curves.

(2)

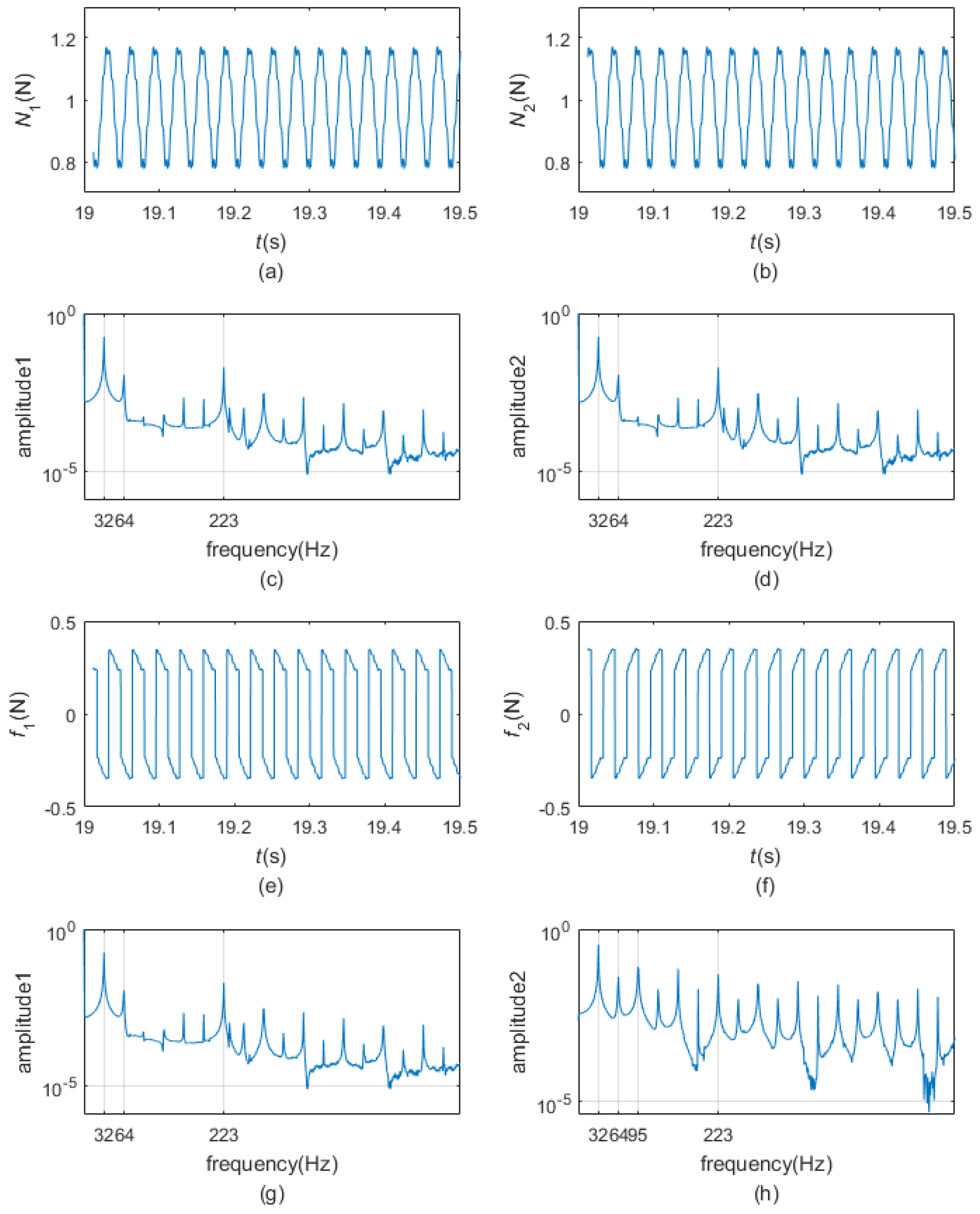
When the pre-load $N_0$ is bigger and appropriate, the two dampers could undergo stick-slip vibration in the steady state. The motion of the blade tip is periodic rather than harmonic. The normal contact forces continue to fluctuate around the preload and are periodic as in gross slip regime. Friction forces $f_1$ and $f_2$ fluctuate between $\pm {\mu }_s{N}_1$ and $\pm {\mu }_s{N}_2$, respectively, and are periodic. At times, $f_1$ equals $\pm {\mu }_k{N}_1$ and $f_2$ equals $\pm {\mu }_k{N}_2$; at any other time, friction forces $f_1$ and $f_2$ could reach $\pm {\mu }_s{N}_1$ and $\pm {\mu }_s{N}_2$, separately. The motions of the dampers are similar to those in the gross slip regime. The phase plane maps of the dampers are closed curves but not smooth.

(3)

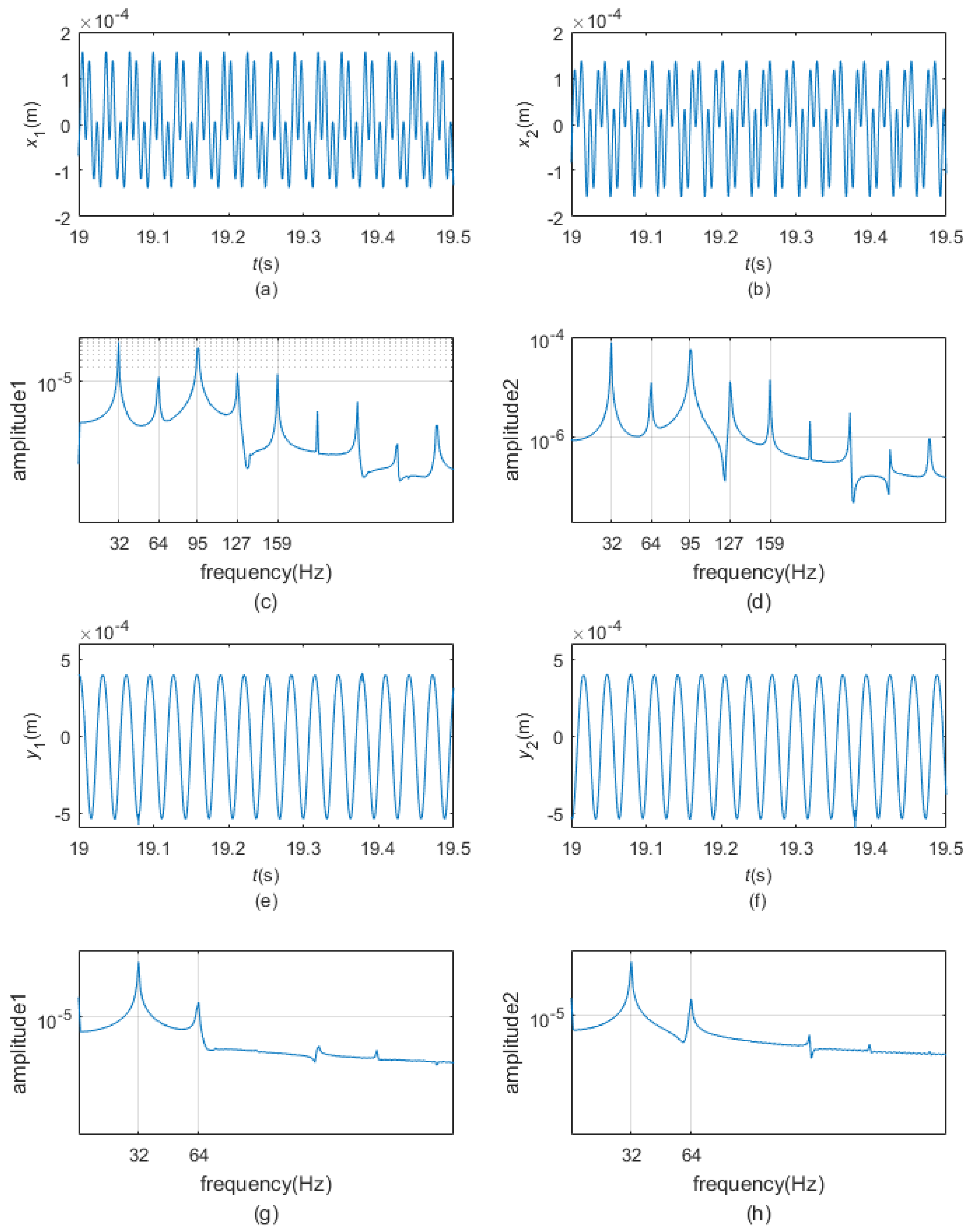
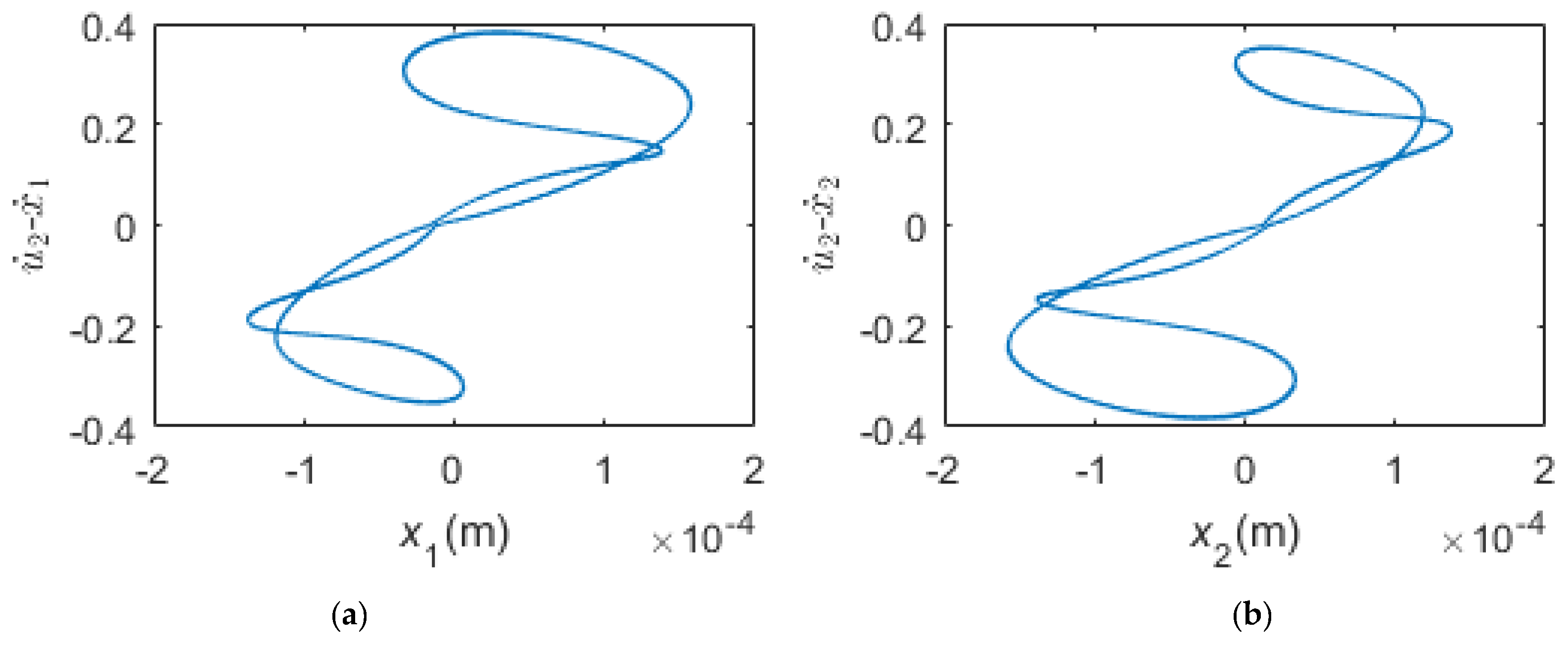
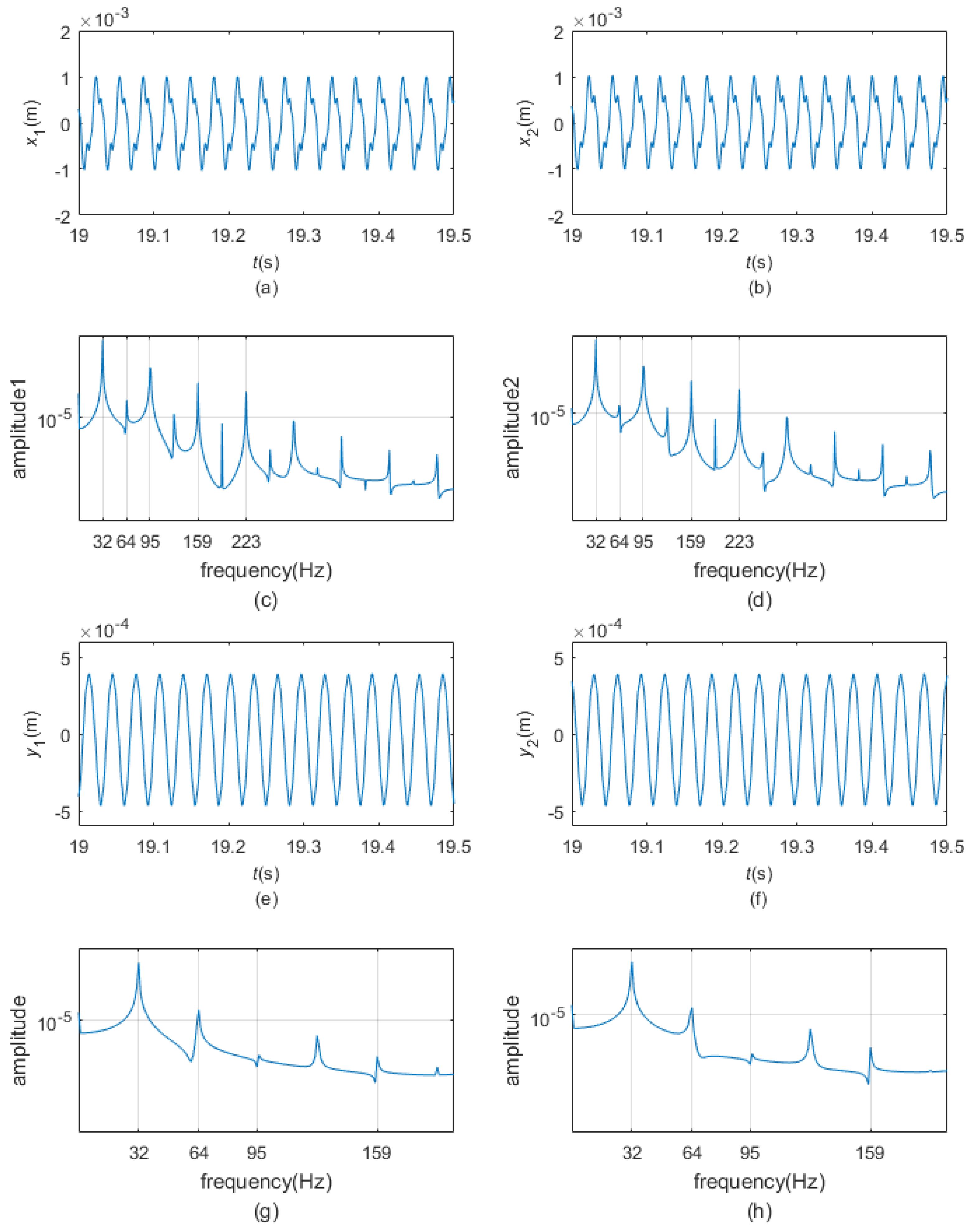
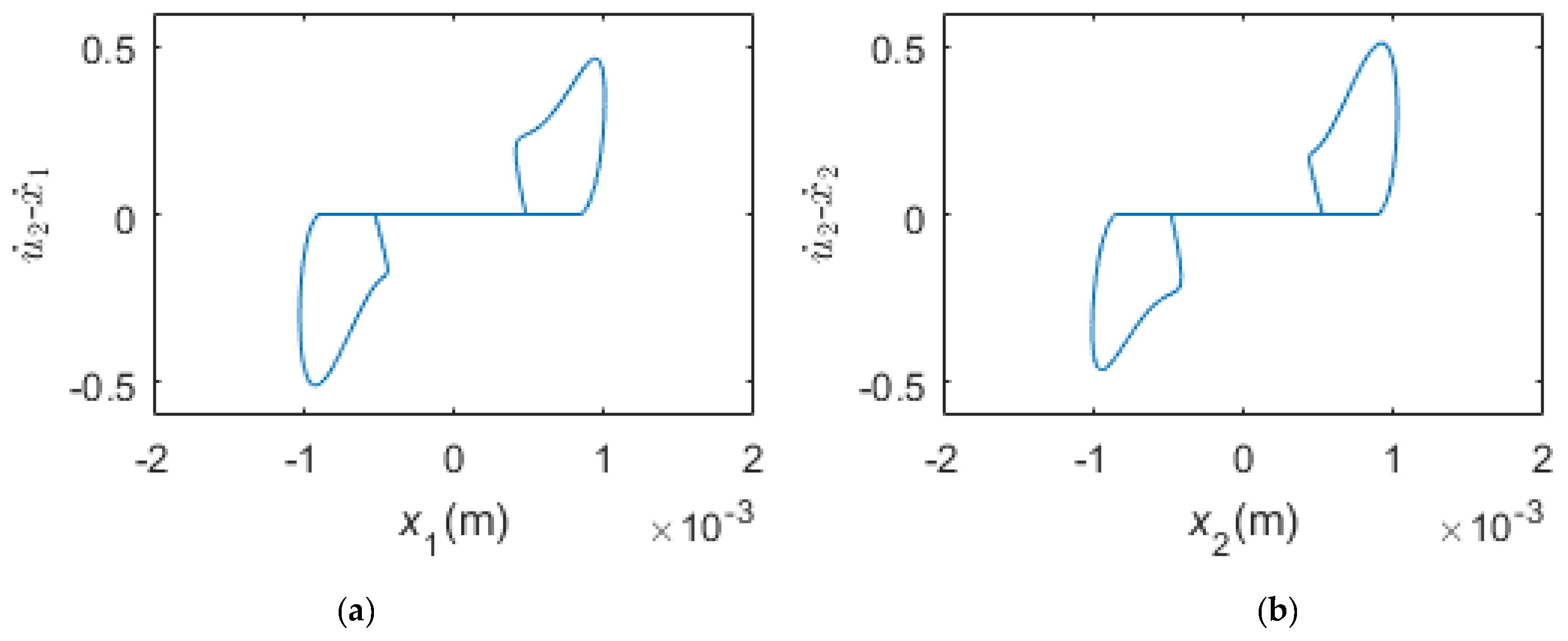
When the pre-load $N_0$ is high enough, the two dampers are all in pure stick regime in the steady state. During pure stick scheme, the blade-platform structure and the dampers form one new system. The normal contact forces and the friction forces display a quasi-periodic variation, and the motion of the blade tip changes to quasi-periodic vibration as well. The motions of the dampers are non-periodic but quasi-periodic. There are three peaks in the frequency spectrum plots: the frequency of the first peak is the same as the excitation frequency, but the frequencies of the second peak and the third peak are now the first-order bending frequency and the fifth-order bending frequency of the whole new system.

(4)

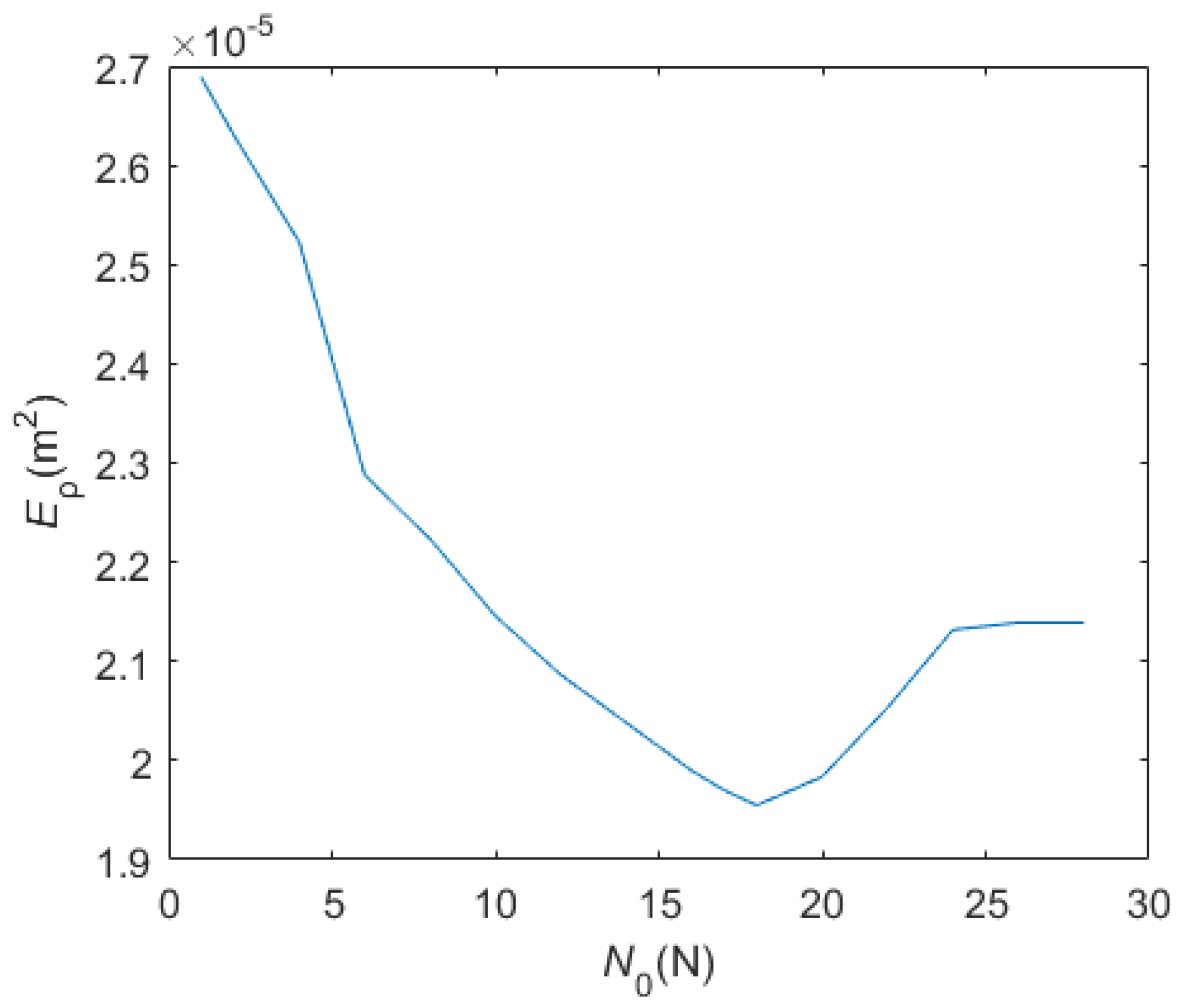
There is an optimal pre-load which can make the biggest vibration reduction.