Low Frequency Interactive Auralization Based on a Plane Wave Expansion
Abstract
:1. Introduction
2. Mathematical Foundations
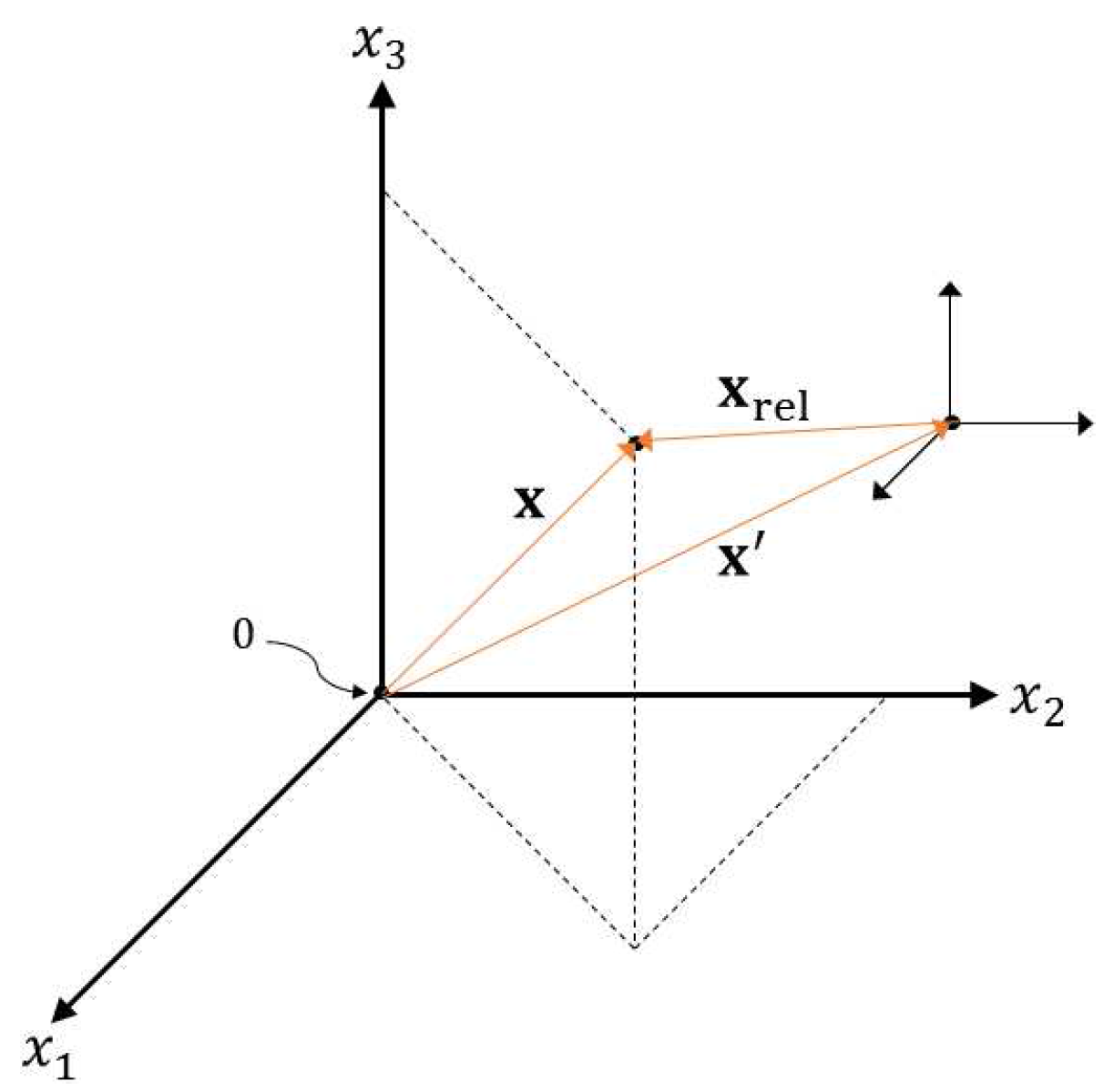
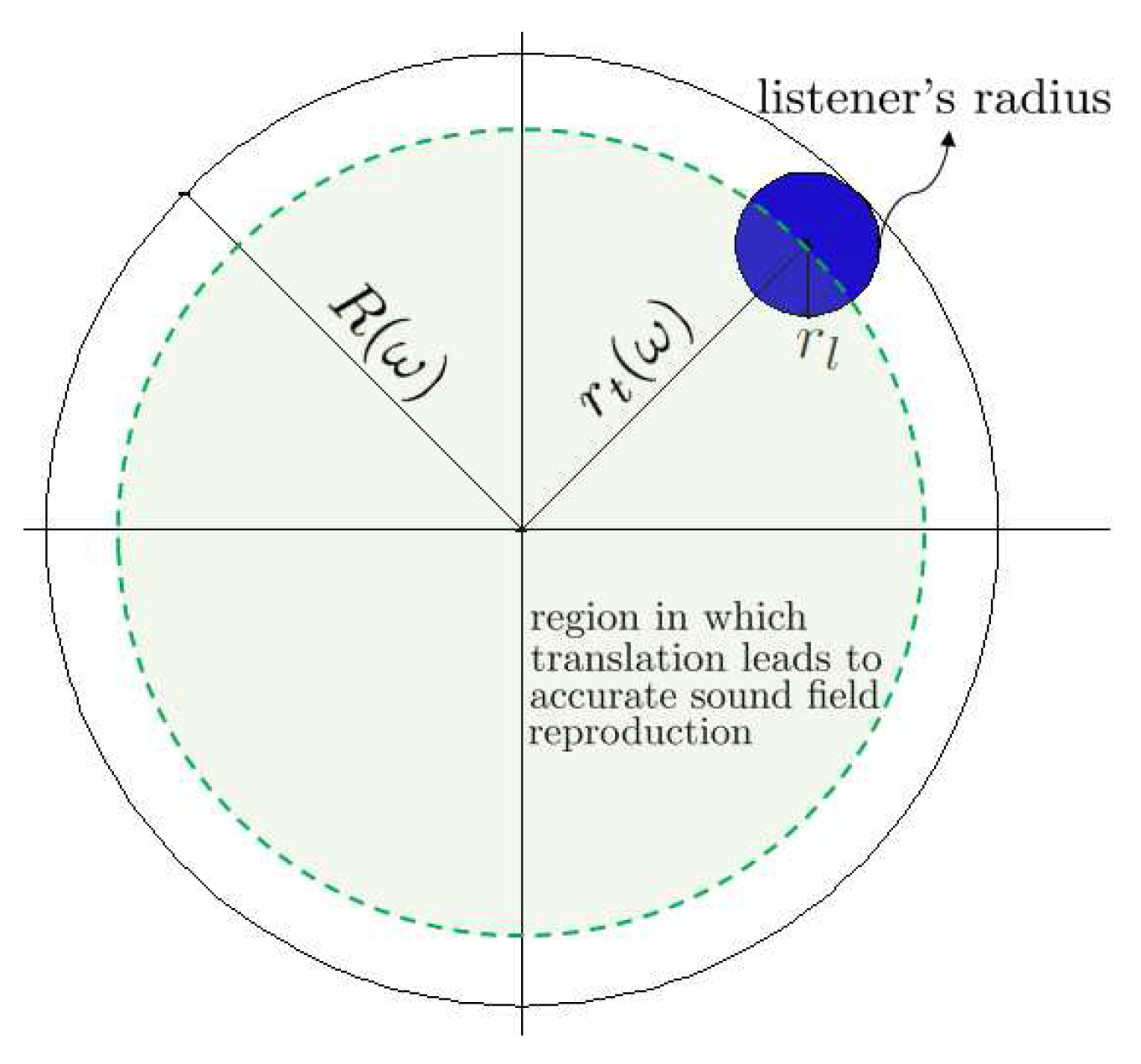
2.1. Translation of the Acoustic Field
2.2. Rotation of the Acoustic Field
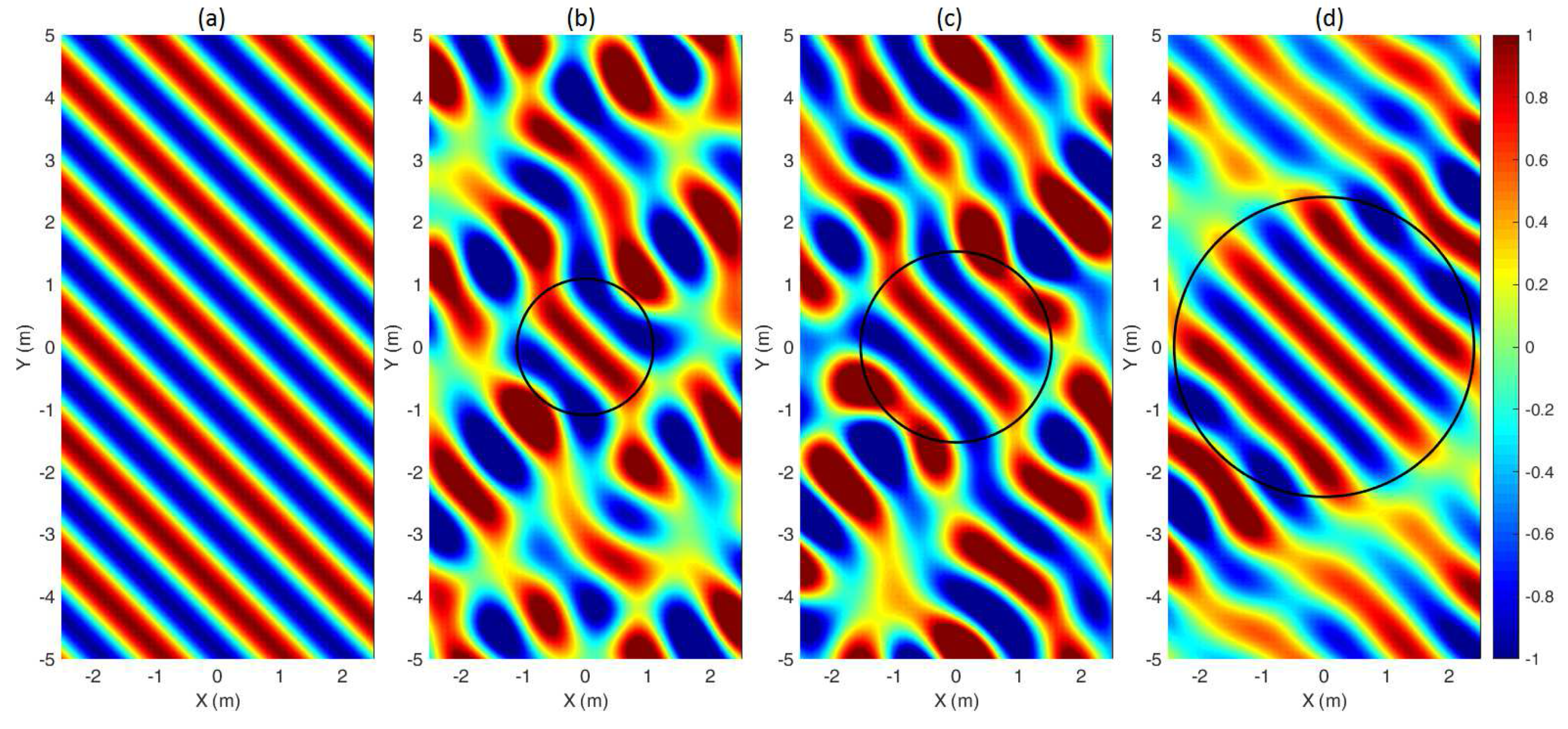
3. Plane Wave Expansion from Finite Element Data
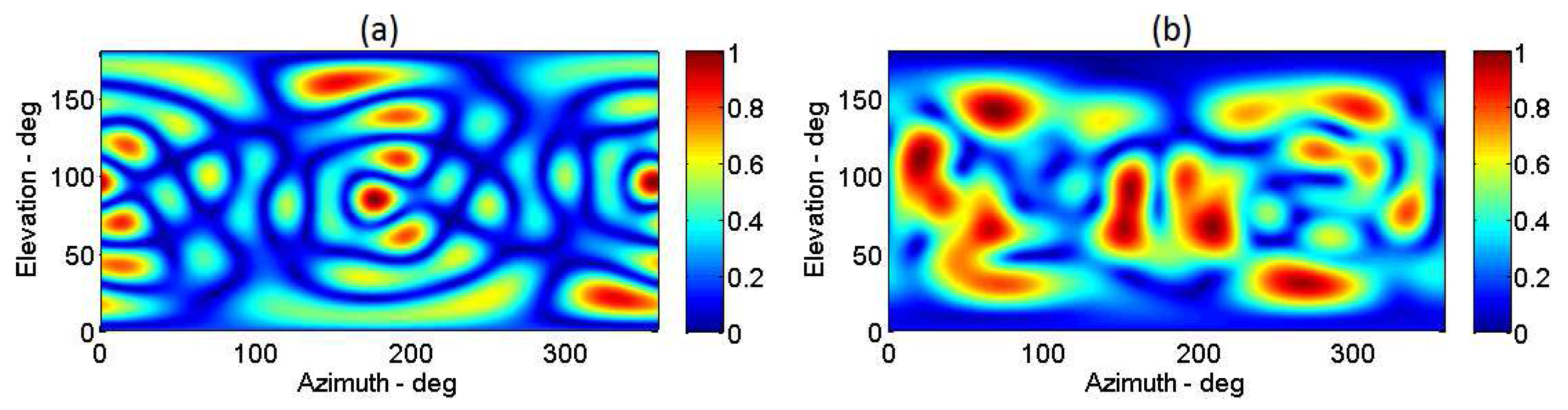
3.1. Reference Case
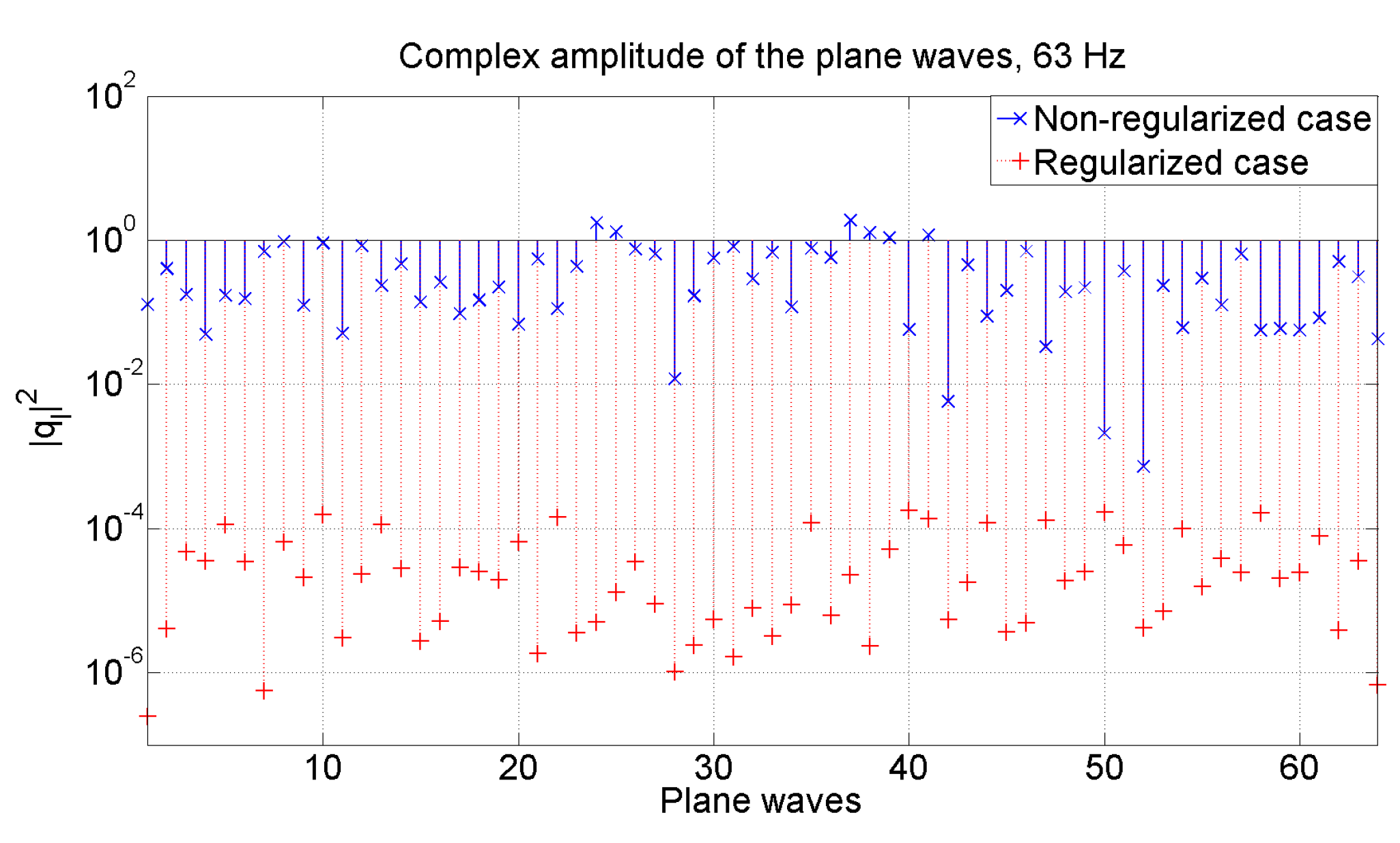
3.1.1. Regularization in the Formulation of the Inverse Problem
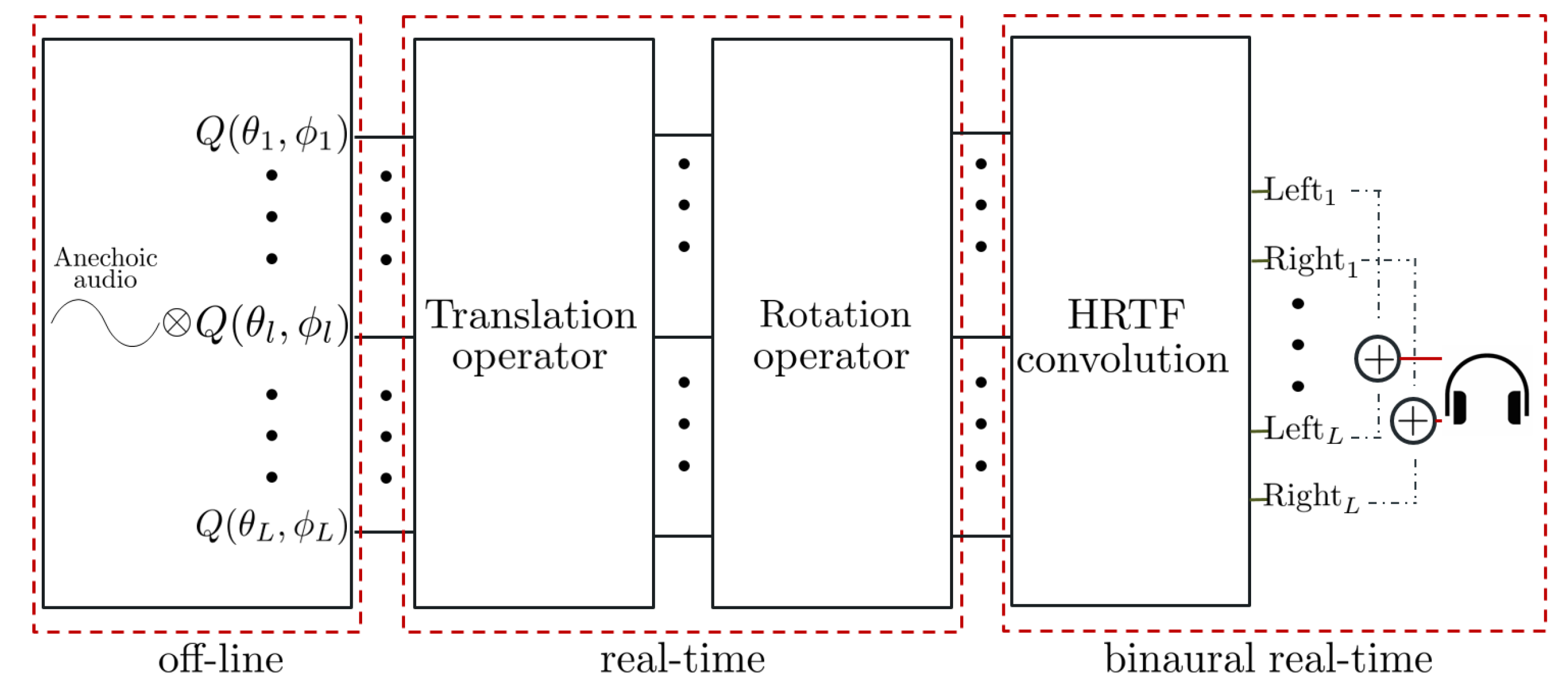
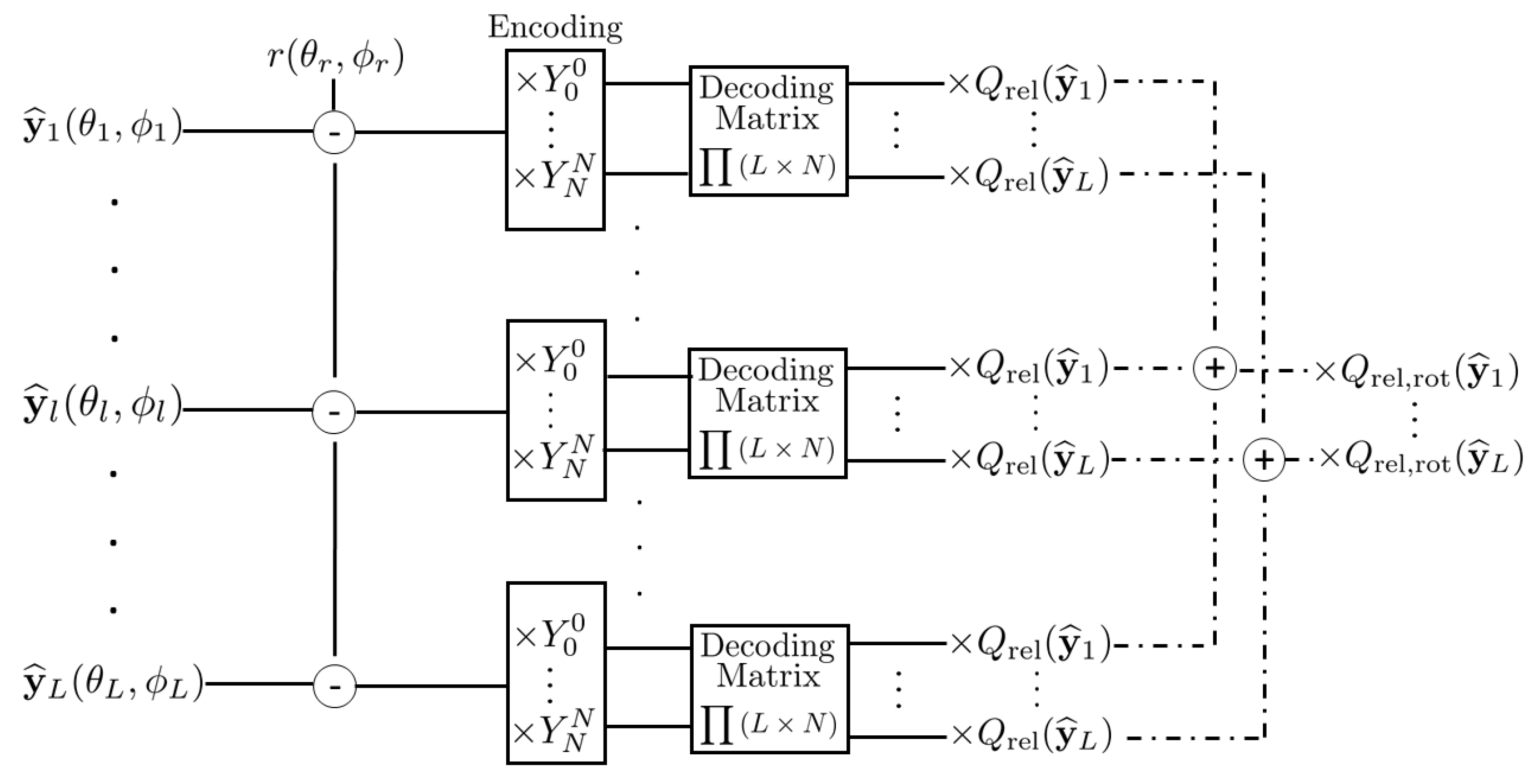
4. Real-Time Implementation of an Auralization System
4.1. Translation of the Acoustic Field
4.2. Rotation of the Acoustic Field
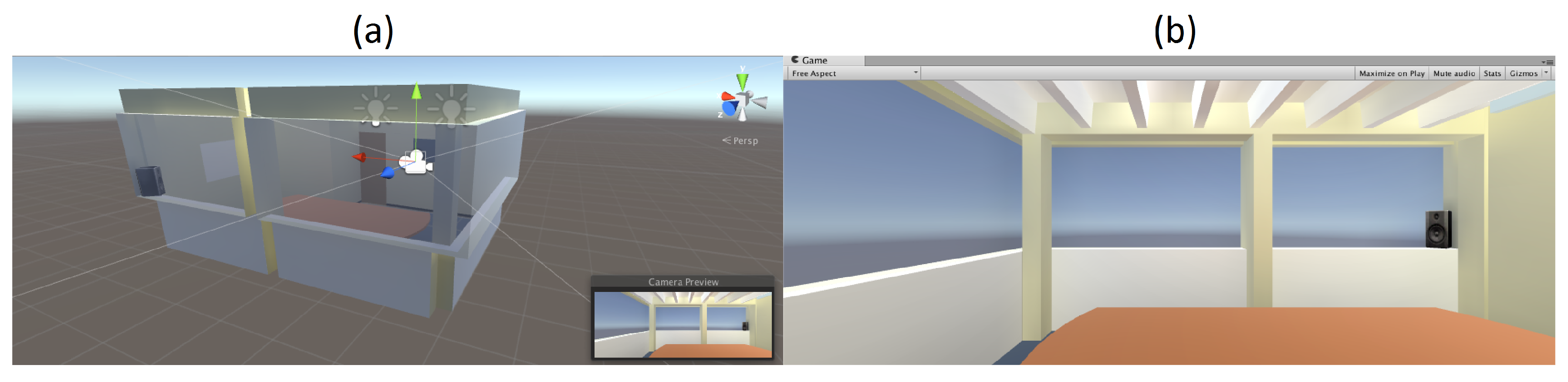
4.3. Graphical Interfaces
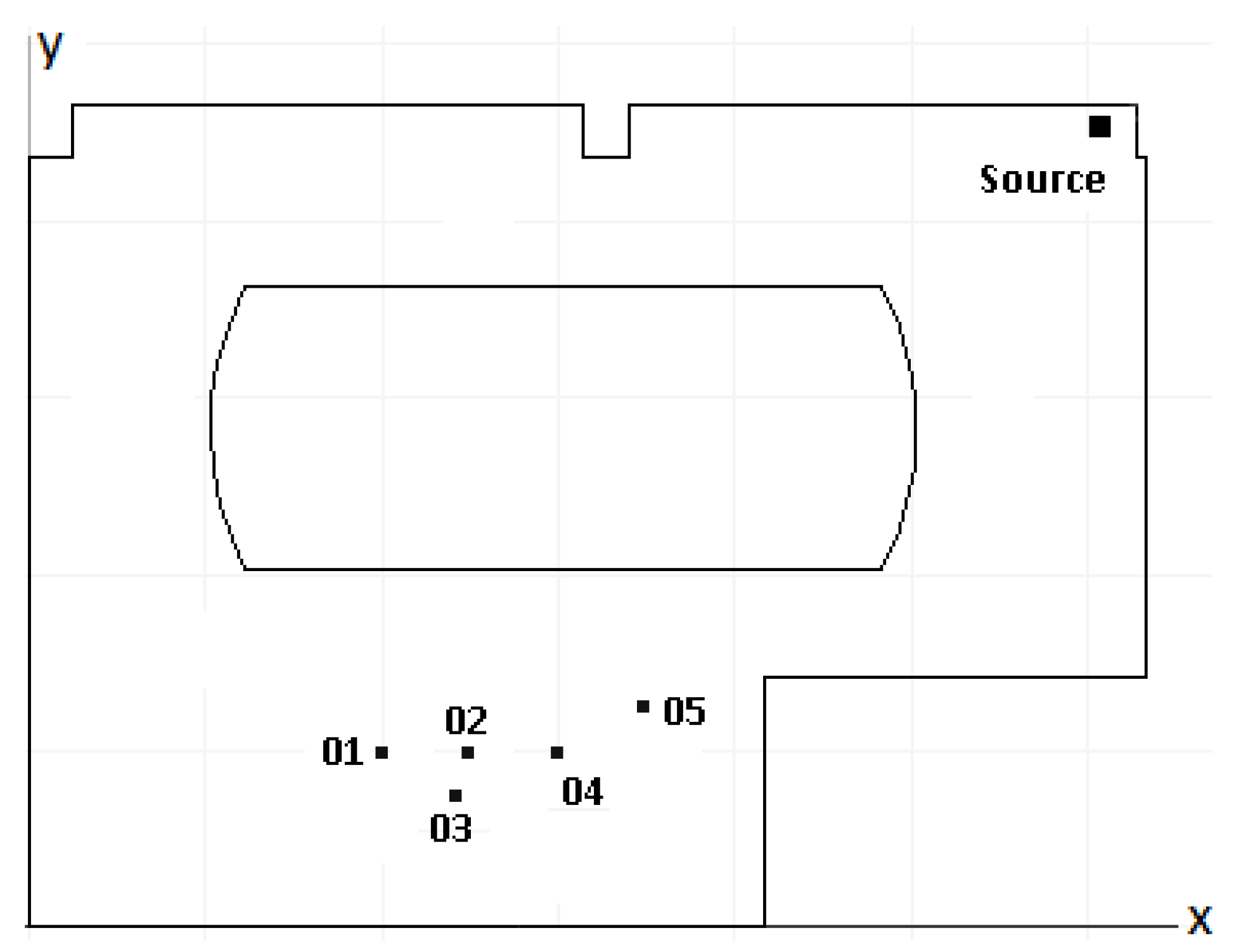
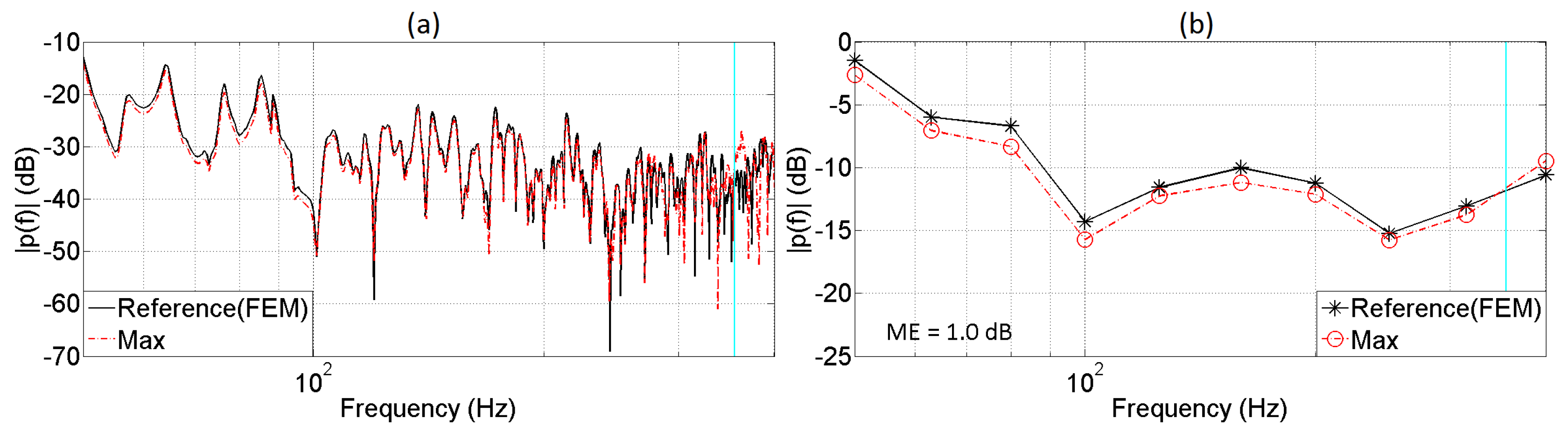
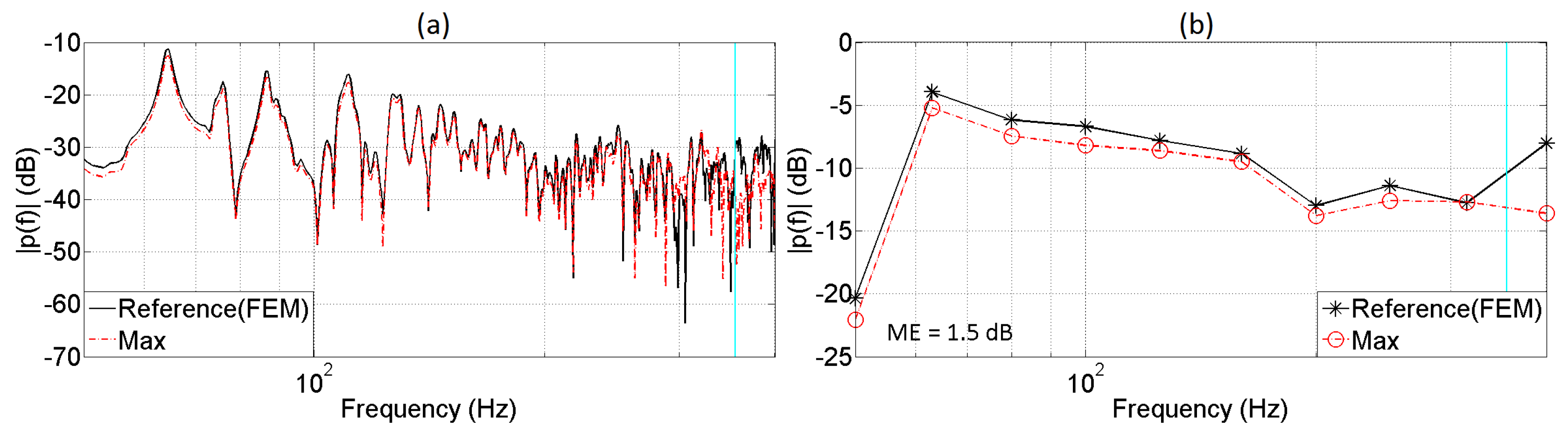
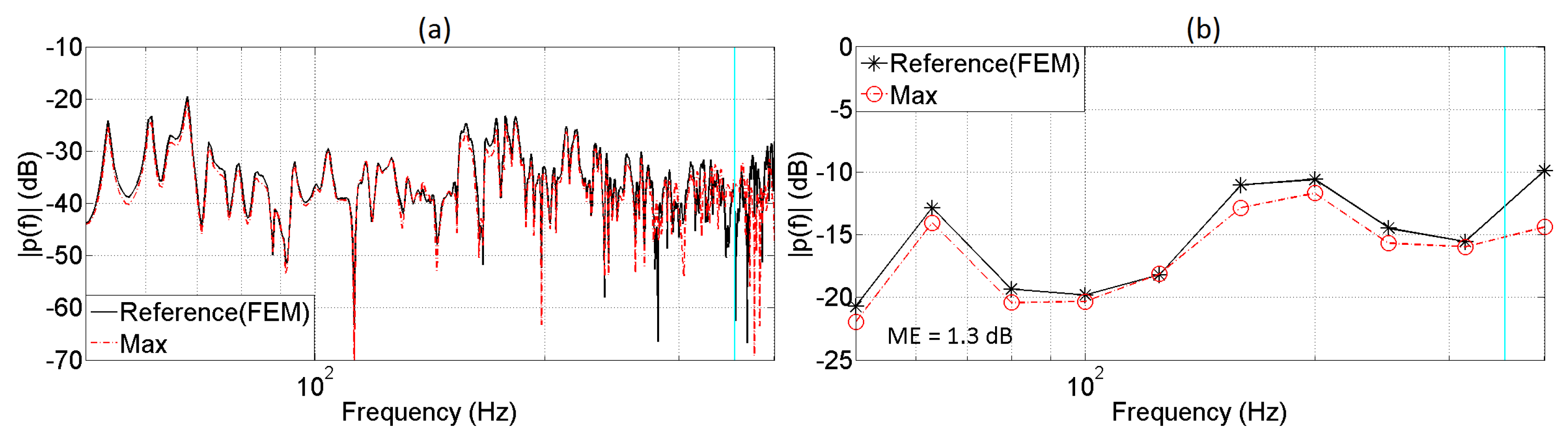
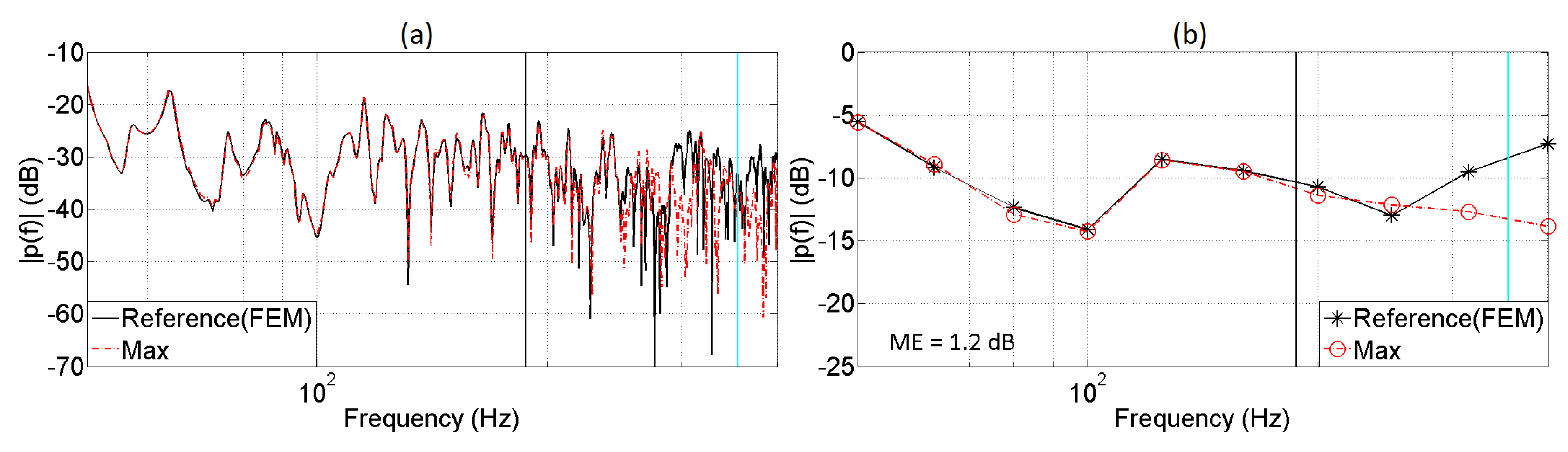
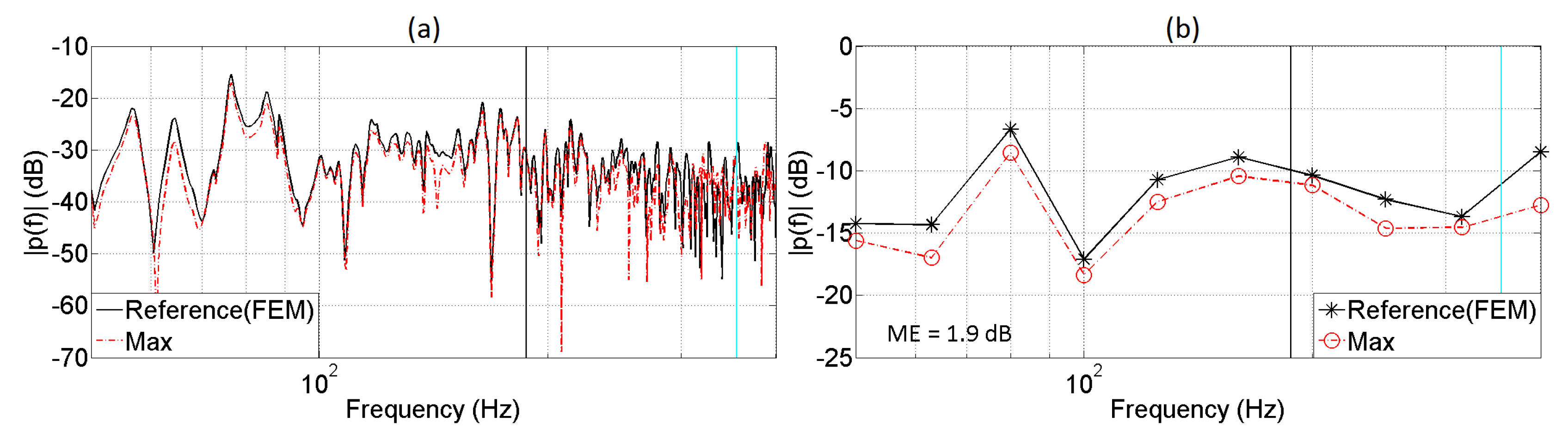
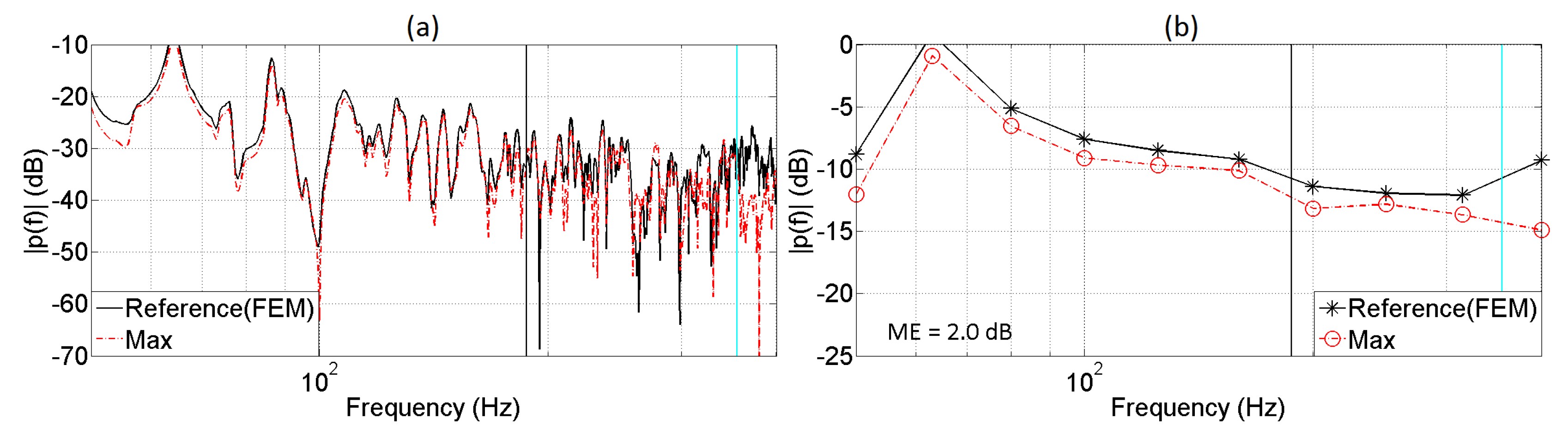
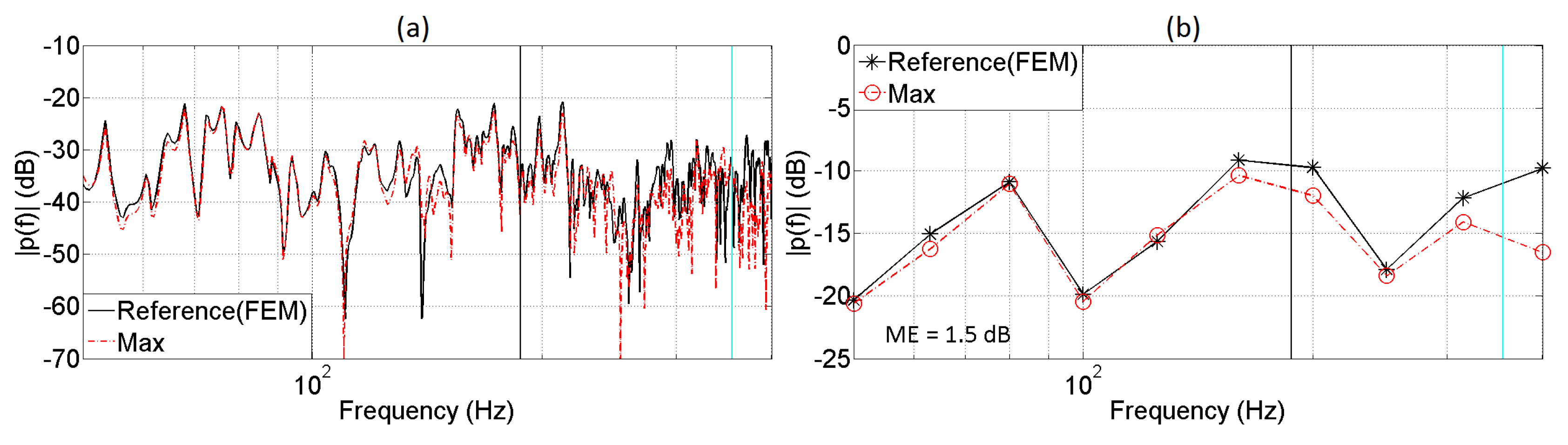
5. Evaluation of the Auralization System
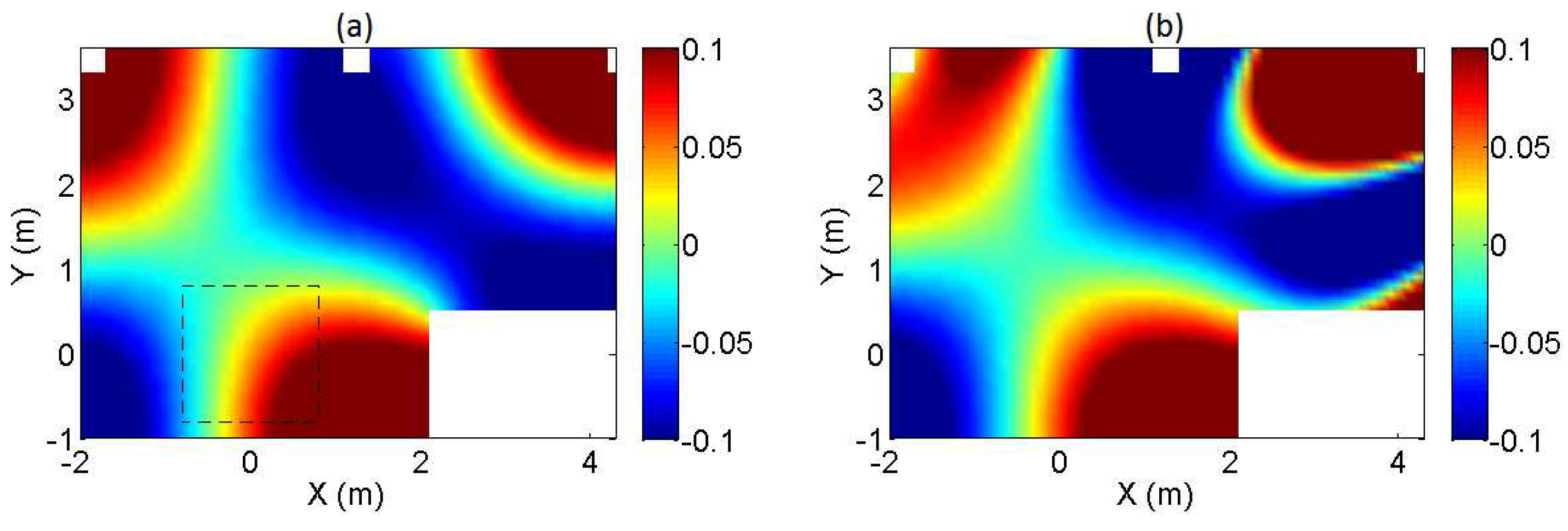
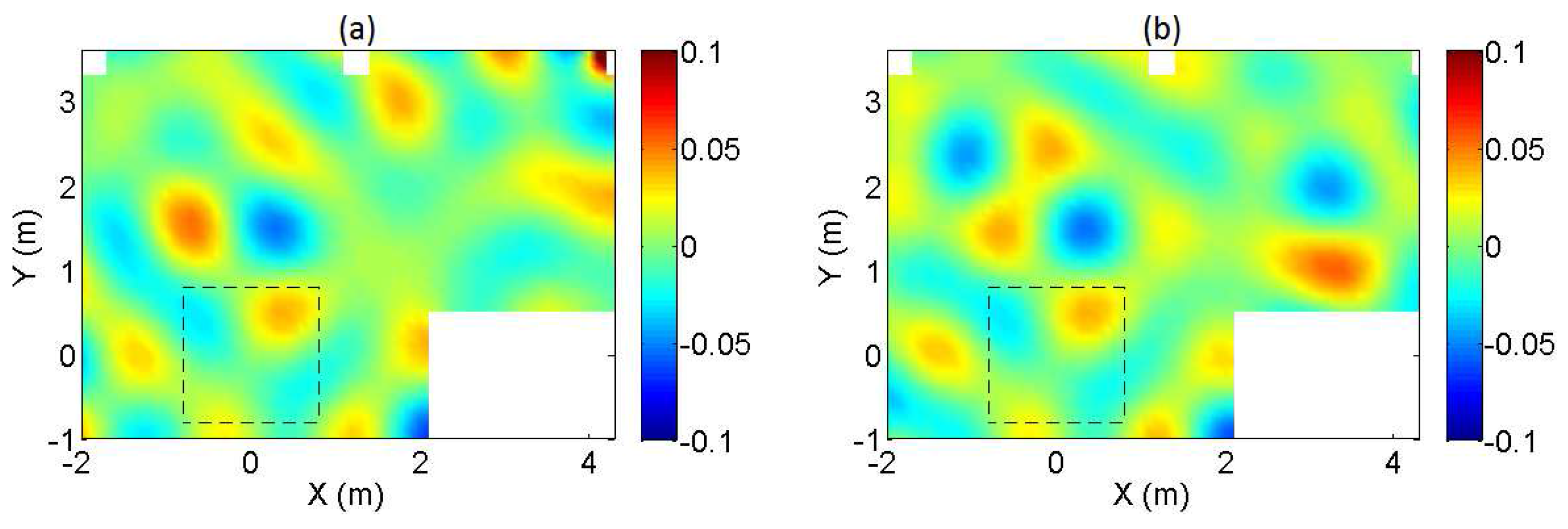
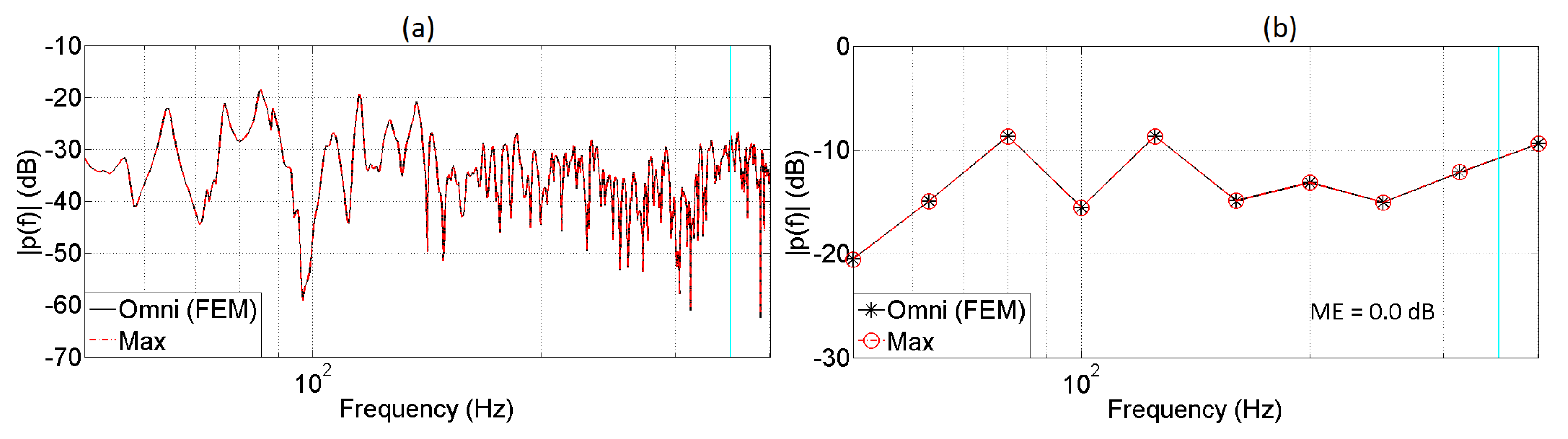
5.1. Monaural Analysis
5.2. Spatial Analysis
6. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| GA | Geometrical Acoustics |
| FEM | Finite Element Method |
| BEM | Boundary Element Method |
| FDTD | Finite Difference Time Domain |
| GPU | Graphics Processor Unit |
| PWE | Plane Wave Expansion |
| WFS | Wave Field Synthesis |
| VBAP | Vector-Based Amplitude Panning |
References
- Vorländer, M. Auralization, 1st ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Savioja, L.; Huopaniemi, T.; Lokki, T.; Vaananen, R. Creating Interactive Virtual Acoustic Environments. J. Audio Eng. Soc. 1999, 47, 675–705. [Google Scholar]
- Funkhouser, T.; Tsingos, N.; Carlbom, I.; Elko, G.; Sondhi, M.; West, J.; Pingali, G.; Min, P.; Ngan, A. A beam tracing method for interactive architectural acoustics. J. Acoust. Soc. Am. 2004, 115, 739–756. [Google Scholar] [CrossRef] [PubMed]
- Noisternig, M.; Katz, B.; Siltanen, S.; Savioja, L. Framework for Real-Time Auralization in Architectural Acoustics. Acta Acust. United Acust. 2008, 94, 1000–1015. [Google Scholar] [CrossRef]
- Chandak, A.; Lauterbach, C.; Taylor, M.; Ren, Z.; Manocha, D. AD-Frustum: Adaptive Frustum Tracing for Interactive Sound Propagation. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1707–1714. [Google Scholar] [PubMed]
- Taylor, M. RESound: Interactive Sound Rendering for Dynamic. In Proceedings of the 17th International ACM Conference on Multimedia 2009, Beijing, China, 19–24 October 2009; pp. 271–280. [Google Scholar]
- Astley, J. Numerical Acoustical Modeling (Finite Element Modeling). In Handbook of Noise and Vibration Control, 1st ed.; Crocker, M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; Chapter 7; pp. 101–115. [Google Scholar]
- Herrin, D.; Wu, T.; Seybert, A. Boundary Element Method. In Handbook of Noise and Vibration Control, 1st ed.; Crocker, M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; Chapter 8; pp. 116–127. [Google Scholar]
- Botteldooren, D. Finite-Difference Time-Domain Simulation of Low-Frequency Room Acoustic Problems. J. Acoust. Soc. Am. 1995, 98, 3302–3308. [Google Scholar] [CrossRef]
- Mehra, R.; Raghuvanshi, N.; Antani, L.; Chandak, A.; Curtis, S.; Manocha, D. Wave-Based Sound Propagation in Large Open Scenes using an Equivalent Source Formulation. ACM Trans. Graph. 2013, 32, 19. [Google Scholar] [CrossRef]
- Mehra, R.; Antani, L.; Kim, S.; Manocha, D. Source and Listener Directivity for Interactive Wave-Based Sound Propagation. IEEE Trans. Vis. Comput. Graph. 2014, 20, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Raghuvanshi, N. Interactive Physically-Based Sound Simulation. Ph.D. Thesis, University of North Carolina, Chapel Hill, NC, USA, 2010. [Google Scholar]
- Savioja, L. Real-Time 3D Finite-Difference Time-Domain Simulation of Low and Mid-Frequency Room Acoustics. In Proceedings of the 13th Conference on Digital Audio Effects, Graz, Austria, 6–10 September 2010. [Google Scholar]
- Southern, A.; Murphy, D.; Savioja, L. Spatial Encoding of Finite Difference Time Domain Acoustic Models for Auralization. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2420–2432. [Google Scholar] [CrossRef]
- Southern, A.; Wells, J.; Murphy, D. Rendering walk-through auralisations using wave-based acoustical models. In Proceedings of the 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 715–716. [Google Scholar]
- Sheaffer, J.; Maarten, W.; Rafaely, B. Binaural Reproduction of Finite Difference Simulation Using Spherical Array Processing. IEEE Trans. Audio Speech Lang. Process. 2015, 23, 2125–2135. [Google Scholar] [CrossRef]
- Støfringsdal, B.; Svensson, P. Conversion of Discretely Sampled Sound Field Data to Auralization Formats. J. Audio Eng. Soc. 2006, 54, 380–400. [Google Scholar]
- Menzies, D.; Al-Akaidi, M. Nearfiled binaural synthesis and ambisonics. J. Acoust. Soc. Am. 2006, 121, 1559–1563. [Google Scholar] [CrossRef]
- Winter, F.; Schultz, F.; Spors, S. Localization Properties of Data-based Binaural Synthesis including Translatory Head-Movements. In Proceedings of the Forum Acusticum, Krakow, Poland, 7–12 September 2014. [Google Scholar]
- Zotter, F. Analysis and Synthesis of Sound-Radiation with Spherical Arrays. Ph.D. Thesis, University of Music and Performing Arts, Graz, Austria, 2009. [Google Scholar]
- Murillo, D. Interactive Auralization Based on Hybrid Simulation Methods and Plane Wave Expansion. Ph.D. Thesis, Southampton University, Southampton, UK, 2016. [Google Scholar]
- Duraiswami, R.; Zotkin, D.; Li, Z.; Grassi, E.; Gumerov, N.; Davis, L. High Order Spatial Audio Capture and Its Binaural Head-Tracked Playback Over Headphones with HRTF Cues. In Proceedings of the 119th Convention of the Audio Engineering Society, New York, NY, USA, 7–10 October 2005. [Google Scholar]
- Fazi, F.; Noisternig, M.; Warusfel, O. Representation of Sound Fields for Audio Recording and Reproduction. In Proceedings of the Acoustics 2012, Nantes, France, 23–27 April 2012; pp. 1–6. [Google Scholar]
- Williams, E. Fourier Acoustics, 1st ed.; Academic Press: London, UK, 1999. [Google Scholar]
- Fliege, J. Sampled Sphere; Technical Report; University of Dortmund: Dortmund, Germany, 1999. [Google Scholar]
- Nelson, P.; Yoon, S. Estimation of Acoustic Source Strength By Inverse Methods: Part I, Conditioning of the Inverse Problem. J. Sound Vib. 2000, 233, 639–664. [Google Scholar] [CrossRef]
- Ward, D.; Abhayapala, T. Reproduction of a Plane-Wave Sound Field Using an Array of Loudspeakers. IEEE Trans. Audio Speech Lang. Process. 2001, 9, 697–707. [Google Scholar] [CrossRef]
- Herlufsen, H.; Gade, S.; Zaveri, H. Analyzers and Signal Generators. Handbook of Noise and Vibration Control, 1st ed. Crocker, M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; Chapter 40. 101–115. [Google Scholar]
- Kim, Y.; Nelson, P. Optimal Regularisation for Acoustic Source Reconstruction by Inverse Methods. J. Sound Vib. 2004, 275, 463–487. [Google Scholar] [CrossRef]
- Yoon, S.; Nelson, P. Estimation of Acoustic Source Strength By Inverse Methods: Part II, Experimental Investigation of Methods for Choosing Regularization Parameters. J. Sound Vib. 2000, 233, 665–701. [Google Scholar] [CrossRef]
- Poletti, M. Unified description of Ambisonics using real and complex spherical harmonics. In Proceedings of the Ambisonics Symposium 2009, Graz, Austria, 25–27 June 2009; pp. 1–10. [Google Scholar]
- Department of Music. Virginia Tech-School of Performing Arts. 2016. Available online: http://disis.music.vt.edu/main/index.php (accessed on 25 February 2017).
- Menzies, D.; Fazi, F. A Theoretical Analysis of Sound Localisation, with Application to Amplitude Panning. In Proceedings of the 138th Convention of Audio Engineering Society, Warsaw, Poland, 7–10 May 2015; pp. 1–5. [Google Scholar]
- Murillo, D.; Fazi, F.; Astley, J. Spherical Harmonic Representation of the Sound Field in a Room Based on Finite Element Simulations. In Proceedings of the 46th Iberoamerican Congress of Acoustics 2015, Valencia, Spain, 21–23 September 2015; pp. 1007–1018. [Google Scholar]



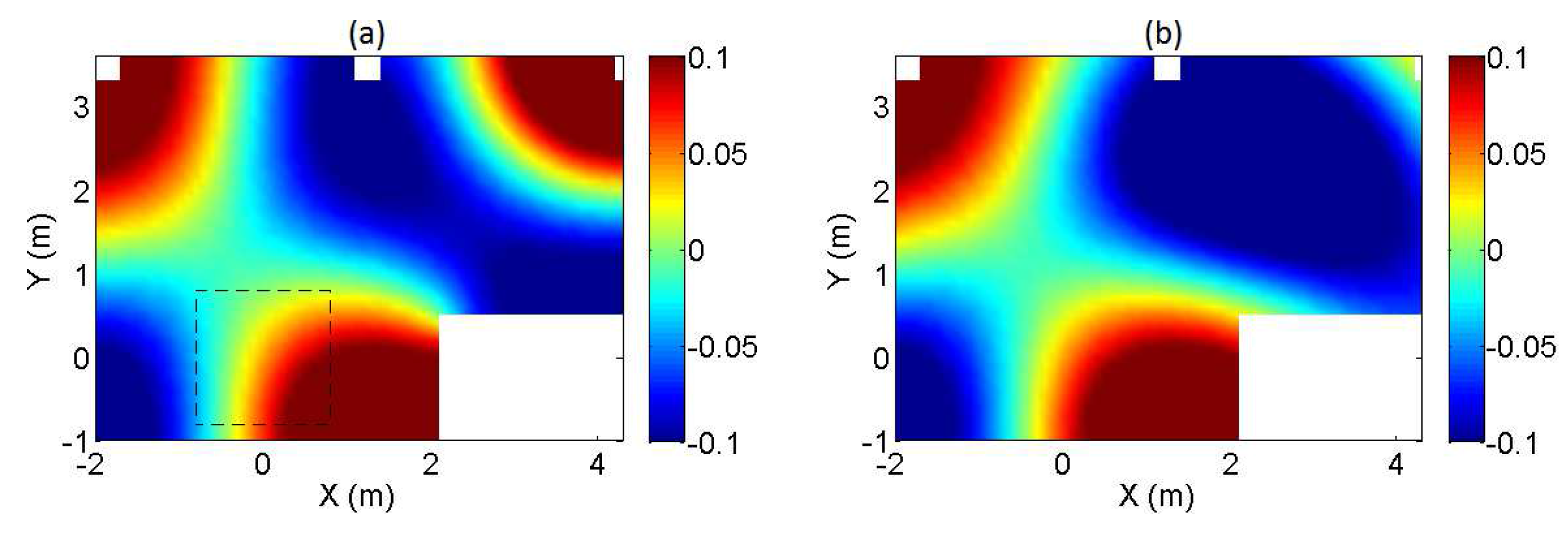
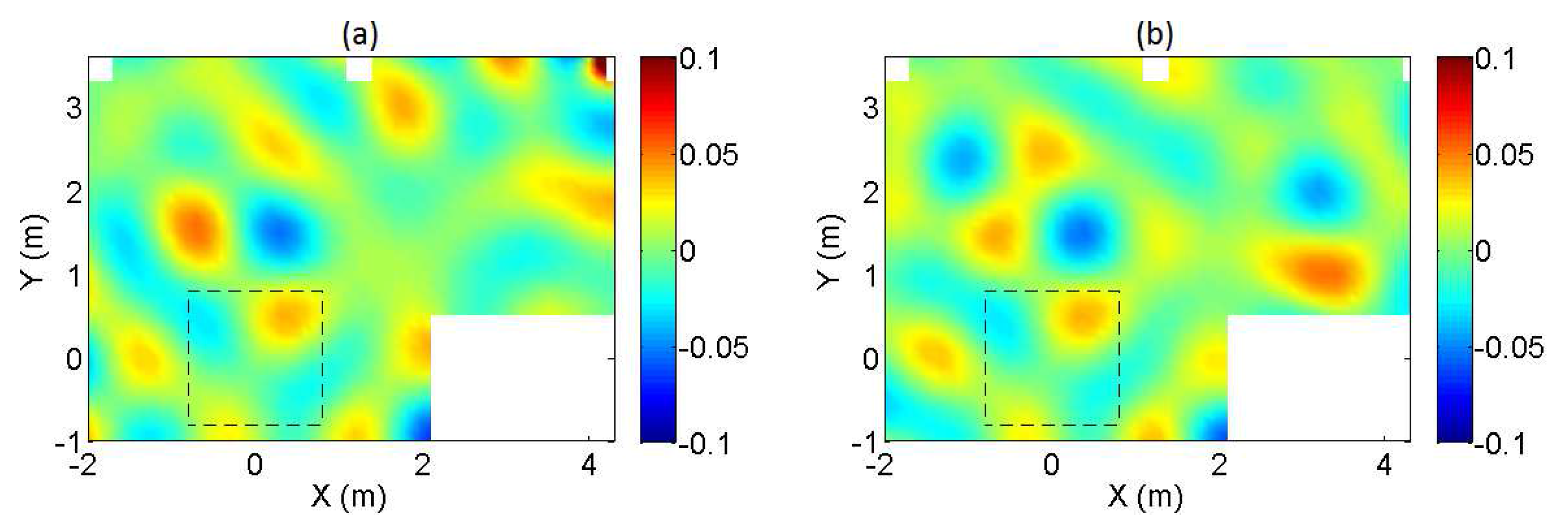
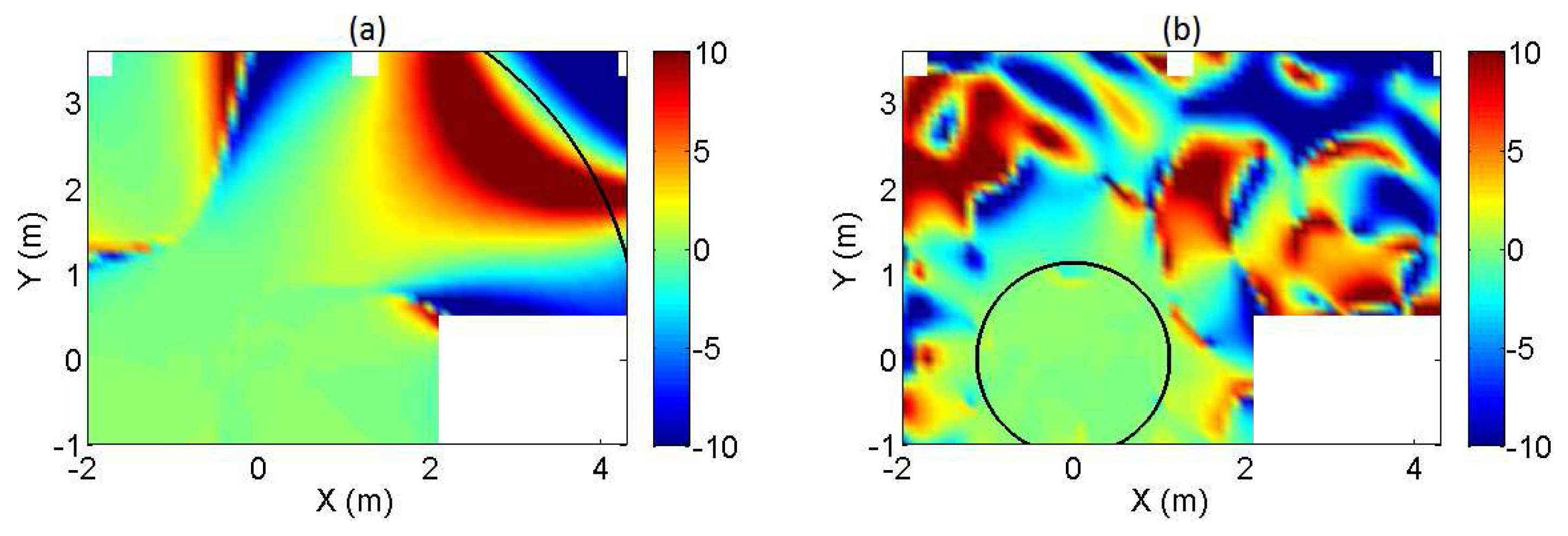
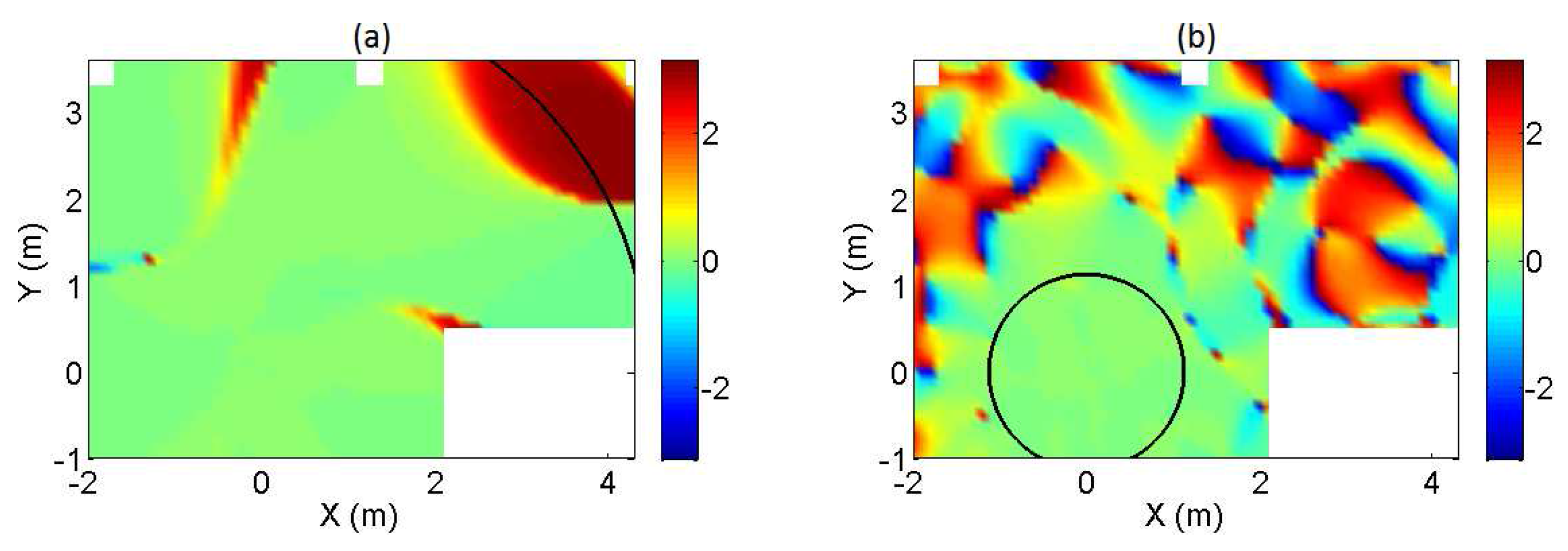

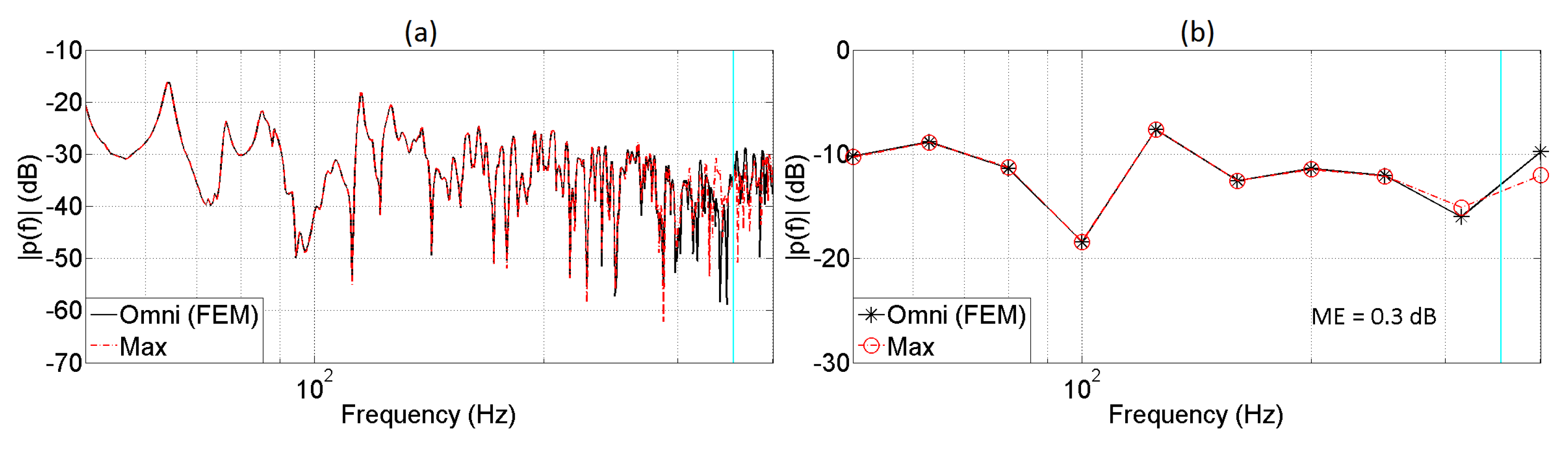
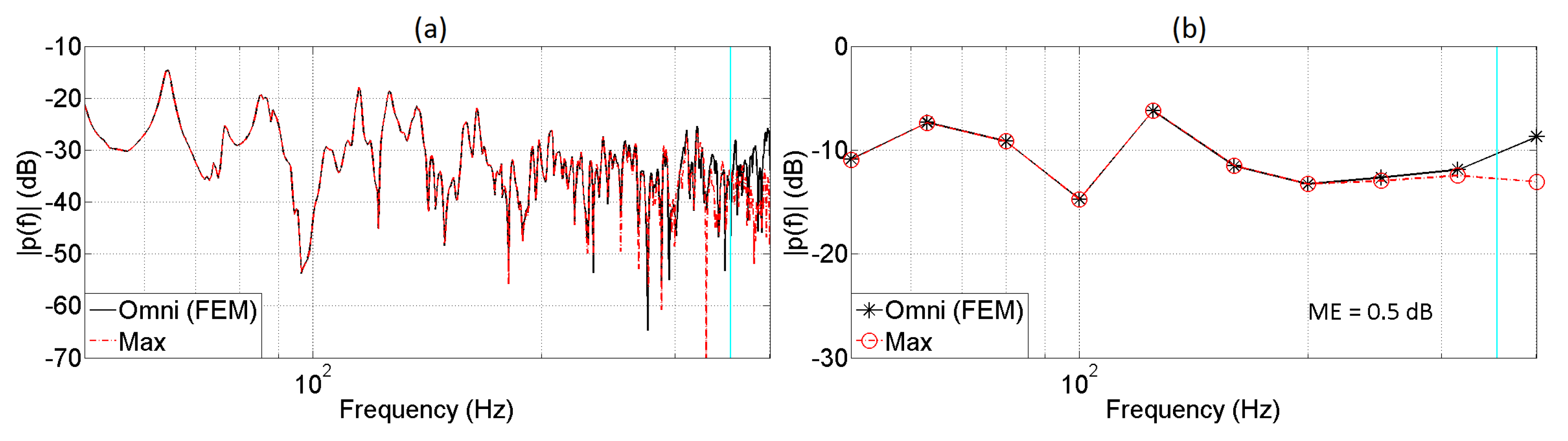
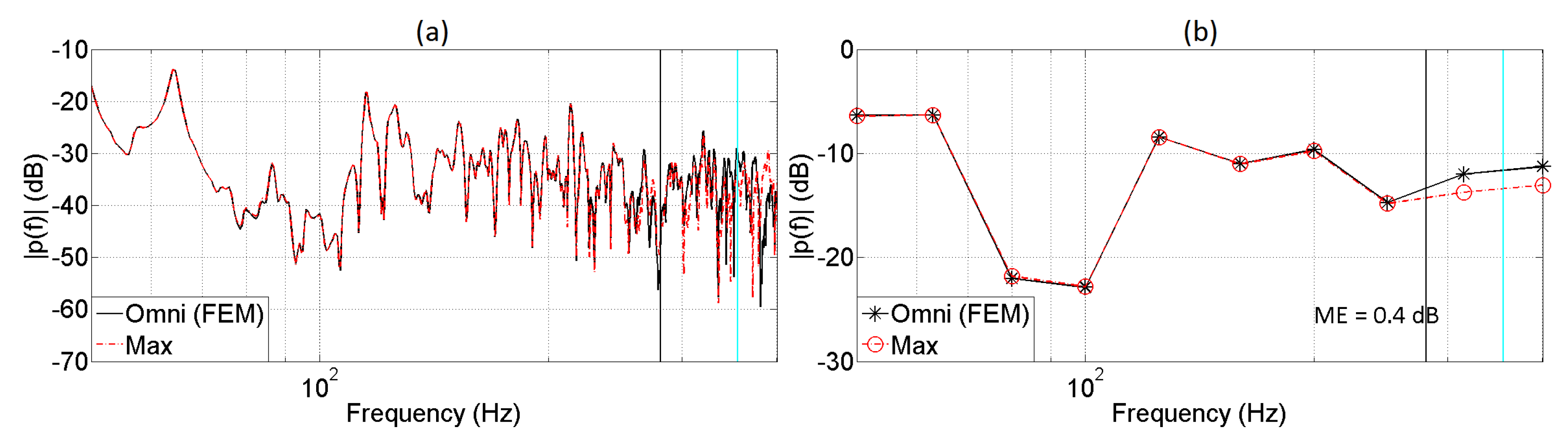
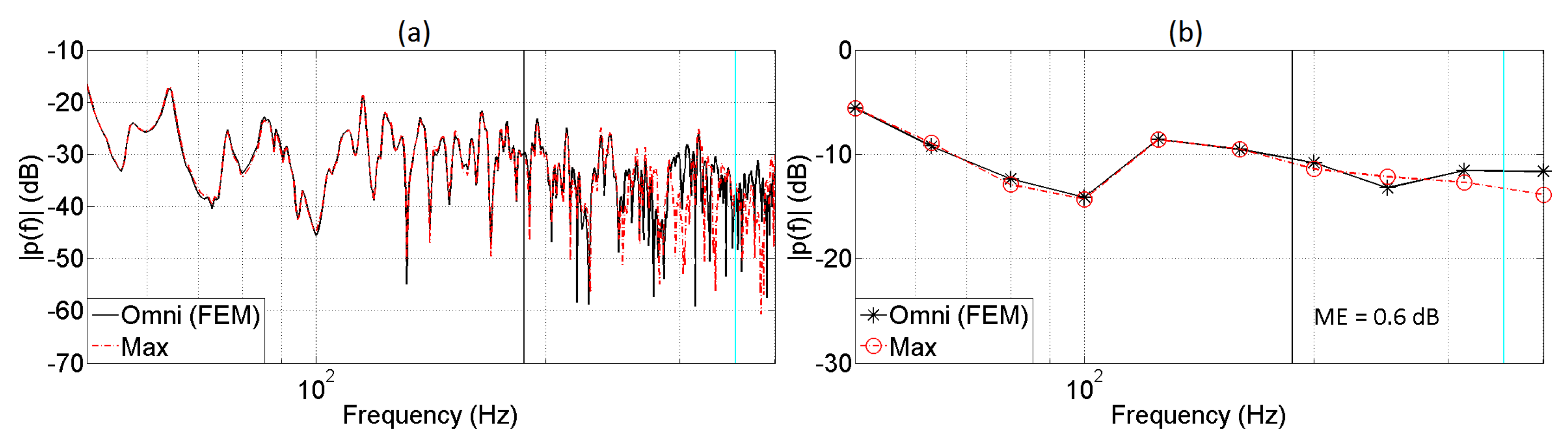

| Length of the Array | |||
|---|---|---|---|
| 1.2 m (343 mics) | |||
| 1.6 m (729 mics) | |||
| 2 m (1331 mics) | |||
| 2.4 m (2197 mics) |
| Receiver | Distance (m) | Frequency (Hz) | ME (dB) |
|---|---|---|---|
| 2 | 0.5 | ≈562 | 1.5 |
| 3 | 0.5 | ≈562 | 1.7 |
| 4 | 1 | ≈281 | 1.9 |
| 5 | 1.5 | ≈187 | 2.0 |
| Receiver | W (dB) | X (dB) | Y (dB) | Z (dB) | Average (dB) |
|---|---|---|---|---|---|
| 2 (0.5 m) | 0.6 | 1.0 | 1.5 | 1.3 | 1.1 |
| 5 (1.5 m) | 1.2 | 1.9 | 2.0 | 1.5 | 1.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, D.M.M.; Astley, J.; Fazi, F.M. Low Frequency Interactive Auralization Based on a Plane Wave Expansion. Appl. Sci. 2017, 7, 558. https://doi.org/10.3390/app7060558
Gómez DMM, Astley J, Fazi FM. Low Frequency Interactive Auralization Based on a Plane Wave Expansion. Applied Sciences. 2017; 7(6):558. https://doi.org/10.3390/app7060558
Chicago/Turabian StyleGómez, Diego Mauricio Murillo, Jeremy Astley, and Filippo Maria Fazi. 2017. "Low Frequency Interactive Auralization Based on a Plane Wave Expansion" Applied Sciences 7, no. 6: 558. https://doi.org/10.3390/app7060558
APA StyleGómez, D. M. M., Astley, J., & Fazi, F. M. (2017). Low Frequency Interactive Auralization Based on a Plane Wave Expansion. Applied Sciences, 7(6), 558. https://doi.org/10.3390/app7060558






