Prediction of Maximum Story Drift of MDOF Structures under Simulated Wind Loads Using Artificial Neural Networks
Abstract
:1. Introduction
2. Theoretical Framework
2.1. Network Training
Calculation of Jacobian Matrix
- Calculate the forward computation with initial weights (randomly generated).
- weights with Equation (22).
- the current total error. If the current total error is increased, then reset the weights to the previous values and increase by a factor of 10. Then, go to Step 2. Otherwise, keep the new weights and decrease by a factor of 10.
- Go to Step 2 until the current total error is smaller than the required value.
2.2. Wind Simulation
Cross-Spectral Density Matrix
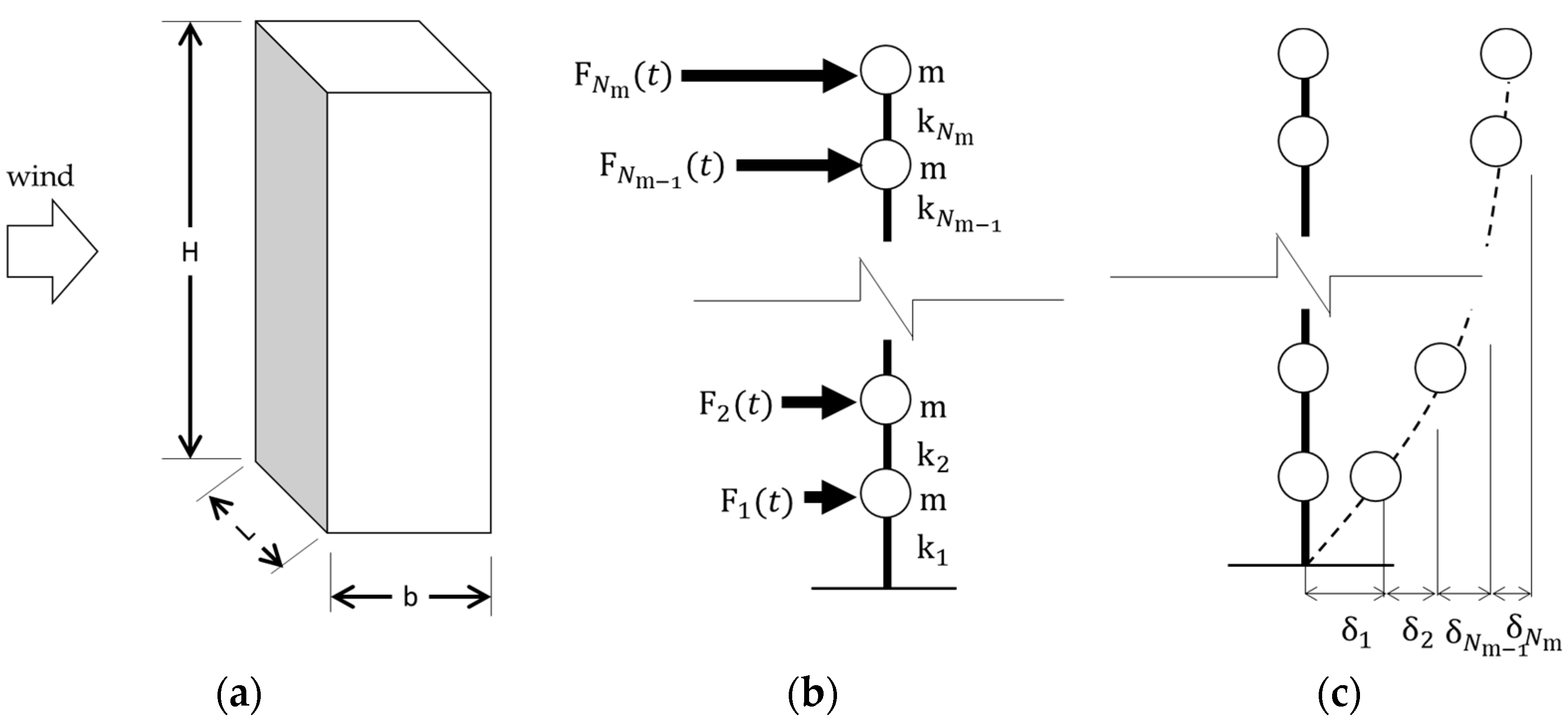
2.3. Dynamic Response
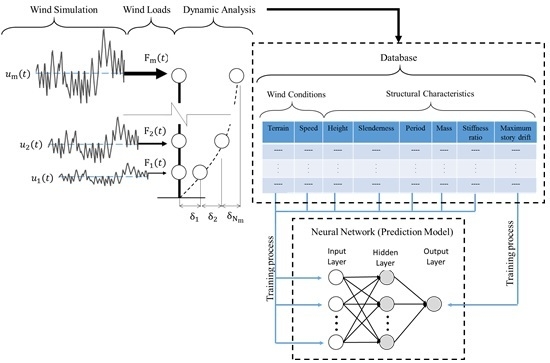
3. Application of Theoretical Framework
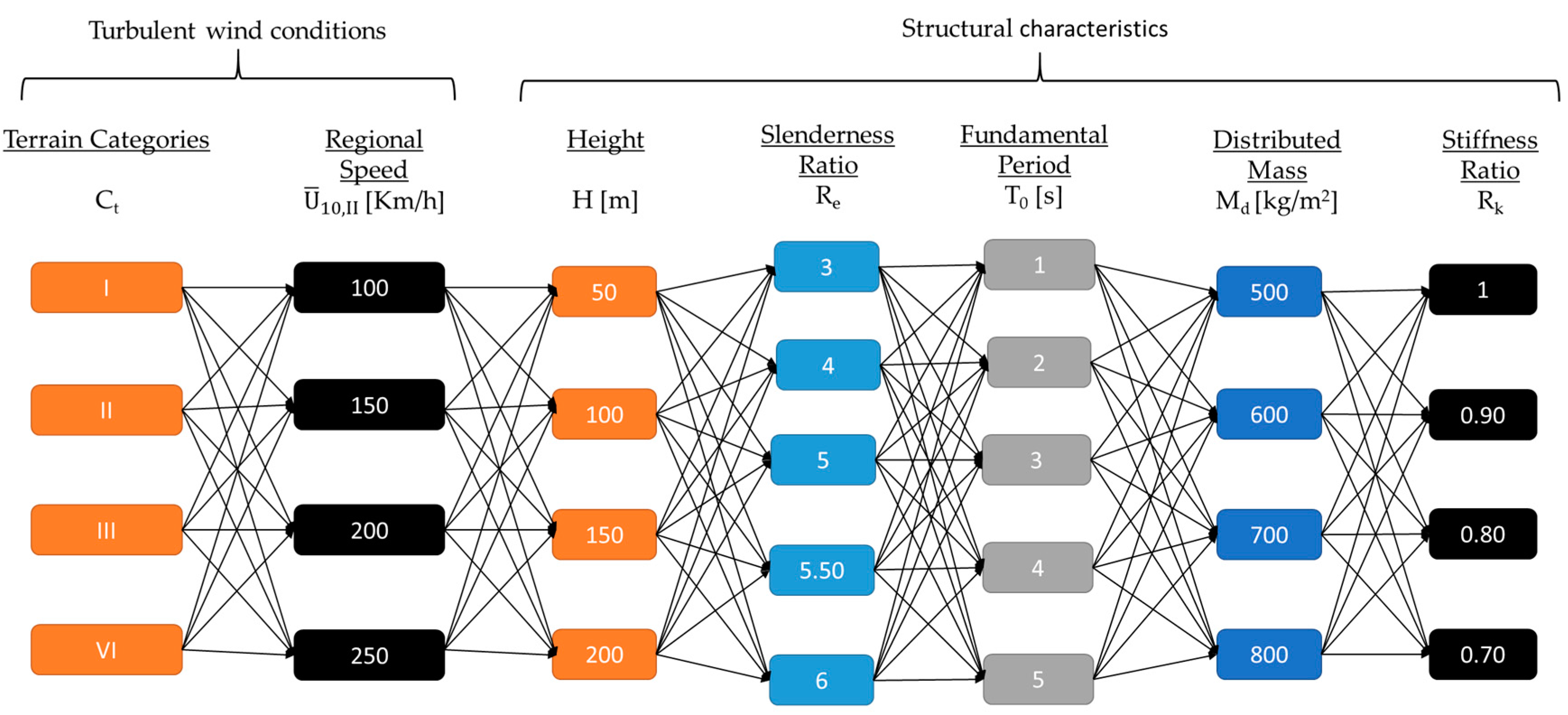
3.1. Data Generation
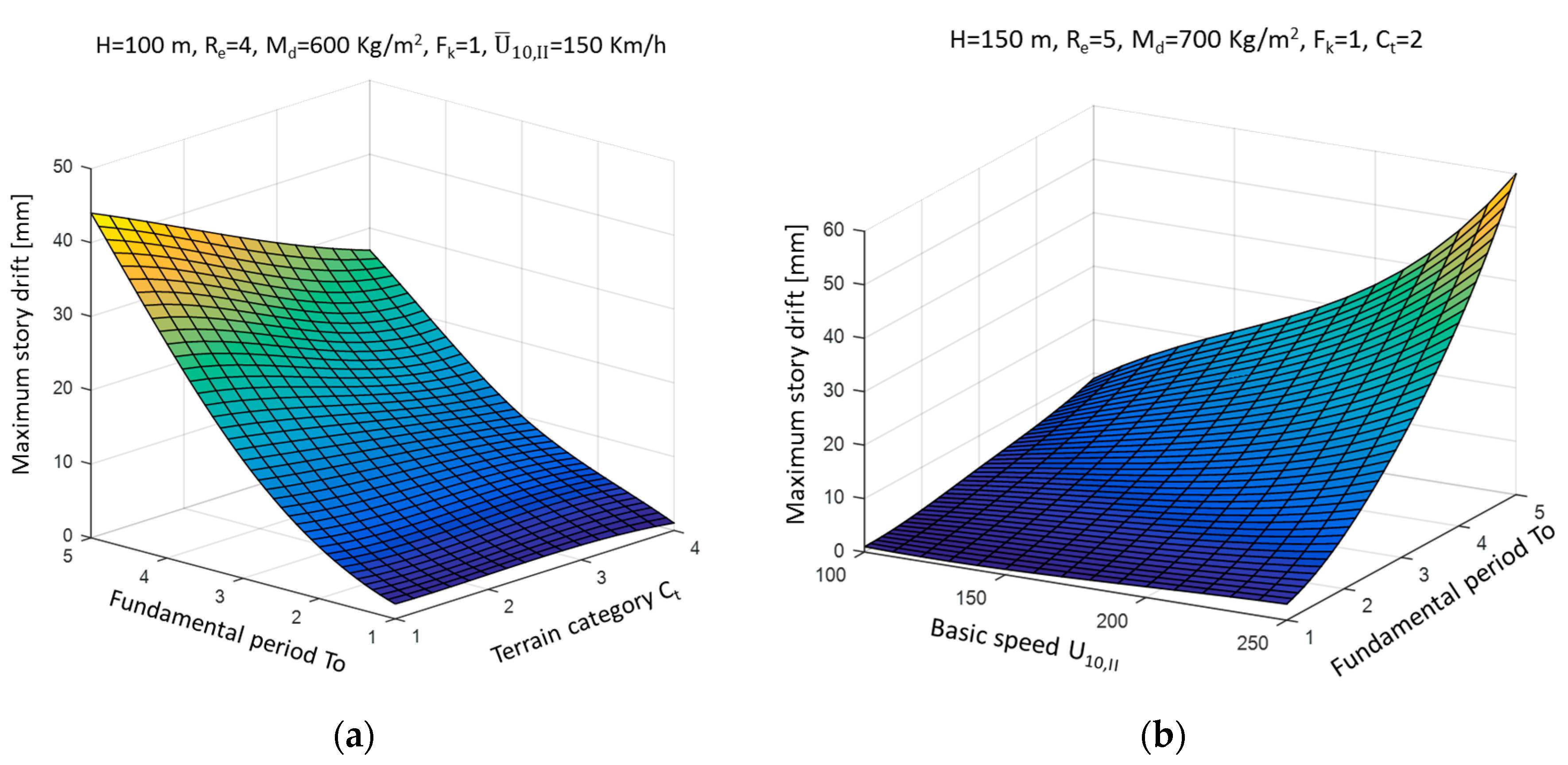
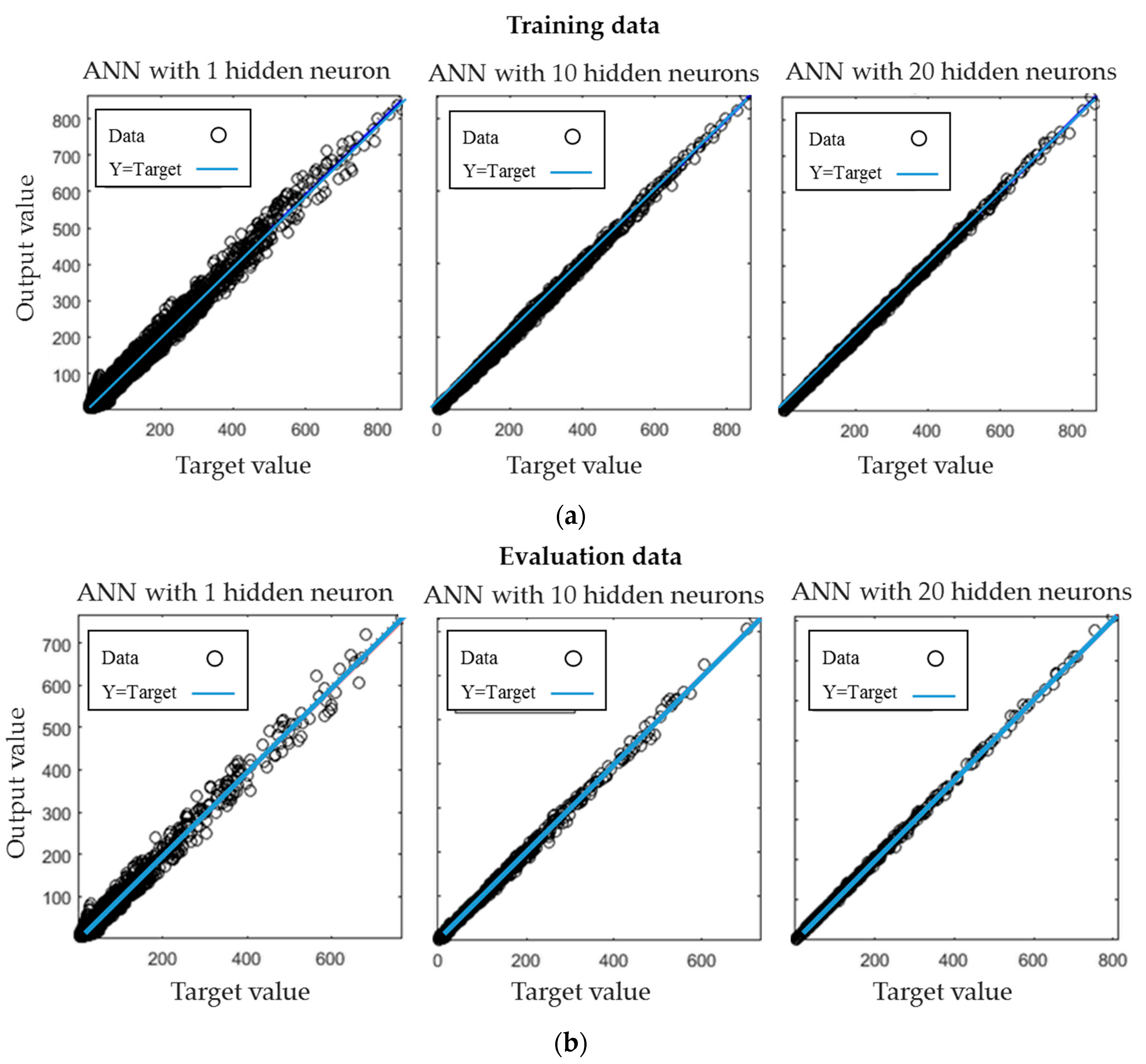
3.2. Results of Network Trainings
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Veers, P.S. Three-Dimensional Wind Simulation; Sandia National Labs: Albuquerque, NM, USA, 1988. [Google Scholar]
- Chay, M.T.; Albermani, F.; Wilson, R. Numerical and analytical simulation of downburst wind loads. Eng. Struct. 2006, 28, 240–254. [Google Scholar] [CrossRef]
- Bojórquez, E.; Payán-Serrano, O.; Reyes-Salazar, A.; Pozos, A. Comparison of spectral density models to simulate wind records. KSCE J. Civ. Eng. 2016, 1, 1–8. [Google Scholar] [CrossRef]
- Davenport, A.G. Gust loading factors. J. Struct. Div. 1967, 93, 11–34. [Google Scholar] [CrossRef]
- Davenport, A.G. The representation of the dynamic effects of turbulent wind by equivalent static wind loads. Proceedings of International Symposium on Structural Steel, Chicago, IL, USA, 1985; pp. 1–13. [Google Scholar]
- Chen, X.; Kareem, A. Equivalent static wind loads on buildings: New model. J. Struct. Eng. 2004, 130, 1425–1435. [Google Scholar] [CrossRef]
- Repetto, M.P.; Solari, G. Equivalent static wind actions on vertical structures. J. Wind Eng. Ind. Aerodyn. 2004, 92, 335–357. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Neurocomputer applications. Neural Comput. 1989, 41, 445–453. [Google Scholar] [CrossRef]
- Conte, J.P.; Durrani, A.J. Seismic Response modeling of multi-story buildings using neural networks. J. Intell. Mater. Syst. Struct. 1994, 5, 392–402. [Google Scholar] [CrossRef]
- Chakraverty, S.; Gupta, P.; Sharma, S. Neural network-based simulation for response identification of two-storey shear building subject to earthquake motion. Neural Comput. Appl. 2010, 19, 367–375. [Google Scholar] [CrossRef]
- Bojórquez, J.; Ruiz, S.; Bojórquez, E.; Reyes-Salazar, A. Probabilistic seismic response transformation factors between SDOF and MDOF systems using artificial neural networks. J. Vibroeng. 2016, 18, 2248–2262. [Google Scholar] [CrossRef]
- Roy, D.; Dash, M.K. Explorations of a family of stochastic Newmark methods in engineering dynamics. Comput. Methods Appl. Mech. Eng. 2005, 194, 4758–4796. [Google Scholar] [CrossRef]
- Krenk, S. Energy conservation in Newmark based time integration algorithms. Comput. Methods Appl. Mech. Eng. 2006, 195, 6110–6124. [Google Scholar] [CrossRef]
- Bourihane, O.; Braikat, B. Dynamic analysis of a thin-walled beam with open cross section subjected to dynamic loads using a high-order implicit algorithm. Eng. Struct. 2016, 120, 133–146. [Google Scholar] [CrossRef]
- Shinozuka, M.; Jam, C.M. Digital simulation of random processes and its applications. J. Sound Vib. 1972, 25, 111–128. [Google Scholar] [CrossRef]
- Rossi, R.; Lazzari, M.; Vitaliani, R. Wind field simulation for structural engineering purposes. Int. J. Num. Method Eng. 2004, 61, 738–763. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain problems in least squares. Q. Appl. Math. 1944, 5, 164–168. [Google Scholar] [CrossRef]
- Suratgar, A.A.; Tavakoli, M.B.; Hoseinabadi, A. Modified Levenberg–Marquardt method for neural networks training. World Acad. Sci. Eng. Technol. 2005, 6, 46–48. [Google Scholar]
- Davenport, A.G. The spectrum of horizontal gustiness near the ground in high winds. Q. J. R. Meteorol. Soc. 1961, 87, 194–211. [Google Scholar] [CrossRef]
- Mackey, S. Gust Factors. In Proceedings of the Seminar USA-Japan Research Seminar: Wind Loads on Structures; University of Hawaii: Honolulu, HI, USA, 1970; pp. 191–202. [Google Scholar]
- Counihan, J. Adiabatic atmospheric boundary layers: A review and analysis of data from the period from 1880–1972. Atmos. Environ. 1967, 9, 871–905. [Google Scholar] [CrossRef]
- Hirt, M.A. Eurocode 1. Basis of design and action on structures Part 1–4. Schweizer Ingenieur Architekt 1993, 16–17, 273–275. [Google Scholar]
- Von Karman, T. Progress in the statistical theory of turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Harris, R.I. On the Spectrum and Auto-correlation Function of Gustiness in High Winds; Electrical Research Association: Leatherhead, UK, 1968. [Google Scholar]
- Lungu, D.; van Gelder, P. Characteristics of wind turbulence with applications to wind codes. In Proceedings of the 2nd European & African Conference on Wind Engineering, Genova, Italy, 22–26 June 1997; pp. 1271–1277. [Google Scholar]
- Xu, Y.L. Wind Effects on Cable-Supported Bridges; John Wiley and Sons: New York, NY, USA, 2013. [Google Scholar]
- McKenna, F.; Fenves, G.L.; Scott, M. Open System for Earthquake Engineering Simulation (OpenSees); University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Carr, A.J. RUAUMOKO-2D Inelastic Time-History Analysis of Two Dimensional Framed Structures; Department of Civil Engineering, University of Canterbury: Christchurch, New Zealand, 2004. [Google Scholar]
- Computer and Structure, Inc. SAP2000 Documentation, Release 15.1.0; University Ave: Berkeley, CA, USA, 2012. [Google Scholar]
- Chopra, A. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Holmes, J.D. Wind Loading of Structures; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]




| Terrain Category | (m) | |
|---|---|---|
| I—Lakes or flat and horizontal area with negligible vegetation and without obstacles | 0.01 | 1.17 |
| II—Area with low vegetation such as grass and isolated obstacles (trees, buildings) with separations of at least 20 obstacle heights | 0.05 | 1.00 |
| III—Area with regular cover of vegetation or buildings or with isolated obstacles with separations of maximum 20 obstacle heights (such as villages, suburban terrain, permanent forest) | 0.30 | 0.77 |
| IV—Area in which at least 15% of the surface is covered with buildings and their average height exceeds 15 m | 1.00 | 0.55 |
| Step-by-step procedure: |
|---|
| Initial calculations: |
| 1.1 |
| 1.2 |
| Calculations for each time step |
| 2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
| 2.5 |
| 2.6 |
| 2.7 |
| Repetition for the next time step. Replace by and implement Steps 2.1 and 2.7 for the next time step. |
| Hidden Neurons | Training Data | Evaluation Data | Training Iterations | MSE Training Data | MSE Evaluation Data |
|---|---|---|---|---|---|
| 1 | 21,760 | 3840 | 1000 | 101.72 | 108.96 |
| 2 | 21,760 | 3840 | 1000 | 65.48 | 62.96 |
| 5 | 21,760 | 3840 | 1000 | 23.92 | 29.22 |
| 10 | 21,760 | 3840 | 1000 | 8.89 | 9.06 |
| 12 | 21,760 | 3840 | 1000 | 5.73 | 5.88 |
| 20 | 21,760 | 3840 | 1000 | 2.59 | 2.91 |
| 30 | 21,760 | 3840 | 1000 | 2.05 | 2.21 |
| Validation Iterations | MSE Training Data | MSE Evaluation Data |
|---|---|---|
| Iteration 1 | 3.51 | 3.71 |
| Iteration 2 | 2.86 | 2.94 |
| Iteration 3 | 2.24 | 3.01 |
| Iteration 4 | 2.58 | 2.82 |
| Iteration 5 | 3.99 | 3.65 |
| Iteration 6 | 3.42 | 3.58 |
| Iteration 7 | 2.79 | 2.74 |
| Iteration 8 | 3.21 | 3.31 |
| Iteration 9 | 2.49 | 2.58 |
| Iteration 10 | 2.73 | 3.00 |
| Procedure | Phase | Memory (MB) | Computer Time (s) |
|---|---|---|---|
| Standard | Wind Simulation | 6850 | 386.41 |
| Calculate stiffness matrix | 13 | 5.93 | |
| Dynamic analyse | 29 | 24.07 | |
| ANN with 20 hidden neurons | Trainging | 424 | 934.15 |
| Execute | 0.01 | 0.001 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Payán-Serrano, O.; Bojórquez, E.; Bojórquez, J.; Chávez, R.; Reyes-Salazar, A.; Barraza, M.; López-Barraza, A.; Rodríguez-Lozoya, H.; Corona, E. Prediction of Maximum Story Drift of MDOF Structures under Simulated Wind Loads Using Artificial Neural Networks. Appl. Sci. 2017, 7, 563. https://doi.org/10.3390/app7060563
Payán-Serrano O, Bojórquez E, Bojórquez J, Chávez R, Reyes-Salazar A, Barraza M, López-Barraza A, Rodríguez-Lozoya H, Corona E. Prediction of Maximum Story Drift of MDOF Structures under Simulated Wind Loads Using Artificial Neural Networks. Applied Sciences. 2017; 7(6):563. https://doi.org/10.3390/app7060563
Chicago/Turabian StylePayán-Serrano, Omar, Edén Bojórquez, Juan Bojórquez, Robespierre Chávez, Alfredo Reyes-Salazar, Manuel Barraza, Arturo López-Barraza, Héctor Rodríguez-Lozoya, and Edgar Corona. 2017. "Prediction of Maximum Story Drift of MDOF Structures under Simulated Wind Loads Using Artificial Neural Networks" Applied Sciences 7, no. 6: 563. https://doi.org/10.3390/app7060563
APA StylePayán-Serrano, O., Bojórquez, E., Bojórquez, J., Chávez, R., Reyes-Salazar, A., Barraza, M., López-Barraza, A., Rodríguez-Lozoya, H., & Corona, E. (2017). Prediction of Maximum Story Drift of MDOF Structures under Simulated Wind Loads Using Artificial Neural Networks. Applied Sciences, 7(6), 563. https://doi.org/10.3390/app7060563