Computational Vibroacoustics in Low- and Medium- Frequency Bands: Damping, ROM, and UQ Modeling
Abstract
:1. Introduction
- Statement of the problem in the frequency domain.
- External inviscid acoustic fluid equations in the frequency domain and acoustic impedance boundary operator.
- Internal dissipative acoustic fluid equations in the frequency domain.
- Structure equations with frequency-dependent constitutive equation.
- Boundary value problem in terms of the structural displacement and the internal pressure field.
- Vibroacoustic computational model.
- Reduced-order vibroacoustic computational model.
- Uncertainty quantification for the vibroacoustic computational model.
- Experimental validation with a complex computational vibroacoustic model of an automobile.
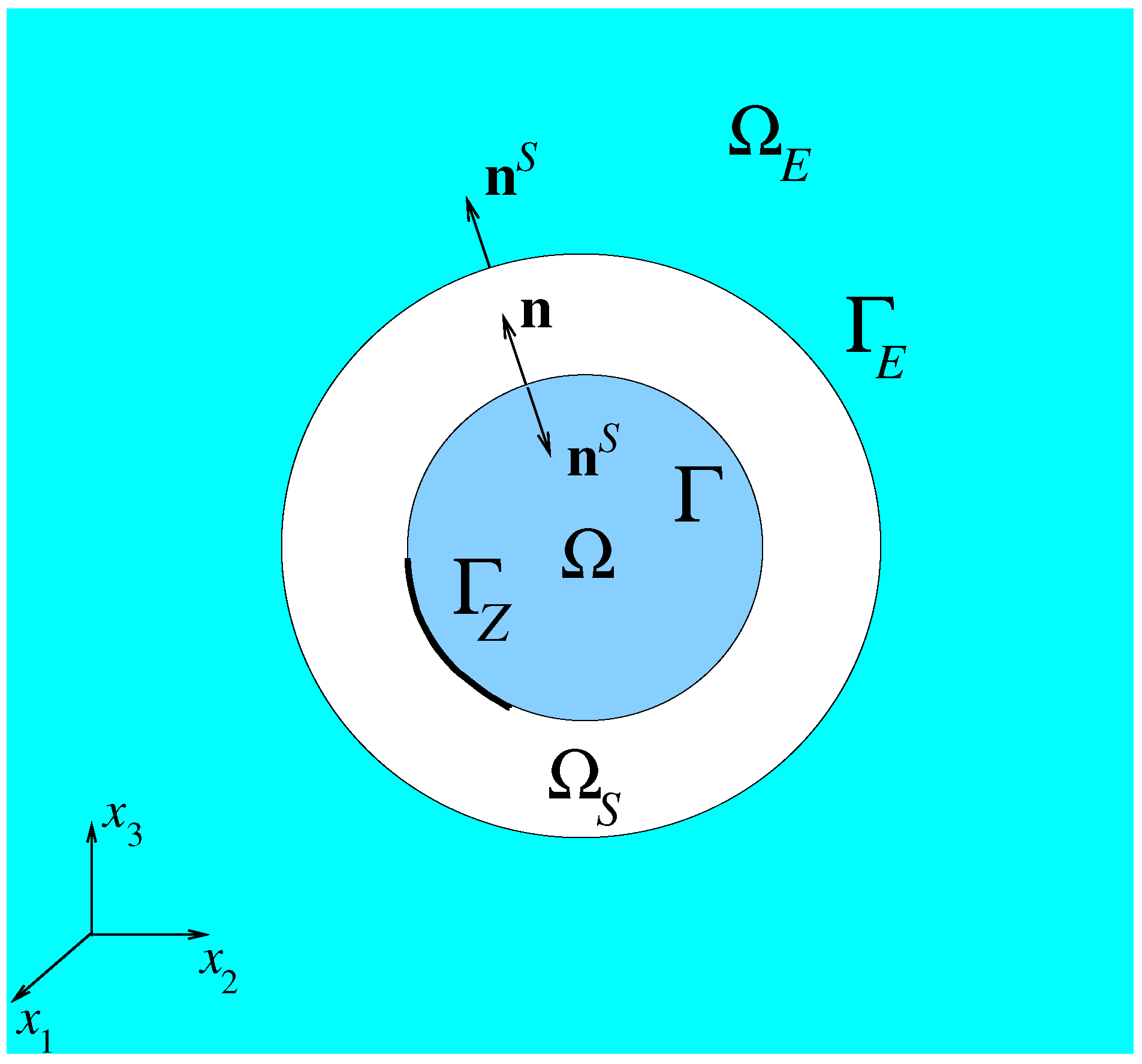
2. Statement of the Problem in the Frequency Domain
3. External Inviscid Acoustic Fluid Equations in the Frequency Domain and Acoustic Impedance Boundary Operator
4. Internal Dissipative Acoustic Fluid Equations in the Frequency Domain
4.1. Internal Dissipative Acoustic Fluid Equations
4.2. Boundary Conditions
4.3. Case of a Free Surface for a Liquid
5. Structure Equations with Frequency-Dependent Constitutive Equation
Structure Equations in the Frequency Domain
6. Boundary Value Problem in Terms of
- It is important to note that the external acoustic pressure field has been eliminated as a function of using the acoustic impedance boundary operator (see Equation (4) of Section 3 and Appendix B), while the internal acoustic pressure field p is kept.
7. Vibroacoustic Computational Model
7.1. Matrix Equation of the Computational Model
7.2. Construction of the Matrices of the Computational Model
7.2.1. Matrices Related to the Equations of the Structure
- Symmetric real mass matrix is positive definite, and corresponds to .
- Symmetric real damping matrix is positive semidefinite with a kernel of dimension 6, and corresponds to .
- Symmetric real stiffness matrix is positive semidefinite with a kernel of dimension 6, and corresponds to .
7.2.2. Matrices Related to the Equations of the Internal Acoustic Fluid
- Symmetric real matrix is positive semidefinite with a kernel of dimension 1, and corresponds to . In the case of a free surface in the internal acoustic cavity (see Section 4.3), the boundary condition defined by Equation (10) is added, and consequently, the corresponding matrix is positive definite.
- Symmetric real matrix is positive definite, and corresponds to .
- Symmetric complex matrix comes from , in which is a complex-valued function and where is the elementary surface area.
7.2.3. Matrices Related to the Coupling Terms
- Rectangular real matrix corresponds to .
7.2.4. Vector of Mechanical and Acoustical Excitations
- Complex vector of external forces corresponds to .
- Complex vector of internal acoustic sources corresponds to .
8. Reduced-Order Vibroacoustic Computational Model
- Projection basis for the structure.
- -
- If the internal acoustic fluid is a gas, the projection basis can be chosen as the undamped elastic structural modes of the structure in vacuo for which the constitutive equation corresponds to elastic materials (see Equation (A5)), and consequently, the stiffness matrix has to be constructed for .
- -
- If the internal acoustic fluid is a liquid (with or without free surface), for the structure, the projection basis can constructed as for a gas but by taking into account the effects of liquid’s added mass.
- Projection basis for the internal acoustic fluid.
- -
- We consider the undamped acoustic modes of an internal acoustic cavity with fixed boundary (and rigid wall) and without wall acoustic impedance. Two cases must be considered: one for which the internal pressure varies with a variation of the volume of the cavity (a cavity with a sealed wall called a closed cavity), and the other one for which the internal pressure does not vary with the variation of the volume of the cavity (a cavity with a non-sealed wall, called an almost-closed cavity).
8.1. Computation of the Projection Basis for the Structure
8.1.1. Case of a Weak Coupling of the Structure with the Internal Acoustic Fluid
8.1.2. Case of a Strong Coupling of the Structure with the Internal Acoustic Fluid
8.2. Computation of the Projection Basis for the Internal Acoustic Fluid
8.2.1. Case of a Gas or a Liquid without Free Surface
- Closed (sealed wall) acoustic cavity. Let be . We introduce the real matrix of the constant eigenvector and of the acoustic modes associated with the first strictly positive eigenvalues,
- Almost-closed (non-sealed wall) acoustic cavity. Let be . We introduce the real matrix of the N acoustic modes associated with the first N strictly positive eigenvalues,
8.2.2. Case of a Liquid with a Free Surface
8.3. Construction of the Reduced-Order Computational Model
9. Uncertainty Quantification for the Vibroacoustic Computational Model
9.1. Preliminary Results for the Stochastic Modeling of the Random Matrices for the Stochastic Reduced-Order Computational Vibroacoustic Model
9.1.1. Ensemble of Random Matrices
- the family of the random entries are independent random variables;
- for , the real-valued random variable is written as in which and where is a real-valued Gaussian random variable with zero mean and variance equal to 1;
- for , the positive-valued random variable is written as in which is a positive-valued Gamma random variable with probability density function in which .
9.1.2. Ensemble of Random Matrices
9.1.3. Cases of Several Random Matrices
9.2. Stochastic Modeling of Random Matrix
9.3. Stochastic Modeling of the Family of Random Matrices Indexed by
- (i)
- For , the construction of the stochastic model of the family of random matrices is carried out as follows:
- Constructing the family of random matrices such thatwhere is such thatand where is a random matrix belonging to ensemble , defined in Section 9.1.2. Its probability distribution and its generator of independent realizations depend only on dimension and on the dispersion parameter that allows the level of uncertainties to be controlled.
- Constructing the family of random matrices using the equation(in which p.v means the Cauchy principal value that is defined in Equation (83)) or equivalently, using the two following equations that are useful for computation:
- Constructing the random matrix such thatin which the deterministic matrix is such thatThe random matrix is a random matrix belonging to ensemble defined in Section 9.1.2 whose probability distribution and generator of independent realizations depend only on dimension and on the dispersion parameter that allows the level of uncertainties to be controlled. Note that random matrix is independent of random matrix .
- Computing the random matrix such that
- Defining the random matrix such that
- Constructing the random matrix such thatIt must be verified that is effectively positive definite. In [101], the following sufficient condition is proven in order for to be a positive-definite random matrix for all : if for all real vector , the random function is decreasing on , then for all , is a positive-definite random matrix.
- (ii)
- For , the family is deduced from the family by using Equation (78).
- (iii)
- A numerical procedure for computing the integrals in Cauchy principal value can be found in [103].
9.4. Stochastic Modeling of Random Matrix
9.5. Stochastic Modeling of Random Matrix
- Closed (sealed wall) acoustic cavity. In such a case, the symmetric positive matrix is of rank and can then be written asin which is a rectangular real matrix. Using the nonparametric probabilistic approach of uncertainties, the stochastic model of the positive symmetric random matrix of rank is then defined [75,91] bywhere is a random matrix belonging to ensemble defined in Section 9.1.2 whose probability distribution and generator of independent realizations depend only on dimension and on the dispersion parameter .
- Almost-closed (non-sealed wall) acoustic cavity or internal liquid with a free surface. Matrix is positive definite and thus invertible. Consequently, it can be written asin which is an upper triangular real matrix. Using the nonparametric probabilistic approach of uncertainties, the stochastic model of this positive symmetric random matrix yieldswhere is a random matrix belonging to ensemble defined in Section 9.1.2 whose probability distribution and generator of independent realizations depend only on dimension N and on the dispersion parameter .
9.6. Stochastic Modeling of Random Matrix
9.7. Hyperparameter of the Stochastic Reduced-Order Model (SROM) and Stochastic Solver
- it is a non-intrusive method,
- it is adapted to massively parallel computation without any software developments,
- it is such that its convergence can be controlled during the computation,
- the speed of convergence is independent of the dimension.
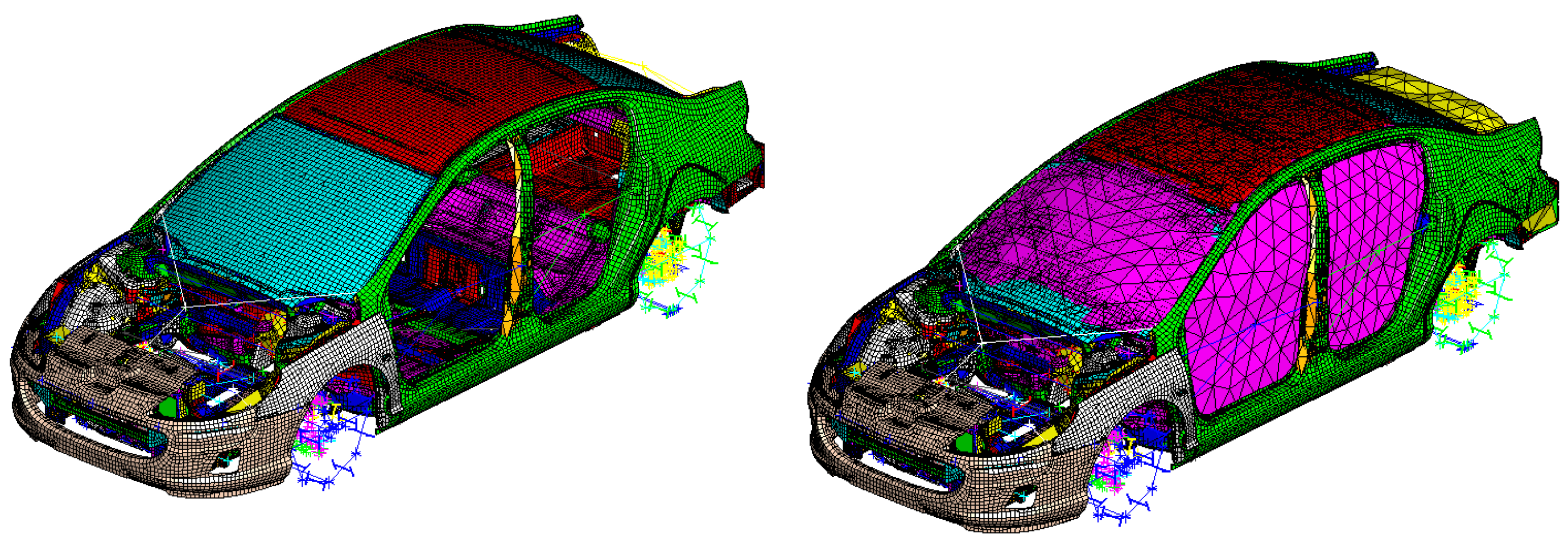
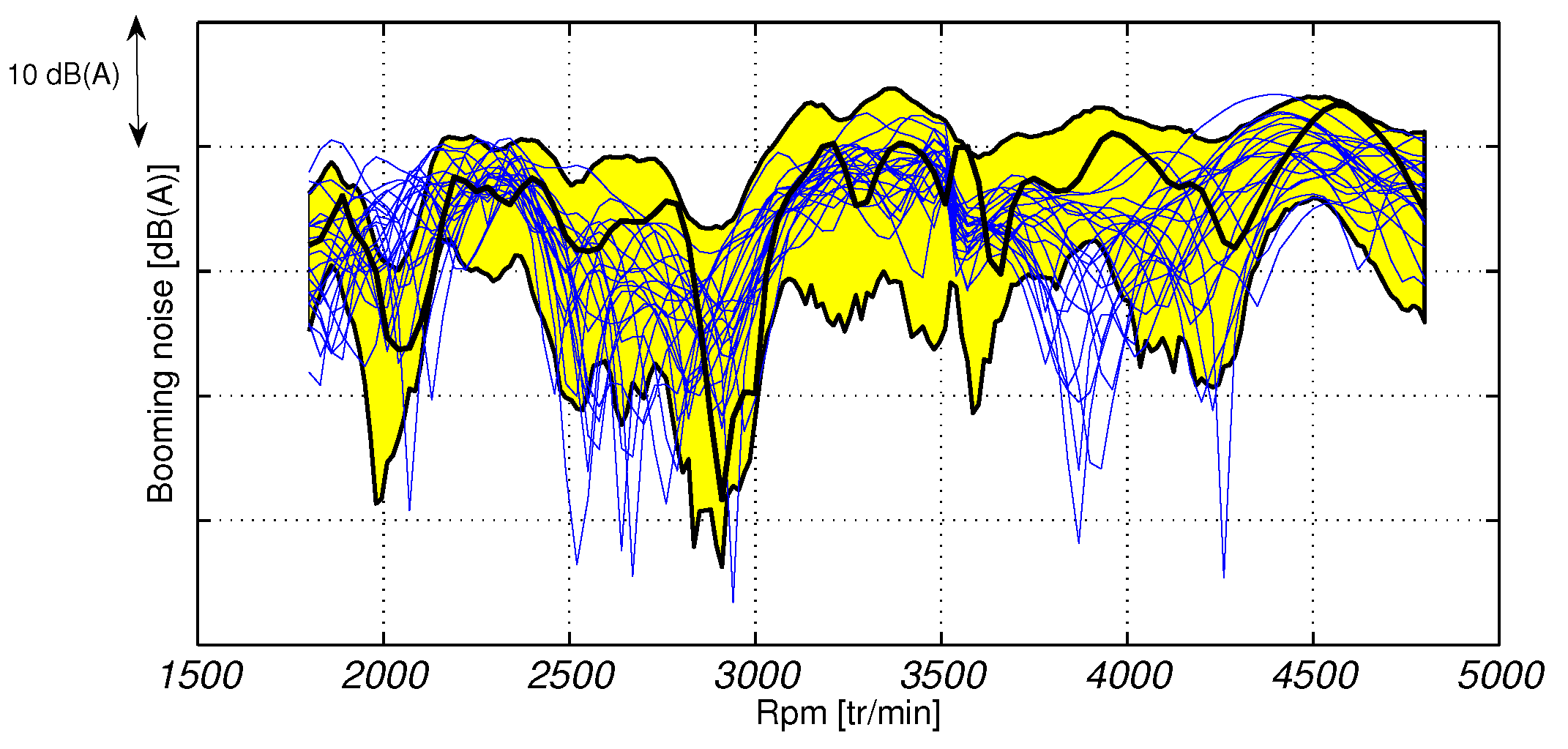
10. Experimental Validation with a Complex Computational Vibroacoustic Model of an Automobile
11. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| BEM | Boundary Element Method |
| DOF | Degree of Freedom |
| FEM | Finite Element Method |
| FRF | Frequency Response Function |
| FSI | Fluid–Structure Interaction |
| LF | Low Frequency |
| MF | Medium Frequency |
| ROM | Reduced-Order Model |
| SROM | Stochastic Reduced-Order Model |
| UQ | Uncertainty Quantification |
| elastic coefficients of the structure | |
| damping coefficients of the structure | |
| speed of sound in the internal acoustic fluid | |
| speed of sound in the external acoustic fluid | |
| vector of the generalized forces for the internal acoustic fluid | |
| vector of the generalized forces for the structure | |
| mechanical body force field in the structure | |
| i | imaginary complex number i |
| k | wave number in the external acoustic fluid |
| n | number of internal acoustic DOF |
| number of structural DOF | |
| component of vector | |
| outward unit normal to | |
| component of vector | |
| outward unit normal to | |
| p | internal acoustic pressure field |
| external acoustic pressure field | |
| value of the external acoustic pressure field on | |
| given external acoustic pressure field | |
| value of the given external acoustic pressure field on | |
| vector of the generalized coordinates for the internal acoustic fluid | |
| vector of the generalized coordinates for the structure | |
| component of the damping stress tensor in the structure | |
| t | time |
| structural displacement field | |
| internal acoustic velocity field | |
| coordinate of point | |
| generic point of | |
| reduced dynamical matrix for the internal acoustic fluid | |
| random reduced dynamical matrix for the internal acoustic fluid | |
| dynamical matrix for the internal acoustic fluid | |
| reduced matrix of the impedance boundary operator for the external acoustic fluid | |
| matrix of the impedance boundary operator for the external acoustic fluid | |
| reduced dynamical matrix for the fluid-structure coupled system | |
| random reduced dynamical matrix for the fluid-structure coupled system | |
| dynamical matrix for the fluid-structure coupled system | |
| reduced dynamical matrix for the structure | |
| random reduced dynamical matrix for the structure | |
| dynamical matrix for the structure | |
| reduced dynamical matrix associated with the wall acoustic impedance | |
| dynamical matrix associated with the wall acoustic impedance | |
| reduced coupling matrix between the internal acoustic fluid and the structure | |
| random reduced coupling matrix between the internal acoustic fluid and the structure | |
| coupling matrix between the internal acoustic fluid and the structure | |
| reduced damping matrix for the internal acoustic fluid | |
| random reduced damping matrix for the internal acoustic fluid | |
| damping matrix for the internal acoustic fluid | |
| reduced damping matrix for the structure | |
| random reduced damping matrix for the structure | |
| damping matrix for the structure | |
| DOF | degrees of freedom |
| vector of discretized acoustic forces | |
| vector of discretized structural forces | |
| initial elasticity tensor for viscoelastic material | |
| relaxation functions for viscoelastic material | |
| mechanical surface force field on | |
| random matrix | |
| random matrix | |
| reduced “stiffness” matrix for the internal acoustic fluid | |
| random reduced “stiffness” matrix for the internal acoustic fluid | |
| “stiffness” matrix for the internal acoustic fluid | |
| reduced stiffness matrix for the structure | |
| random reduced stiffness matrix for the structure | |
| stiffness matrix for the structure | |
| reduced “mass” matrix for the internal acoustic fluid | |
| random reduced “mass” matrix for the internal acoustic fluid | |
| “mass” matrix for the internal acoustic fluid | |
| reduced mass matrix for the structure | |
| random reduced mass matrix for the structure | |
| mass matrix for the structure | |
| internal acoustic mode | |
| matrix of internal acoustic modes | |
| Q | internal acoustic source density |
| external acoustic source density | |
| random vector of the generalized coordinates for the internal acoustic fluid | |
| random vector of the generalized coordinates for the structure | |
| random vector of internal acoustic pressure DOF | |
| vector of internal acoustic pressure DOF | |
| random vector of structural displacement DOF | |
| vector of structural displacement DOF | |
| elastic structural mode | |
| matrix of elastic structural modes | |
| Z | wall acoustic impedance |
| impedance boundary operator for external acoustic fluid | |
| dispersion parameter | |
| component of the strain tensor in the structure | |
| circular frequency in rad/s | |
| mass density of the internal acoustic fluid | |
| mass density of the external acoustic fluid | |
| mass density of the structure | |
| stress tensor in the structure | |
| component of the stress tensor in the structure | |
| component of the elastic stress tensor in the structure | |
| damping coefficient for the internal acoustic fluid | |
| boundary of | |
| boundary of equal to | |
| boundary of | |
| coupling interface between the structure and the internal acoustic fluid | |
| coupling interface between the structure and the external acoustic fluid | |
| coupling interface between the structure and the internal acoustic fluid with acoustic properties | |
| internal acoustic fluid domain | |
| external acoustic domain | |
| structural domain |
Appendix A. Frequency-Dependent Constitutive Equation for the Dissipative Structure
Appendix A.1. Linear Viscoelastic Constitutive Equation in the Frequency Domain
Appendix A.2. Compatibility Equation between a ijkh and b ijkh
Appendix A.3. Construction of the Linear Viscoelastic Constitutive Equation in the Frequency Domain
- (i) Particular case. A family of linear viscoelastic constitutive equations can be constructed in the time domain using linear differential equations in and . The associated frequency-dependent coefficients and automatically verified Equation (A12). In this framework, some examples for and can be found in the literature (e.g., [41,98,112,113,122,123,124,125,126,127]).
- (ii) General case. In the general case for which and are not derived from such an algebraic representation but correspond to a general integral operator in the time domain (e.g., constructed using experimental curves), a rigorous method of construction is proposed below to satisfy the causality principle.
- The given functions cannot be arbitrarily chosen, but must satisfy some hypotheses to ensure the coherence of the viscoelastic model:(1) For all fixed and , the tensor must be symmetric and positive definite.(2) For , Equation (A3) must hold, which means that functions decrease at infinity at least in with .(3) Functions that satisfy (1) and (2) are then extended to using the even property defined by Equation (A6).
- For all fixed and , the tensor must be symmetric and positive definite. For all , functions are then constructed using the following equation (see Equation (A12)),and are extended to using the even property.
- As seen above, for all fixed and , symmetric tensor must be positive definite. This property must then be checked at the end of the construction, and if it is not satisfied, functions must be modified. In [101], it has been shown that the following sufficient condition allows this property to be satisfied: if functions are decreasing functions for , then the property is verified.
Appendix A.4. Linear Dissipative Constitutive Equation for Modeling Damping Effects
- (1)
- For , function must decrease at infinity at least in in which .
- (2)
- Function is even, .
Appendix B. Boundary Element Method for the External Acoustic Fluid
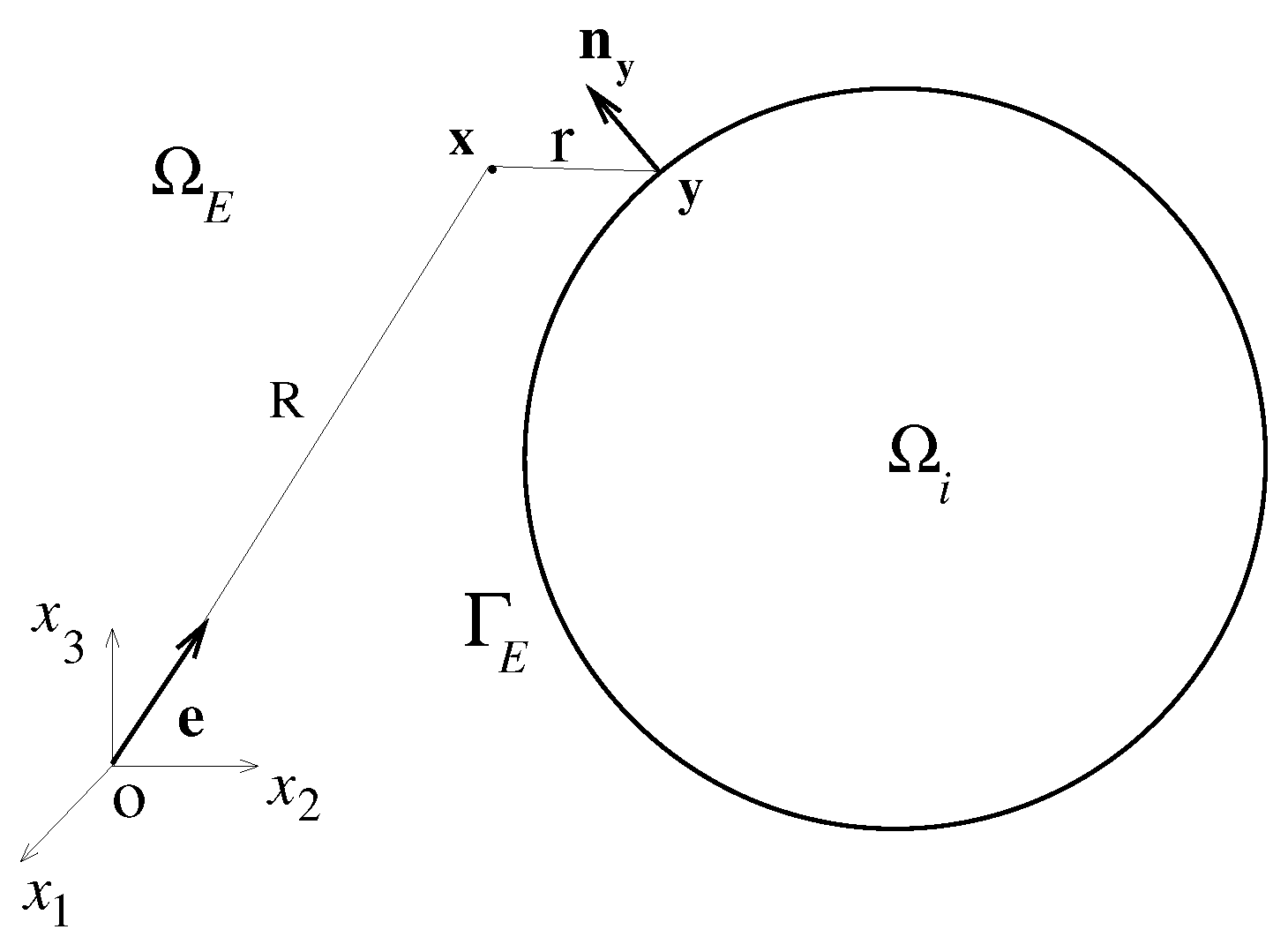
Appendix B.1. Exterior Neumann Boundary Value Problem Related to the Helmholtz Equation
Appendix B.2. Introduction of the Acoustic Impedance Boundary Operator and Radiation Impedance Operator
Appendix B.3. Algebraic Properties of the Acoustic Impedance Boundary Operator
Appendix B.4. Construction of the Acoustic Impedance Boundary Operator for All Real Values of the Frequency
Appendix B.5. Construction of the Radiation Impedance Operator
Appendix B.6. Symmetric Boundary Element Method without Spurious Frequencies
Appendix B.7. Acoustic Response to Prescribed Wall Displacement Field and Acoustic Source Density
Appendix B.8. Asymptotic Formula for the Radiated Pressure Far Field
References
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Lighthill, J. Waves in Fluids; Cambridge University Press: Boston, MA, USA, 1978. [Google Scholar]
- Cremer, L.; Heckl, M.; Ungar, E.E. Structure-Born Sound; Springer: Berlin, Germany, 1988. [Google Scholar]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; Originally Published in 1981, McGraw-Hill, New York, NY, USA; Acoustical Society of America Publications on Acoustics: Woodbury, NY, USA, 1989. [Google Scholar]
- Crighton, D.G.; Dowling, A.P.; Ffowcs-Williams, J.E.; Heckl, M.; Leppington, F.G. Modern Methods in Analytical Acoustics; Springer: Berlin, Germany, 1992. [Google Scholar]
- Landau, L.; Lifchitz, E. Fluid Mechanics; Pergamon Press: Oxford, UK, 1992. [Google Scholar]
- Junger, M.C.; Feit, D. Sound, Structures and Their Interaction; Originally Published in 1972, MIT Press, Cambridge, UK; Acoustical Society of America Publications on Acoustics: Woodbury, NY, USA, 1993. [Google Scholar]
- Blackstock, D.T. Fundamentals in Physical Acoustics; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Bruneau, M. Fundamentals of Acoustics; ISTE USA: Newport Beach, CA, USA, 2006. [Google Scholar]
- Fahy, F.J.; Gardonio, P. Sound and Structural Vibration, Second Edition: Radiation, Transmission and Response; Academic Press: Oxford, UK, 2007. [Google Scholar]
- Howe, M.S. Acoustics of Fluid-Structure Interactions; Cambridge Monographs on Mechanics, Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Bathe, K.J.; Wilson, E.L. Numerical Methods in Finite Element Analysis; Prentice-Hall: New York, NY, USA, 1976. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: New York, NY, USA, 2000. [Google Scholar]
- Fish, J.; Belytshko, T. A First Course in Finite Elements; John Wiley and Sons: Chichester, UK, 2007. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Fox, D.D. The Finite Element Method For Solid and Structural Mechanics, 7th ed.; Elsevier, Butterworth-Heinemann: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Geers, T.L.; Felippa, C.A. Doubly asymptotic approximations for vibration analysis of submerged structures. J. Acoust. Soc. Am. 1983, 173, 1152–1159. [Google Scholar] [CrossRef]
- Harari, I.; Hughes, T.J.R. Finite element methods for the Helmholtz equation in an exterior domain: Model problems. Comput. Methods Appl. Mech. Eng. 1991, 87, 59–96. [Google Scholar] [CrossRef]
- Givoli, D. Numerical Methods for Problems in Infinite Domains; Elsevier: Amsterdam, The Netherlands; London, UK; New York, NY, USA; Tokyo, Japan, 1992. [Google Scholar]
- Harari, I.; Grosh, K.; Hughes, T.J.R.; Malhotra, M.; Pinsky, P.M.; Stewart, J.R.; Thompson, L.L. Recent development in finite element methods for structural acoustics. Arch. Comput. Methods Eng. 1996, 3, 131–309. [Google Scholar] [CrossRef]
- Astley, R.J. Infinite elements for wave problems: A review of current formulations and assessment of accuracy. Int. J. Numer. Methods Eng. 2000, 49, 951–976. [Google Scholar] [CrossRef]
- Farhat, C.; Tezaur, R.; Toivanen, J. A domain decomposition method for discontinuous Galerkin discretizations of Helmholtz problems with plane waves and Lagrange multipliers. Int. J. Numer. Methods Eng. 2009, 78, 1513–1531. [Google Scholar] [CrossRef]
- Oden, J.T.; Prudhomme, S.; Demkowicz, L. A posteriori error estimation for acoustic wave propagation. Arch. Comput. Methods Eng. 2005, 12, 343–389. [Google Scholar] [CrossRef]
- Bergen, B.; van Genechten, B.; Vandepitte, D.; Desmet, W. An efficient Trefftz-based method for three-dimensional Helmholtz in unbounded domain. Comput. Model. Eng. Sci. 2010, 61, 155–175. [Google Scholar]
- Ihlenburg, F. Finite Element Analysis of Acoustic Scattering; Springer: New York, NY, USA, 2013. [Google Scholar]
- Farhat, C.; Harari, I.; Hetmaniuk, U. The discontinuous enrichment method for medium-frequency Helmholtz problems with a spatially variable wavenumber. Comput. Methods Appl. Mech. Eng. 2014, 268, 126–140. [Google Scholar]
- Costabel, M.; Stephan, E. A direct boundary integral equation method for transmission problems. J. Math. Anal. Appl. 1985, 106, 367–413. [Google Scholar] [CrossRef]
- Kress, R. Linear Integral Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Brebbia, C.A.; Dominguez, J. Boundary Elements: An Introductory Course; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Chen, G.; Zhou, J. Boundary Element Methods; Academic Press: New York, NY, USA, 1992. [Google Scholar]
- Colton, D.L.; Kress, R. Integral Equation Methods in Scattering Theory; Krieger Publishing Company: Malabar, FL, USA, 1992. [Google Scholar]
- Hackbusch, W. Integral Equations, Theory and Numerical Treatment; Birkhauser Verlag: Basel, Switzerland, 1995. [Google Scholar]
- Bonnet, M. Boundary Integral Equation Methods for Solids and Fluids; John Wiley: New York, NY, USA, 1999. [Google Scholar]
- Gaul, L.; Kögl, M.; Wagner, M. Boundary Element Methods for Engineers and Scientists; Springer: Heidelberg, Germany; New York, NY, USA, 2003. [Google Scholar]
- Schanz, M.; Steinbach, O.E. Boundary Element Analysis; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Hsiao, G.C.; Wendland, W.L. Boundary Integral Equations; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Sauter, S.A.; Schwab, C. Boundary Elements Methods; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Jones, D.S. Integral equations for the exterior acoustic problem. Q. J. Mech. Appl. Math. 1974, 1, 129–142. [Google Scholar] [CrossRef]
- Jones, D.S. Acoustic and Electromagnetic Waves; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Greengard, L.; Rokhlin, V. A fast algoritm for particle simulations. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
- Ohayon, R.; Soize, C. Structural Acoustics and Vibration; Academic Press: London, UK, 1998. [Google Scholar]
- Von Estorff, O.; Coyette, J.P.; Migeot, J.L. Governing formulations of the BEM in acoustics. In Boundary Elements in Acoustics—Advances and Applications; Von Estorff, O., Ed.; WIT Press: Southampton, UK, 2000; pp. 1–44. [Google Scholar]
- Nedelec, J.C. Acoustic and Electromagnetic Equations. Integral Representation for Harmonic Problems; Springer: New York, NY, USA, 2001. [Google Scholar]
- Gumerov, N.A.; Duraiswami, R. Fast Multipole Methods for the Helmholtz Equation in Three Dimension; Elsevier Ltd.: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Bonnet, M.; Chaillat, S.; Semblat, J.F. Multi-level fast multipole BEM for 3-D elastodynamics. In Recent Advances in Boundary Element Methods; Manomis, G.D., Polyzos, D., Eds.; Springer: Berlin, Germany, 2009; pp. 15–27. [Google Scholar]
- Brunner, D.; Junge, M.; Gaul, L. A comparison of FE-BE coupling schemes for large scale problems with fluid-structure interaction. Int. J. Numer. Methods Eng. 2009, 77, 664–688. [Google Scholar] [CrossRef]
- Lee, M.; Park, Y.S.; Park, Y.; Park, K.C. New approximations of external acoustic-structural interactions: Derivation and evaluation. Comput. Methods Appl. Mech. Eng. 2009, 198, 1368–1388. [Google Scholar] [CrossRef]
- Chen, L.; Chen, H.; Zheng, C.; Marburg, S. Structural-acoustic sensitivity analysis of radiated sound power using a finite element/discontinuous fast multipole boundary element scheme. Int. J. Numer. Methods Fluids 2016, 82, 858–878. [Google Scholar] [CrossRef]
- Ryckelynck, D. A priori hyperreduction method: An adaptive approach. J. Comput. Phys. 2005, 202, 346–366. [Google Scholar] [CrossRef]
- Grepl, M.A.; Maday, Y.; Nguyen, N.C.; Patera, A. Efficient reduced-basis treatment of nonaffine and nonlinear partial differential equations. ESAIM Math. Model. Numer. Anal. 2007, 41, 575–605. [Google Scholar] [CrossRef]
- Nguyen, N.; Peraire, J. An efficient reduced-order modeling approach for non-linear parametrized partial differential equations. Int. J. Numer. Methods Eng. 2008, 76, 27–55. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Stat. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Degroote, J.; Virendeels, J.; Willcox, K. Interpolation among reduced-order matrices to obtain parameterized models for design, optimization and probabilistic analysis. Int. J. Numer. Methods Fluids 2010, 63, 207–230. [Google Scholar] [CrossRef]
- Carlberg, K.; Bou-Mosleh, C.; Farhat, C. Efficient non-linear model reduction via a least-squares Petrov-Galerkin projection and compressive tensor approximations. Int. J. Numer. Methods Eng. 2011, 86, 155–181. [Google Scholar] [CrossRef]
- Carlberg, K.; Farhat, C. A low-cost, goal-oriented compact proper orthogonal decomposition basis for model reduction of static systems. Int. J. Numer. Methods Eng. 2011, 86, 381–402. [Google Scholar] [CrossRef]
- Amsallem, D.; Zahr, M.J.; Farhat, C. Nonlinear model order reduction based on local reduced-order bases. Int. J. Numer. Methods Eng. 2012, 92, 891–916. [Google Scholar] [CrossRef]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef]
- Zahr, M.; Farhat, C. Progressive construction of a parametric reduced-order model for PDE-constrained optimization. Int. J. Numer. Methods Eng. 2015, 102, 1077–1110. [Google Scholar] [CrossRef]
- Farhat, C.; Avery, P.; Chapman, T.; Cortial, J. Dimensional reduction of nonlinear finite element dynamic models with finite rotations and energy-based mesh sampling and weighting for computational efficiency. Int. J. Numer. Methods Eng. 2014, 98, 625–662. [Google Scholar] [CrossRef]
- Amsallem, D.; Zahr, M.J.; Choi, Y.; Farhat, C. Design optimization using hyper-reduced-order models. Struct. Multidiscip. Optim. 2015, 51, 919–940. [Google Scholar] [CrossRef]
- Farhat, C.; Chapman, T.; Avery, P. Structure-preserving, stability, and accuracy properties of the Energy-Conserving Sampling and Weighting (ECSW) method for the hyper reduction of nonlinear finite element dynamic models. Int. J. Numer. Methods Eng. 2015, 102, 1077–1110. [Google Scholar] [CrossRef]
- Paul-Dubois-Taine, A.; Amsallem, D. An adaptive and efficient greedy procedure for the optimal training of parametric reduced-order models. Int. J. Numer. Methods Eng. 2015, 102, 1262–1292. [Google Scholar] [CrossRef]
- Clough, R.W. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Meirovitch, L. Computational Methods in Structural Dynamics; Sijthoff and Noordhoff: Alphen aan den Rijn, The Netherlands, 1980. [Google Scholar]
- Argyris, J.; Mlejnek, H.P. Dynamics of Structures; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Morand, H.P.; Ohayon, R. Fluid Structure Interaction; Wiley: Chichester, UK, 1995. [Google Scholar]
- Craig, R.R., Jr.; Kurdila, A.J. Fundamentals of Structural Dynamics; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- De Klerk, D.; Rixen, D.J.; Voormeeren, S.N. General framework for dynamic substructuring: History, review and classification of techniques. AIAA J. 2008, 46, 1169–1181. [Google Scholar] [CrossRef]
- Preumont, A. Twelve Lectures on Structural Dynamics; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Ohayon, R.; Soize, C. Advanced Computational Vibroacoustics—Reduced-Order Models and Uncertainty Quantification; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Ohayon, R.; Soize, C. Variational-based reduced-order model in dynamic substructuring of coupled structures through a dissipative physical interface: Recent advances. Arch. Comput. Methods Eng. 2014, 21, 321–329. [Google Scholar] [CrossRef]
- Peters, H.; Kessissoglou, N.; Marburg, S. Modal decomposition of exterior acoustic-structure interaction problems with model order reduction. J. Acoust. Soc. Am. 2014, 135, 2706–2717. [Google Scholar] [CrossRef] [PubMed]
- Geradin, M.; Rixen, D. Mechanical Vibrations, Third Edition: Theory and Application to Structural Dynamics; Wiley: Chichester, UK, 2015. [Google Scholar]
- Gruber, F.M.; Rixen, D.J. Evaluation of substructure reduction techniques with fixed and free interfaces. J. Mech. Eng. 2016, 62, 452–462. [Google Scholar] [CrossRef]
- Soize, C. Uncertainty Quantification. An Accelerated Course with Advanced Applications in Computational Engineering (Interdisciplinary Applied Mathematics); Springer: New York, NY, USA, 2017. [Google Scholar]
- Ghanem, R.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991. [Google Scholar]
- Ghanem, R.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Revised Edition; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Mace, B.; Worden, W.; Manson, G. Uncertainty in Structural Dynamics. J. Sound Vib. 2005, 288, 431–790. [Google Scholar] [CrossRef]
- Schueller, G.I. Uncertainties in Structural Mechanics and Analysis-Computational Methods. Comput. Struct. 2005, 83, 1031–1150. [Google Scholar]
- Schueller, G.I. On the treatment of uncertainties in structural mechanics and analysis. Comput. Struct. 2007, 85, 235–243. [Google Scholar] [CrossRef]
- Arnst, M.; Ghanem, R. Probabilistic equivalence and stochastic model reduction in multiscale analysis. Comput. Methods Appl. Mech. Eng. 2008, 197, 3584–3592. [Google Scholar] [CrossRef]
- Deodatis, G.; Spanos, P.D. Proceedings of the 5th International Conference on Computational Stochastic Mechanics. Probab. Eng. Mech. 2008, 23, 103–346. [Google Scholar] [CrossRef]
- LeMaitre, O.P.; Knio, O.M. Spectral Methods for Uncertainty Quantification with Applications to Computational Fluid Dynamics; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Soize, C. Stochastic Models of Uncertainties in Computational Mechanics; Lecture Notes in Mechanics Series; Engineering Mechanics Institute (EMI) of the American Society of Civil Engineers (ASCE): Reston, VA, USA, 2012. [Google Scholar]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Beck, J.L.; Au, S.K. Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation. J. Eng. Mech. ASCE 2002, 128, 380–391. [Google Scholar] [CrossRef]
- Spall, J.C. Introduction to Stochastic Search and Optimization; John Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kaipio, J.; Somersalo, E. Statistical and Computational Inverse Problems; Springer: New York, NY, USA, 2005. [Google Scholar]
- Soize, C. A nonparametric model of random uncertainties on reduced matrix model in structural dynamics. Probab. Eng. Mech. 2000, 15, 277–294. [Google Scholar] [CrossRef]
- Soize, C. Maximum entropy approach for modeling random uncertainties in transient elastodynamics. J. Acoust. Soc. Am. 2001, 109, 1979–1996. [Google Scholar] [CrossRef] [PubMed]
- Soize, C. Random matrix theory for modeling uncertainties in computational mechanics. Comput. Methods Appl. Mech. Eng. 2005, 194, 1333–1366. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–659. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Revised and Enlarged Second Edition; Academic Press: New York, NY, USA, 1991. [Google Scholar]
- Soize, C.; Farhat, C. A nonparametric probabilistic approach for quantifying uncertainties in low- and high-dimensional nonlinear models. Int. J. Numer. Methods Eng. 2017, 109, 837–888. [Google Scholar] [CrossRef]
- Fernandez, C.; Soize, C.; Gagliardini, L. Fuzzy structure theory modeling of sound-insulation layers in complex vibroacoustic uncertain systems—Theory and experimental validation. J. Acoust. Soc. Am. 2009, 125, 138–153. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Hubert, J.; Sanchez-Palencia, E. Vibration and Coupling of Continuous Systems. Asymptotic Methods; Springer: Berlin, Germany, 1989. [Google Scholar]
- Dautray, R.; Lions, J.L. Mathematical Analysis and Numerical Methods for Science and Technology; Springer: Berlin, Germany, 1992. [Google Scholar]
- MSC Nastran, T.M. Dynamic Analysis User’s Guide, Chapter 12—Mid-Frequency Acoustics; MSC Nastran, MSC Software Cooporation: Newport Beach, CA, USA, 2017. [Google Scholar]
- Soize, C. Construction of probability distributions in high dimension using the maximum entropy principle. Applications to stochastic processes, random fields and random matrices. Int. J. Numer. Methods Eng. 2008, 76, 1583–1611. [Google Scholar]
- Soize, C.; Poloskov, I.E. Time-domain formulation in computational dynamics for linear viscoelastic media with model uncertainties and stochastic excitation. Comput. Math. Appl. 2012, 64, 3594–3612. [Google Scholar] [CrossRef]
- Papoulis, A. Signal Analysis; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Capillon, R.; Desceliers, C.; Soize, C. Uncertainty quantification in computational linear structural dynamics for viscoelastic composite structures. Comput. Methods Appl. Mech. Eng. 2016, 305, 154–172. [Google Scholar] [CrossRef]
- Fishman, G. Monte Carlo: Concepts, Algorithms, and Applications; Springer: New York, NY, USA, 1996. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Chebli, H.; Soize, C. Experimental validation of a nonparametric probabilistic model of non homogeneous uncertainties for dynamical systems. J. Acoust. Soc. Am. 2004, 115, 697–705. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Duhamel, D.; Soize, C. Probabilistic approach for model and data uncertainties and its experimental identification in structural dynamics: Case of composite sandwich panels. J. Sound Vib. 2006, 294, 64–81. [Google Scholar] [CrossRef]
- Duchereau, J.; Soize, C. Transient dynamics in structures with nonhomogeneous uncertainties induced by complex joints. Mech. Syst. Signal Process. 2006, 20, 854–867. [Google Scholar] [CrossRef]
- Soize, C.; Capiez-Lernout, E.; Durand, J.F.; Fernandez, C.; Gagliardini, L. Probabilistic model identification of uncertainties in computational models for dynamical systems and experimental validation. Comput. Methods Appl. Mech. Eng. 2008, 198, 150–163. [Google Scholar] [CrossRef]
- Durand, J.F.; Soize, C.; Gagliardini, L. Structural-acoustic modeling of automotive vehicles in presence of uncertainties and experimental identification and validation. J. Acoust. Soc. Am. 2008, 124, 1513–1525. [Google Scholar] [CrossRef] [PubMed]
- Capiez-Lernout, E.; Soize, C.; Mignolet, M.P. Post-buckling nonlinear static and dynamical analyses of uncertain cylindrical shells and experimental validation. Comput. Methods Appl. Mech. Eng. 2014, 271, 210–230. [Google Scholar] [CrossRef]
- Truesdell, C. Encyclopedia of Physics, Vol. VIa/3, Mechanics of Solids III; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1973. [Google Scholar]
- Bland, D.R. The Theory of Linear Viscoelasticity; Pergamon: London, UK, 1960. [Google Scholar]
- Fung, Y.C. Foundations of Solid Mechanics; Prentice Hall: Englewood Cliffs, NJ, USA, 1968. [Google Scholar]
- Coleman, B.D. On the thermodynamics, strain impulses and viscoelasticity. Arch. Ration. Mech. Anal. 1964, 17, 230–254. [Google Scholar] [CrossRef]
- Hahn, S.L. Hilbert Transforms in Signal Processing; Artech House Signal Processing Library: Boston, MA, USA, 1996. [Google Scholar]
- Pandey, J.N. The Hilbert Transform of Schwartz Distributions and Applications; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- King, F.W. Hilbert Transforms; Vol 1 and Vol 2, Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Feldman, M. Hilbert Transform Applications in Mechanical Vibration; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Kronig, R.D. On the theory of dispersion of X-rays. J. Opt. Soc. Am. 1926, 12, 547–557. [Google Scholar] [CrossRef]
- Kramers, H.A. La diffusion de la lumière par les atomes, Atti del Congresso Internazionale dei Fisica. In Proceedings of the Transactions of Volta Centenary Congress, Como, Italy, 11–20 September 1927; Volume 2, pp. 545–557. [Google Scholar]
- Bagley, R.; Torvik, P. Fractional calculus—A different approach to the analysis of viscoelastically damped struture. AIAA J. 1983, 5, 741–748. [Google Scholar] [CrossRef]
- Golla, D.F.; Hughes, P.C. Dynamics of viscoelastic structures—A time domain, finite element formulation. J. Appl. Mech. 1985, 52, 897–906. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Mingori, D. Finite element modeling of frequency-dependent material damping using augmenting thermodynamic fields. J. Guid. Control Dyn. 1990, 13, 1040–1050. [Google Scholar] [CrossRef]
- Mc Tavish, D.J.; Hughes, P.C. Modeling of linear viscoelastic space structures. J. Vib. Acoust. 1993, 115, 103–113. [Google Scholar] [CrossRef]
- Dovstam, K. Augmented Hooke’s law in frequency domain. Three dimensional material damping formulation. Int. J. Solids Struct. 1995, 32, 2835–2852. [Google Scholar] [CrossRef]
- Lesieutre, G.A. Damping in structural dynamics. In Encyclopedia of Aerospace Engineering; Blockley, R., Shyy, W., Eds.; John Wiley: New York, NY, USA, 2010. [Google Scholar]
- Burton, A.J.; Miller, G.F. The application of integral equation methods to the numerical solution of some exterior boundary value problems. Proc. R. Soc. Lond. Ser. A 1971, 323, 201–210. [Google Scholar] [CrossRef]
- Jones, D.S. Low-frequency scattering by a body in lubricated contact. Q. J. Mech. Appl. Math. 1983, 36, 111–137. [Google Scholar] [CrossRef]
- Luke, C.J.; Martin, P.A. Fluid-solid interaction: Acoustic scattering by a smooth elastic obstacle. SIAM J. Appl. Math. 1995, 55, 904–922. [Google Scholar] [CrossRef]
- Jentsch, L.; Natroshvili, D. Non-local approach in mathematical problems of fluid-structure interaction. Math. Method Appl. Sci. 1999, 22, 13–42. [Google Scholar] [CrossRef]
- Panich, O.I. On the question of solvability of the exterior boundary value problems for the wave equation and Maxwell’s equations. Russ. Math. Surv. 1965, 20, 221–226. [Google Scholar]
- Schenck, H.A. Improved integral formulation for acoustic radiation problems. J. Acoust. Soc. Am. 1968, 44, 41–58. [Google Scholar] [CrossRef]
- Mathews, I.C. Numerical techniques for three-dimensional steady-state fluid-structure interaction. J. Acoust. Soc. Am. 1986, 79, 1317–1325. [Google Scholar] [CrossRef]
- Amini, S.; Harris, P.J. A comparison between various boundary integral formulations of the exterior acoustic problem. Comput. Methods Appl. Mech. Eng. 1990, 84, 59–75. [Google Scholar] [CrossRef]
- Amini, S.; Harris, P.J.; Wilton, D.T. Coupled Boundary and Finite Element Methods for the Solution of the Dynamic Fluid-Structure Interaction Problem; Lecture Notes in Engineer; Springer: New York, NY, USA, 1992; Volume 77. [Google Scholar]
- Angelini, J.J.; Hutin, P.M. Exterior Neumann problem for Helmholtz equation. Problem of irregular frequencies. La Recherche Aérospatiale 1983, 3, 43–52. (In English) [Google Scholar]
- Golub, G.H.; van Loan, C.F. Matrix Computations; The Johns Hopkins University Press: Baltimore, MD, USA; London, UK, 1989. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohayon, R.; Soize, C. Computational Vibroacoustics in Low- and Medium- Frequency Bands: Damping, ROM, and UQ Modeling. Appl. Sci. 2017, 7, 586. https://doi.org/10.3390/app7060586
Ohayon R, Soize C. Computational Vibroacoustics in Low- and Medium- Frequency Bands: Damping, ROM, and UQ Modeling. Applied Sciences. 2017; 7(6):586. https://doi.org/10.3390/app7060586
Chicago/Turabian StyleOhayon, Roger, and Christian Soize. 2017. "Computational Vibroacoustics in Low- and Medium- Frequency Bands: Damping, ROM, and UQ Modeling" Applied Sciences 7, no. 6: 586. https://doi.org/10.3390/app7060586




