1. Introduction
For a linear passive vibration isolation system, the vibration isolation performance is effective only when the frequency of external disturbance is more than
times the natural frequency. In order to attenuate vibration in the low-frequency band, one must reduce the stiffness of the linear vibration isolation system. However, reduction of the stiffness will diminish load bearing capacity of linear vertical vibration isolation system, resulting in undesirable excess deflection and over-stress of spring material. Finally, the linear vibration isolation system will fail to work well. In order to settle this problem, nonlinear vibration isolation systems attract great interests, because they exhibit the typical characteristics of high static stiffness and low dynamic stiffness (HSLDS), which are very different from the invariant stiffness characteristic of linear vibration isolation system [
1]. At the static equilibrium point, nonlinear vibration isolation systems can not only provide sufficiently large static stiffness to reduce static deflection, but also offer very small dynamic stiffness to obtain good low-frequency vibration isolation performance.
So far, nonlinear vibration isolation systems are mainly realized by integrating negative stiffness structures with linear positive stiffness springs. There are several methods to achieve negative stiffness characteristics. Inclined spring negative stiffness structure is the most studied one in the literature. Carrella et al. [
2,
3,
4] firstly reported a quasi-zero-stiffness system in which two inclined springs connected in parallel with one vertical spring. Typically, this system outperforms the linear system provided that the system parameters are chosen appropriately. Based on this work, Ahn [
5] put forward design guidelines for the quasi-zero-stiffness isolator and solved the performance limit of this isolator. To further improve vibration isolation effectiveness of the vehicle seat, the quasi-zero-stiffness vibration isolation model was developed [
6,
7], and it is experimentally confirmed that the proposed system offers a larger isolation frequency range and a higher attenuation rate than that of the linear system. After that, various methods were conducted to develop the quasi-zero-stiffness vibration isolator, and the effects of various loads and archetypal dynamical model of this quasi-zero stiffness isolator were discussed in the literature [
8,
9]. Moreover, a quasi-zero stiffness isolator using Euler buckled beams as negative stiffness corrector was reported and the results showed that introducing the negative stiffness was an effective way to lower the resonance frequency even with the stiffness and load imperfections [
10,
11]. Although quasi-zero stiffness vibration isolation systems (QZS-VIS) are potentially advantageous in many practical applications, QZS-VIS have many disadvantages, such as the easiness to lose stability, low loading capability and potential bifurcation effect at equilibrium [
3,
5,
11,
12].
Utilizing permanent magnets and electromagnets to produce negative stiffness is another method for the negative stiffness characteristics [
13,
14,
15,
16]. Xu et al. [
17] presented the geometric nonlinear magnetic vibration isolation devices with the quasi-zero-stiffness characteristic. In comparison to the corresponding linear system, the vibration isolation range of the proposed system can be largely extended to the lower frequency domain. Zheng et al. [
18] employed a pair of coaxial ring permanent magnets installed in parallel with the mechanical spring to reduce the resonance frequency of the linear isolator, and the proposed quasi-zero-stiffness isolator can really outperform a linear isolator. Zhu et al. [
19] designed a novel six degrees of freedom vibration isolator system utilizing magnetic levitation, which realized inherent quasi-zero stiffness in the vertical direction, and zero stiffness in other five degrees of freedoms. The negative stiffness structures that originated from the permanent magnets and electromagnets were very effective. However, they were quite thermally sensitive and may induce unwanted couplings to external electromagnetic fields.
In addition, there are many other novel designs for quasi-zero-stiffness vibration isolation systems reported, such as sliding beam structure [
20], composite bi-stable plate [
21], scissor-like structured platform [
22], and super elastic shape memory alloy bars [
23]. However, because of structural complexity or unknown structural stability or environmental dependence, much deep-in research work still needs to be done, with the objective of further industrial application.
The geometrical anti-spring structure was first proposed by Bertolini [
24] and Cella [
25] for the purpose of seismic attenuation. It was successfully applied in optical table prototype designed for advanced LIGO (Laser Interferometer Gravitational wave Observatory) [
26] and external injection bench of the Advanced Virgo gravitational wave detector [
27,
28]. Due to its nonlinear characteristics of high static low dynamic stiffness, the geometric anti-spring structure would be a perfect candidate for the design of low-frequency vibration isolation system. In contrast to other designs for the nonlinear isolator, the advantages of geometric anti-spring isolator include structuralicity simple and compactness, space saving and insensitive to temperatures or external electromagnetic fields, and so on. However, expect for the seismic attenuation in gravitational wave observatory, the geometric anti-spring isolator has not been applied in any other vibration reduction application. And the detailed nonlinear stiffness characteristic of the geometric anti-spring structure have not been intensively investigated. The effect of load and stiffness imperfection on the performance of this nonlinear isolation structure has not been discussed, which is very important for its further application in the field of vehicles, ships, and other precision equipment, especially for the situation under the excitation of low frequency (several Hz) and large amplitude.
In this study, aiming at settling the pressing issue for isolating the disturbance of several Hz in precision instruments in vehicles and ships, a novel geometric anti-spring isolator for the low-frequency vibration isolation is developed and its vibration isolation performance and nonlinearity characteristic are investigated mathematically and experimentally. In
Section 2, the genetic algorithm was used to achieve the numerical solution to the differential boundary value problem that describes the mechanical properties of the blade spring. The stiffness nonlinearity is investigated and the dimensionless optimal design parameters of the geometric anti-spring vibration isolation structure for different nonlinear geometric parameters are obtained. Mathematical simulation based on four order Runge-Kutta algorithm is carried out to investigate the transmissibility characteristic of the geometric anti-spring isolator in
Section 3. The influence of geometric parameter, excitation amplitude, load weight and viscous damping on the transmissibility of the geometric anti-spring isolator are investigated theoretically. Then, a geometric anti-spring isolator with a nonlinear geometric parameter of 0.92 is fabricated and experimentally studied. The experiment setup and results are presented in
Section 4. Conclusions are drawn in
Section 5. This work will enhance the understanding of vibration attenuation mechanism of geometric anti-spring structure and provide further design guidelines for the broader application of the geometric anti-spring isolator.
2. Geometric Anti-Spring Structure
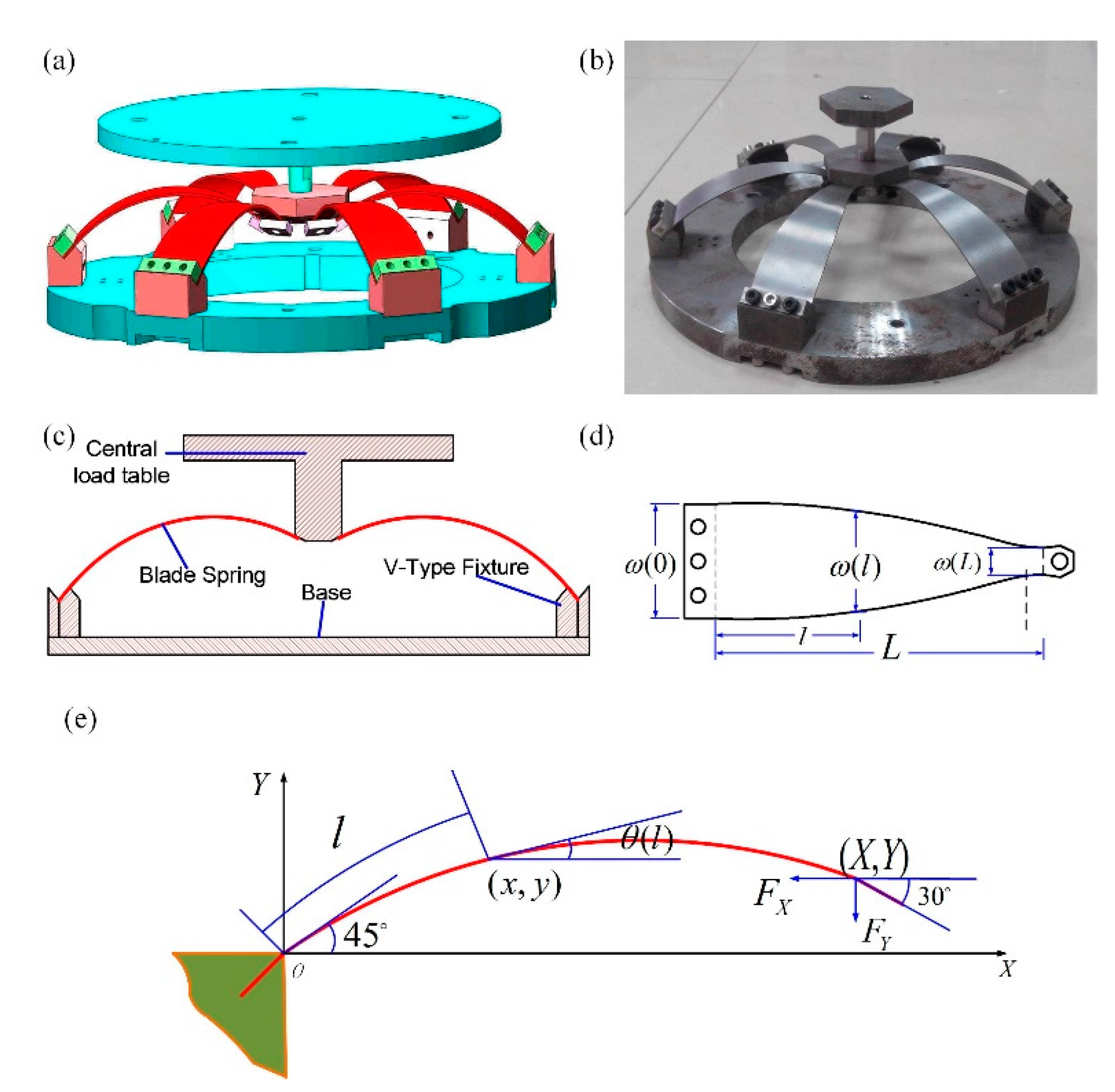
The geometric anti-spring isolator (
Figure 1a) consists of several quasi-trapezoid cantilever blade springs. The bottoms of blade springs are fixed to a massive base with V-type fixtures and their vertices are connected to each other through a central load plate. Both the bottoms and the vertices of the blade spring are kept at a constant angle to the horizontal direction. The central load plate connected with the mass load is limited to move along the vertical direction. The shape of cantilever blade spring is shown in
Figure 1d. The effective length of spring is
, and the width of the blade spring is represented by
, with
. The shape function of the blade spring is
where
,
,
and
. This particular shape is chosen to achieve a uniform inner stress distribution [
25]. Meanwhile, total stress of the spring will be the smallest in comparison to that with other shapes when the vibration isolation structure works at the low stiffness area. The blade spring has a constant thickness, which is much smaller than both the length and the width of the spring.
According to the geometric symmetry, the mechanical property of the geometric anti-spring structure can be obtained through mechanical analysis of single blade spring.
Figure 1e shows a one dimension mechanical model of the blade spring, in which the influence of thickness is ignored. Rectangular coordinate system O-(X,Y), of which the origin O is sited at the bottom of the blade spring, X axis represents the horizontal direction and Y axis is for the vertical direction, is established to analyze the mechanical property of the blade spring. The variable
is the curvilinear coordinate along the length direction of the blade spring. It is convenient to define
as the angle between the tangent of curvilinear and the positive direction of X axis of the rectangular coordinate system. The quantity
represents horizontal constraint force and the quantity
represents vertical payload applied on the vertex of the blade spring. The relationship between the dimensionless force
and actual force
is shown as follows.
Here,
is Young’s modulus of the material of blade spring. Dimensionless vertical coordinate
and dimensionless horizontal coordinate
of blade spring’s vertex are given by
Here, is dimensionless arc length.
According to the literature [
25], the mechanical properties of the blade spring can be described by the first order differential boundary equations as follows:
Here, is an intermediate parameter. Boundary conditions are , .
In general, the exact analytical solution of Equation (4) cannot be obtained theoretically with an explicit expression formulation. The dimensionless horizontal coordinate
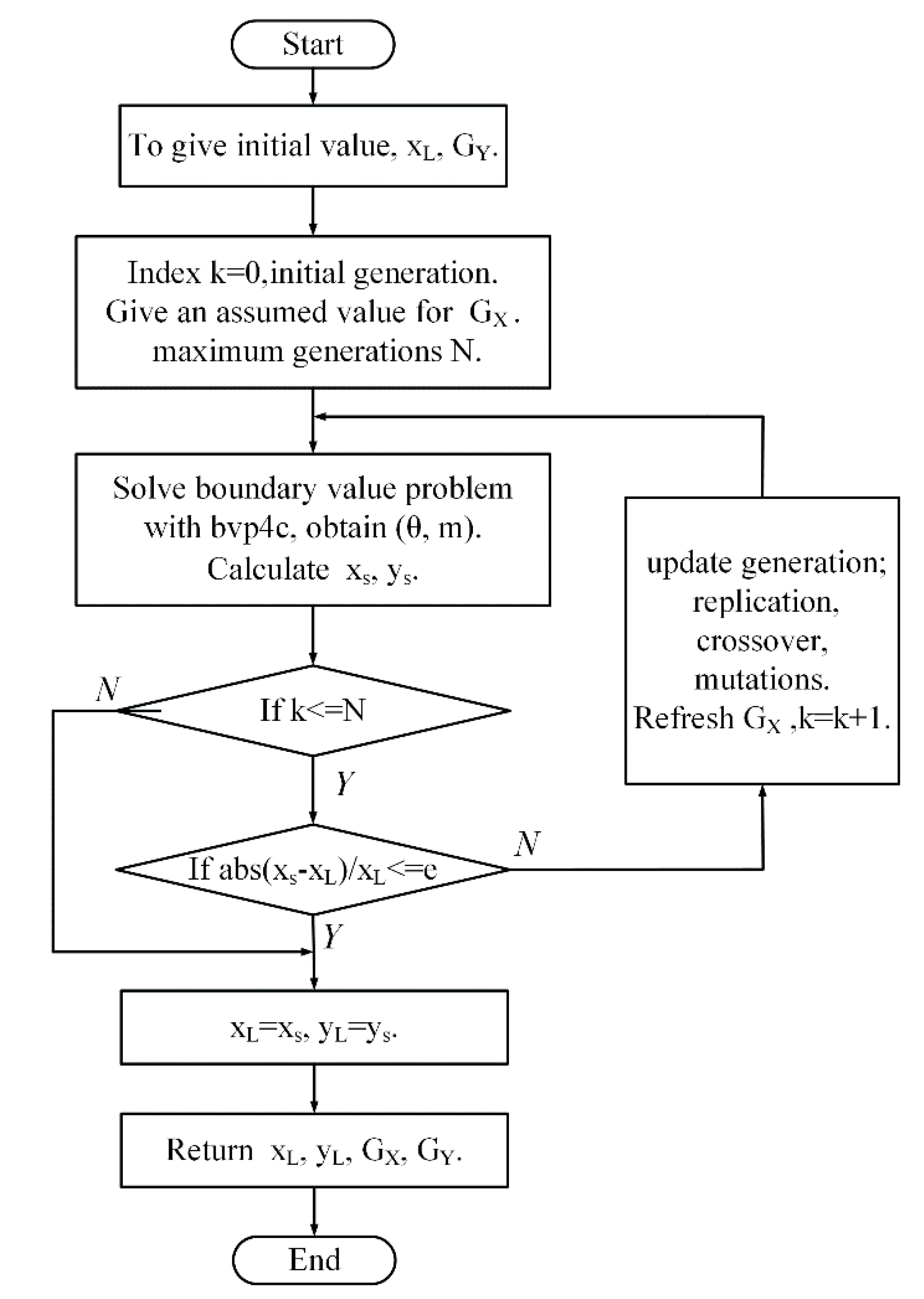
of spring’s vertex is the key parameter to distinguish the mechanical characteristic of the geometric anti-spring isolator under different work state. For the sake of simplicity, the dimensionless horizontal coordinate of the vertex of the spring is referred to the nonlinear geometric parameter in this paper. Utilizing a MATLAB program based on genetic algorithm, the approximately numerical solution of Equation (4) was obtained. The flow chart of the algorithm to solve the boundary problem of Equation (4) is shown in
Figure 2. This solution algorithm transforms the differential boundary problem to an optimization problem. The horizontal constraint force
is unknown in Equation (4). The objective of the optimization algorithm is to gain the horizontal constraint force
of the blade spring under certain a vertical load and a nonlinear geometric parameter. The procedure of the solution algorithm is given as follow.
Step 1: Giving an initial assuming value of horizontal constraint force for the given vertical load and nonlinear geometric parameter .
Step 2: Solve the boundary problem mathematically and get the horizontal coordinate of the vertex of the spring.
Step 3: Calculate the relative error between and . If the calculated error is less than the required accuracy e (=1 × 10−9), record the horizontal force and go to Step 5. Otherwise, go to Step 4.
Step 4: Update the assuming value of the horizontal constraints force using the genetic algorithm function ga() given by Matlab software (Matlab 2012a) and repeat Step 2 and Step 3.
Step 5: Solve the boundary problem mathematically under the given vertical force and the recorded optimal horizontal force . And get the vertical coordinate of the vertex of the spring.
In this optimization problem, the number of variables for the genetic algorithm function ga() is 1. Some key arguments in the options of the genetic algorithm function ga() are listed in
Table 1. The other arguments are the defaults.
In the solution procedure, when the geometric parameter is larger than 0.9027, optimization terminates when the average change in the fitness value is less than the options.TolFun. The maximum iteration generation is less than 100. The optimization algorithm is time-saving. There is no multi-value solution obtained, which means that the vertical force
and the vertical coordinate
of the blade spring’s vertex are one to one correspondence and no negative stiffness appears. According to the literature [
25], the negative stiffness appears when the nonlinear geometric parameter is smaller than 0.9027. And for the situation that the geometric parameter is less than 0.9027, the time of optimization progress is long when the nondimensional vertical force is close to −1.75 and the multi-value solution can not be achieved. Therefore, the negative stiffness characteristics of the geometric anti-spring isolator when the nonlinear geometric parameter is smaller than 0.9027 are not discussed in this paper. This will be studied in the future work.
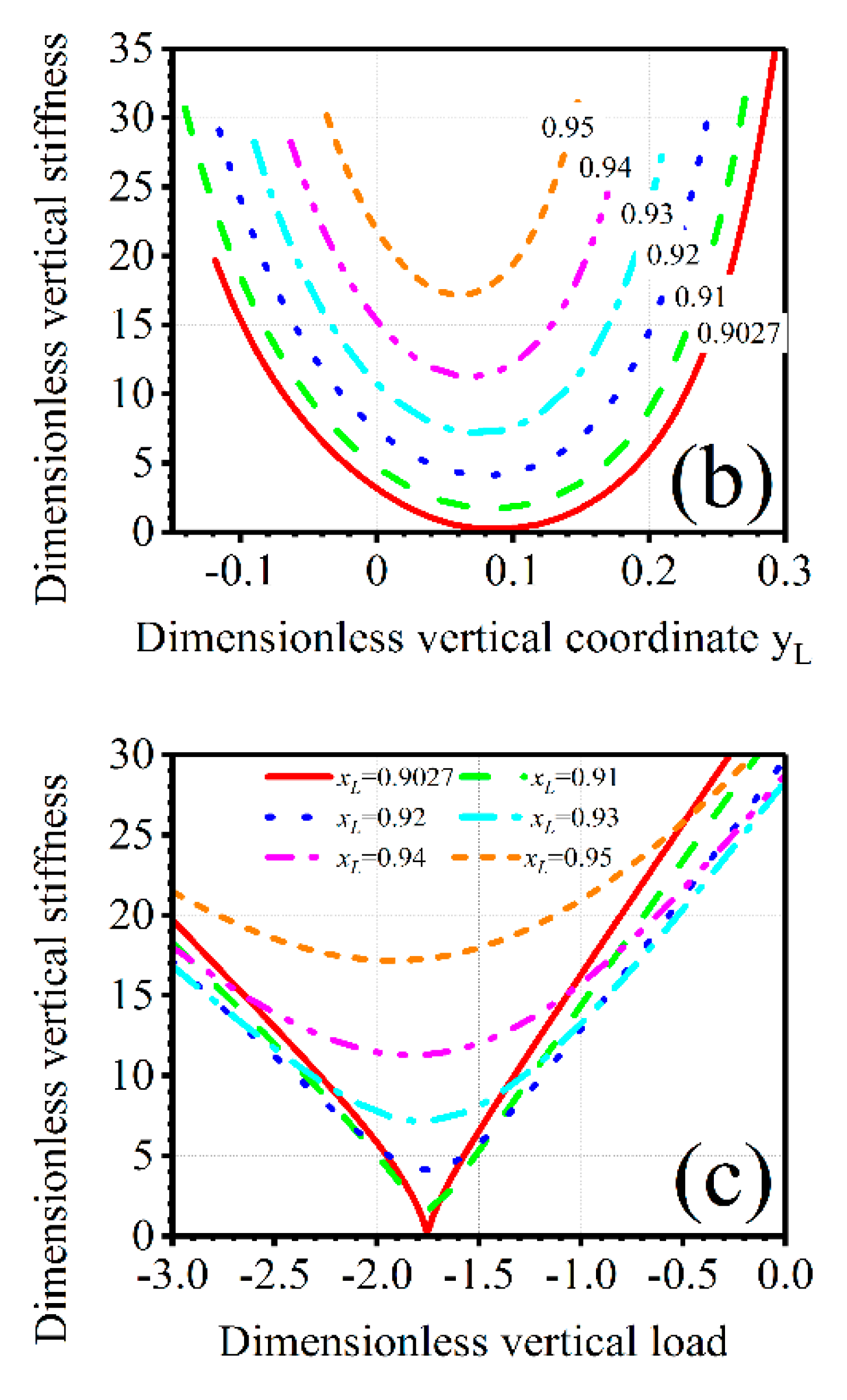
Figure 3a depicts the relationship between dimensionless vertical force
and dimensionless vertical coordinate
of spring’s vertex. As the nonlinear geometric parameter
decreases, the curve of dimensionless vertical force
vs. dimensionless vertical coordinate
changes from an approximately straight line to a nonlinear curve. When the dimensionless vertical coordinate
approaches to 0.1, dimensionless vertical force
grows slowly, which means that the geometric anti-spring isolator possesses very low local stiffness in these load range.
Taking a first order derivative to
with respect to
, dimensionless dynamic stiffness
is obtained (
Figure 3b,c). With the decreasing of the nonlinear geometric parameter
, the nonlinearity of the geometric anti-spring isolator is largely enhanced and the dimensionless lowest dynamic stiffness decreases. When
, the minimum stiffness approaches zero. In order to achieve better vibration isolation performance, it is essential to settle the static equilibrium point of the isolator at the minimum stiffness point, which is called the optimal or rated working point. As the nonlinear geometric parameter decreases, the range of displacement for low stiffness is enlarged but the range of the load goes to be narrow. When the nonlinear geometric parameter is small, the change of the load will largely increase the dynamic stiffness of the isolator in low stiffness area.
According to the vibration theory, the natural angular frequency of the geometric anti-spring structure can be calculated as follows,
And the dimensionless angular frequency is given by:
The dimensionless minimum dynamic stiffness
and corresponding dimensionless natural angular frequency for different dimensionless horizontal coordinates
are shown in
Table 2. The corresponding dimensionless vertical coordinate
and vertical force
at the rated working point are given at the same time.
As the nonlinear geometric parameter decreases, dimensionless minimum dynamic stiffness and natural angular frequency decrease. The dimensionless vertical coordinate increases with the decrement of the nonlinear geometric parameter but vertical force slightly decreases. The carrying capacity of the geometric anti-spring structure reduces with the reduction of the nonlinear geometric parameter.
According to the mathematically theoretical analysis results, the relationship between dimensionless restoring force and displacement of the geometric anti-spring isolator for different nonlinear geometric parameters can be accurately fitted with a seven order polynomial function:
Here,
is the dimensionless vertical displacement of the geometric anti-spring isolator and
are the fitting coefficients, which are shown in
Table 3.
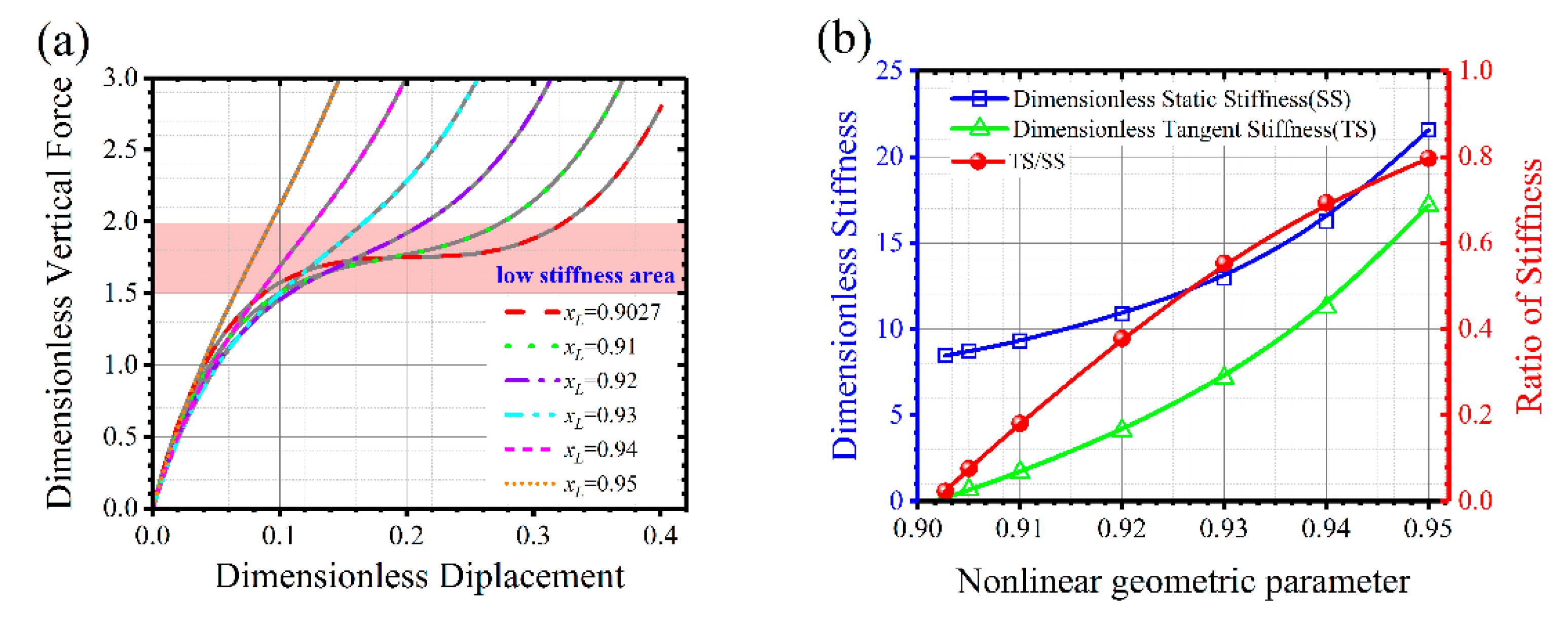
Figure 4a shows the dimensionless vertical force of the geometric anti-spring isolator for different nonlinear geometric parameters, where the gray solid line represents the mathematical calculated results based on the genetic algorithm and different types of color lines represent the polynomial fitting results. It can be seen that the curve of force vs. displacement of the geometric anti-spring isolator in low-frequency area goes much flatter with the decrement of the geometric parameter. The low dynamic stiffness characteristic is also apparent. However, the static displacement of the geometric anti-spring isolator in the low stiffness area increases as the nonlinear geometric parameter decreases, which means that the static stiffness of the isolator will reduce with the decrement of the nonlinear geometric parameter.
Figure 4b shows the dimensionless dynamic stiffness characteristic at the rated working point. As the nonlinear geometric parameter decreases, both the static stiffness and dynamic tangent stiffness of the geometric anti-spring isolator decrease. However, the dynamic stiffness is always less than the static stiffness at the rated working point. The ratio of dynamic stiffness to static stiffness at the rated working load decreases with the decrement of the nonlinear geometric parameter. When the nonlinear geometric parameter is 0.9027, the ratio of dynamic stiffness to static stiffness tend to zero. Therefore, the geometric anti-spring isolator possesses a good high static low dynamic stiffness characteristic. When the nonlinear geometric parameter tends to be 0.9027, the quasi-zero stiffness can even be realized.
3. Mathematical Simulation
In order to theoretically analyze the vibration isolation performance of the geometric anti-spring isolator, a mathematical simulation based on a four order Runge-Kutta algorithm is carried out. When subjected to base excitation
, the governing equation of motion in the geometric anti-spring isolator is
where
represents the relative motion between the excitation displacement
of base and the displacement
of mass.
is the load weight.
is the static displacement. The relationship between the load weight and the static displacement is given by
.
Introducing the dimensionless parameters
Equation (8) can be written as
where
and
denote the second and first derivative of the dimensionless relative displacement
with respect to the dimensionless time
. The intermediate variable
is the angular frequency of the equivalent linear isolator. For the equivalent linear vibration isolation system, the dimensionless initial isolation frequency
is
.
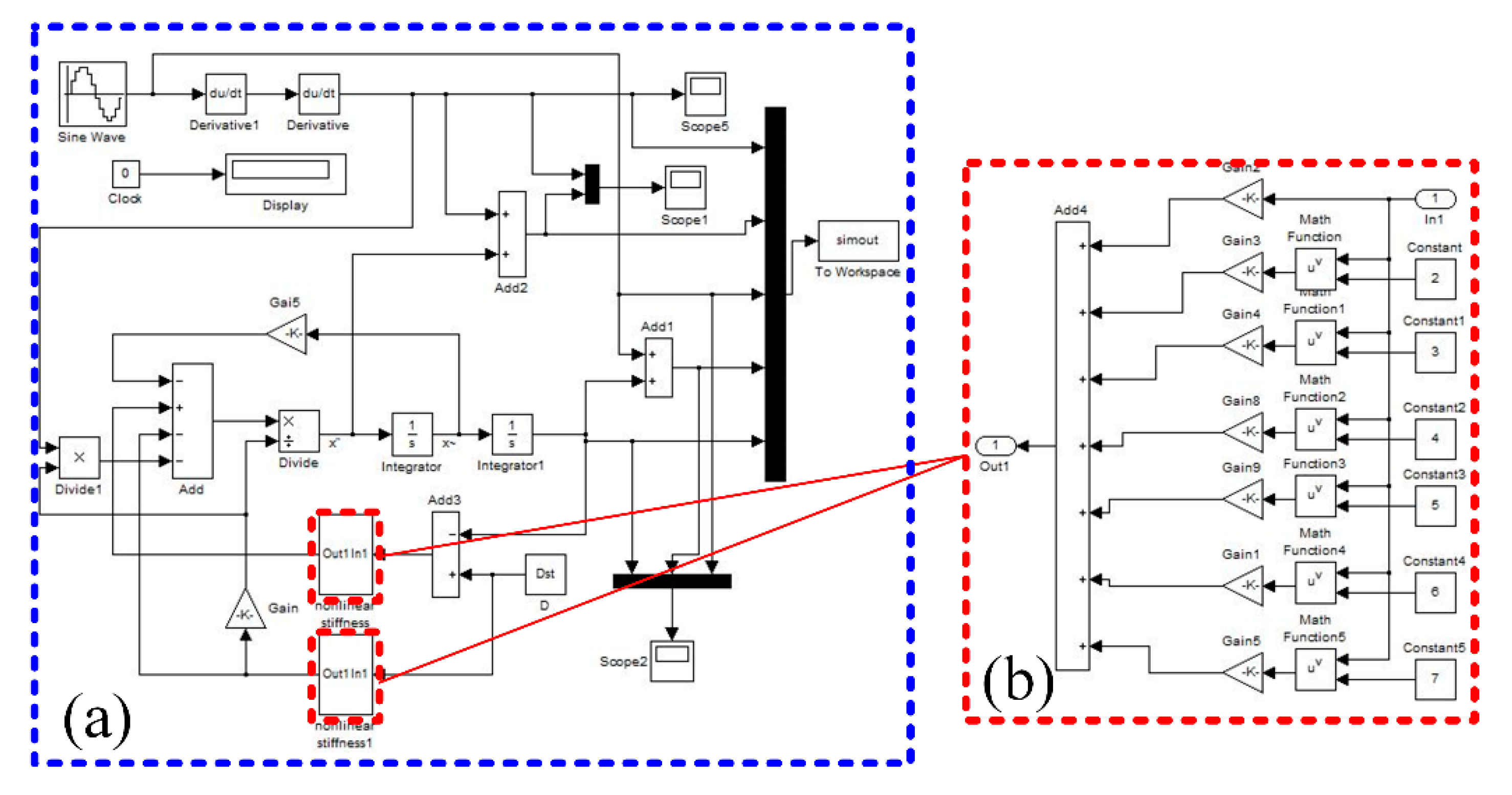
Figure 5 shows the Matlab/Simulink program (Matlab 2012a) used for solving the nonlinear dynamic differential equation (Equation (9)) of motion of the geometric anti-spring isolator. The model of nonlinear restoring force (
Figure 5b) is set up based on Equation (7). Giving the initial state conditions (initial displacement and initial velocity), time domain solution of Equation (9) can be obtained using four order Runge-Kutta algorithm. Calculating the ratio of the absolute acceleration amplitude
of the load mass to the excitation acceleration amplitude
, the acceleration transmissibility of the geometric anti-spring isolator can be obtained. Here, the effects of the nonlinear geometric parameter, excitation displacement amplitude, static payload weight and viscous damping ratio on the transmissibility of the geometric anti-spring isolator are considered.
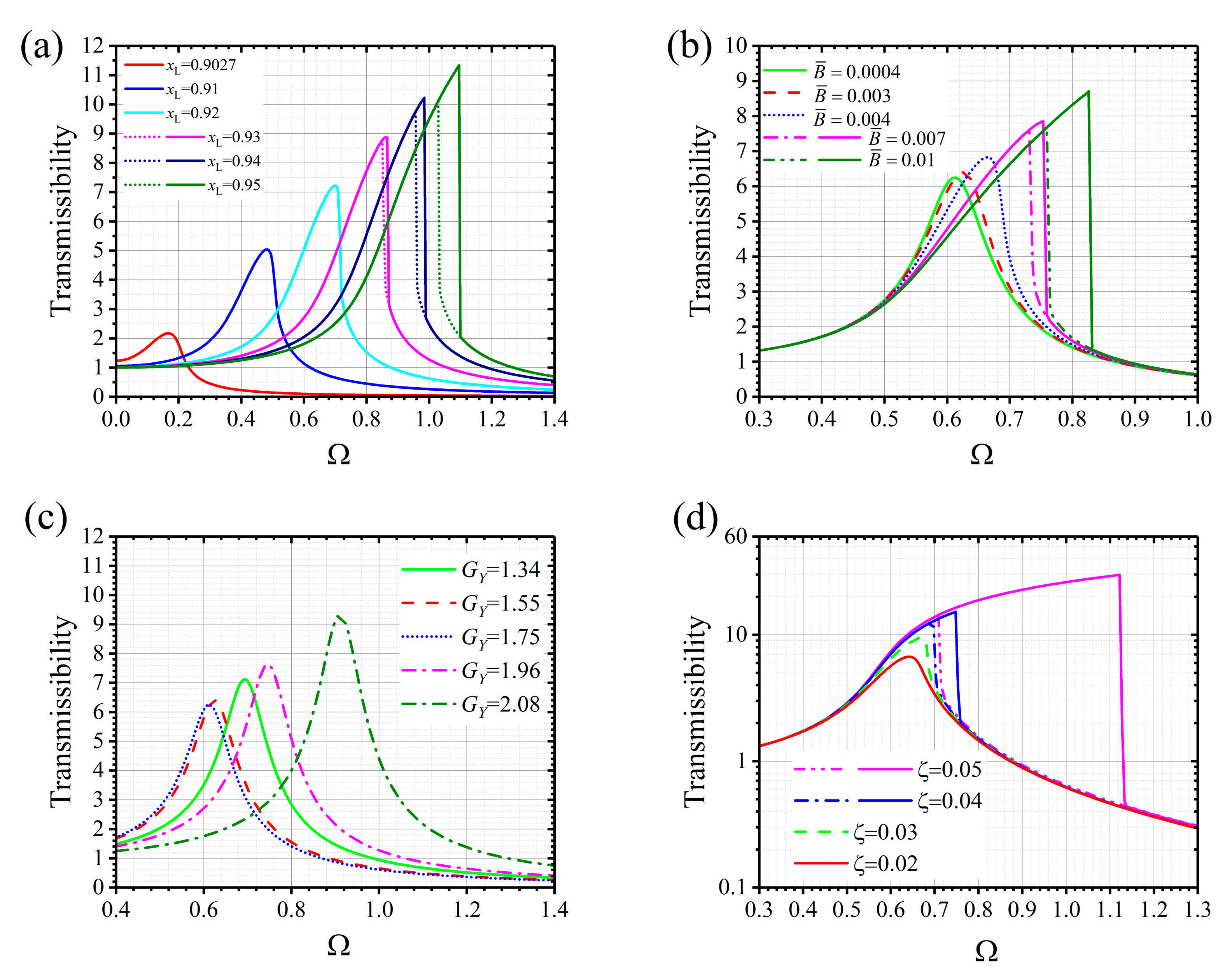
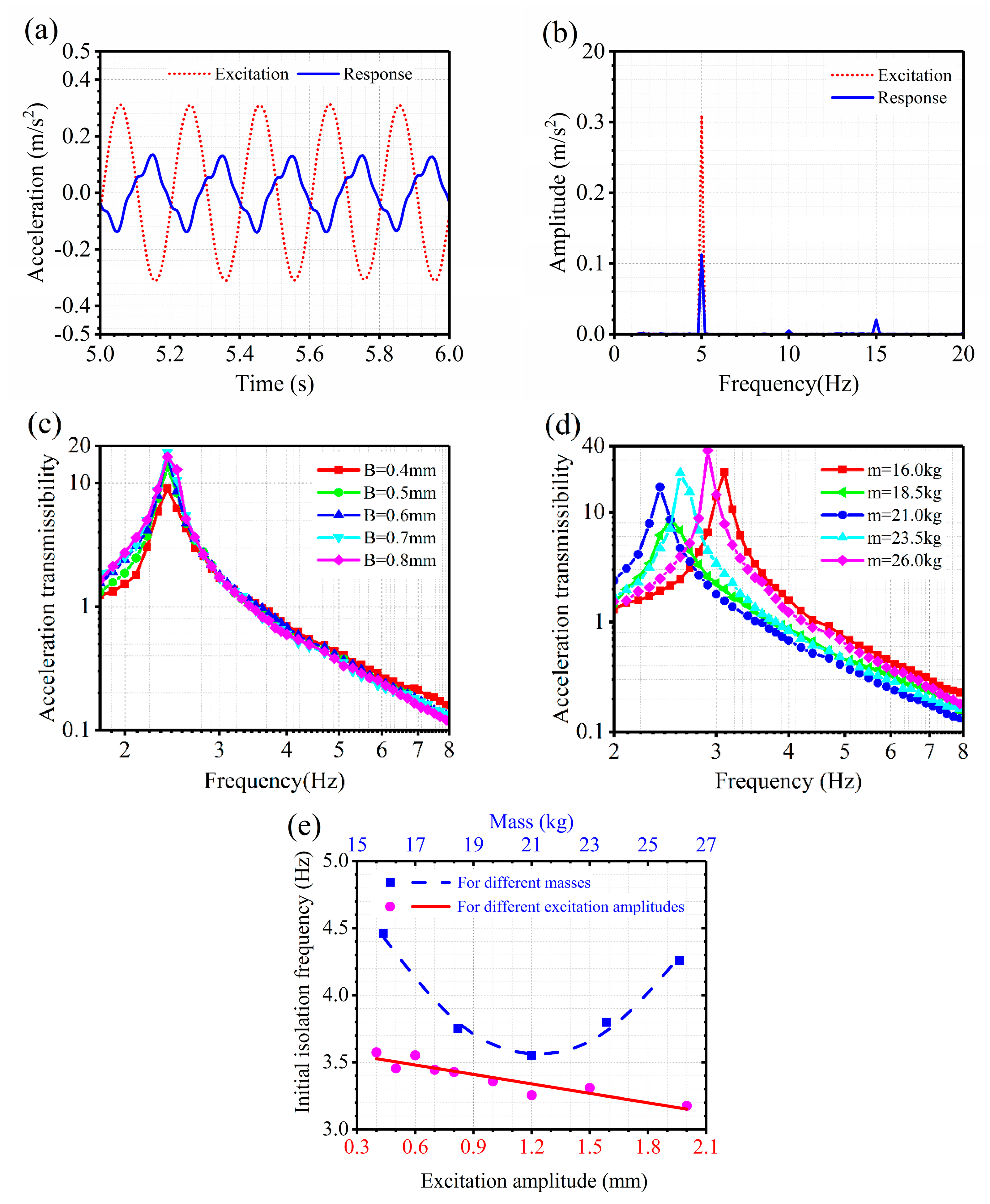
The transmissibility curves of the geometric anti-spring isolator are shown in
Figure 6. Due to the existence of the nonlinearity, the response of the geometric anti-spring isolator under certain excitation levels is dependent on the initial condition. The transmissibility curves of the geometric anti-spring isolator for the situation of gradually increasing frequency and decreasing frequency are different when the nonlinearity is strong, which are distinguished by different types of lines.
From
Figure 6a, it can be seen that as the nonlinear geometric parameter grows, the resonance frequency of the geometric anti-spring isolator increases and the nonlinearity enhances as well. When
is larger than 0.93, the transmissibility curves in the resonance area do not follow the same path. When the excitation frequency is gradually accumulated, a downward jumping phenomena is observed (as is shown by the solid line). When the excitation frequency is gradually reduced, an upward jumping phenomenon is observed (as is shown by the dotted line). The geometric anti-spring isolator shows a hardening-type stiffness characteristic at the rated load.
As the excitation amplitude increases, the peak area of transmissibility curve deflects to the right and the peak of curve increases (
Figure 6b). The nonlinearity of the geometric anti-spring isolator enhances with the increment of excitation amplitude. However, the transmissibility of the isolator in the isolation area for different excitation amplitude does not change too much.
When the geometric parameter is 0.92 and the excitation amplitude is 0.01, the transmissibility peak first decreases and then increases with the increment of the load weight (
Figure 6c). When the dimensionless load weight is 1.75 (the rated working load), the resonance frequency reaches to the minimum value. The increment of the resonance frequency of the geometric anti-spring isolator is slow when reducing the load but fast when increasing the load.
As shown in
Figure 6d, with increasing of the damping, the peak of the transmissibility curve reduces and the nonlinearity is weakened. The attenuation rate of the transmissibility curve in the isolation area does not change when the damping is not too large. So providing appropriate damping will be profitable to weaken the nonlinearity and retain the good vibration isolation performance of the isolator.
The imperfection of load weight will largely change the nonlinearity characteristic of the geometric anti-spring isolator.
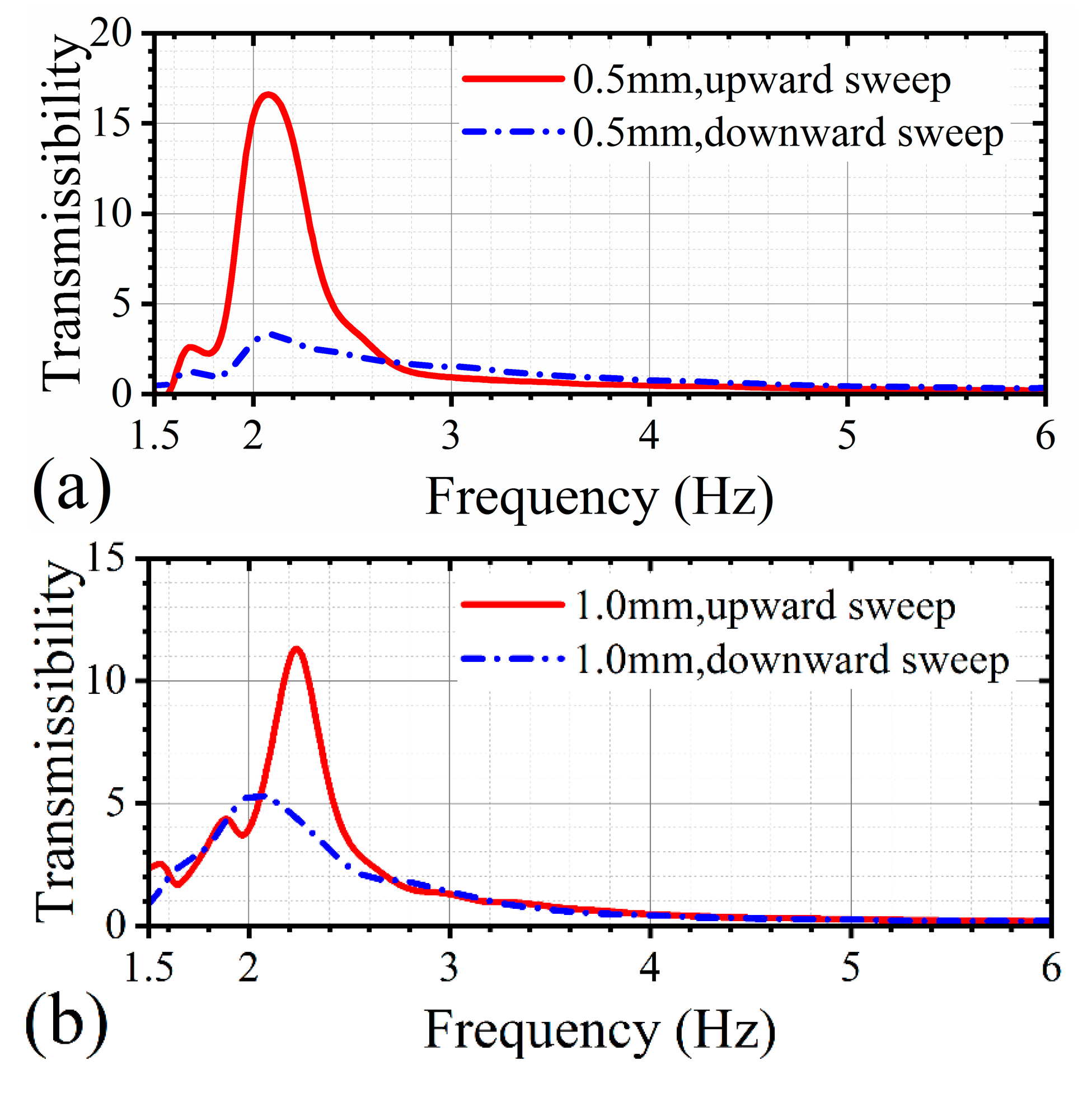
Figure 7 shows the transmissibility curves of the geometric anti-spring isolator for different load weights when the nonlinear geometric parameter is 0.92. When the load weight is 1.55 or 1.96, the transmissibility curve deflects toward the right, nearly the same as the situation for the rated load. However, when the load weight is 1.34 or 2.08, the transmissibility curve deflects to the left when the excitation amplitude is small. When the excitation amplitude is large, the transmissibility deflects to the right again. The isolator shows a softening-type stiffness characteristic when the excitation level is low and a hardening-type stiffness characteristic appears when the excitation level is gradually enhanced.
5. Conclusions
In this paper, a geometric anti-spring isolator made up of several cantilever blade springs is developed. The idea of optimization based on the genetic algorithm is utilized to mathematically solve the differential boundary problem of static mechanical of the geometric anti-spring isolation structure. The dimensionless optimal design parameters of geometric anti-spring isolation structure for different nonlinear geometric parameters are achieved. A Matlab/Simulink program is used to explore the transmissibility of the geometric anti-spring isolator under base excitation. The effects of the nonlinear geometric parameter, excitation displacement amplitude, load weight and damping on the transmissibility of the geometric anti-spring isolator are discussed. A single degree of the freedom vibration evaluation system is established to investigate the vibration isolation performance and nonlinearity characteristics of the geometric anti-spring isolator with a nonlinear geometric parameter of 0.92. Discrete sine excitation experiment and linear frequency sweep excitation experiment are carried out. The initial isolation frequency is used to describe the low-frequency vibration isolation range of the isolator. Some conclusions are as follows:
(1) The nonlinear geometric parameter i.e., the dimensionless horizontal coordinate of blades spring’s vertex is the key parameter to decide the mechanical property of the geometric anti-spring isolator. With the decrement of the nonlinear geometric parameter, the dynamic stiffness of the isolator decreases quickly. When the nonlinear geometric parameter is 0.9027, the minimum dynamic stiffness approaches zero.
(2) The geometric anti-spring isolator under the rated load has a hardening-type stiffness characteristic. As the excitation amplitude increases, the nonlinearity of the isolator enhances.
(3) The imperfection of load weight will largely change the resonance frequency and nonlinearity characteristic of the geometric anti-spring isolator. When the working load goes away from the rated load, the resonance frequency of the geometric anti-spring isolator increases and the nonlinearity type of the isolator varies with the increment of the excitation amplitude. When the excitation amplitude is small, the isolator shows a softening-type stiffness characteristic. When the excitation amplitude is large, the isolator shows a hardening-type stiffness characteristic.
(4) By increasing the damping, the nonlinearity of the isolator will be weakened. The attenuation rate in the isolation area does not change if the damping is not too large.
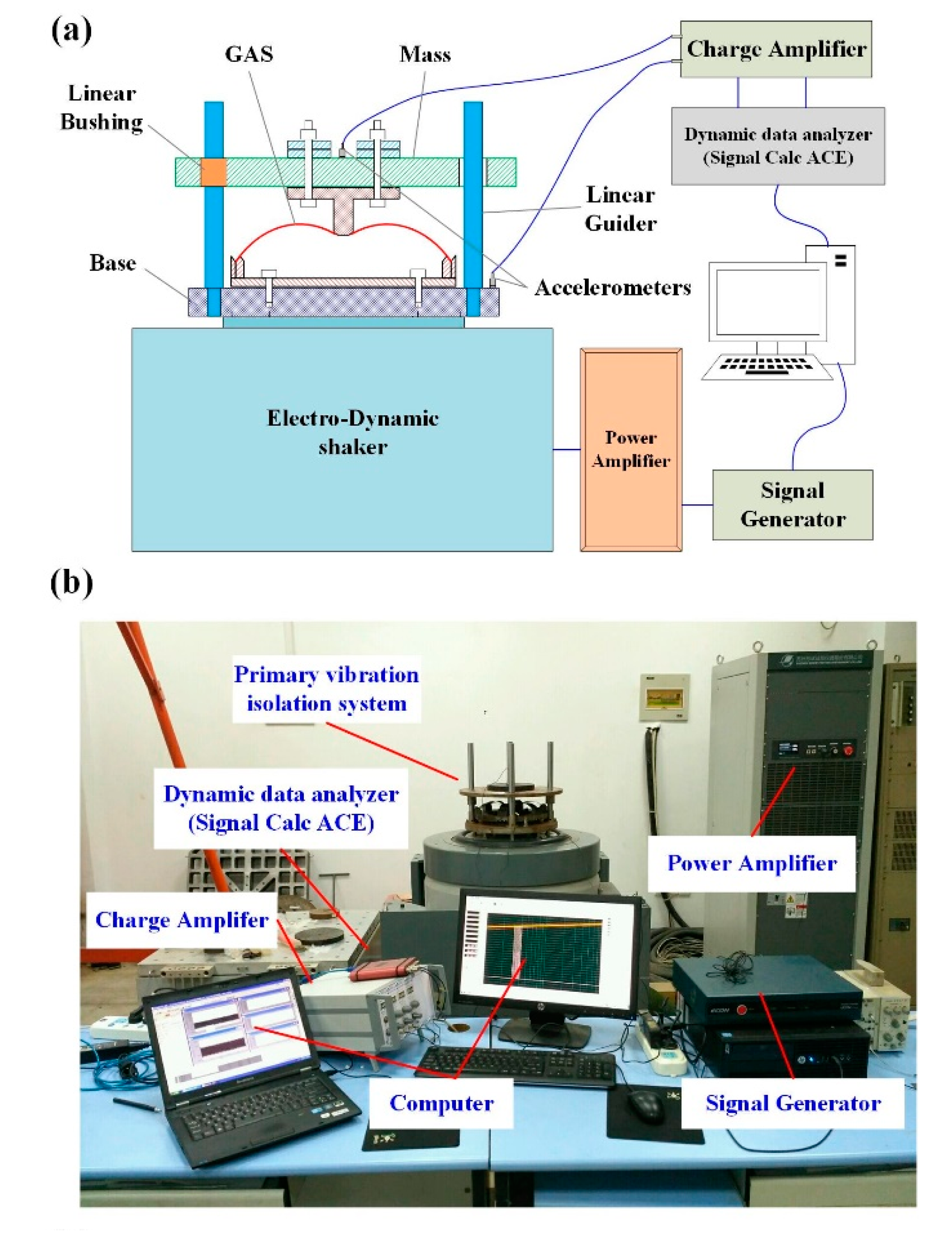
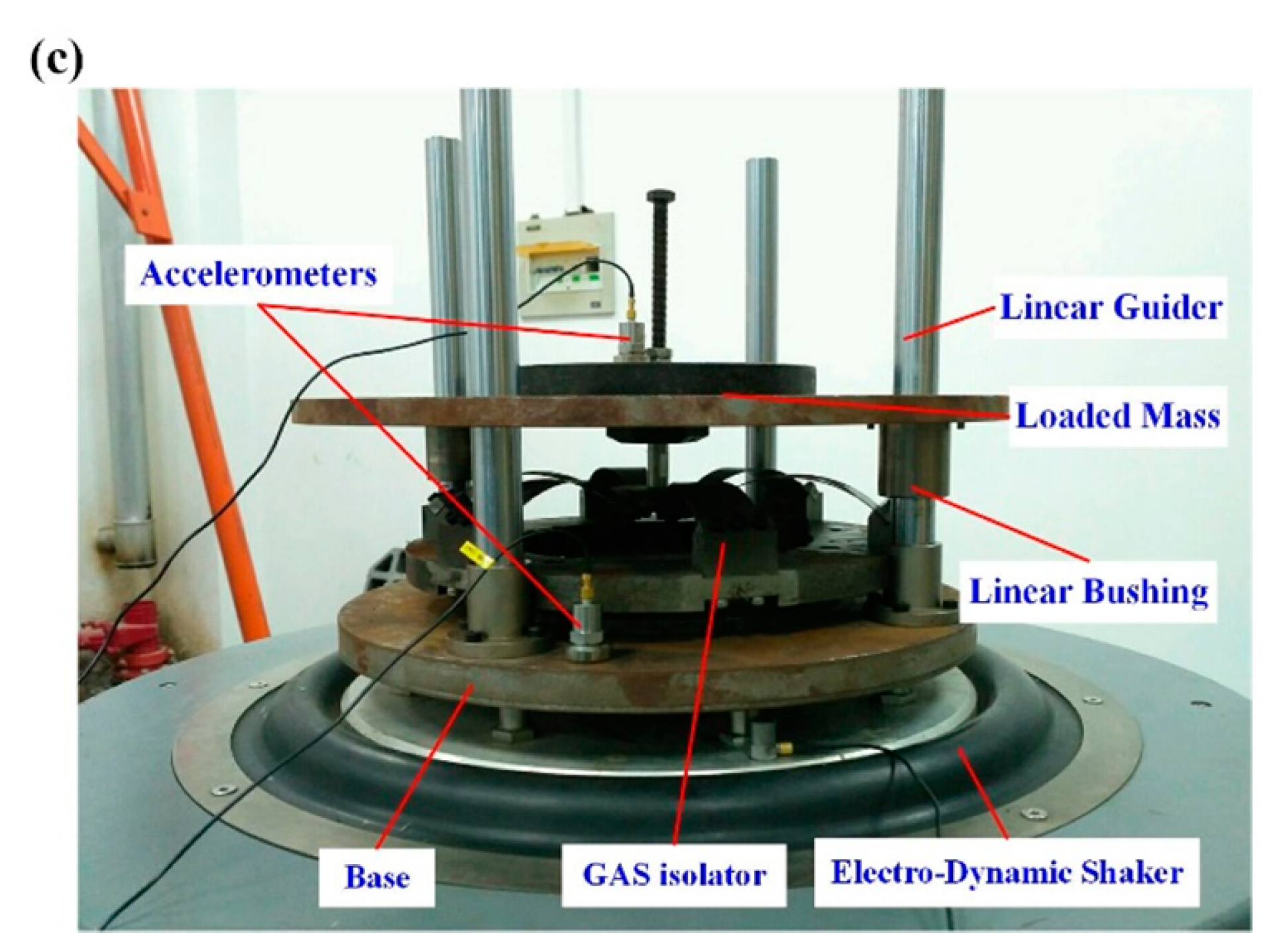
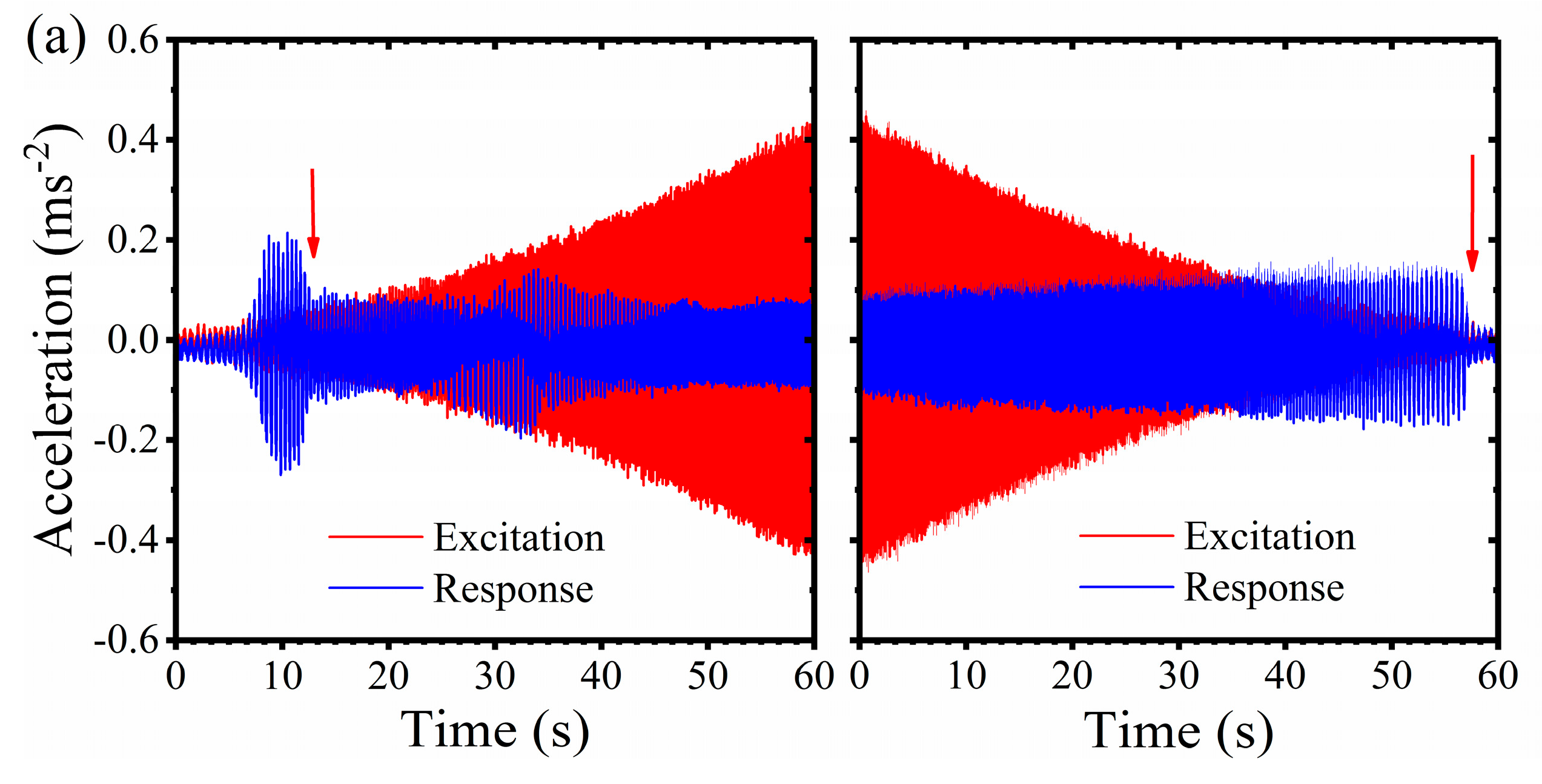
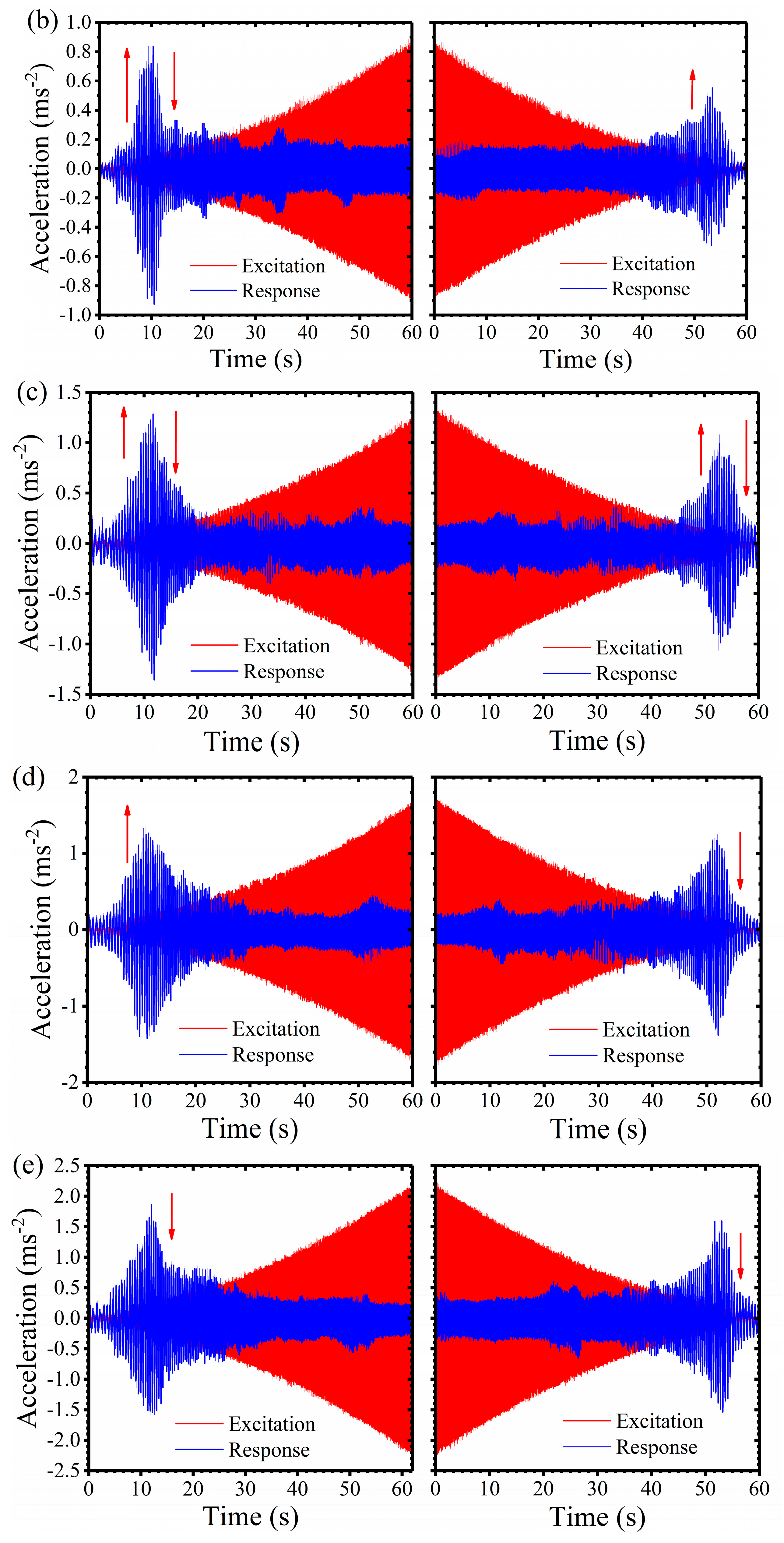
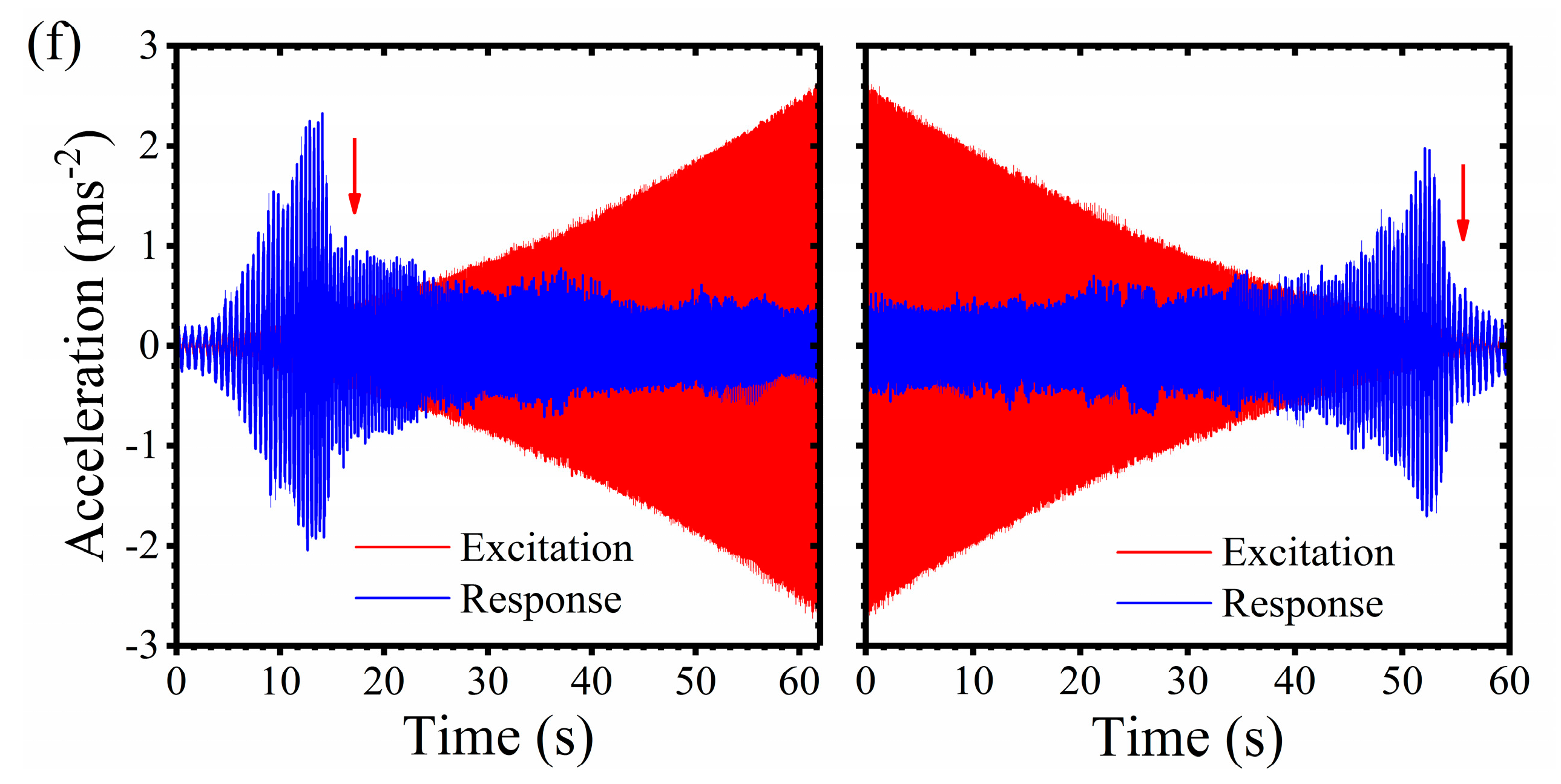
(5) The experiment shows that the designed isolator has good low-frequency isolation performance. Under the rated working load, the initial isolation frequency is not larger than 3.6 Hz. With the excitation amplitude increases, the initial isolation frequency of the isolator decreases linearly. When the working load is changed, the initial isolation frequency will be enlarged. In the frequency sweep excitation experiment, both upward jumping and downward jumping phenomena are observed, which demonstrates that the geometric anti-spring isolator had complex nonlinearity characteristics when damping is light. The nonlinearity characteristics of the geometric anti-spring isolator vary as the excitation amplitude increases.