Member Discrete Element Method for Static and Dynamic Responses Analysis of Steel Frames with Semi-Rigid Joints
Abstract
:Featured Application
Abstract
1. Introduction
2. Member Discrete Element Method (MDEM)
2.1. Particle Motion Equations and Internal Forces
2.1.1. Particle Motion Equations
2.1.2. Particle Internal Forces
2.2. MDEM for Modelling Geometric Nonlinearity
2.3. MDEM for Modeling Facture Behavior
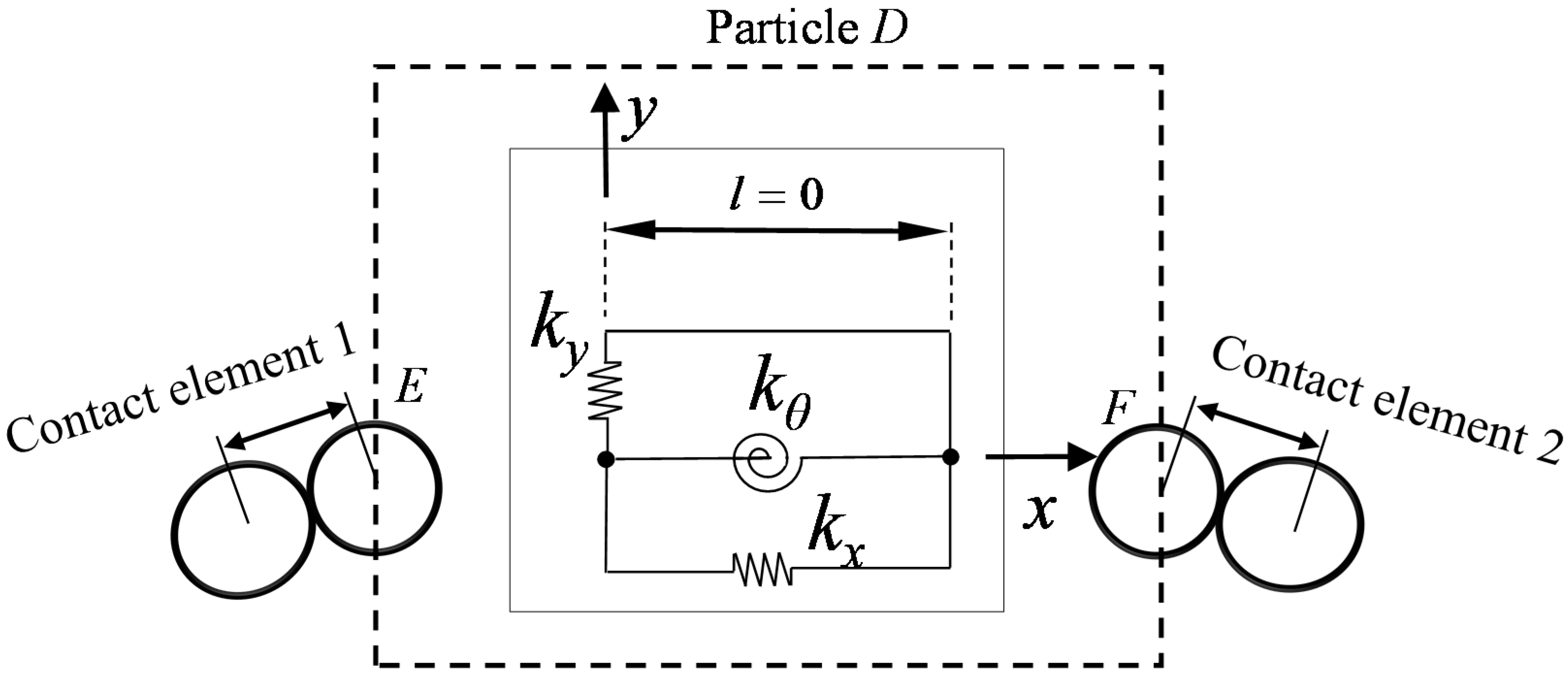
3. Member Discrete Element Modeling for Semi-Rigid Connections
3.1. Virtual Zero-Length Spring Element
3.2. Semi-Rigid Connection Models
3.3. Cyclic Behavior Modelling of Semi-Rigid Connections
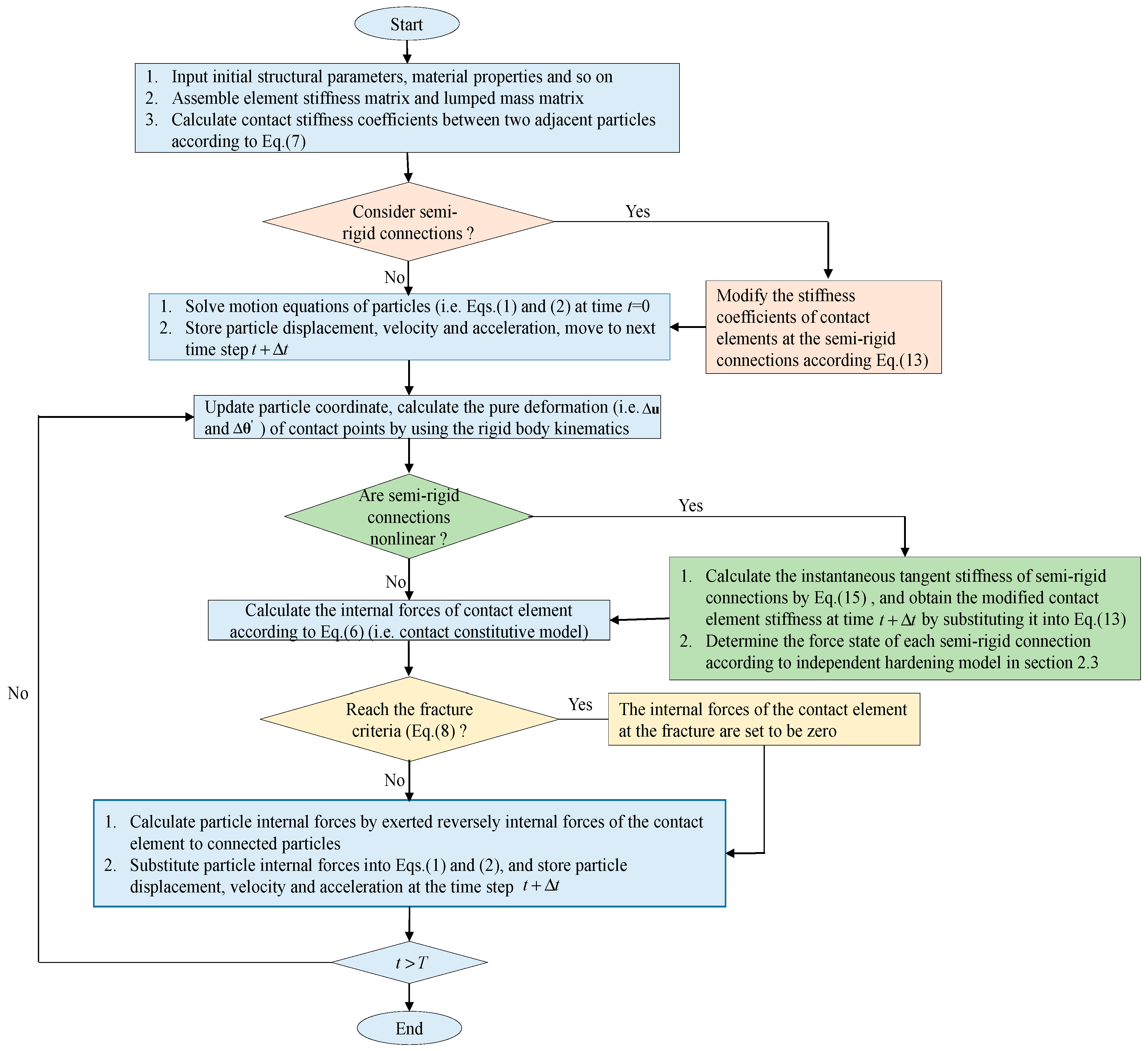
3.4. Computational Procedures for Static and Dynamic Analysis of Steel Frames with Semi-Rigid Joints
4. Examples
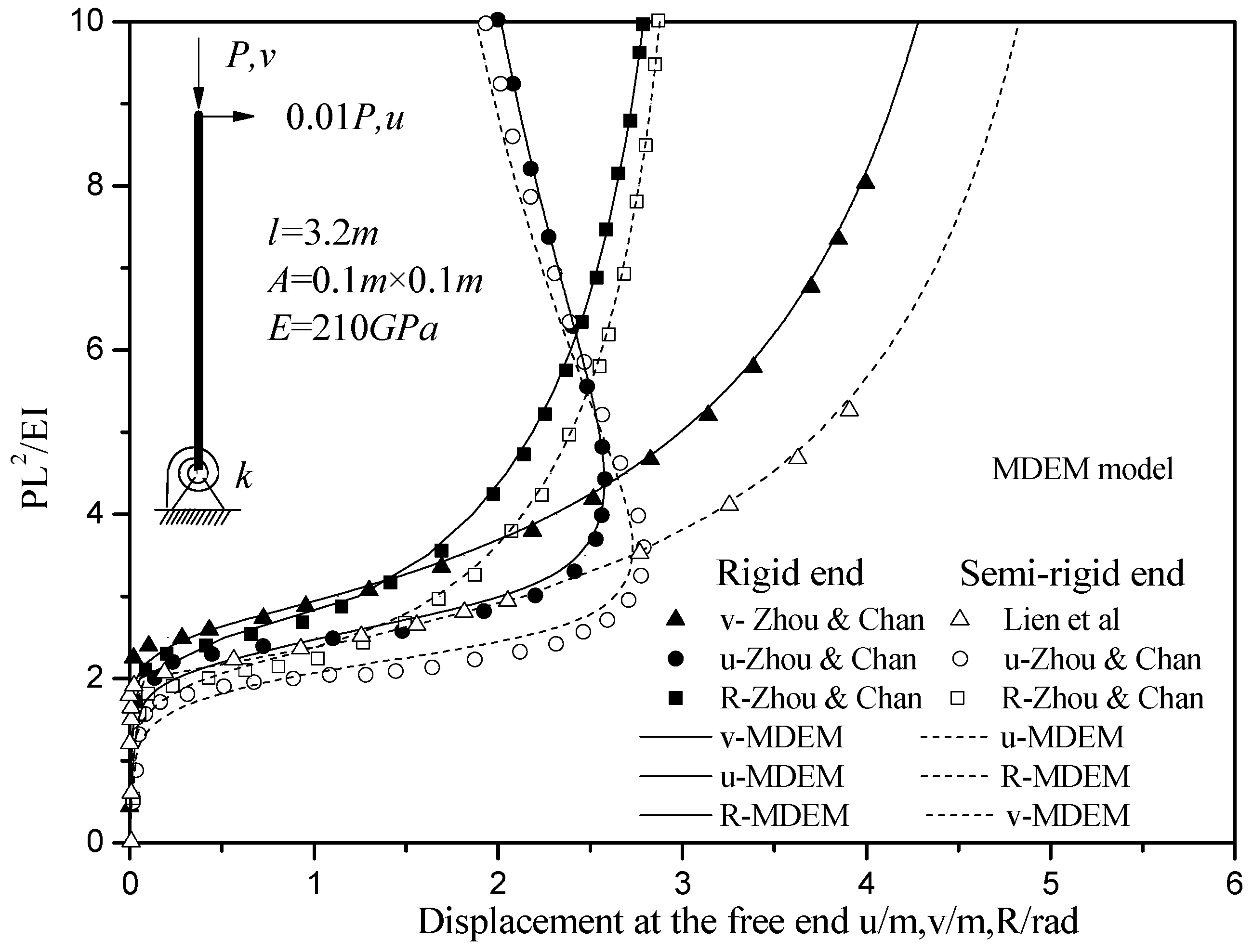
4.1. Geometrically Nonlinear Analysis of a Column with Elastic Support
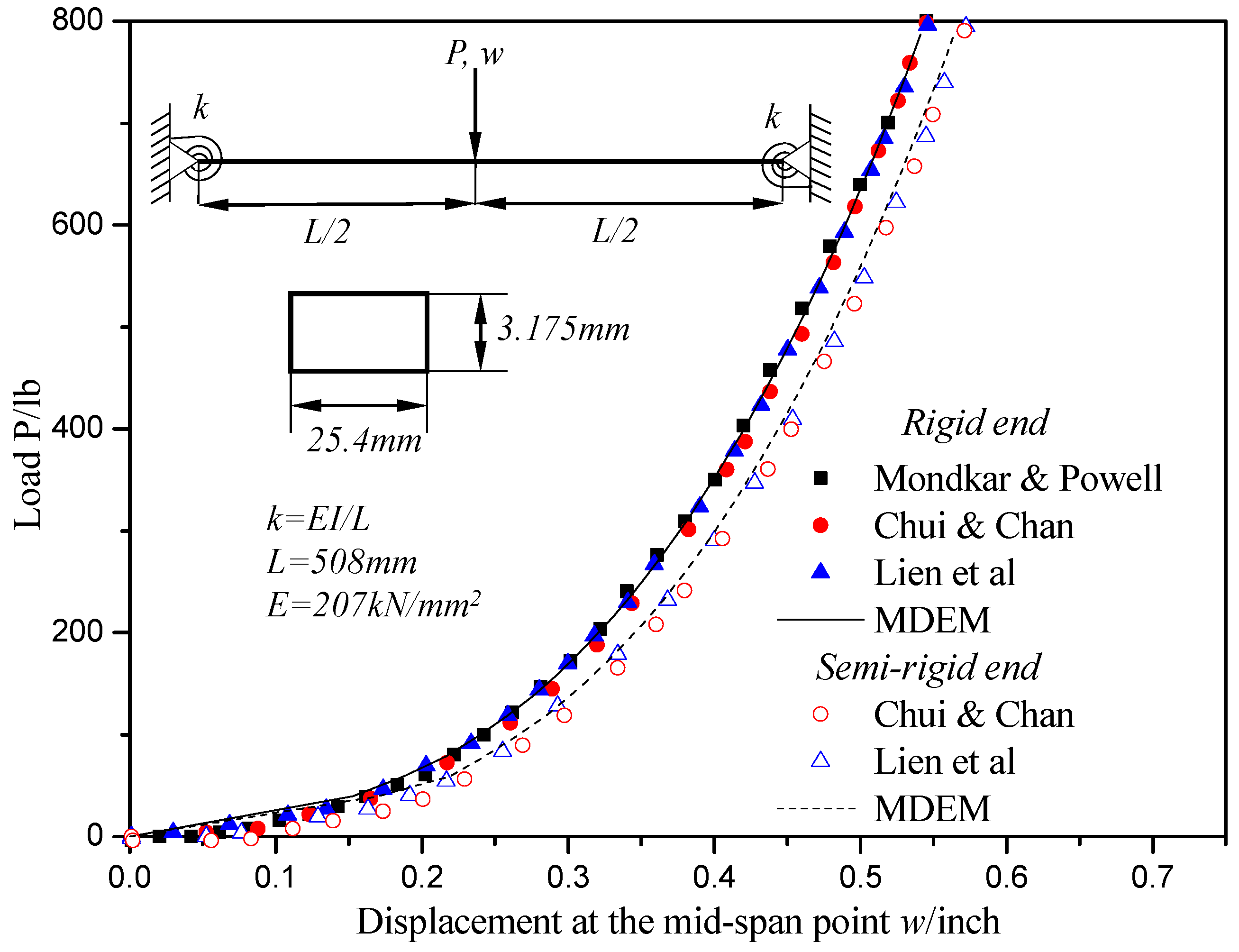
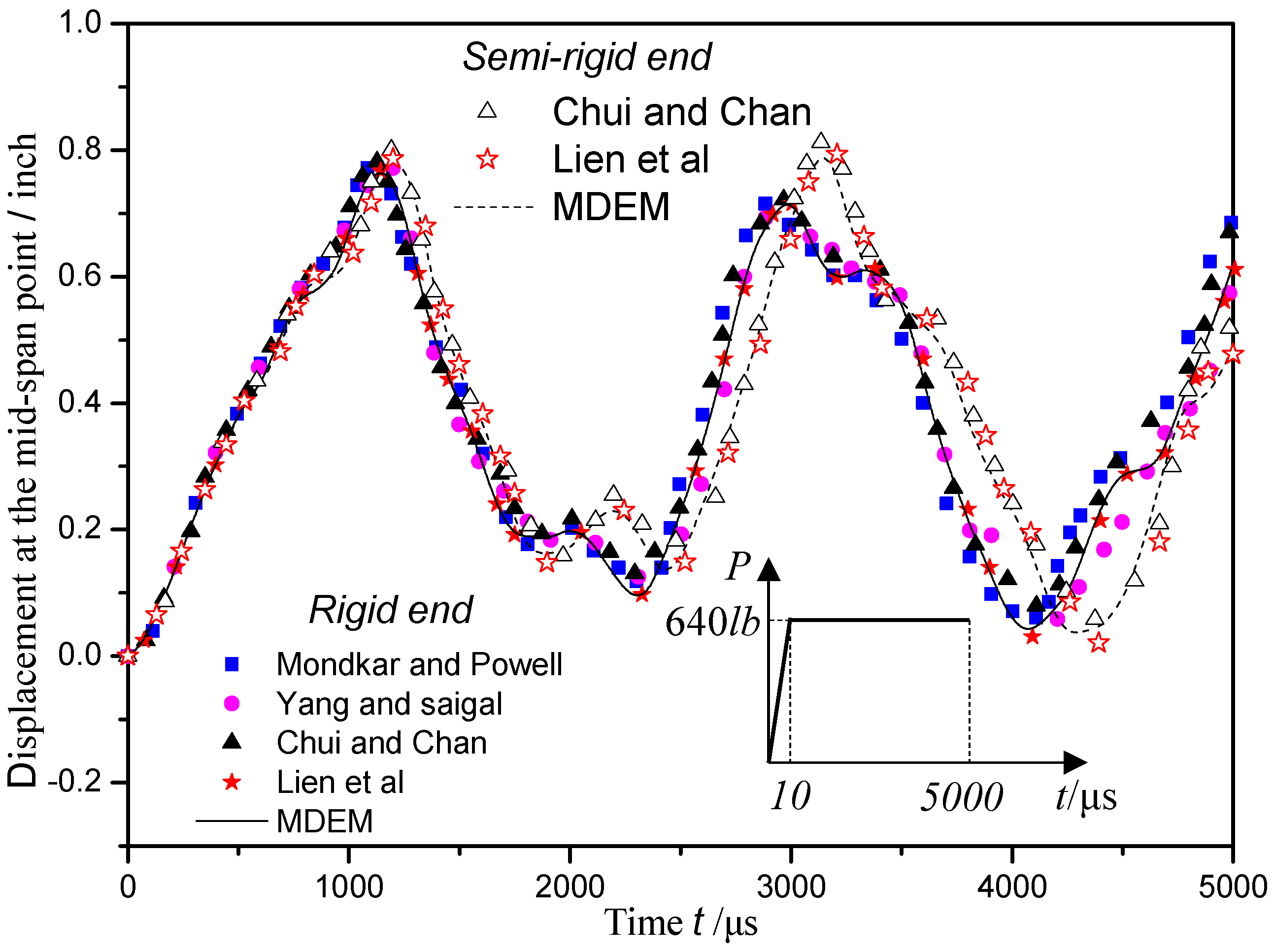
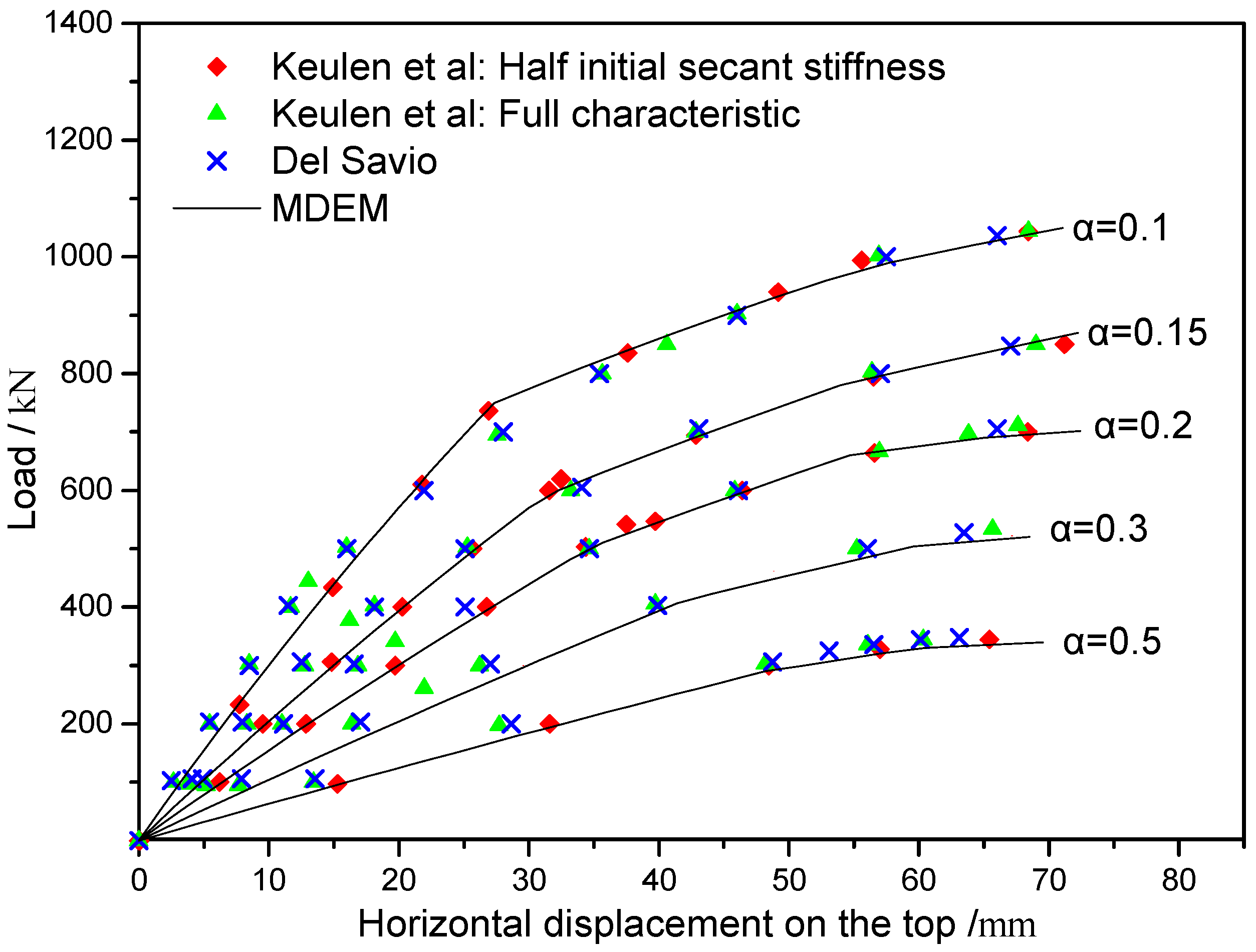
4.2. Static and Dynamic Response of a Beam with Elastic Ends
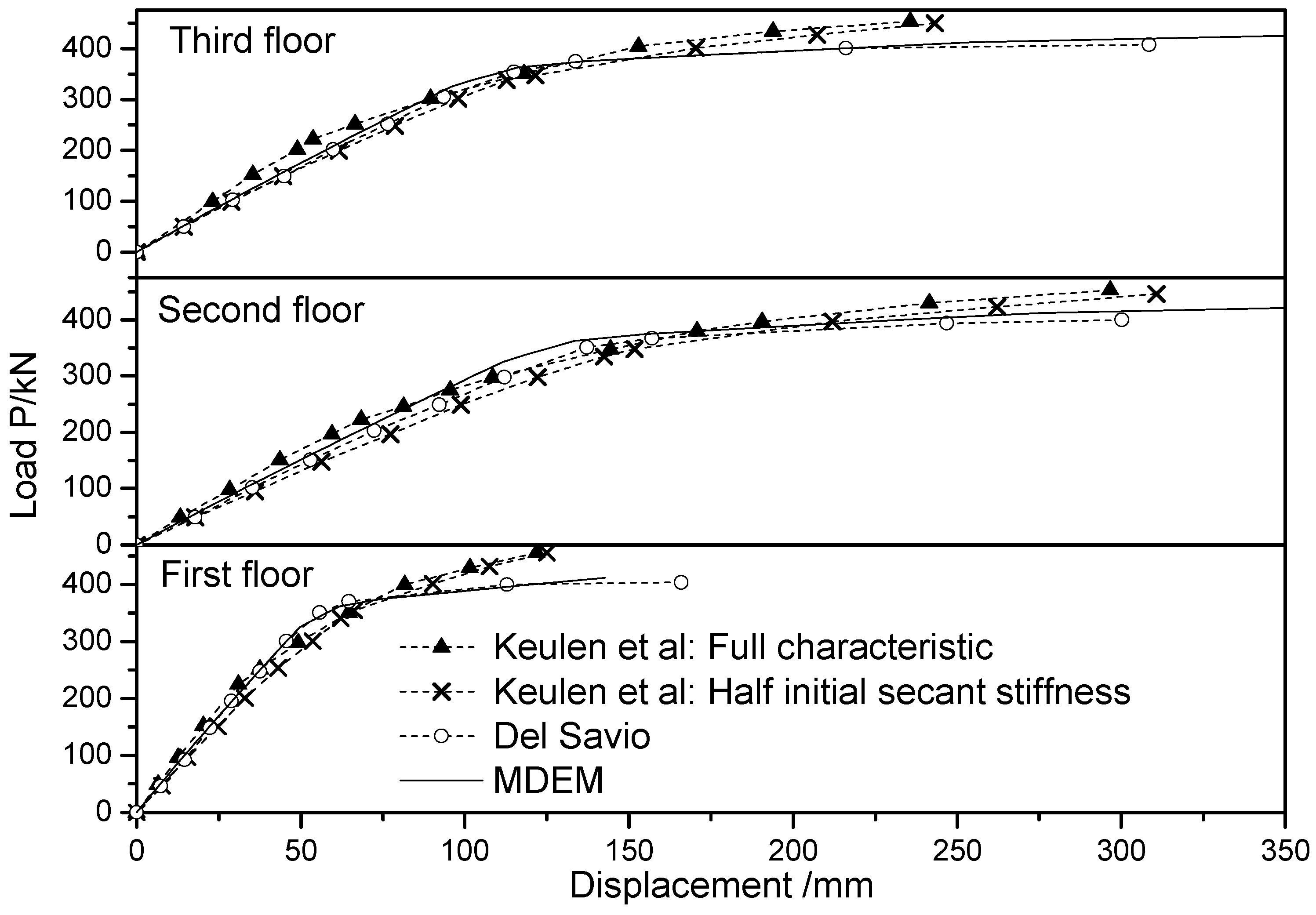
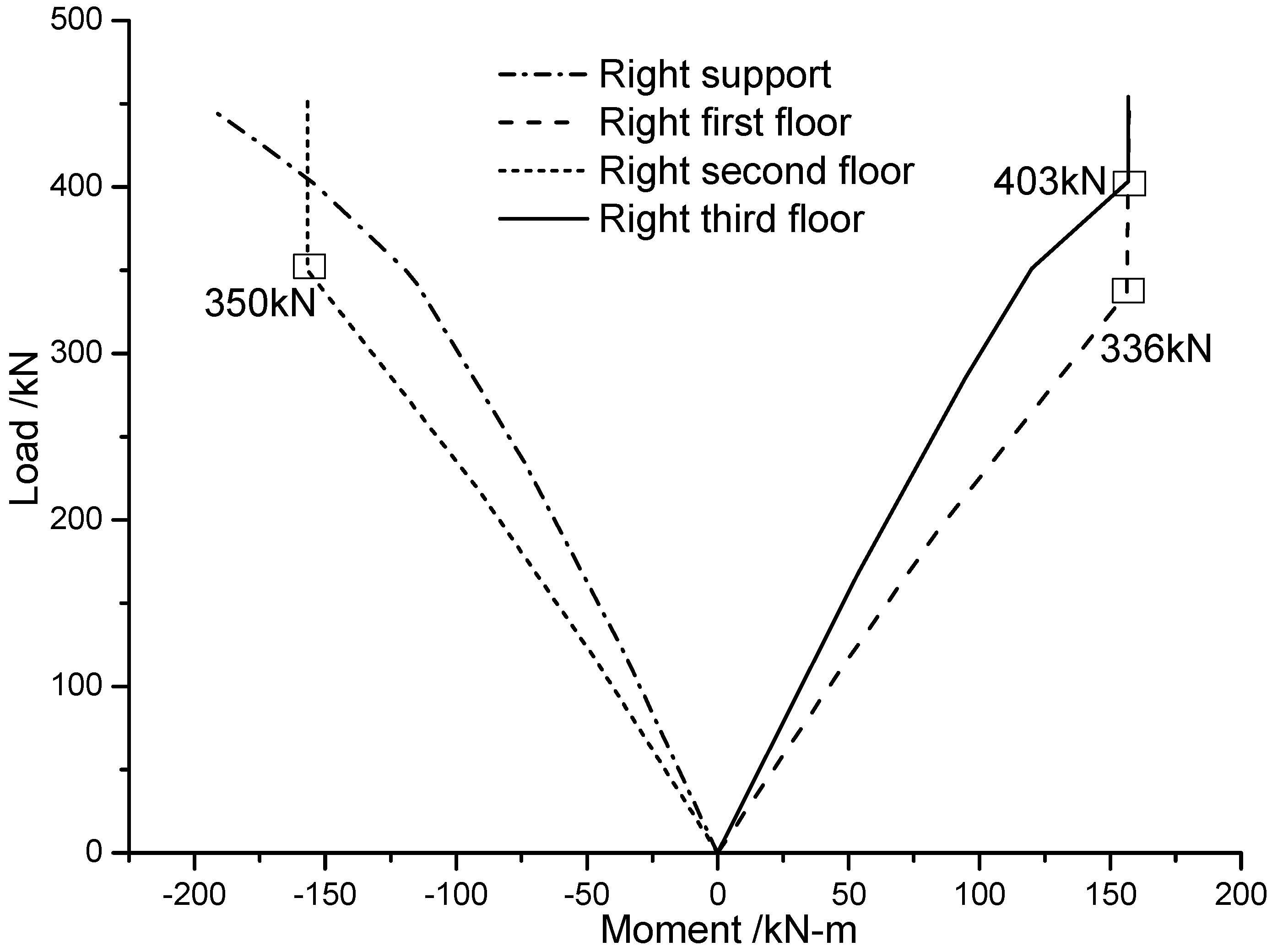
4.3. Static and Dynamic Response Analysis of Steel Frames with Linear Semi-Rigid Connections
4.4. Snap-Through Buckling Analysis of the Williams Toggle Frame with Linear Semi-Rigid Connections and Supports
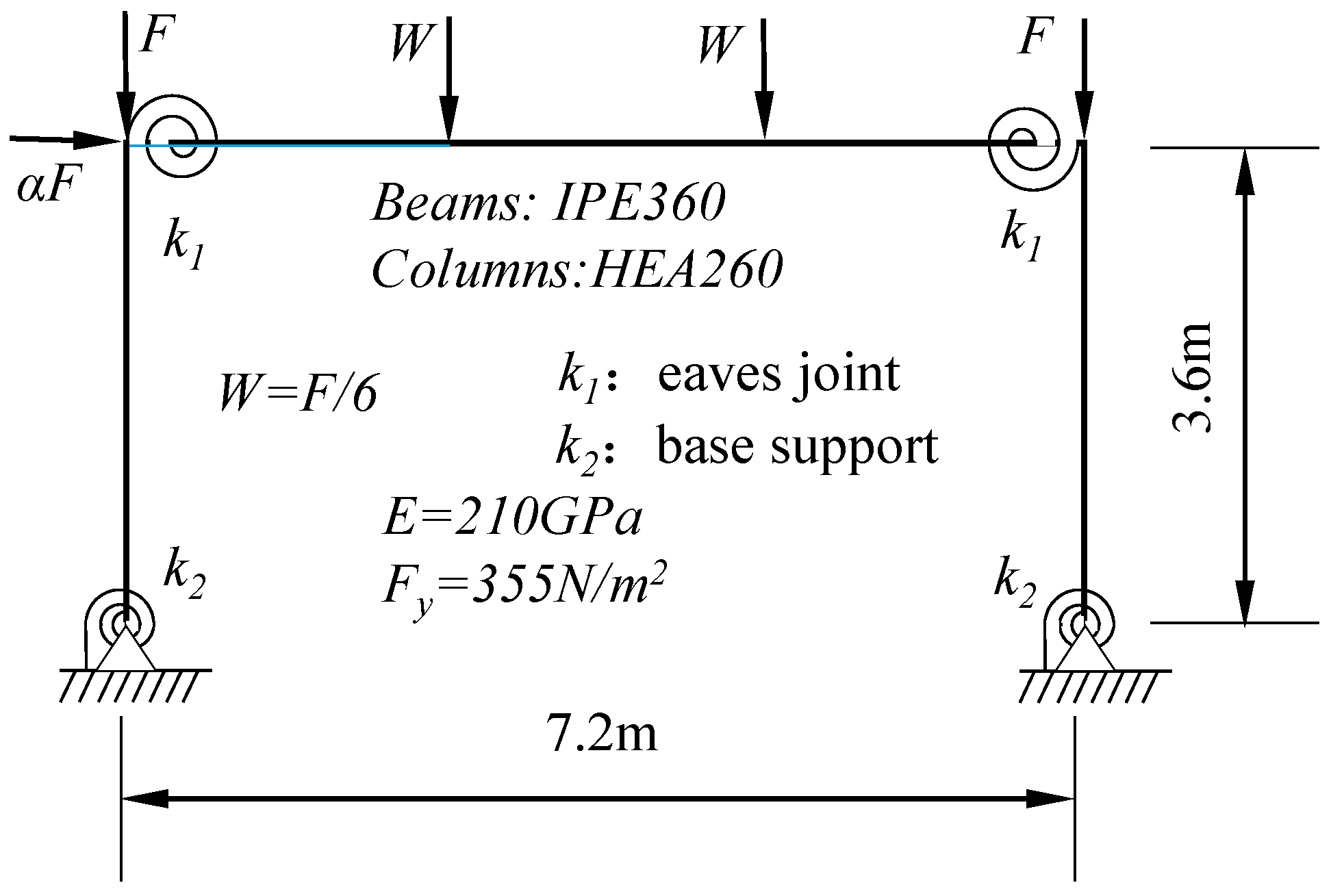
4.5. Static Analysis of a Steel Portal Frame with Bilinear Semi-Rigid Connections
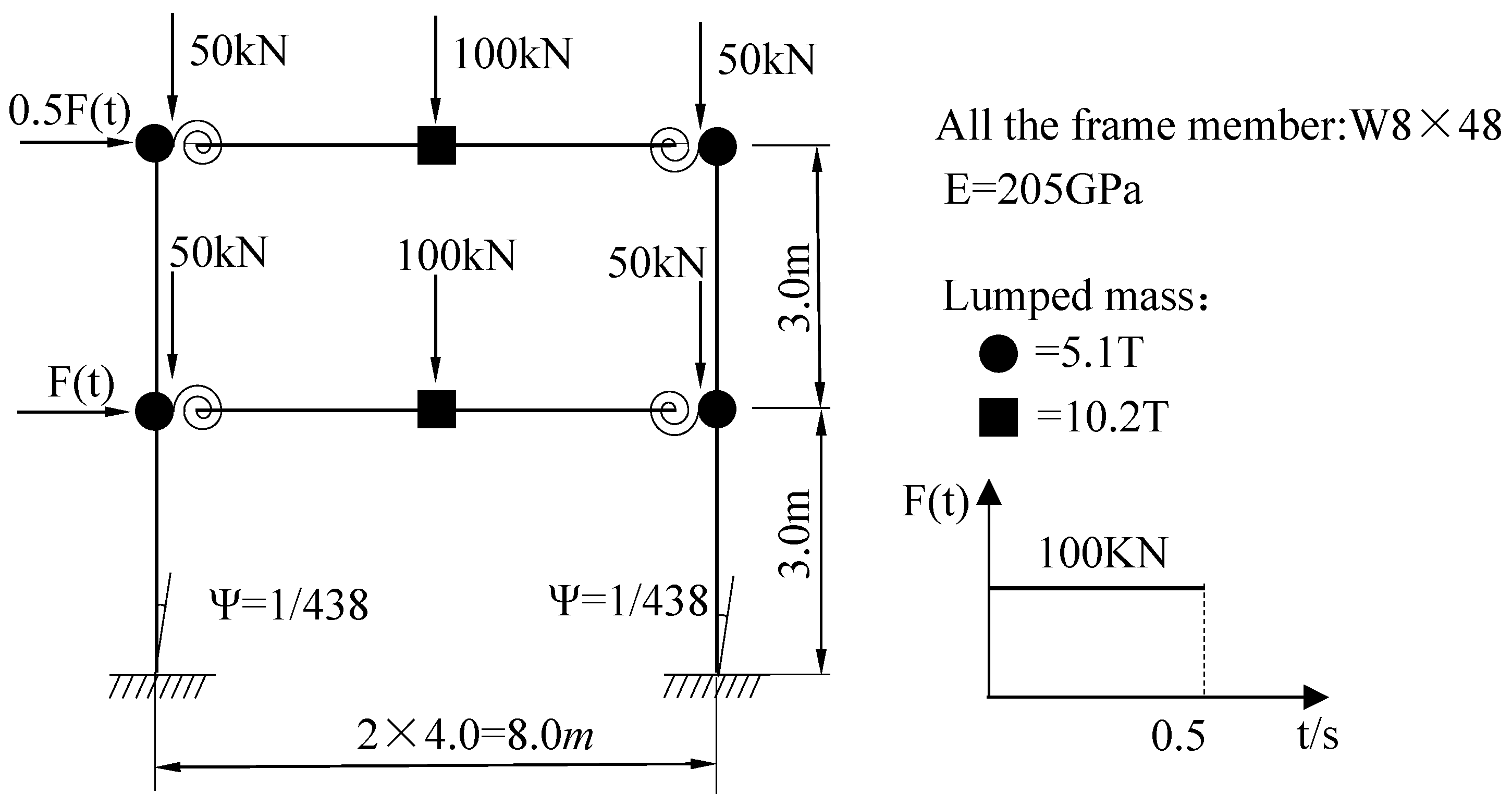
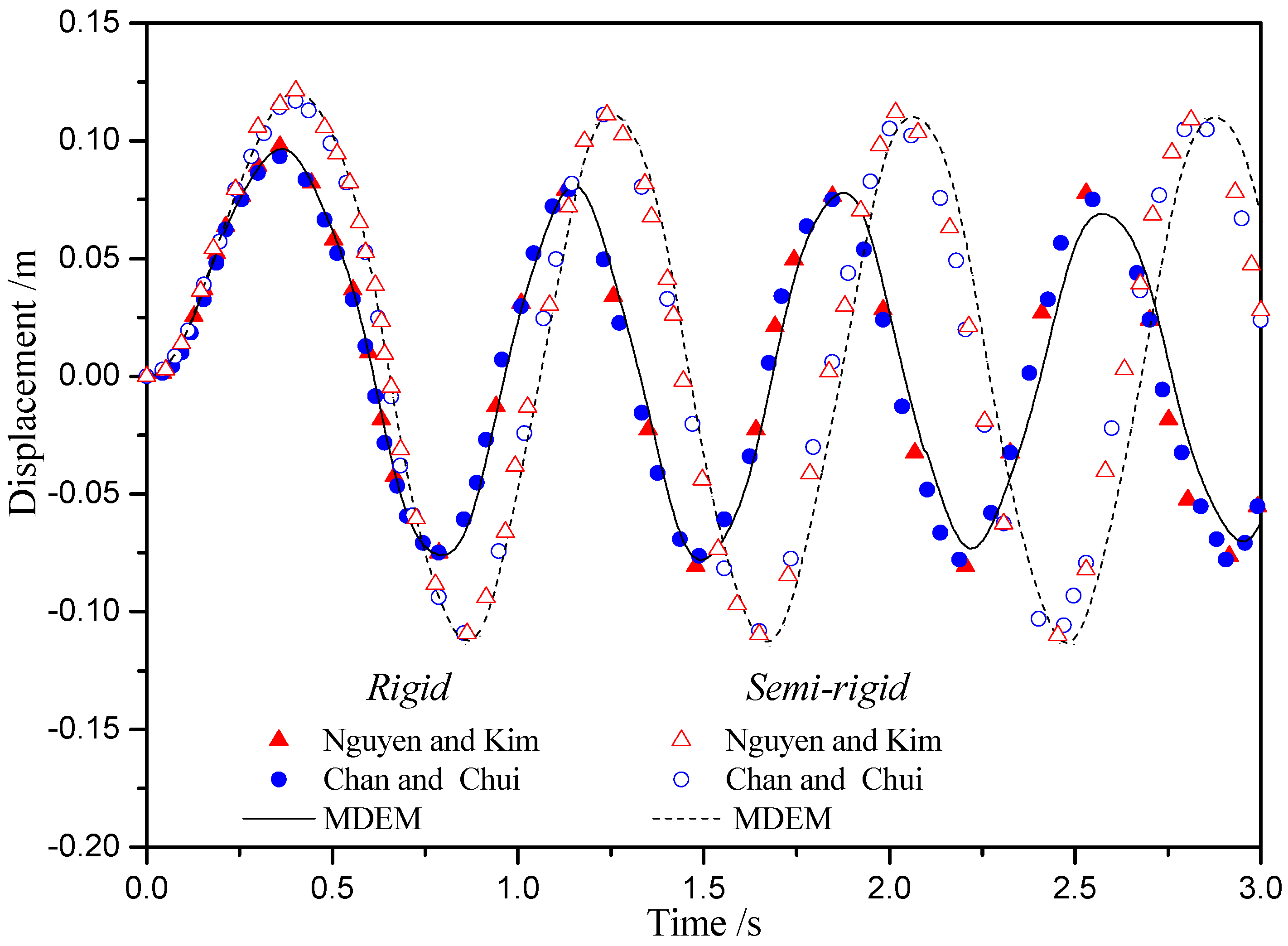
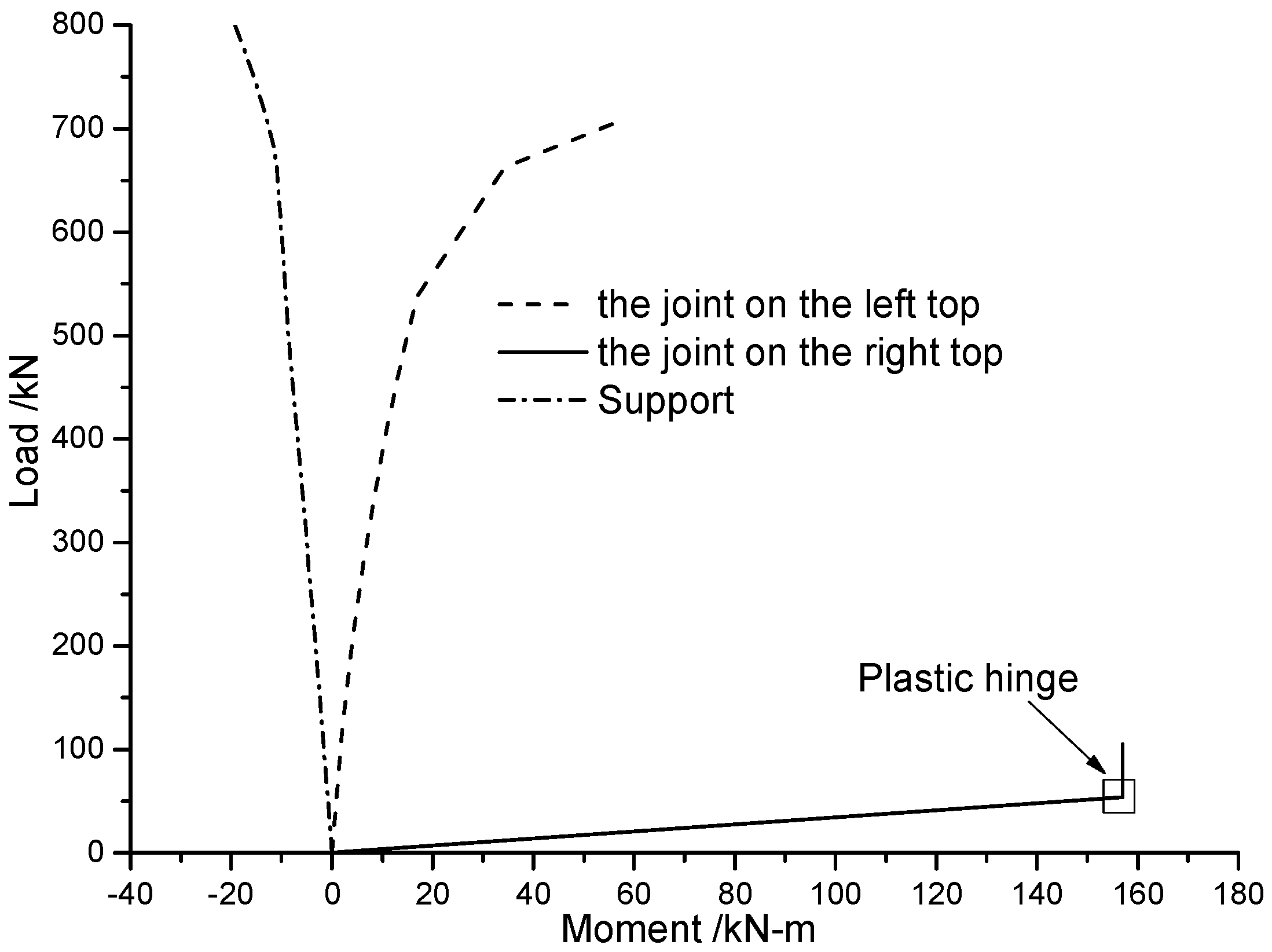
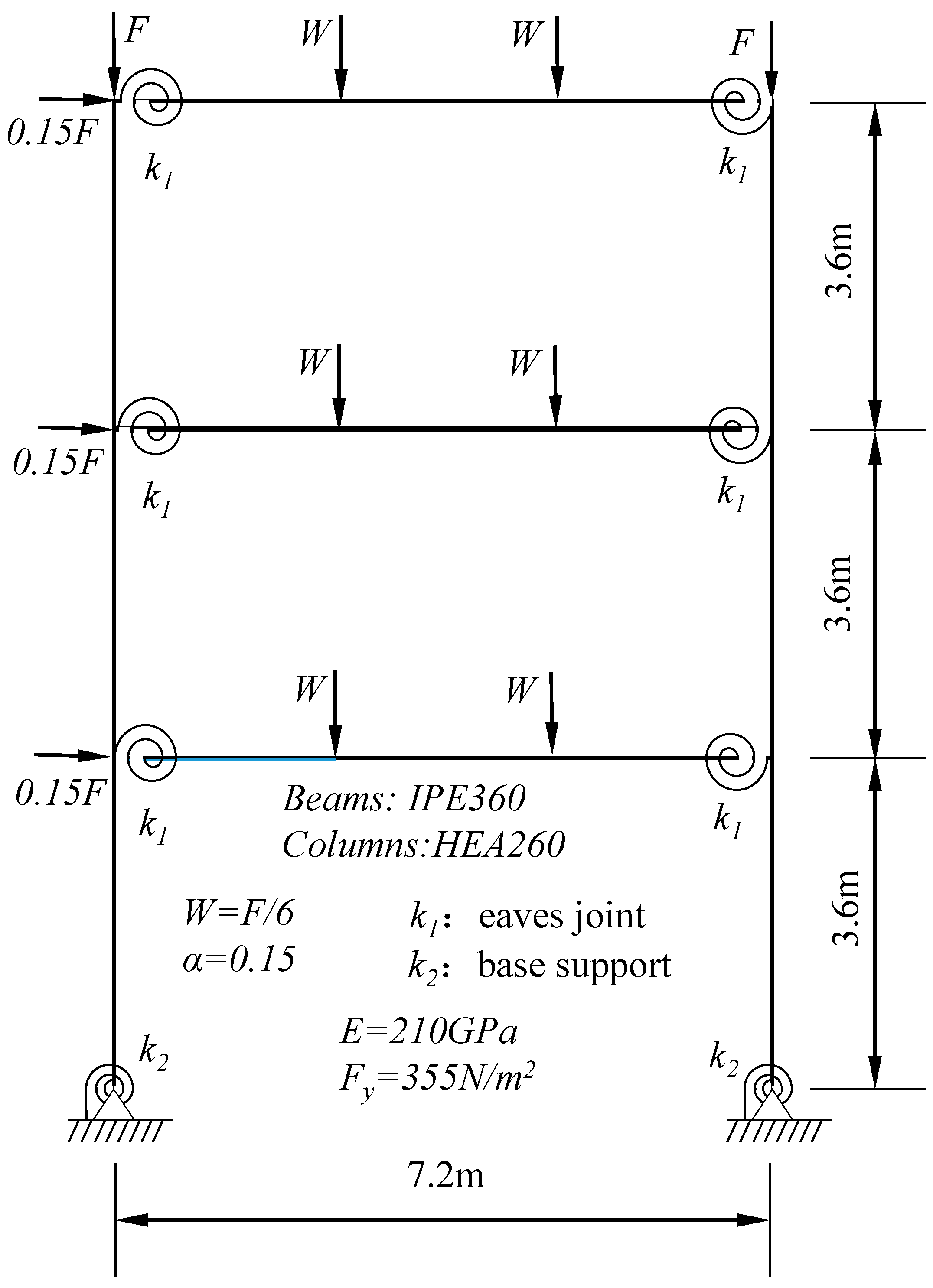
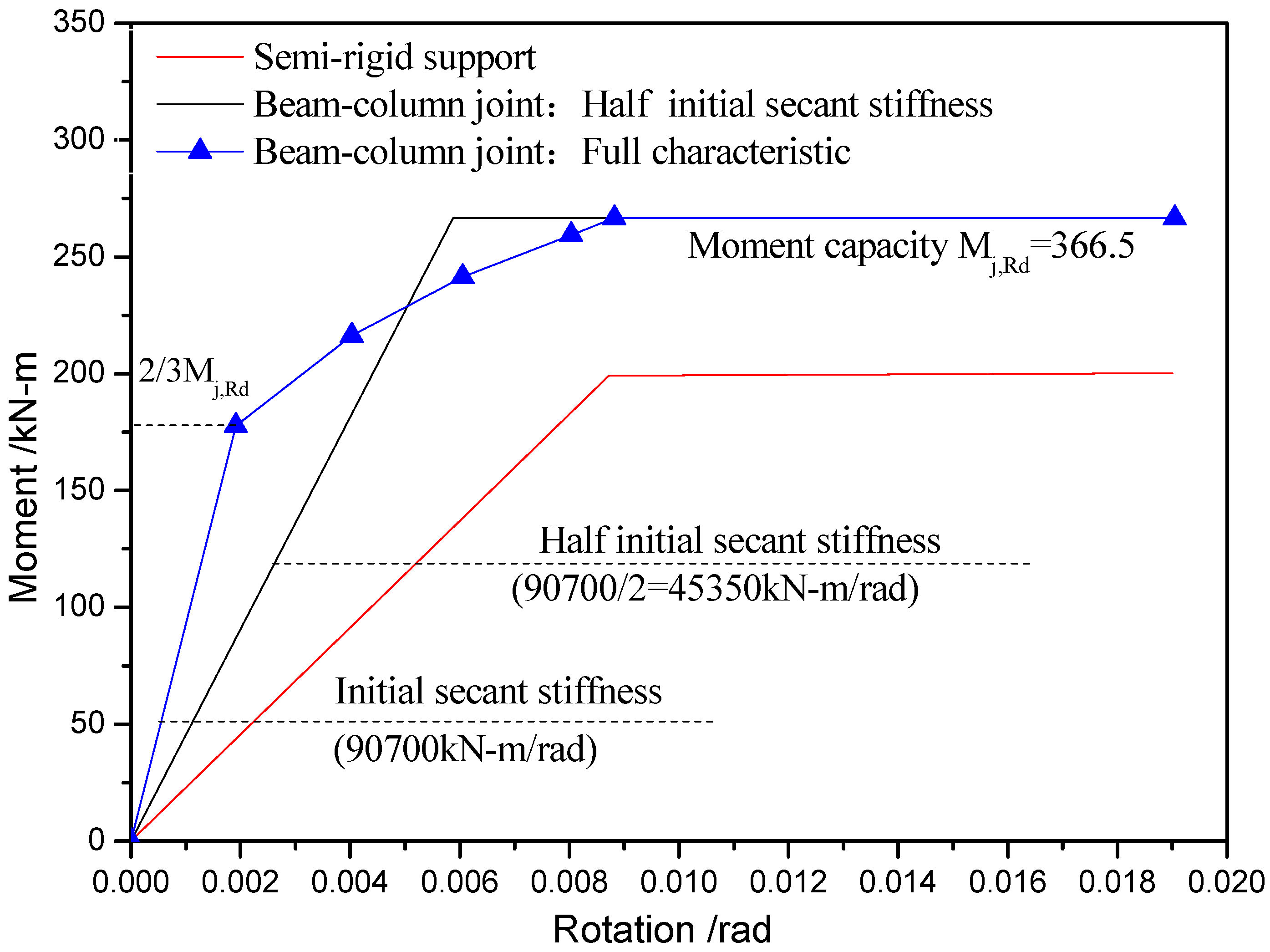
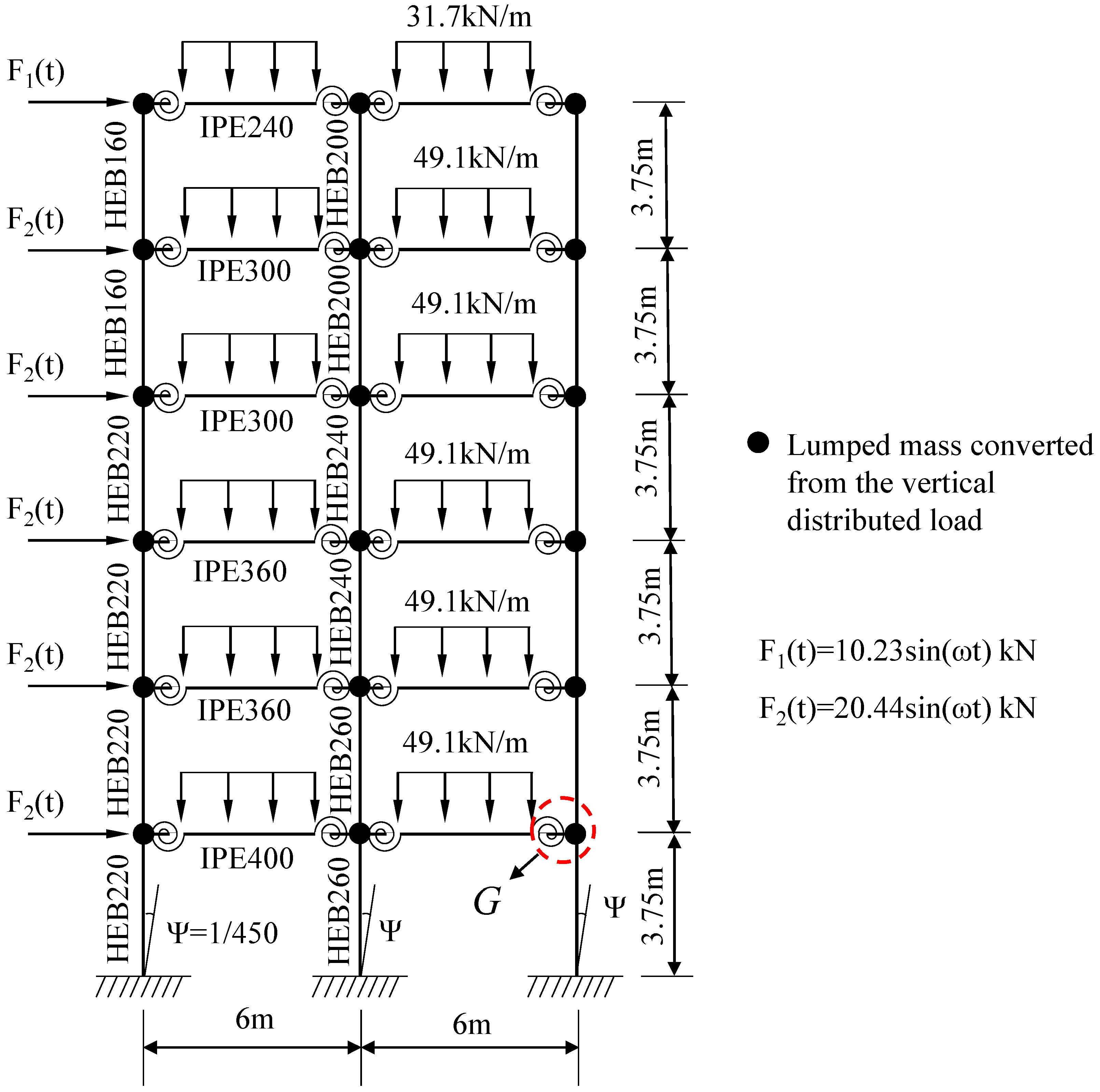
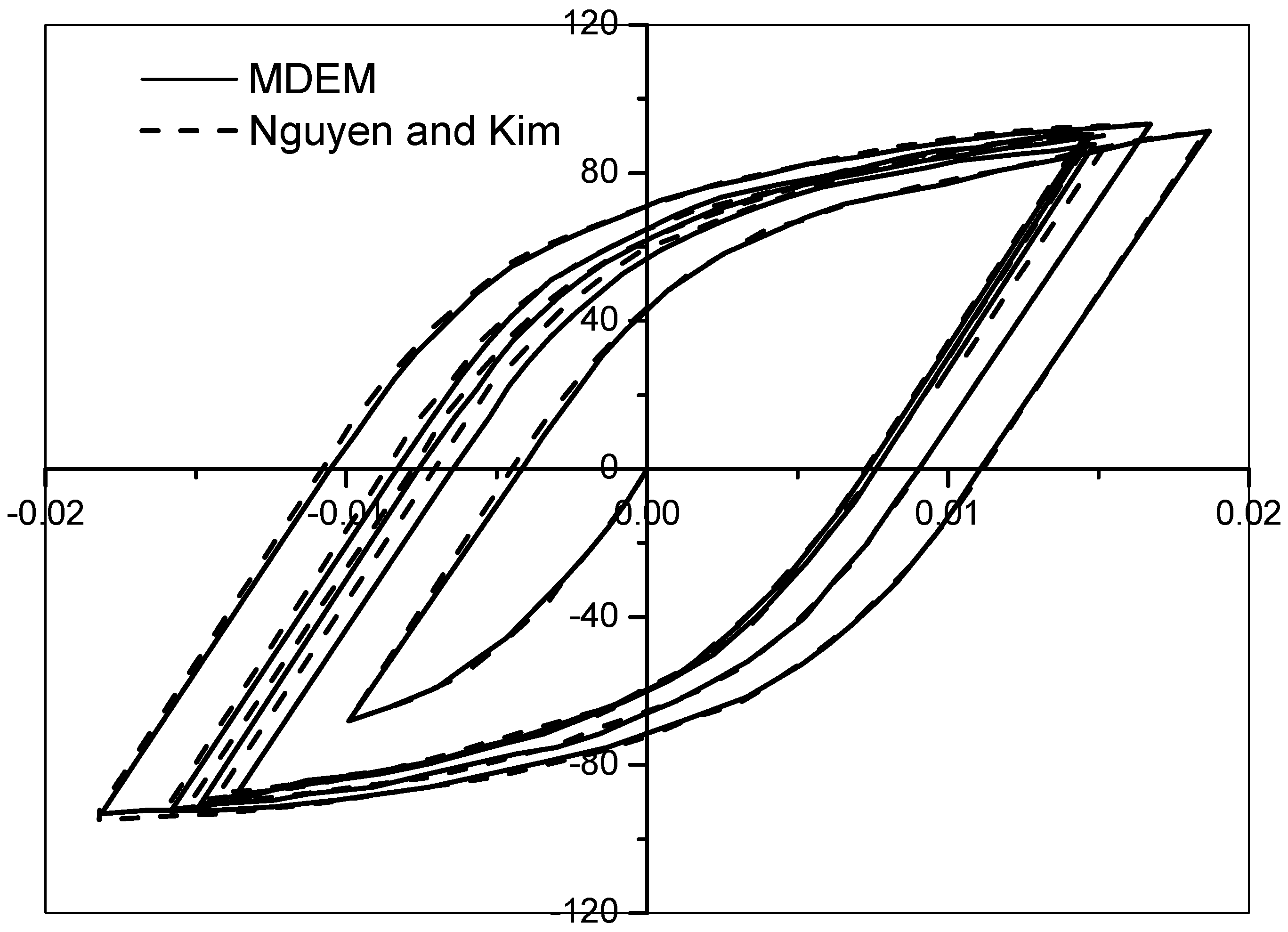
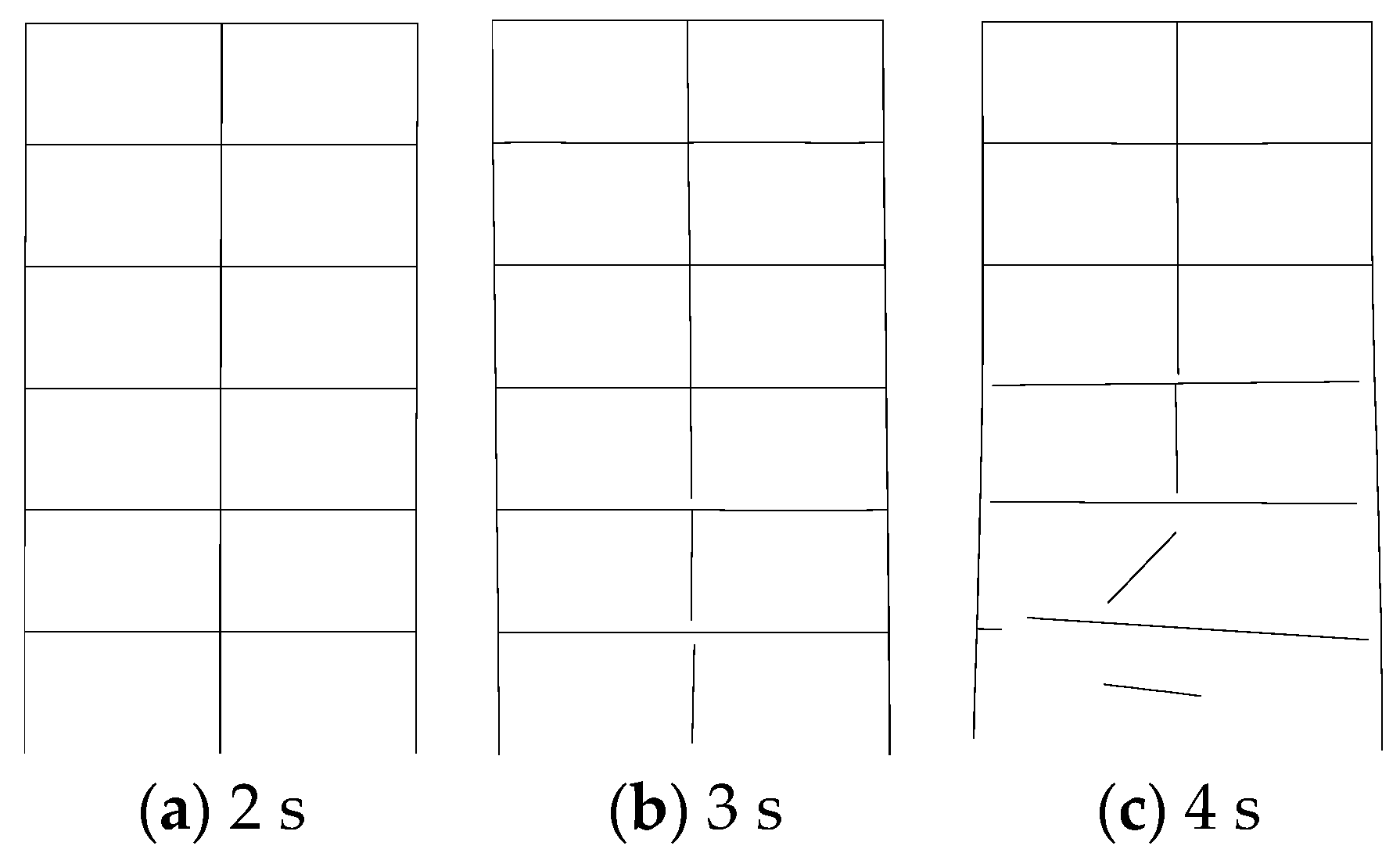
4.6. Dynamic Analysis of the Two-Span, Six-Story Vogel Steel Frame with Nonlinear Semi-Rigid Connections
5. Conclusions
- (1)
- This paper presented an effective numerical approach for static and dynamic behavior simulation of steel frames with semi-rigid joints based on the Member Discrete Element Method (MDEM). In the MDEM, a structure is discretized into a set of finite rigid particles, as well as geometric nonlinearity and fracture behaviors can be naturally captured. A virtual spring element without actual length is applied to simulate the semi-rigid connection. On this basis, the modified formula of the contact element stiffness at the semi-rigid connection is derived. Finally, the numerical approach proposed is verified by complex behaviors of steel frames with semi-rigid connections such as geometric nonlinearity, snap-through buckling, dynamic responses and fracture. In addition, compared with other numerical approaches taking the FEM as a representation, the approach proposed is simple and feasible for simulating the semi-rigid connections because the zero-length spring element is not directly involved in the calculation.
- (2)
- The comparison of the analysis results of the proposed approach and the existing researches shows that the modified MDEM can accurately capture linear and nonlinear behaviors of semi-rigid connections. Some common conclusions can be drown as follow: the semi-rigid connections may significantly reduce structural stiffness, and structural bearing capacity under static loading will be overestimated if the semi-rigid connections are ignored; When the frequency of dynamic load applied is close to structural fundamental frequency, resonance occurs in the frames with rigid or linear semi-rigid connections, but not in the frame with nonlinear semi-rigid connections, the reason is that the hysteresis damping of the nonlinear connection causes energy dissipation. Fracture behavior analysis also indicates that frames with semi-rigid connection possess more anti-collapse capacity.
- (3)
- The MDEM can avoid the difficulties of finite element method (FEM) in dealing with strong nonlinearity and discontinuity. A unified computational framework is applied for static and dynamic analyses. The method is simple and generally good, which is an effective tool to investigate complex behaviors of steel frames with semi-rigid connections. In the follow-up study, material nonlinearity will be taken into account to simulate the collapse process of steel frames with semi-rigid connections under strong earthquake or impact loading action.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nguyen, P.-C.; Kim, S.-E. Second-order spread-of-plasticity approach for nonlinear time-history of space semi-rigid steel frames. Finite Elem. Anal. Des. 2015, 105, 1–15. [Google Scholar] [CrossRef]
- Abdalla, K.M.; Chen, W.F. Expanded database of semirigid steel connections. Comput. Struct. 1995, 56, 553–564. [Google Scholar] [CrossRef]
- Brown, N.D.; Anderson, D. Structural properties of composite major axis end plate connections. J. Constr. Steel Res. 2001, 57, 327–349. [Google Scholar] [CrossRef]
- Chen, W.F.; Kishi, N. Semirigid steel beam-to-column connections- data-base and modeling. J. Struct. Eng. ASCE 1989, 115, 105–119. [Google Scholar] [CrossRef]
- Richard, R.M.; Abbott, B.J. Versatile elastic-plastic stress–strain formula. J. Eng. Mech. Div. ASCE 1975, 101, 511–515. [Google Scholar]
- Wang, X.; Ye, J.; Yu, Q. Improved equivalent bracing model for seismic analysis of mid-rise CFS structures. J. Constr. Steel Res. 2017, 136, 256–264. [Google Scholar] [CrossRef]
- Eurocode 3. Design of Steel Structures-Joints Inbuilding Frames; ENV-1993-1-1:1992/A2; Annex, J., Ed.; European Committee for Standardization (CEN): Brussels, Belgium, 1998. [Google Scholar]
- Keulen, D.C.; Nethercot, D.A.; Snijder, H.H.; Bakker, M.C.M. Frame analysis incorporating semirigid joint action: Applicability of the half initial secant stiffnes approach. J. Constr. Steel Res. 2003, 59, 1083–1100. [Google Scholar] [CrossRef]
- Lui, E.M.; Chen, W.F. Analysis and behavior of flexibly-jointed frames. Eng. Struct. 1986, 8, 107–118. [Google Scholar] [CrossRef]
- Ho, W.M.G.; Chan, S.L. Semibifurcation and bifurcation analysis of flexibly connected steel frames. J. Struct. Eng. ASCE 1991, 117, 2298–2318. [Google Scholar] [CrossRef]
- Yau, C.Y.; Chan, S.L. Inelastic and stability analysis of flexibly connected steel frames by springs-in-series model. J. Struct. Eng. 1994, 120, 2803–2819. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Chan, S.L. Self-equilibrating element for second-order analysis of semirigid jointed frames. J. Eng. Mech. 1995, 121, 896–902. [Google Scholar] [CrossRef]
- Chui, P.P.T.; Chan, S.L. Transient response of moment-resistant steel frames with flexible and hysteretic joints. J. Constr. Steel Res. 1996, 39, 221–243. [Google Scholar] [CrossRef]
- Chan, S.L.; Chui, P.T. Non-Linear Static and Cyclic Analysis of Steel Frames with Semi-Rigid Connections; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Sophianopoulos, D.S. The effect of joint flexibility on the free elastic vibration characteristics of steel plane frames. J. Constr. Steel Res. 2003, 59, 995–1008. [Google Scholar] [CrossRef]
- Li, T.Q.; Choo, B.S.; Nethercot, D.A. Connection element method for the analysis of semirigid frames. J. Constr. Steel Res. 1995, 32, 143–171. [Google Scholar] [CrossRef]
- Raftoyiannis, I.G. The effect of semi-rigid joints and an elastic bracing system on the buckling load of simple rectangular steel frames. J. Constr. Steel Res. 2005, 61, 1205–1225. [Google Scholar] [CrossRef]
- Nguyen, P.-C.; Kim, S.-E. Nonlinear elastic dynamic analysis of space steel frames with semi-rigid connections. J. Constr. Steel Res. 2013, 84, 72–81. [Google Scholar] [CrossRef]
- Nguyen, P.-C.; Kim, S.-E. Nonlinear inelastic time-history analysis of three-dimensional semi-rigid steel frames. J. Constr. Steel Res. 2014, 101, 192–206. [Google Scholar] [CrossRef]
- Lien, K.H.; Chiou, Y.J.; Hsiao, P.A. Vector form intrinsic finite-element analysis of steel frames with semi-rigid joints. J. Struct. Eng. 2012, 138, 327–336. [Google Scholar] [CrossRef]
- Ying, Y.; Xing, Y.Z. Nonlinear dynamic collapse analysis of semi-rigid steel frames based on the finite particle method. Eng. Struct. 2016, 118, 383–393. [Google Scholar]
- Ye, J.; Qi, N. Progressive collapse simulation based on DEM for single-layer reticulated domes. J. Constr. Steel Res. 2017, 128, 721–731. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete element model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Ye, J.; Qi, N. Collapse process simulation of reticulated shells based on coupled DEM/FEM model. J. Build. Struct. 2017, 38, 52–61. (In Chinese) [Google Scholar]
- Qi, N.; Ye, J. Nonlinear dynamic analysis of space frame structures by discrete element method. Appl. Mech. Mater. 2014, 638–640, 1716–1719. [Google Scholar] [CrossRef]
- Xu, L.; Ye, J. DEM algorithm for progressive collapse simulation of single-layer reticulated domes under multi-support excitation. J. Earthq. Eng. 2017. [Google Scholar] [CrossRef]
- Wang, X.C. Finite Element Method; Tsinghua University Press: Beijing, China, 2003. [Google Scholar]
- Qi, N.; Ye, J.H. Geometric nonlinear analysis with large deformation of member structures by discrete element method. J. Southeast Univ. (Nat. Sci. Ed.) 2013, 43, 917–922. (In Chinese) [Google Scholar]
- Lynn, K.M.; Isobe, D. Finite element code for impact collapse problem. Int. J. Numer. Method. Eng. 2007, 69, 2538–2563. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Mondkar, D.P.; Powell, G.H. Finite element analysis of nonlinear static and dynamic response. Int. J. Numer. Method. Eng. 1977, 11, 499–520. [Google Scholar] [CrossRef]
- Yang, T.Y.; Saigal, S. A simple element for static and dynamic response of beams with material and geometric nonlinearities. Int. J. Numer. Method. Eng. 1984, 20, 851–867. [Google Scholar] [CrossRef]
- Yang, Y.B.; Chiou, H.T. Analysis with beam elements. J. Eng. Mech. 1987, 113, 1404–1419. [Google Scholar] [CrossRef]
- Williams, F.W. An approach to the nonlinear behaviour of the members of a rigid jointed plane framework with finite deflection. Q. J. Mech. Appl. Maths 1964, 17, 451–469. [Google Scholar] [CrossRef]
- Del Savio, A.A.; Andrade, S.A.L.; Vellasco, P.C.G.S.; Martha, L.F. A nonlinear system for semirigid steel portal frame analysis. In Proceedings of the 7th International Conference on Computational Structures Technology, Tecnologiaem Computação Gráfica, Rio de Janeiro, Brazil, 10–11 January 2004; Volume 1, pp. 1–12. [Google Scholar]





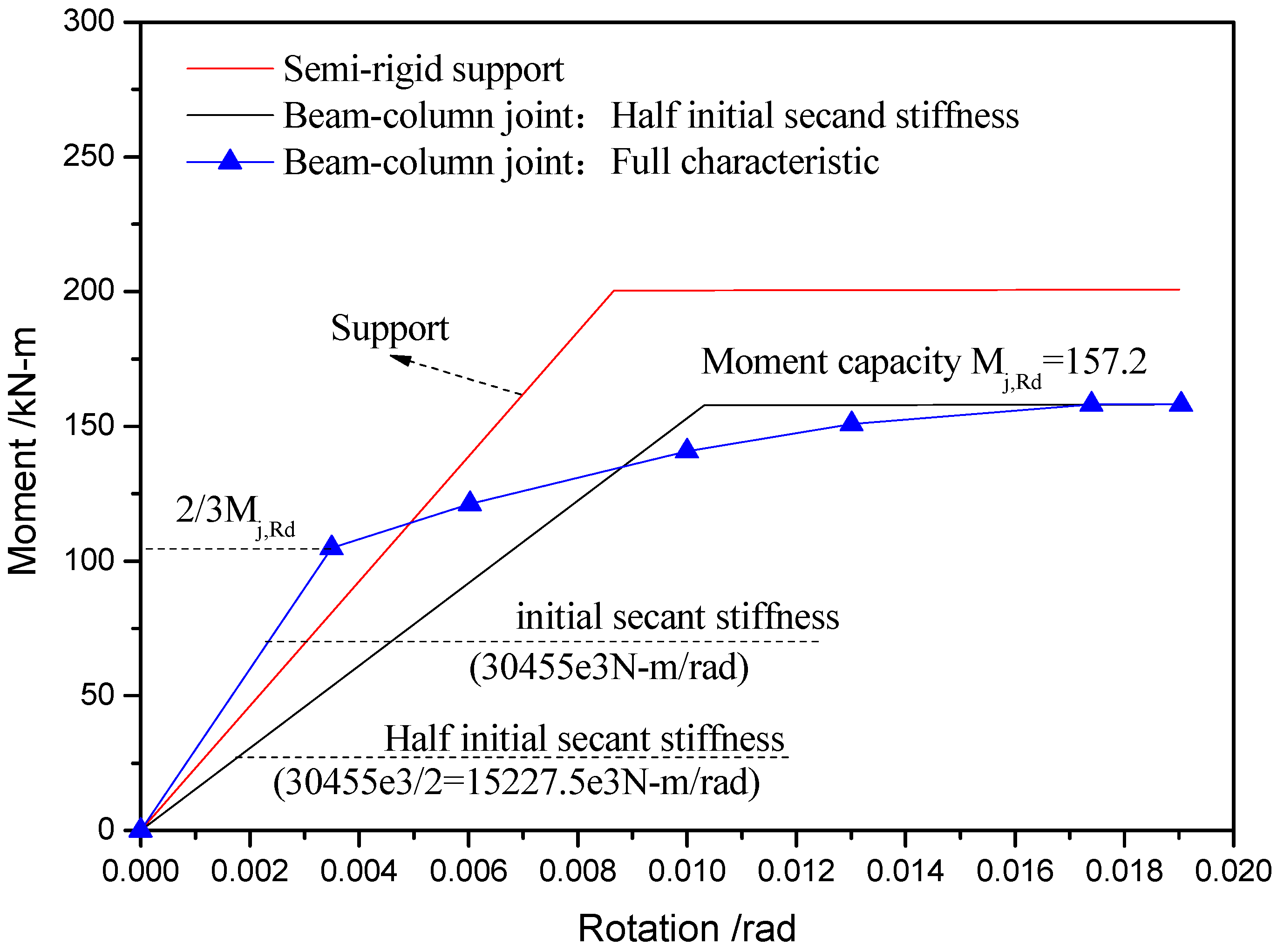


| Semi-Rigid Connection Types | Configuration | Formulas |
|---|---|---|
| Elastic support |  | |
| Couple-bar joint |  | (for two same bars) |
| Beam-column joint |  | (for semi-rigid connections on the beam) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Xu, L. Member Discrete Element Method for Static and Dynamic Responses Analysis of Steel Frames with Semi-Rigid Joints. Appl. Sci. 2017, 7, 714. https://doi.org/10.3390/app7070714
Ye J, Xu L. Member Discrete Element Method for Static and Dynamic Responses Analysis of Steel Frames with Semi-Rigid Joints. Applied Sciences. 2017; 7(7):714. https://doi.org/10.3390/app7070714
Chicago/Turabian StyleYe, Jihong, and Lingling Xu. 2017. "Member Discrete Element Method for Static and Dynamic Responses Analysis of Steel Frames with Semi-Rigid Joints" Applied Sciences 7, no. 7: 714. https://doi.org/10.3390/app7070714





