Dynamic Behavior of a Simple Rolling Seismic Isolator with a Position Restoring Device
Abstract
:1. Introduction
- Performance that returns the object to the initial position after the earthquake
- Improvement of damping, which is a disadvantage of the RIS system.
- Suppression of movement during weak earthquakes.
- Control of resonance generation in the RIS system.
2. Equation of Motion
2.1. Description of Analysis Model
2.2. Equation of Motion
3. Numerical Analysis
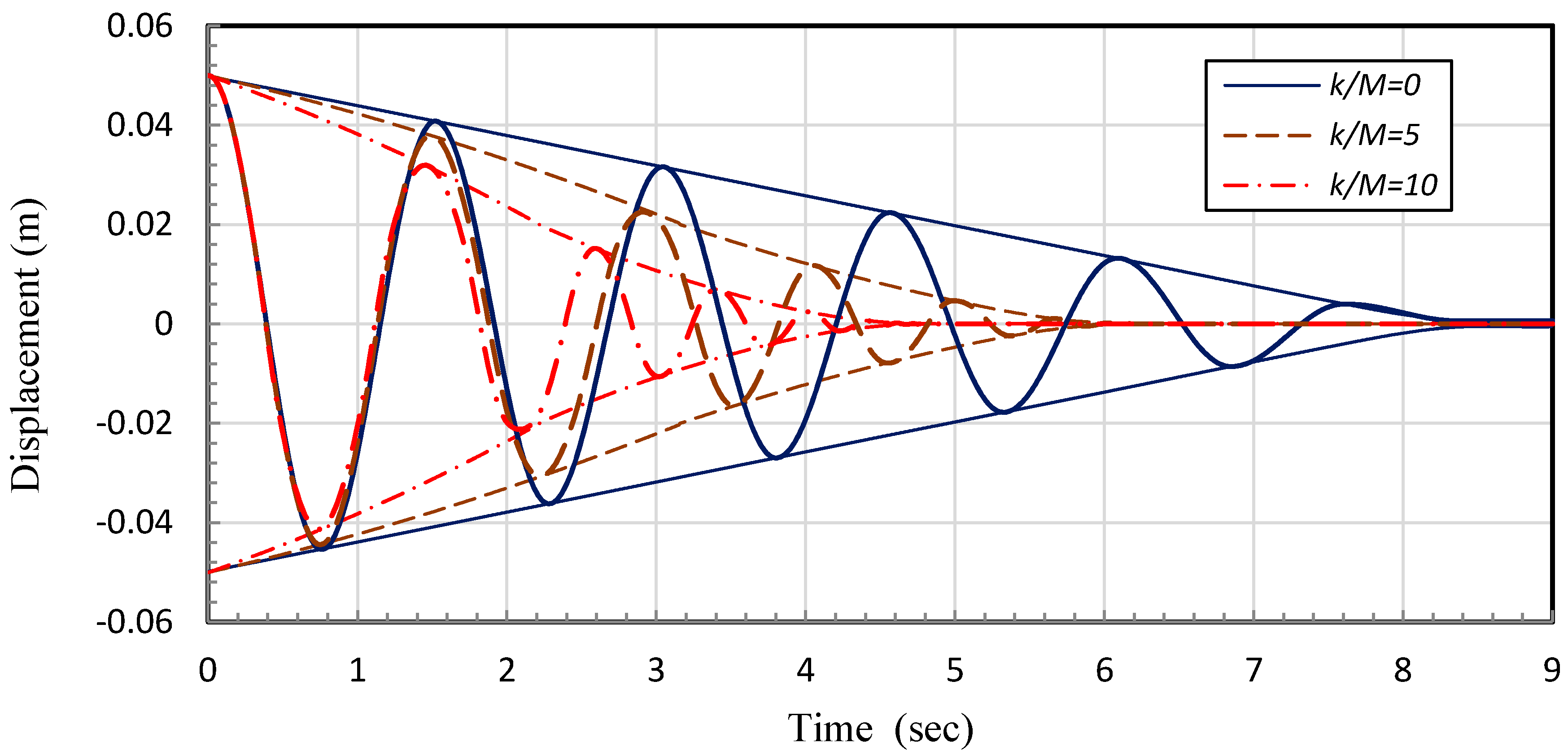
3.1. Position Restoration
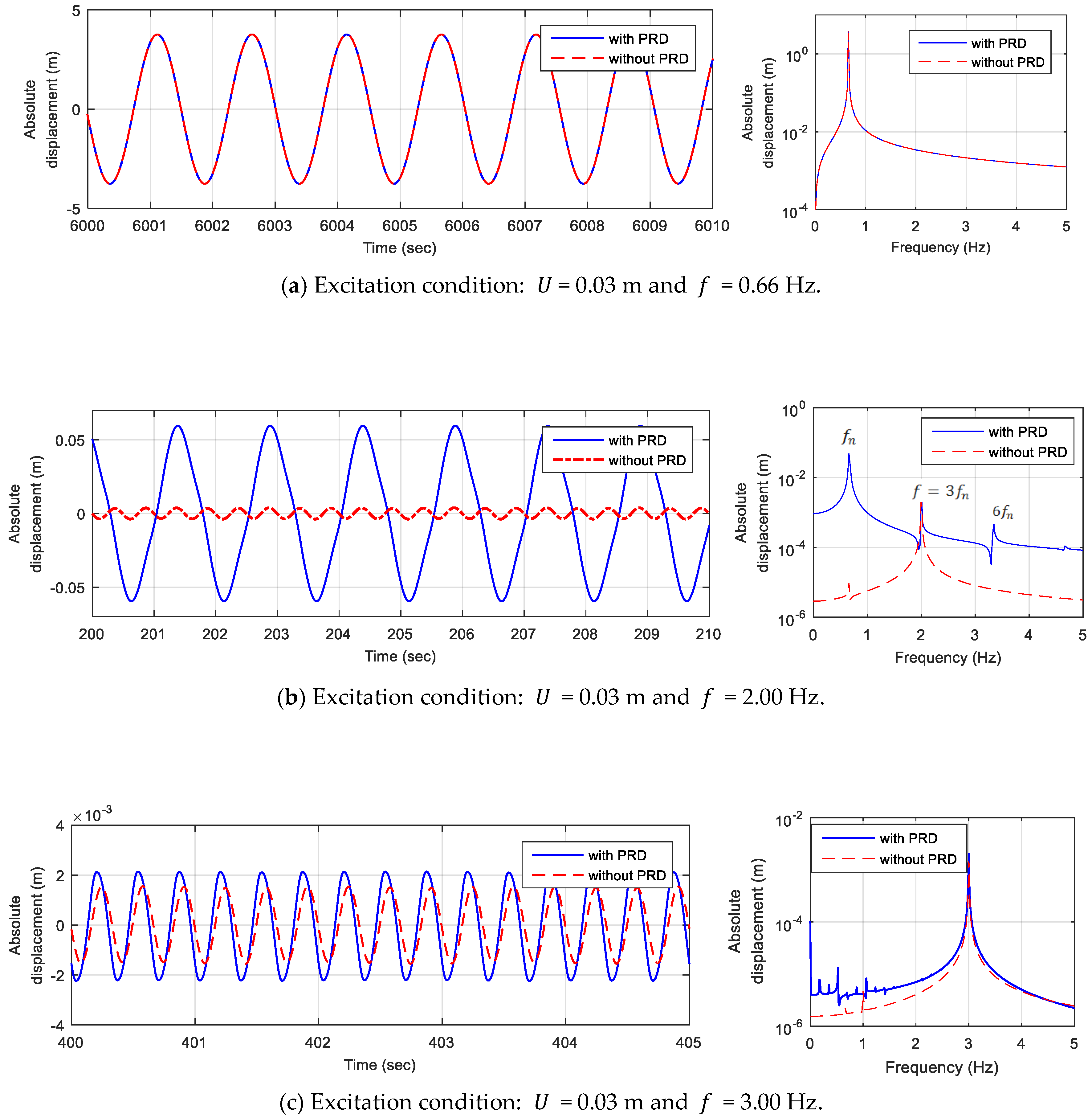
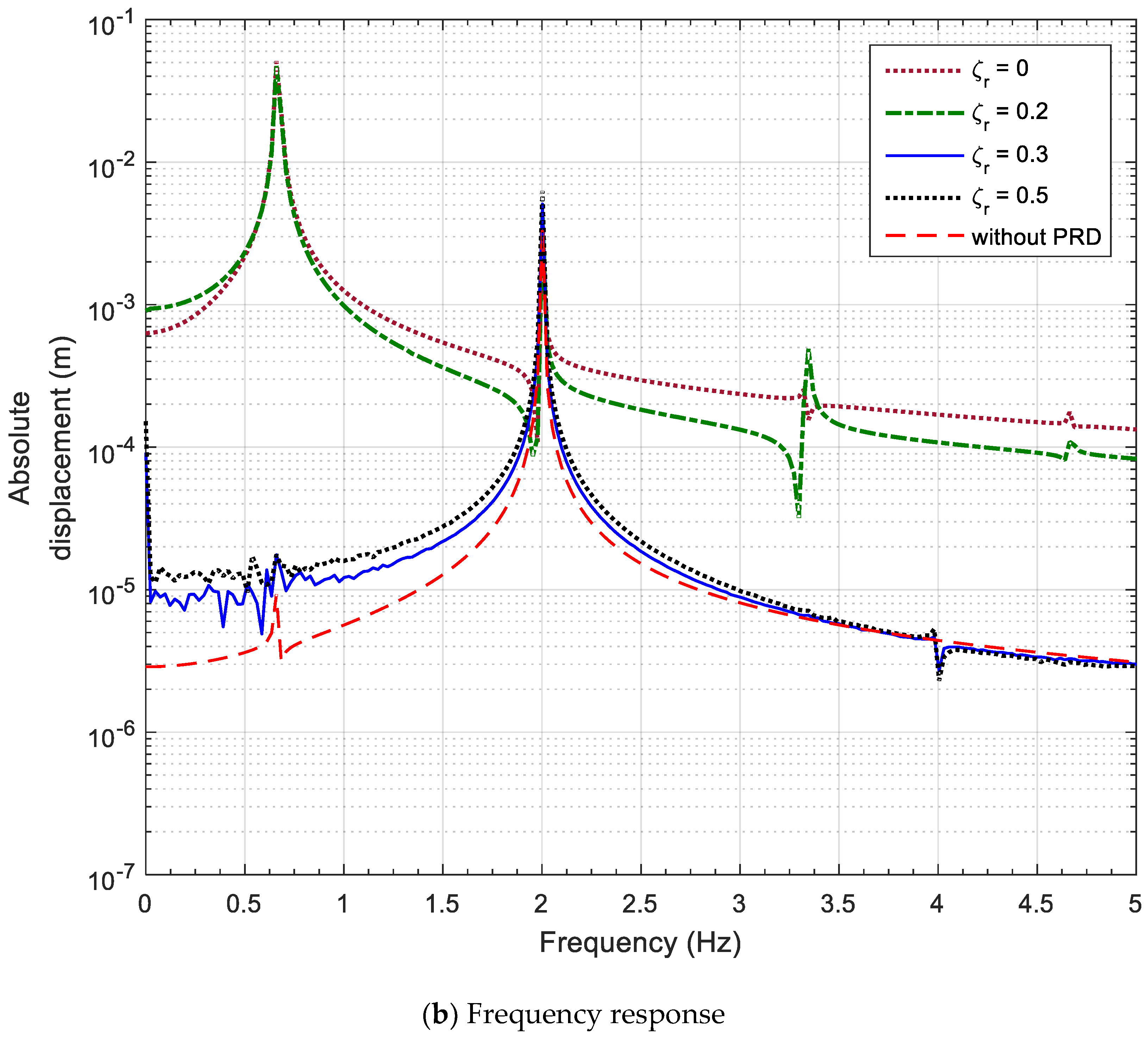
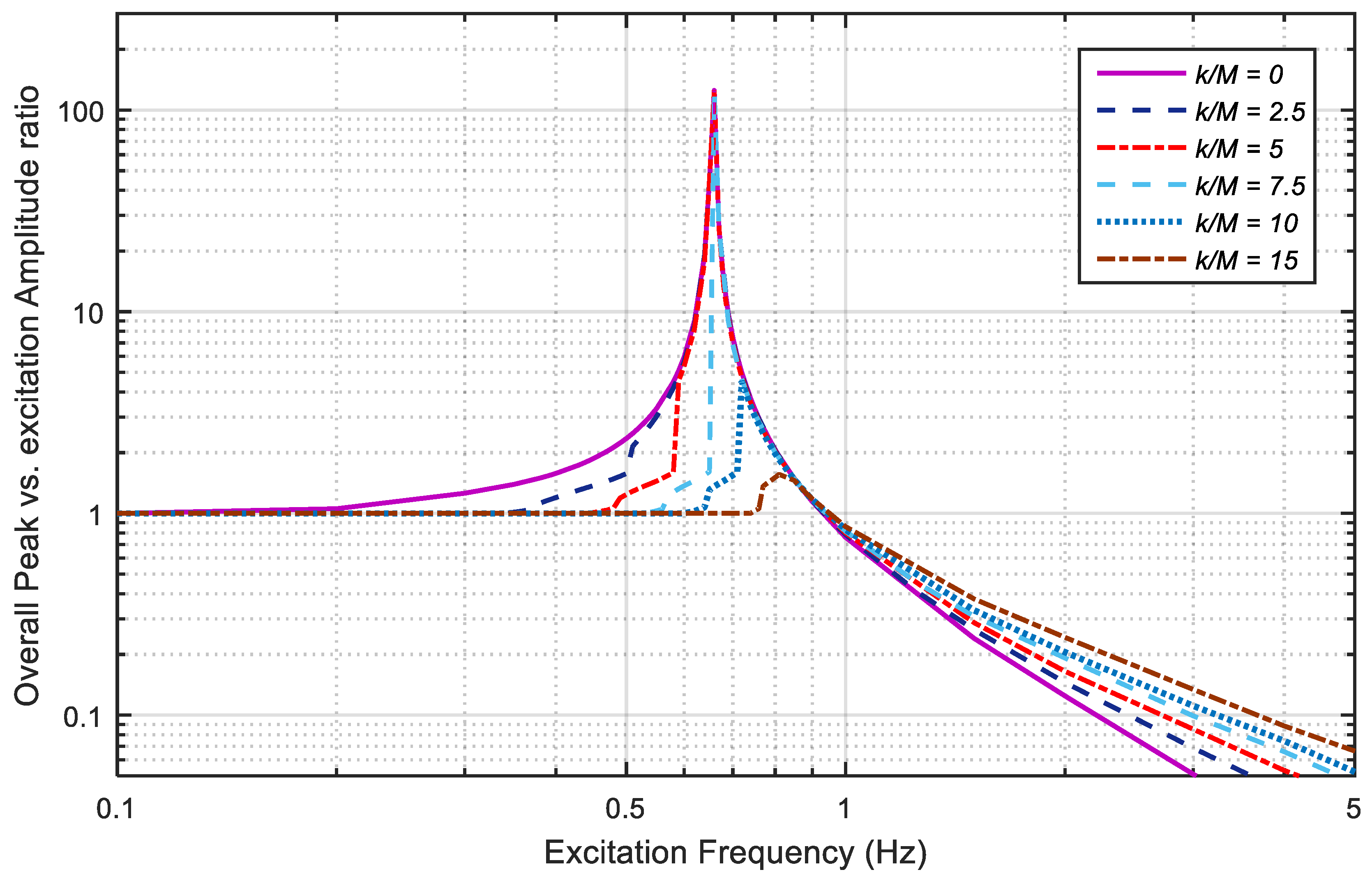
3.2. Steady-State Response and Frequency Response
3.3. System Response Analysis for El Centro Earthquake Waveform
4. Conclusions
- (1)
- The PRD is an effective device to control the deviation of the original position and stop position after disturbance of the seismic isolation system, and to return quickly to the home position. Further, it is expected to solve the disadvantages of a general rolling type seismic isolation system.
- (2)
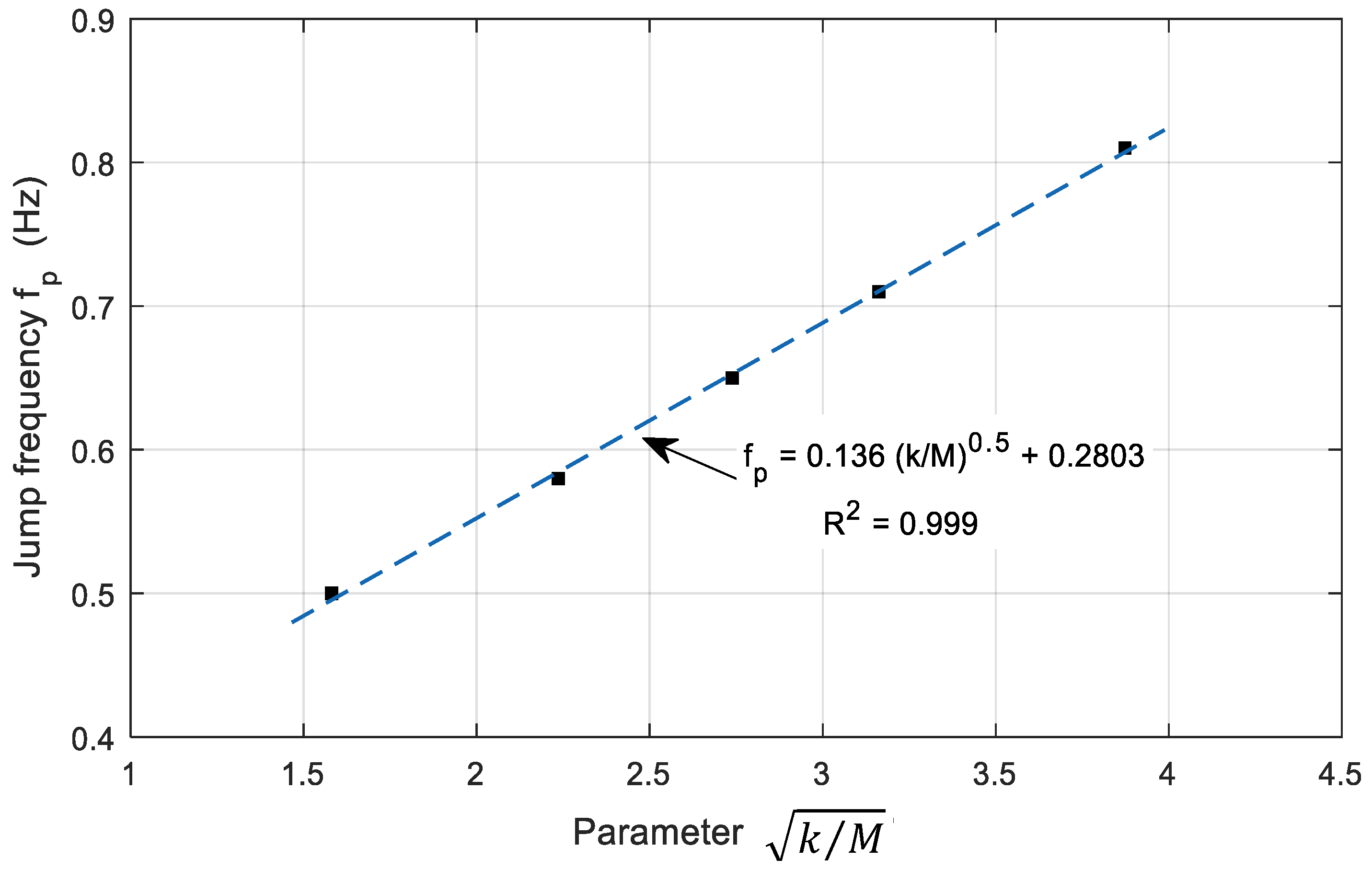
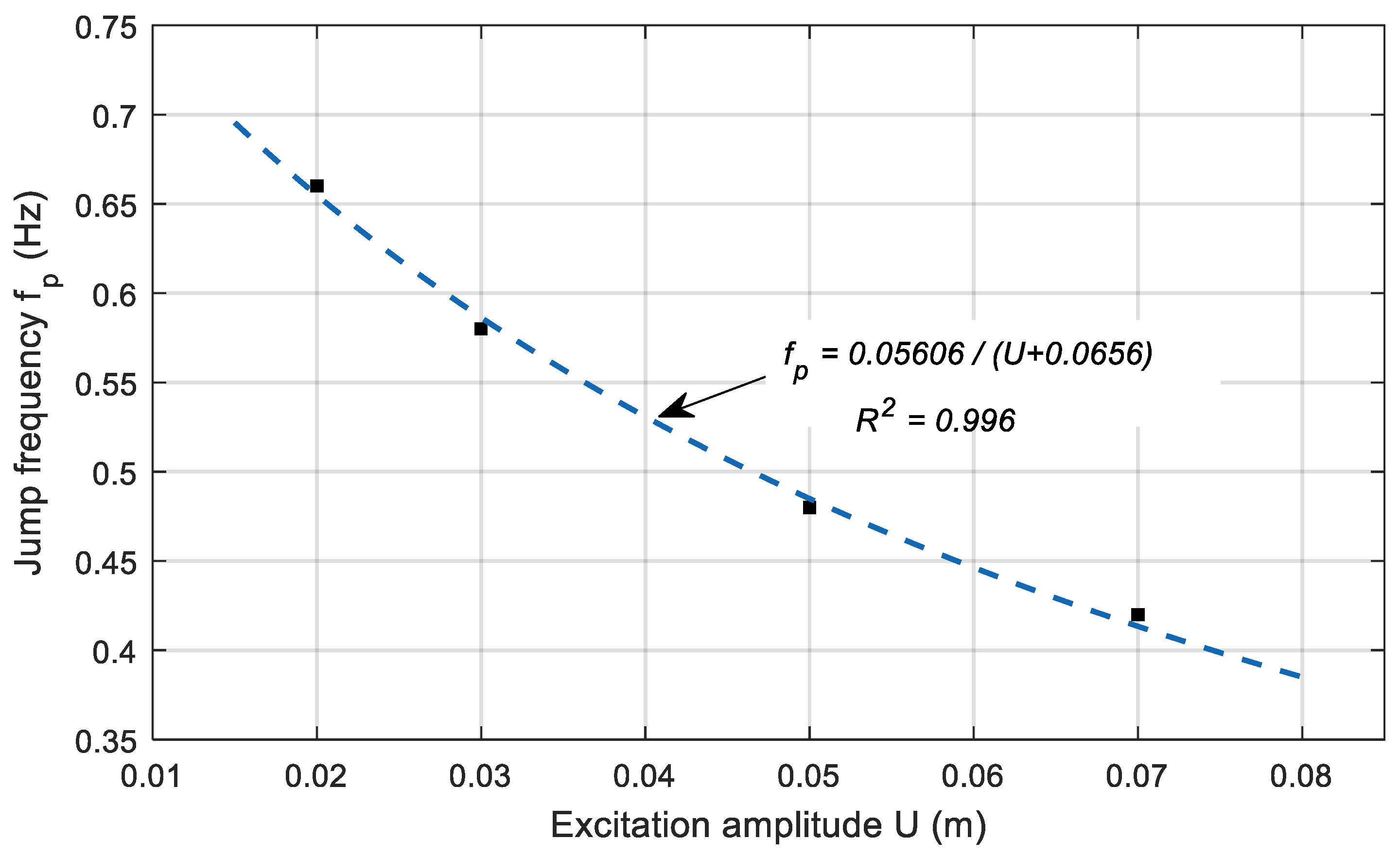
- The frequency response characteristics of the seismic isolation system equipped with PRD show that the relative displacement of the upper and lower parts and the magnitude of the response rise sharply at a specific frequency, depending on the magnitude of the spring–mass ratio and the amplitude of the excitation. It can be seen that the resonance can be avoided by controlling the design parameters because the jump frequency at which the response amplitude increases sharply is proportional to the stiffness to mass ratio and inversely proportional to the excitation amplitude .
- (3)
- The response characteristics of the rolling-type seismic system have been determined. It was found that the harmonic characteristics at the excitation frequency of an integral multiple of the resonant frequency appear, and that they can be controlled by the damping value.
- (4)
- When the El Centro earthquake excitation is applied, the PRD has good vibration damping effects, which reduce the maximum acceleration. Further, the relative displacement response is small, so the stroke of the seismic table can be designed to be small.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| radius of the concave surface of the base table | |
| radius of the roller | |
| displacement of the base table | |
| relative horizontal displacements of the superstructure | |
| absolute horizontal displacements of the superstructure | |
| vertical displacement | |
| total mass of the superstructure | |
| friction coefficient of the wedge hole surface | |
| ratio of the rolling resistant coefficient to the roller radius | |
| half width of the wedge hole | |
| b | height of the wedge hole |
| compression displacement for preload | |
| spring constant of the PRD | |
| damping coefficient of the PRD | |
| damping ratio of PRD | |
| natural frequency | |
| stiffness to mass ratio | |
| excitation amplitude or exciting displacement amplitude | |
| excitation frequency | |
| fp | jump frequency |
| displacement transmissibility ratio (overall peak vs. excitation amplitude) |
References
- Esfeh, M.A.; Caldera, H.J.; Heshami, S.; Moshahedi, N.; Wirasinghe, S.C. The severity of earthquake events-statistical analysis and classfication. Int. J. Urban Sci. 2016, 20, 4–24. [Google Scholar] [CrossRef]
- Girish, M.; Pranesh, M. Sliding Isolation Systems: State-of-the-Art Review. IOSR-JMCE 2013, 6, 30–35. [Google Scholar]
- Girish, M.; Pranesh, M. Comparative Study of Sliding Isolation Systems for Near-Fault Ground Motion. Int. J. Inf. & Futuristic Res. 2014, 2, 1154–1168. [Google Scholar]
- Tsai, C.S. Advanced base isolation systems for light weight equipments. In Earthquake Resistant Structures–Design, Assessment and Rehabilitation; In-Tech: Guangdong, China, 2012; pp. 79–130. [Google Scholar]
- Hosseini, M.; Kangarloo, K. Introducing Orthogonal Roller Pairs as an effective isolating system for low rise buildings. In Seismic Control. System; WIT Press: London, UK, 2013; pp. 65–76. [Google Scholar]
- Lu, Z.; Chen, X.Y.; Zhou, Y. An equivalent method for optimization of particle tuned mass damper based on experimental parametric study. J. Sound Vib. 2018, 419, 571–584. [Google Scholar] [CrossRef]
- Dai, K.S.; Wang, J.Z.; Mao, R.F.; Lu, Z.; Chen, S.E. Experimental investigation on dynamic characterization and seismic control performance of a TLPD system. Struct. Des. Tall Spec. Build. 2016, 26, e1350. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, X.Y.; Lu, X.L.; Yang, Z. Shaking table test and numerical simulation of an RC frame-core tube structure for earthquake-induced collapse. Earthquake Eng. Struct. Dyn. 2016, 45, 1537–1556. [Google Scholar] [CrossRef]
- Muhamad, F.I.; Kang, H.S.; Lee, K.Q.; Siow, C.L. Experimental analysis on variable stiffness and variable damping device. 2nd Multi. Conf. Mech. Eng. 2017, 1, 269–277. [Google Scholar]
- Hu, Y.; Liu, L.; Rahimi, S. Seismic Vibration Control of 3D Steel Frames with Irregular Plans Using Eccentrically Placed MR Damper. Sustainability 2017, 9, 1255. [Google Scholar] [CrossRef]
- Shin, Z.; Cheng, Z.; Xiang, H. Seismic isolation foundations with effective attenuation zones. Int. J. Soil Dyn. Earthquake Eng. 2014, 57, 143–151. [Google Scholar]
- Castaldo, P.; Palazzo, B.; Vecchia, P.D. Seismic reliability of base-isolated structures with friction pendulum bearings. Eng. Struct. 2015, 95, 80–93. [Google Scholar] [CrossRef]
- Kanyilmaz, A.; Castiglioni, C.A. Reducing the seismic vulnerability of existing elevated silos by means of base isolation devices. Eng. Struct. 2017, 143, 477–497. [Google Scholar] [CrossRef]
- Lin, T.W.; Chern, C.C.; Hone, C.C. Experimental study of base isolation by free rolling rods. Earthquake Eng. Struct. Dyn. 1995, 24, 1645–1650. [Google Scholar] [CrossRef]
- Lin, T.W.; Hone, C.C. Base isolation by free rolling rods under basement. Earthquake Eng. Struct. Dyn. 1993, 22, 261–273. [Google Scholar] [CrossRef]
- Mosleh, A.; Rodrigues, H.; Varum, H.; Costa, A.; Arêde, A. Seismic behavior of RC building structures designed according to current codes. Structures 2016, 7, 1–13. [Google Scholar] [CrossRef]
- Mosleh, A.; Varum, H.; Jara, J.; Razzaghi, M.S. Development of fragility curves for RC bridges subjected to reverse and strike-slip seismic sources. Eng. Struct. 2016, 11, 517–538. [Google Scholar] [CrossRef]
- Tsai, M.H.; Wu, S.Y.; Chang, K.C.; Lee, G.C. Shaking table tests of a scale bridge model with rolling-type seismic isolation bearings. Eng. Struct. 2007, 29, 694–704. [Google Scholar] [CrossRef]
- Harvey, P.S., Jr.; Gavin, H.P. The nonholonomic and chaotic nature of a rolling isolation system. J. Sound Vib. 2013, 332, 3535–3551. [Google Scholar] [CrossRef]
- Krishnamoorthy, A. Seismic Control of Continuous Bridges Using Variable Radius Friction Pendulum Systems and Viscous Fluid Dampers. Int. J. Acoust. Vibr. 2015, 20, 24–60. [Google Scholar] [CrossRef]
- Krishnamoorthy, A. Variable curvature pendulum isolator and viscous fluid damper for seismic isolation of structures. Int. J. Vibr. Control 2011, 17, 1779–1790. [Google Scholar] [CrossRef]
- Krishnamoorthy, A. Seismic isolation of bridges using variable frequency and variable friction pendulum isolator system. Struct. Eng. Int. 2010, 20, 178–184. [Google Scholar] [CrossRef]
- Pranesh, M.; Sinha, R. VFPI: An isolation device for aseismic design. Earthquake Eng. Struct. Dyn. 2000, 29, 603–627. [Google Scholar] [CrossRef]
- Tsai, C.S.; Chiang, T.C.; Chen, B.J. Finite element formulations and theoretical study for variable curvature friction pendulum system. Eng. Struct. 2003, 25, 1719–1730. [Google Scholar] [CrossRef]
- Ghidelli, M.; Sebastiani, M.; Johanns, K.E.; Pharr, G.M. Effects of indenter angle on micro-scale fracture toughness measurement by pillar splitting. J. Am. Ceram. Soc. 2017, 100, 5731–5738. [Google Scholar] [CrossRef]
- Gu, L.X.; Xu, Z.Y.; Liu, Z.F. Effect of the Fracture Toughness of Materials (Kc) on Fatigue Crack Propagation Rate. Adv. Mater. Res. 2012, 594–597, 1005–1008. [Google Scholar] [CrossRef]
- Kotzalas, M.N.; Harris, T.A. Fatigue Failure and Ball Bearing Friction. Tribol. Trans. 2008, 43, 137–143. [Google Scholar] [CrossRef]
- Iemura, H.; Miyamoto, A.; Akahashi, Y. Influence of failure of steel bearings on damage modes of bridges under strong Earthquake motion. J. Struct. Eng. 1998, 44, 659–666. [Google Scholar]
- Hibbeler, R.C.; Schiavone, P.; Yap, K.B. Chapter 8. In Mechanics for Engineers: Statics; Pearson: London, UK, 2015. [Google Scholar]







| Parameters | Dimensions |
|---|---|
| 200 kg | |
| 600 mm | |
| 25 mm | |
| 0–2 kN/m | |
| 30 mm | |
| 0–0.5 | |
| 20 mm | |
| 20 mm | |
| 0.2 | |
| [29] | 0.004 |
| The Ratio of | 0 (without PRD) | 5 | 10 |
|---|---|---|---|
| Time Taken to Return (s) | 16.6 | 12.55 (▼23.4%) | 10.05 (▼39.3%) |
| Offset (mm) | 1.2 | - | - |
| Damping Ratio | 0 | 0.3 | 0.5 |
| Time Taken to Return (s) | 8.14 | 5.06 (▼37.8%) | 3.71 (▼54.4%) |
| El Centro Earthquake | Isolator with PRD | Isolator without PRD | |
|---|---|---|---|
| Maximum Relative Displacement | - | 6.11 cm | 13.14 cm |
| Maximum Absolute Acceleration | 0.319 g | 0.115 g (▼0.204 g) | 0.233 g (▼0.086 g) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.C.; Hur, D.-J. Dynamic Behavior of a Simple Rolling Seismic Isolator with a Position Restoring Device. Appl. Sci. 2018, 8, 1910. https://doi.org/10.3390/app8101910
Hong SC, Hur D-J. Dynamic Behavior of a Simple Rolling Seismic Isolator with a Position Restoring Device. Applied Sciences. 2018; 8(10):1910. https://doi.org/10.3390/app8101910
Chicago/Turabian StyleHong, Sung Chul, and Deog-Jae Hur. 2018. "Dynamic Behavior of a Simple Rolling Seismic Isolator with a Position Restoring Device" Applied Sciences 8, no. 10: 1910. https://doi.org/10.3390/app8101910





