A Space-Variant Deblur Method for Focal-Plane Microwave Imaging

Abstract

In the research of passive millimetre wave (PMMW) imaging, the focal plane array (FPA) can realize fast, wide-range imaging and detection. However, it has suffered from a limited aperture and off-axis aberration. Thus, the result of FPA is usually blurred by space-variant point spread function (SVPSF) and is hard to restore. In this paper, a polar-coordinate point spread function (PCPSF) model is presented to describe the circle symmetric characteristic of space-variant blur, and a log-polar-coordinate transformation (LPCT) method is propagated as the pre-processing step before the Lucy–Richardson algorithm to eliminate the space variance of blur. Compared with the traditional image deblur method, LPCT solves the problem by analyzing the physical model instead of the approximating it, which has proved to be a feasible way to deblur the FPA imaging system.

1. Introduction

In the research of passive millimetre wave (PMMW) imaging, focal plane array (FPA) is widely applied for object detection, scene monitoring, and security checks, because of its fast and wide-range of imaging abilities. In the area of electromagnetic compatibility (EMC) detection, we adopt the FPA system to take an image of spatial electromagnetic leakage of electronic equipment (working in the microwave band), which can be called the passive focal-plane microwave (PFPM) imaging system, as shown in Figure 1. The reflector of the PFPM system is offset to offset center obscuring, and its aperture is much larger than that in PMMW to match the microwave wavelengths according to diffraction theory.

Compared with PMMW imaging, due to the much lower frequency of the source (3–6 GHz) and the limited aperture of the parabolic reflector, the PFPM imaging system is more diffraction-limited, so the image has larger blur degradation. Moreover, the aberration of the system caused by the off-axis parabolic (OAP) reflector is pretty serious, which increases the space-variant characteristic of the point spread function(PSF). The two reasons both make the blurred image restoration of the PFPM image much harder than PMMW. In the field of optical imaging, several restoration algorithms of the degraded image caused by space-variant blur have been proposed. There are three main kinds of methods: direct restoration, segmentation restoration, and space coordinate transformation restoration.

The direct recovery method considers image degradation from a global perspective. It decomposes, collates, and compresses a large amount of PSF data into smaller storage quantities and performs recovery by an iterative or non-iterative method. Both Jain and Angel [1] proposed solving the SVPSF image restoration problem with the conjugate gradient method and experimenting with the 31 × 31 image. In 1977, John [2] proposed the Kalman filtering method, and it was subsequently revised and improved [3]. Mehmet [4] used the projection onto convex set (POCS) method for space-variant blurred image restoration. Fish [5] improved the singular value decomposition method and sped up the calculation. James [6] used the interpolation method to process the PSF when performing image restoration on the Hubble telescope image. After analyzing the SVPSF with the diffraction limit and aberrations of the optical system, Thomas et al. [7] completed the image restoration using the Gauss–Seidel iterative algorithm.

The segmentation algorithm divides the image into several sub-blocks whose PSF are considered space-invariant. Then, the space-invariant restoration method is used to complete the image restoration in each image sub-block, and finally, the sub-blocks are spliced to obtain the final image. Trussell and Hunt proposed an image block-based restoration algorithm in 1978 [8,9]. Thomas [10] discussed, in detail, the effects of different segmentation methods on the image restoration quality, and the results were affected by the computational complexity and the edge ringing effect. Guo et al. [11] used the image maximization algorithm to estimate the PSF after image segmentation, and then, used the spatial adaptive least squares method to complete image restoration. Du Xin [12] proposed a new segmentation method based on the mean-shift algorithm to split the signal region out in an electromagnetic image.

The coordinate transformation restoration (CTR) method is mainly used for the degradation of linear motion blur, radial symmetric blur, and so on. By transforming the image into a certain coordinate space where the point spread function is spatially invariant, restoration of degraded image can be simplified and achieved effectively and accurately. In reference [13], the author used polar-coordinate transformation to realize space-invariant transformation in the azimuth direction in optical imaging.

Recently, some new approaches have been proposed to solve this problem. Camera [14] improved the sectioning approach and applied a deconvolution method with boundary effect correction in the segmentation algorithm and accelerated the method with scaled gradient projection (SGP). Mourya [15] proposed a distributed shift-variant image deblurring algorithm to solve the limited resource problem when the image is extremely large (up to gigapixels). Zhang [16] estimated the blur map and adopted the BM3D-based, non-blind deconvolution algorithm to reconstruct the image. In the area of artificial intelligence, Schuler [17] improved a neural network with a deep layered architecture and trained it to estimate the blur kernel and reconstruct the image alternately. Sun [18] used a convolutional neural network to predict the distribution of the motion blur and extend it by image rotation. Then, a Markov random field model was applied to remove the motion blur using the prior patch-level image. The method was proved to effectively estimate and remove complex non-uniform motion blur.

In the field of PMMW, Li Liangchao [19] studied the relationship between the focal plane and the image plane and presented the spherical anti-projection transformation method to eliminate the space-variant characteristic of the PSF. After analyzing the PSF of our system, we proposed the use of a log-polar-coordinate transformation (LPCT) method before the Lucy–Richardson algorithm to eliminate the space-variant blur in both the angular direction and the radial direction. In this paper, we introduce the PCPSF model of OAP firstly in Section 2, and then our algorithm is explained in detail in Section 3. Finally, we apply the algorithm to both the simulation and experiment results displayed in Section 4, and the conclusions are given in the final section.

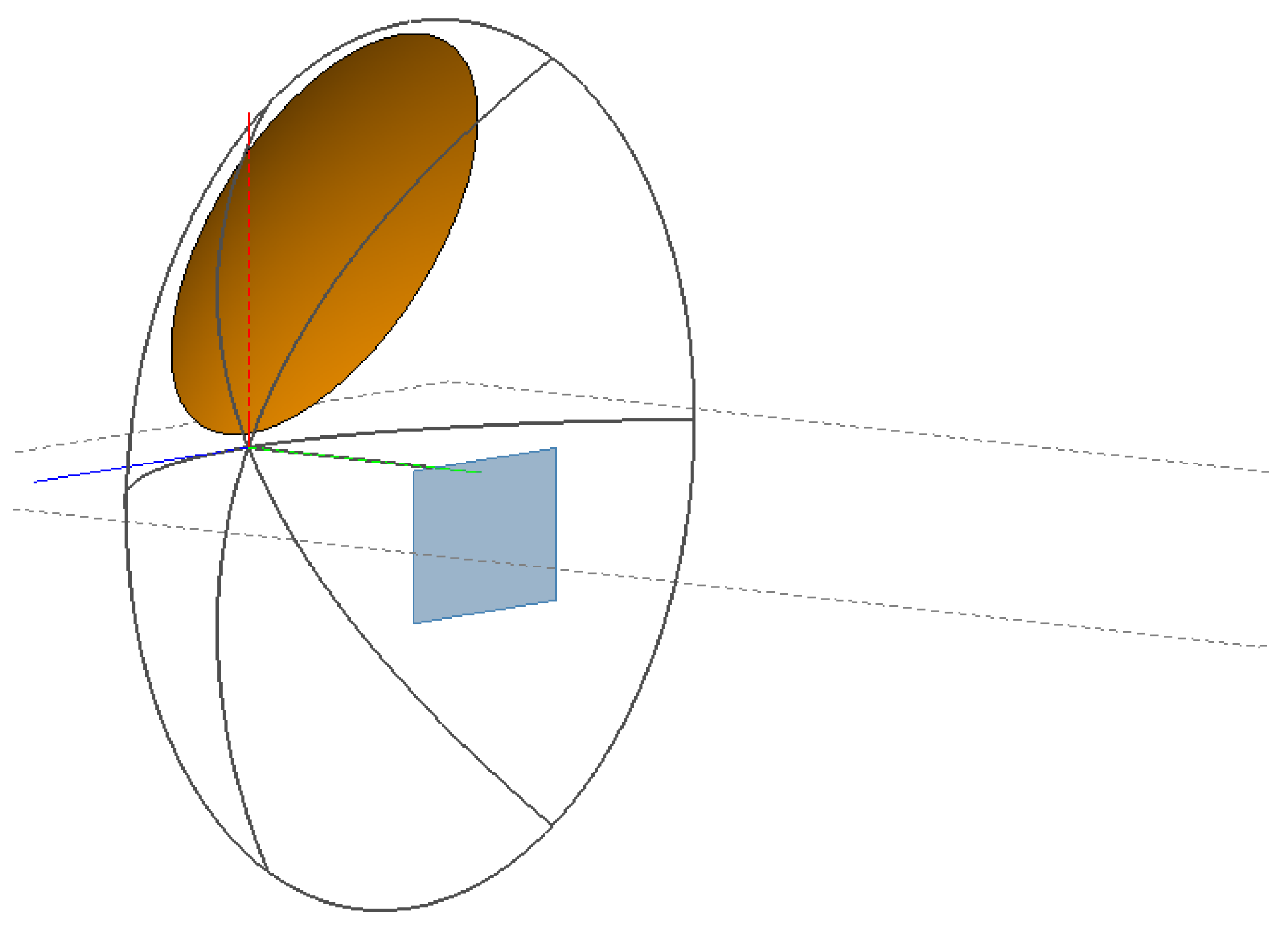
2. Space-Variant PSF of OAP System

The OAP is usually designed as the intersection of a symmetric parabolic, which is called the parent parabolic, with a circular object, as shown in Figure 2. So, the research on PSF of OAP can be carried out in two steps: the diffraction limited effect of parent parabolic without aberration and the inherent aberration caused by the off-axis characteristic. In the next two subsections, we give a detailed explanation of how these two factors cause the space-variant blur.

2.1. Space-Variance Correction in the Angular Direction

Usually the research on propagation and the focus of the light or electromagnetic field relies on the Fresnel diffraction integral formula, Kirchhoff formula, or Rayleigh–Sommerfeld diffraction integrals. To avoid these complex formulas, we derive the PSF of the parent parabolic by the Collins formula, which has proved to be consistent with the Fresnel diffraction integral formula for the numerical analyses of symmetric paraxial optical systems [20]. As mentioned in [21], the parabolic mirror has the same function of light field transformation as a lens. Therefore, we can derive the ideal imaging of the parabolic reflector using the mature method of lens. According to [20], the PSF of the parent parabolic can be written as follows:

$$\begin{array}{cc}h(x_2,y_2;{\xi }_2,{\eta }_2)=\frac{k^{2}exp(jkL)}{4{\pi }^2{d}_1{d}_2}\hfill & exp(jk\frac{x_2^2+y_2^2}{2d_2})exp[-jk\frac{A({\xi }_1^2+{\eta }_1^2)}{2d_1}]\hfill \\ & \hfill ·{\int }_0^{2\pi }{\int }_0^{\frac{D}{2}}{r}_{0}exp\frac{-jk}{d_2}[(x_2-A{\xi }_1)r_{0}cos{\theta }_0+(y_2-A{\eta }_1)r_{0}sin{\theta }_0]d{r}_{0}d{\theta }_0.\end{array}$$

(1)

In Equation (1), $u_1({\xi }_1,{\eta }_1)$ is the object plane, $u_2(x_2,y_2)$ is the image plane, and $u_0(r_0,{\theta }_0)$ is the pupil plane. So it is obvious that the PSF is variant along with the coordinate parameter. Inspired by the symmetrical, circlular characteristics of the blur, we transform the object plane and image plane from Cartesian-coordinates into polar-coordinates followed by Equation (2):

$$r_1^2={\xi }_1^2+{\eta }_1^2{\theta }_1=tan({\eta }_1/{\xi }_1);r_2^2=x_2^2+y_2^2{\theta }_2=tan(y_2/x_2).$$

(2)

Then, we derive the PSF under the polar-coordinate:

$$h(r_2,{\theta }_2;r_1,{\theta }_1)=\frac{k^{2}exp(jkL)}{4{\pi }^2{d}_1{d}_2}exp(jk\frac{r_2^2}{2d_2})exp[-jk\frac{A(r_1^2)}{2d_1}]·{\int }_0^{2\pi }{\int }_0^{\frac{D}{2}}{r}_{0}exp[\frac{2jk}{d_2}{r}_0{r}_{2}cos({\theta }_2-{\theta }_0)]d{r}_{0}d{\theta }_0.$$

(3)

In particular, we take the integral about $\theta$ into consideration to get Equation (4):

$${\int }_0^{2\pi }exp[Mcos({\theta }_2-{\theta }_0)]d{\theta }_0,$$

(4)

where $M=\frac{2jk{r}_0{r}_2}{d_2}$, and if ${\theta }_2-{\theta }_0=t$, then $d{\theta }_0=-dt$. Equation (4) can be calculated as follows according to the properties of trigonometric functions:

$$\begin{array}{c}{\int }_{{\theta }_2}^{{\theta }_2-2\pi }-exp[Mcos(t)]dt\hfill \\ ={\int }_{{\theta }_2-2\pi }^{{\theta }_2}-exp[Mcos(t)]dt\hfill \\ ={\int }_0^{2\pi }-exp[Mcos(t)]dt.\hfill \end{array}$$

(5)

So, as we can see, the PSF is not related to $\theta$ under the polar-coordinate. In other words, the PSF is invariant to $\theta$ after the coordinate transformation. The PSF in polar-coordinates can be called the PCPSF model, which decouples the two-dimensional space-variant blur from the angular direction.

2.2. Space Variance Correction in the Radial Direction

Since the object and image planes of the focal plane imaging system are on the same side of the reflector, most systems use an off-axis approach to avoid center occlusion. For parabolic reflectors, the characteristics of off-axis and non-parallel incident rays cause relatively large aberrations. In the literature [22,23], Arguijo used the ray tracing method in geometric optics to analyze the aberration of the off-axis parabolic reflection mirror in optical imaging systems, pointing out that the aberration mainly includes astigmatism and coma. According to Seidel’s primary aberration theory, the astigmatism and coma can be described by polar-coordinates as follows [12,24]:

$$\begin{array}{cc}\hfill x_r-u_r& =(2C+D)u_r^2{ϵ}_{r}cos{ϵ}_{\theta }\hfill \\ \hfill x_{\theta }-u_{\theta }& =arctan[D{u}_r{ϵ}_{r}sin{ϵ}_{\theta }/(1+(2C+D)u_r^2{ϵ}_{r}cos{ϵ}_{\theta })]\hfill \\ \hfill x_r-u_r& =u_{r}F{ϵ}_r^2(2+cos2{ϵ}_{\theta })\hfill \\ \hfill x_{\theta }-u_{\theta }& =arctan[(-F{ϵ}_r^{2}sin2{ϵ}_{\theta })/(1-F{ϵ}_r^2(2+cos2{ϵ}_{\theta }))].\hfill \end{array}$$

(6)

In Equation (6), the two rows above represent the astigmatism aberration and the two rows below denote the coma aberration. Obviously, the aberration above has nothing to do with $x_{\theta }$ nor $u_{\theta }$, which means that there is no variance caused by $\theta$, the same as the PSF of the parent parabolic. So, the work on the restoration of blurred image is focused on the radial direction after the polar-coordinate transformation.

In Equation (6), the $u_r$ contributes a little to astigmatism and nothing to the coma abberation of the direction of $\theta$, but it has a significant impact on the direction of r. Since the radial blur in Equation (6) is related to $u_r$ or $u_r^2$, we can put an logarithm operation into the r direction in the polar-coordinate transformation, which can be helpful to depress the radial variance. After that, the radial aberration described in Equation (6) can be written as follows, where the blur is in weak or has no relationship with $u_r$ anymore:

$$\begin{array}{cc}\hfill ln(x_r)-ln(u_r)& =ln[1+(2C+D)u_r{ϵ}_{r}cos{ϵ}_{\theta }]\hfill \\ \hfill ln(x_r)-ln(u_r)& =ln[1+F{ϵ}_r^2(2+cos2{ϵ}_{\theta })].\hfill \end{array}$$

(7)

Here, we give an example of the effect of logarithm in Figure 3. After the logarithm operation in the radial direction, the variance along r has been almost removed.

In Section 2, the description and correction in the angular and radial directions is given by analyzing the PSF under the polar-coordinate. By combining the two subsections, we set up an log-polar-coordinate transformation method to eliminate the space variance of the blurred image. The realization of this method is given in the next section.

3. Methods

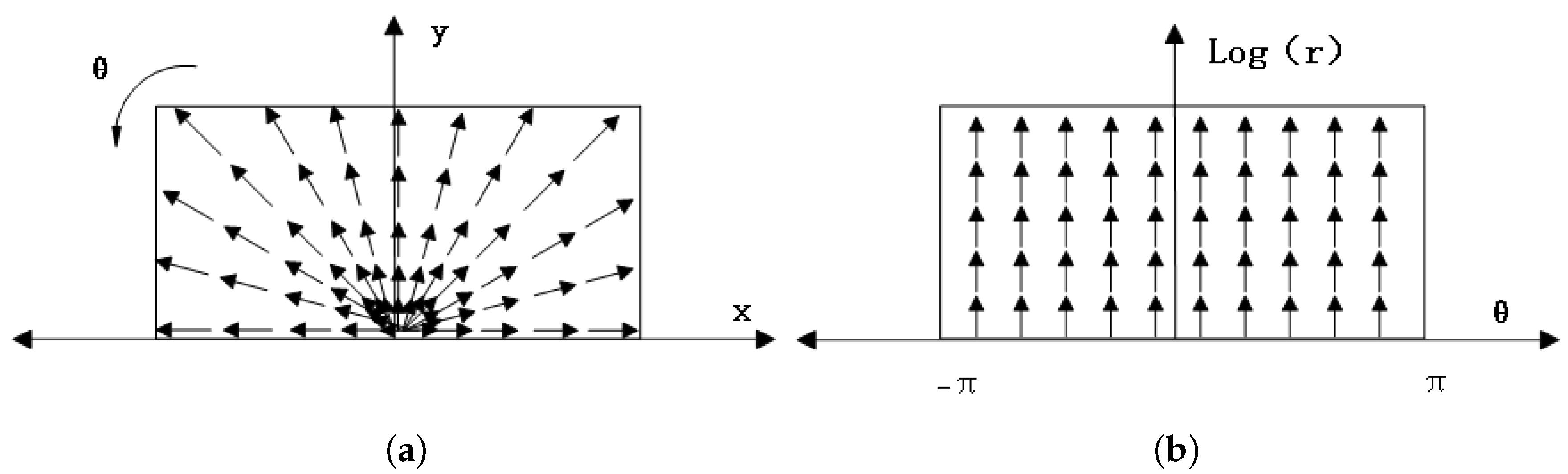
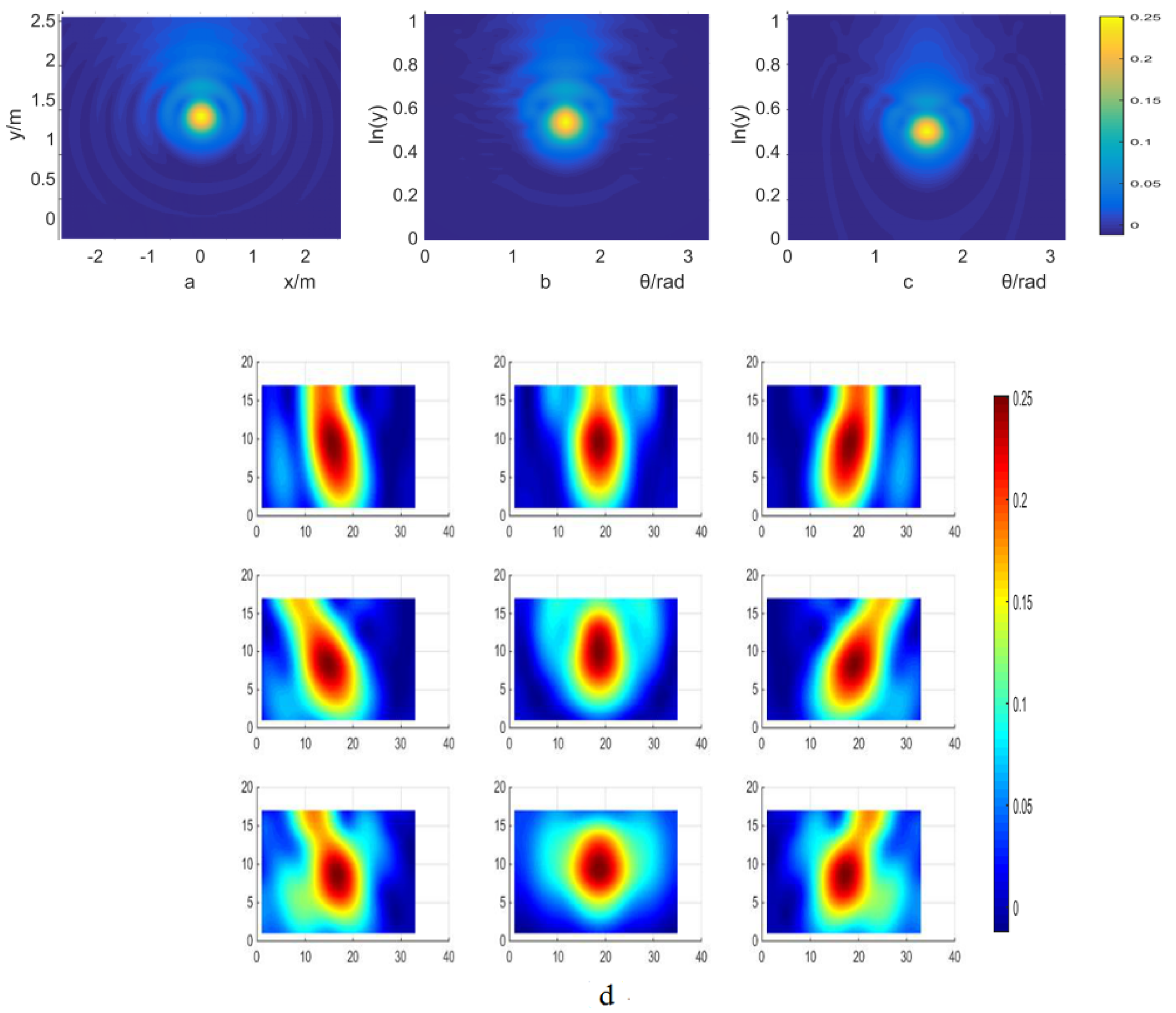
3.1. Log-Polar Transformation

In the image processing algorithm, the log-polar transformation has the characteristics of scaling invariance and rotation invariance and is usually used for target extraction and recognition [25,26]. However, the log-polar transformation in our method is inspired by analyzing the characteristics of the imaging system, as derived above. Here, we present the steps and flow charts that describe the application of the log-polar transformation method to achieve resolution recovery.

• Step 1 Obtain the image data $f(x,y)$ of M*N by photoelectric sensors and the point spread function $PSF(x,y)$ of M*N by simulation of the ideal point source in FEKO.
• Step 2 Transform the image data $f(x,y)$ and $PSF(x,y)$ coordinate into the polar-coordinate to get the new image $g(r,\theta )$ and the new $PSF(r,\theta )$ Equation (8), and interpolate the new image using the bicubic interpolation method.

  $$r=log(\sqrt{x^2+y^2})\theta =arctan(y/x)$$

  (8)
• Step 3 Use the Lucy–Richardson algorithm with $g(r,\theta )$ and $PSF(r,\theta )$ to reconstruct the high-resolution image $g^{\prime }(r,\theta )$.
• Step 4 Inverse transform $g^{\prime }(r,\theta )$ into the Cartesian coordinate system and interpolate it by the bicubic method to obtain the final result with resolution recovery.

Figure 4 shows the transformation process. As we can see, the space-variant blur in the Cartesian-coordinate turns to be space-invariant in the log-polar-coordinate. However, this method has a blind spot at r = 0, and it will not work well close to the blind spot since there is too few pixels to be sampled. The mathematical method can hardly improve it, and now, the feasible way is to avoid putting the detected object around the blind point.

In the process of transformation, bicubic interpolation will result in an uneven rise of values in the different locations of the image, which can be depressed by choosing appropriate filter methods, such as median filter, or by improving the interpolation procedure.

3.2. Lucy–Richardson Iterative Algorithm

According to the Fourier optics theory, the finite aperture is equivalent to a low-pass filter in the spatial light field transformation, which will cause a cutoff effect on the spatial frequency in cases above a certain value [20]. It is represented in the airspace as a high-resolution image convolved with the point spread function, resulting in image blur, as described in Equation (9):

$$g(x,y)=\int \int h(x,y,ϵ,\eta )f(ϵ,\eta )dϵd\eta +n(x,y).$$

(9)

Unlike the super-resolution recovery of ordinary under-sampled images, whose goal is to recover high frequency components from the aliased spectrum, the main purpose of super-resolution in our system is to recover the high-frequency components that are filtered out by the finite aperture, which is called the inverse problem. To solve this problem, many methods have been proposed, such as the Winner inverse filter, projection onto convex sets, etc. Our system adopts the Lucy–Richardson iterative algorithm, and its main principle is the maximum likelihood criterion theory. As shown in Equation (10), it attempts to find a high-resolution image estimate $f(x,y)$ to maximize the likelihood function $P(g|f)$, where g is the low resolution image, resulting in a maximum likelihood estimate $\widehat{f}(x,y)$,

$$\widehat{f}=argmaxP(g|f),$$

(10)

where $P(g|f)$ is a statistical model that reflects the radiation distribution of the object plane. The iterative equation of this algorithm is as follows:

$${\widehat{f}}_{k+1}={\widehat{f}}_k[\frac{g(x,y)}{h(x,y)\ast {\widehat{f}}_k(x,y)}\ast \widehat{h}(x,y)].$$

(11)

In Equation (11), * denotes the convolution operation, $h(x,y)$ is the PSF obtained from the simulation result of an ideal point source in FEKO, and $\sum h(x,y)=1$, $\widehat{h}(x,y)$ represents the spatially inverse value of $h(x,y)$. In addition, the initial iteration condition is generally set to ${\widehat{f}}_0=g(x,y)$. To solve the ill-posed problem, the iteration number should be limited [27,28] and is set to 300 in this paper based on the restoration effect. Finally, the $f_{k+1}$ that satisfies the iteration requirement is the estimated high-resolution image.

In conclusion, the flow chart of our LPCT and L-R iterative method that was presented in Section 3 is shown in Figure 5.

4. Results and Analysis

To verify the effectiveness of the algorithm, we applied it to the super-resolution process with simulation results and experimental results. In addition, we did a comparison with the typical algorithms for solving such problems in optical imaging, including the direct L-R method and the segmentation method in the literature [29]. Since the super-resolution process is a typical inverse process, the corresponding high-resolution image cannot be compared with the low-resolution one, so the traditional image processing evaluation method could not be used here, and the high-resolution does not mean that the visual effect is better either. Considering the requirements for imaging and locating the electromagnetic leakage of electronic equipment, here, we used the correctness of position and the number of radiation sources as the criteria for evaluating the super-resolution algorithm.

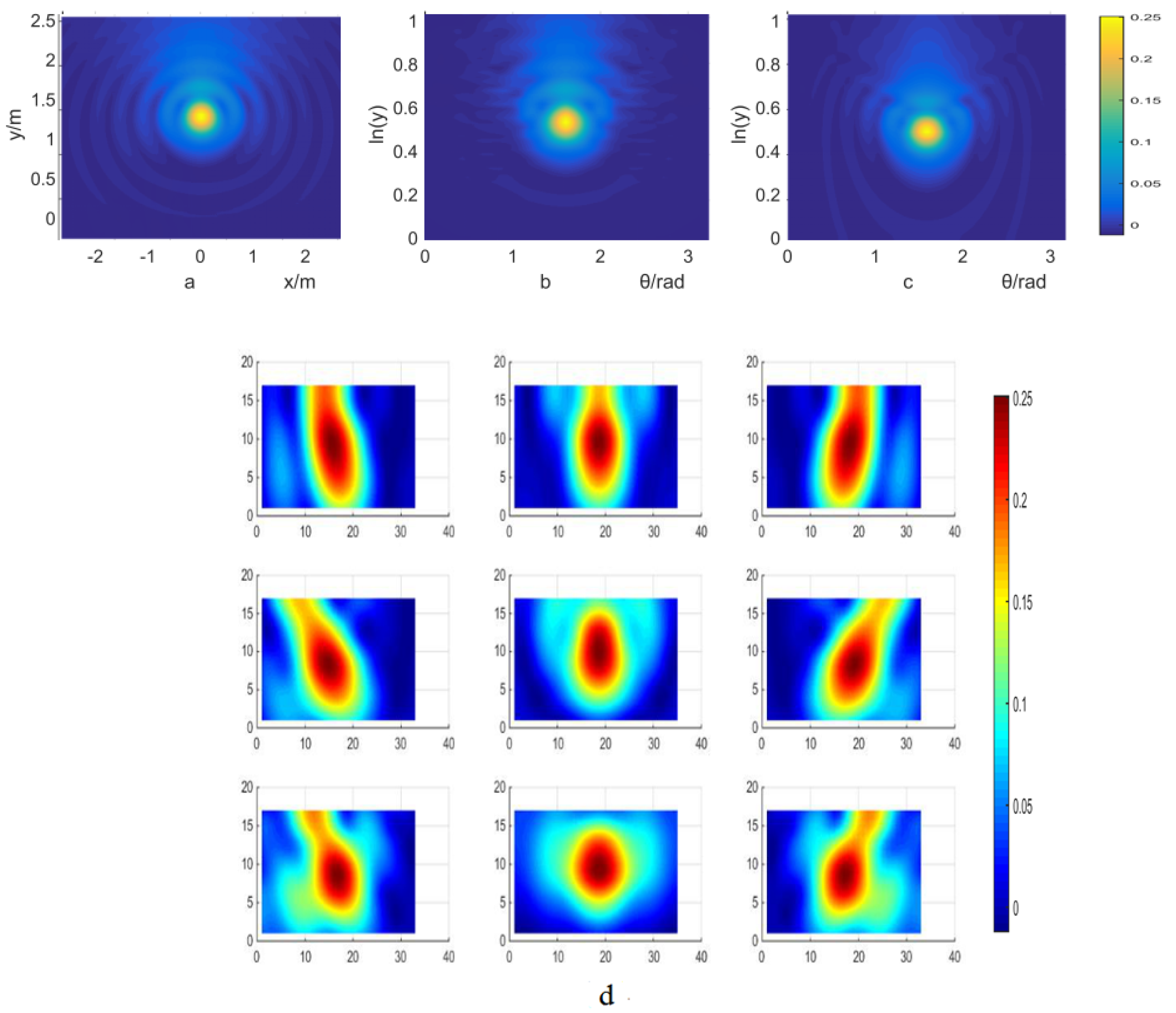
4.1. PSF Used for the Results

Since the L-R iterative algorithm is a non-blind deconvolution method, the selection of the PSF is important. In our algorithm, the PSF is acquired by the simulation result in FEKO with each frequency being the same as the experiment and the size of the PSF and image are both 51 × 101. In Figure 6, the PSF values of different methods at 3 GHz are shown: a is the PSF of the direct deconvolution algorithm; b is the polar transformation’s PSF; c is the PSF of our method, whose axes are set with the same range as the acquisition image; d is the 9 sub-PSFs of the PSF set in the segmentation method which includes the sub-PSFs acquired at different locations. The axis represents the pixel number of each sub-block, which is usually 17 × 33 or 17 × 35.

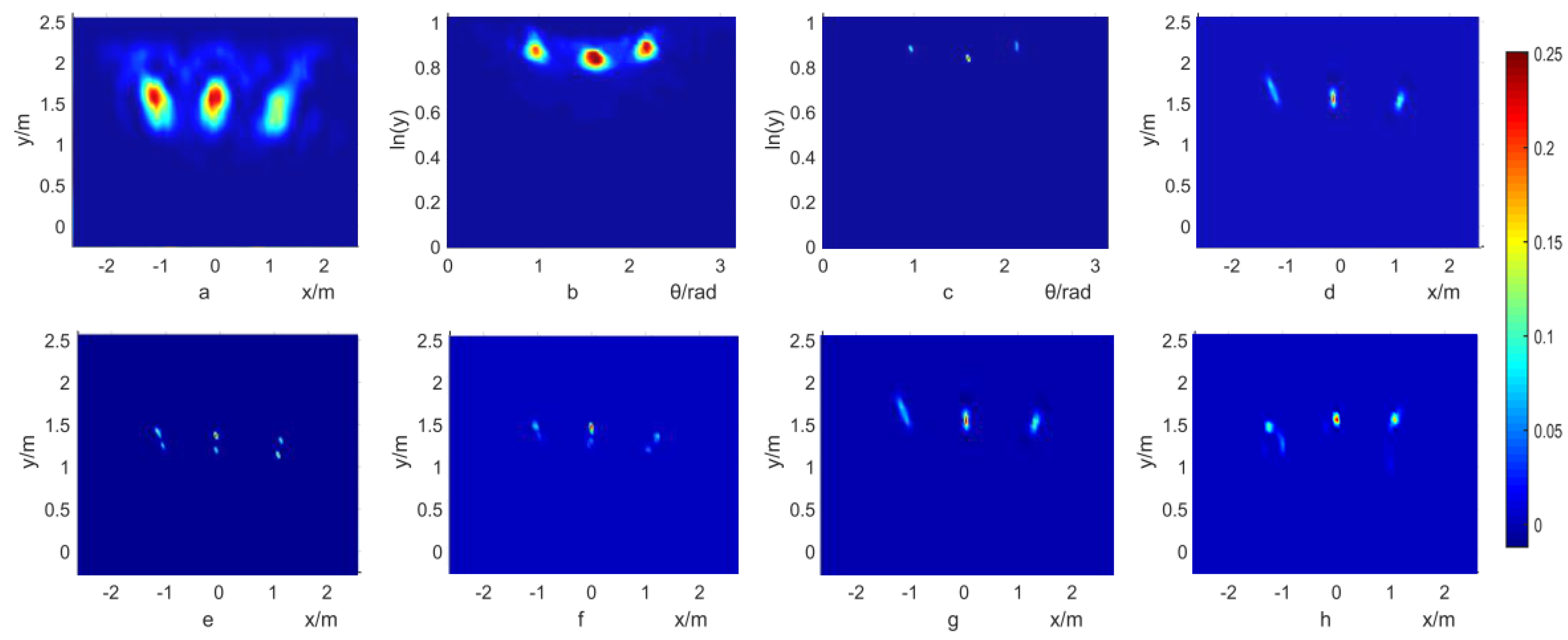
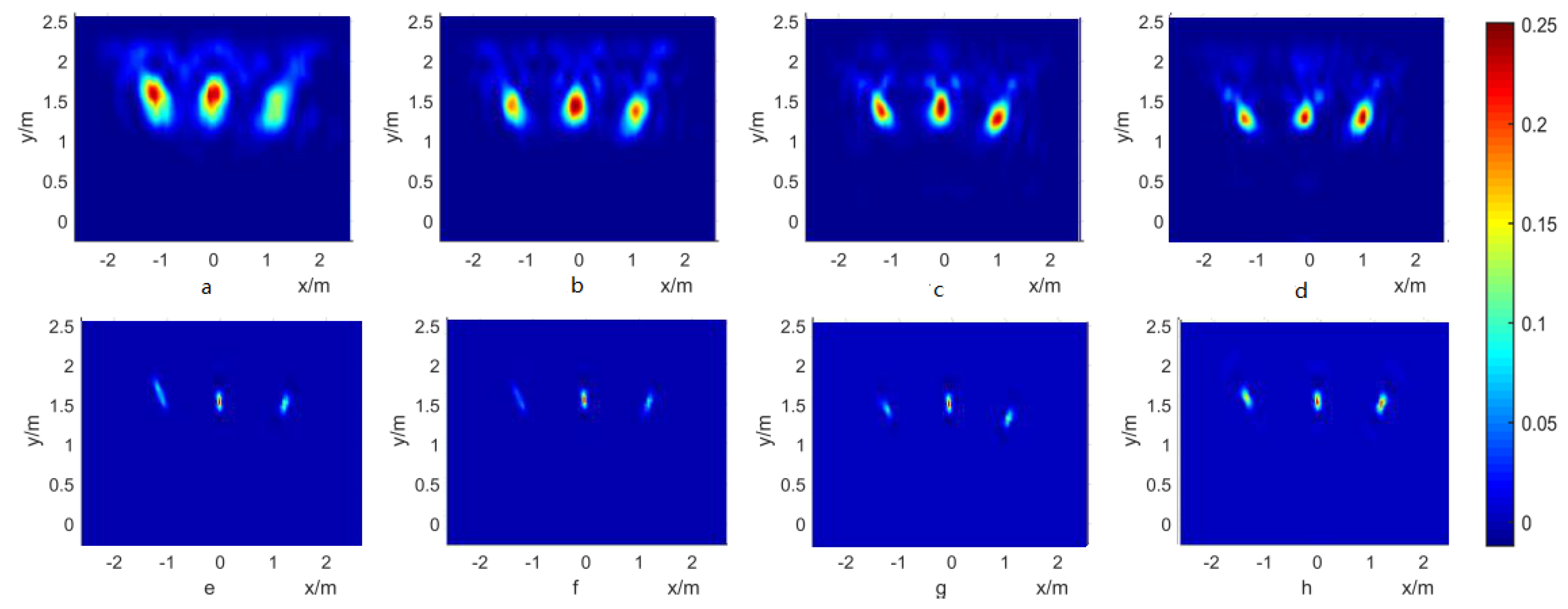
4.2. Deblur of Simulation Results

We used FEKO to build a system model and simulated the imaging of ten dipole sources (4 GHz) placed in a circle shape on the object plane. The model structure and the degraded pictures are shown in Figure 7.

As shown in Figure 8, the row above is the step result of the log-polar transformation algorithm. It can be seen that the log-polar transformation basically eliminates the spatial variation characteristics of the blur, and the number and position of the electromagnetic radiation source are consistent with the real conditions. The row below is the result of applying other algorithms to Figure 8a. It can be seen that due to the large blur and the obvious spatial variation characteristics, the direct super-resolution (SR) algorithm and segmentation SR algorithm cannot satisfy the space-invariant hypothesis which results in some speckle noise and false signals. In addition, the only polar transformation method can recover part of the blur, leaving the noise caused by the radial variant blur.

4.3. Deblur of Experiment Results

We built an imaging system in a microwave darkroom and performed imaging experiments on three horizontally-placed, double-ridged horn antennas (3–6 GHz, 10 dBm), as shown in Figure 9. The results are shown in Figure 10.

The row above in Figure 10 is the step result of the log-polar transformation algorithm, and the row below shows the results of the other algorithms. It can be seen that the direct SR and segmentation SR algorithms still generate noise and interfere, which will cause mistakes in the judgment and localization of the electromagnetic leakage. The log-polar algorithm can effectively suppress this problem. Figure 11 below shows the results of the imaging (upper) and resolution recovery (lower) results of radiation sources of different frequencies. So, as we can see, the algorithm can be applied to a wide-range spectrum if we can get the PSF.

In theory, the recovered image should have the same resolution and position as the target signal. The resolution can be measured by the beamwidth of the recovered signal. So, we evaluated the results in Figure 11 by the consistency of position and beamwidth of the three signals.

In the evaluation, the positions of different antennae were determined by the x and y-axes (unit: pixel) of the maximum value of their beams. The beamwidth used in this evaluation was introduced from the antenna area and was set at a beamwidth of −6 dB, which means the area (unit: pixel) of the value that is 6 dB less than the peak of the beam. In this paper, it was calculated by the following:

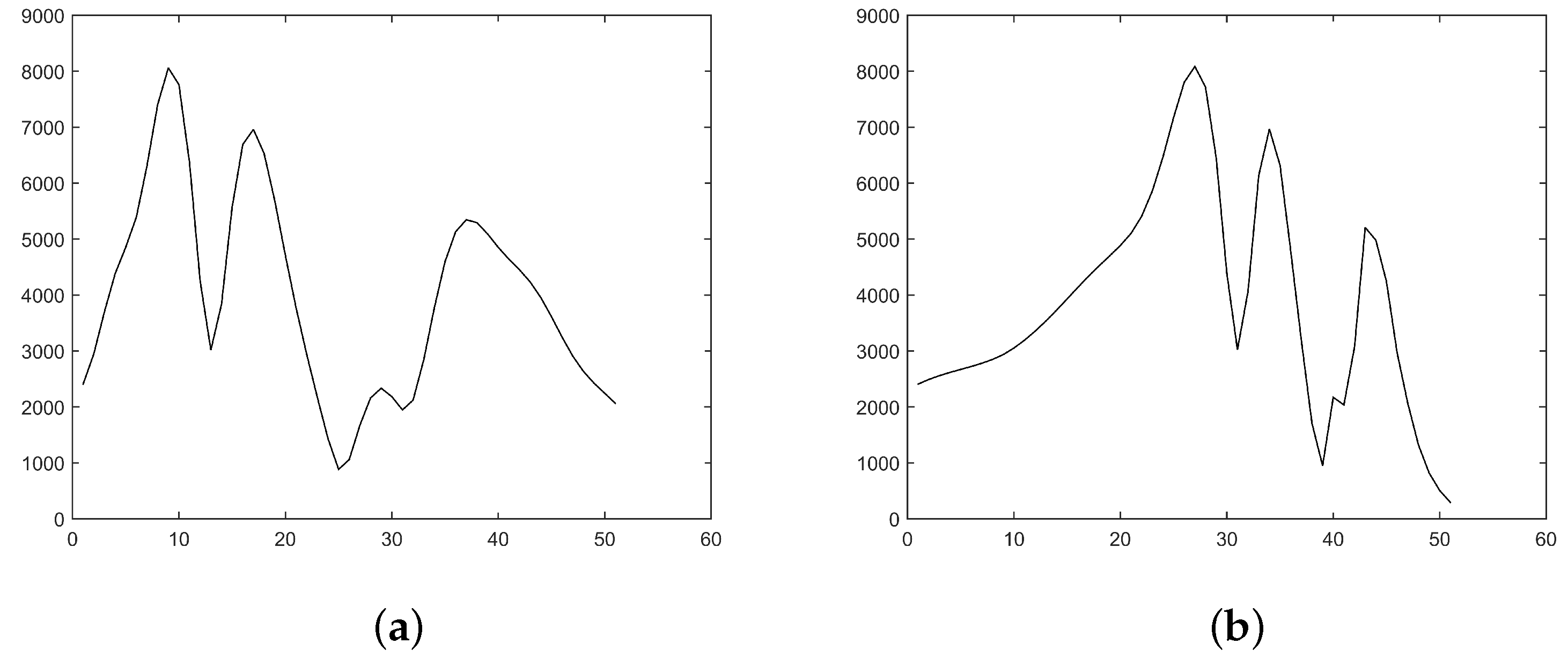
• Step 1 Convert the z-axis of the image matrix into a dB area by log operation.
• Step 2 Mark the pixel as 1 if its value is larger than the peak subtracted by 6 dB and 0 if not.
• Step 3 Calculate the number of 1 in the whole image as the −6 dB beamwidth.

The results are as follows. In

Table 1. The positions of recovered signals at all frequencies.

	3 GHz	4 GHz	5 GHz	6 GHz
Left	(36,28)	(32,28)	(32,28)	(34,25)
Center	(33,50)	(33,50)	(33,50)	(33,50)
Right	(33,73)	(33,73)	(30,71)	(33,73)

and

Table 2. The beamwidth of recovered signals at all frequencies.

	3 GHz	4 GHz	5 GHz	6 GHz
Left	2	2	2	3
Center	6	6	6	6
Right	7	7	8	10

, left means the left signal on the recovered image, and similarly with the center and right. The units of both tables are pixels. Table 1 shows that the positions of the three signals were almost the same and met up with the real antenna. Table 2 shows that the recovery signals had good consistency in beamwidth with each other at different frequencies. The position and beamwidth prove that the method is suitable for wide-frequencies.

The transformation is not complex and the size of image is also not too big, so the time that the algorithm consumes (on the laptop with MatLAB R2014b, Windows 7, Intel I5) is within 1 s. The number of iterations in the L-R iteration method is set to 300 for regularization.

5. Conclusions

In the deblurring processing of focal-plane image, the space-variant characteristic is hard to eliminatedue to its large dimensions. This problem is particularly acute in our focal-plane microwave imaging systems due to the low frequency and off-axis aberration. In this paper, we analyzed the physics model of the space-variant blur and proposed an LPCT method as the preprocessing method before Lucy–Richardson restoration. This algorithm starts from the principle of image blur instead of approximating it, and proved to be effective for the space-variant deblurring of focal-plane microwave imaging. It improves the resolution and accuracy of electromagnetic imaging and detecting in EMC detection significantly. However, this method brings a blind spot, as discussed above, and there is no better solution but to avoid it. In addition, in future work, the interpolation of transformation will be studied further to depress the uneven rise of values and regularization with the L-R algorithm to help to improve the noise problem.