Continuum Damage-Healing and Super Healing Mechanics in Brittle Materials: A State-of-the-Art Review
Abstract
:1. Introduction
2. Damage and Healing Configurations
3. Damage-Healing Formulations
3.1. Healing Model Based on Parameter Recovery
3.2. Fracture Mechanics Based Healing Model
3.3. Creep Damage-Healing Model for Salt Rock
3.4. Micro-Damage Healing Models for Asphalt Mixtures
3.5. Curing-Based Damage Healing Law
3.6. Damage-Healing Law for Concrete
- History of loading and damage;
- Rest period;
- Material characteristics that were reflected mathematically in this present work represented by the parameter .
3.7. Unilateral-Effects-Based Models
4. Anisotropic Damage-Healing Formulations
5. Super Healing Theory
6. Self-Healing Metals
6.1. Liquid State Healing Mechanism
6.2. Solid State Healing Mechanism (Precipitation Healing)
7. Conclusions and Perspectives
- The measure and presentation of the healing variable in both autonomous and autogenous self-healing mechanisms.
- The evolution equations of the healing models based on CDHM.
- The influence of different mechanical and environmental parameters on the healing efficiency.
- The effect of the self-healing and super healing on the mechanical behavior of the material.
- The anisotropic presentation of damage-healing and super healing with tensorial formulation.
- The effect of the new strengthening theory based on the super healing and CDHM.
Author Contributions
Funding
Conflicts of Interest
References
- Hilloulin, B.; Grondin, F.; Matallah, M.; Loukili, A. Modelling of autogenous healing in ultra high performance concrete. Cem. Concr. Res. 2014, 61, 64–70. [Google Scholar] [CrossRef]
- Yang, Y.; Lepech, M.D.; Yang, E.H.; Li, V.C. Autogenous healing of engineered cementitious composites under wet–dry cycles. Cem. Concr. Res. 2009, 39, 382–390. [Google Scholar] [CrossRef]
- Giannaros, P.; Kanellopoulos, A.; Al-Tabbaa, A. Sealing of cracks in cement using microencapsulated sodium silicate. Smart Mater. Struct. 2016, 25, 084005. [Google Scholar] [CrossRef]
- White, S.R.; Sottos, N.; Geubelle, P.; Moore, J.; Kessler, M.; Sriram, S.; Brown, E.; Viswanathan, S. Autonomic healing of polymer composites. Nature 2001, 409, 794–797. [Google Scholar] [CrossRef] [PubMed]
- Barbero, E.J.; Greco, F.; Lonetti, P. Continuum damage-healing mechanics with application to self-healing composites. Int. J. Damage Mech. 2005, 14, 51–81. [Google Scholar] [CrossRef]
- Herbst, O.; Luding, S. Modeling particulate self-healing materials and application to uni-axial compression. Int. J. Fract. 2008, 154, 87–103. [Google Scholar] [CrossRef] [Green Version]
- Hall, J.; Qamar, I.; Rendall, T.; Trask, R. A computational model for the flow of resin in self-healing composites. Smart Mater. Struct. 2015, 24, 037002. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Rabczuk, T.; Gracie, R.; Song, J.H.; Belytschko, T. Immersed particle method for fluid–structure interaction. Int. J. Numer. Methods Eng. 2010, 81, 48–71. [Google Scholar] [CrossRef]
- Rabczuk, T.; Zi, G.; Bordas, S.; Nguyen-Xuan, H. A simple and robust three-dimensional cracking-particle method without enrichment. Comput. Methods Appl. Mech. Eng. 2010, 199, 2437–2455. [Google Scholar] [CrossRef]
- Zhou, S.; Zhu, H.; Ju, J.W.; Yan, Z.; Chen, Q. Modeling microcapsule-enabled self-healing cementitious composite materials using discrete element method. Int. J. Damage Mech. 2017, 26, 340–357. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T.D.; de Sá, J.C. A novel two-stage discrete crack method based on the screened Poisson equation and local mesh refinement. Comput. Mech. 2016, 58, 1003–1018. [Google Scholar] [CrossRef]
- Gui, Y.L.; Bui, H.H.; Kodikara, J.; Zhang, Q.B.; Zhao, J.; Rabczuk, T. Modelling the dynamic failure of brittle rocks using a hybrid continuum-discrete element method with a mixed-mode cohesive fracture model. Int. J. Impact Eng. 2016, 87, 146–155. [Google Scholar] [CrossRef]
- Rabczuk, T.; Eibl, J. Simulation of high velocity concrete fragmentation using SPH/MLSPH. Int. J. Numer. Methods Eng. 2003, 56, 1421–1444. [Google Scholar] [CrossRef]
- Kalameh, H.A.; Karamali, A.; Anitescu, C.; Rabczuk, T. High velocity impact of metal sphere on thin metallic plate using smooth particle hydrodynamics (SPH) method. Front. Struct. Civ. Eng. 2012, 6, 101–110. [Google Scholar]
- Rabczuk, T.; Xiao, S.P.; Sauer, M. Coupling of mesh-free methods with finite elements: Basic concepts and test results. Commun. Numer. Methods Eng. 2006, 22, 1031–1065. [Google Scholar] [CrossRef]
- Rabczuk, T.; Eibl, J.; Stempniewski, L. Numerical analysis of high speed concrete fragmentation using a meshfree Lagrangian method. Eng. Fract. Mech. 2004, 71, 547–556. [Google Scholar] [CrossRef]
- Triantafyllou, S.P.; Chatzis, M.N. A new damage-healing smooth hysteretic formulation for the modeling of self-healing materials. In Proceedings of the 8th GRACM International Congress on Computational Mechanics, Volos, Greece, 12–15 July 2015. [Google Scholar]
- Rabczuk, T.; Areias, P.; Belytschko, T. A meshfree thin shell method for non-linear dynamic fracture. Int. J. Numer. Methods Eng. 2007, 72, 524–548. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Zi, G.; Bordas, S. Enriched Finite Element and Meshfree Methods for Dynamic Crack Propagation Problems. In Proceedings of the 5th Australasian Congress on Applied Mechanics, Brisbane, Australia, 10–12 December 2007; p. 570. [Google Scholar]
- Zi, G.; Rabczuk, T.; Wall, W. Extended meshfree methods without branch enrichment for cohesive cracks. Comput. Mech. 2007, 40, 367–382. [Google Scholar] [CrossRef]
- Rabczuk, T.; Bordas, S.; Zi, G. A three-dimensional meshfree method for continuous multiple-crack initiation, propagation and junction in statics and dynamics. Comput. Mech. 2007, 40, 473–495. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Areias, P. A meshfree thin shell for arbitrary evolving cracks based on an extrinsic basis. Comput. Model. Eng. Sci. 2006, 16, 115–130. [Google Scholar]
- Rabczuk, T.; Samaniego, E. Discontinuous modelling of shear bands using adaptive meshfree methods. Comput. Methods Appl. Mech. Eng. 2008, 197, 641–658. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, Z.; Zhang, S.; Duan, Q. Multiscale modeling and characterization of coupled damage-healing-plasticity for granular materials in concurrent computational homogenization approach. Comput. Methods Appl. Mech. Eng. 2018, 342, 354–383. [Google Scholar] [CrossRef]
- Talebi, H.; Silani, M.; Rabczuk, T. Concurrent multiscale modeling of three dimensional crack and dislocation propagation. Adv. Eng. Softw. 2015, 80, 82–92. [Google Scholar] [CrossRef]
- Budarapu, P.R.; Gracie, R.; Bordas, S.P.; Rabczuk, T. An adaptive multiscale method for quasi-static crack growth. Comput. Mech. 2014, 53, 1129–1148. [Google Scholar] [CrossRef]
- Talebi, H.; Silani, M.; Bordas, S.P.; Kerfriden, P.; Rabczuk, T. A computational library for multiscale modeling of material failure. Comput. Mech. 2014, 53, 1047–1071. [Google Scholar] [CrossRef]
- Budarapu, P.R.; Gracie, R.; Yang, S.W.; Zhuang, X.; Rabczuk, T. Efficient coarse graining in multiscale modeling of fracture. Theor. Appl. Fract. Mech. 2014, 69, 126–143. [Google Scholar] [CrossRef]
- Budarapu, P.; Javvaji, B.; Reinoso, J.; Paggi, M.; Rabczuk, T. A three dimensional adaptive multiscale method for crack growth in Silicon. Theor. Appl. Fract. Mech. 2018, 96, 576–603. [Google Scholar] [CrossRef]
- Pan, Y.; Tian, F.; Zhong, Z. A continuum damage-healing model of healing agents based self-healing materials. Int. J. Damage Mech. 2018, 27, 754–778. [Google Scholar] [CrossRef]
- Amiri, F.; Millán, D.; Shen, Y.; Rabczuk, T.; Arroyo, M. Phase-field modeling of fracture in linear thin shells. Theor. Appl. Fract. Mech. 2014, 69, 102–109. [Google Scholar] [CrossRef] [Green Version]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Msekh, M.A.; Silani, M.; Jamshidian, M.; Areias, P.; Zhuang, X.; Zi, G.; He, P.; Rabczuk, T. Predictions of J integral and tensile strength of clay/epoxy nanocomposites material using phase field model. Compos. Part B Eng. 2016, 93, 97–114. [Google Scholar] [CrossRef]
- Msekh, M.A.; Cuong, N.; Zi, G.; Areias, P.; Zhuang, X.; Rabczuk, T. Fracture properties prediction of clay/epoxy nanocomposites with interphase zones using a phase field model. Eng. Fract. Mech. 2018, 188, 287–299. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T. Steiner-point free edge cutting of tetrahedral meshes with applications in fracture. Finite Elem. Anal. Des. 2017, 132, 27–41. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Rabczuk, T. Dual-horizon peridynamics: A stable solution to varying horizons. Comput. Methods Appl. Mech. Eng. 2017, 318, 762–782. [Google Scholar] [CrossRef] [Green Version]
- Nguyen-Thanh, N.; Zhou, K.; Zhuang, X.; Areias, P.; Nguyen-Xuan, H.; Bazilevs, Y.; Rabczuk, T. Isogeometric analysis of large-deformation thin shells using RHT-splines for multiple-patch coupling. Comput. Methods Appl. Mech. Eng. 2017, 316, 1157–1178. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Cai, Y.; Rabczuk, T. Dual-horizon peridynamics. Int. J. Numer. Methods Eng. 2016, 108, 1451–1476. [Google Scholar] [CrossRef] [Green Version]
- Areias, P.; Rabczuk, T.; Msekh, M. Phase-field analysis of finite-strain plates and shells including element subdivision. Comput. Methods Appl. Mech. Eng. 2016, 312, 322–350. [Google Scholar] [CrossRef]
- Nguyen, B.; Tran, H.; Anitescu, C.; Zhuang, X.; Rabczuk, T. An isogeometric symmetric Galerkin boundary element method for two-dimensional crack problems. Comput. Methods Appl. Mech. Eng. 2016, 306, 252–275. [Google Scholar] [CrossRef]
- Areias, P.; Msekh, M.; Rabczuk, T. Damage and fracture algorithm using the screened Poisson equation and local remeshing. Eng. Fract. Mech. 2016, 158, 116–143. [Google Scholar] [CrossRef]
- Kachanov, L. On the creep fracture time. IZV AKAD 1958, 8, 26–31. [Google Scholar]
- Rabotnov, Y.N. Creep rupture in applied mechanics. In Proceedings of the 12th International Congress on Applied Mechanics, Stanford, CA, USA, 26–31 August 1968; pp. 342–349. [Google Scholar]
- Rabotnov, Y.N. Creep Problems in Structural Members; North-Holland Publishing Company: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Lemaitre, J.; Chaboche, J. A Non-Linear Model of Creep Fatigue Damage Cumulation; ONERA: Palaiseau, France, 1394; p. 174. [Google Scholar]
- Hayhurst, D. Creep rupture under multi-axial states of stress. J. Mech. Phys. Solids 1972, 20, 381–382. [Google Scholar] [CrossRef]
- Leckie, F.A.; Hayhurst, D. Constitutive equations for creep rupture. Acta Metall. 1977, 25, 1059–1070. [Google Scholar] [CrossRef]
- Chaboche, J. Continuum damage mechanics: Present state and future trends. Nucl. Eng. Des. 1987, 105, 19–33. [Google Scholar] [CrossRef]
- Lin, J.; Dunne, F.; Hayhurst, D. Aspects of testpiece design responsible for errors in cyclic plasticity experiments. Int. J. Damage Mech. 1999, 8, 109–137. [Google Scholar] [CrossRef]
- Murakami, S.; Ohno, N. Creep damage analysis in thin-walled tubes. Inelast. Behav. Press. Vessel Pip. Compon. 1978, 55–69. [Google Scholar]
- Murakami, S. Effect of cavity distribution in constitutive equations of creep and creep damage. In Proceedings of the EUROMECH Colloquium on Damage Mechanics, Cachan, France, 7–11 September 1981. [Google Scholar]
- Murakami, S.; Ohno, N. A continuum theory of creep and creep damage. In Creep in Structures; Springer: Berlin, Germany, 1981; pp. 422–444. [Google Scholar]
- Murakami, S. Damage mechanics approach to damage and fracture of materials. Rairo 1982, 3, 1–13. [Google Scholar]
- Chaboche, J.L. Continuous damage mechanics—A tool to describe phenomena before crack initiation. Nucl. Eng. Des. 1981, 64, 233–247. [Google Scholar] [CrossRef]
- Chaboche, J. Une loi Différentielle D’Endommagement de Fatigue Avec Cumulation Non Linéaire; Office Nationale d’Etudes et de Recherches Aérospatiales: Palaiseau, France, 1974. [Google Scholar]
- Chaboche, J.L. Continuum damage mechanics: Part I. general concepts. J. Appl. Mech. 1988, 55, 59–72. [Google Scholar] [CrossRef]
- Chaboche, J.L. Continuum damage mechanics: Part II—Damage growth, crack initiation, and crack growth. J. Appl. Mech. 1988, 55, 65–72. [Google Scholar] [CrossRef]
- Simo, J.; Ju, J. Strain-and stress-based continuum damage models—II. Computational aspects. Int. J. Solids Struct. 1987, 23, 841–869. [Google Scholar] [CrossRef]
- Simo, J.; Ju, J. Strain-and stress-based continuum damage models—I. Formulation. Math. Comput. Model. 1989, 12, 378. [Google Scholar] [CrossRef]
- Simo, J.; Ju, J.; Taylor, R.; Pister, K. On strain-based continuum damage models: Formulation and computational aspects. Const. Laws Eng. Mater. 1987, 1, 233–245. [Google Scholar]
- Simo, J.; Ju, J. On continuum damage-elastoplasticity at finite strains. Comput. Mech. 1989, 5, 375–400. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. A plasticity-damage theory for large deformation of solids? I. Theoretical formulation. Int. J. Eng. Sci. 1992, 30, 1089–1108. [Google Scholar] [CrossRef]
- Voyiadjis, G.; Park, T. Anisotropic damage effect tensors for the symmetrization of the effective stress tensor. J. Appl. Mech. 1997, 64, 106–110. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Park, T. Local and interfacial damage analysis of metal matrix composites using the finite element method. Eng. Fract. Mech. 1997, 56, 483–511. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z. Advances in Damage Mechanics: Metals and Metal Matrix Composites; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Cordier, G.; Van, K.D. Strain hardening effects and damage in plastic fatigue. In Physical Non-Linearities in Structural Analysis; Springer: Berlin, Germany, 1981; pp. 52–55. [Google Scholar]
- Bodner, S. A procedure for including damage in constitutive equations for elastic-viscoplastic work-hardening materials. In Physical Non-Linearities in Structural Analysis; Springer: Berlin, Germany, 1981; pp. 21–28. [Google Scholar]
- Kachanov, L. Introduction to Continuum Damage Mechanics; Springer Science & Business Media: Berlin, Germany, 2013; Volume 10. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Aspect phénoménologique de la rupture par endommagement. J. Méc. Appl. 1978, 2, 317–365. [Google Scholar]
- Lemaitre, J.; Dufailly, J. Modelization and identification of endommagement plasticity of material. In Proceedings of the 3rd French Congress of Mechanics, Grenoble, France, 1977; pp. 17–21. [Google Scholar]
- Voyiadjis, G.Z. Degradation of elastic modulus in elastoplastic coupling with finite strains. Int. J. Plast. 1988, 4, 335–353. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Decomposition of elastic stiffness degradation in continuum damage mechanics. J. Eng. Mater. Technol. 2017, 139, 021005. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Damage mechanics with fabric tensors. Mech. Adv. Mater. Struct. 2006, 13, 285–301. [Google Scholar] [CrossRef]
- Kattan, P.I.; Voyiadjis, G.Z. Decomposition of damage tensor in continuum damage mechanics. J. Eng. Mech. 2001, 127, 940–944. [Google Scholar] [CrossRef]
- Rabczuk, T.; Akkermann, J.; Eibl, J. A numerical model for reinforced concrete structures. Int. J. Solids Struct. 2005, 42, 1327–1354. [Google Scholar] [CrossRef]
- Dunant, C.F.; Bordas, S.P.; Kerfriden, P.; Scrivener, K.L.; Rabczuk, T. An algorithm to compute damage from load in composites. Front. Archit. Civ. Eng. China 2011, 5, 180–193. [Google Scholar] [CrossRef]
- Silani, M.; Ziaei-Rad, S.; Talebi, H.; Rabczuk, T. A semi-concurrent multiscale approach for modeling damage in nanocomposites. Theor. Appl. Fract. Mech. 2014, 74, 30–38. [Google Scholar] [CrossRef]
- Silani, M.; Talebi, H.; Hamouda, A.M.; Rabczuk, T. Nonlocal damage modelling in clay/epoxy nanocomposites using a multiscale approach. J. Comput. Sci. 2016, 15, 18–23. [Google Scholar] [CrossRef]
- Thai, T.Q.; Rabczuk, T.; Bazilevs, Y.; Meschke, G. A higher-order stress-based gradient-enhanced damage model based on isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2016, 304, 584–604. [Google Scholar] [CrossRef]
- Abiri, O.; Lindgren, L.E. Non-local damage models in manufacturing simulations. Eur. J. Mech. A/Solids 2015, 49, 548–560. [Google Scholar] [CrossRef]
- Geers, M.; Peerlings, R.; Brekelmans, W.; de Borst, R. Phenomenological nonlocal approaches based on implicit gradient-enhanced damage. Acta Mech. 2000, 144, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Rojas-Solano, L.B.; Grégoire, D.; Pijaudier-Cabot, G. Interaction-based non-local damage model for failure in quasi-brittle materials. Mech. Res. Commun. 2013, 54, 56–62. [Google Scholar] [CrossRef]
- Simone, A.; Askes, H.; Sluys, L.J. Incorrect initiation and propagation of failure in non-local and gradient-enhanced media. Int. J. Solids Struct. 2004, 41, 351–363. [Google Scholar] [CrossRef]
- Peerlings, R.; Geers, M.; De Borst, R.; Brekelmans, W. A critical comparison of nonlocal and gradient-enhanced softening continua. Int. J. Solids Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Oucif, C.; Voyiadjis, G.Z.; Kattan, P.I.; Rabczuk, T. Investigation of the super healing theory in continuum damage and healing mechanics. Int. J. Damage Mech. 2018. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. A comparative study of damage variables in continuum damage mechanics. Int. J. Damage Mech. 2009, 18, 315–340. [Google Scholar] [CrossRef]
- Oucif, C.; Voyiadjis, G.Z.; Rabczuk, T. Modeling of damage-healing and nonlinear self-healing concrete behavior: Application to coupled and uncoupled self-healing mechanisms. Theor. Appl. Fract. Mech. 2018, 96, 216–230. [Google Scholar] [CrossRef]
- Oucif, C.; Voyiadjis, G.Z.; Kattan, P.I.; Rabczuk, T. Nonlinear Superhealing and Contribution to the Design of a New Strengthening Theory. J. Eng. Mech. 2018, 144, 04018055. [Google Scholar] [CrossRef]
- Darabi, M.K.; Al-Rub, R.K.A.; Little, D.N. A continuum damage mechanics framework for modeling micro-damage healing. Int. J. Solids Struct. 2012, 49, 492–513. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Shojaei, A.; Li, G.; Kattan, P. Continuum damage-healing mechanics with introduction to new healing variables. Int. J. Damage Mech. 2012, 21, 391–414. [Google Scholar] [CrossRef]
- Wool, R.; O’connor, K. A theory crack healing in polymers. J. Appl. Phys. 1981, 52, 5953–5963. [Google Scholar] [CrossRef]
- Schapery, R. On the mechanics of crack closing and bonding in linear viscoelastic media. Int. J. Fract. 1989, 39, 163–189. [Google Scholar] [CrossRef]
- Little, D.N.; Bhasin, A. Exploring Mechanism of H ealing in Asphalt Mixtures and Quantifying its Impact. In Self Healing Materials; Springer: Berlin, Germany, 2007; pp. 205–218. [Google Scholar]
- Bhasin, A.; Little, D.N.; Bommavaram, R.; Vasconcelos, K. A framework to quantify the effect of healing in bituminous materials using material properties. Road Mater. Pavement Des. 2008, 9, 219–242. [Google Scholar] [CrossRef]
- Chan, K.; Bodner, S.; Fossum, A.; Munson, D. Constitutive Representation of Damage Development and Healing in WIPP Salt; Technical report; Sandia National Labs.: Livermore, CA, USA, 1994.
- Chan, K.; Bodner, S.; Munson, D. Recovery and healing of damage in WIPP salt. Int. J. Damage Mech. 1998, 7, 143–166. [Google Scholar] [CrossRef]
- Miao, S.; Wang, M.L.; Schreyer, H.L. Constitutive models for healing of materials with application to compaction of crushed rock salt. J. Eng. Mech. 1995, 121, 1122–1129. [Google Scholar] [CrossRef]
- Xu, H.; Arson, C.; Chester, F. Stiffness and Deformation of Salt Rock Subject to Anisotropic Damage and Temperature-Dependent Healing. In Proceedings of the 46th US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; American Rock Mechanics Association. [Google Scholar]
- Arson, C.; Xu, H.; Chester, F.M. On the definition of damage in time-dependent healing models for salt rock. Géotech. Lett. 2012, 2, 67–71. [Google Scholar] [CrossRef]
- Zhu, C.; Arson, C. Theoretical Bases of Thermomechanical Damage and DMT-Healing Model for Rock. In Proceedings of the Geo-Congress 2014: Geo-Characterization and Modeling for Sustainability, Atlanta, GA, USA, 23–26 February 2014; pp. 2785–2794. [Google Scholar]
- Zhu, C.; Arson, C. Using Microstructure Descriptors to Model Thermo-Mechanical Damage and Healing in Salt Rock; Georgia Institute of Technology: Atlanta, GA, USA, 2014. [Google Scholar]
- Zhu, C.; Arson, C. A model of damage and healing coupling halite thermo-mechanical behavior to microstructure evolution. Geotech. Geol. Eng. 2015, 33, 389–410. [Google Scholar] [CrossRef]
- Zhu, C.; Arson, C. Fabric-Enriched Modeling of Anisotropic Healing Induced by Diffusion in Granular Salt; Georgia Institute of Technology: Atlanta, GA, USA, 2015. [Google Scholar]
- Xu, J.; Qu, J.; Gao, Y.; Xu, N. Study on the Elastoplastic Damage-Healing Coupled Constitutive Model of Mudstone. Math. Probl. Eng. 2017, 2017, 6431607. [Google Scholar] [CrossRef]
- Ju, J.; Yuan, K. New strain-energy-based coupled elastoplastic two-parameter damage and healing models for earth-moving processes. Int. J. Damage Mech. 2012, 21, 989–1019. [Google Scholar] [CrossRef]
- Ju, J.; Yuan, K.; Kuo, A. Novel strain energy based coupled elastoplastic damage and healing models for geomaterials—Part I: Formulations. Int. J. Damage Mech. 2012, 21, 525–549. [Google Scholar] [CrossRef]
- Ju, J.W.; Yuan, K.Y.; Kuo, A.W.; Chen, J.S. Novel Strain Energy Based Coupled Elastoplastic Damage and Healing Models for Geomaterials—Part II: Computational Aspects. Int. J. Damage Mech. 2012, 21, 551–576. [Google Scholar] [CrossRef]
- Yuan, K.; Ju, J. New strain energy–based coupled elastoplastic damage-healing formulations accounting for effect of matric suction during earth-moving processes. J. Eng. Mech. 2012, 139, 188–199. [Google Scholar] [CrossRef]
- Hampel, A. Description of damage reduction and healing with the CDM constitutive model for the thermo-mechanical behavior of rock salt. In Mechanical Behavior of Salt VIII; Taylor & Francis Group: London, UK, 2012; pp. 1–10. [Google Scholar]
- Hong, S.; Yuan, K.; Ju, J. New strain energy-based thermo-elastoviscoplastic isotropic damage–self-healing model for bituminous composites—Part I: Formulations. Int. J. Damage Mech. 2017, 26, 651–671. [Google Scholar] [CrossRef]
- Hong, S.; Yuan, K.; Ju, J. New strain energy-based thermo-elastoviscoplastic isotropic damage–self-healing model for bituminous composites—Part II: Computational aspects. Int. J. Damage Mech. 2017, 26, 672–696. [Google Scholar] [CrossRef]
- Hong, S.; Yuan, K.; Ju, J. Initial strain energy-based thermo-elastoviscoplastic two-parameter damage–self-healing models for bituminous composites—Part I: Formulations. Int. J. Damage Mech. 2016, 25, 1082–1102. [Google Scholar] [CrossRef]
- Hong, S.; Yuan, K.; Ju, J. Initial strain energy-based thermo-elastoviscoplastic two-parameter damage self-healing model for bituminous composites—Part II: Computational aspects. Int. J. Damage Mech. 2016, 25, 1103–1129. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, Y.R. Viscoelastic continuum damage model of asphalt concrete with healing. J. Eng. Mech. 1998, 124, 1224–1232. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, Y.R. Viscoelastic constitutive model for asphalt concrete under cyclic loading. J. Eng. Mech. 1998, 124, 32–40. [Google Scholar] [CrossRef]
- Schapery, R.A. Correspondence principles and a generalizedJ integral for large deformation and fracture analysis of viscoelastic media. Int. J. Fract. 1984, 25, 195–223. [Google Scholar] [CrossRef]
- Carpenter, S.; Shen, S. A Dissipated Energy Approach to Study HMA Healing 36 in Fatigue. Transp. Res. Rec. 2006, 1970, 178–185. [Google Scholar] [CrossRef]
- Kim, B.; Roque, R. Evaluation of healing property of asphalt mixtures. Transp. Res. Rec. 2006, 1970, 84–91. [Google Scholar] [CrossRef]
- Prager, S.; Tirrell, M. The healing process at polymer–polymer interfaces. J. Chem. Phys. 1981, 75, 5194–5198. [Google Scholar] [CrossRef]
- Shen, S.; Carpenter, S. Application of the dissipated energy concept in fatigue endurance limit testing. Transp. Res. Rec. 2005, 1929, 165–173. [Google Scholar] [CrossRef]
- Shen, S.; Airey, G.D.; Carpenter, S.H.; Huang, H. A dissipated energy approach to fatigue evaluation. Road Mater. Pavement Des. 2006, 7, 47–69. [Google Scholar] [CrossRef]
- Menozzi, A.; Garcia, A.; Partl, M.N.; Tebaldi, G.; Schuetz, P. Induction healing of fatigue damage in asphalt test samples. Constr. Build. Mater. 2015, 74, 162–168. [Google Scholar] [CrossRef]
- Riara, M.; Tang, P.; Mo, L.; Javilla, B.; Chen, M.; Wu, S. Systematic evaluation of fracture-based healing indexes of asphalt mixtures. J. Mater. Civ. Eng. 2018, 30, 04018264. [Google Scholar] [CrossRef]
- Al-Rub, R.K.A.; Darabi, M.K.; Little, D.N.; Masad, E.A. A micro-damage healing model that improves prediction of fatigue life in asphalt mixes. Int. J. Eng. Sci. 2010, 48, 966–990. [Google Scholar] [CrossRef]
- Darabi, M.K.; Al-Rub, R.K.A.; Masad, E.A.; Little, D.N. Constitutive modeling of fatigue damage response of asphalt concrete materials with consideration of micro-damage healing. Int. J. Solids Struct. 2013, 50, 2901–2913. [Google Scholar] [CrossRef]
- Alsheghri, A.A.; Al-Rub, R.K.A. Thermodynamic-based cohesive zone healing model for self-healing materials. Mech. Res. Commun. 2015, 70, 102–113. [Google Scholar] [CrossRef]
- Alsheghri, A.A.; Al-Rub, R.K.A. Finite element implementation and application of a cohesive zone damage-healing model for self-healing materials. Eng. Fract. Mech. 2016, 163, 1–22. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Shojaei, A.; Li, G. A generalized coupled viscoplastic–viscodamage–viscohealing theory for glassy polymers. Int. J. Plast. 2012, 28, 21–45. [Google Scholar] [CrossRef]
- Darabi, M.K.; Al-Rub, R.K.A.; Masad, E.A.; Huang, C.W.; Little, D.N. A thermo-viscoelastic–viscoplastic–viscodamage constitutive model for asphaltic materials. Int. J. Solids Struct. 2011, 48, 191–207. [Google Scholar] [CrossRef]
- Shojaei, A.; Li, G.; Voyiadjis, G.Z. Cyclic viscoplastic-viscodamage analysis of shape memory polymers fibers with application to self-healing smart materials. J. Appl. Mech. 2013, 80, 011014. [Google Scholar] [CrossRef]
- Underwood, B.; Zeiada, W. Characterization of microdamage healing in asphalt concrete with a smeared continuum damage approach. Transp. Res. Rec. 2014, 2447, 126–135. [Google Scholar] [CrossRef]
- Karki, P.; Li, R.; Bhasin, A. Quantifying overall damage and healing behaviour of asphalt materials using continuum damage approach. Int. J. Pavement Eng. 2015, 16, 350–362. [Google Scholar] [CrossRef]
- Mergheim, J.; Steinmann, P. Phenomenological modelling of self-healing polymers based on integrated healing agents. Comput. Mech. 2013, 52, 681–692. [Google Scholar] [CrossRef]
- Mergheim, J.; Possart, G.; Steinmann, P. Modelling and computation of curing and damage of thermosets. Comput. Mater. Sci. 2012, 53, 359–367. [Google Scholar] [CrossRef]
- Wu, M.; Johannesson, B.; Geiker, M. A review: Self-healing in cementitious materials and engineered cementitious composite as a self-healing material. Constr. Build. Mater. 2012, 28, 571–583. [Google Scholar] [CrossRef]
- Sanada, K.; Mizuno, Y.; Shindo, Y. Damage progression and notched strength recovery of fiber-reinforced polymers encompassing self-healing of interfacial debonding. J. Compos. Mater. 2015, 49, 1765–1776. [Google Scholar] [CrossRef]
- Ahmed, A.; Sanada, K.; Fanni, M.; El-Moneim, A.A. A practical methodology for modeling and verification of self-healing microcapsules-based composites elasticity. Compos. Struct. 2018, 184, 1092–1098. [Google Scholar] [CrossRef]
- Mauludin, L.M.; Zhuang, X.; Rabczuk, T. Computational modeling of fracture in encapsulation-based self-healing concrete using cohesive elements. Compos. Struct. 2018, 196, 63–75. [Google Scholar] [CrossRef]
- Mauludin, L.M.; Oucif, C. Interaction between matrix crack and circular capsule under uniaxial tension in encapsulation-based self-healing concrete. Undergr. Space 2018, 3, 181–189. [Google Scholar] [CrossRef]
- Mauludin, L.M.; Oucif, C. The effects of interfacial strength on fractured microcapsule. Front. Struct. Civ. Eng. 2018, 1–11. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Mechanics of damage, healing, damageability, and integrity of materials: A conceptual framework. Int. J. Damage Mech. 2017, 26, 50–103. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Decomposition of healing tensor: In continuum damage and healing mechanics. Int. J. Damage Mech. 2018, 27, 1020–1057. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, S.; Yan, Z.; Ju, J.W.; Chen, Q. A two-dimensional micromechanical damage-healing model on microcrack-induced damage for microcapsule-enabled self-healing cementitious composites under tensile loading. Int. J. Damage Mech. 2015, 24, 95–115. [Google Scholar] [CrossRef]
- Li, X.; Du, Y.; Duan, Q.; Ju, J.W. Thermodynamic framework for damage-healing-plasticity of granular materials and net damage variable. Int. J. Damage Mech. 2016, 25, 153–177. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, S.; Yan, Z.; Ju, J.W.; Chen, Q. A two-dimensional micromechanical damage–healing model on microcrack-induced damage for microcapsule-enabled self-healing cementitious composites under compressive loading. Int. J. Damage Mech. 2016, 25, 727–749. [Google Scholar] [CrossRef]
- Shahsavari, H.; Baghani, M.; Sohrabpour, S.; Naghdabadi, R. Continuum damage-healing constitutive modeling for concrete materials through stress spectral decomposition. Int. J. Damage Mech. 2016, 25, 900–918. [Google Scholar] [CrossRef]
- Ozaki, S.; Osada, T.; Nakao, W. Finite element analysis of the damage and healing behavior of self-healing ceramic materials. Int. J. Solids Struct. 2016, 100, 307–318. [Google Scholar] [CrossRef]
- Davies, R.; Jefferson, A. Micromechanical modelling of self-healing cementitious materials. Int. J. Solids Struct. 2017, 113, 180–191. [Google Scholar] [CrossRef]
- Kazemi, A.; Baghani, M.; Shahsavari, H.; Abrinia, K.; Baniassadi, M. Application of elastic-damage-heal model for self-healing concrete thick-walled cylinders through thermodynamics of irreversible processes. Int. J. Appl. Mech. 2017, 9, 1750082. [Google Scholar] [CrossRef]
- Chaboche, J.L. Damage induced anisotropy: On the difficulties associated with the active/passive unilateral condition. Int. J. Damage Mech. 1992, 1, 148–171. [Google Scholar] [CrossRef]
- Cormery, F.; Welemane, H. A critical review of some damage models with unilateral effect. Mech. Res. Commun. 2002, 29, 391–395. [Google Scholar] [CrossRef] [Green Version]
- Welemane, H.; Goidescu, C. Isotropic brittle damage and unilateral effect. C. R. Méc. 2010, 338, 271–276. [Google Scholar] [CrossRef] [Green Version]
- Alliche, A. A continuum anisotropic damage model with unilateral effect. Mech. Sci. 2016, 7, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Bielski, J.; Skrzypek, J.; Kuna-Ciskal, H. Implementation of a model of coupled elastic-plastic unilateral damage material to finite element code. Int. J. Damage Mech. 2006, 15, 5–39. [Google Scholar] [CrossRef]
- Zhu, C.; Arson, C. A thermo-mechanical damage model for rock stiffness during anisotropic crack opening and closure. Acta Geotech. 2014, 9, 847–867. [Google Scholar] [CrossRef]
- Xianda, S.; Zhu, C.; Arson, C. Chemo-Mechanical Damage and Healing of Granular Salt: Micro-Macro Modeling; Georgia Institute of Technology: Atlanta, GA, USA, 2016. [Google Scholar]
- He, W.; Wu, Y.F.; Xu, Y.; Fu, T.T. A thermodynamically consistent nonlocal damage model for concrete materials with unilateral effects. Comput. Methods Appl. Mech. Eng. 2015, 297, 371–391. [Google Scholar] [CrossRef]
- Matallah, M.; La Borderie, C. Inelasticity–damage-based model for numerical modeling of concrete cracking. Eng. Fract. Mech. 2009, 76, 1087–1108. [Google Scholar] [CrossRef]
- Murakami, S. Mechanical modeling of material damage. J. Appl. Mech. 1988, 55, 280–286. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Shojaei, A.; Li, G.; Kattan, P.I. A theory of anisotropic healing and damage mechanics of materials. Proc. R. Soc. A 2012, 468, 163–183. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Yousef, M.A.; Kattan, P.I. New tensors for anisotropic damage in continuum damage mechanics. J. Eng. Mater. Technol. 2012, 134, 021015. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. On the decomposition of the damage variable in continuum damage mechanics. Acta Mech. 2017, 228, 2499–2517. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Shojaei, A.; Li, G. A thermodynamic consistent damage and healing model for self healing materials. Int. J. Plast. 2011, 27, 1025–1044. [Google Scholar] [CrossRef]
- Balieu, R.; Kringos, N.; Chen, F.; Córdoba, E. Multiplicative viscoelastic-viscoplastic damage-healing model for asphalt-concrete materials. In Proceedings of the 8th RILEM International Conference on Mechanisms of Cracking and Debonding in Pavements, Nantes, France, 7–9 June 2016; pp. 235–240. [Google Scholar]
- Voyiadjis, G.Z.; Kattan, P.I. Mechanics of damage processes in series and in parallel: A conceptual framework. Acta Mech. 2012, 223, 1863–1878. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Healing and super healing in continuum damage mechanics. Int. J. Damage Mech. 2014, 23, 245–260. [Google Scholar] [CrossRef]
- Wang, J.; Soens, H.; Verstraete, W.; De Belie, N. Self-healing concrete by use of microencapsulated bacterial spores. Cem. Concr. Res. 2014, 56, 139–152. [Google Scholar] [CrossRef]
- Dong, B.; Fang, G.; Wang, Y.; Liu, Y.; Hong, S.; Zhang, J.; Lin, S.; Xing, F. Performance recovery concerning the permeability of concrete by means of a microcapsule based self-healing system. Cem. Concr. Compos. 2017, 78, 84–96. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Introduction to the mechanics and design of undamageable materials. Int. J. Damage Mech. 2013, 22, 323–335. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. On the theory of elastic undamageable materials. J. Eng. Mater. Technol. 2013, 135, 021002. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. Governing differential equations for the mechanics of undamageable materials. Eng. Trans. 2014, 62, 241–267. [Google Scholar]
- Ghosh, S.K. Self-Healing Materials: Fundamentals, Design Strategies, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Files, B.S. Design of a Biomimetic Self-Healing Superalloy Composite. Ph.D. Thesis, Northwestern University, Evanston, IL, USA, 1997. [Google Scholar]
- Manuel, M.V. Design of a Biomimetic Self-Healing Alloy Composite. Ph.D. Thesis, Northwestern University, Evanston, IL, USA, 2007. [Google Scholar]
- Manuel, M.V.; Olson, G.B. Biomimetic self-healing metals. In Proceedings of the 1st International Conference on Self-Healing Materials, Noordwijik aan Zee, The Netherlands, 18–20 April 2007; pp. 18–20. [Google Scholar]
- Burton, D.; Gao, X.; Brinson, L. Finite element simulation of a self-healing shape memory alloy composite. Mech. Mater. 2006, 38, 525–537. [Google Scholar] [CrossRef]
- Zhu, P.; Cui, Z.; Kesler, M.S.; Newman, J.A.; Manuel, M.V.; Wright, M.C.; Brinson, L.C. Characterization and modeling of three-dimensional self-healing shape memory alloy-reinforced metal-matrix composites. Mech. Mater. 2016, 103, 1–10. [Google Scholar] [CrossRef]
- Araki, S.; Ono, H.; Saito, K. Micromechanical analysis of crack closure mechanism for intelligent material containing TiNi fibers. JSME Int. J. Ser. Solid Mech. Mater. Eng. 2002, 45, 208–216. [Google Scholar]
- Bor, T.C.; Warnet, L.; Akkerman, R.; de Boer, A. Modeling of stress development during thermal damage healing in fiber-reinforced composite materials containing embedded shape memory alloy wires. J. Compos. Mater. 2010, 44, 2547–2572. [Google Scholar] [CrossRef]
- Kawai, M.; Ogawa, H.; Baburaj, V.; Koga, T. Micromechamical analysis for hysteretic behavior of unidirectional TiNi SMA fiber composites. J. Intell. Mater. Syst. Struct. 1999, 10, 14–28. [Google Scholar] [CrossRef]
- Grabowski, B.; Tasan, C.C. Self-healing metals. In Self-Healing Materials; Springer: Berlin, Germany, 2016; pp. 387–407. [Google Scholar]
- Lumley, R.; Polmear, I. Advances in self-healing metals. In Proceedings of the First International Conference on Self Healing Materials, Series in Materials Science, Noordwijk aan Zee, The Netherlands, 18–20 April 2007; Volume 24. [Google Scholar]
- Lumley, R.; Morton, A.; Polmear, I. Enhanced creep performance in an Al–Cu–Mg–Ag alloy through underageing. Acta Mater. 2002, 50, 3597–3608. [Google Scholar] [CrossRef]
- Shinya, N.; Kyono, J.; Laha, K.; Masuda, C. Self-healing of creep damage through autonomous boron segregation and boron nitride precipitation during high temperature use of austenitic stainless steels. In Proceedings of the First International Conference on Self-Healing Materials, Noordwijk aan Zee, The Netherlands, 18–20 April 2007. [Google Scholar]
- Laha, K.; Kyono, J.; Sasaki, T.; Kishimoto, S.; Shinya, N. Improved creep strength and creep ductility of type 347 austenitic stainless steel through the self-healing effect of boron for creep cavitation. Metall. Mater. Trans. A 2005, 36, 399–409. [Google Scholar] [CrossRef]
- Li, S.; Gao, K.; Qiao, L.; Zhou, F.; Chu, W. Molecular dynamics simulation of microcrack healing in copper. Comput. Mater. Sci. 2001, 20, 143–150. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Kewei, G.; Lijie, Q.; Wuyang, C.; Fuxin, Z. Molecular dynamics simulation of the role of dislocations in microcrack healing. Acta Mech. Sin. 2000, 16, 366–373. [Google Scholar] [CrossRef]
- Zhou, G.; Gao, K.; Qiao, L.; Wang, Y.; Chu, W. Atomistic simulation of microcrack healing in aluminium. Model. Simul. Mater. Sci. Eng. 2000, 8, 603. [Google Scholar] [CrossRef]
- Wei, D.; Han, J.; Tieu, K.; Jiang, Z. Simulation of crack healing in BCC Fe. Scr. Mater. 2004, 51, 583–587. [Google Scholar] [CrossRef]
- Huang, P.; Li, Z.; Sun, J. Shrinkage and splitting of microcracks under pressure simulated by the finite-element method. Metall. Mater. Trans. A 2002, 33, 1117–1124. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z. The shrinkage of grain-boundary voids under pressure. Metall. Mater. Trans. A 2003, 34, 1493–1500. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z. Stability and shrinkage of a cavity in stressed grain. J. Appl. Phys. 2004, 95, 6025–6031. [Google Scholar] [CrossRef]
- Kukudzhanov, K. Modeling the healing of damage of metal by high-energy pulsed electromagnetic field. Lett. Mater. PIS Mater. 2018, 8, 27–32. [Google Scholar]
- Versteylen, C.; Sluiter, M.; van Dijk, N. Modelling the formation and self-healing of creep damage in iron-based alloys. J. Mater. Sci. 2018, 53, 14758–14773. [Google Scholar] [CrossRef]


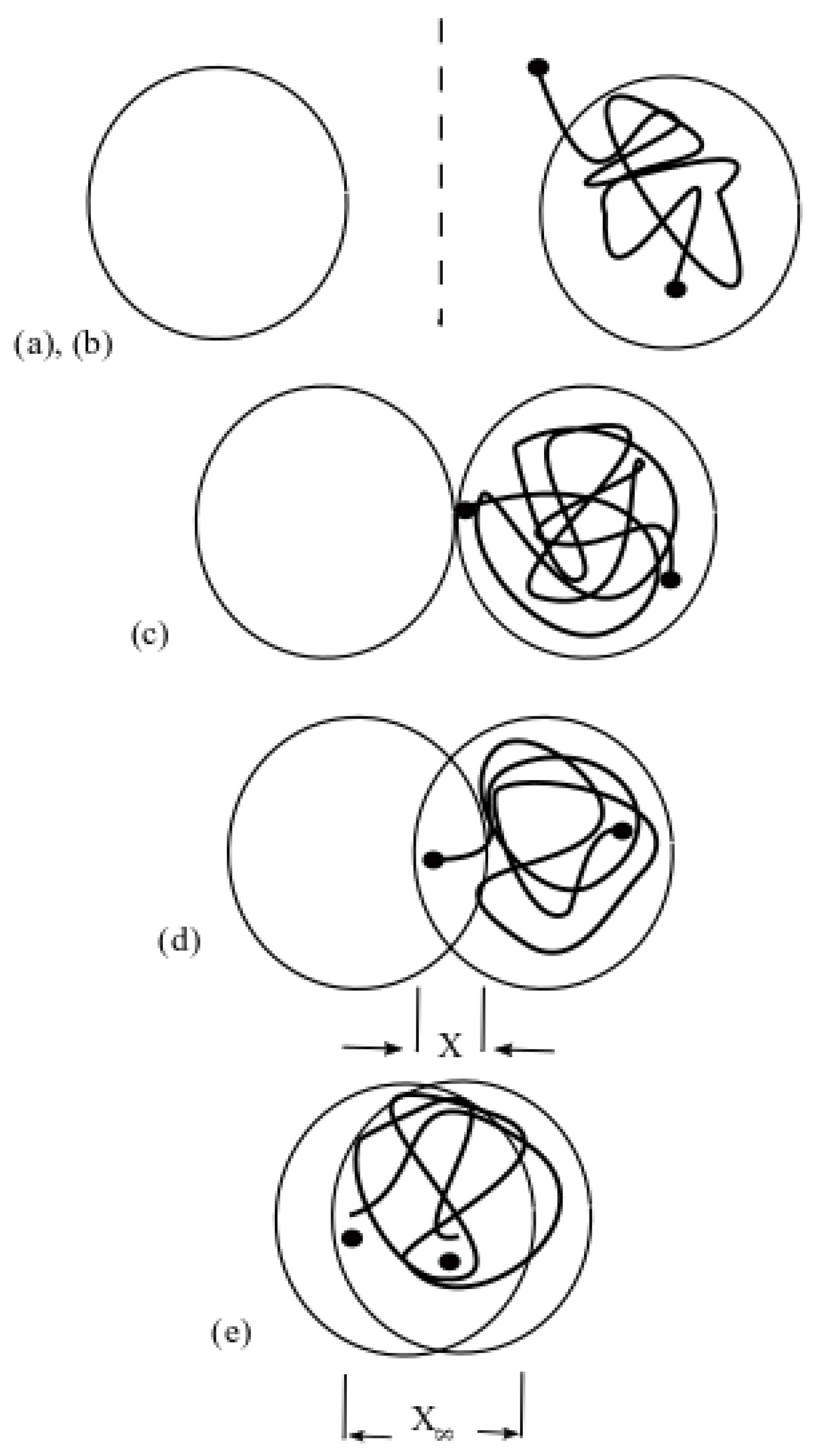
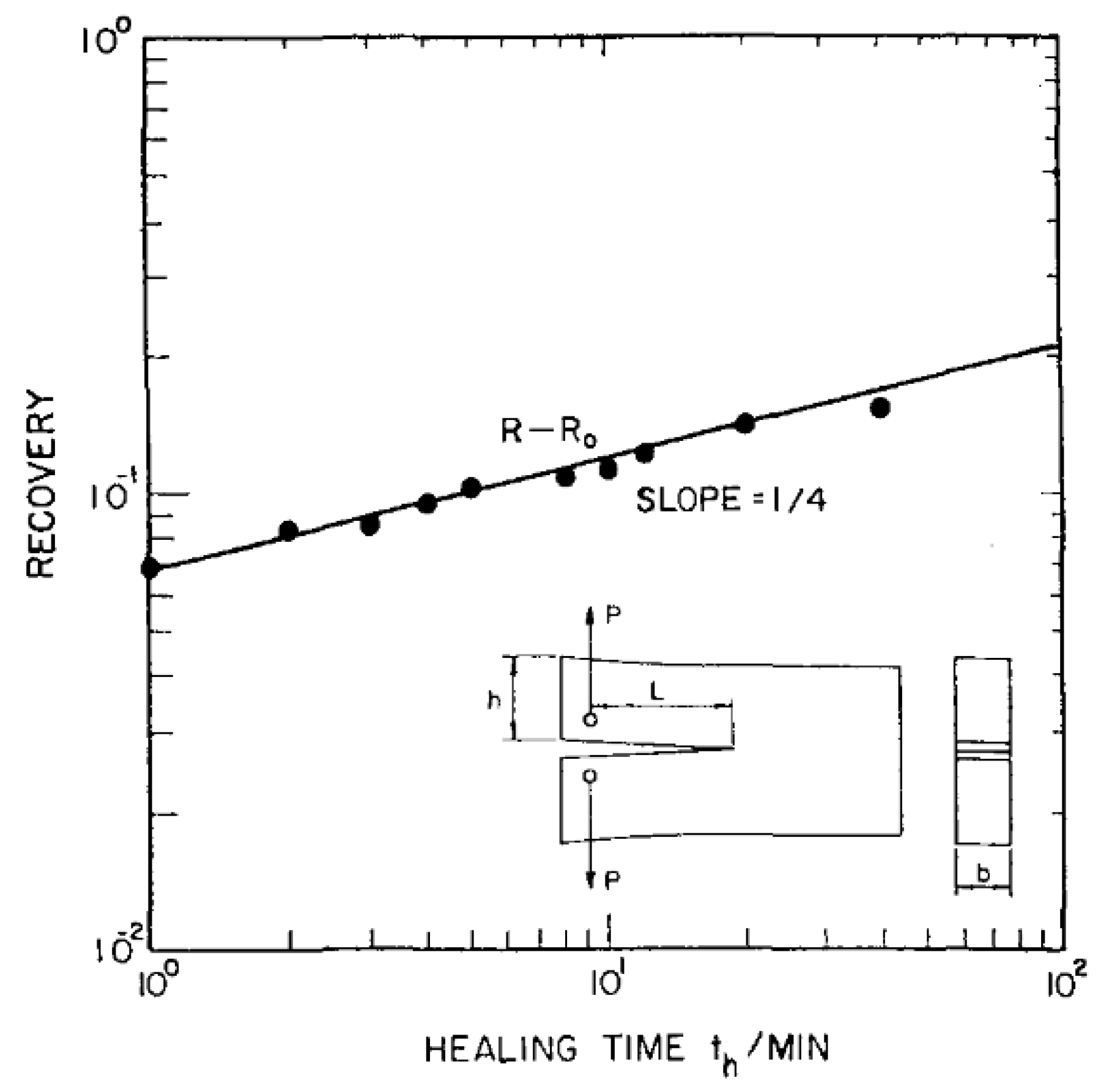




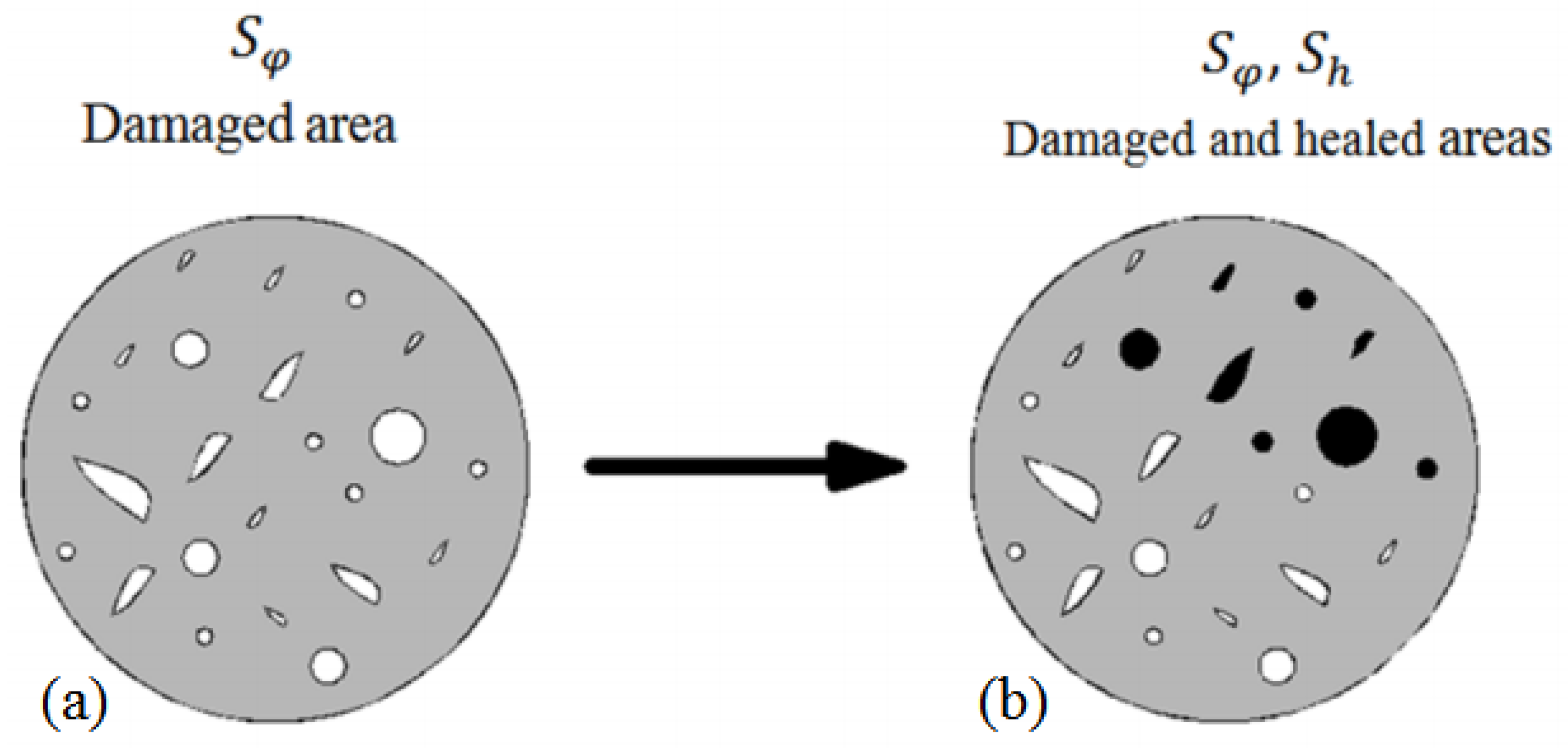

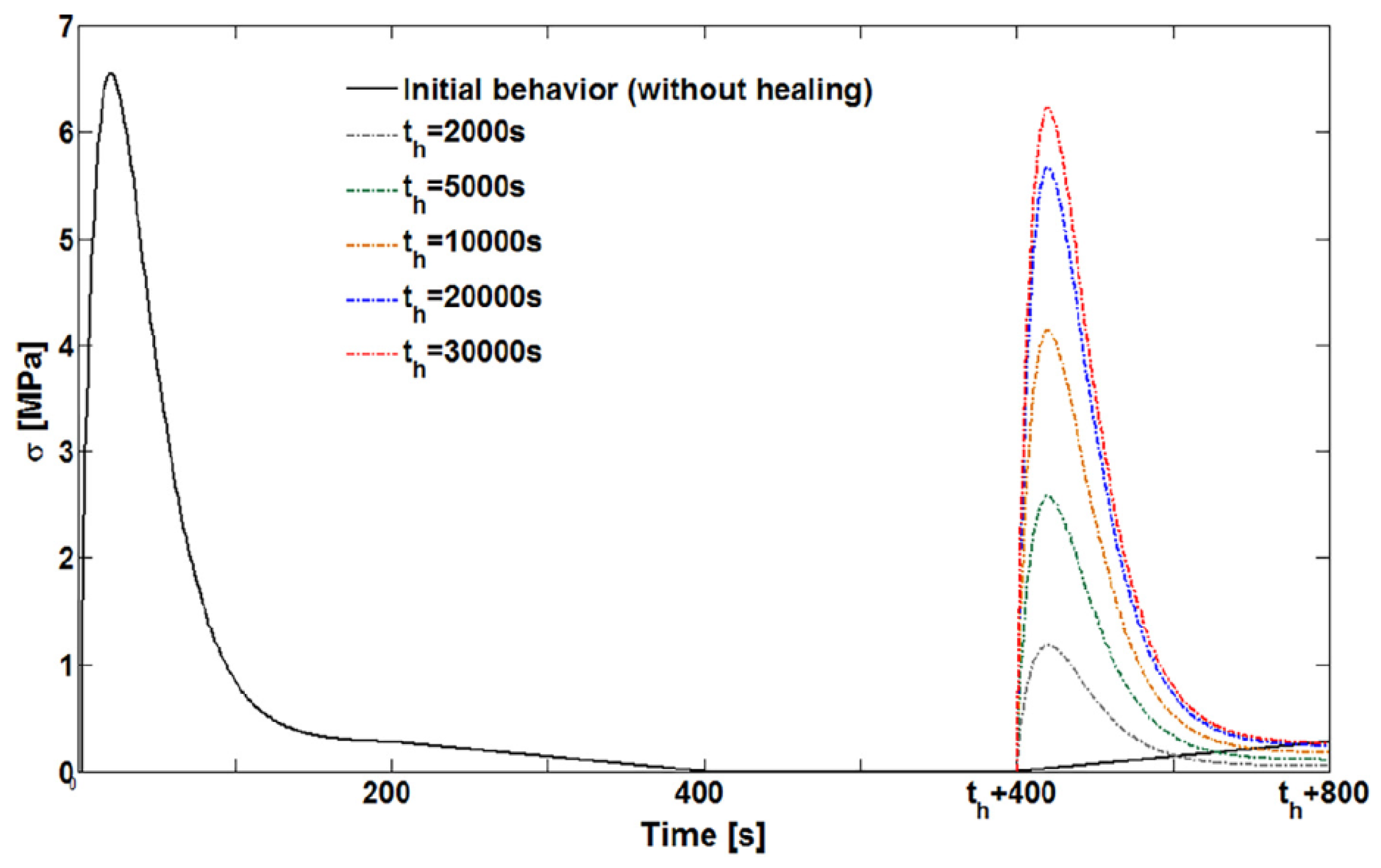

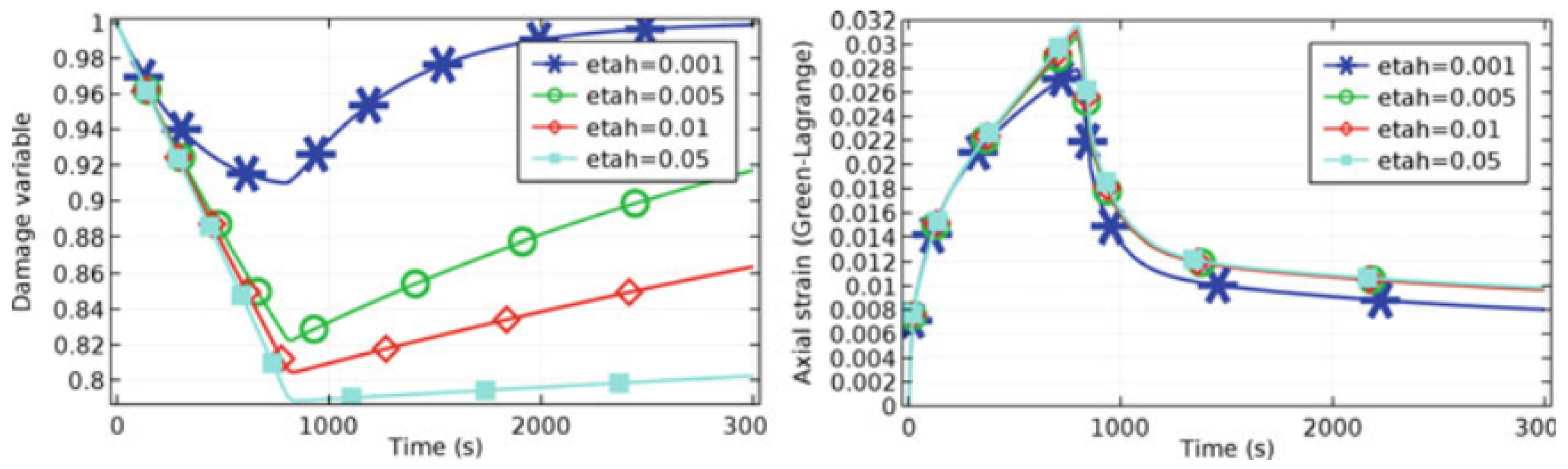

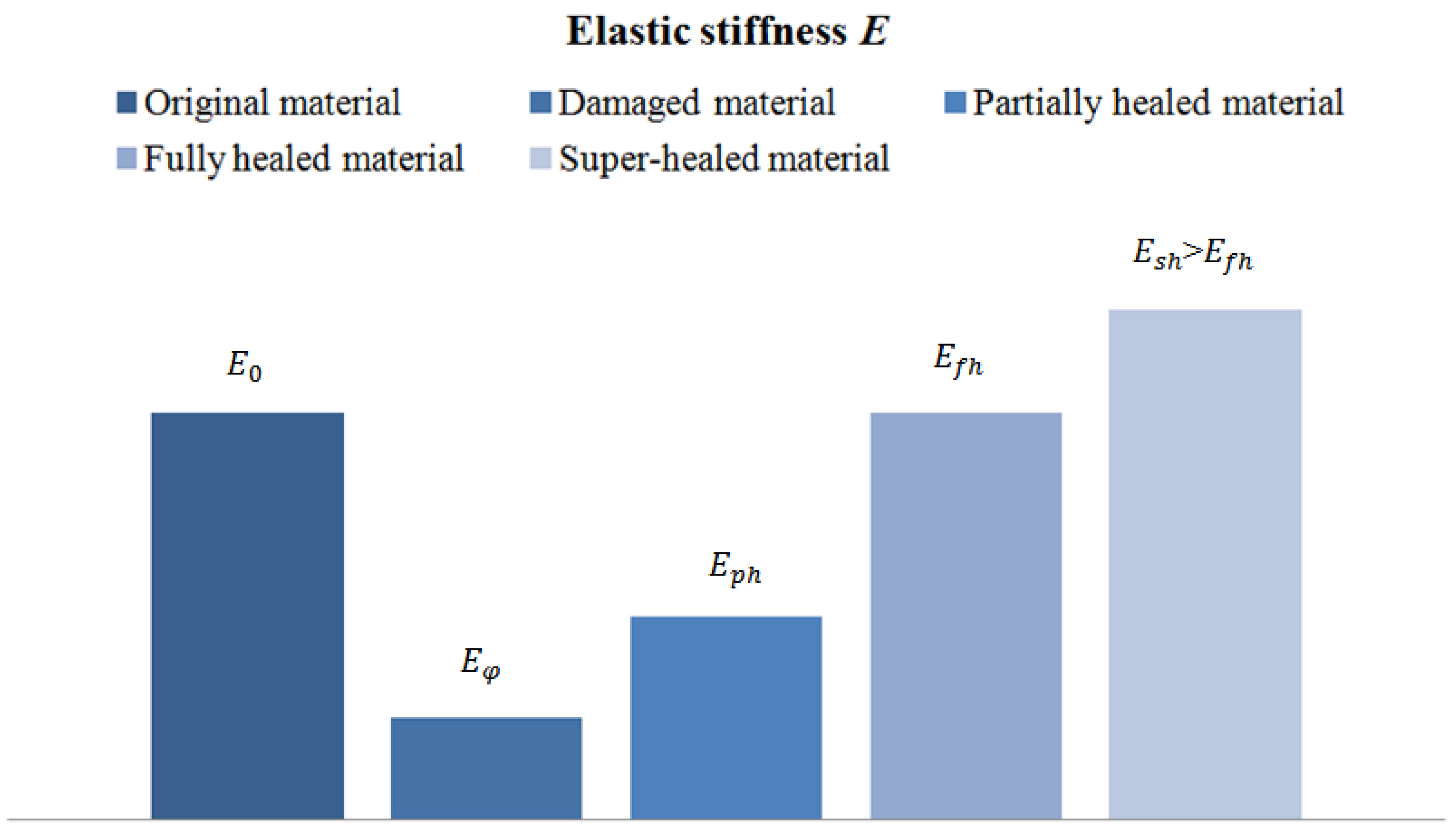

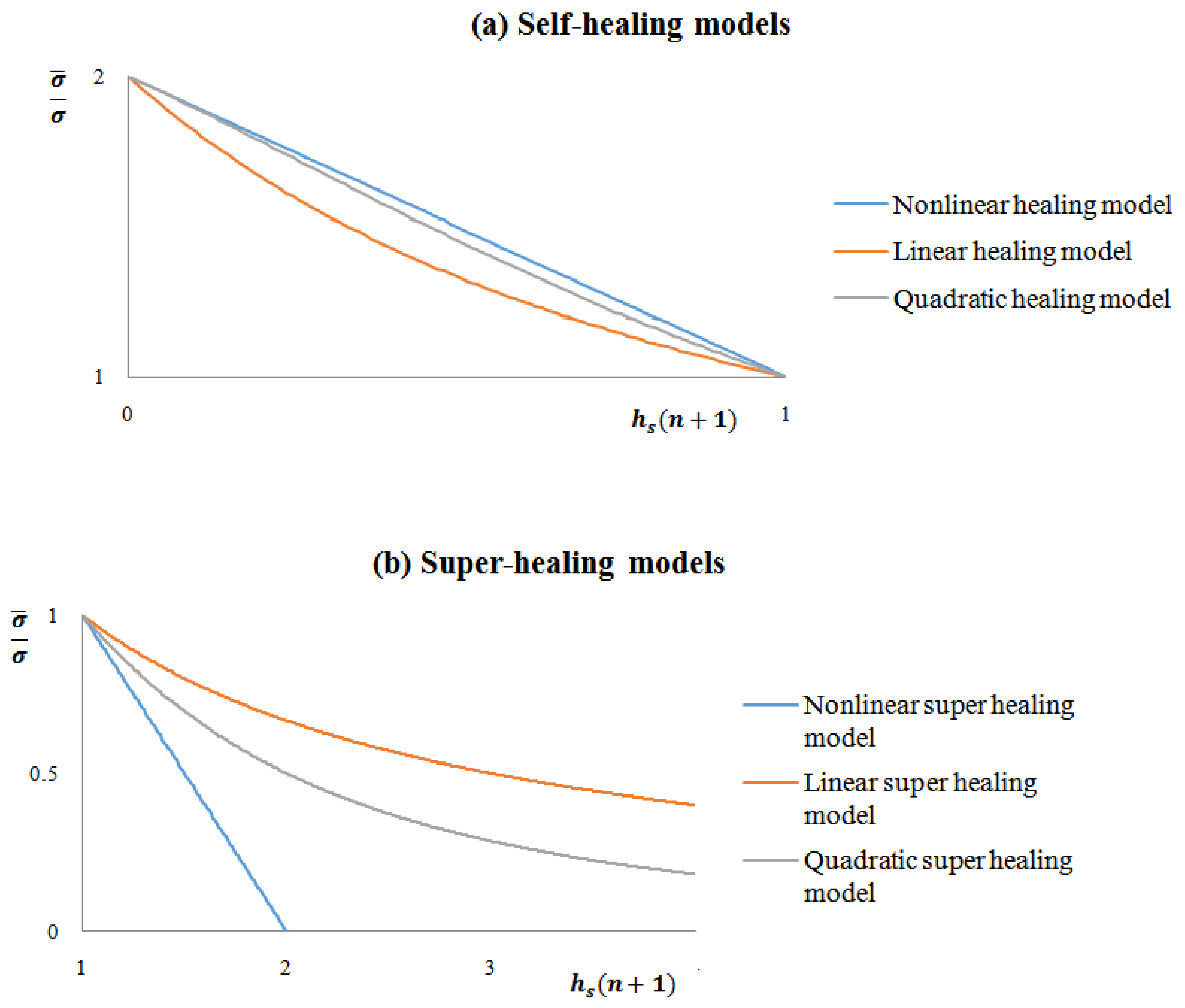

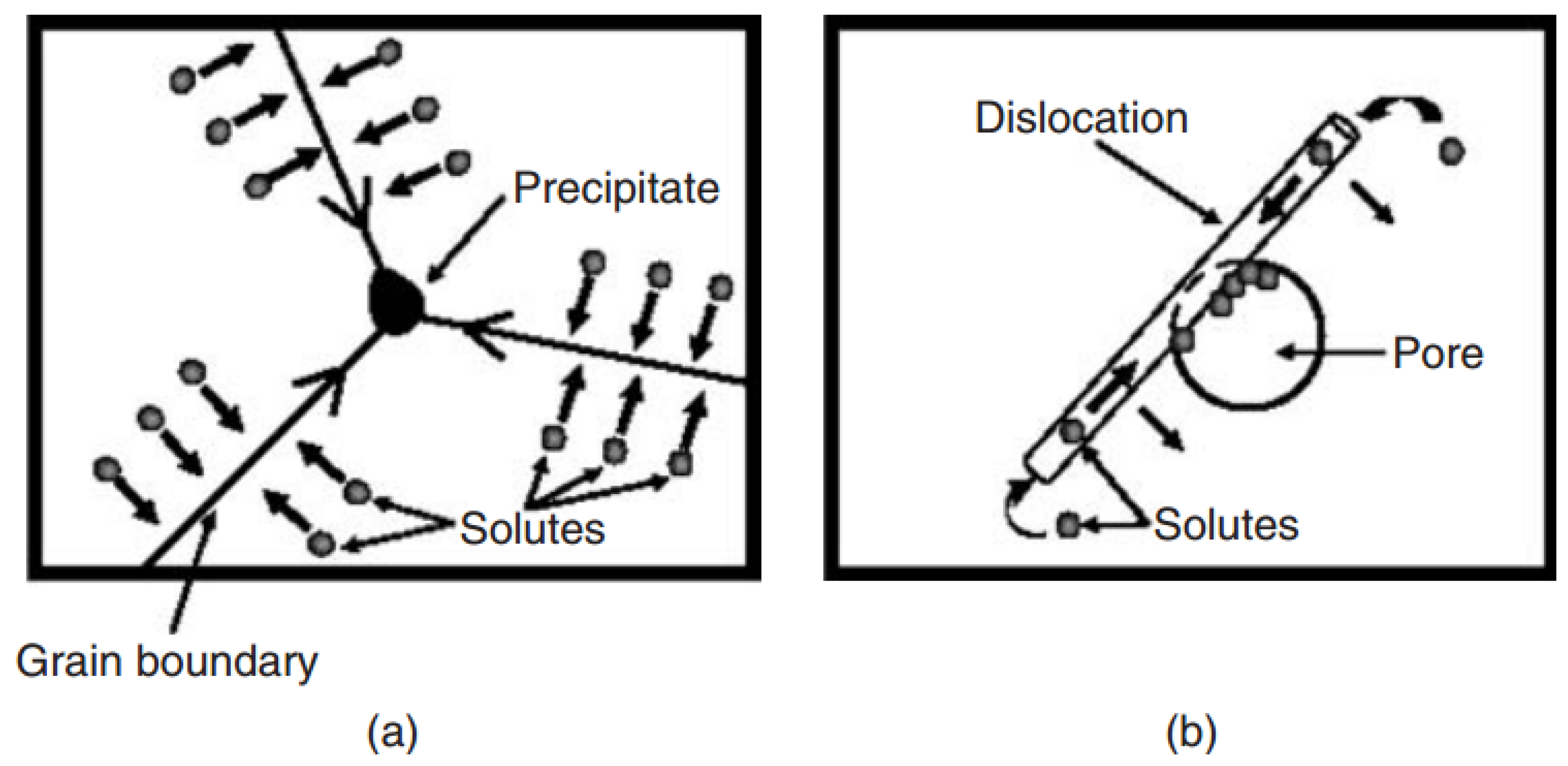
| Super Healing Model | Equation of the Ratio | Equation of the Ratio |
|---|---|---|
| Linear super healing (LSH) | ||
| Generalized nonlinear super healing (NSH) | ||
| Quadratic super healing (QSH) |
| Elastic Strain Equivalence | Elastic Energy Equivalence | |||
|---|---|---|---|---|
| Phase | Elastic Modulus | Variable | Elastic Modulus | Variable |
| Damage | ||||
| Healing | ||||
| Super healing | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oucif, C.; Mauludin, L.M. Continuum Damage-Healing and Super Healing Mechanics in Brittle Materials: A State-of-the-Art Review. Appl. Sci. 2018, 8, 2350. https://doi.org/10.3390/app8122350
Oucif C, Mauludin LM. Continuum Damage-Healing and Super Healing Mechanics in Brittle Materials: A State-of-the-Art Review. Applied Sciences. 2018; 8(12):2350. https://doi.org/10.3390/app8122350
Chicago/Turabian StyleOucif, Chahmi, and Luthfi Muhammad Mauludin. 2018. "Continuum Damage-Healing and Super Healing Mechanics in Brittle Materials: A State-of-the-Art Review" Applied Sciences 8, no. 12: 2350. https://doi.org/10.3390/app8122350




