Depth Retrieval Procedures in Pulsed Thermography: Remarks in Time and Frequency Domain Analyses
Abstract
:Featured Application
Abstract
1. Introduction
1.1. Quantitative Depth Estimation in the Time Domain
1.2. Quantitative Depth Estimation in the Frequency Domain
2. Materials and Methods
3. Results and Discussion
3.1. Depth Retrieval with Thermal-Contrast Peak Slope Time
3.2. Depth Retrieval with Blind Frequency
3.3. Comparison of Temporal and Frequency Domain Analysis for the Acquisition of Depth Information
4. Evaluation of Analysis Parameters for Depth Prediction
4.1. Selection of Sampling Frequency
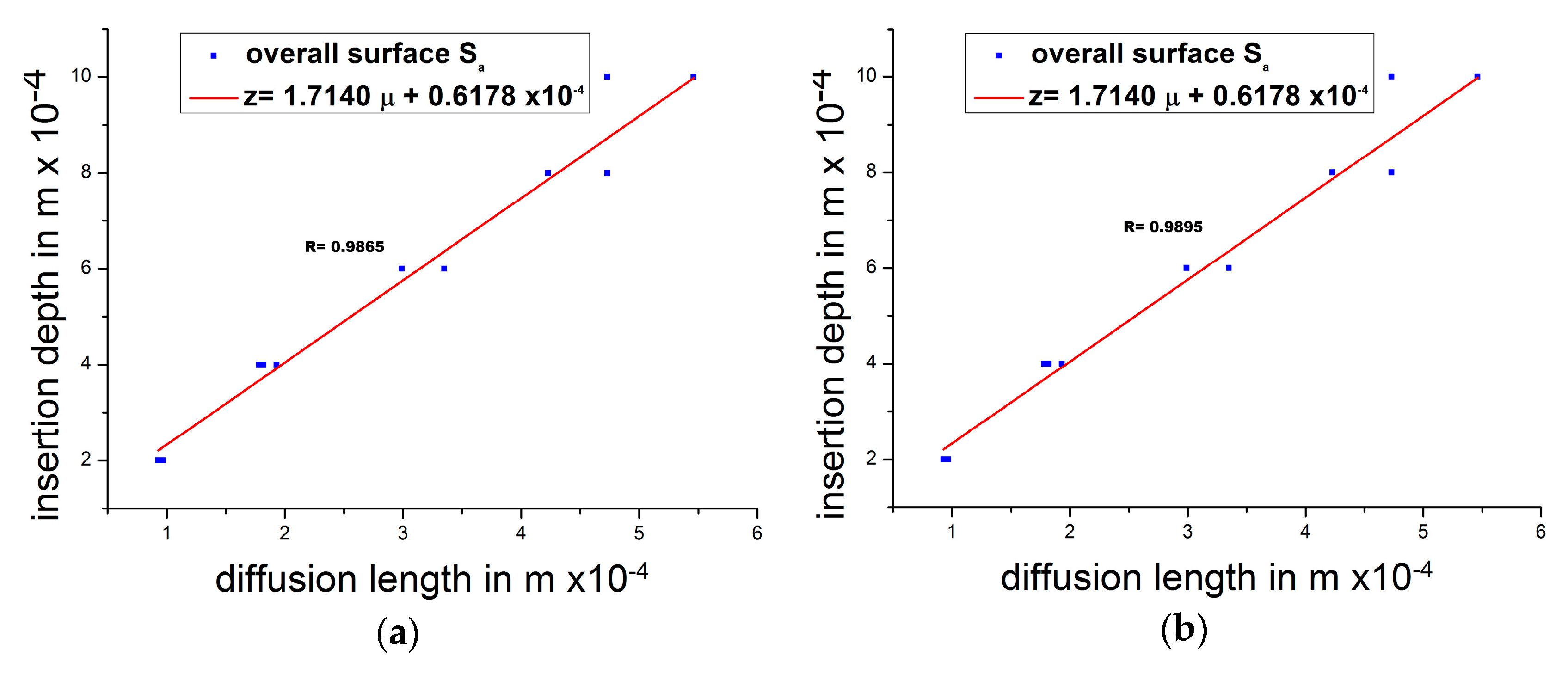
4.2. Selection of Sound Area
4.3. Assessment of Correlation Factor C in Frequency Domain Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Def. No | Measured Peak Slope | Measured Peak Slope Time in s | Calculated Depth in ×10−1 mm | Error (%) | Def. No | Measured Peak Slope | Measured Peak Slope Time in s | Calculated Depth in ×10−1 mm | Error (%) |
|---|---|---|---|---|---|---|---|---|---|
| A5 | 52.95 | 0.0254 | 1.70 | −15 | D5 | 0.15 | 0.7643 | 9.32 | 16.5 |
| A4 | 46.57 | 0.0254 | 1.70 | −15 | D4 | 0.29 | 0.6624 | 8.68 | 8.51 |
| A3 | 18.01 | 0.0254 | 1.70 | −15 | D3 | 0.17 | 0.6879 | 8.84 | 10.6 |
| A2 | 17.99 | 0.0254 | 1.70 | −15 | D2 | 0.07 | 0.7643 | 9.32 | 16.5 |
| A1 | 8.19 | 0.0254 | 1.70 | −15 | D1 | N/D | N/D | N/D | N/D |
| B5 | 2.39 | 0.2547 | 5.38 | 34.5 | E5 | 0.08 | 0.9936 | 10.63 | 6.3 |
| B4 | 1.40 | 0.2802 | 5.65 | 41.25 | E4 | 0.15 | 0.9681 | 10.49 | 4.9 |
| B3 | 1.66 | 0.2547 | 5.38 | 34.5 | E3 | 0.09 | 0.9171 | 10.21 | 2.1 |
| B2 | 0.63 | 0.2802 | 5.65 | 41.25 | E2 | 0.06 | 0.9936 | 10.63 | 6.3 |
| B1 | 0.03 | 0.3057 | 5.89 | 47.4 | E1 | N/D | N/D | N/D | N/D |
| C5 | 0.57 | 0.4331 | 7.01 | 16.8 | |||||
| C4 | 0.94 | 0.4076 | 6.8 | 13.3 | |||||
| C3 | 0.41 | 0.4588 | 7.22 | 20.4 | |||||
| C2 | 0.34 | 0.4076 | 6.8 | 13.3 | |||||
| C1 | 0.10 | 0.4840 | 7.42 | 23.6 | |||||
| Sound Area Top Left Corner | Sound Area All Pixels | ||||||
|---|---|---|---|---|---|---|---|
| Def. No | Nominal Depth in ×10−1 mm | Blind Frequency fb (Hz) | Measured Depth z in ×10−1 mm | Error (%) | Blind Frequency fb (Hz) | Measured Depth z in ×10−1 mm | Error (%) |
| A5 | 2 | 14.476 | 1.74 | −13 | 15.222 | 1.70 | −15 |
| A4 | 2 | 15.371 | 1.69 | −15.5 | 15.222 | 1.70 | −15 |
| A3 | 2 | 16.267 | 1.65 | −17.5 | 15.222 | 1.70 | −15 |
| A2 | 2 | 15.222 | 1.70 | −15 | 15.222 | 1.70 | −15 |
| A1 | 2 | 15.073 | 1.71 | −14.5 | 14.028 | 1.77 | −11.5 |
| B5 | 4 | 3.730 | 3.44 | −14 | 4.029 | 3.31 | −17.2 |
| B4 | 4 | 3.880 | 3.37 | −15.7 | 4.029 | 3.31 | −17.2 |
| B3 | 4 | 3.880 | 3.37 | −15.7 | 4.178 | 3.25 | −18.7 |
| B2 | 4 | 3.581 | 3.51 | −12.2 | 3.581 | 3.51 | −12.2 |
| B1 | 4 | 3.880 | 3.37 | −12.2 | 3.581 | 3.51 | −12.2 |
| C5 | 6 | 1.492 | 5.44 | −7.3 | 1.492 | 5.44 | −7.3 |
| C4 | 6 | 1.641 | 5.19 | −13.5 | 1.492 | 5.44 | −7.3 |
| C3 | 6 | 1.044 | 6.51 | 8.5 | 1.193 | 6.09 | 1.5 |
| C2 | 6 | 1.193 | 6.09 | 1.5 | 1.492 | 5.44 | −7.3 |
| C1 | 6 | 1.044 | 6.51 | 8.5 | 1.492 | 5.44 | −7.3 |
| D5 | 8 | 0.746 | 7.70 | −3.7 | 0.746 | 7.70 | −3.7 |
| D4 | 8 | 0.596 | 8.61 | 7.6 | 0.596 | 8.61 | 7.6 |
| D3 | 8 | 0.596 | 8.61 | 7.6 | 0.746 | 7.70 | −3.7 |
| D2 | 8 | 0.596 | 8.61 | 7.6 | 0.596 | 8.61 | 7.6 |
| D1 | 8 | 0.596 | 8.61 | 7.6 | 0.596 | 8.61 | 7.6 |
| E5 | 10 | 0.447 | 9.94 | −0.6 | 0.447 | 9.94 | −0.6 |
| E4 | 10 | 0.447 | 9.94 | −0.6 | 0.447 | 9.94 | −0.6 |
| E3 | 10 | 0.447 | 9.94 | −0.6 | 0.447 | 9.94 | −0.6 |
| E2 | 10 | 0.447 | 9.94 | −0.6 | 0.447 | 9.94 | −0.6 |
| E1 | 10 | 0.596 | 8.61 | −16.1 | 0.596 | 8.61 | −16.1 |
References
- Maldague, X.P.V. Nondestructive Evaluation of Materials by Infrared Thermography, 1st ed.; Springer-Verlag: London, UK, 1993; pp. 73–99. ISBN 978-1-4471-1995-1. [Google Scholar]
- Shepard, S.M. Thermal nondestructive evaluation of composite materials and structures. In Comprehensive Composite Materials II, 2nd ed.; Zweben, C.H., Beaumont, P.W.R., Eds.; Elsevier Science: Cambridge, MA, USA, 2017; Volume 7, pp. 250–269. ISBN 978-0-08-100534-7. [Google Scholar]
- Maierhofer, C.; Röllig, M.; Krankenhagen, R.; Myrach, P. Comparison of quantitative defect characterization using pulse-phase and lock-in thermography. Appl. Opt. 2016, 55, 76–86. [Google Scholar] [CrossRef] [PubMed]
- Krishnapillai, M.; Jones, R.; Marshall, I.H.; Bannister, M.; Rajic, N. NDTE using pulse thermography: Numerical modeling of composite subsurface defects. Compos. Struct. 2006, 75, 241–249. [Google Scholar] [CrossRef]
- Theodorakeas, P.; Avdelidis, N.P.; Hatziioannidis, I.; Cheilakou, E.; Marini, R.; Koui, M. Comparative evaluation of aerospace composites using thermography and ultrasonic NDT techniques. In Proceedings of the SPIE 9485, Thermosense: Thermal Infrared Applications XXXVII, Baltimore, MD, USA, 20–24 April 2015. [Google Scholar]
- Maldague, X.P.V. Theory and Practice of Infrared Technology for Nondestructive Testing, 1st ed.; John-Wiley & Sons: New York, NY, USA, 2001; ISBN 0471181900. [Google Scholar]
- Peeters, J.; Ibarra-Castanedo, C.; Khodayar, F.; Mokhtari, Y.; Sfarra, S.; Zhang, H.; Maldague, X.; Dirckx, J.J.J.; Steenackers, G. Optimised Dynamic line scan thermographic detection of CFRP inserts using FE updating and POD analysis. NDT E Int. 2018, 93, 141–149. [Google Scholar] [CrossRef]
- Theodorakeas, P.; Avdelidis, N.P.; Hrissagis, K.; Ibarra-Castanedo, C.; Koui, M.; Malague, X.P.V. Automated transient thermography for the inspection of CFRP structures: Experimental results and developed procedures. In Proceedings of the SPIE 8013, Thermosense: Thermal Infrared Applications XXXIII, Orlando, FL, USA, 25–29 April 2011. [Google Scholar]
- Avdelidis, N.P.; Ibarra-Castanedo, C.; Theodorakeas, P.; Bendada, A.; Saarimaki, E.; Kauppinen, T.; Koui, M.; Maldague, X.P.V. NDT characterisation of carbon-fibre and glass-fibre composites using non-invasive imaging techniques. In Proceedings of the 10th Quantitative Infrared Thermography Conference (QIRT10), Quebec City, QC, Canada, 27–30 July 2010; pp. 703–710. [Google Scholar]
- Montanini, R. Quantitative determination of subsurface defects in a reference specimen made of Plexiglas by means of lock-in and pulse phase infrared thermography. Infrared Phys. Technol. 2010, 53, 363–371. [Google Scholar] [CrossRef]
- Ibarra- Castanedo, C.; Avdelidis, N.P.; Grinzato, E.G.; Bison, P.G.; Marinetti, S.; Chen, L.; Genest, M.; Maldague, X.P.V. Quantitative inspection of non-planar composite specimens by pulsed phase thermography. QIRT 2006, 3, 25–40. [Google Scholar] [CrossRef]
- James, P.H.; Welch, C.S.; Winfree, W.P. A numerical grid generation scheme for thermal simulation in laminated structures. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Plenum Press: New York, NY, USA, 1989; Volume 8, pp. 801–809. [Google Scholar]
- Krapez, J.C.; Maldague, X.P.V.; Cielo, P. Thermographic nondestructive evaluation: Data inversion procedures part II: 2-D Analysis and Experimental Results. Res. Nondestruct. Eval. 1991, 3, 101–124. [Google Scholar] [CrossRef]
- Zeng, Z.; Tao, N.; Feng, L.; Zhang, C. Specified value based defect depth prediction using pulsed thermography. J. Appl. Phys. 2012, 112, 023112. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Maldague, X.P.V. Defect depth retrieval from pulsed phase thermographic data on Plexiglas and aluminum samples. In Proceedings of the SPIE 5405, Thermosense XXVI, Orlando, FL, USA, 12–16 April 2004. [Google Scholar]
- Deemer, C.; Sun, J.G.; Ellingson, W.A.; Short, S. Front-flash thermal imaging characterisation of continuous fiber ceramic composites. In 23rd Annual Conference on Composites, Advanced Ceramics, Materials, and Structures: A: Ceramic Engineering and Science Proceedings; Ustundag, E., Fischman, G., Eds.; The American Ceramic Society: Westerville, OH, USA, 1999; Volume 20, pp. 317–324. [Google Scholar]
- Theodorakeas, P. Quantitative Analysis and Defect Assessment Using Infrared Thermographic Approaches. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2013. [Google Scholar]
- Ibarra-Castanedo, C.; Gonzalez, D.; Maldague, X. Automatic algorithm for quantitative pulsed phase thermography calculations. In Proceedings of the 16th World Conference on Nondestructive Testing, Montreal, QC, Canada, August 30–September 3 2004. [Google Scholar]
- Schlichting, J.; Maierhofer, C.; Kreutzbruck, M. Defect sizing by local excitation thermography. QIRT 2011, 8, 51–63. [Google Scholar] [CrossRef]
- Plotnikov, Y.A.; Winfree, W.P. Advanced image processing for defect visualization in infrared thermography. In Proceedings of the SPIE 3361, Thermosense XX, Orlando, FL, USA, 13–17 April 1998; pp. 331–338. [Google Scholar]
- Hamzah, A.R.; Delpech, P.; Saintey, M.B.; Almond, D.P. Experimental investigations of defect sizing by transient thermography. Insight 1996, 38, 167–171. [Google Scholar]
- Bison, P.; Bortolin, A.; Cadelano, G.; Ferrarini, G.; Grinzato, E. Comparison of some thermographic techniques applied to thermal properties characterisation of porous materials. In Proceedings of the 11th Quantitative Infrared Thermography Conference (QIRT2012), Naples, Italy, 11–14 June 2012. [Google Scholar]
- Maierhofer, C.; Brink, A.; Rolling, M.; Wiggenhauser, H. Quantitative impulse- thermography as non-destructive testing method in civil engineering—Experimental results and numerical simulations. Constr. Build. Mater. 2005, 19, 731–737. [Google Scholar] [CrossRef]
- Theodorakeas, P.; Avdelidis, N.P.; Cheilakou, E.; Koui, M. Quantitative analysis of plastered mosaics by means of active infrared thermography. Constr. Build. Mater. 2014, 73, 417–425. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, C.; Tao, N.; Feng, L.; Zhang, C. Depth prediction of non-air interface defect using pulsed thermography. NDT E Int. 2012, 48, 39–45. [Google Scholar] [CrossRef]
- Almond, D.P.; Patel, P.M. Photothermal Science and Techniques, 1st ed.; Chapman & Hall: London, UK, 1996; ISBN 978-0-412-57880-9. [Google Scholar]
- Lau, S.K.; Almond, D.P.; Milne, J.M. A quantitative analysis of pulsed video thermography. NDT E Int. 1991, 24, 195–202. [Google Scholar] [CrossRef]
- Krapez, J.C.; Lepoutre, F.; Balageas, D. Early Detection of thermal contrast in pulsed stimulated thermography. J. Phys. IV 1994, 4, C7.47–C7.50. [Google Scholar] [CrossRef]
- Krapez, J.C.; Balageas, D.; Deom, A.; Lepoutre, F. Early Detection by stimulated infrared thermography. Comparison with Ultrasonics and Holo/Shearography. In Advances in Signal Processing for Nondestructive Evaluation of Materials; Maldague, X.P.V., Ed.; Springer: Dordrecht, The Netherlands, 1994; Volume 262, pp. 303–321. ISBN 978-94-011-1056-3. [Google Scholar]
- Plotnikov, Y.A.; Winfree, W.P. Temporal treatment of a thermal response for defect depth estimation. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Plenum Press: New York, NY, USA, 1999; Volume 19, pp. 587–594. [Google Scholar]
- Favro, L.D.; Han, X.; Kuo, P.K.; Thomas, R.L. Imaging the early time behaviour of reflected thermal wave pulses. In Proceedings of the SPIE 2473, Thermosense XVIII, Orlando, FL, USA, 8–12 April 1996; 1996; pp. 331–338. [Google Scholar]
- Sun, J.G. Analysis of pulsed thermography methods for defect depth prediction. J. Heat Transf. 2006, 128, 329–338. [Google Scholar] [CrossRef]
- Ringermacher, H.I.; Archacki, R.J.; Veronesi, W.A. Nondestructive Testing: Transient Depth Thermography. U.S. Patent US5711603, 1998. [Google Scholar]
- Ibarra-Castanedo, C.; Maldague, X.P.V. Pulsed Phase Thermography Reviewed. QIRT 2004, 1, 47–70. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Maldague, X.P.V. Interactive methodology for Optimized Defect characterization by quantitative pulsed phase thermography. Res. Nondestruct. Eval. 2005, 16, 175–193. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C. Quantitative subsurface defect evaluation by pulsed phase thermography: Depth retrieval with the phase. Ph.D. Thesis, Université Laval, Quebec City, QC, Canada, 2005. [Google Scholar]
- Busse, G. Optoacoustic phase angle measurement for probing a metal. Appl. Phys. Lett. 1979, 35, 759–760. [Google Scholar] [CrossRef]
- Thomas, R.L.; Pouch, J.J.; Wong, H.Y.; Favro, L.D.; Kuo, P.K. Subsurface flaw detection in metals by photoacustic microscopy. Appl. Phys. 1980, 51, 1152–1156. [Google Scholar] [CrossRef]
- Meloa, C.; Carlomagno, G.M. Recent advances in the use of infrared thermography. J. Meas. Sci. Technol. 2004, 15, R27–R58. [Google Scholar] [CrossRef]
- Theodorakeas, P.; Avdelidis, N.P.; Ibarra-Castanedo, C.; Koui, M.; Maldague, X. Pulsed thermographic inspection of CFRP structures: Experimental results and image analysis tools. In Proceedings of the SPIE 9062: Smart Sensor Phenomena, Technology, Networks, and Systems Integration, San Diego, CA, USA, 9–13 March 2014. [Google Scholar]
- Shepard, S.M.; Lhota, J.R.; Rubadeux, A.; Wang, D.; Ahmed, T. Reconstruction and Enhancement of active thermographic image sequences. Opt. Eng. 2003, 42, 1337–1342. [Google Scholar] [CrossRef]
- Peeters, J.; Ibarra-Castanedo, C.; Sfarra, S.; Maldague, X.; Dirckx, J.J.J.; Steenackers, G. Robust Quantitative Depth Estimation on CFRP samples using active thermography inspection & numerical simulation updating. NDT E Int. 2017, 87, 119–123. [Google Scholar] [CrossRef]
- Tabatabaei, N.; Mandelis, A. Thermal-wave radar: A novel subsurface imaging modality with extended depth-resolution dynamic range. Rev. Sci. Instrum. 2009, 034902. [Google Scholar] [CrossRef] [PubMed]
- Ghali, V.S.; Jonnalagadda, N.; Mulaveesala, R. Three-dimensional pulse compression for infrared nondestructive testing. IEEE Sens. J. 2009, 9, 832–833. [Google Scholar] [CrossRef]
- Silipigni, G.; Burrascano, P.; Hutchins, D.A.; Laureti, S.; Petrucci, R.; Senni, L.; Torre, L.; Ricci, M. Optimization of the pulse compression technique applied to the infrared thermography nondestructive evaluation. NDT E Int. 2017, 87, 100–110. [Google Scholar] [CrossRef]













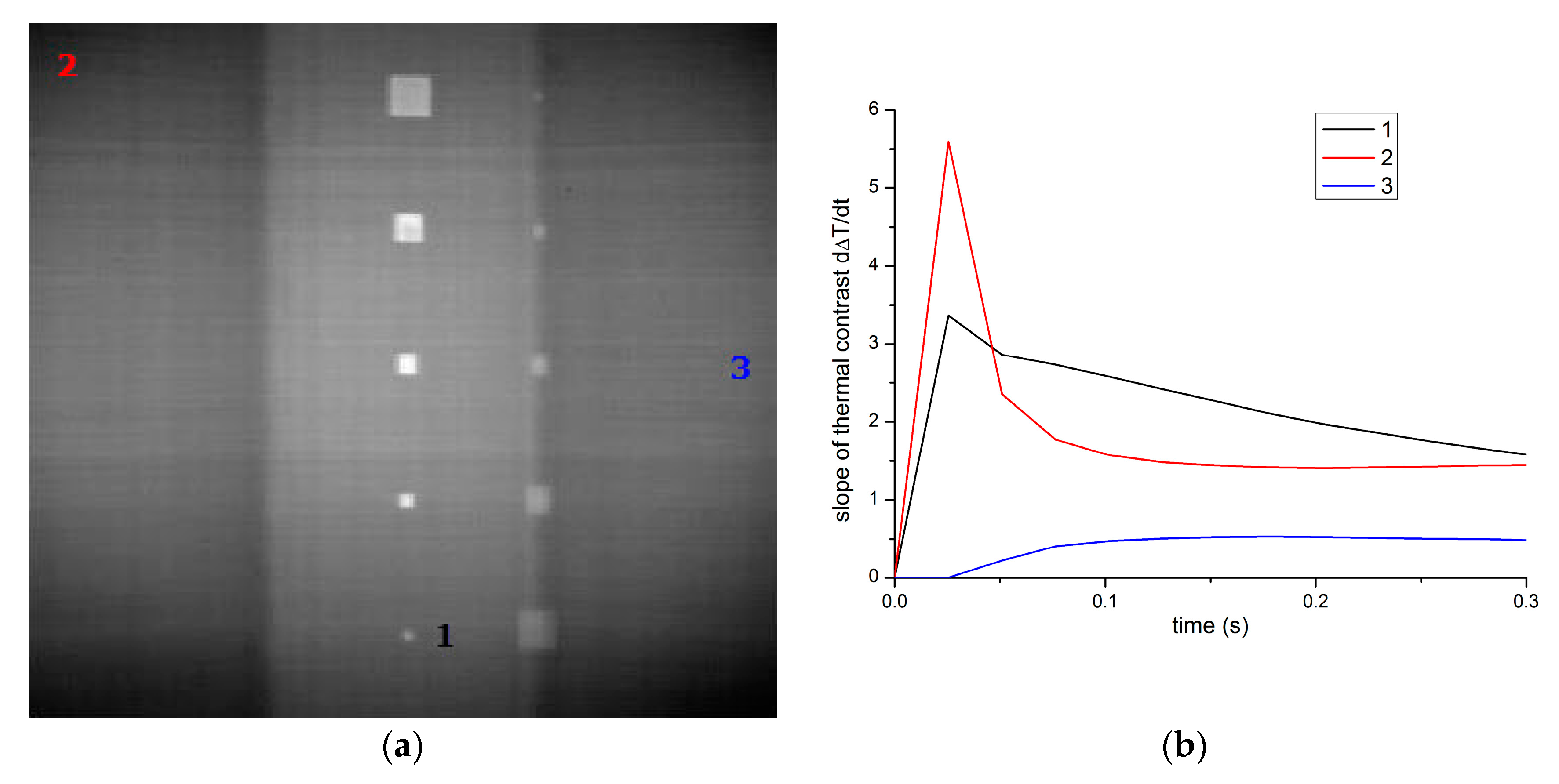

| Experimental Equipment | Acquisition Parameters | |
|---|---|---|
| Thermal stimulation: Photographic Flashes: Balcar FX 60 pulse duration: 5 ms thermal pulse, deposited energy: 3.2 KJ/ flash (total energy deposited 6.4 KJ) Thermographic monitoring: Santa Barbara infrared camera, Focal Plane Array, nitrogen cooled, InSb, 320 × 256 pixels | Sampling rate, | 157 Hz |
| Acquisition duration, | 6.7 s | |
| Time interval, | 6.3 ms | |
| Total number of frames, N | 1052 | |
| Def. No | Measured Peak Slope Time in s | Calculated Depth in ×10−1 mm | Error (%) | Def. No | Measured Peak Slope Time in s | Calculated Depth in ×10−1 mm | Error (%) |
|---|---|---|---|---|---|---|---|
| A5 | 0.0341 | 1.97 | −1.5 | B5 | 0.2045 | 4.82 | 20.5 |
| A4 | 0.0341 | 1.97 | −1.5 | B4 | 0.1932 | 4.69 | 17.2 |
| A3 | 0.0341 | 1.97 | −1.5 | B3 | 0.1818 | 4.55 | 13.7 |
| A2 | 0.0341 | 1.97 | −1.5 | B2 | 0.2045 | 4.82 | 20.5 |
| A1 | 0.0341 | 1.97 | −1.5 | B1 | 0.2159 | 4.96 | 24 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Theodorakeas, P.; Koui, M. Depth Retrieval Procedures in Pulsed Thermography: Remarks in Time and Frequency Domain Analyses. Appl. Sci. 2018, 8, 409. https://doi.org/10.3390/app8030409
Theodorakeas P, Koui M. Depth Retrieval Procedures in Pulsed Thermography: Remarks in Time and Frequency Domain Analyses. Applied Sciences. 2018; 8(3):409. https://doi.org/10.3390/app8030409
Chicago/Turabian StyleTheodorakeas, Panagiotis, and Maria Koui. 2018. "Depth Retrieval Procedures in Pulsed Thermography: Remarks in Time and Frequency Domain Analyses" Applied Sciences 8, no. 3: 409. https://doi.org/10.3390/app8030409
APA StyleTheodorakeas, P., & Koui, M. (2018). Depth Retrieval Procedures in Pulsed Thermography: Remarks in Time and Frequency Domain Analyses. Applied Sciences, 8(3), 409. https://doi.org/10.3390/app8030409






