Three-Dimensional Electromagnetic Mixing Models for Dual-Phase Steel Microstructures
Abstract
:1. Introduction
2. The Generation of 3D Microstructure Models
2.1. The Generation of Random Close Packing of Spheres
2.2. The Generation of RCPS-VM
2.3. Volume Fraction Analysis
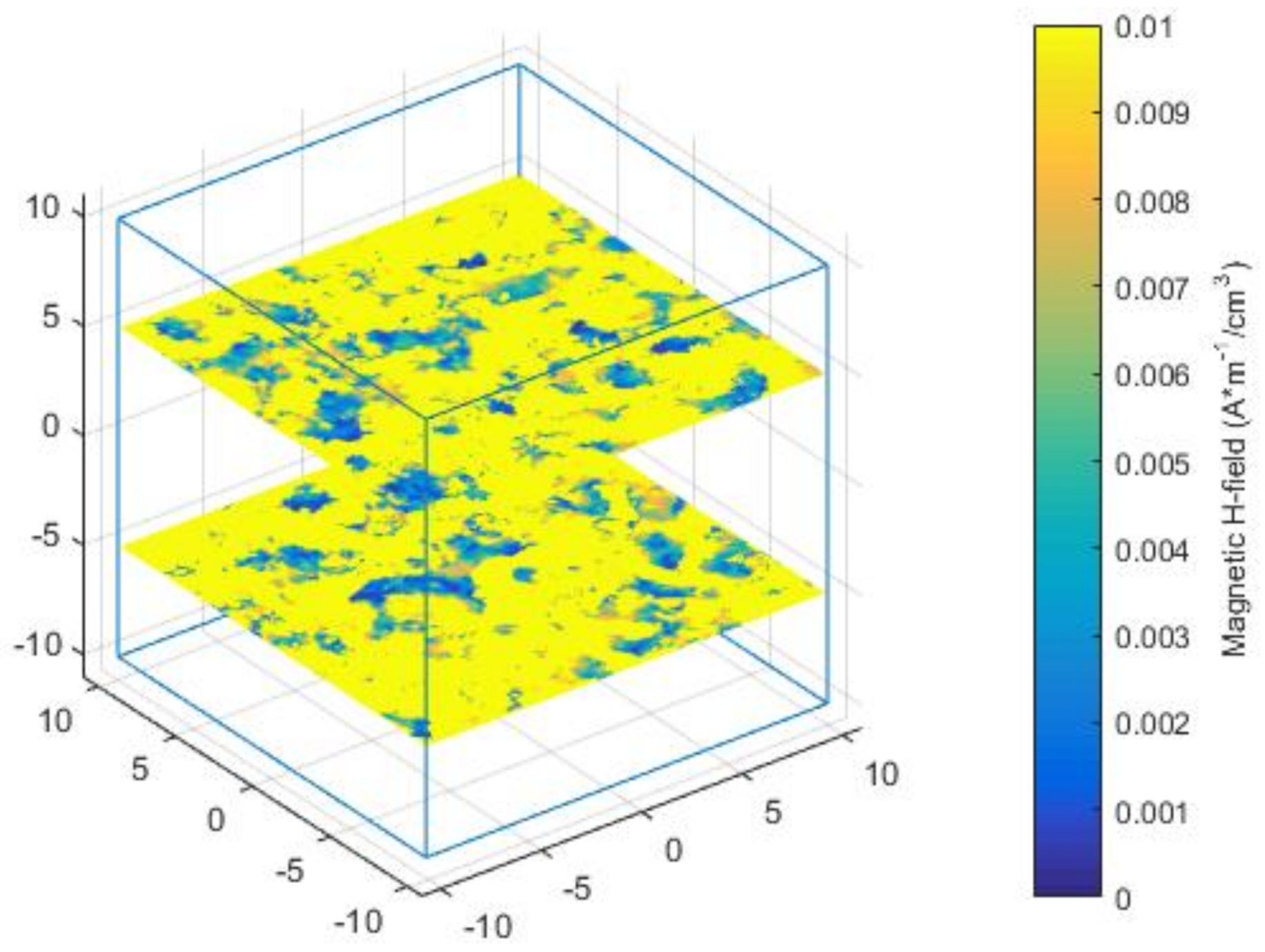
3. Tetrahedron Meshing for FEM
4. Methods of the Edge-Element FEM Solver
5. The Effect of Ferrite Fraction on Relative Permeability
6. The Effect of Mesh Element Density
7. The Effect of the Background Field Tensor
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yin, W.; Hao, X.J.; Peyton, A.J.; Strangwood, M.; Davis, C.L. Measurement of permeability and ferrite/austenite phase fraction using a multi-frequency electromagnetic sensor. NDT E Int. 2009, 42, 64–68. [Google Scholar] [CrossRef]
- Hao, X.J.; Yin, W.; Strangwood, M.; Peyton, A.J.; Morris, P.F.; Davis, C.L. Modelling the electromagnetic response of two-phase steel microstructures. NDT E Int. 2010, 43, 305–315. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, J.; Hao, X.J.; Strangwood, M.; Peyton, A.J.; Davis, C.L. Quantification of the phase fraction in steel using an electromagnetic sensor. NDT E Int. 2014, 67, 31–35. [Google Scholar] [CrossRef]
- Lu, M.; Zhu, W.; Yin, L.; Peyton, A.J.; Yin, W.; Qu, Z. Reducing the Lift-Off Effect on Permeability Measurement for Magnetic Plates from Multifrequency Induction Data. IEEE Trans. Instrum. Meas. 2018, 67, 167–174. [Google Scholar] [CrossRef]
- Lu, M.; Xu, H.; Zhu, W.; Yin, L.; Zhao, Q.; Peyton, A.J.; Yin, W. Conductivity Lift-off Invariance and measurement of permeability for ferrite metallic plates. NDT E Int. 2018, 95, 36–44. [Google Scholar] [CrossRef]
- Avila, J.R.; How, K.Y.; Lu, M.; Yin, W. A Novel Dual Modality Sensor with Sensitivities to Permittivity, Conductivity, and Permeability. IEEE Sens. J. 2018, 18, 356–362. [Google Scholar] [CrossRef]
- Lu, M.; Yin, L.; Peyton, A.J.; Yin, W. A novel compensation algorithm for thickness measurement immune to lift-off variations using eddy current method. IEEE Trans. Instrum. Meas. 2016, 65, 2773–2779. [Google Scholar] [CrossRef]
- Lu, M.; Zhao, Q.; Hu, P.; Yin, W.; Peyton, A.J. Prediction of the asymptotical magnetic polarization tensors for cylindrical samples using the boundary element method. In Proceedings of the 2015 IEEE Sensors Applications Symposium (SAS), Zadar, Croatia, 13–15 April 2015. [Google Scholar]
- Yang, T.; Zhao, Q.; How, K.Y.; Xu, K.; Lu, M.; Xie, Y.; Yin, W. Level measurement for saline with a small surface area using high frequency electromagnetic sensing technique. Measurement 2017, 101, 118–125. [Google Scholar] [CrossRef]
- Peyton, A.J.; Yin, W.; Dickinson, S.J.; Davis, C.L.; Strangwood, M.; Hao, X.; Douglas, A.J.; Morris, P.F. Monitoring microstructure changes in rod online by using induction spectroscopy. Ironmak. Steelmak. 2010, 37, 135–139. [Google Scholar] [CrossRef]
- Hao, X.J.; Yin, W.; Strangwood, M.; Peyton, A.J.; Dickinson, S.J.; Morris, P.F.; Davis, C.L. Monitoring of Steel Microstructures using Electromagnetic Sensors. In Proceedings of the International Conference on Non Destructive Evaluation for Steel and Allied Industries—NDESAI 2011, Jamshedpur, India, 2–3 December 2011. [Google Scholar]
- Zhu, W.; Yin, W.; Peyton, A.J.; Ploegaert, H. Modelling and experimental study of an electromagnetic sensor with an H-shaped ferrite core used for monitoring the hot transformation of steel in an industrial environment. NDT E Int. 2011, 44, 547–552. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. (TOMS) 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Sugihara, K. Three-dimensional convex hull as a fruitful source of diagrams. Theor. Comput. Sci. 2000, 235, 325–337. [Google Scholar] [CrossRef]
- Yin, W.; Peyton, A.J.; Strangwood, M.; Davis, C.L. Exploring the relationship between ferrite fraction and morphology and the electromagnetic properties of steel. J. Mater. Sci. 2007, 42, 6854–6861. [Google Scholar] [CrossRef]
- Yadegari, S.; Turteltaub, S.; Suiker, A.S.; Kok, P.J. Analysis of banded microstructures in multiphase steels assisted by transformation-induced plasticity. Comput. Mater. Sci. 2014, 84, 339–349. [Google Scholar] [CrossRef]
- Van-Den-Berg, F.; Kok, P.; Yang, H.; Aarnts, M.; Vink, J.J.; Beugeling, W.; Meilland, P.; Kebe, T.; Stolzemberg, M.; Krix, D.; et al. In-line characterisation of microstructure and mechanical properties in the manufacturing of steel strip for the purpose of product uniformity control. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
- Zhou, L.; Davis, C.L.; Kok, P.; Van-Den-Berg, F. Magnetic NDT for Steel Microstructure Characterisation–Modelling the Effect of Second Phase Distribution on Magnetic Relative Permeabilty. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
- Wang, K.; Chang, B.; Chen, J.; Fu, H.; Lin, Y.; Lei, Y. Effect of molybdenum on the microstructures and properties of stainless steel coatings by laser cladding. Appl. Sci. 2017, 7, 1065. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, W.; Wang, B.; Yang, F. Modeling and characterization of two-phase composites by Voronoi diagram in the Laguerre geometry based on random close packing of spheres. Comput. Mater. Sci. 2010, 47, 951–961. [Google Scholar] [CrossRef]
- Han, K.; Feng, Y.T.; Owen, D.R. Sphere packing with a geometric based compression algorithm. Powder Technol. 2005, 155, 33–41. [Google Scholar] [CrossRef]
- Al-Raoush, R.; Alsaleh, M. Simulation of random packing of polydisperse particles. Powder Technol. 2007, 176, 47–55. [Google Scholar] [CrossRef]
- He, D.; Ekere, N.N. Computer simulation of powder compaction of spherical particles. J. Mater. Sci. Lett. 1998, 17, 1723–1725. [Google Scholar] [CrossRef]
- Wu, Y.; Fan, Z.; Lu, Y. Bulk and interior packing densities of random close packing of hard spheres. J. Mater. Sci. 2003, 38, 2019–2025. [Google Scholar] [CrossRef]
- Tetgen Software Package. Available online: http://wias-berlin.de/ (accessed on 28 February 2018).
- Bíró, O. Edge element formulations of eddy current problems. Comput. Methods Appl. Mech. Eng. 1999, 169, 391–405. [Google Scholar] [CrossRef]
- Lu, M.; Peyton, A.J.; Yin, W. Acceleration of Frequency Sweeping in Eddy-Current Computation. IEEE Trans. Magn. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Ryzhakov, P.; Marti, J. A Semi-Explicit Multi-Step Method for Solving Incompressible Navier-Stokes Equations. Appl. Sci. 2018, 8, 119. [Google Scholar] [CrossRef]
- Papaelias, M.P.; Strangwood, M.; Peyton, A.J.; Davis, C.L. Measurement and modeling of the electromagnetic response to phase transformation in steels. Metall. Mater. Tran. A 2004, 2004 35, 965–972. [Google Scholar] [CrossRef]
- Haldane, R.J.; Yin, W.; Strangwood, M.; Peyton, A.J.; Davis, C.L. Multi-frequency electromagnetic sensor measurement of ferrite/austenite phase fraction—Experiment and theory. Scr. Mater. 2006, 54, 1761–1765. [Google Scholar] [CrossRef]









| Group No. | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Volume fraction of ferrite phase spheres | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| Volume fraction of ferrite phase grains | 0.1017 | 0.2019 | 0.3072 | 0.4071 | 0.5018 |
| Mean number of grains | 6425 | 6416 | 6423 | 6411 | 6435 |
| Mean number of ferrite phase grains | 1031 | 1287 | 1958 | 2607 | 3230 |
| Mean volume of grains | 1.2362 | 1.2374 | 1.2362 | 1.2405 | 1.2361 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Lu, M.; Chen, Z.; Zhou, L.; Yin, L.; Zhao, Q.; Peyton, A.; Li, Y.; Yin, W. Three-Dimensional Electromagnetic Mixing Models for Dual-Phase Steel Microstructures. Appl. Sci. 2018, 8, 529. https://doi.org/10.3390/app8040529
Zhou W, Lu M, Chen Z, Zhou L, Yin L, Zhao Q, Peyton A, Li Y, Yin W. Three-Dimensional Electromagnetic Mixing Models for Dual-Phase Steel Microstructures. Applied Sciences. 2018; 8(4):529. https://doi.org/10.3390/app8040529
Chicago/Turabian StyleZhou, Weibin, Mingyang Lu, Ziqi Chen, Lei Zhou, Liyuan Yin, Qian Zhao, Anthony Peyton, Yu Li, and Wuliang Yin. 2018. "Three-Dimensional Electromagnetic Mixing Models for Dual-Phase Steel Microstructures" Applied Sciences 8, no. 4: 529. https://doi.org/10.3390/app8040529
APA StyleZhou, W., Lu, M., Chen, Z., Zhou, L., Yin, L., Zhao, Q., Peyton, A., Li, Y., & Yin, W. (2018). Three-Dimensional Electromagnetic Mixing Models for Dual-Phase Steel Microstructures. Applied Sciences, 8(4), 529. https://doi.org/10.3390/app8040529







