Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations
Abstract
1. Introduction
2. Governing Equations for a Piezoelectric Coupled Beam
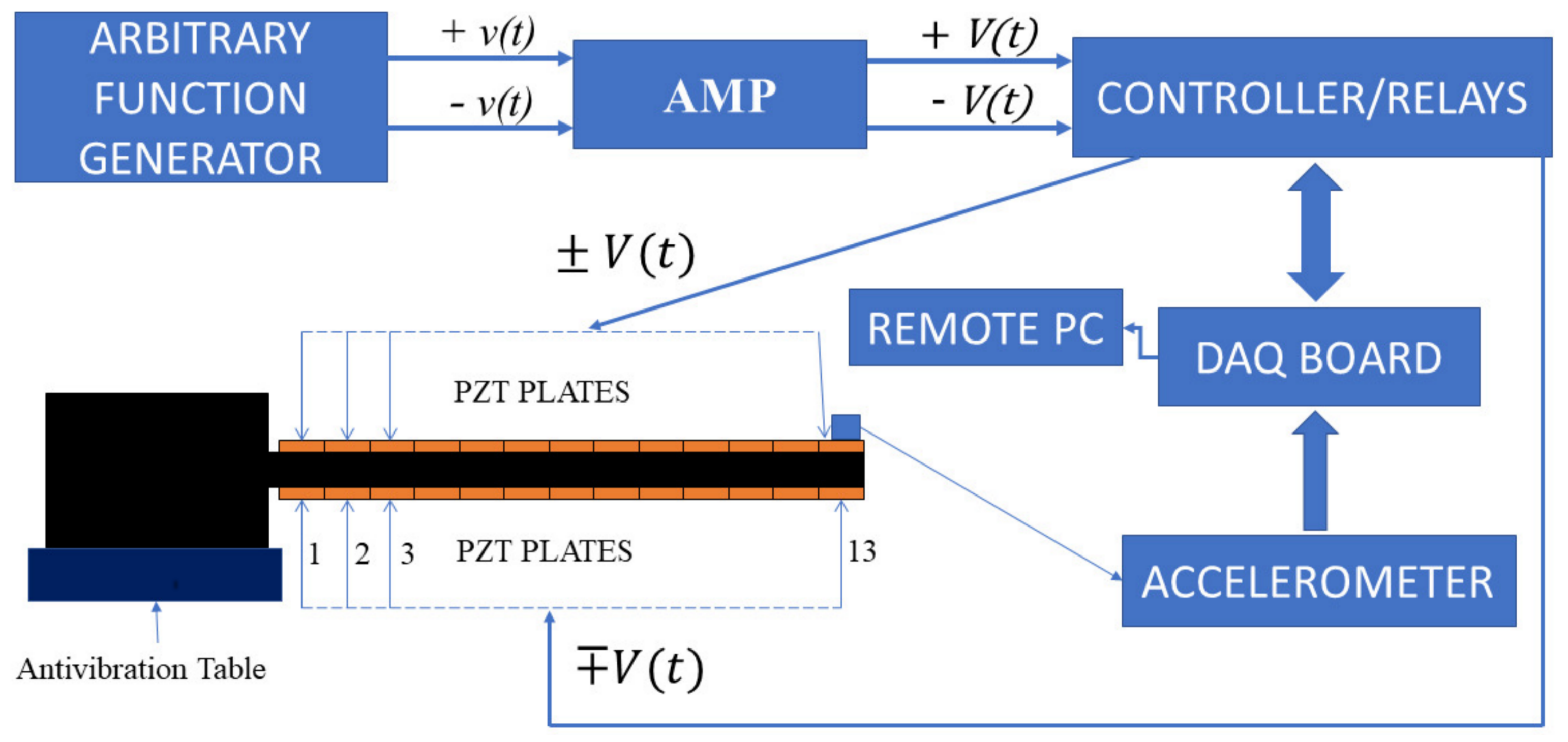
3. Experimental and Numerical Tests
4. Results and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| B | control vector |
| C | damping matrices |
| piezoelectric coefficient | |
| Young’s modulus of the piezoelectric material | |
| Young’s modulus of the beam | |
| K | stiffness matrices |
| beam length | |
| M | piezoelectric bending moment |
| M | mass matrices |
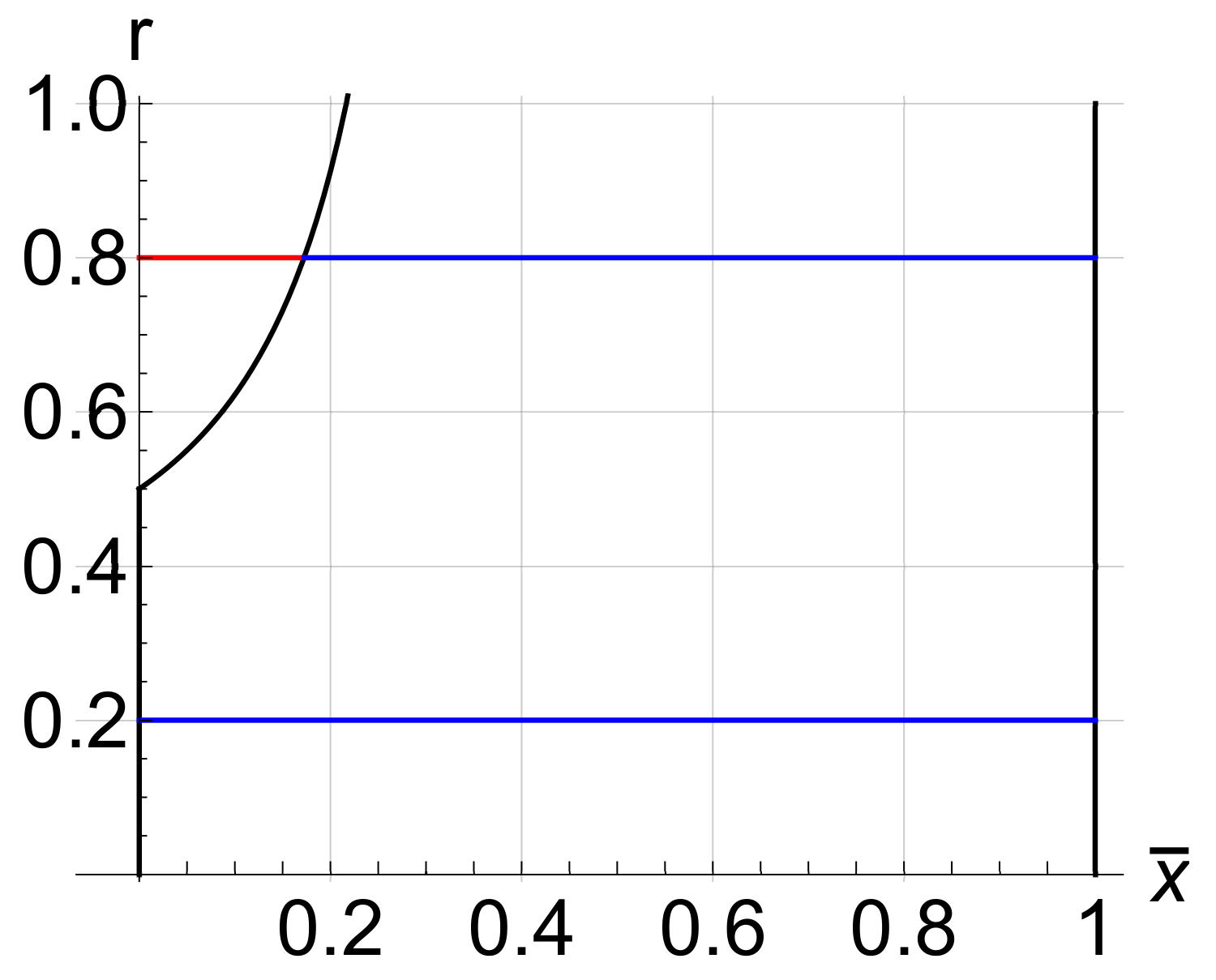
| r | ratio of the j-th component of the tension |
| piezoelectric thickness | |
| beam thickness | |
| V | voltage applied to the piezoelectric plates |
| w | vertical displacement |
| virtual vertical displacement | |
| damping coefficient | |
| i-th flexural mode of the cantilever beam | |
| adimensional length of the beam: | |
| points where the potential changes its sign | |
| natural frequency |
References
- Poursaeidi, E.; Salavatian, M. Fatigue grow simulation in a generator fan blade. Eng. Fail. Anal. 2009, 16, 888–898. [Google Scholar] [CrossRef]
- Witek, L. Experimental crack propagation and failure analysis of the first stage compressor blade subject to vibration. Eng. Fail. Anal. 2009, 16, 2163–2170. [Google Scholar] [CrossRef]
- Kubiac, S.J.; Urquiza, G.B.; Garcia, C.J.; Sierra, E.F. Failure analysis of steam turbine last stage blade tenon and shroud. Eng. Fail. Anal. 2007, 14, 1476–1487. [Google Scholar] [CrossRef]
- Motta, V.; Malzacher, L.; Peitsch, D. Numerical Assessment of Virtual Control Surfaces for Load Alleviation on Compressor Blades. Appl. Sci. 2018, 8, 125. [Google Scholar] [CrossRef]
- Yan, B.; Wang, K.; Hu, Z.; Wu, C.; Zhang, X. Shunt Damping Vibration Control Technology: A Review. Appl. Sci. 2017, 7, 494. [Google Scholar] [CrossRef]
- Guo, K.; Xu, Y. Random Vibration Suppression of a Truss Core Sandwich Panel Using Independent Modal Resonant Shunt and Modal Criterion. Appl. Sci. 2017, 7, 496. [Google Scholar] [CrossRef]
- Crawley, E.F.; de Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA J. 1987, 25, 1373–1385. [Google Scholar] [CrossRef]
- Kim, B.; Yoon, J.-Y. Enhanced Adaptive Filtering Algorithm Based on Sliding Mode Control for Active Vibration Rejection of Smart Beam Structures. Appl. Sci. 2017, 7, 750. [Google Scholar] [CrossRef]
- Lou, J.; Liao, J.; Wei, Y.; Yang, Y.; Li, G. Experimental Identification and Vibration Control of A Piezoelectric Flexible Manipulator Using Optimal Multi-Poles Placement Control. Appl. Sci. 2017, 7, 309. [Google Scholar] [CrossRef]
- Frecker, M.I. Recent Advances in Optimization of Smart Structures and Actuators. J. Intell. Mater. Syst. Sruct. 2003, 14, 207–216. [Google Scholar] [CrossRef]
- Gupta, V.; Sharma, M.; Nagesh, T. Optimization Criteria for Optimal Placement of Piezoelectric Sensors and Actuators on a Smart Structure: A Technical Review. J. Intell. Mater. Syst. Sruct. 2010, 21, 1227–1243. [Google Scholar] [CrossRef]
- Dhuri, K.D.; Seshu, P. Piezo actuator placement and sizing for good control effectiveness and minimal change in original system dynamics. Smart Mater. Struct. 2006, 15, 1661–1672. [Google Scholar] [CrossRef]
- Kumar, K.R.; Narayanan, S. Active vibration control of beams with optimal placement of piezoelectric sensor/actuator pairs. Smart Mater. Struct. 2008, 17, 055008. [Google Scholar] [CrossRef]
- Demetriou, M.A. A Numerical Algorithm for the Optimal Placement of Actuators and Sensors for Flexible Structures. In Proceedings of the American Control Conference, Chicago, IL, USA, 28–30 June 2000; pp. 2290–2294. [Google Scholar]
- Bruant, I.; Coffignal, G.; Lene, F.; Verge, M. A methodology for determination of piezoelectric actuator and sensor location on beam structures. J. Sound Vib. 2001, 245, 861–882. [Google Scholar] [CrossRef]
- Sunar, M.; Rao, S.S. Distribuited Modeling and Actuator Location for Piezoelectric Control System. AIAA J. 1996, 34, 2209–2211. [Google Scholar] [CrossRef]
- Yang, Y.; Zhanli, J.; Soh, C.K. Integrated optimal design of vibration control system for smart beams using genetic algorithms. J. Sound Vib. 2005, 119, 487–508. [Google Scholar] [CrossRef]
- Barboni, R.; Mannini, A.; Fantini, E.; Gaudenzi, P. Optimal placement of PZT actuators for the control of beam dynamics. Smart Mater. Struct. 2000, 9, 110–120. [Google Scholar] [CrossRef]
- Aldraihem, O.J.; Singh, T.; Wetherhold, R.C. Optimal Size and Location of Piezoelectric Actuator/Sensors: Practical Considerations. J. Guid. Control Dyn. 2000, 23, 509–515. [Google Scholar] [CrossRef]
- Baz, A.; Poh, S. Performance of an active control system with piezoelectric actuators. J. Sound Vib. 1988, 126, 327–343. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, C.M. Optimal placement and size of piezoelectric patches on beams from the controllability perspective. Smart Mater. Struct. 2000, 9, 558–567. [Google Scholar] [CrossRef]
- Botta, F.; Dini, D.; Schwingshackl, C.; di Mare, L.; Cerri, G. Optimal Placement of Piezoelectric Plates to Control Multimode Vibrations of a Beam. Adv. Acoust. Vib. 2013, 2013. [Google Scholar] [CrossRef]
- Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Sciuto, S.A.; Di Giminiani, R. A preliminary characterization of a whole body vibration platform prototype for medical and rehabilitation application. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 15–18 May 2016. art. no. 7533721. [Google Scholar]
- Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Sciuto, S.A.; Di Giminiani, R. A preliminary uncertainty analysis of acceleration and displacement measurements on a novel WBV platform for biologic response studies. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 15–18 May 2016. art. no. 7533722. [Google Scholar]
- Hohl, A.; Neubauer, M.; Schwarzendahl, S.M.; Panning, L.; Wallaschek, J. Active and semiactive Vibration Damping of Turbine Blades with Piezoceramics. Proc. SPIE 2009, 7288, 72881H1–72881H10. [Google Scholar]
- Goltz, I.; Bohmer, H.; Nollau, R.; Belz, J.; Grueber, B.; Seume, J.R. Piezo-electric actuation of rotor blades in an axial compressor with Piezoceramics. In Proceedings of the 8th European Conference on Turbomachinery (ETC), Graz, Austria, 23–27 March 2009. [Google Scholar]
- Provenza, A.J.; Morrison, C.R. Control of fan blade vibrations using piezoelectric and bi-directional telemetry. In Proceedings of the ASME Turbo Expo, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Lin, S.M.; Lin, J.M. Vibration of Rotating Smart Beam. AIAA J. 2007, 4, 382–389. [Google Scholar] [CrossRef][Green Version]


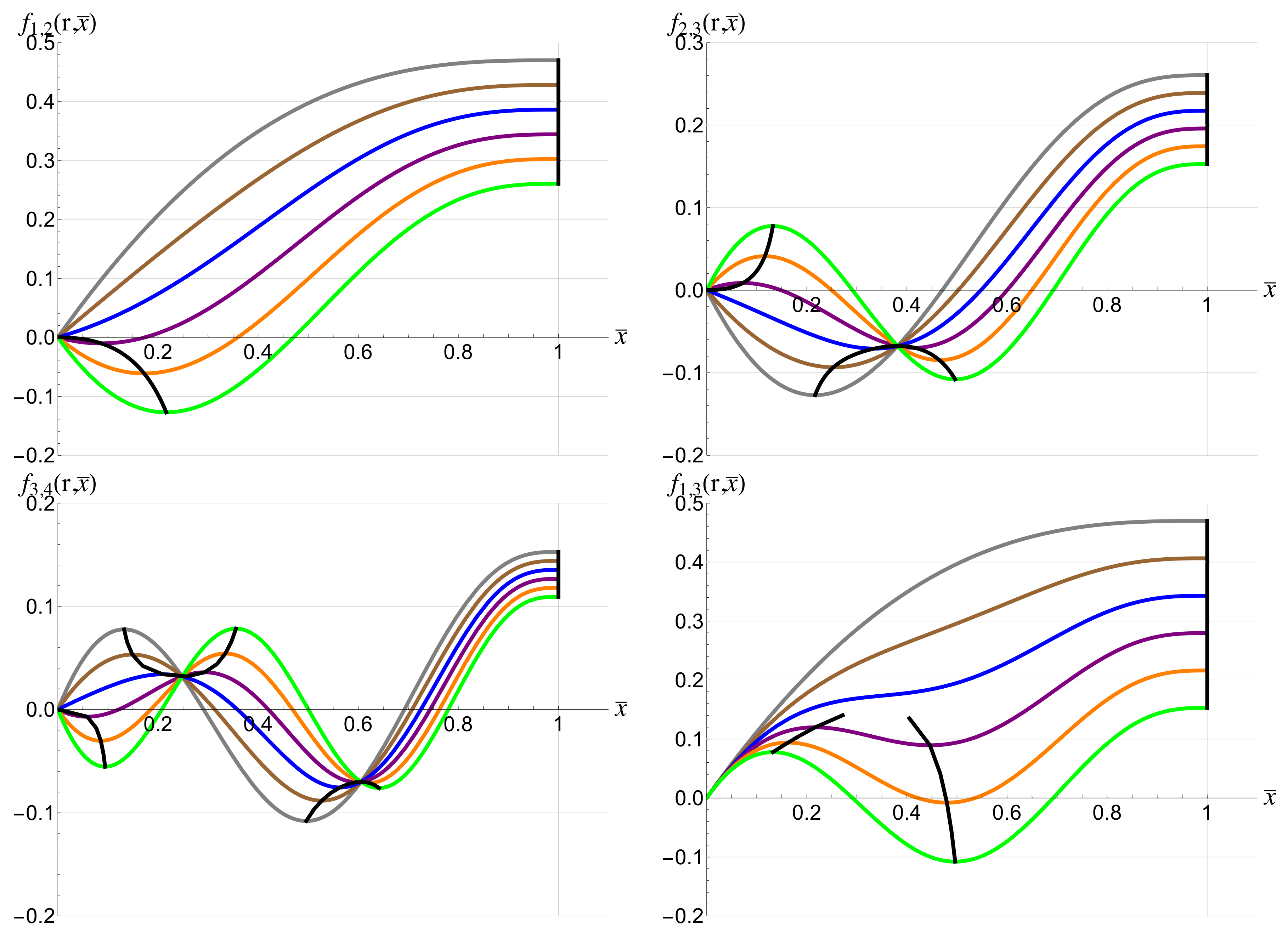




 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.
 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.
 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.
 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.
 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.
 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.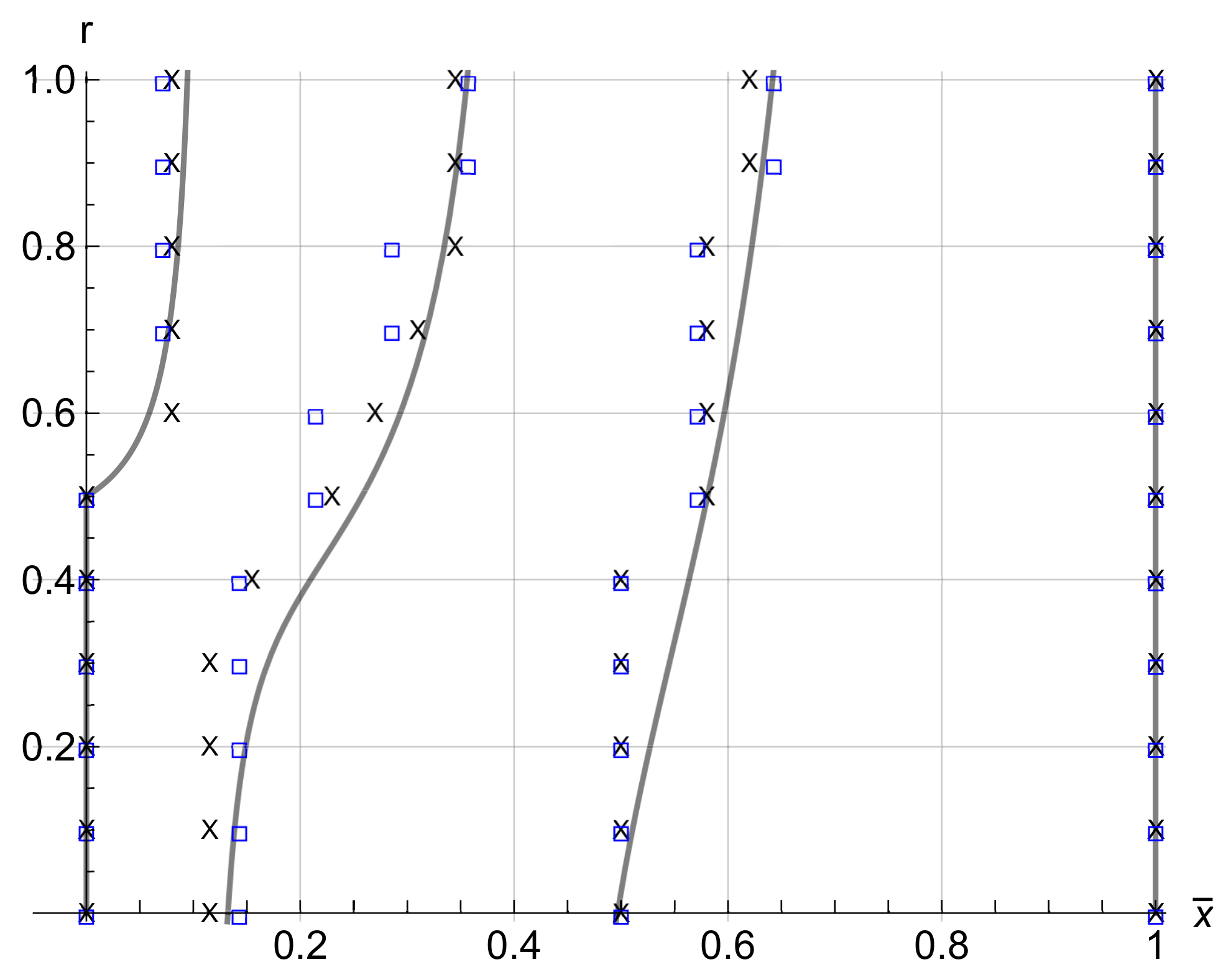
 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.
 = model solution; = FEM simulations; × = experimental results.
= model solution; = FEM simulations; × = experimental results.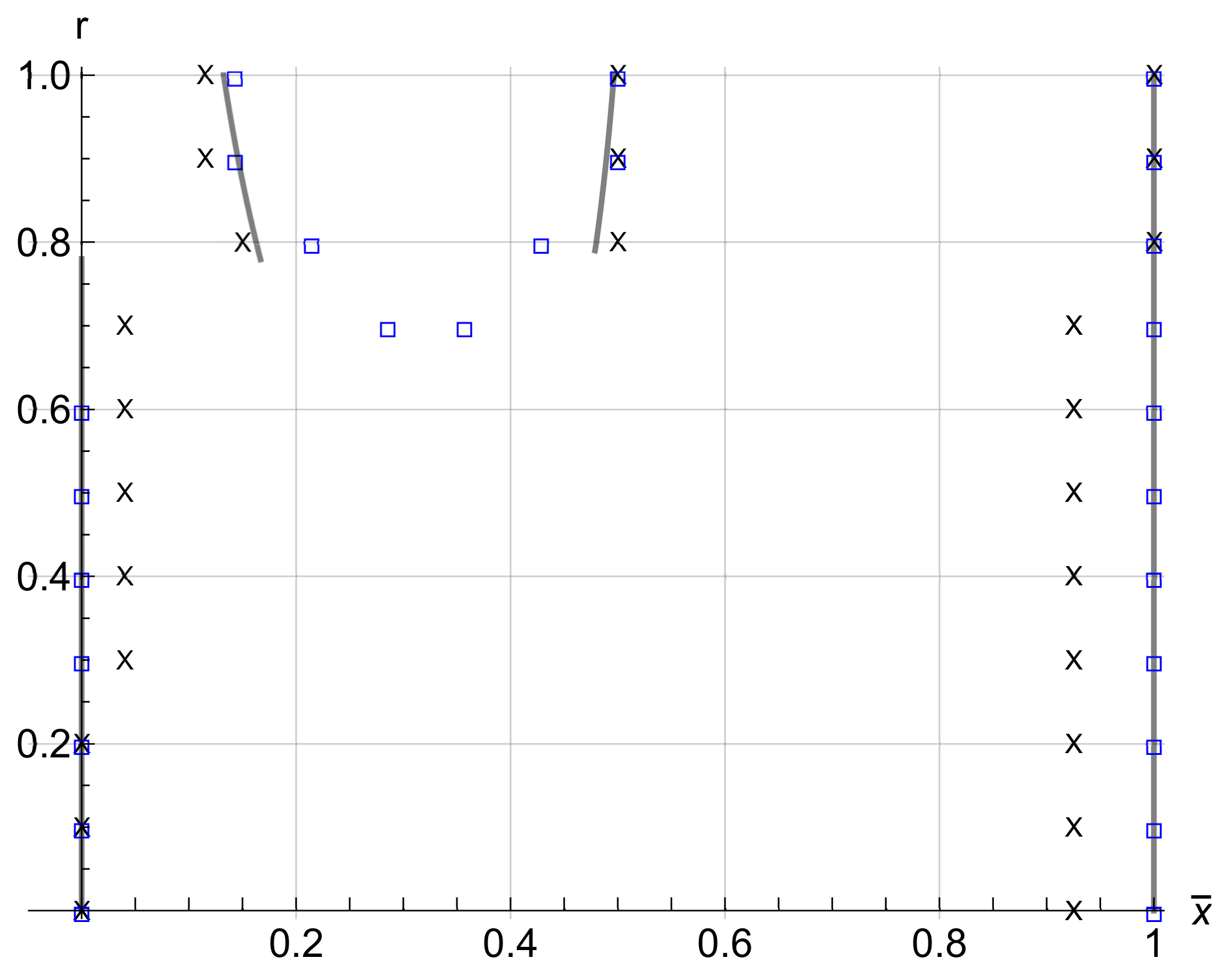





| Material | Length | Width | Thickness | |
|---|---|---|---|---|
| Beam | Aluminium | 185 | 36 | 1.5 |
| PZT plate | PIC 255 (PI Ceramic) | 40 | 14 | 0.5 |
| Combination\Plates Couple | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
| 2 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 |
| 3 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | +1 |
| 4 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | −1 |
| 5 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | −1 | +1 | +1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Botta, F.; Scorza, A.; Rossi, A. Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations. Appl. Sci. 2018, 8, 551. https://doi.org/10.3390/app8040551
Botta F, Scorza A, Rossi A. Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations. Applied Sciences. 2018; 8(4):551. https://doi.org/10.3390/app8040551
Chicago/Turabian StyleBotta, Fabio, Andrea Scorza, and Andrea Rossi. 2018. "Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations" Applied Sciences 8, no. 4: 551. https://doi.org/10.3390/app8040551
APA StyleBotta, F., Scorza, A., & Rossi, A. (2018). Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations. Applied Sciences, 8(4), 551. https://doi.org/10.3390/app8040551






