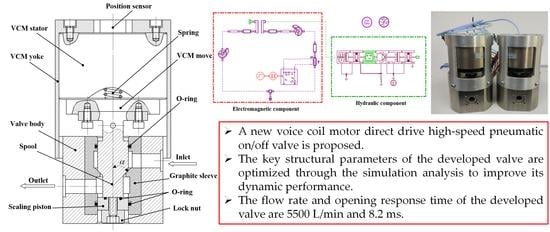
Development of a High-Pressure Pneumatic On/Off Valve with High Transient Performances Direct-Driven by Voice Coil Motor
Abstract
:1. Introduction
2. Characterization and Methodology
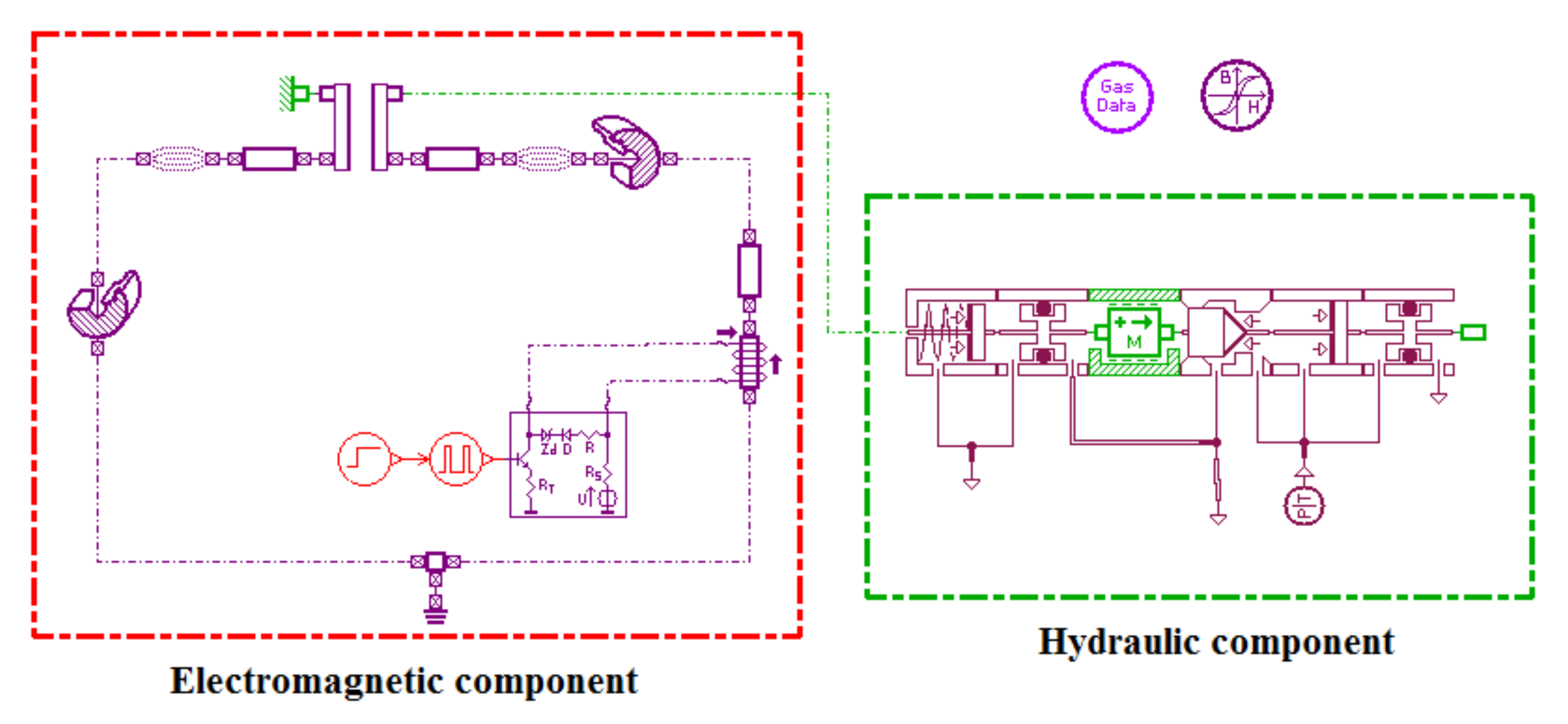
2.1. Description of VCM-DHPV
2.2. Mathematical Model
- A constant stable gas supply is considered.
- Flowing process of gas through valve port of VCM-DHPV is isentropic.
- The pressure and thermal fields are uniformly distributed inside every cavity of VCM-DHPV.
- The spring of VCM-DHPV is assumed to be linear. In addition, the masses of spool, piston, and spring are integrated into one inertial parameter.
- Dynamic flow forces, gas inertia and pressure loss in tubes can be neglected.
- Steady state flow forces are considered only.
3. Simulation Analysis
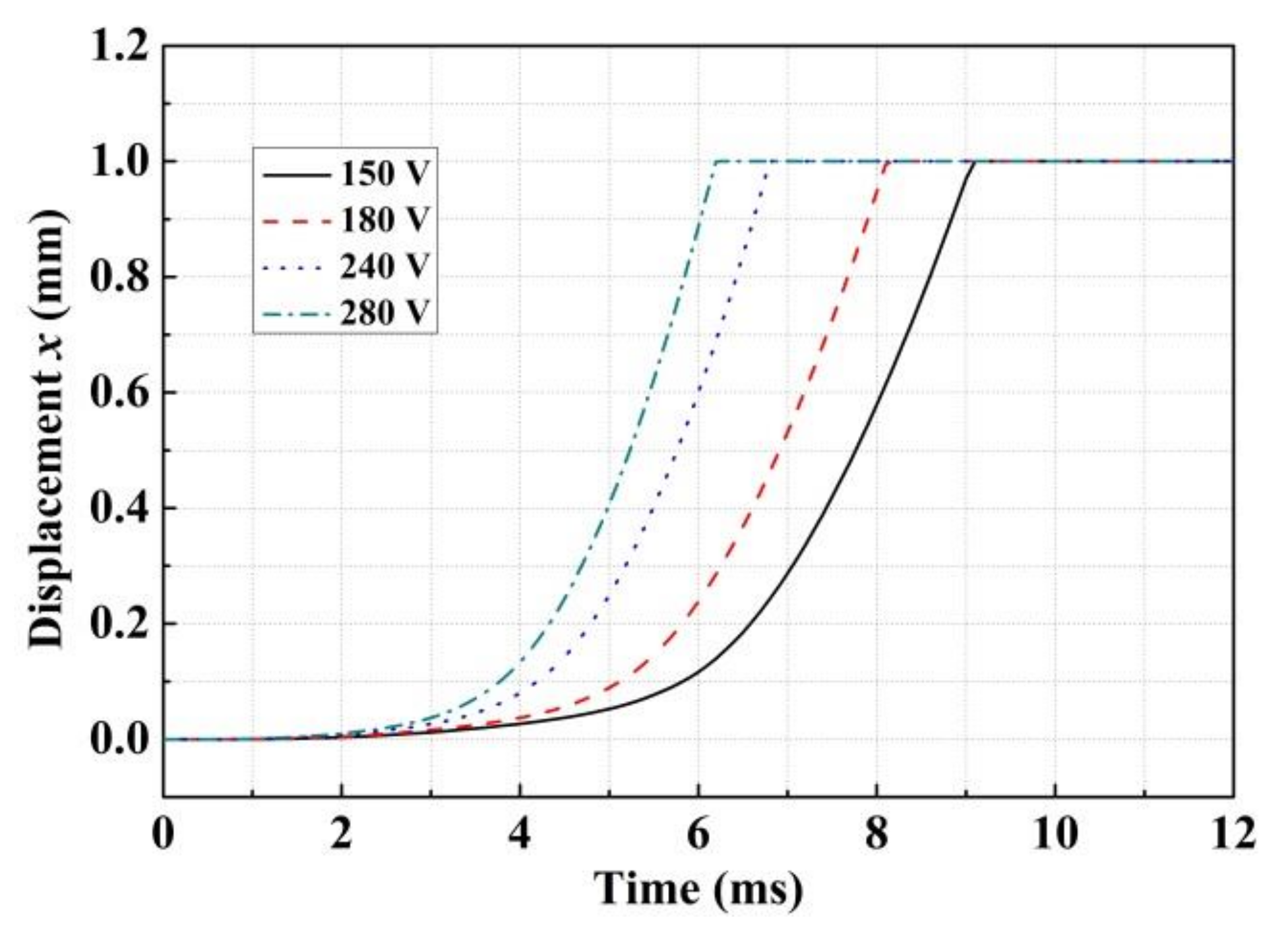
3.1. Influence of the Exciting Voltage
3.2. Influence of the Supply Pressure
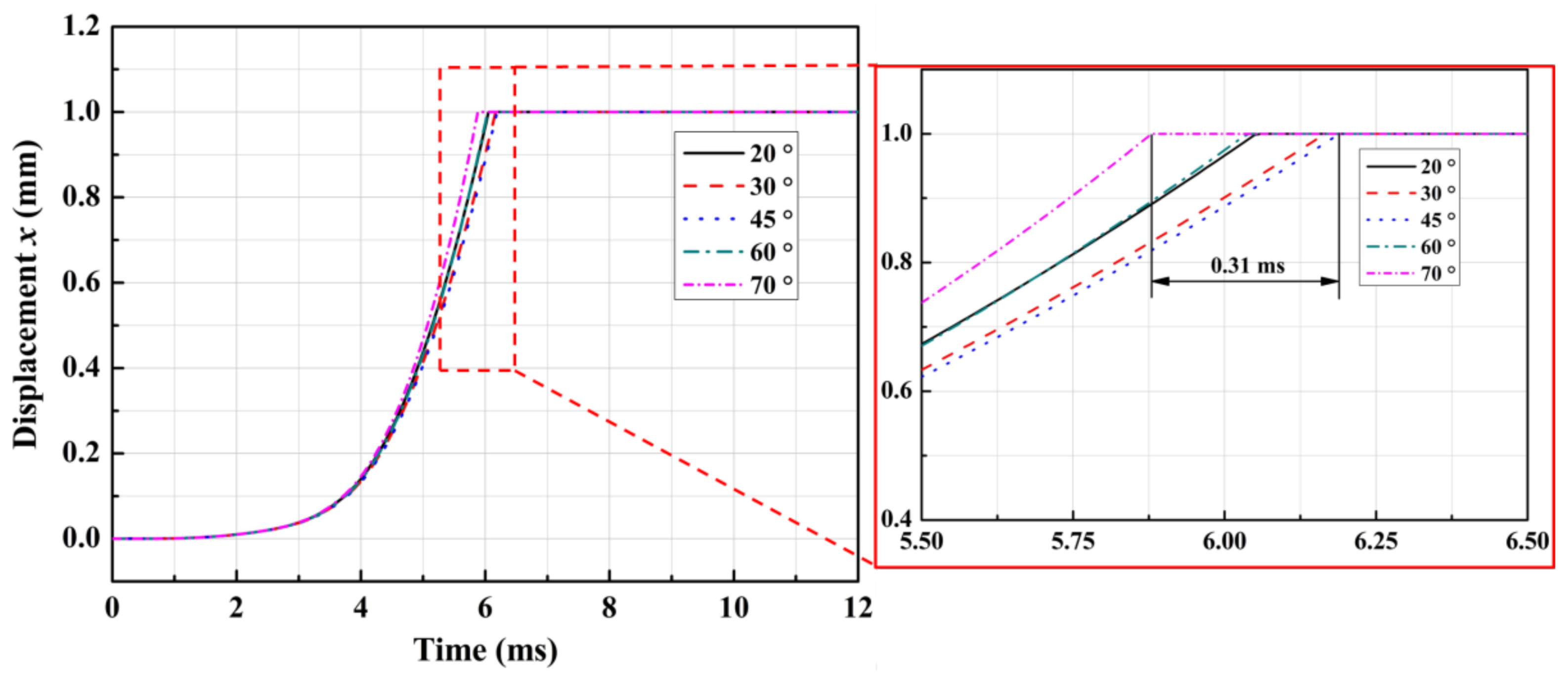
3.3. Influence of the Half Cone Angle
4. Experiment Verification
4.1. Experiment Apparatus
- Open the stop valve and regulate the pressure reducing valve to make the compressed air as a certain pressure.
- Use the computer to collect the pressure signal, flow signal and displacement signal when opening the on/off valve.
- Set a new pressure and repeat Steps (1) and (2).
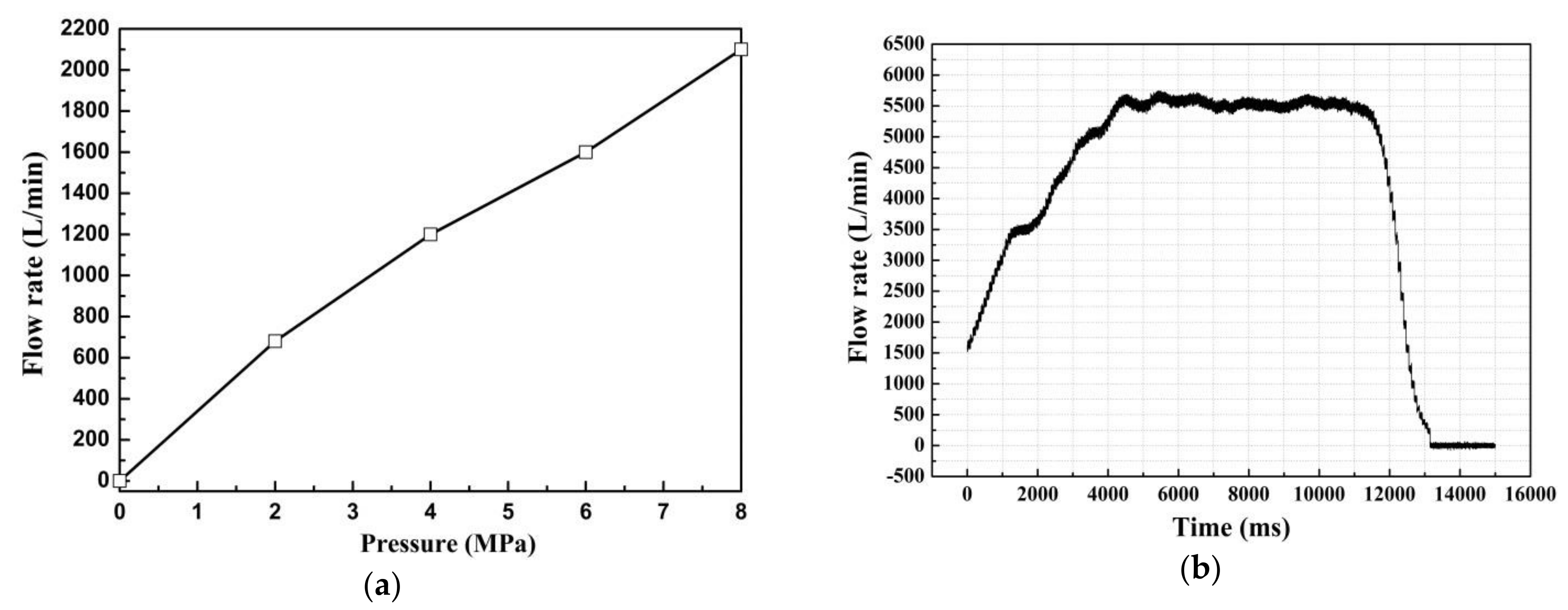
4.2. Experiment Results and Discussion
4.2.1. Static Characteristics Experiments
4.2.2. Dynamic Characteristics Experiments
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, H.; Pan, M. Engineering research in fluid power: A review. J. Zhejiang Univ. Sci. A 2015, 16, 427–442. [Google Scholar] [CrossRef]
- Simic, M.; Herakovic, N. Reduction of the flow forces in a small hydraulic seat valve as alternative approach to improve the valve characteristics. Energy Convers. Manag. 2015, 89, 708–718. [Google Scholar] [CrossRef]
- Richer, E.; Hurmuzlu, Y. A High Performance Pneumatic Force Actuator System: Part 1—Nonlinear Mathematical Model. J. Dyn. Syst. Meas. Control 2000, 122, 416–425. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Y.; Cai, M.; Zhang, B.; Zhu, J. Study on the Aviation Oxygen Supply System Based on a Mechanical Ventilation Model. Chin. J. Aeronaut. 2018, 31, 197–204. [Google Scholar] [CrossRef]
- Ren, S.; Cai, M.L.; Shi, Y.; Xu, W.Q.; Zhang, X.D. Influence of bronchial diameter change on the airflow dynamics based on a pressure-controlled ventilation system. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2929. [Google Scholar] [CrossRef] [PubMed]
- Taghizadeh, M.; Ghaffari, A.; Najafi, F. Modeling and identification of a solenoid valve for PWM control applications. C. R. Mac. 2009, 337, 131–140. [Google Scholar] [CrossRef]
- Heikkil, M.; Linjama, M. Displacement control of a mobile crane using a digital hydraulic power management system. Mechatronics 2013, 23, 452–461. [Google Scholar] [CrossRef]
- Topcu, E.E.; Ibrahim, Y.; Kamis, Z. Development of electro-pneumatic fast switching valve and investigation of its characteristics. Mechatronics 2006, 16, 365–378. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, B.L.; Cai, M.L.; Xu, W.Q. Coupling Effect of double lungs on a VCV ventilator with automatic secretion clearance function. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 99, 1. [Google Scholar] [CrossRef] [PubMed]
- Kamelreiter, M.; Kemmetmüller, W.; Kugi, A. Digitally controlled electrorheological valves and their application in vehicle dampers. Mechatronics 2012, 22, 629–638. [Google Scholar] [CrossRef]
- Lee, G.S.; Sung, H.J.; Kim, H.C. Multiphysics analysis of a linear control solenoid valve. J. Fluid Eng. 2013, 135, 011104. [Google Scholar] [CrossRef]
- Ahn, K.; Yokota, S. Intelligent switching control of pneumatic actuator using on/off solenoid valves. Mechatronics 2005, 15, 683–702. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, B.; Zhong, Q. Study on control performance of pilot high-speed switching valve. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Li, B.R.; Gao, L.L.; Yang, G. Modeling and control of a novel high-pressure pneumatic servo valve direct-driven by voice coil motor. J. Dyn. Syst. 2013, 135, 014507. [Google Scholar]
- Li, B.R.; Gao, L.L.; Yang, G. Evaluation and compensation of steady gas flow force on the high-pressure electro-pneumatic servo valve direct-driven by voice coil motor. Energy Convers. Manag. 2013, 67, 92–102. [Google Scholar] [CrossRef]
- Guo, H.; Wang, D.Y.; Xu, J.Q. Research on a high-frequency response direct drive valve system based on voice coil motor. IEEE Trans. Power Electron. 2013, 28, 2483–2492. [Google Scholar] [CrossRef]
- Wu, S.; Jiao, Z.X.; Yan, L.; Zhang, R.; Yu, J.T.; Chen, C.Y. A fault-tolerant triple-redundant voice coil motor for direct drive valves: Design, optimization, and experiment. Chin. J. Aeronaut. 2013, 26, 1071–1079. [Google Scholar] [CrossRef]
- Wu, S.; Jiao, Z.X.; Yan, L.; Yu, J.T.; Chen, C.Y. Development of a direct-drive servo valve with high-frequency voice coil motor and advanced digital controller. IEEE/ASME Trans. Mechatron. 2014, 19, 932–942. [Google Scholar] [CrossRef]
- Miyajima, T.; Fujita, T.; Sakaki, K. Development of a digital control system for high-performance pneumatic servo valve. Precis. Eng. 2007, 31, 156–161. [Google Scholar] [CrossRef]
- Yao, J.; Zhao, L.; Deng, Q. High precision locating control system based on VCM for Talbot lithography. In Proceedings of the Eighth International Symposium on Advanced Optical Manufacturing and Testing Technology, Suzhou, China, 25 October 2016. [Google Scholar]
- Chi, W.; Cao, D.; Wang, D. Design and experimental study of a VCM-based Stewart parallel mechanism used for active vibration isolation. Energies 2015, 8, 8001–8019. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, B.L.; Cai, M.L.; Zhang, X.D. Numerical Simulation of volume-controlled mechanical ventilated respiratory system with two different lungs. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2852. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.P.; Wang, X.Y. Development of a Novel High Pressure Electronic Pneumatic Pressure Reducing Valve. J. Dyn. Syst. 2011, 133, 011011. [Google Scholar]
- Shi, Y.; Wang, Y.X.; Xu, W.Q.; Liang, H.W.; Cai, M.L. Power characteristics of a new kind of air-powered vehicle. Int. J. Energy Res. 2016, 40, 1112–1121. [Google Scholar] [CrossRef]
- Shi, Y.; Wu, T.C.; Cai, M.L.; Wang, Y.X.; Xu, W.Q. Energy conversion characteristics of a hydropneumatic transformer in a sustainable-energy vehicle. Appl. Energy 2016, 171, 77–85. [Google Scholar] [CrossRef]
- Niu, J.L.; Shi, Y.; Cai, M.L.; Cao, Z.X.; Wang, D.D.; Zhang, Z.Z.; Zhang, X.D. Detection of Sputum by Interpreting the Time-frequency Distribution of respiratory sound signal using image processing techniques. Bioinformatics 2018, 34, 820–827. [Google Scholar] [CrossRef] [PubMed]










| Description | Notation | Value | Unit |
|---|---|---|---|
| Mass of coil and spool | m | 0.28 | kg |
| Maximum stroke of the spool | xmax | 1.0 | mm |
| Nominal mass flow rate | qtmax | 0.5 | g/s |
| Gain of VCM | Ke | 44.2 | N/A |
| Maximum coil current | I | 8.4 | A |
| Coil resistance | R | 4.6 | Ω |
| Coil inductance | Ls | 220 | mH/kHz |
| Viscous friction coefficient | kf | 8 × 10-3 | N/(m/s) |
| Spring stiffness | ks | 0.02 | N/m |
| Description | Notation | Value | Unit |
|---|---|---|---|
| Orifice diameter of the valve | D | 24 | mm |
| Spool diameter | dr | 16 | mm |
| Half cone angle | α | 45 | ° |
| Inlet diameter | di | 11 | mm |
| Outlet diameter | do | 11 | mm |
| VCM electromagnetic force | Fe | 376 | N |
| Test pressure | Ps | 8 | MPa |
| Supply Pressure | Opening Response time | Deviation | |
|---|---|---|---|
| Simulation | Experiment | ||
| 2 MPa | 5.7 ms | 7.3 ms | 1.6 ms |
| 4 MPa | 5.9 ms | 7.4 ms | 1.5 ms |
| 6 MPa | 6.1 ms | 7.9 ms | 1.8 ms |
| 8 MPa | 6.2 ms | 8.2 ms | 2.0 ms |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, S.; Liu, X.; Yin, F.; Ji, H.; Zhang, J. Development of a High-Pressure Pneumatic On/Off Valve with High Transient Performances Direct-Driven by Voice Coil Motor. Appl. Sci. 2018, 8, 611. https://doi.org/10.3390/app8040611
Nie S, Liu X, Yin F, Ji H, Zhang J. Development of a High-Pressure Pneumatic On/Off Valve with High Transient Performances Direct-Driven by Voice Coil Motor. Applied Sciences. 2018; 8(4):611. https://doi.org/10.3390/app8040611
Chicago/Turabian StyleNie, Songlin, Xiangyang Liu, Fanglong Yin, Hui Ji, and Jingxiu Zhang. 2018. "Development of a High-Pressure Pneumatic On/Off Valve with High Transient Performances Direct-Driven by Voice Coil Motor" Applied Sciences 8, no. 4: 611. https://doi.org/10.3390/app8040611
APA StyleNie, S., Liu, X., Yin, F., Ji, H., & Zhang, J. (2018). Development of a High-Pressure Pneumatic On/Off Valve with High Transient Performances Direct-Driven by Voice Coil Motor. Applied Sciences, 8(4), 611. https://doi.org/10.3390/app8040611