Determination of Nonlinear Creep Parameters for Hereditary Materials
Abstract
:1. Introduction
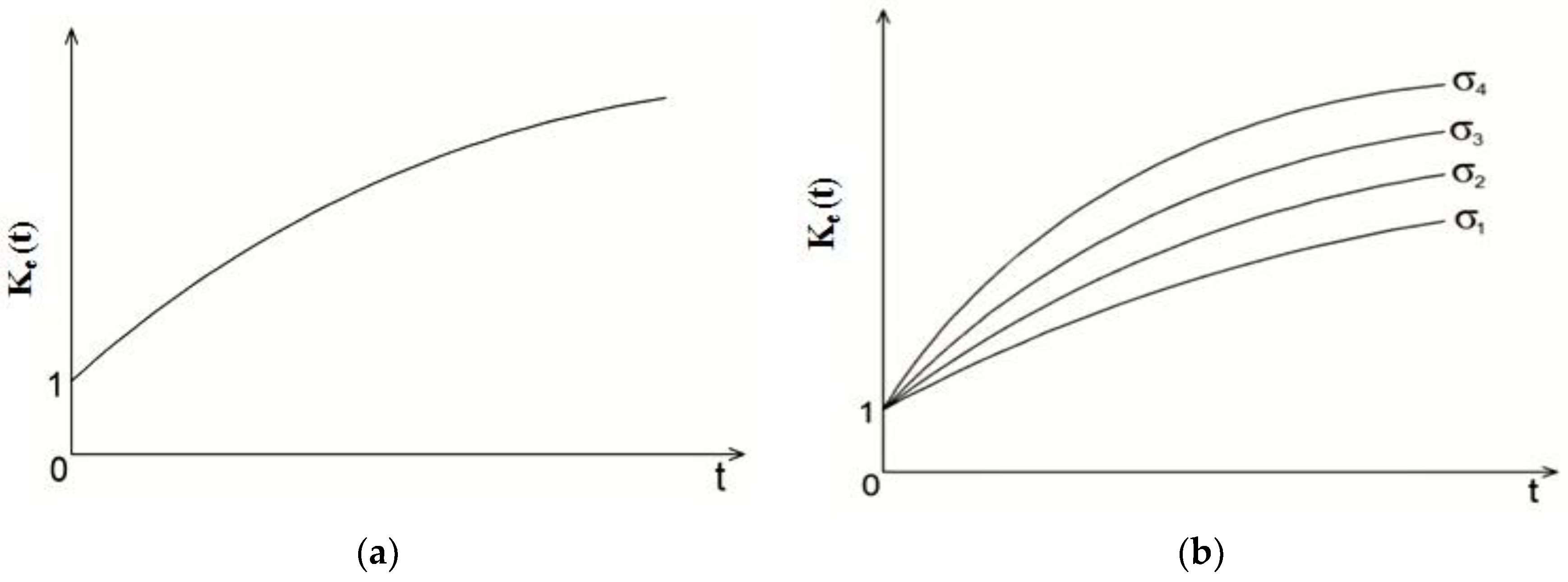
2. Method of Isochronous Creep Curves of Yu. N. Rabotnov
2.1. Short Description of Method
2.2. Nonlinear Equation and Creep Kernel
3. Methods of Determination of Linear Creep Parameters for Hereditary Materials
3.1. Parameters α, ε0, and δ
3.2. Parameters β and λ
4. Algorithm for Description of Nonlinear Deformation of Hereditary Materials
5. Application of Proposed Algorithm and Methods
5.1. Material Nylon 6
5.2. Glass-Reinforced Plastic TC 8/3-250
5.2.1. Ѳ = 90°
5.2.2. Ѳ = 45°
5.3. Asphalt Concrete
6. Conclusions
- Using the schematic creep curves and isochronous curves, Yu. N. Rabotnov’s isochronous creep curve method has been visually explained. The nonlinear integral equation has been shown for mathematical description of the nonlinear deformation process for hereditary materials, proposed by Yu. N. Rabotnov.
- Relevant equations have been determined from the nonlinear integral equation of Yu. N. Rabotnov for the application cases of Rabotnov’s fractional exponential kernel and Abel’s kernel for nonlinear deformation of hereditary materials at creep. The improved methods have been given for determination of creep parameters α, ε0, δ, β, and λ.
- The detailed method has been developed for description of the nonlinear deformation process for hereditary materials. The notions have been introduced for experimental and model rheological parameters and similarity coefficients of isochronous curves. It has been shown how using them, one can find instantaneous strains at various stress levels for description of nonlinear deformation of hereditary materials at creep.
- By processing and using test results for material Nylon 6 and glass-reinforced plastic TС 8/3-250, the process has been shown for sequential implementation of the developed methods for description of linear and nonlinear deformation of these materials at creep. The accuracy of the proposed methods is high.
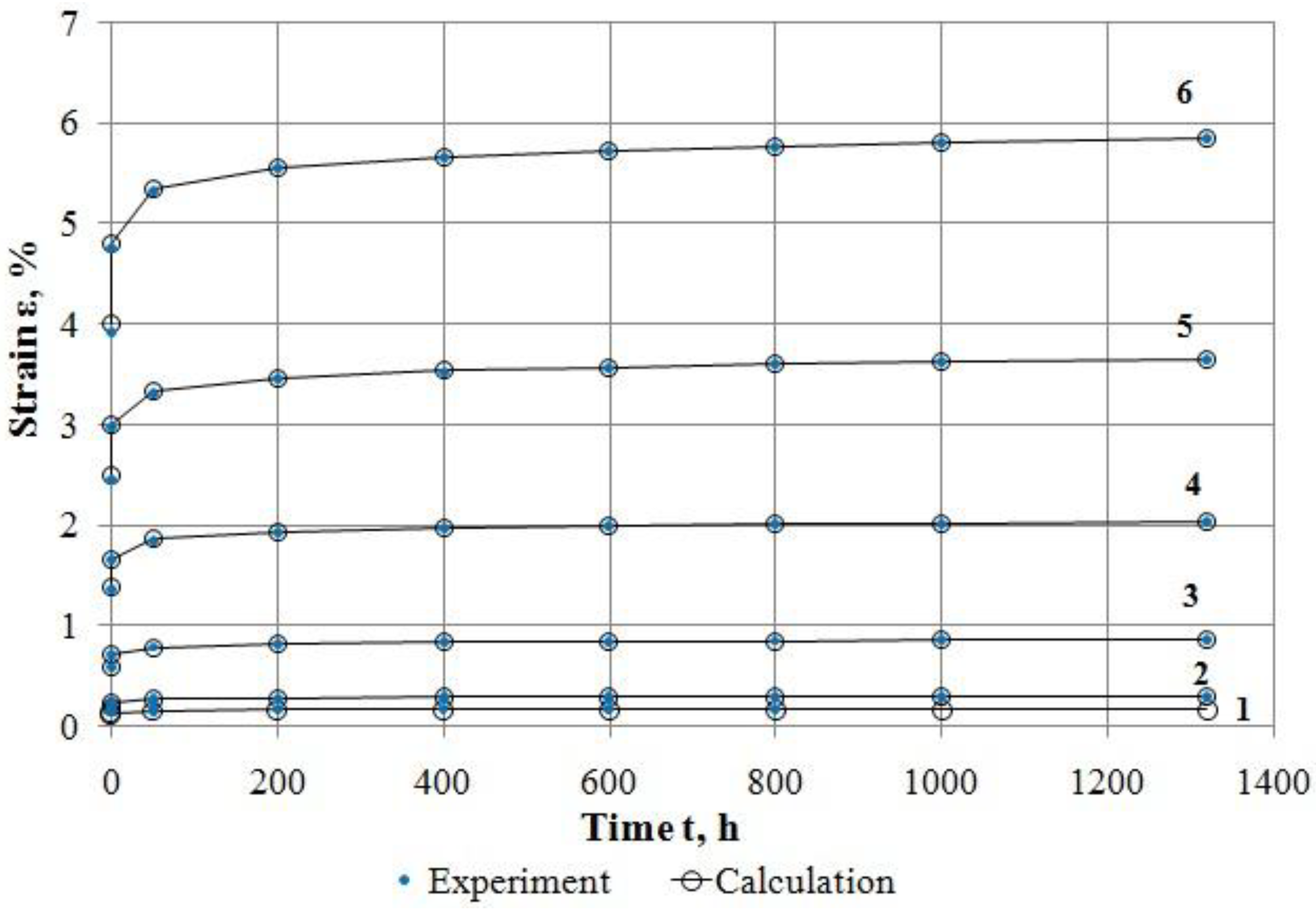
- By the results of experimental investigation, performed by the authors of this paper, it has been determined that fine-grained dense asphalt concrete at the temperature of 20 ± 2 °С and stresses up to 0.183 MPa at direct tension is deformed considerably in a nonlinear way. It has been shown in an illustrative way by construction of isochronous creep curves at various load durations and curves of experimental rheological parameter at various stresses. Nonlinear deformation of the asphalt concrete at creep is adequately described by the proposed methods.
Author Contributions
Conflicts of Interest
References
- Cristensen, R. Theory of Viscoelasticity: An Introduction; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Tschoegl, N. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Ferry, J. Viscoelastic Properties of Polymers, 3rd ed.; Willey: New York, NY, USA, 1980. [Google Scholar]
- Rabotnov, Y. Mechanics of Deformed Solid Body; Nauka: Moscow, Russia, 1988. [Google Scholar]
- Rabotnov, Y. Creep of Structure Elements; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Rabotnov, Y. Elements of Hereditary Mechanics of Solids; Nauka: Moscow, Russia, 1977. [Google Scholar]
- Georgievskiy, D.V.; Klimov, D.M.; Pobedrya, B.E. Peculiarities for behavior of viscoelastic materials. Solid Mech. 2004, 1, 119–157. [Google Scholar]
- Timoshenko, S.; Goodier, J. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Lurie, A.I. Theory of Elasticity; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Volterra, V. LeconsSurles Fonctions de Lignes; Gautheir-Villard: Paris, France, 1913. [Google Scholar]
- Rabotnov, Y.N. Balance of the elastic medium with an aftereffect. Appl. Math. Mech. 1948, 12, 53–62. [Google Scholar]
- Rabotnov, Y.; Mileiko, S. Short-Term Creep; Nauka: Moscow, Russia, 1970. [Google Scholar]
- Rabotnov, Y. Introduction to Fracture Mechanics; Nauka: Moscow, Russia, 1987. [Google Scholar]
- Iskakbayev, A.; Teltayev, B.; Alexandrov, S. Determining the creep parameters of linear viscoelastic materials. J. Appl. Math. 2016, 2016, 6568347. [Google Scholar] [CrossRef]
- Rabotnov, Y.; Papernik, L.; Zvonov, E. Tables of a Fractional Exponential Function of Negative Parameter and Its Integral; Nauka: Moscow, Russia, 1969. [Google Scholar]
- Golub, V.P.; Fernati, P.V.; Lyashenko, Y.G. Determining the parameters of the fractional exponential heredity kernels of linear viscoelastic materials. Int. Appl. Mech. 2008, 44, 963–974. [Google Scholar] [CrossRef]
- Zvonov, E.N.; Malinin, N.I.; Papernik, L.K.; Tseitlin, B.M. Determination of the creep characteristics of linear elastic hereditary materials by using a digital computer. Mech. Solid 1968, 5, 76–82. [Google Scholar]
- Gavrilov, D.А.; Markov, B.A. Numerical method of determining the rheologic parameters of composites from test results. Mech. Compos. Mater. 1987, 22, 417–421. [Google Scholar] [CrossRef]
- Mosin, A.V. Calculation of parameters for nonlinear determining equation of hereditary type. Probl. Mech. Eng. Reliab. Mach. 2002, 2, 83–88. [Google Scholar]
- Suvorova, Y.V.; Alekseyeva, S.I. Engineering applications of nonlinear-hereditary model considering the temperature. Industrial laboratory. Diagn. Mater. 2000, 66, 48–52. [Google Scholar]
- Suvorova, Y.V.; Mosin, A.V. Determination of parameters of the Rabotnov’s fractional exponential function with use of integral transform and modern software. Probl. Mech. Eng. Autom. 2002, 4, 54–56. [Google Scholar]
- Suvorova, Y.V.; About, Y.N. Rabotnov’s nonlinear hereditary equation and its applications. News Russ. Acad. Sci. Mech. Solids 2004, 1, 174–181. [Google Scholar]
- Osokin, A.E.; Suvorova, Y.V. Nonlinear governing equation of hereditary media and methods for determination of its parameters. Appl. Math. Mech. 1978, 42, 1108–1114. [Google Scholar]
- Rozovskii, M.I. Some features of elasticity hereditary media. News USSR Acad. Sci. 1961, 2, 30–36. [Google Scholar]
- Lodge, A.S. Elastic Liquids: An Introductory Vector Treatment of Finite-Strain Polymer Rheology; Academic Press: London, UK; New York, NY, USA, 1964. [Google Scholar]
- Iskakbayev, A.I.; Teltayev, B.B.; Andriadi, F.K.; Estayev, K.Z.; Suppes, E.A.; Iskakbayeva, A.A. Experimental research of creep, recovery and fracture processes of asphalt concrete under tension. In Proceedings of the 24th International Congress on Theoretical and Applied Mechanics, Montreal, QC, Canada, 21–26 August 2016. [Google Scholar]
- Iskakbayev, A.I.; Teltayev, B.B.; Rossi, C.O. Deformation and strength of asphalt concrete under static and step loadings. In Proceedings of the AIIT International Congress on Transport Infrastructure and Systems (TIS 2017), Rome, Italy, 10–12 April 2017; pp. 3–8. [Google Scholar]
- Iskakbayev, A.I.; Teltayev, B.B.; Rossi, C.O. Steady-state creep of asphalt concrete. Appl. Sci. 2017, 7, 142. [Google Scholar] [CrossRef]
- Annin, B.D. Asymptotic expansion of an exponential function of fractional order. Appl. Math. Mech. 1961, 25, 796–798. [Google Scholar] [CrossRef]
- Maksimov, R.D.; Jirgens, L.; Jansons, J.; Plume, E. Mechanical properties of polyester polymer-concrete. Mech. Compos. Mater. 1999, 35, 99–110. [Google Scholar] [CrossRef]
- Rabotnov, Y.N.; Papernik, L.H.; Stepanychev, E.I. Nonlinear creep of glass-reinforced plastic TС8/3-250. Mech. Polym. 1971, 3, 391–397. [Google Scholar]
- ST RK 1225-2013. Hot Mix Asphalt for Roads and Airfields; Technical Specifications: Astana, Kazakhstan, 2013. [Google Scholar]
- ST RK 1284-2004. Crushed Stone and Gravel of Dense Rock for Construction Works; Technical Specifications: Astana, Kazakhstan, 2004. [Google Scholar]
- ST RK 1373-2013. Bitumens and Bitumen Binders. Oil Road Viscous Bitumens; Technical Specifications: Astana, Kazakhstan, 2013. [Google Scholar]
- Asphalt Institute. Performance Graded Asphalt Binder Specification and Testing; Superpave Series No. 1; Asphalt Institute: Lexington, MA, USA, 2003. [Google Scholar]
- EN 12697-33. Bituminous Mixtures. Test Methods for Hot Mix Asphalt. Part 33: Specimen Prepared by Roller Compactor; European Committee for Standardization: Brussels, Belgium, 2003. [Google Scholar]
- Fitzgerald, J.E.; Vakili, J. Non linear characterization of sand-asphalt concrete by means of permanent-memory norms. Exp. Mech. 1973, 13, 504–510. [Google Scholar] [CrossRef]
- Basalov, Y.G.; Kuznetsov, V.N.; Shesterikov, S.A. Determination of ratio for rheonom material. Mech. Solid Body 2000, 6, 69–89. [Google Scholar]
- Yoder, E.J.; Witczak, M.W. Principles of Pavement Design; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1975; p. 736. [Google Scholar]
- Huang, Y.H. Pavement Analysis and Design, 2nd ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- MS-4. The Asphalt Handbook, 7th ed.; Asphalt Institute: Lexington, MA, USA, 2008. [Google Scholar]
- Papagiannakis, A.; Masad, E. Pavement Design and Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]


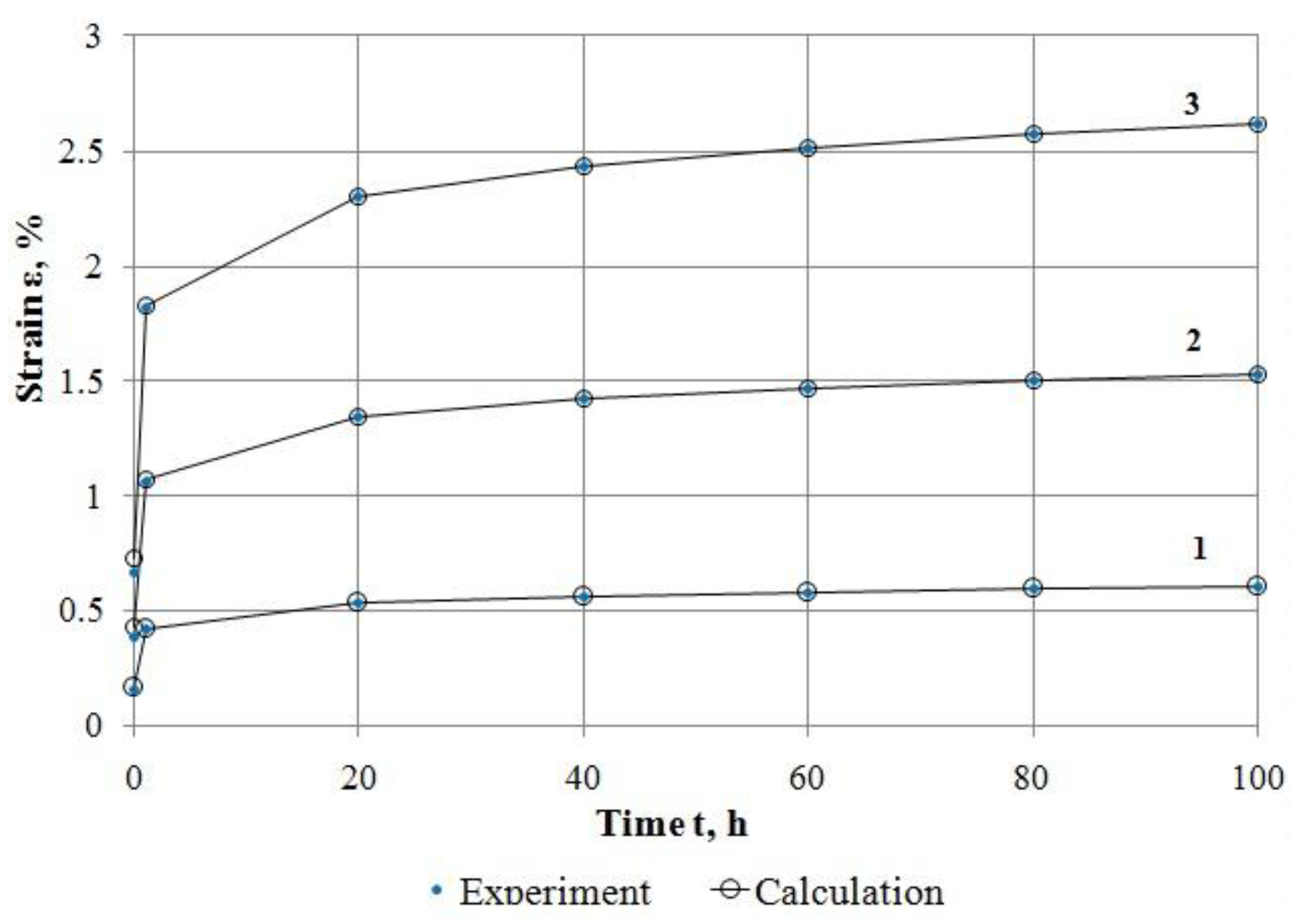






| Time t, h | Strain εе (t), %, at Stress σ, MPa | ||
|---|---|---|---|
| 5 | 10 | 15 | |
| 0 | 0.1537 | 0.3873 | 0.6650 |
| 1 | 0.4200 | 1.0585 | 1.8174 |
| 20 | 0.5321 | 1.3408 | 2.3022 |
| 40 | 0.5621 | 1.4164 | 2.4319 |
| 60 | 0.5804 | 1.4624 | 2.5110 |
| 80 | 0.5937 | 1.4961 | 2.5689 |
| 100 | 0.6043 | 1.5229 | 2.6148 |
| Time t, h | Strain εе (t), %, at Stress σ, MPa | |||
|---|---|---|---|---|
| 104.7 | 209.4 | 279.2 | 349.0 | |
| 0 | 0.3478 | 0.6957 | 0.9276 | 1.1595 |
| 1 | 0.3616 | 0.7232 | 0.9643 | 1.2054 |
| 10 | 0.3668 | 0.7337 | 0.9782 | 1.2228 |
| 50 | 0.3709 | 0.7419 | 0.9892 | 1.2365 |
| 100 | 0.3728 | 0.7457 | 0.9942 | 1.2428 |
| 200 | 0.3746 | 0.7493 | 0.9991 | 1.2489 |
| 300 | 0.3757 | 0.7515 | 1.0020 | 1.2525 |
| 400 | 0.3765 | 0.7530 | 1.0040 | 1.2550 |
| 500 | 0.3771 | 0.7542 | 1.0056 | 1.2570 |
| Time t, h | Strain εе (t), %, at Stress σ, MPa | |||||
|---|---|---|---|---|---|---|
| 20.3 | 40.6 | 60.9 | 81.2 | 101.5 | 121.8 | |
| 0 | 0.1074 | 0.1946 | 0.5805 | 1.3624 | 2.4430 | 3.9262 |
| 1 | 0.1302 | 0.2359 | 0.7037 | 1.6515 | 2.9614 | 4.7593 |
| 50 | 0.1457 | 0.2639 | 0.7873 | 1.8478 | 3.3134 | 5.3251 |
| 200 | 0.1518 | 0.2750 | 0.8204 | 1.9255 | 3.4527 | 5.5489 |
| 400 | 0.1548 | 0.2806 | 0.8370 | 1.9643 | 3.5222 | 5.6608 |
| 600 | 0.1566 | 0.2838 | 0.8466 | 1.9869 | 3.5629 | 5.7260 |
| 800 | 0.1579 | 0.2861 | 0.8533 | 2.0027 | 3.5912 | 5.7715 |
| 1000 | 0.1588 | 0.2878 | 0.8586 | 2.0150 | 3.6132 | 5.8068 |
| 1320 | 0.1600 | 0.2900 | 0.8649 | 2.0300 | 3.6401 | 5.8500 |
| Time t, h | Strain εе (t), %, at Stress σ, MPa | ||||
|---|---|---|---|---|---|
| 0.041 | 0.074 | 0.111 | 0.148 | 0.183 | |
| 0 | 0.0475 | 0.0543 | 0.0805 | 0.1313 | 0.1782 |
| 30 | 0.0633 | 0.0728 | 0.1018 | 0.1584 | 0.2305 |
| 90 | 0.0849 | 0.0932 | 0.1338 | 0.1782 | 0.2855 |
| 150 | 0.0988 | 0.1102 | 0.1491 | 0.2084 | 0.3310 |
| 210 | 0.1099 | 0.1232 | 0.1643 | 0.2484 | 0.3710 |
| 270 | 0.1194 | 0.1346 | 0.1795 | 0.2696 | 0.4081 |
| 330 | 0.1255 | 0.1457 | 0.1937 | 0.2839 | 0.4482 |
| 390 | 0.1339 | 0.1546 | 0.2055 | 0.3184 | 0.4812 |
| 450 | 0.1415 | 0.1627 | 0.2158 | 0.3293 | 0.5105 |
| 510 | 0.1460 | 0.1713 | 0.2273 | 0.3478 | 0.5433 |
| 570 | 0.1488 | 0.1759 | 0.2349 | 0.3632 | 0.5741 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iskakbayev, A.; Teltayev, B.; Oliviero Rossi, C.; Yensebayeva, G. Determination of Nonlinear Creep Parameters for Hereditary Materials. Appl. Sci. 2018, 8, 760. https://doi.org/10.3390/app8050760
Iskakbayev A, Teltayev B, Oliviero Rossi C, Yensebayeva G. Determination of Nonlinear Creep Parameters for Hereditary Materials. Applied Sciences. 2018; 8(5):760. https://doi.org/10.3390/app8050760
Chicago/Turabian StyleIskakbayev, Alibai, Bagdat Teltayev, Cesare Oliviero Rossi, and Gulzat Yensebayeva. 2018. "Determination of Nonlinear Creep Parameters for Hereditary Materials" Applied Sciences 8, no. 5: 760. https://doi.org/10.3390/app8050760





