Design & Manufacture of a High-Performance Bicycle Crank by Additive Manufacturing

Featured Application

The research presented in this article is focused on the design, manufacture, and validation of an elite bicycle crank.

Abstract

A new practical workflow for the laser Powder Bed Fusion (PBF) process, incorporating topological design, mechanical simulation, manufacture, and validation by computed tomography is presented, uniquely applied to a consumer product (crank for a high-performance racing bicycle), an approach that is tangible and adoptable by industry. The lightweight crank design was realised using topology optimisation software, developing an optimal design iteratively from a simple primitive within a design space and with the addition of load boundary conditions (obtained from prior biomechanical crank force–angle models) and constraints. Parametric design modification was necessary to meet the Design for Additive Manufacturing (DfAM) considerations for PBF to reduce build time, material usage, and post-processing labour. Static testing proved performance close to current market leaders with the PBF manufactured crank found to be stiffer than the benchmark design (static load deflection of 7.0 ± 0.5 mm c.f. 7.67 mm for a Shimano crank at a competitive mass (155 g vs. 175 g). Dynamic mechanical performance proved inadequate, with failure at 2495 ± 125 cycles; the failure mechanism was consistent in both its form and location. This research is valuable and novel as it demonstrates a complete workflow from design, manufacture, post-treatment, and validation of a highly loaded PBF manufactured consumer component, offering practitioners a validated approach to the application of PBF for components with application outside of the accepted sectors (aerospace, biomedical, autosports, space, and power generation).

1. Introduction

A high-performance bicycle crank is considered to be one that would be installed on a racing bicycle, the elite of which are operated by professional cycling teams such as those competing in the Tour de France. There has been a considerable effort in developing an understanding of the effect of crank design on the force delivered by the rider [1,2,3,4,5], although there has been very little study of innovation of the crank design itself away from the norm [2]. This is likely in part due to lack of innovation in crank manufacturing methods. The vast majority of common crank designs are effectively box section in their form and are either machined from aluminium in halves then bonded together, or manufactured using Carbon-Fibre-Reinforced Polymer (CFRP) [6] with titanium or aluminium inserts for mechanical interfaces. These methods offer limited opportunity for design innovation.

Component mass is a significant factor in the competitiveness of a racing bicycle and has been driven down to a low level, particularly with the incorporation of CFRP. With cranks, however, stiffness is also a major consideration in order to cycle more efficiently and effectively, maximising performance over both long and short distances through improved power transmission and reduced fatigue. These objectives are suited to topology optimisation (TO), a computer-aided design (CAD) technique. TO has been used previously for designing minimal weight structures [7,8,9] where low mass is critical to high component performance in the end-use application (e.g., in saving fuel [7,9], increasing stability, and decreasing cost [8]). The effectiveness of TO techniques are often limited by conventional manufacturing techniques due to the complex natural form of the resulting geometry, making the optimal design un-manufacturable.

Additive Manufacturing (AM) introduces an opportunity whereby this theoretically idealised geometry can be manufactured with a greater degree of economic sensibility. TO for AM has therefore become an active research area, utilizing the approach for a number of component performance objectives, such as heat transfer efficiency [10], stiffness [11], and mass [12]. A design produced using this combination of techniques could therefore exhibit maximum stiffness at a minimum mass, achieving ultimate product performance.

The build quality of the complex geometry produced by AM, and the results of functional testing, can both be verified by using Computed Tomography (CT) scanning [13], comparing a CT-generated model with the original CAD data. A similar design investigation has been completed in the high-performance automotive sector, successfully improving the performance of engine valves by designing for AM [14].

Application of this approach to the design and manufacture of an elite bicycle crank to obtain a combination of low mass and high stiffness has not previously been seen. This research paper demonstrates a complete workflow from design, manufacture, post-treatment, and validation of a highly loaded, spiderless, non-drive-side (NDS) crank, offering practitioners a validated approach to the application of Powder Bed Fusion (PBF) to highly loaded components.

2. Methodology

The method developed and followed for the design, manufacture, and testing of a high-performance crank is given in Figure 1.

The optimised design was benchmarked against leading metallic cranks: Hollowtech II [15] and Hollowgram SiSL2 [16], as they offer a similar cost–performance balance.

2.1. Design

Crank design began from first principles, optimising for AM whilst maximising stiffness and minimising mass. Ergonomics was considered throughout, with regards to both performance efficiency and comfort.

2.1.1. Design Variables

Design variable selection was made based on a common usage and a worst-case scenario. The lower end crank boss was designed to fit a 113 mm square taper cartridge Bottom Bracket (BB), BS 6102-14 (ISO 6696), with 68 mm frame shell width, BS 6102-9 (ISO 6696). A top boss was designed for attachment of the pedal spindle (a 9/16’’X 20 TPI British Standard Cycling Thread). The ‘crank length’, the distance between the pedal centre spindle hole and BB taper, was set as 175 mm. The distance between the outboard face of each crank was set to 147 mm (standard for road products).

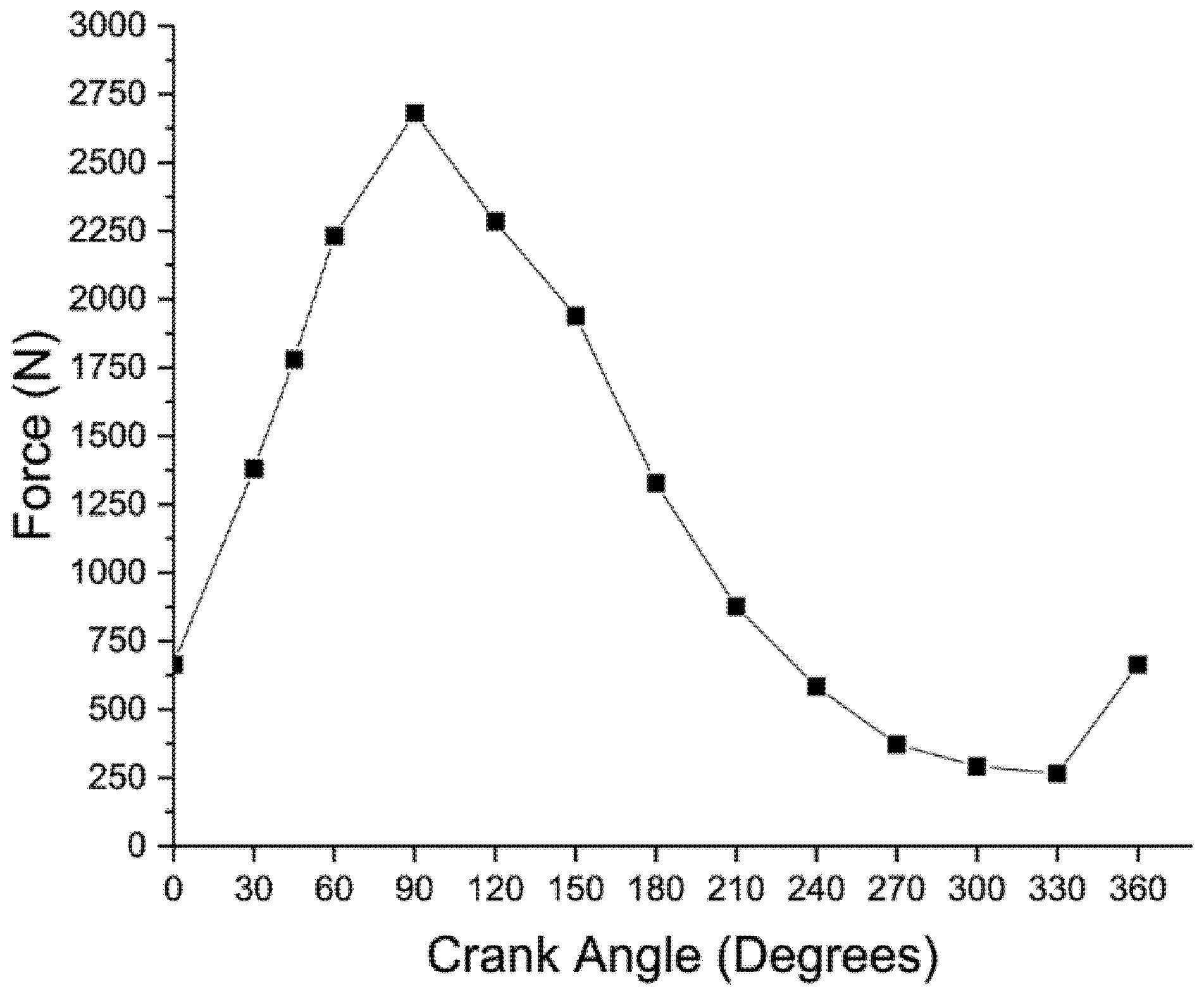
2.1.2. Boundary Conditions

Both optimisation and Finite Element Analysis (FEA) require accurate input boundary conditions. Crank assemblies must pass a 100,000-cycle fatigue test, alternating loading of each crank (set at 45°) with 1800 N applied 65 mm from its pedal-side face (BS EN ISO 4210-8).

Many studies have developed models to relate crank power to the crank angle. Kautz & Hull [17] defined crank force to be muscular and non-muscular (gravitational or inertial). Bertuccia et al. [18] used horizontal and vertical components of these forces at 70 rpm to produce a force vector profile for realistic loading. The author has scaled this force vector profile to provide the desired 1800 N at 45° to comply with the BS EN ISO 4210 testing conditions. The forces obtained for various crank angles from the resulting force vector profile (Figure 2) agree with those found in numerous studies: maximum load crank angle [19], hip and knee angles of 38°–50° and 73°–145° [20].

The calculated loads from Figure 2 were applied 65 mm from the outboard crank face. An RBE3 (Rigid Body Element) connected this point to the inside face of the pedal spindle hole. This RBE represents the pedal spindle, transferring applied load to a singular external grid to the hole’s face. Loads at 30° crank angle intervals were applied to ensure realistic loading and acceptable processing time. Lateral loads were not considered, as with a correctly adjusted Q-Factor, these would be zero.

All degrees of freedom were constrained by a Single-Point Constraint (SPC) at the centre of the square taper void. Each tapered face was connected to this with an infinitely stiff RBE2 element. This infinitely stiff RBE simulates the connection to a BB axle which cannot undergo translational or rotational displacement. While in reality, rotation is allowed about one axis, this produces an unsolvable model for optimisation and this configuration may thus produce an overly stiff result.

2.1.3. Material Selection

A high specific stiffness and specific strength is required for high performance at low mass. Therefore density, Young’s Modulus, and Yield Strength were identified as key factors. Based on these requirements, Titanium Ti64 and Maraging Steel MS1 are the most favourable options [21] (EOS 1), as shown by the mechanical properties in

Table 1. EOS Material Properties [22,23].

Parameter	EOS Ti64	EOS MS1
Density (g/cm3)	4.41	8.05
Young’s Mod. (GPa)	115 ± 10	180 ± 20
Yield Strength (MPa)	860 ± 20	1990 ± 100

.

2.1.4. Optimisation

Topology optimisation was selected as it provides a conceptual geometry for design development. In this case, the design objective was to produce maximum stiffness at minimum mass.

The size of the design space (Figure 3) was limited by physical realities during cycling. Firstly, the limb of the cyclist prevents any protrusions on the pedal-side of the crank so the design space was trimmed in accordance with the Q-Factor and an approximate foot width. The opposite side was made parallel to a hypothetical chain stay to prevent contact with the frame.

HyperMesh 13.0 (Altair Engineering, Bristol, UK) was used to preprocess and mesh the geometry created in CAD. Genesis Design Studio 14.0 (GRM Consulting, Leamington Spa, UK) was used to perform the geometry optimisation. The Boundary Conditions (Section 2.1.2) were inputs into the model. The mechanical properties of Ti64 were used as the material of choice. Elements of the model were separated into Design Space (DES) (optimised) and Fixed Geometry (FIX) (non-optimised), given as red and blue, respectively. The model configuration can be seen in Figure 4.

Since AM enables freeform manufacture, no manufacturing constraints were imposed. The design objective was set to minimise strain energy (maximising stiffness). Mass was also defined as a design objective, the ‘weighting’ of which was increased with progressive iterations.

A relatively coarse initial mesh was used to increase optimisation efficiency. Once reasonable results were obtained, the mesh was refined, increasing the number of tetrahedral elements 10-fold to 504,495 (average element size of 1.09 mm²), increasing the accuracy of the resulting isosurfaces (the surface form of the topology optimisation). Use of tetrahedral elements allowed for more effective packing of the complex solid body. This made an increased mesh resolution possible, which both increases accuracy of results and produces a more precise resulting surface for improved interpretation during CAD modelling.

2.1.5. Geometry Creation and Computer-Aided Design

The isosurfaces were exported from Design Studio as an STL file and imported into SolidWorks 2015 (Dassault Systèmes, Vélizy-Villacoublay, France) and directly traced over to produce a practical crank model.

Consideration of AM build direction influenced the development of the design. A vertical build direction starting from the BB boss was selected based on the geometry to reduce the likelihood of manufacturing defects as well as maximise yield.

2.1.6. Design Evaluation

FEA was performed in SolidWorks Simulation 2015 (Dassault Systèmes, Vélizy-Villacoublay, France) for each load case; two methods were predominantly used as they would be ultimately replicated by physical testing. The constitutive model for the FEA performed in the SolidWorks static study was a nonlinear elastic model, for both the performance benchmarking and fatigue analysis.

The first test was conducted to provide benchmarking information. Benchmark data for the Hollowtech II and Hollowgram SiSL2 [24] was used, collected by setting the crank at 90°, applying 890 N (225 N preload and 667.5 N main load) 60 mm from the outboard face. This method was repeated 3 times per crank and the average deflection (due to main load) published.

Secondly, the BS EN ISO 4210-8 fatigue test parameters described in Section 2.1.2 were replicated in a static scenario in order to analyse the response of the part under loading.

2.2. Manufacture

2.2.1. Model Preprocessing

To improve the stability of the build, a solid block base was added to the bottom of the part. The CAD model was exported as an STL file and imported into Magics v19.0 (Materialise Ltd., Sheffield, UK) and support material was generated for the pedal spindle hole as well as the square taper (Figure 5, support material in red). The solid bar was included for calibration of the wire EDM machine for accurate part removal from the build plate.

2.2.2. Additive Manufacturing

Parts were manufactured on an M280 (EOS GmbH, Eschweiler, Germany) in 60 μm layers using standard parameters “Ti64_060_110 Speed” and HSS steel recoater blade. Powder was sieved using the EOS IPCM-M equipment to < 63 μm from a single batch of Ti64 (EOS GmbH, Eschweiler, Germany). The finished build prior to its removal from the machine can be seen in Figure 6.

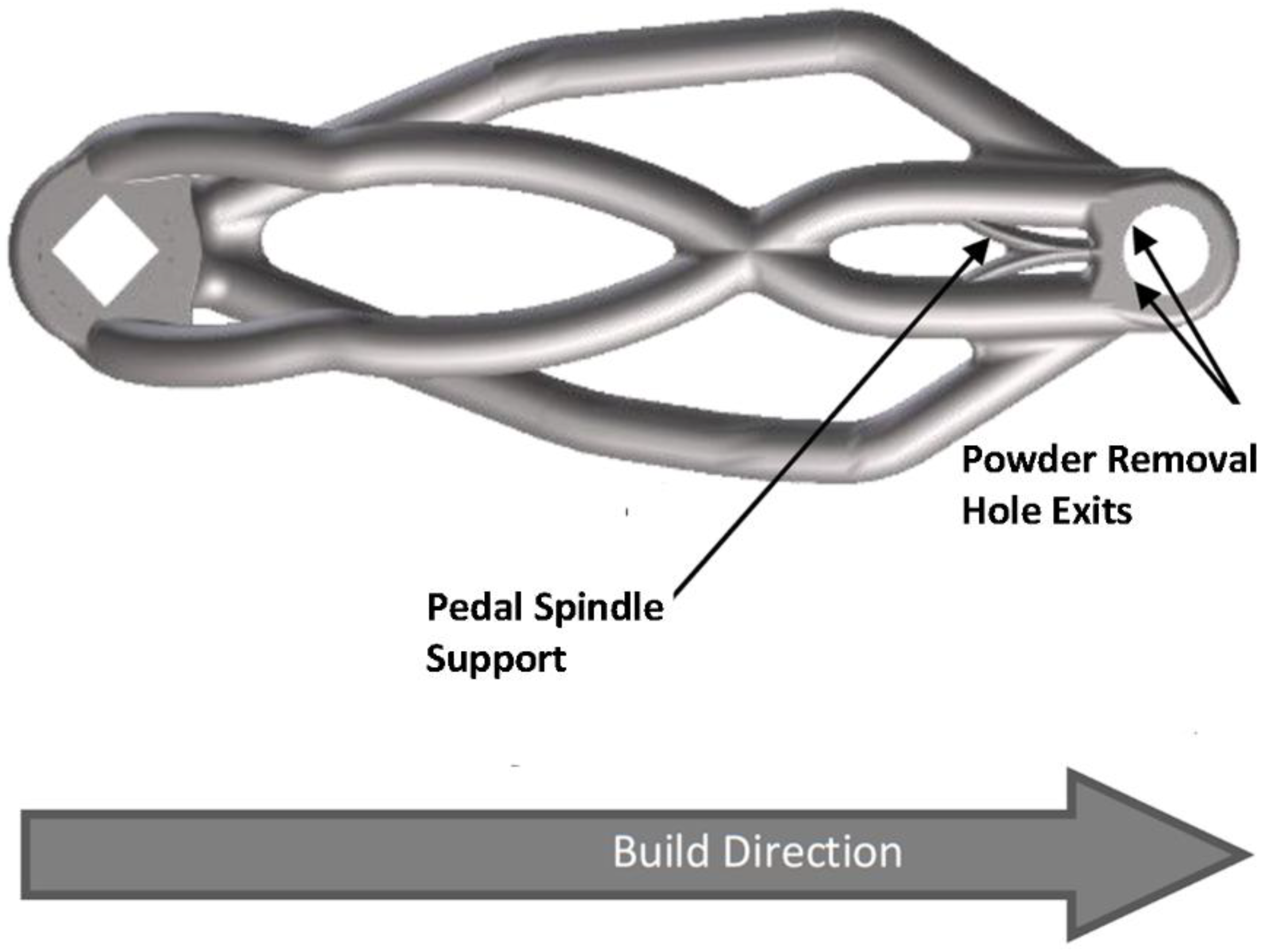
2.2.3. Powder Removal

Once out of the machine, a hydraulic line was attached securely to the build platform to deliver short pulses which produced a vibration in the plate and thus the parts, improving the effectiveness of material removal. The plate was manipulated by hand to ensure that all loose powder had been evacuated.

2.2.4. Post-treatment

The parts were heat treated (Tamworth Heat Treatment Ltd., Tamworth, UK) at 800 °C for 4 h in a vacuum [22] to reduce anisotropy [25]. Heat treatment also reduces yield strength, increases elastic modulus, and most importantly, improves fatigue properties.

The components wire EDM were removed from the build platform and the square taper cut into the BB boss (Exetek V500G) (Excetek Technologies Ltd., Shengang, Taiwan). The pedal spindle boss was tapped using an ISO M12 tap. As this was a worst-case scenario design, no surface finishing processes were carried out as this would improve the fatigue characteristics of the components [26].

2.3. Validation

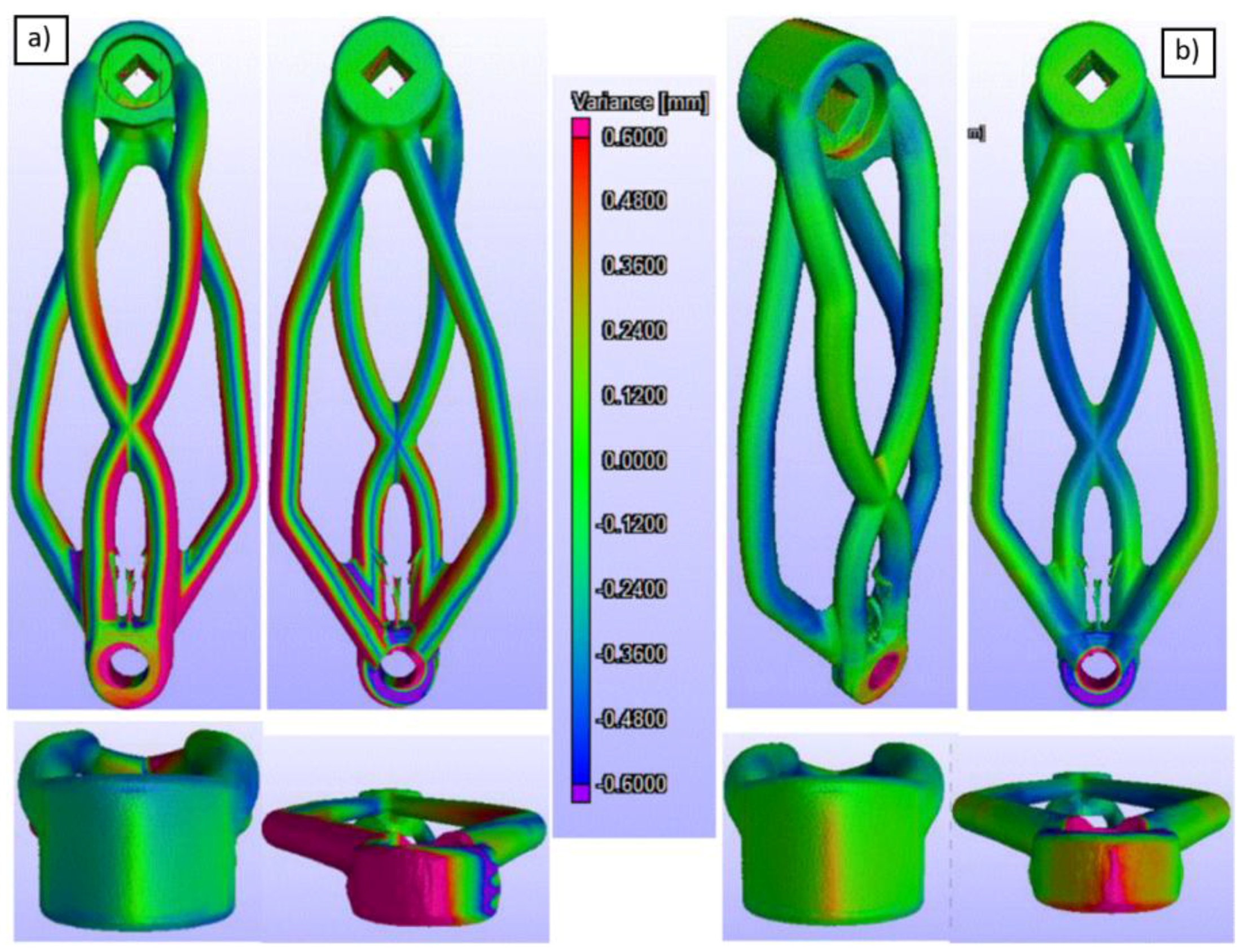
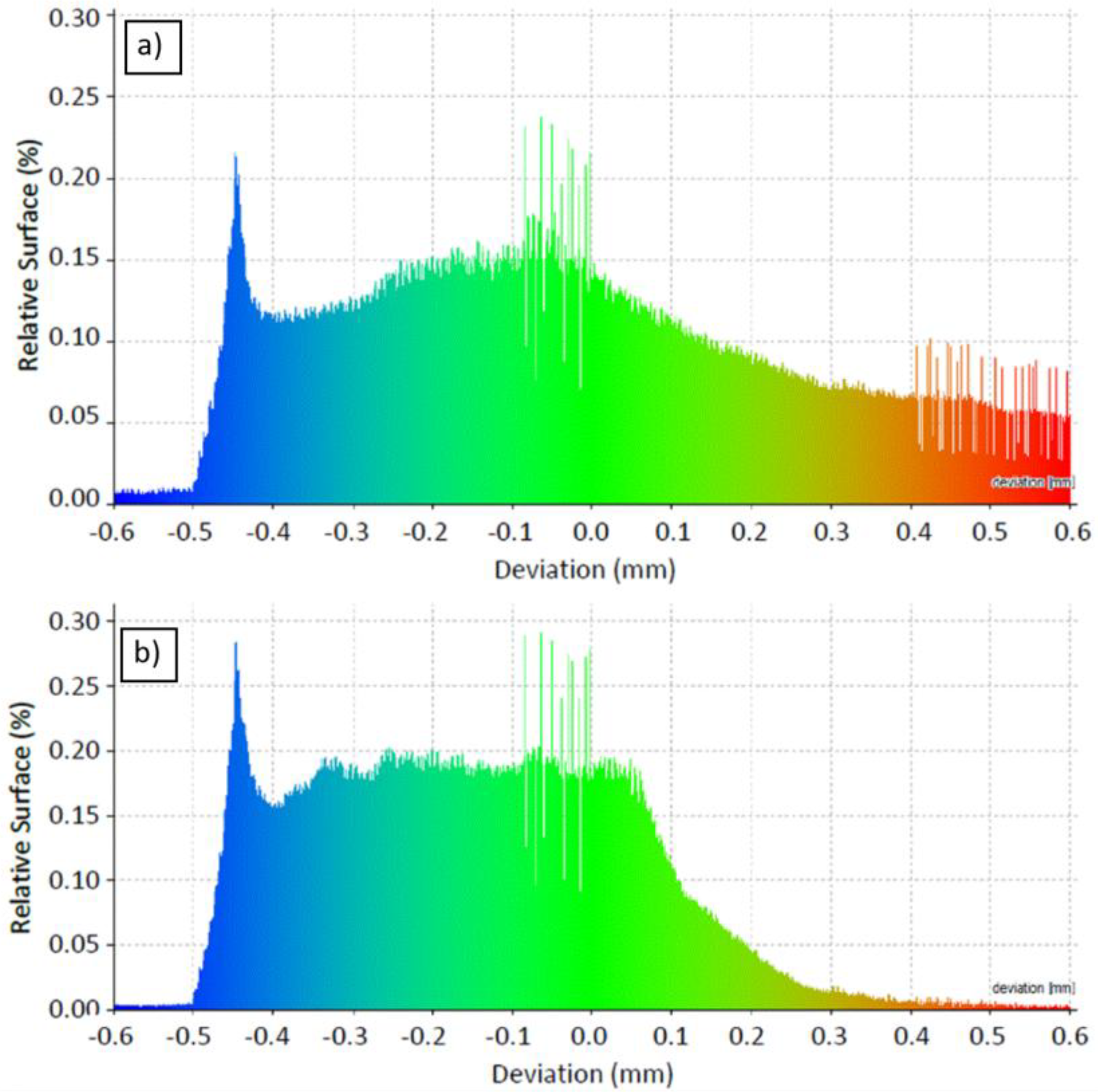
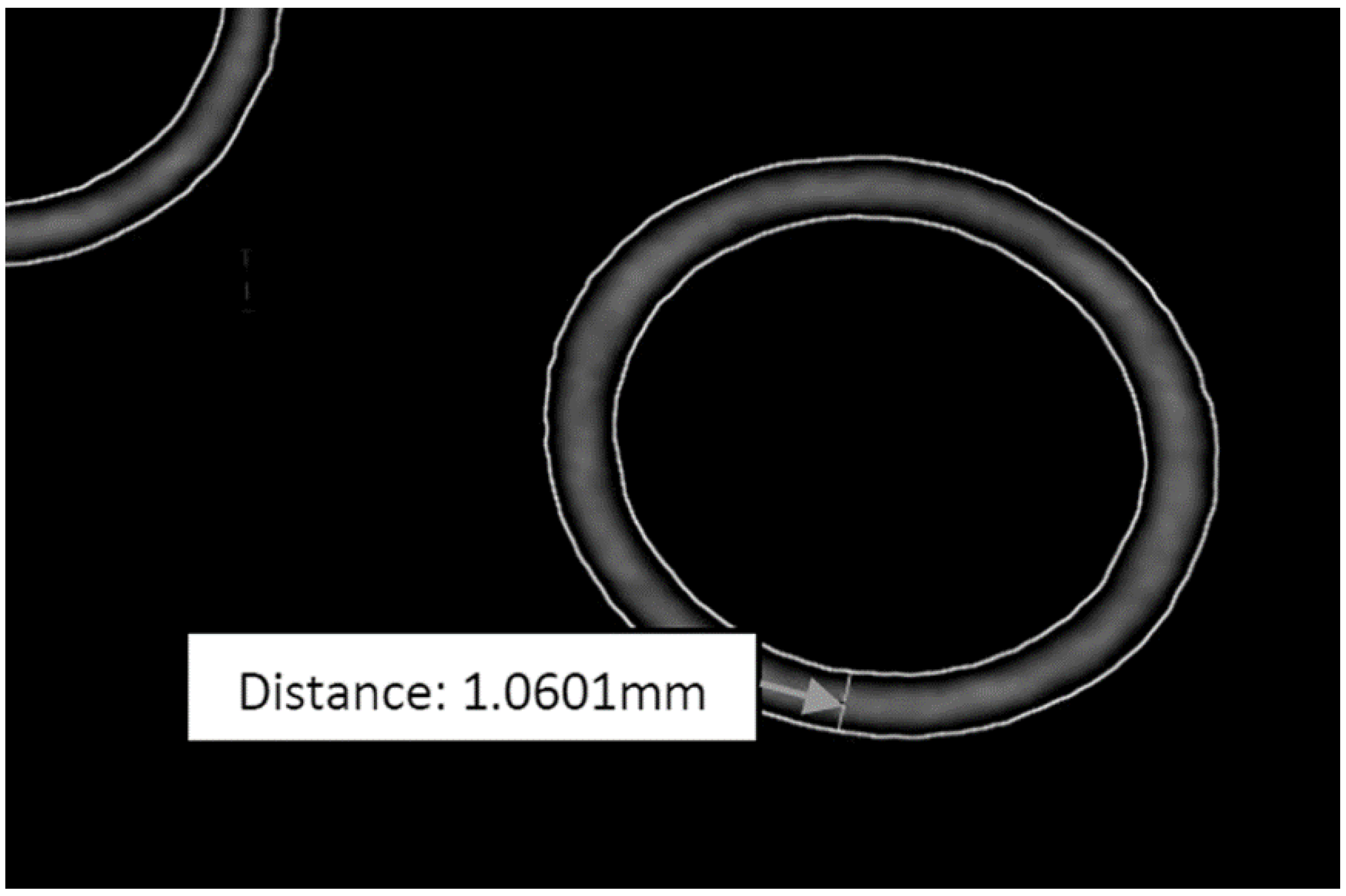
2.3.1. Post-manufacture Inspection

CT scanning of the part removed from the build plate was completed using an X-Metris TEK XTH 320 LC (Nikon Metrology, Derby, UK). The exposure was set to 300 kV or 40 W for a time of 4 s, a magnification of 1.8× and a gain of 24 dB and a 2 mm Sn filter. The CT scan (3145 projections over 20 h) used a voxel size of 111.11 μm and unsharpness size of 114.05 μm.

The digital 3D model ‘actual model’ from the scan was compared to the CAD ‘nominal model’. The actual and nominal models were aligned using the datum method. The flat faces of the BB boss were used as a datum as they were the most stable during the build and had best flatness, parallelism and dimensional accuracy. A secondary “best fit” method was also used, where an algorithm fitted the models together by identifying the greatest number of common surface points.

2.3.2. Functional Validation

Physical testing was conducted to BS EN ISO 4210 by Bureau Veritas UK Ltd., Manchester, UK, using a hydraulic rig to test.

Static Loading

This test was conducted to benchmark against the Fairwheel Bikes data [24] with the crank set at 90°, 890 N was applied at 65 mm (5 mm further out than the simulation) from the outboard face (Figure 7). A fixed identical crank was placed on the opposite end of the axle to prevent rotation. The magnitude of deflection was manually measured with a steel rule on the crank itself at the pedal spindle boss.

Fatigue

The crank (set at 45°) was loaded with 1800 N 65 mm from its outboard face (Figure 8) at 0.5 Hz (1 s force on; 1 s force off). A solid commercial crank was used to prevent rotation. Two samples from the same PBF build were tested.

3. Results and Discussion

3.1. Material Selection

Both Ti64 and MS1 exhibit excellent specific properties, however, while the exceedingly high strength of Maraging Steel MS1 may enable a lower mass to be used for a similar performance, its reduced ductility may degrade the fatigue capability of the component. Therefore, Ti64 was selected as the material of choice.

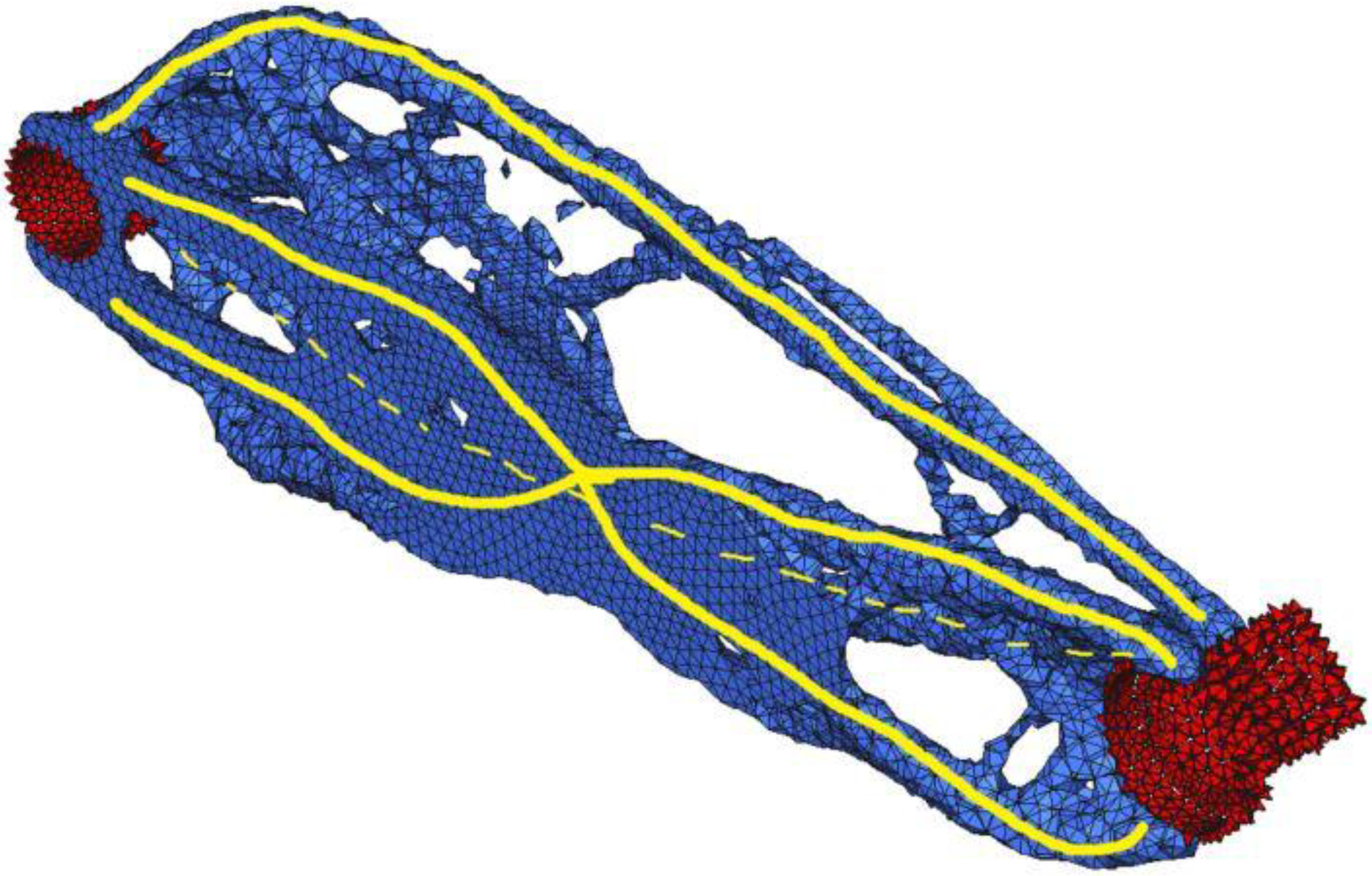
3.2. Optimisation

The topology optimisation isosurface results produced are given in Figure 9. Theoretically, this is the ideal design of a solid crank with increasing levels of weight reduction. The complex geometry shown suggests that ALM would be the favoured, if not the only possible method of manufacture for producing this design.

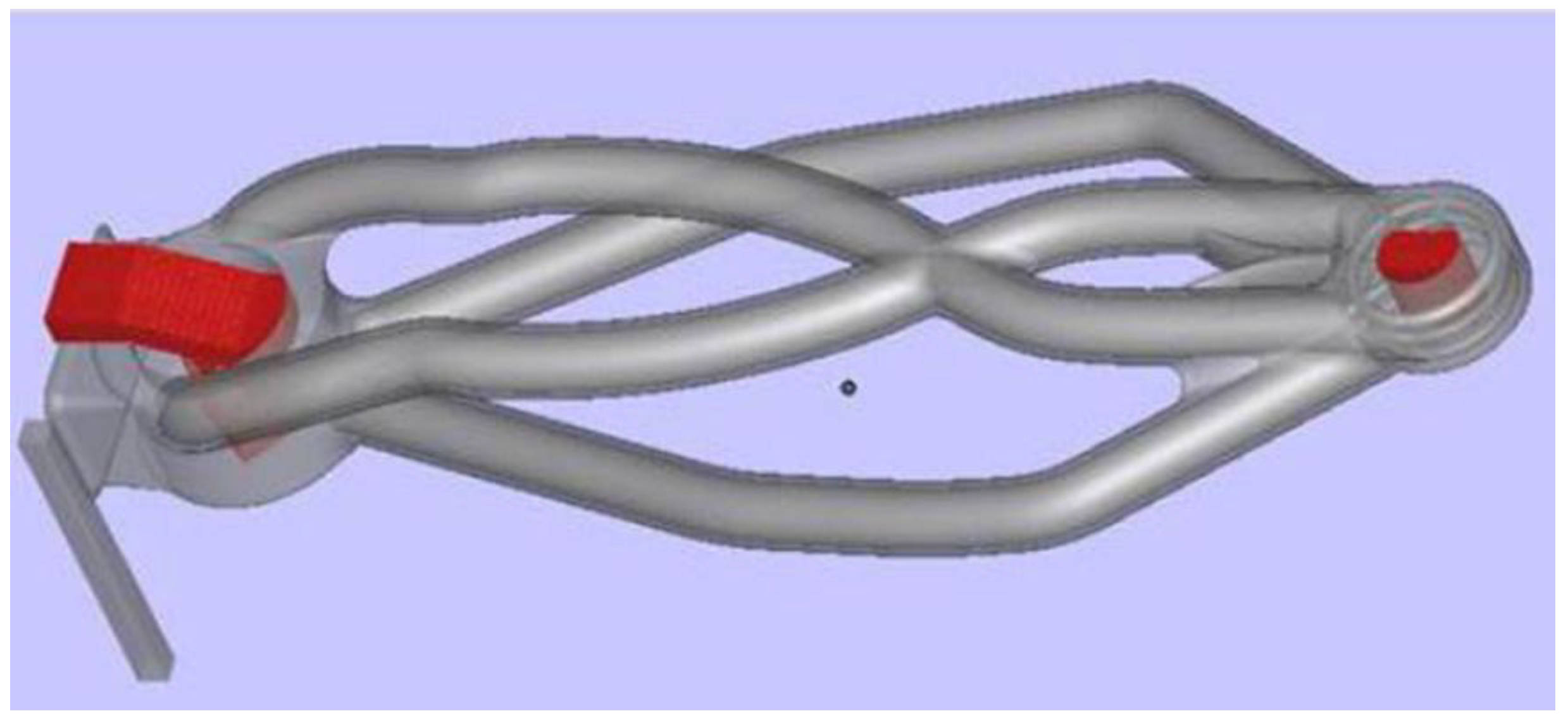
3.3. Geometry Creation & Computer-Aided Design

It is clear from Figure 9 that the results from the optimisation could not simply be printed. “Design interpretation” is a key stage of this process; using some of the optimisation results directly may implement too high a level of mass reduction which may not perform functionally. In order to account for this, common features present in all results were identified. These could then be traced in CAD, at which stage each feature could be easily modified using FEA guidance to reach the optimal level of mass reduction. These common features included the 4 primary “limbs” as well as the “auxiliary spars” stemming from these (highlighted yellow and pink, respectively, in Figure 10).

The design interpretation produces beam-like structures which can fail through fracture or deflection, determined by their strength and stiffness, respectively. In pure bending, the value for second moment of area (I) is key, where a greater I decreases stress and deflection. Torsion, however, is dependent upon the polar second moment of area (J), where a greater J reduces shear stress and twist. J should be maximised for strength and stiffness [27]. Application of this theory identified three design variables:

• Tube Diameter ‘D’: Increased D results in increased J and M
• Wall Thickness ‘WT’: Increased WT results in reduced J and increased M
• Auxiliary Tubing: Addition as per topology results

D = tube diameter, J = polar second moment of area, M = tube mass, WT = tube wall thickness.

As this was a feasibility assessment with regards to building the component, a “worst-case” of these variables was used.

Design for Additive Manufacturing

The current design is produced entirely through focusing on performance; modifications have to be made with regards to Design for Additive Manufacture (DfAM) (Figure 11). Due to its complex geometry, support material would likely be removed by hand and thus be time-consuming and uneconomical. Therefore, all proceeding design work aimed to require no further support material for manufacture (now only required at the pedal spindle, BB taper, and base), reducing waste material, cost, and build time.

A feature was added to support the bottom of the pedal spindle boss (Figure 11). To enable powder removal from inside the part, holes were routed through the component.

The model was heavily filleted both internally and externally to ease stress concentrations and reduce the risk of manufacturing defects. The fillet radius was dependent upon the geometry of the feature, and external radii were matched by corresponding internal fillets to achieve uniform wall thickness throughout.

3.4. Design Evaluation

Inconsistencies between the Fairwheel test method [24] and the simulation exist. Fairwheel used a 222.5 N preload before increasing to 890 N, reporting deflection between these two values. The simulated deflection, however, included preload deflection. The simulation used fixed constraints on the square taper faces, whereas in the actual test this was connected to a BB and therefore torsion and bending of this component were not accounted for in the simulated results, whilst approximately 70% of total deflection measured at the pedal came from axle twist [28]. Finally, the Fairwheel test deflection was measured with force applied to the pedal spindle, thus including deformation of the pedal spindle in its measurement. The results are shown in Figure 12a, with a resultant displacement of 2.258 mm.

The fatigue test was replicated identically in SolidWorks as per BS EN ISO 4210. While this also used fixed constraints on the square taper faces, this would only increase the stress levels and therefore produce a worst-case. Accounting for this, no regions of the results (see Figure 12b) were significantly beyond the yield stress value.

3.5. Powder Removal

As this process was performed manually, it was difficult to ensure that all powder was completely removed from the internals of the component. Examination of the CT scanned layers showed no signs of powder remaining within the structure, confirming that powder removal routes were satisfactory.

3.6. Post-manufacture Inspection

The datum method showed significant differences at the top of the part. The best fit method, however, produced lower levels of variation (Figure 13). The variance distribution % for both methods is given in Figure 14, where the datum method results in a significant % exceeding 0.5 mm deviation, whereas the best fit does not significantly exceed 0.3 mm.

The maximum geometry variance of under 1 mm is deemed insignificant with regards to its application, and therefore build quality is acceptable. The majority of the deviation is most likely caused by recoater blade contact during the PBF powder layering process as opposed to the effect of residual stresses.

Scans of the internal geometry confirmed that the wall thickness produced is identical to the desired value (Figure 15). Modelling of the pedal spindle support was affected by CT noise reduction algorithms and threshold selection and, due to its smaller wall thickness, geometry comparison of this feature was limited.

3.7. Functional Validation

3.7.1. Static Loading

Under the Fairwheel Bikes method, the crank deflection was 14.0 ± 0.5 mm. As an identical crank was used to prevent rotation on the opposite side, it can be assumed that this deformed equally, therefore producing a deflection of 7.0 ± 0.5 mm per crank. Twisting of the part could not be accounted for. Lateral displacement occurred at the red patches during simulation seen on the rear main tubes in Figure 5, suggesting twisting of the crank under load, and therefore this effect was not insignificant but was not being recorded in its own right.

The simulation of this method produced a deflection of just 2.258 mm (c.f. 7.0 ± 0.5 mm). It is likely that much of this deviation was due to the simulation not measuring torsion of the BB. This is reinforced by claims that roughly 70% of deflection was due to BB torsion [29], with the simulated value of 2.258 mm being 32% of the measured value.

A comparison of this design with the benchmark cranks is given in

Table 2. Benchmarked Results.

Parameter	Shimano	Cannondale	AM
Mass (g)	175	125	155
Deflection (mm)	7.67 *	6.91 *	7.0 ± 0.5

* 50–200 lb distance only [24].

and indicates that this worst-case design for the AM crank is stiffer than current market leading designs, and at a competitive weight.

3.7.2. Fatigue

Both of the tests completed failed catastrophically, through identical mechanisms, after similar durations (2370 and 2620 cycles) (Figure 16). During the design phase, yield stress (860 MPa) had been used as the mechanical limit, whereas the actual capability of a part under fatigue is lower than this. Rekedal [30] investigated high cycle fatigue life of Ti64 using identical build and heat treatment parameters to those here. The Rekedal study suggests that peak stress below 250 MPa would be required to achieve 100,000 cycles. Edwards and Ramulu [25] found that we would expect failure earlier than when it physically occurred.

The fatigue configuration was simulated in a static test (Figure 12b). At the centre section where critical failure occurred, a higher stress can be seen (green). Combining this with the components post-fatigue (Figure 16), it is likely that the fracture initiated at this location and propagated across the part under cyclic loading. The other noncritical area of damage (Figure 16) is also a region of higher stress. The area located near the pedal spindle, however, where the maximum stress is identified, showed no signs of external damage, although this is an area of high material concentration and therefore had better stress-relieving characteristics.

4. Conclusions

It is expected that the UK’s High Value Manufacturing sector can capture over £3.5 bn GVA per year for the UK of the rapidly growing global market for AM products and services by 2025 [31]. Despite the exciting potential and progress to date, many UK companies, especially within the SME community, lack the awareness, resources, or confidence to apply AM as a core and integral part of their manufacturing toolkit. Lack of design capability and the knowledge required to take full advantage of the benefits offered by AM were highlighted in this recent UK Government report [31].

The research presented in this paper provides a methodology through which a product can be fundamentally redesigned, manufactured using state of the art AM metals technology, and validated, an approach that can be adopted by industry to engage with this technology and harness the benefits. A novel aspect of this research lies in the product focus; unusually, this research is not aimed at very high value products, such as for aerospace [32] or biomedical [33] applications, but is focused on consumer market product, making the approach more tangible for industry, and in particular, for the SME sector, which accounts for 60% of the UK’s manufacturing output.

A further novelty of this research is that it describes the product realisation approach across design, manufacture, and validation, rather than exploring these as individual aspects. In developing and demonstrating this process flow, we have demonstrated the efficacy of PBF, particularly when designing specifically towards using this as a manufacturing tool. Topology optimisation was free from conventional manufacturing constraints to profit from a fully maximised design space, enabling the design of a crank that was stiffer than the benchmark design (static load deflection of 7.0 ± 0.5 mm c.f. 7.67 mm for a Shimano crank at a competitive mass (155 g vs. 175 g).

The successful use of CT scanning as a method of post-manufacture inspection proved an acceptable build quality of a tall, complex design, and that powder removal was complete such that the physical part represented the digital model. Nonlinear elastic simulation could then be used to accurately model component performance, as well as diagnose catastrophic failure of the part under fatigue. The physical testing validated both simulation studies and gives confidence that it provides an accurate representation of a component produced by AM.

The value of this research is in the demonstration of the realisation of a design through topology optimisation which is unlikely to have been produced by human invention. The computational nature of topology optimisation reduced manual analysis and an iterative design optimisation process. Its incorporation increased both the efficiency and effectiveness of the design phase significantly, whilst increasing functional performance to a degree that may have been unachievable without its inclusion. Manual design for AM was required, however, with the addition of features purely to enable a successful build. This might suggest that a limitation of topology optimisation is that it is almost too free, and that the development of design for AM considerations would be beneficial.

Furthermore, incorporation of biomechanics specific to the realistic loading conditions enabled the production of a product which has the potential to outperform more conventional designs.

The results of this research also saw physical fatigue testing which surpassed the lifetime expected for titanium components produced by PBF [25]. This might suggest that technology advancements are seeing the quality of PBF components improve and that further research into the quality and integrity of the resulting specimens may need to be maintained, where improved mechanical properties would enable the design capability to be pushed further.

Further value lies in the quality of the resulting component itself, whereby this worst-case scenario design performed within the region of existing market leader products, design development of which will likely see their performance surpassed. This further reinforces the success of this optimised process for design, manufacture, and validation of components manufactured by PBF using the techniques demonstrated here. Again, this provides industry with confidence in the PBF process for application to highly loaded components, ultimately moving towards the AM-UK National Strategy [31] goal of increasing awareness and confidence in AM as a manufacturing tool.