Propagation Characteristics of a Twisted Cosine-Gaussian Correlated Radially Polarized Beam
Abstract
:Featured Application
Abstract
1. Introduction
2. Theory
- the spectral density
- the spectral degree of coherence (DOC)
- and the degree of polarization (DOP)
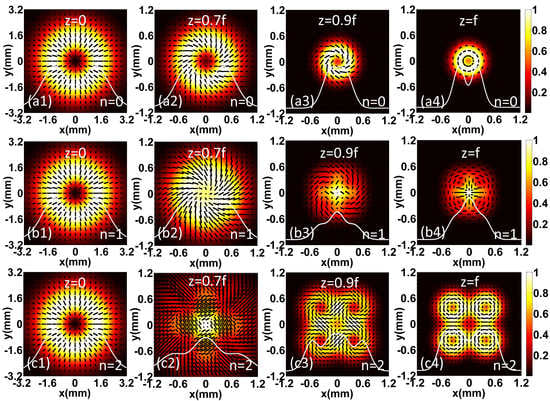
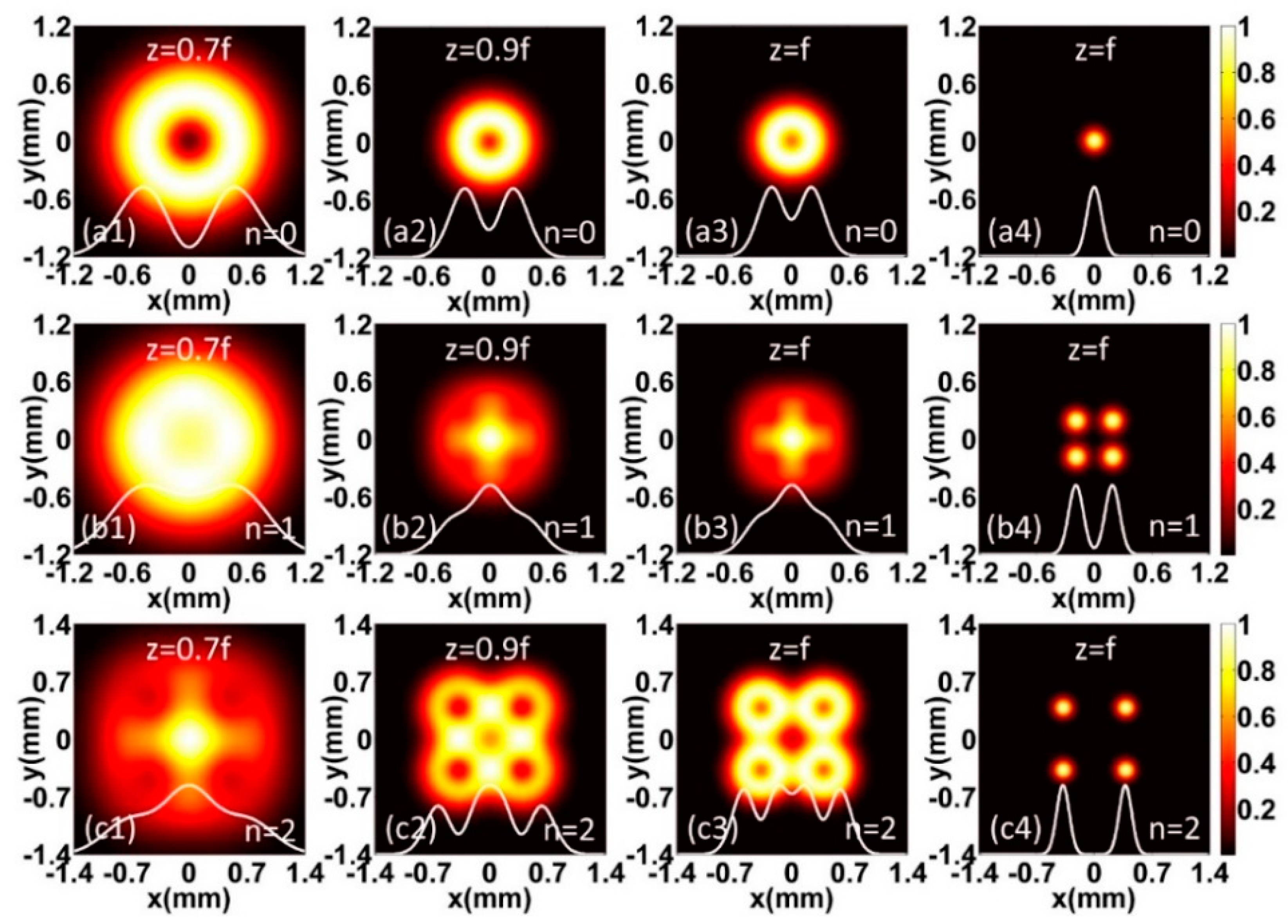
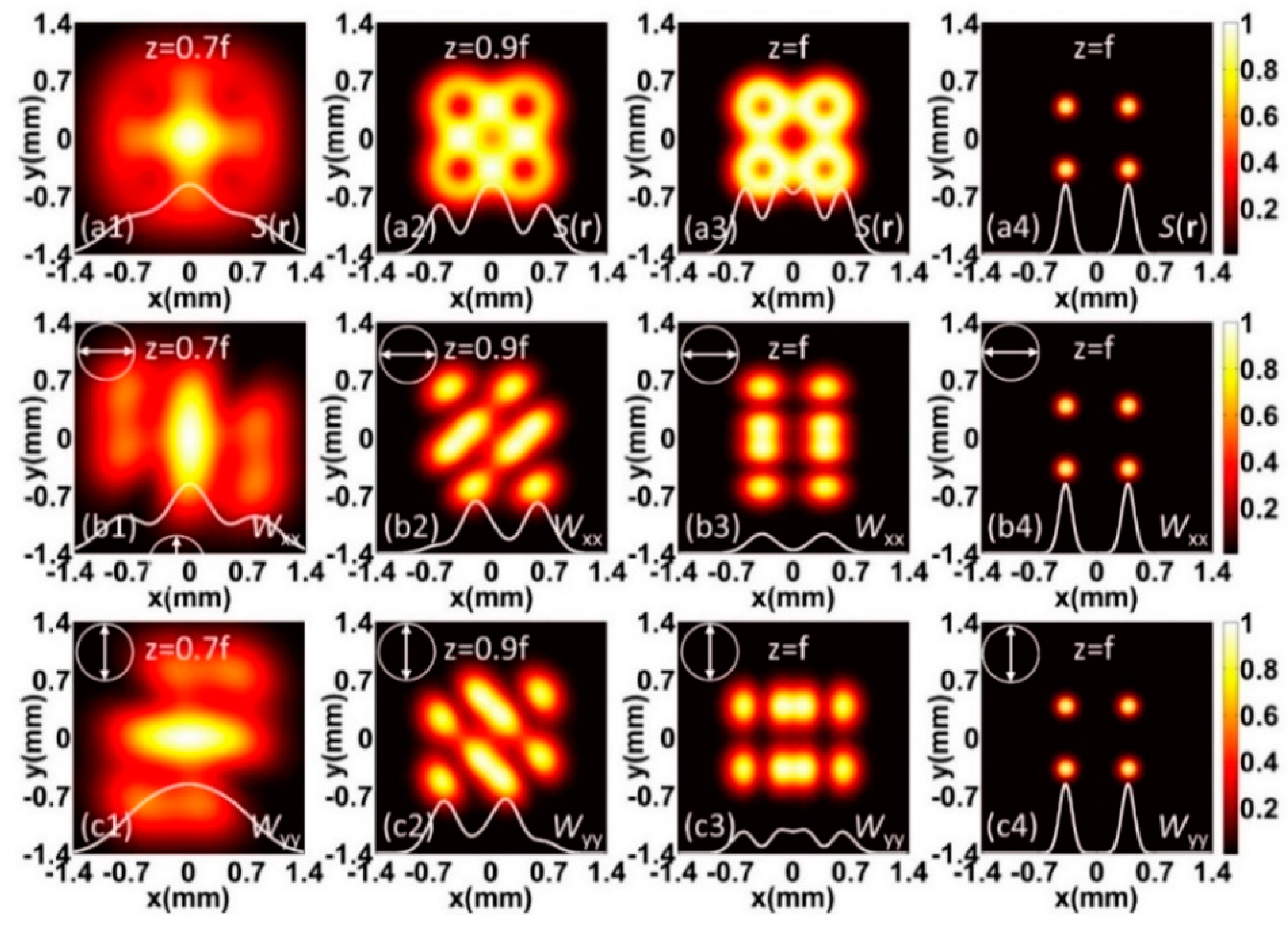
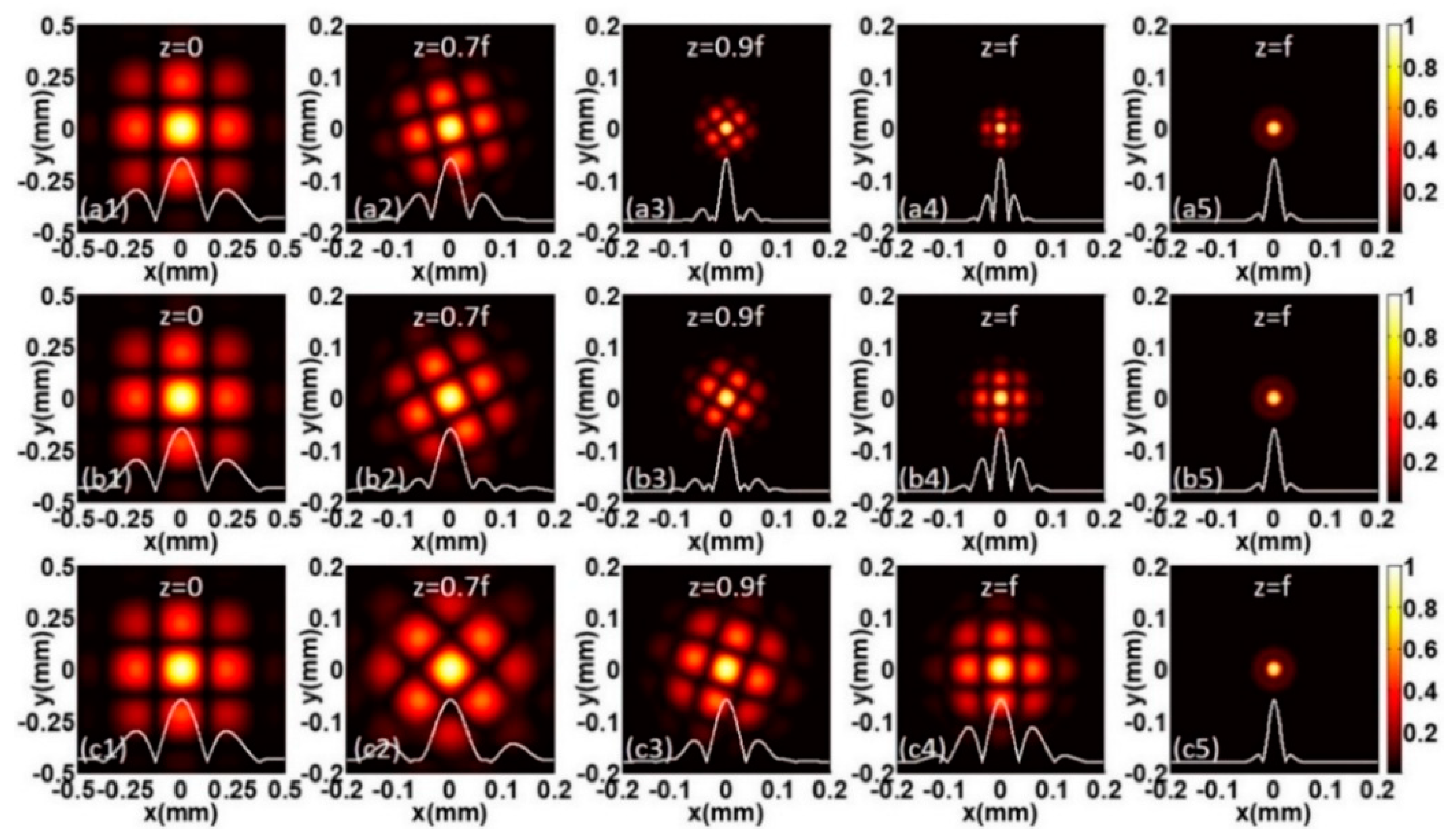
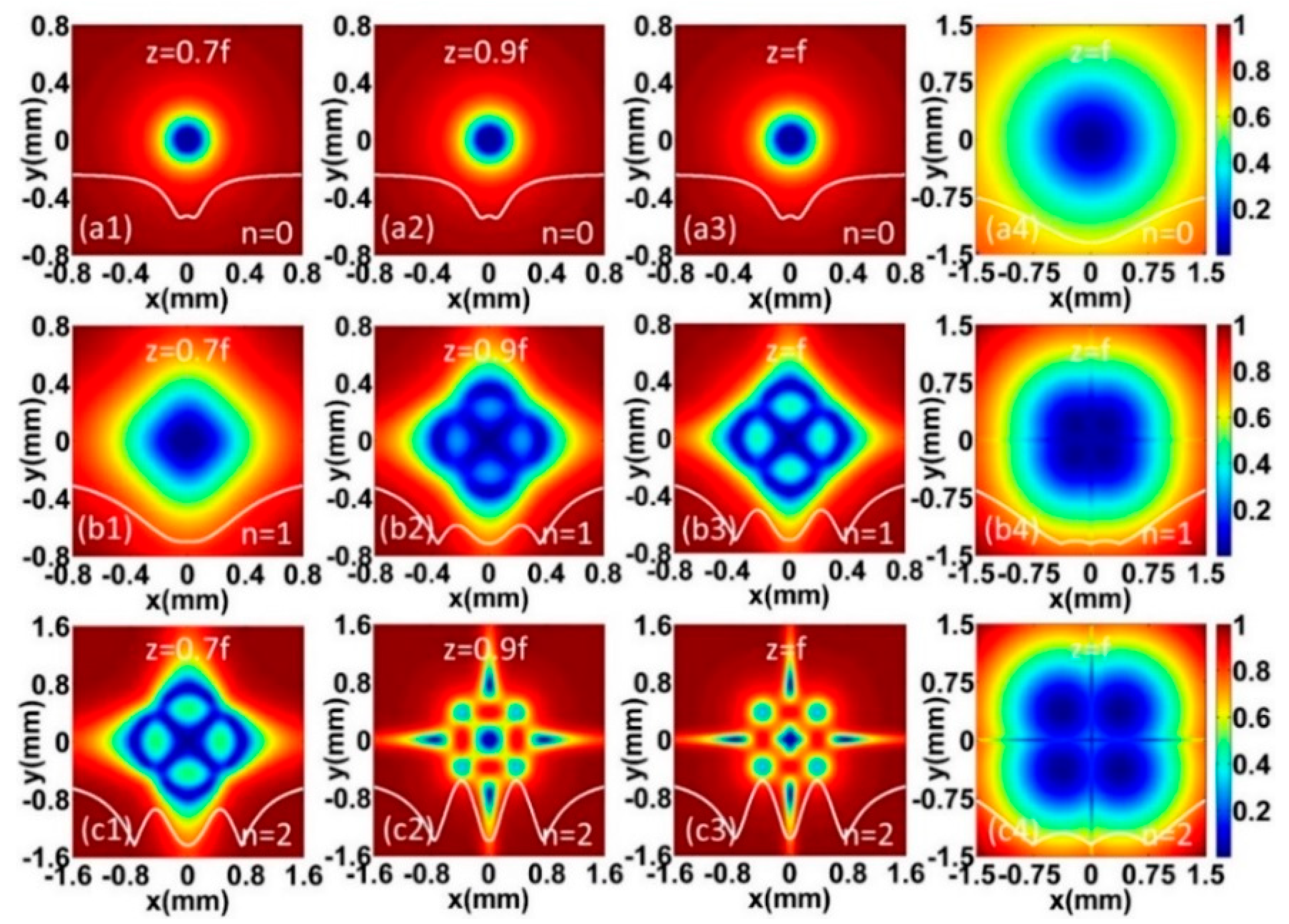
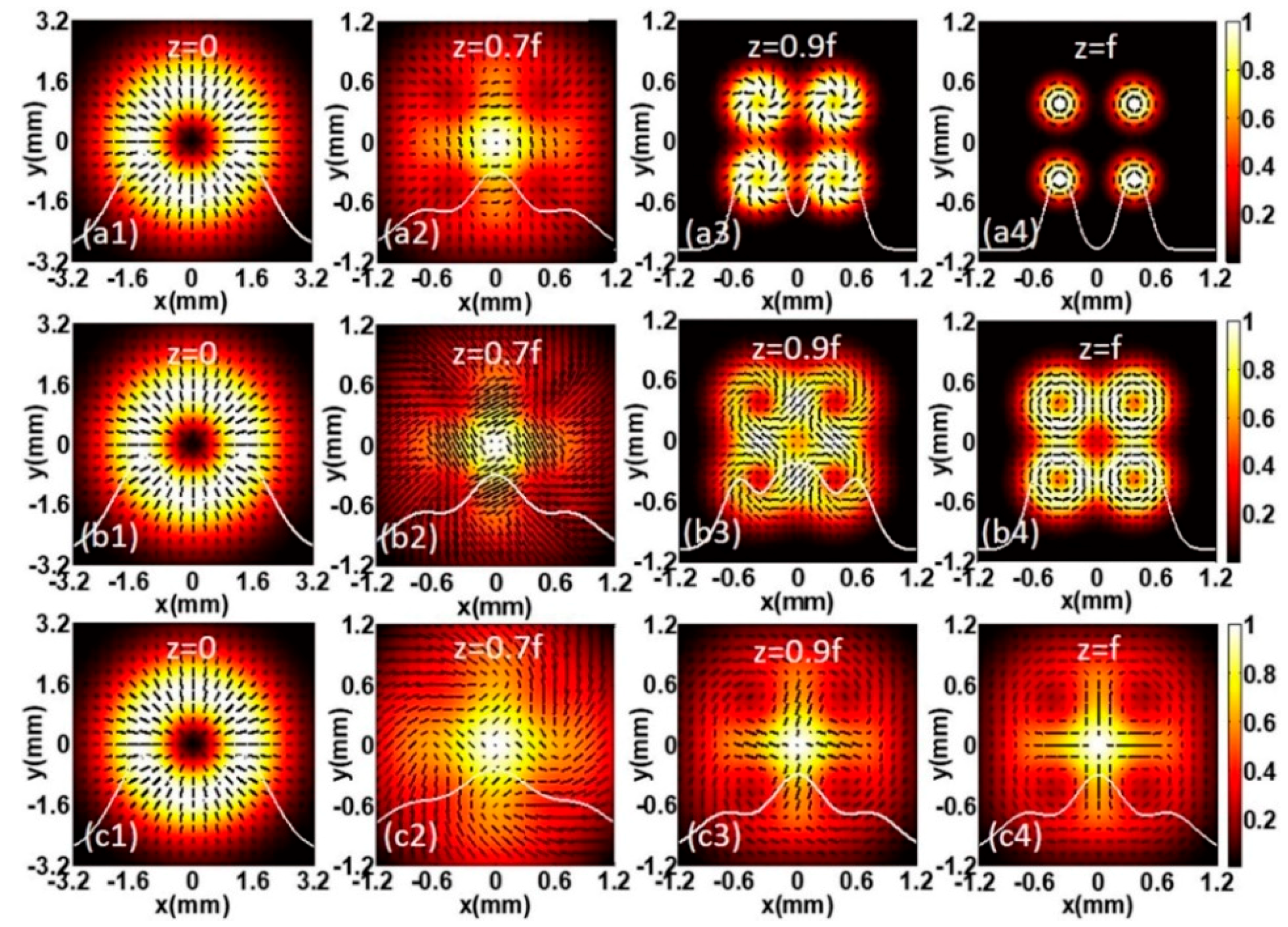
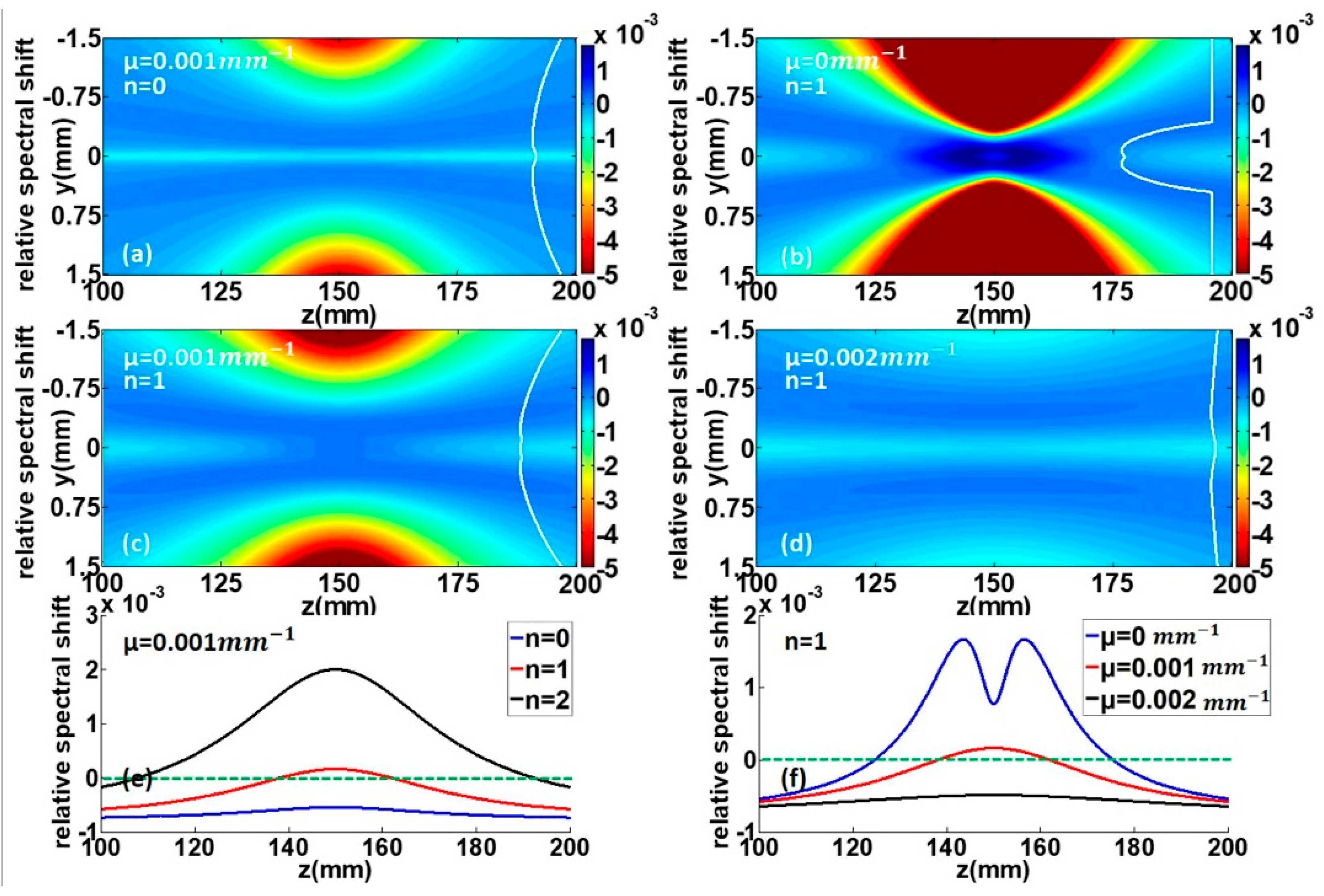
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University: Cambridge, UK, 1995. [Google Scholar]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University: Cambridge, UK, 2007. [Google Scholar]
- Martínez-Herrero, R.; Mejías, P.M.; Piquero, G. Characterization of Partially Polarized Light Fields; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Friberg, A.T.; Sudol, R.J. Propagation parameters of Gaussian Schell-model beams. Opt. Commun. 1982, 41, 383–387. [Google Scholar] [CrossRef]
- Wolf, E. Invariance of the Spectrum of Light on Propagation. Phys. Rev. Lett. 1986, 56, 1370–1372. [Google Scholar] [CrossRef] [PubMed]
- Pu, J.; Zhang, H.; Nemoto, S. Spectral shifts and spectral switches of partially coherent light passing throug an aperture. Opt. Commun. 1999, 162, 57–63. [Google Scholar] [CrossRef]
- James, D.F.V. Changes of polarization of light beams on propagation in free space. J. Opt. Soc. Am. A 1994, 11, 1641–1643. [Google Scholar] [CrossRef]
- Korotkova, O.; Wolf, E. Changes in the state of polarization of a random electromagnetic beam on propagation. Opt. Commun. 2005, 246, 35–43. [Google Scholar] [CrossRef]
- Tervo, J.; Setälä, T.; Friberg, A.T. Degree of coherence for electromagnetic fields. Opt. Express 2003, 11, 1137–1143. [Google Scholar] [CrossRef] [PubMed]
- Ellis, J.; Dogariu, A.; Ponomarenko, S.A.; Wolf, E. Correlation matrix of a completely polarized, statistically stationary electromagnetic field. Opt. Lett. 2004, 29, 1536–1538. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Sanchez, V.R.; Santarsiero, M.; Shirai, T. On genuine cross–spectral density matrices. J. Opt. A 2009, 11, 085706. [Google Scholar] [CrossRef]
- Borghi, R. Superposition scheme for J0-Correlated partially coherent sources. IEEE J. Quantum Electron. 2002, 35, 65–130. [Google Scholar]
- Ponomarenko, S.A. A class of partially coherent beams carrying optical vortices. J. Opt. Soc. Am. A 2001, 18, 150–156. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef] [PubMed]
- Sahin, S.; Korotkova, O. Light sources generating far fields with tunable flat profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.; Korotkova, O. Non-uniformly correlated light beams in uniformly correlated media. Opt. Lett. 2012, 37, 3240–3242. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.; Korotkova, O. Random sources generating ring-shaped beams. Opt. Lett. 2013, 38, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Chen, Y.; Wang, F. Generation and propagation of partially coherent beams with non-conventional correlation functions: A review. J. Opt. Soc. Am. A 2014, 31, 2083–2096. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, X.; Yuan, Y.; Cai, Y. Experimental generation of partially coherent beams with different complex degrees of coherence. Opt. Lett. 2013, 38, 1814–1816. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Gu, J.; Wang, F.; Cai, Y. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys. Rev. A 2014, 91, 013832. [Google Scholar] [CrossRef]
- Ma, L.; Ponomarenko, S.A. Optical coherence gratings and lattices. Opt. Lett. 2014, 39, 6656–6659. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Ponomarenko, S.A. Free-space propagation of optical coherence lattices and periodicity reciprocity. Opt. Express 2015, 23, 1848–1856. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.; Zhao, D.; Korotkova, O. Gaussian Schell-model arrays. Opt. Lett. 2015, 40, 5662–5665. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Chen, Y.; Wang, J.; Wang, H.; Li, Z.; Cai, Y. Generation and propagation of a vector cosine-Gaussian correlated beam with radial polarization. Opt. Express 2015, 23, 33099–33115. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Wang, J.; Liu, X.; Cai, Y.; Li, Z. Generation of arbitrary radially polarized array beams by manipulating correlation structure. Appl. Phys. Lett. 2016, 109, 161904. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Yu, J.; Cai, Y.; Ponomarenko, S.A. Propagation of optical coherence lattices in the turbulent atmosphere. Opt. Lett. 2016, 41, 4182–4185. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhu, S.; Li, Z. Vector properties of a tunable random electromagnetic beam in non-Kolmogrov turbulence. Chin. Opt. Lett. 2016, 14, 080101. [Google Scholar] [CrossRef]
- Santarsiero, M.; Martínez-Herrero, R.; Maluenda, D.; de Sande, J.C.G.; Piquero, G.; Gori, F. Partially coherent sources with circular coherence. Opt. Lett. 2017, 42, 1512–1515. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Koivurova, M.; Turunen, J.; Pan, L. Self-focusing of a partially coherent beam with circular coherence. J. Opt. Soc. Am. A 2017, 34, 1441–1447. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, J.; Huang, L.; Zhu, S.; Li, Z. Propagation of a vector cosine-Gaussian correlated beam through an active GRIN medium. IEEE Photon. J. 2017, 7908312. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Optical coherence grids and their propagation characteristics. Opt. Express 2018, 26, 2168–2180. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Zhu, X.; Mi, C.; Peng, X.; Wang, F.; Cai, Y.; Ponomarenko, S.A. High-quality partially coherent Bessel beam array generation. Opt. Lett. 2018, 43, 3188–3191. [Google Scholar] [CrossRef] [PubMed]
- Youngworth, K. S.; Brown, T.G. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef] [PubMed]
- Kozawa, Y.; Sato, S. Generation of a radially polarized laser beam by use of a conical Brewster prism. Opt. Lett. 2005, 30, 3063–3065. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Guo, Q. Analytical vectorial structure of radially polarized light beams. Opt. Lett. 2007, 32, 2711–2713. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Shi, L.; Lukyanchuk, B.; Sheppard, C.J.R.; Chong, C.T. Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nat. Photonics 2008, 2, 501–505. [Google Scholar] [CrossRef]
- Wróbel, P.; Pniewski, J.; Antosiewicz, T.J.; Szoplik, T. Focusing radially polarized light by a concentrically corrugated silver film without a hole. Phys. Rev. Lett. 2009, 102, 183902. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Abeysinghe, D.C.; Nelson, R.L.; Zhan, Q. Plasmonic lens made of multiple concentric metallic rings under radially polarized illumination. Nano Lett. 2009, 9, 4320–4325. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Korotkova, O.; Gbur, G. Scintillation of nonuniformly polarized beams in atmospheric turbulence. Opt. Lett. 2009, 34, 2261–2263. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lan, T.H.; Tien, C.H.; Gu, M. Three-dimensional orientation-unlimited polarization encryption by a single optically configured vectorial beam. Nat. Commun. 2012, 3, 998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, Y.; Feng, F.; Chen, Y.; Zhao, C.; Cai, Y. Statistical properties of a nonparaxial cylindrical vector partially coherent field in free space. Opt. Express 2012, 20, 15908–15927. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Wang, F.; Cai, Y. Coherence and polarization properties of a radially polarized beam with variable spatial coherence. Opt. Express 2012, 20, 28301–28318. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Dong, Y.; Wang, F.; Cai, Y. Statistical properties of a cylindrical vector partially coherent beam in turbulent atmosphere. Appl. Phys. B 2013, 112, 247–259. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Dong, Y.; Korotkova, O. Experimental generation of a radially polarized beam with controllable spatial coherence. Appl. Phys. Lett. 2012, 100, 051108. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, X.; Liu, L.; Wang, F.; Cai, Y. Theoretical and experimental studies of the spectral changes of a polychromatic partially coherent radially polarized beam. Opt. Express 2013, 21, 27682–27696. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Wang, F.; Chen, Y.; Li, Z.; Cai, Y. Statistical properties in Young’s interference pattern formed with a radially polarized beam with controllable spatial coherence. Opt. Express 2014, 22, 28697–28710. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Herrero, R.; Prado, F. Polarization evolution of radially polarized partially coherent vortex fields: role of Gouy phase of Laguerre–Gauss beams. Opt. Express 2015, 23, 5043–5051. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, X.; Liu, L.; Yuan, Y.; Cai, Y. Experimental study of the scintillation index of a radially polarized beam with controllable spatial coherence. Appl. Phys. Lett. 2013, 103, 091102. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, S.; Wang, H.; Cai, Y.; Li, Z. Second-order statistics of a radially polarized cosine-Gaussian correlated Schell-model beam in anisotropic turbulence. Opt. Express 2016, 24, 11626–11639. [Google Scholar] [CrossRef] [PubMed]
- Simon, R.; Mukunda, N. Twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1993, 10, 95–109. [Google Scholar] [CrossRef]
- Friberg, A.T.; Tervonen, E.; Turunen, J. Interpretation and experimental demonstration of twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1994, 11, 1818–1826. [Google Scholar] [CrossRef]
- Borghi, R.; Gori, F.; Guattari, G.; Santarsiero, M. Twisted Schell-model beams with axial symmetry. Opt. Lett. 2015, 40, 4504–4507. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Devising genuine twisted cross-spectral densities. Opt. Lett. 2018, 43, 595–598. [Google Scholar] [CrossRef] [PubMed]
- Ambrosini, D.; Bagini, V.; Gori, F.; Santarsiero, M. Twisted Gaussian Schell-model beams: A superposition model. J. Mod. Opt. 1994, 41, 1391–1399. [Google Scholar] [CrossRef]
- Simon, R.; Friberg, A.T.; Wolf, E. Transfer of radiance by twisted Gaussian Schell-model beams in paraxial systems. Pure Appl. Opt. 1996, 5, 331–343. [Google Scholar] [CrossRef]
- Ponomarenko, S.A. Twisted Gaussian Schell-model solitons. Phys. Rev. E 2001, 64, 036618. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Cai, Y. Tensor ABCD law for partially coherent twisted anisotropic Gaussian-Schell model beams. Opt. Lett. 2002, 27, 216–218. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Cai, Y. Spectral shift of a twisted electromagnetic Gaussian Schell-model beam focused by a thin lens. App. Phys. B 2010, 99, 317–323. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, Y.; Korotkova, O. Radiation force of scalar and electromagnetic twisted Gaussian Schell-model beams. Opt. Express 2009, 17, 21472–21487. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Cai, Y. Second-order statistics of a twisted Gaussian Schell-model beam in turbulent atmosphere. Opt. Express 2010, 18, 24661–24672. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Cai, Y.; Eyyuboğlu, H.T.; Baykal, Y. Twist phase-induced reduction in scintillation of a partially coherent beam in turbulent atmosphere. Opt. Lett. 2015, 40, 4504–4507. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, H.; Zhu, S.; Li, Z. Second-order moments of a twisted Gaussian Schell-model beam in anisotropic turbulence. J. Opt. Soc. Am. A 2018, 35, 1173–1179. [Google Scholar] [CrossRef] [PubMed]
- Serna, J.; Movilla, J.M. Orbital angular momentum of partially coherent beams. Opt. Lett. 2001, 26, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Zhu, S. Orbital angular moment of a partially coherent beam propagating through an astigmatic ABCD optical system with loss or gain. Opt. Lett. 2014, 39, 1968–1971. [Google Scholar] [CrossRef] [PubMed]
- Kandpal, H.C.; Vaishya, J.S.; Joshi, K.C. Wolf shift and its application in spectroradiometry. Opt. Commun. 1989, 73, 169–172. [Google Scholar] [CrossRef]
- James, D.F.; Kandpal, H.C.; Wolf, E. A new method for determining the angular separation of double stars. Astrophys. J. 1995, 445, 406–410. [Google Scholar] [CrossRef]
- Zhu, S.; Zhao, C.; Chen, Y.; Cai, Y. Experimental generation of a polychromatic partially coherent dark hollow beam. Optik 2013, 124, 5271–5273. [Google Scholar] [CrossRef]
- Zhu, S.; Li, Z. Theoretical and experimental studies of the spectral changes of a focused polychromatic partially coherent flat-topped beam. Appl. Phys. B 2015, 118, 481–487. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, J.; Huang, H.; Wang, H.; Zhu, S.; Li, Z.; Lu, J. Propagation Characteristics of a Twisted Cosine-Gaussian Correlated Radially Polarized Beam. Appl. Sci. 2018, 8, 1485. https://doi.org/10.3390/app8091485
Zhang J, Wang J, Huang H, Wang H, Zhu S, Li Z, Lu J. Propagation Characteristics of a Twisted Cosine-Gaussian Correlated Radially Polarized Beam. Applied Sciences. 2018; 8(9):1485. https://doi.org/10.3390/app8091485
Chicago/Turabian StyleZhang, Jipeng, Jing Wang, Hongkun Huang, Haiyan Wang, Shijun Zhu, Zhenhua Li, and Jian Lu. 2018. "Propagation Characteristics of a Twisted Cosine-Gaussian Correlated Radially Polarized Beam" Applied Sciences 8, no. 9: 1485. https://doi.org/10.3390/app8091485
APA StyleZhang, J., Wang, J., Huang, H., Wang, H., Zhu, S., Li, Z., & Lu, J. (2018). Propagation Characteristics of a Twisted Cosine-Gaussian Correlated Radially Polarized Beam. Applied Sciences, 8(9), 1485. https://doi.org/10.3390/app8091485