Effect of Ionic Liquids on the Isobaric Vapor-Liquid Equilibrium Behavior of Acetone-Chloroform
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Apparatus and Procedure
3. Results and Discussion
3.1. VLE Data
3.2. Modeling Results
4. Quantum Chemical Calculations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
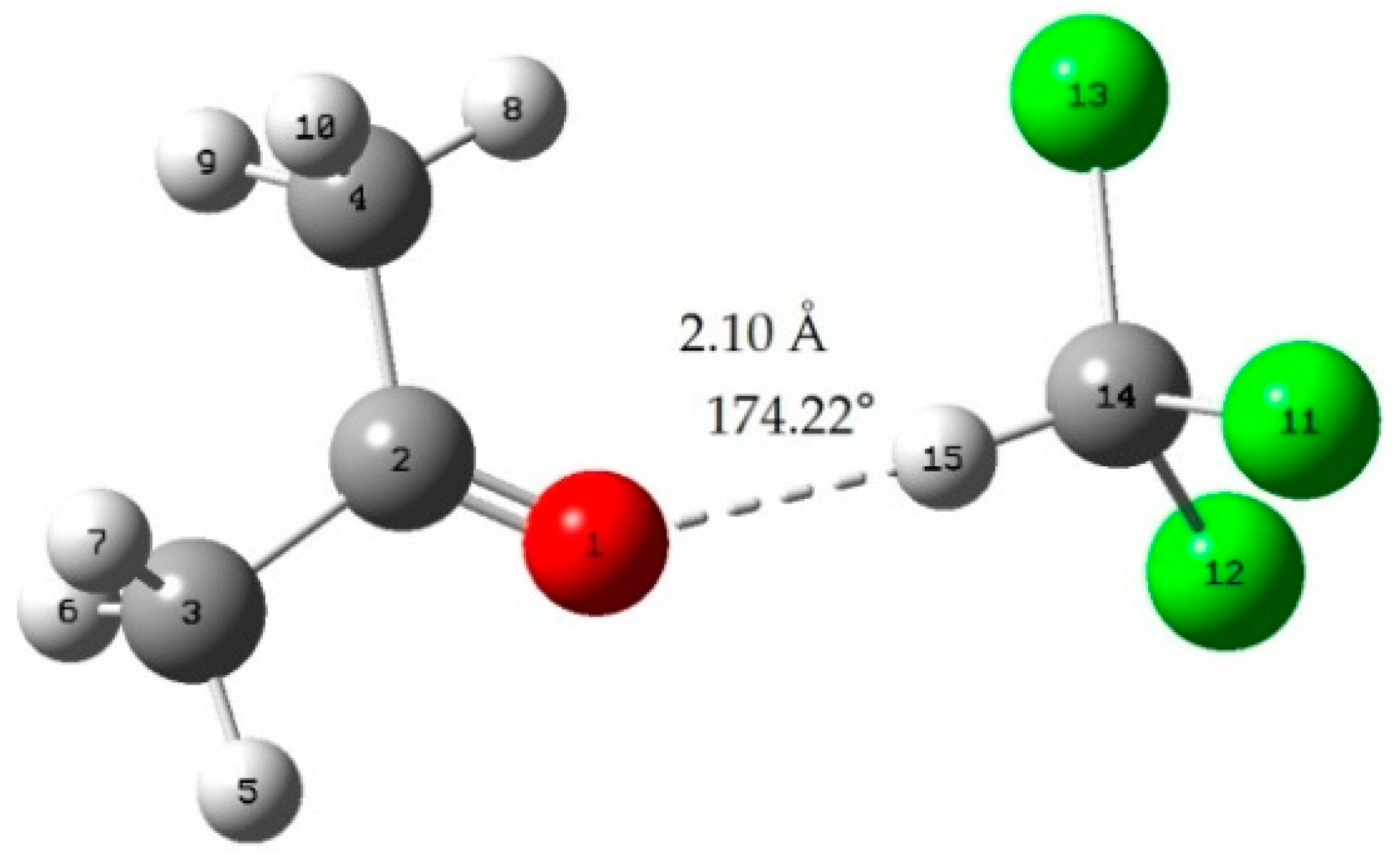
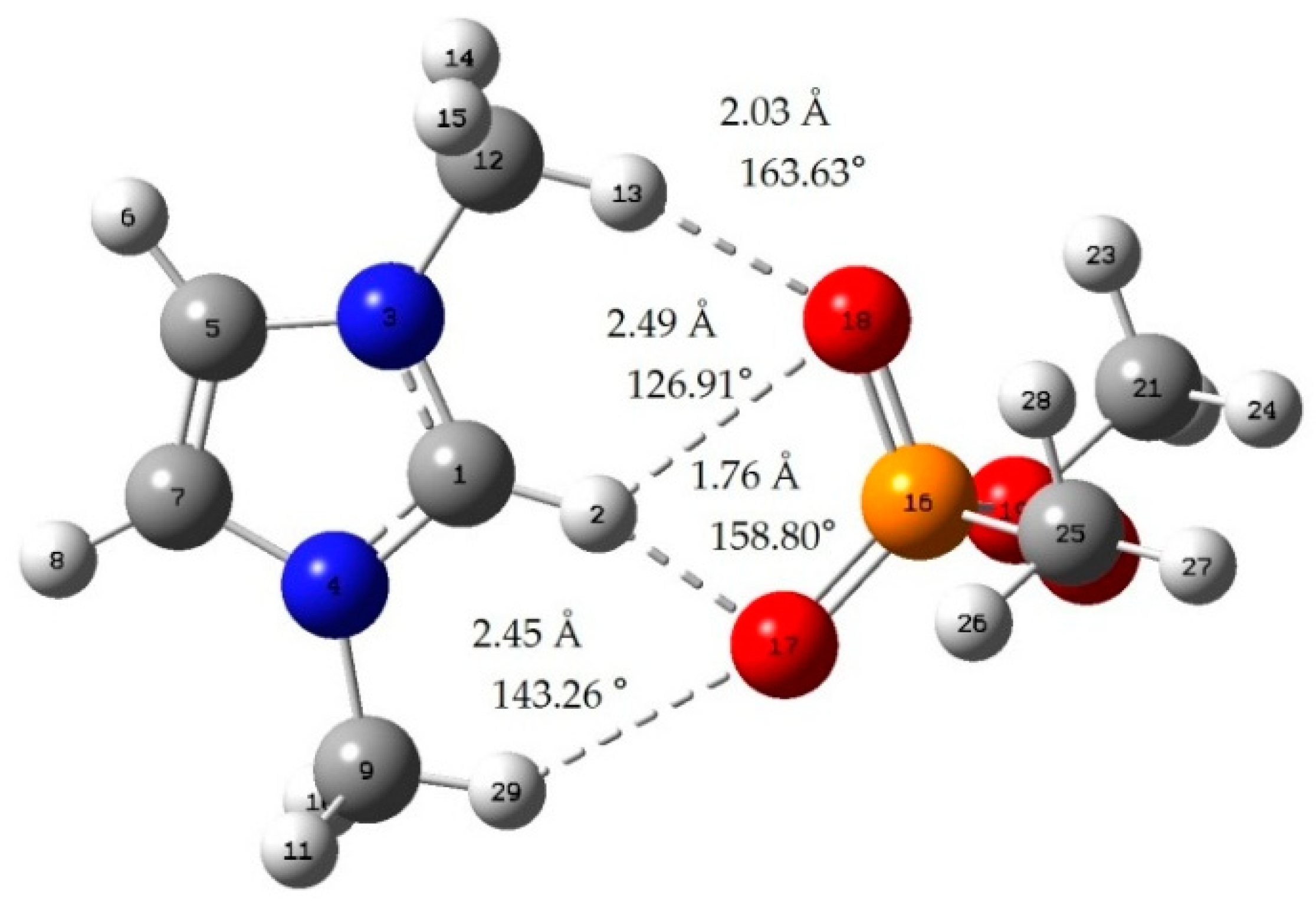
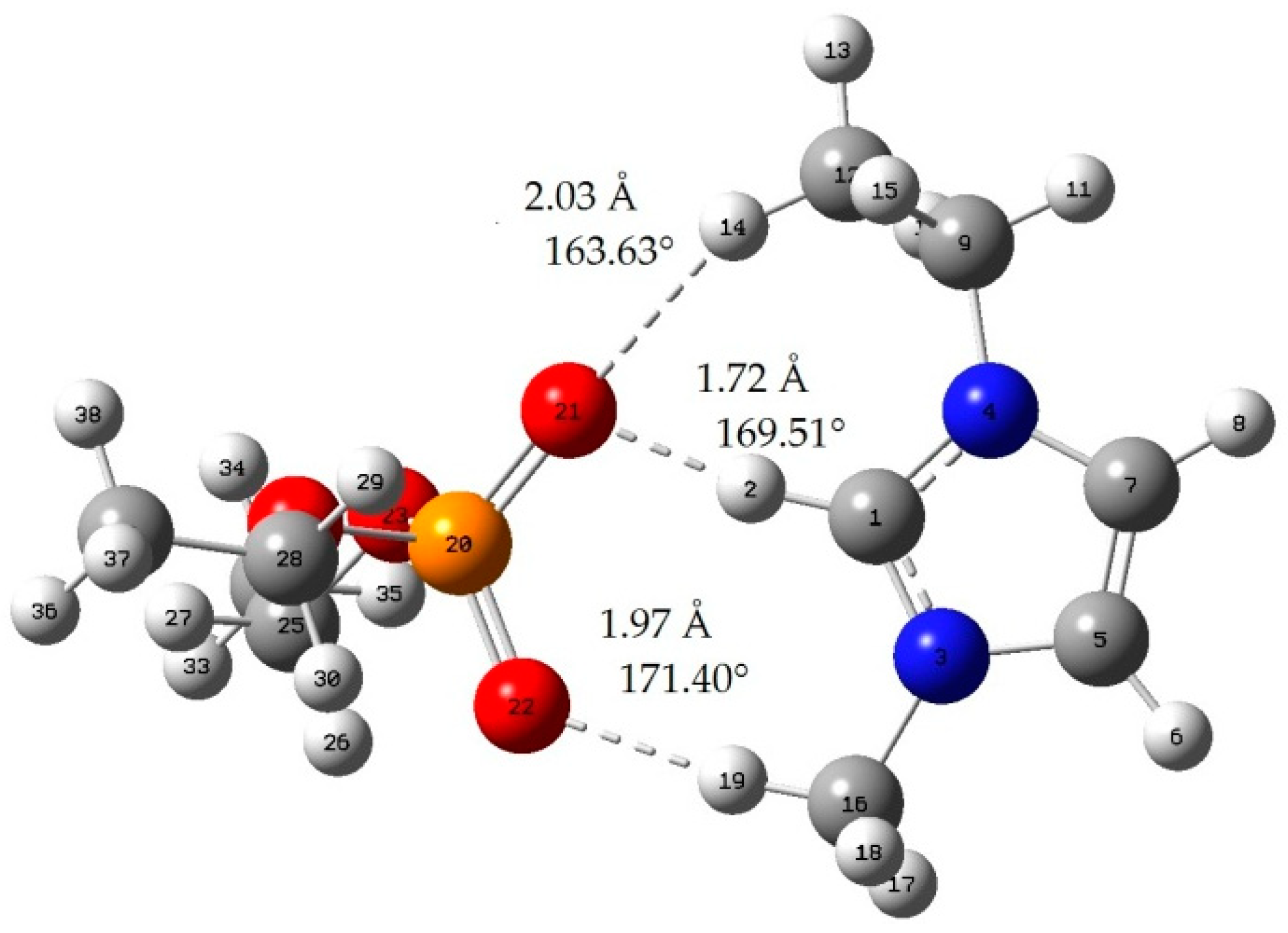
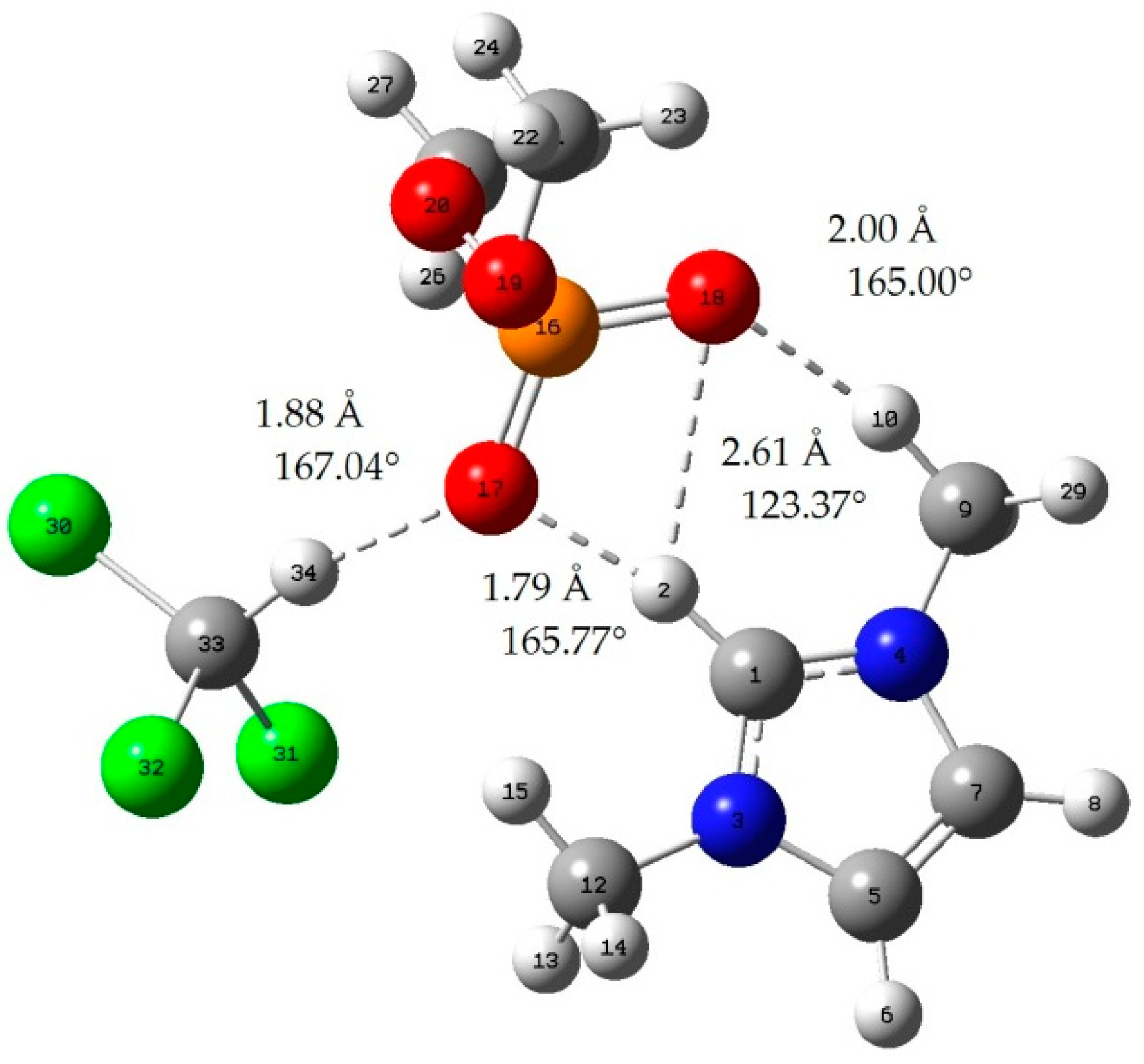
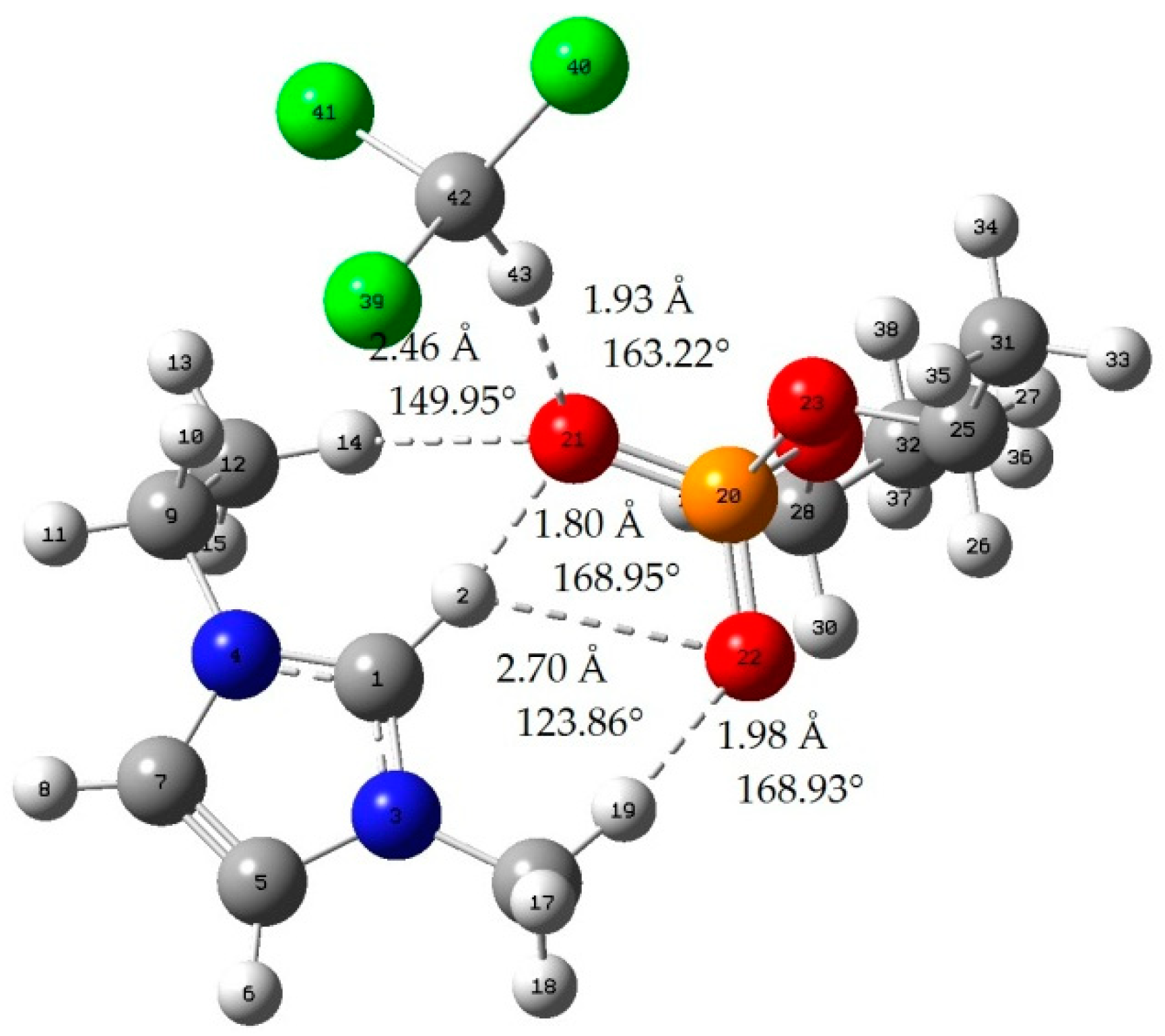
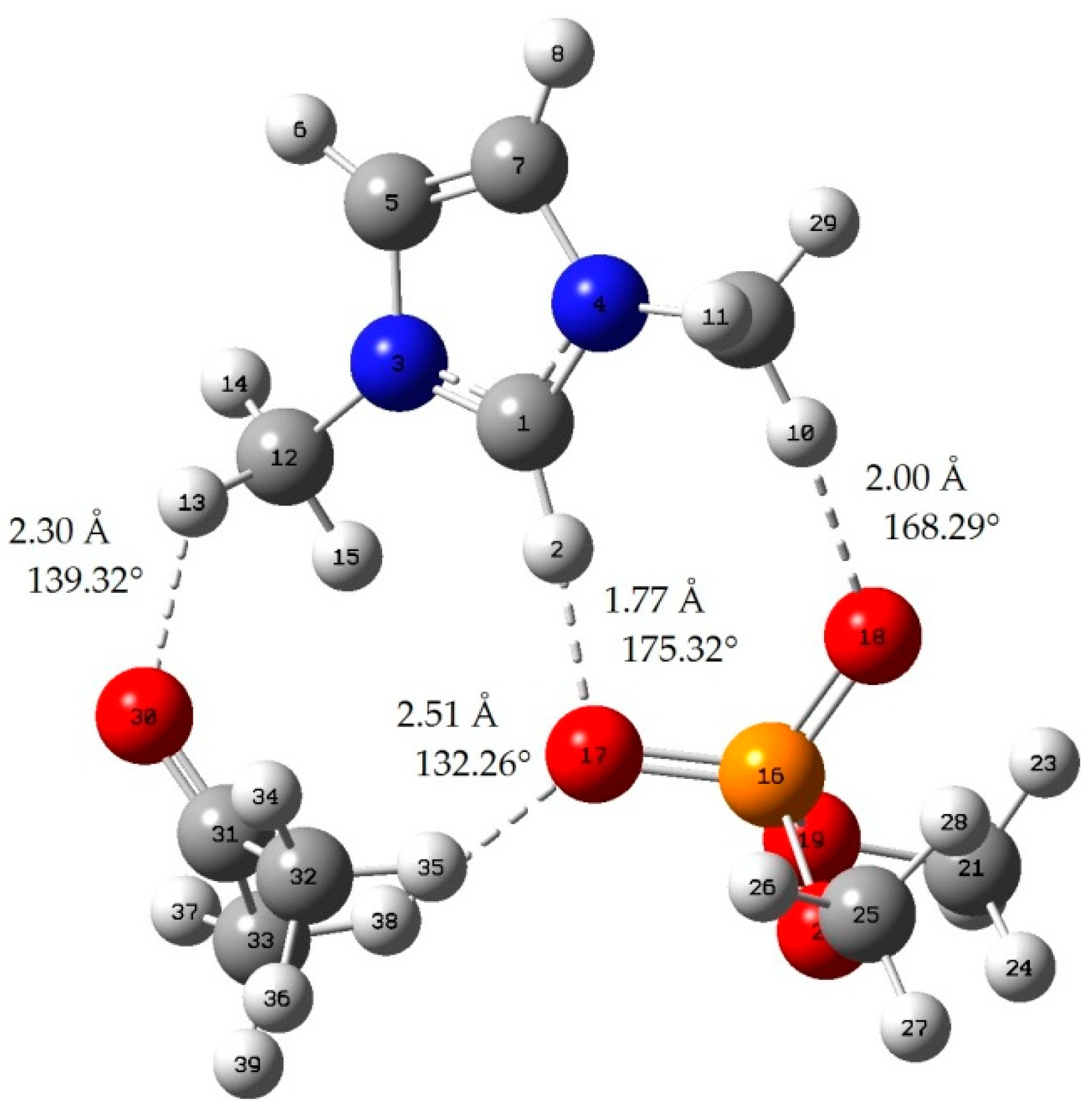
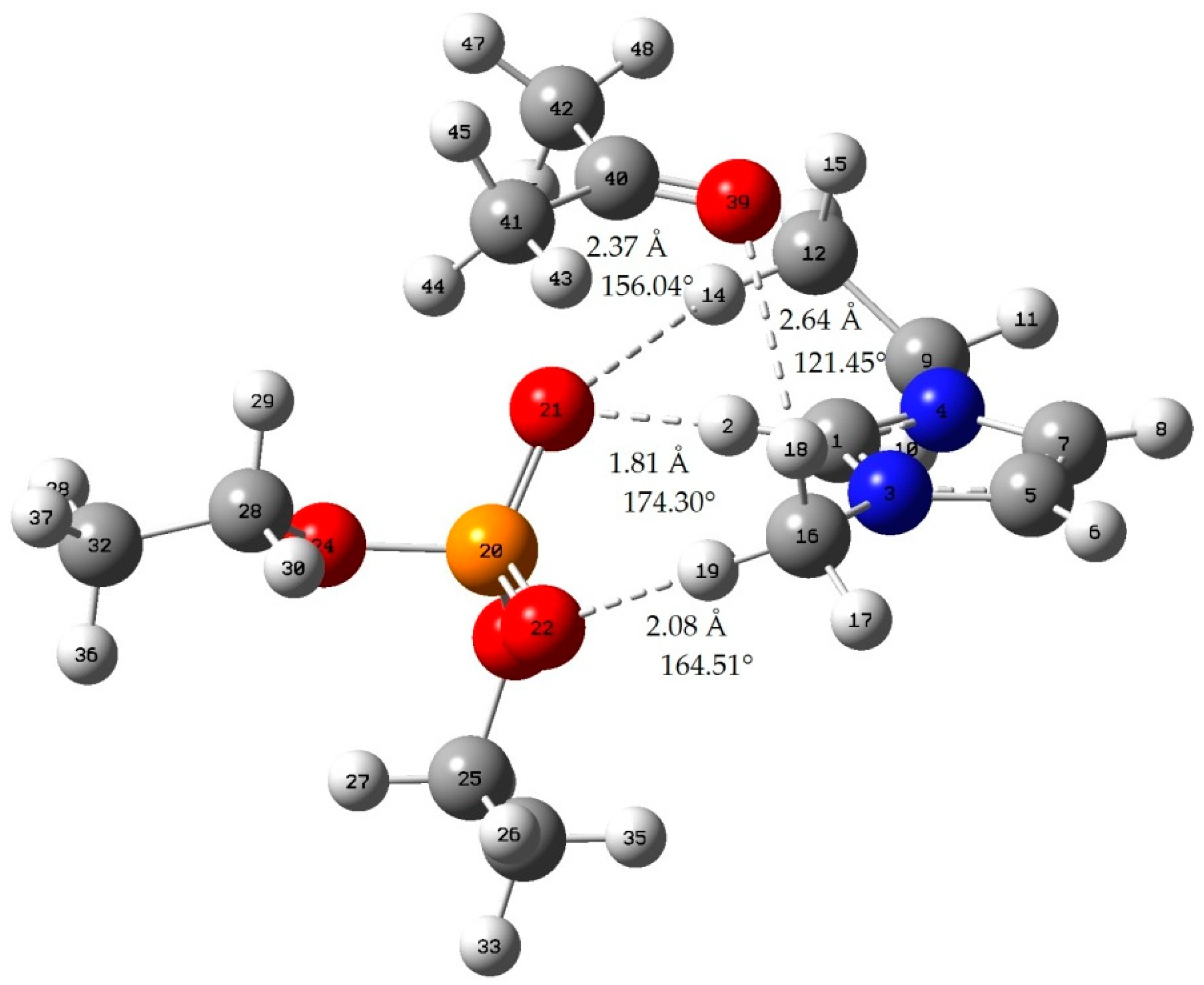
Appendix B
| T/K | x1 | y1 |
|---|---|---|
| 335.7 | 0.102 | 0.067 |
| 336.9 | 0.202 | 0.160 |
| 337.6 | 0.301 | 0.280 |
| 337.6 | 0.396 | 0.401 |
| 336.9 | 0.494 | 0.544 |
| 335.9 | 0.587 | 0.660 |
| 334.5 | 0.679 | 0.765 |
| 332.5 | 0.786 | 0.866 |
| 331.0 | 0.893 | 0.945 |
| x3 | T/K | x1′ | y1exp | y1cal | α12 |
|---|---|---|---|---|---|
| 0.103 | 337.39 | 0.104 | 0.098 | 0.102 | 0.971 |
| 0.100 | 338.67 | 0.202 | 0.211 | 0.226 | 1.060 |
| 0.100 | 339.31 | 0.290 | 0.339 | 0.354 | 1.257 |
| 0.100 | 338.93 | 0.396 | 0.485 | 0.509 | 1.435 |
| 0.100 | 338.23 | 0.476 | 0.610 | 0.617 | 1.723 |
| 0.100 | 336.51 | 0.583 | 0.732 | 0.742 | 1.956 |
| 0.100 | 334.7 | 0.678 | 0.831 | 0.832 | 2.334 |
| 0.100 | 332.58 | 0.785 | 0.910 | 0.908 | 2.776 |
| 0.100 | 330.97 | 0.887 | 0.960 | 0.960 | 3.068 |
| 0.150 | 338.8 | 0.100 | 0.109 | 0.116 | 1.111 |
| 0.152 | 340.21 | 0.194 | 0.242 | 0.252 | 1.326 |
| 0.151 | 340.45 | 0.282 | 0.382 | 0.387 | 1.571 |
| 0.150 | 339.84 | 0.372 | 0.513 | 0.521 | 1.780 |
| 0.150 | 338.34 | 0.486 | 0.665 | 0.672 | 2.104 |
| 0.151 | 336.65 | 0.578 | 0.773 | 0.773 | 2.476 |
| 0.150 | 334.78 | 0.672 | 0.852 | 0.852 | 2.810 |
| 0.150 | 332.75 | 0.782 | 0.921 | 0.921 | 3.254 |
| 0.150 | 330.94 | 0.884 | 0.968 | 0.966 | 3.994 |
| 0.199 | 342.07 | 0.107 | 0.153 | 0.149 | 1.506 |
| 0.200 | 343.07 | 0.187 | 0.279 | 0.279 | 1.679 |
| 0.199 | 343.16 | 0.266 | 0.418 | 0.407 | 1.983 |
| 0.200 | 341.34 | 0.369 | 0.575 | 0.564 | 2.317 |
| 0.201 | 339.6 | 0.468 | 0.697 | 0.692 | 2.619 |
| 0.200 | 337.61 | 0.553 | 0.791 | 0.780 | 3.065 |
| 0.201 | 335.23 | 0.671 | 0.874 | 0.873 | 3.400 |
| 0.201 | 333.06 | 0.784 | 0.930 | 0.934 | 3.689 |
| 0.202 | 331.04 | 0.883 | 0.970 | 0.971 | 4.341 |
| x3 | T/K | x1′ | y1exp | y1cal | α12 |
|---|---|---|---|---|---|
| 0.100 | 338.18 | 0.100 | 0.099 | 0.105 | 0.989 |
| 0.100 | 339.39 | 0.195 | 0.215 | 0.230 | 1.128 |
| 0.100 | 339.83 | 0.287 | 0.348 | 0.365 | 1.325 |
| 0.100 | 339.68 | 0.376 | 0.484 | 0.495 | 1.563 |
| 0.100 | 338.74 | 0.477 | 0.614 | 0.634 | 1.746 |
| 0.100 | 337.33 | 0.573 | 0.742 | 0.746 | 2.143 |
| 0.100 | 335.10 | 0.679 | 0.834 | 0.843 | 2.382 |
| 0.101 | 333.18 | 0.788 | 0.919 | 0.917 | 3.031 |
| 0.100 | 331.37 | 0.897 | 0.970 | 0.968 | 3.665 |
| 0.150 | 340.81 | 0.097 | 0.115 | 0.124 | 1.216 |
| 0.150 | 341.67 | 0.192 | 0.256 | 0.267 | 1.443 |
| 0.150 | 342.21 | 0.269 | 0.392 | 0.389 | 1.756 |
| 0.150 | 341.41 | 0.365 | 0.535 | 0.536 | 1.998 |
| 0.150 | 340.03 | 0.456 | 0.664 | 0.658 | 2.354 |
| 0.149 | 337.91 | 0.567 | 0.788 | 0.779 | 2.837 |
| 0.150 | 336.30 | 0.663 | 0.863 | 0.859 | 3.198 |
| 0.150 | 333.88 | 0.781 | 0.933 | 0.929 | 3.920 |
| 0.150 | 332.20 | 0.877 | 0.971 | 0.968 | 4.726 |
| 0.199 | 344.21 | 0.093 | 0.143 | 0.144 | 1.626 |
| 0.199 | 344.81 | 0.178 | 0.293 | 0.290 | 1.913 |
| 0.200 | 345.48 | 0.251 | 0.423 | 0.414 | 2.186 |
| 0.200 | 344.37 | 0.345 | 0.563 | 0.562 | 2.443 |
| 0.200 | 342.76 | 0.430 | 0.690 | 0.675 | 2.946 |
| 0.205 | 339.93 | 0.556 | 0.812 | 0.809 | 3.446 |
| 0.200 | 337.70 | 0.664 | 0.882 | 0.884 | 3.783 |
| 0.199 | 335.58 | 0.766 | 0.937 | 0.936 | 4.525 |
| 0.198 | 332.63 | 0.908 | 0.981 | 0.982 | 5.201 |
References
- Luyben, W.L. Comparison of extractive distillation and pressure-swing distillation for acetone/chloroform separation. Comput. Chem. Eng. 2013, 50, 1–7. [Google Scholar] [CrossRef]
- Dai, C.; Lei, Z.; Xi, X.; Zhu, J.; Chen, B. Extractive distillation with a mixture of organic solvent and ionic liquid as entrainer. Ind. Eng. Chem. Res. 2014, 53, 15786–15791. [Google Scholar] [CrossRef]
- Lei, Z.; Dai, C.; Zhu, J.; Chen, B. Extractive distillation with ionic liquids: A review. AIChE J. 2014, 60, 3312–3329. [Google Scholar] [CrossRef]
- Luyben, W.L. Control of the maximum-boiling acetone/chloroform azeotropic distillation system. Ind. Eng. Chem. Res. 2008, 47, 6140–6149. [Google Scholar] [CrossRef]
- Lei, Z.; Chen, B.; Ding, Z. Special Distillation Processes; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Rezabal, E.; Schäfer, T. First principle approach to solvation by methylimidazolium-based ionic liquids. J. Phys. Chem. B 2013, 117, 553–562. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Z.; Zhou, T.; Chen, L.; Ye, Y.; Kai, S.; Qi, Z. Simulation based ionic liquid screening for benzene–cyclohexane extractive separation. Chem. Eng. Sci. 2014, 115, 186–194. [Google Scholar] [CrossRef]
- Dong, K.; Song, Y.; Liu, X.; Cheng, W.; Yao, X.; Zhang, S. Understanding structures and hydrogen bonds of ionic liquids at the electronic level. J. Phys. Chem. B 2012, 116, 1007–1017. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Liu, P.; Cao, L.; Wen, F.; Zhang, S.; Wang, B. Vapor–liquid equilibrium for tetrahydrofuran + methanol + tetrafluoroborate-based ionic liquids at 101.3 kPa. Fluid Phase Equilibr. 2013, 360, 439–444. [Google Scholar] [CrossRef]
- Hiaki, T.; Kawai, A. Vapor–liquid equilibria determination for a hydrofluoroether with several alcohols. Fluid Phase Equilibr. 1999, 158, 979–989. [Google Scholar] [CrossRef]
- Kojima, K.; Tochigi, K.; Kurihara, K.; Nakamichi, M. Isobaric vapor-liquid equilibria for acetone + chloroform + benzene and the three constituent binary systems. J. Chem. Eng. Data 1991, 36, 343–345. [Google Scholar] [CrossRef]
- Yaws, C.L.; Yang, H.C. To estimate vapor pressure easily. Hydrocarbon Process. 1989, 68, 10. [Google Scholar]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Li, Q.; Cao, L.; Sun, X.; Liu, P.; Wang, B. Isobaric vapor–liquid equilibrium for ethyl acetate + acetonitrile + 1-butyl-3-methylimidazolium hexafluorophosphate at 101.3 kPa. J. Chem. Eng. Data 2013, 58, 1112–1116. [Google Scholar] [CrossRef]
- Simoni, L.D.; Ficke, L.E.; Lambert, C.A.; Stadtherr, M.A.; Brennecke, J.F. Measurement and prediction of vapor-liquid equilibrium of aqueous 1-ethyl-3-methylimidazolium-based ionic liquid systems. Ind. Eng. Chem. Res. 2010, 49, 3893–3901. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, S.; Ding, B.; Cao, L.; Liu, P.; Jiang, Z.; Wang, B. Isobaric vapor-liquid equilibrium for methanol + dimethyl carbonate + trifluoromethanesulfonate-based ionic liquids at 101.3 kpa. J. Chem. Eng. Data 2014, 59, 3488–3494. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. Gaussian 09, Rev. A. 01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Steiner, T. The hydrogen bond in the solid state. Angew. Chem. Int. Ed. 2010, 41, 48–76. [Google Scholar] [CrossRef]






| i Component | j Component | αij | Δgij/J·mol−1 | Δgji/J·mol−1 |
|---|---|---|---|---|
| acetone | chloroform | 0.399 | −198.209 | −11.766 |
| acetone | [MMIM][DMP] | 0.217 | 1006.802 | 2707.172 |
| chloroform | [MMIM][DMP] | 0.780 | 117.775 | 10.602 |
| acetone | [EMIM][DEP] | 0.023 | 1547.298 | −725.432 |
| chloroform | [EMIM][DEP] | 0.200 | −298.873 | −407.809 |
| A | B | ΔE(AB) |
|---|---|---|
| acetone | chloroform | −14.290 |
| [MMIM]+ | [DMP]− | −387.833 |
| [EMIM]+ | [DEP]− | −381.524 |
| acetone | [MMIM][DMP] | −24.519 |
| acetone | [EMIM][DEP] | −14.892 |
| chloroform | [MMIM][DMP] | −30.939 |
| chloroform | [EMIM][DEP] | −30.421 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Zhao, Z.; Jia, P.; Zhang, X. Effect of Ionic Liquids on the Isobaric Vapor-Liquid Equilibrium Behavior of Acetone-Chloroform. Appl. Sci. 2018, 8, 1519. https://doi.org/10.3390/app8091519
Gao Q, Zhao Z, Jia P, Zhang X. Effect of Ionic Liquids on the Isobaric Vapor-Liquid Equilibrium Behavior of Acetone-Chloroform. Applied Sciences. 2018; 8(9):1519. https://doi.org/10.3390/app8091519
Chicago/Turabian StyleGao, Qinglin, Zongchang Zhao, Peng Jia, and Xiaodong Zhang. 2018. "Effect of Ionic Liquids on the Isobaric Vapor-Liquid Equilibrium Behavior of Acetone-Chloroform" Applied Sciences 8, no. 9: 1519. https://doi.org/10.3390/app8091519
APA StyleGao, Q., Zhao, Z., Jia, P., & Zhang, X. (2018). Effect of Ionic Liquids on the Isobaric Vapor-Liquid Equilibrium Behavior of Acetone-Chloroform. Applied Sciences, 8(9), 1519. https://doi.org/10.3390/app8091519




