Effect of Excitation Beam Divergence on the Goos–Hänchen Shift Enhanced by Bloch Surface Waves
Abstract
:1. Introduction
2. Theory and Analysis
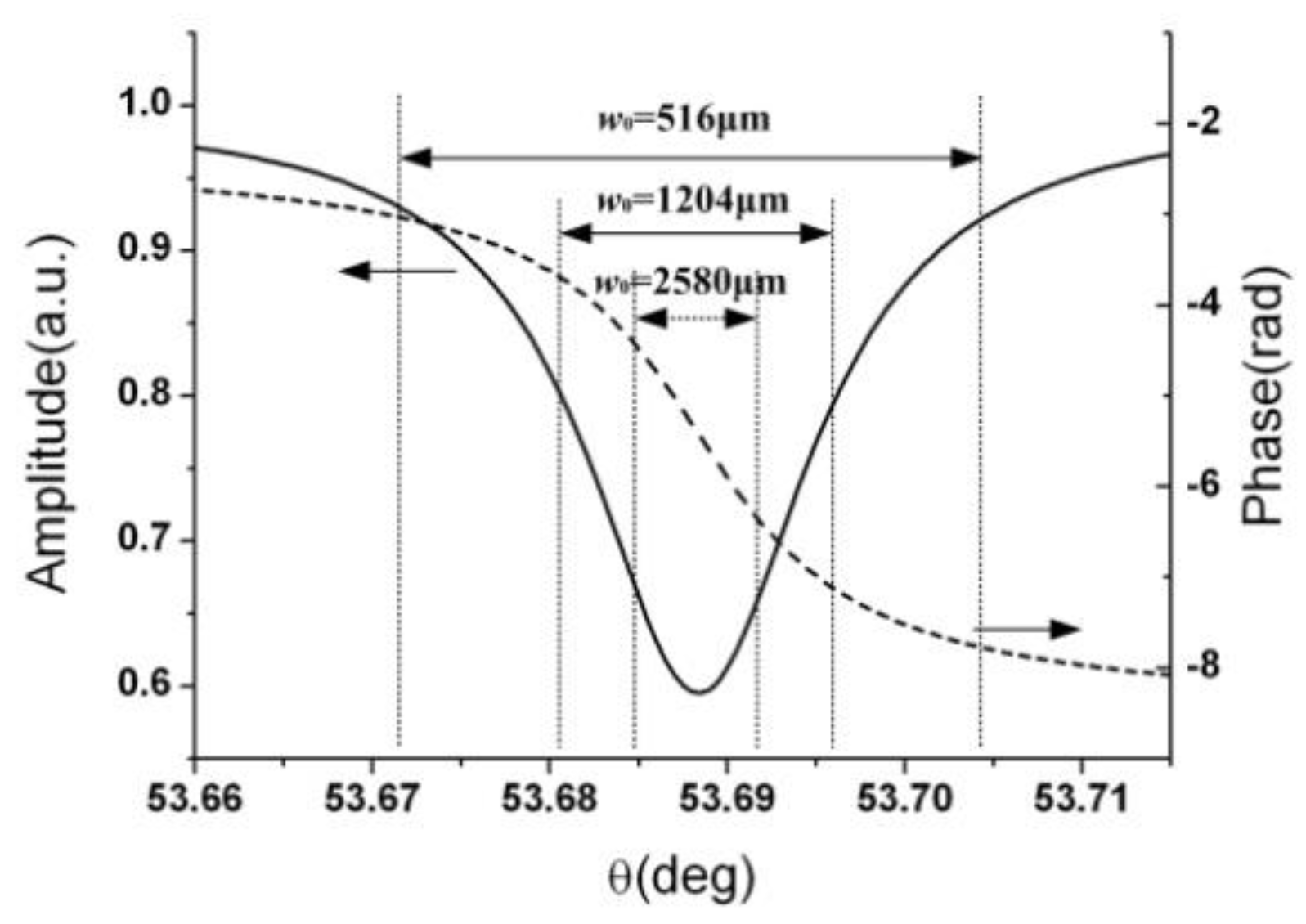
3. Simulation
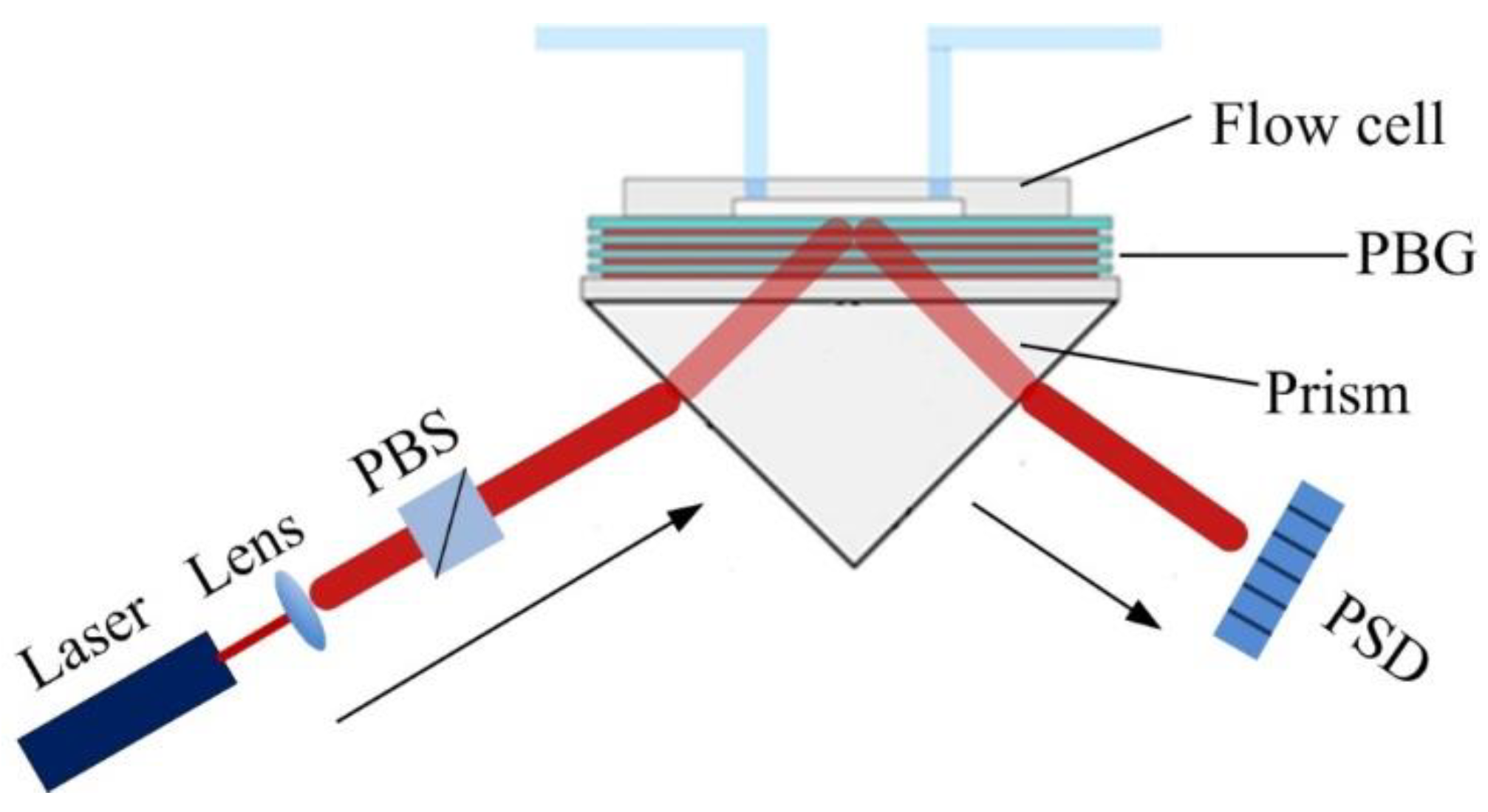
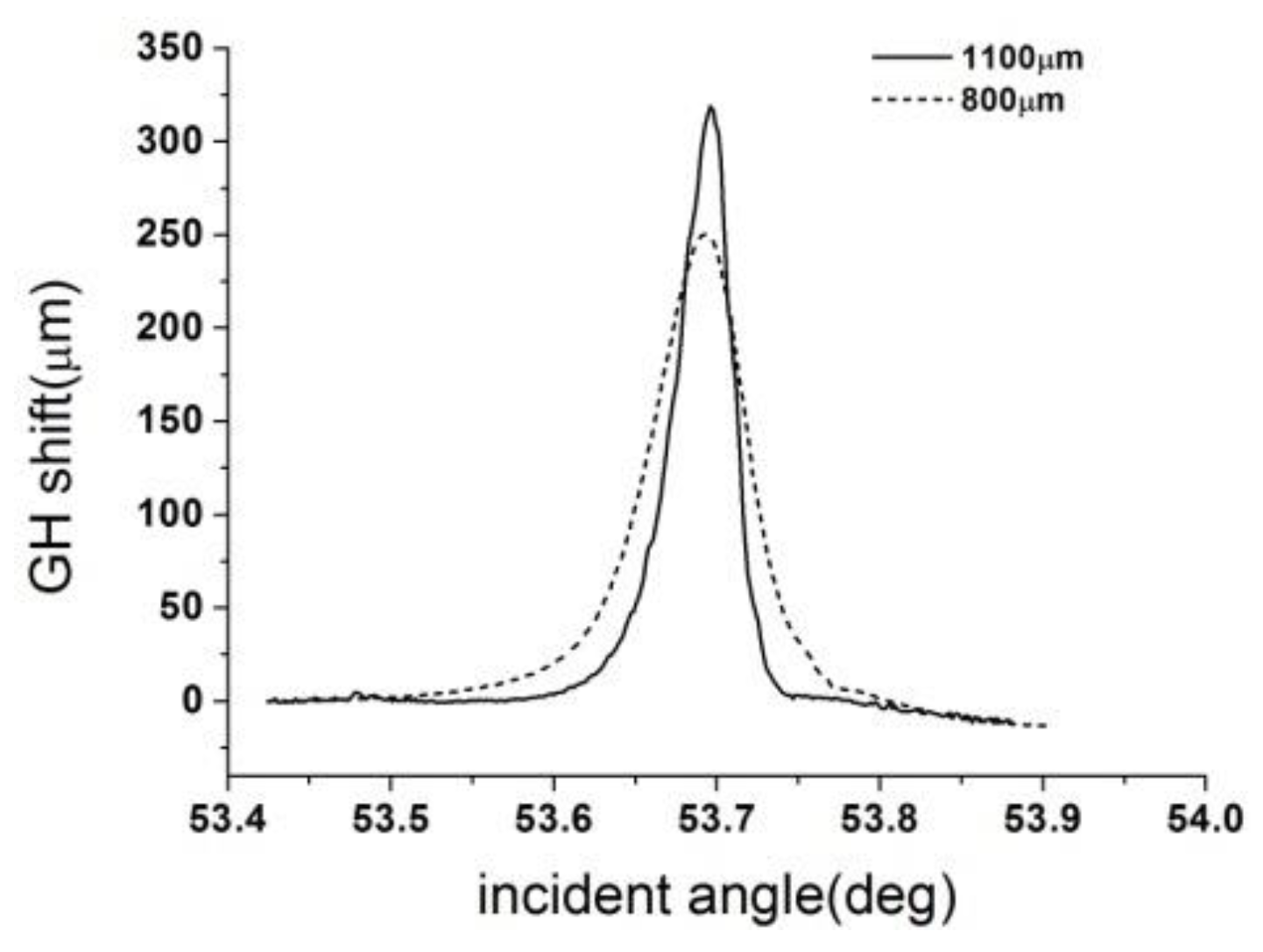
4. Experiment and Result
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Artmann, K. Berechnung der Seitenversetzung des totalreflektierten Strahles. Ann. Phys. 1948, 437, 87–102. [Google Scholar] [CrossRef]
- Imbert, C. Calculation and experimental proof of the transverse shift induced by total internal reflection of a circularly polarized light beam. Phys. Rev. D 1972, 5, 787. [Google Scholar] [CrossRef]
- Leung, P.; Chen, C.; Chiang, H.-P. Large negative Goos–Hanchen shift at metal surfaces. Opt. Commun. 2007, 276, 206–208. [Google Scholar] [CrossRef]
- Merano, M.; Aiello, A.; GW’t Hooft, M.; van Exter, M.P.; Eliel, E.R.; Woerdman, J.P. Observation of Goos-Hanchen shifts in metallic reflection. Opt. Express 2007, 15, 15928–15934. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Zheng, Z.; Kong, W.; Liu, Y.; Lu, Z.; Bian, Y. Direct experimental observation of giant Goos–Hänchen shifts from bandgap-enhanced total internal reflection. Opt. Lett. 2011, 36, 3539–3541. [Google Scholar] [CrossRef] [PubMed]
- Soboleva, I.V.; Moskalenko, V.V.; Fedyanin, A.A. Giant Goos-Hänchen Effect and Fano Resonance at Photonic Crystal Surfaces. Phys. Rev. Lett. 2012, 108, 123901. [Google Scholar] [CrossRef] [PubMed]
- Matthews, A.; Kivshar, Y. Tunable Goos–Hänchen shift for self-collimated beams in two-dimensional photonic crystals. Phys. Lett. A 2008, 372, 3098–3101. [Google Scholar] [CrossRef]
- Yin, X.; Hesselink, L. Goos-Hänchen shift surface plasmon resonance sensor. Appl. Phys. Lett. 2006, 89, 261108. [Google Scholar] [CrossRef]
- Wan, Y.; Zheng, Z.; Zhu, J. Propagation-dependent beam profile distortion associated with the Goos-Hanchen shift. Opt. Express 2009, 17, 21313–21319. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-G.; Zhu, S.-Y. Large positive and negative Goos-Hänchen shifts from a weakly absorbing left-handed slab. J. Appl. Phys. 2005, 98, 043522. [Google Scholar] [CrossRef]
- Fan, J.; Dogariu, A.; Wang, L. Amplified total internal reflection. Opt. Express 2003, 11, 299–308. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M. Goos-Hänchen shift in bilayer graphene. Eur. Phys. J. B 2012, 85, 1–4. [Google Scholar] [CrossRef]
- Song, Y.; Wu, H.-C.; Guo, Y. Giant Goos-Hänchen shift in graphene double-barrier structures. Appl. Phys. Lett. 2012, 100, 253116. [Google Scholar] [CrossRef]
- Wan, Y.; Zheng, Z.; Kong, W.; Zhao, X.; Liu, Y.; Bian, Y.; Liu, J. Nearly three orders of magnitude enhancement of Goos-Hanchen shift by exciting Bloch surface wave. Opt. Express 2012, 20, 8998–9003. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Kong, W.; Zheng, Z.; Zhao, X.; Liu, Y.; Bian, Y. Fiber-pigtailed optical switch based on gigantic bloch-surface-wave-induced Goos-Hanchen shifts. In Proceedings of the 2012 IEEE Photonics Conference, Burlingame, CA, USA, 23–27 September 2012; pp. 36–37. [Google Scholar]
- Merano, M.; Hermosa, N.; Aiello, A.; Woerdman, J.P. Demonstration of a quasi-scalar angular Goos-Hanchen effect. Opt. Lett. 2010, 35, 3562–3564. [Google Scholar] [CrossRef]
- Narayanaswamy, R.; Wolfbeis, O.S. Optical Sensors: Industrial, Environmental and Diagnostic Applications; Springer: Berlin/Heidelberg, Germany, 2004; Volume 1. [Google Scholar]
- Yeh, P.; Yariv, A.; Hong, C.-S. Electromagnetic propagation in periodic stratified media. I. General theory. J. Opt. Soc. Am. 1977, 67, 423–438. [Google Scholar] [CrossRef]
- Kong, W.; Zheng, Z.; Wan, Y.; Li, S.; Liu, J. High-sensitivity sensing based on intensity-interrogated Bloch surface wave sensors. Sens. Actuators B Chem. 2014, 193, 467–471. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wan, Y.; Liu, J.; Kong, W.; Zheng, Z. Effect of Excitation Beam Divergence on the Goos–Hänchen Shift Enhanced by Bloch Surface Waves. Appl. Sci. 2019, 9, 40. https://doi.org/10.3390/app9010040
Li S, Wan Y, Liu J, Kong W, Zheng Z. Effect of Excitation Beam Divergence on the Goos–Hänchen Shift Enhanced by Bloch Surface Waves. Applied Sciences. 2019; 9(1):40. https://doi.org/10.3390/app9010040
Chicago/Turabian StyleLi, Shuna, Yuhang Wan, Jiansheng Liu, Weijing Kong, and Zheng Zheng. 2019. "Effect of Excitation Beam Divergence on the Goos–Hänchen Shift Enhanced by Bloch Surface Waves" Applied Sciences 9, no. 1: 40. https://doi.org/10.3390/app9010040
APA StyleLi, S., Wan, Y., Liu, J., Kong, W., & Zheng, Z. (2019). Effect of Excitation Beam Divergence on the Goos–Hänchen Shift Enhanced by Bloch Surface Waves. Applied Sciences, 9(1), 40. https://doi.org/10.3390/app9010040



