Propagation Property of an Astigmatic sin–Gaussian Beam in a Strongly Nonlocal Nonlinear Media
Abstract
:1. Introduction
2. Theoretical Formulation
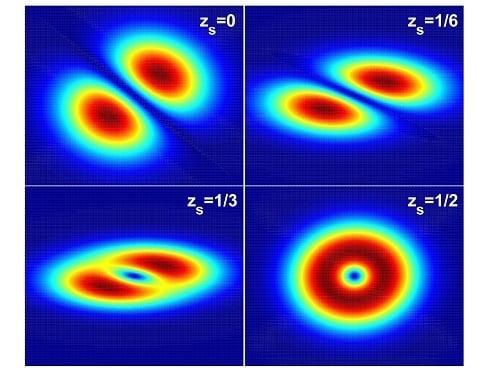
3. Evolutions of Wave Front Dislocations and Intensity Patterns Occurring in an Astigmatic Sin-Gaussian Beam
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Snyder, A.W.; Mitchell, D.J. Accessible solitons. Science 1997, 276, 1538–1541. [Google Scholar] [CrossRef]
- Peccianti, M.; Conti, C.; Assanto, G.; De Luca, A.; Umeton, C. All Optical Switching and Logic Gating with Spatial Solitons in Liquid Crystals. Appl. Phys. Lett. 2002, 81, 3335–3337. [Google Scholar] [CrossRef]
- Briedis, D.; Petersen, D.E.; Edmundson, D.; Krolikowski, W.; Bang, O. Ring vortex solitons in nonlocal nonlinear media. Opt. Express 2005, 13, 435–443. [Google Scholar] [CrossRef]
- Lu, D.Q.; Hu, W. Multiringed breathers and rotating breathers in strongly nonlocal nonlinear media under the off-waist incident condition. Phys. Rev. A 2009, 79, 043833. [Google Scholar] [CrossRef]
- Deng, D.M.; Guo, Q.; Hu, W. Complex-variable-function Gaussian solitons. Opt. Lett. 2009, 34, 43–45. [Google Scholar] [CrossRef]
- Zhang, S.W.; Yin, L. Two-dimensional Hermite–Gaussian solitons in strongly nonlocal nonlinear medium with rectangular boundaries. Opt. Commun. 2009, 282, 1654–1658. [Google Scholar] [CrossRef]
- Yang, Z.J.; Ma, X.K.; Zheng, Y.Z.; Gao, X.H.; Lu, D.Q.; Hu, W. Dipole solitons in nonlinear media with an exponential-decay nonlocal response. Chin. Phys. Lett. 2011, 28, 074213. [Google Scholar] [CrossRef]
- Ge, L.J.; Wang, Q.; Shen, M.; Shi, J.L. Dipole solitons in nonlocal nonlinear media with anisotropy. Opt. Commun. 2011, 284, 2351–2356. [Google Scholar] [CrossRef]
- Bai, Z.Y.; Deng, D.M.; Guo, Q. Elegant Ince Gaussian breathers in strongly nonlocal nonlinear media. Chin. Phys. B 2012, 21, 064218. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.Z. Hermite-Gaussian Vector soliton in strong nonlocal media. Opt. Commun. 2014, 333, 253–260. [Google Scholar] [CrossRef]
- Lopez-Aguayo, S.; Gutierrez-Vega, J.C. Elliptically modulated self-trapped singular beams in nonlocal nonlinear media: ellipticons. Opt. Express 2007, 15, 18326–18338. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.M.; Guo, Q. Propagation of Laguerre-Gaussian beams in nonlocal nonlinear media. J. Opt. A. Pure Appl. Opt. 0351. [Google Scholar] [CrossRef]
- Yang, Z.J.; Lu, D.Q.; Deng, D.M.; Li, S.H.; Hu, W.; Guo, Q. Propagation of four-petal Gaussian beams in strongly nonlocal nonlinear media. Opt. Commun. 2010, 283, 595–603. [Google Scholar] [CrossRef]
- Yang, Z.J.; Lu, D.Q.; Hu, W.; Zheng, Y.Z.; Gao, X.H. Hollow Gaussian beams in strongly nonlocal nonlinear media. Chin. Phys. B 2010, 19, 124212. [Google Scholar] [CrossRef]
- Yang, Z.J.; Lu, D.Q.; Hu, W.; Zheng, Y.Z.; Gao, X.H.; Guo, Q. Propagation of optical beams in strongly nonlocal nonlinear media. Phys. Lett. A 2010, 374, 4007–4013. [Google Scholar] [CrossRef]
- Deng, D.M.; Guo, Q. Propagation of Cartesian beams in nonlocal nonlinear media. Eur. Phys. J. D 2010, 60, 355–359. [Google Scholar] [CrossRef]
- Mishra, M.; Hong, W.P. Investigation on propagation characteristics of super-Gaussian beam in highly nonlocal medium. Prog. Electromagn. Res. B 2011, 31, 175–188. [Google Scholar] [CrossRef]
- Deng, D.M. Propagation of rotating parabolic cylindrical beams in nonlocal nonlinear medium. Opt. Commun. 2012, 285, 3976–3981. [Google Scholar] [CrossRef]
- Deng, D.; Li, H. Propagation properties of Airy–Gaussian beams. Appl. Phys. B 2012, 106, 677–681. [Google Scholar] [CrossRef]
- Guan, Y.; Zhong, L.X.; Chew, K.H.; Chen, H.; Wu, Q.Y.; Chen, R.P. Evolution of cos-Gaussian beams in a strongly nonlocal nonlinear medium. Prog. Electromagn. Res. 2013, 141, 403–414. [Google Scholar] [CrossRef]
- Honarasa, G.; Keshavarz, A. Propagation of the two-dimensional elegant Hermite-cosh-Gaussian beams in strongly nonlocal nonlinear media. Optik 2013, 124, 6535–6538. [Google Scholar] [CrossRef]
- Zhou, G.Q. Propagation property of a Lorentz–Gauss vortex beam in a strongly nonlocal nonlinear media. Opt. Commun. 2014, 330, 106–112. [Google Scholar] [CrossRef]
- Zhou, G.Q.; Chen, R.P.; Ru, G.Y. Propagation of an Airy beam in a strongly nonlocal nonlinear media. Laser Phys. Lett. 2014, 11, 105001. [Google Scholar] [CrossRef]
- Dai, Z.P.; Yang, Z.J.; Zhang, S.M.; Pang, Z.G. Propagation of anomalous vortex beams in strongly nonlocal nonlinear media. Opt. Commun. 2015, 350, 19–27. [Google Scholar] [CrossRef]
- Zhu, W.; Guan, J.; Deng, F.; Deng, D.M.; Huang, J.W. The propagation properties of the first-order and the second-order Airy vortex beams through strongly nonlocal nonlinear medium. Opt. Commun. 2016, 380, 434–441. [Google Scholar] [CrossRef]
- Zhang, X.P. Conversion of the high-mode solitons in strongly nonlocal nonlinear media. J. Mod. Opt. 2017, 64, 170–176. [Google Scholar] [CrossRef]
- Guo, Q.; Luo, B.; Yi, F.; Chi, S.; Xie, Y. Large phase shift of nonlocal optical spatial solitons. Phys. Rev. E 2004, 69, 016602. [Google Scholar] [CrossRef] [PubMed]
- Nie, H.X.; Zhang, H.F.; Li, L. Propagation and interaction of beams with initial phase-front curvature in highly nonlocal media. Opt. Commun. 2008, 281, 5429–5438. [Google Scholar] [CrossRef]
- Casperson, L.W.; Hall, D.G.; Tovar, A.A. Sinusoidal-Gaussian beams in complexoptical systems. J. Opt. Soc. Am. A 1997, 14, 3341–3348. [Google Scholar] [CrossRef]
- Casperson, L.W.; Tovar, A.A. Hermite-sinusoidal-Gaussian beams in complex optical systems. J. Opt. Soc. Am. A 1998, 15, 954–961. [Google Scholar] [CrossRef]
- Eyyuboglu, H.T.; Baykal, Y. Hermite-sine-Gaussian and Hermite-sinh-Gaussian laser beams in turbulent atmosphere. J. Opt. Soc. Am. A 2005, 22, 2709–2718. [Google Scholar] [CrossRef]
- Chen, R.P.; Zheng, H.P.; Chu, X.X. Propagation properties of a sinh-Gaussian beam in a Kerr medium. Appl. Phys. B 2011, 102, 695–698. [Google Scholar] [CrossRef]
- Baykal, Y. Sinusoidal Gaussian beam field correlations. J. Opt. 2012, 14, 075707. [Google Scholar] [CrossRef]
- Sun, Q.G.; Zhou, K.Y.; Fang, G.Y.; Zhang, G.Q.; Liu, Z.J.; Liu, S.T. Hollow sinh-Gaussian beams and their paraxial properties. Opt. Express 2012, 20, 9682–9691. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.Q.; Zhu, K.C. Generation of dark hollow beam by focusing a sine-Gaussian beam using a cylindrical lens and a focusing lens. Opt. & Laser Technology 2013, 54, 68–71. [Google Scholar]
- Zhu, K.C.; Tang, H.Q.; Tang, Y.; Xia, H. Gyrator transform of generalized sine-Gaussian beams and conversion an edge-dislocation into a vortex. Opt. & Laser Technol. 2014, 64, 11–16. [Google Scholar]
- Zhu, J.; Zhu, K.C.; Tang, H.Q.; Xia, H. Average intensity and spreading of an astigmatic sinh-Gaussian beam with small beam width propagating in atmospheric turbulence. Journal of Modern Optics 2017, 64, 1915–1921. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, K.C.; Li, X.L.; Su, Q.; Tang, H.Q. Gyrator transform of phase-flipped Gaussian beams and conversion of an edge-dislocation into a vortex. Optik 2018, 156, 684–688. [Google Scholar] [CrossRef]
- Serna, J.; Nemels, G. Decoupling of coherent Gaussian beams with general astigmatism. Opt. Lett. 1994, 18, 1774–1776. [Google Scholar] [CrossRef]
- Lu, D.Q.; Hu, W.; Zheng, Y.J.; Liang, Y.B.; Cao, L.G.; Lan, S.; Guo, Q. Self-induced fractional Fourier transform and revivable higher-order spatial solitons in strongly nonlocal nonlinear media. Phys. Re. A 2008, 78, 043815. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.Q.; Guo, Q. The relation between optical beam propagation in free space and in strongly nonlocal nonlinear media. Europhys. Lett. 2009, 86, 44004. [Google Scholar] [CrossRef] [Green Version]
- Conti, C.; Peccianti, M.; Assanto, G. Route to nonlocality and observation of accessible solitons. Phys. Rev. Lett. 2003, 91, 073901. [Google Scholar] [CrossRef] [PubMed]
- Conti, C.; Peccianti, M.; Assanto, G. Observation of optical spatial solitons in a highly nonlocal Medium. Phys. Rev. Lett. 2004, 92, 113902. [Google Scholar] [CrossRef] [PubMed]
- Rotschild, C.; Cohen, O.; Manela, O.; Segev, M.; Carmon, T. Solitons in nonlinear medium with an infinite range of nonlocality: first observation of coherent elliptic solitons and of vortex-ring solitons. Phys. Rev. Lett. 2005, 95, 213904. [Google Scholar] [CrossRef] [PubMed]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, K.; Zhu, J.; Su, Q.; Tang, H. Propagation Property of an Astigmatic sin–Gaussian Beam in a Strongly Nonlocal Nonlinear Media. Appl. Sci. 2019, 9, 71. https://doi.org/10.3390/app9010071
Zhu K, Zhu J, Su Q, Tang H. Propagation Property of an Astigmatic sin–Gaussian Beam in a Strongly Nonlocal Nonlinear Media. Applied Sciences. 2019; 9(1):71. https://doi.org/10.3390/app9010071
Chicago/Turabian StyleZhu, Kaicheng, Jie Zhu, Qin Su, and Huiqin Tang. 2019. "Propagation Property of an Astigmatic sin–Gaussian Beam in a Strongly Nonlocal Nonlinear Media" Applied Sciences 9, no. 1: 71. https://doi.org/10.3390/app9010071