Ultra-Small Fiber Bragg Grating Accelerometer
Abstract
:1. Introduction
2. Theory
2.1. Relationships among the Sensitivity, Resonant Frequency and Length of the Spring
2.2. Calculation of Pre-Stretch Based on the Mass and Stretch at Equilibrium
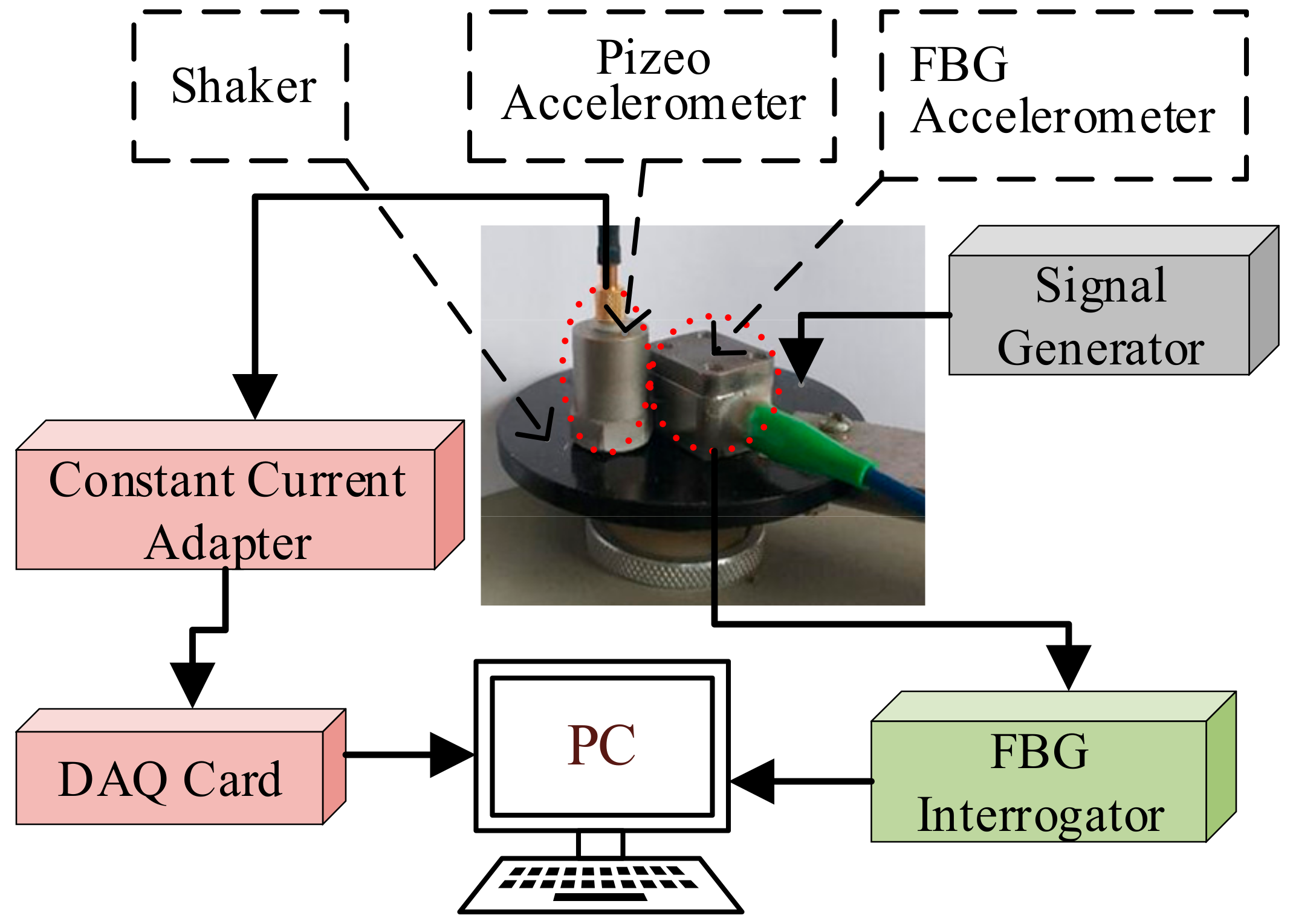
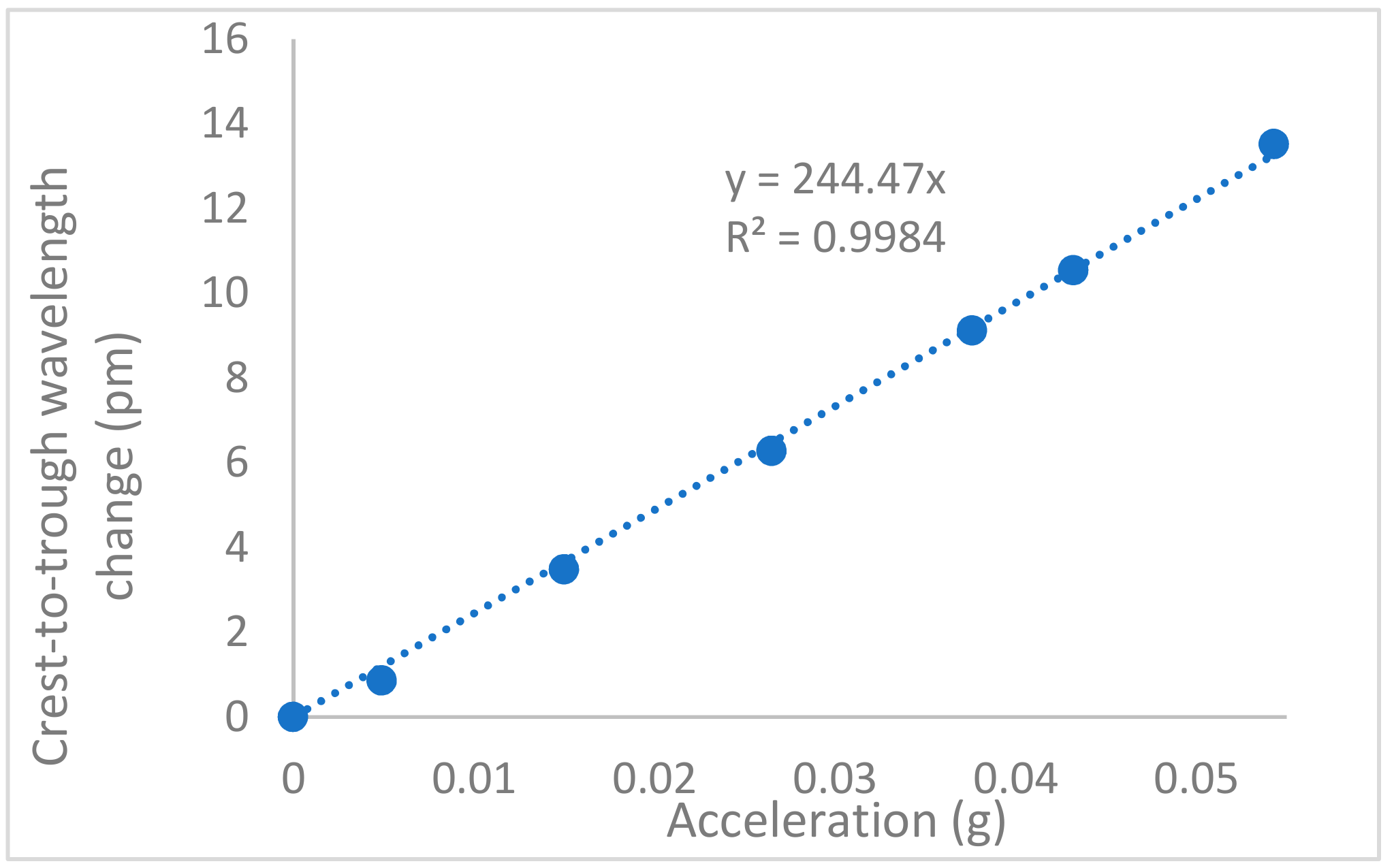
3. Experiments
4. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Li, K.; Chan, T.H.T.; Yau, M.H.; Nguyen, T.; Thambiratnam, D.P.; Tam, H.Y. Very sensitive fiber Bragg grating accelerometer using transverse forces with an easy over-range protection and low cross axial sensitivity. Appl. Opt. 2013, 52, 6401–6410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Berkoff, T.A.; Kersey, A.D. Experimental demonstration of a fiber Bragg grating accelerometer. IEEE Photon. Technol. Lett. 1996, 8, 1677–1679. [Google Scholar] [CrossRef]
- Todd, M.D.; Johnson, G.A.; Althouse, B.A.; Vohra, S.T. Flexural beam-based fiber Bragg grating accelerometers. IEEE Photon. Technol. Lett. 1998, 10, 1605–1607. [Google Scholar] [CrossRef]
- Laudati, A.; Mennella, F.; Giordano, M.; D’Altrui, G.; Tassini, C.C.; Cusano, A. A fiber-optic Bragg grating seismic sensor. IEEE Photon. Technol. Lett. 2007, 19, 1991–1993. [Google Scholar] [CrossRef]
- Basumallick, N.; Biswas, P.; Chakraborty, R.; Chakraborty, S.; Dasgupta, K.; Bandyopadhyay, S. Fibre bragg grating based accelerometer with extended bandwidth. Meas. Sci. Technol. 2016, 27, 035008. [Google Scholar] [CrossRef]
- Antunes, P.; Varum, H.; Andre, P. Uniaxial fiber Bragg grating accelerometer system with temperature and cross axis insensitivity. Measurement 2011, 44, 55–59. [Google Scholar] [CrossRef]
- Antunes, P.; Marques, C.A.; Varum, H.; Andre, P. Biaxial optical accelerometer and high-angle inclinometer with temperature and cross-axis insensitivity. IEEE Sens. J. 2012, 12, 2399–2406. [Google Scholar] [CrossRef]
- Stefani, A.; Andresen, S.; Yuan, W.; Herholdt-Rasmussen, N.; Bang, O. High Sensitivity Polymer Optical Fiber-Bragg-Grating-Based Accelerometer. IEEE Photon. Technol. Lett. 2012, 24, 763–765. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Zhang, Y.; Chen, L.; Yan, T.; Wang, S.; Yu, L.; Li, Y. 2-d medium–high frequency fiber bragg gratings accelerometer. IEEE Sens. J. 2017, 17, 614–618. [Google Scholar] [CrossRef]
- Wang, J.; Wei, L.; Li, R.; Liu, Q.; Yu, L.; Tan, Y. An FBG-based 2-D Vibration Sensor with Adjustable Sensitivity. IEEE Sens. J. 2017, 17, 4716–4724. [Google Scholar] [CrossRef]
- Guo, Y.X.; Zhang, D.S.; Zhou, Z.D.; Xiong, L.; Deng, X.W. Welding-packaged accelerometer based on metal-coated FBG. Chin. Opt. Lett. 2013, 11, 070604. [Google Scholar]
- Li, K.; Chan, T.H.T.; Yau, M.H.; Thambiratnam, D.P.; Tam, H.Y. Biaxial fiber Bragg grating accelerometer using axial and transverse forces. IEEE Photon. Technol. Lett. 2014, 26, 1549–1552. [Google Scholar] [CrossRef]
- Li, T.; Tan, Y.; Zhou, Z.; Wei, Q. Pasted type distributed two-dimensional fiber Bragg grating vibration sensor. Rev. Sci. Instrum. 2015, 86, 075009. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Chan, T.H.T.; Yau, M.H.; Thambiratnam, D.P.; Tam, H.Y. Experimental verification of the modified spring-mass theory of fiber Bragg grating accelerometers using transverse forces. Appl. Opt. 2014, 53, 1200–1211. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Yau, M.H.; Chan, T.H.T.; Thambiratnam, D.; Tam, H.Y. Fiber Bragg grating strain modulation based on nonlinear string transverse-force amplifier. Opt. Lett. 2013, 38, 311–313. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Chan, T.H.T.; Yau, M.H.; Thambiratnam, D.P.; Tam, H.Y. Fiber Bragg grating accelerometer based on a transversely rotating stick. Optik 2015, 126, 4337–4341. [Google Scholar] [CrossRef] [Green Version]



| Length of the Vibration Arm (mm) | Mass of the Inertial Object (gram) | Crest-to-Trough Sensitivity (pm/g) | Resonant Frequency (Hz) | Vibration Direction of the Inertial Object (Axial: Along the Fiber; Transverse: Perpendicular to the Fiber) | Ref. |
|---|---|---|---|---|---|
| 7 | 4.41 | 244 | 90 | transvers | here |
| 24 | 3 | 770 | 41 | transvers | Ref. [15] |
| 30 | 1.29 | 16 | 1300 | axial | Ref. [14] |
| 40 | 4.8 | 1.7 | 3600 | axial | Ref. [12] |
| 47 | 1.76 | 23 | 900 | axial | Ref. [13] |
| 47 | 1.76 | 545 | 34 | transvers | Ref. [13] |
| 50 | 5.71 | 1290 | 26 | transvers | Ref. [15] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Liu, G.; Li, Y.; Yang, J.; Ma, W. Ultra-Small Fiber Bragg Grating Accelerometer. Appl. Sci. 2019, 9, 2707. https://doi.org/10.3390/app9132707
Li K, Liu G, Li Y, Yang J, Ma W. Ultra-Small Fiber Bragg Grating Accelerometer. Applied Sciences. 2019; 9(13):2707. https://doi.org/10.3390/app9132707
Chicago/Turabian StyleLi, Kuo, Guoyong Liu, Yuqing Li, Jun Yang, and Wenlong Ma. 2019. "Ultra-Small Fiber Bragg Grating Accelerometer" Applied Sciences 9, no. 13: 2707. https://doi.org/10.3390/app9132707





