Effects of Boundary Condition Models on the Seismic Responses of a Container Crane
Abstract
:Featured Application
Abstract
1. Introduction
2. Description of a Numerical Model of the Container Crane
2.1. Modeling of Boundary Conditions
2.2. Dynamic Analysis of the Container Crane
2.3. Defining Damage Criteria for the Container Crane
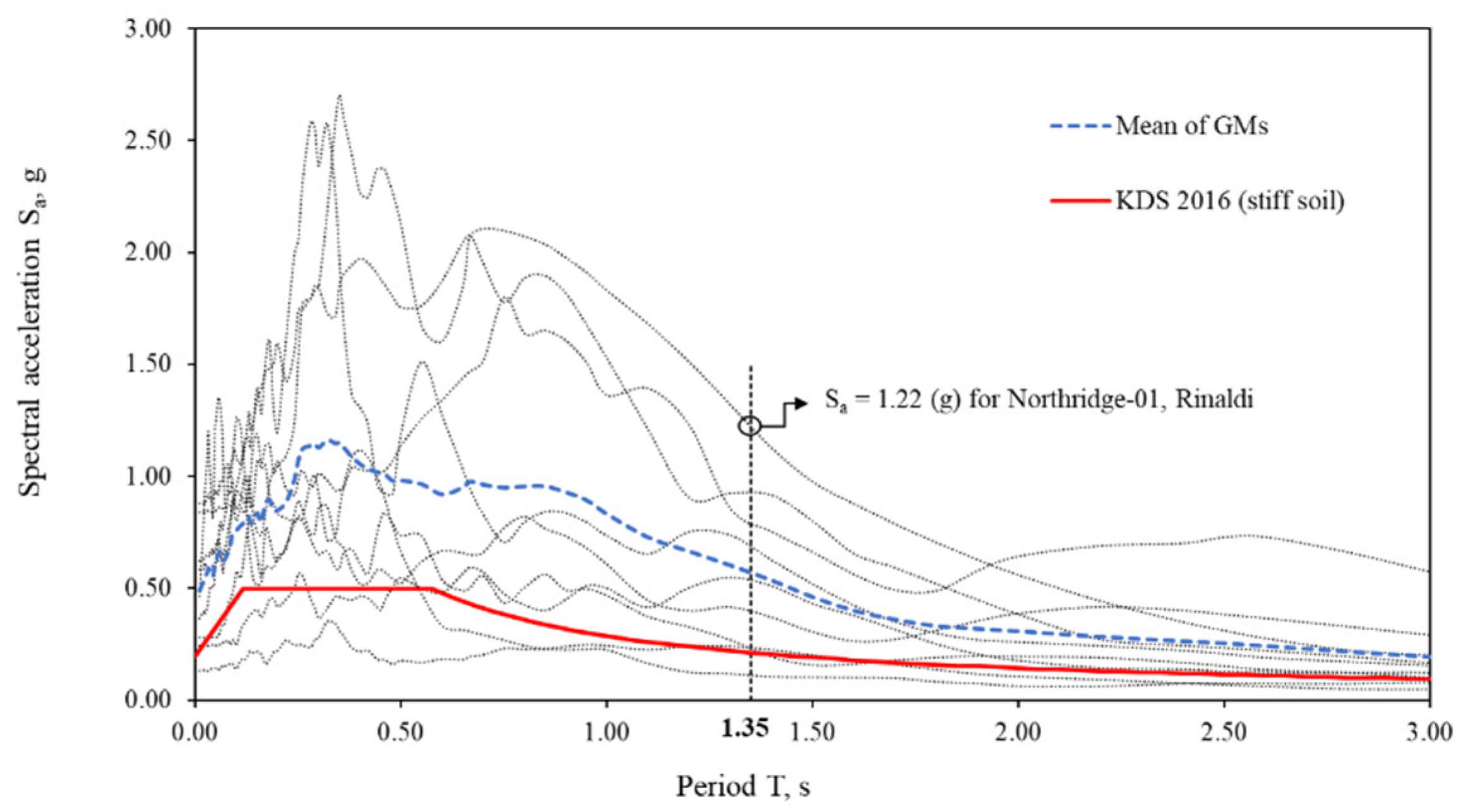
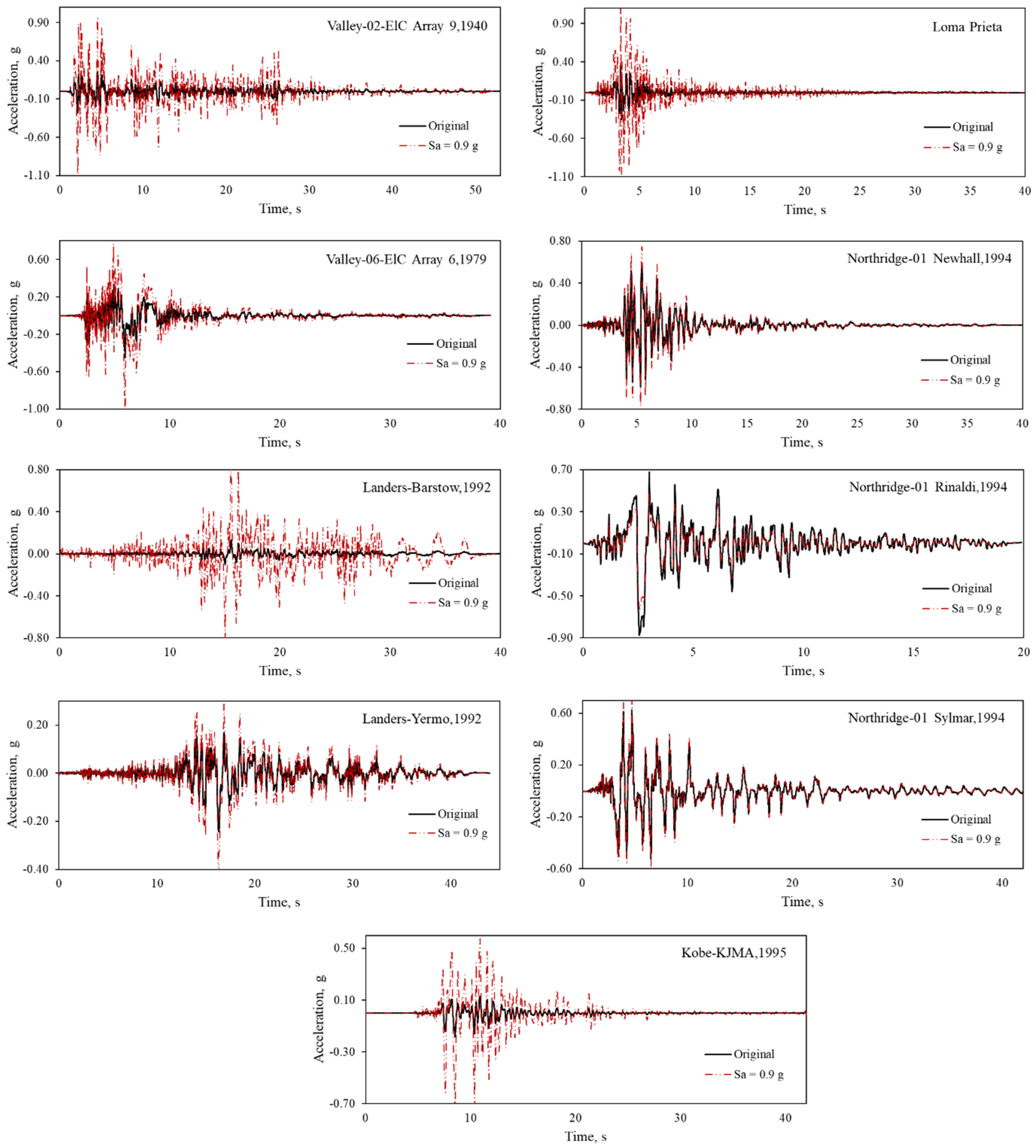
3. Recorded Ground Motions
- Compute the elastic spectral acceleration Sao at the fundamental period of the container crane (T = 1.35 s) with damping 5% from original ground motions; Table 2 shows the Sao.
- Determine the scaled factor (αi) by αi = Sai/Sao.
- The ground motions that were obtained times the original ground motion with αi are used in the time history analysis.
4. Results and Discussions
4.1. Displacement of Legs
4.2. Lateral Displacement of Portal Frames
4.3. Reaction of Legs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, S.E. Disasters and transport systems: Loss, recovery and competition at the Port of Kobe after the 1995 earthquake. J. Transp. Geogr. 2000, 8, 53–65. [Google Scholar] [CrossRef]
- Jacobs, L.D.; Kosbab, B.D.; Leon, R.T.; DesRoches, R. Seismic behavior of a jumbo container crane including uplift. Earthq. Spectra 2011, 27, 745–773. [Google Scholar] [CrossRef]
- Azeloglu, C.O.; Edincliler, A.; Sagirli, A. Investigation of seismic behavior of container crane structures by shake table tests and mathematical modeling. Shock Vib. 2014, 682647. [Google Scholar] [CrossRef]
- Kanayama, T.; Kashiwazki, A.; Shimizu, N.; Nakamaura, I.; Kobayashi, N. Large shaking table test of a container crane by strong ground excitation. Seism Eng. 1998, 364, 243–248. [Google Scholar]
- Kanayama, T.; Kashiwazaki, A. A study on the dynamic behavior of container cranes under strong earthquakes. Seism Eng. 1998, 364, 276–284. [Google Scholar]
- Kobayashi, N.; Kuribara, H.; Honda, T.; Watanabe, M. Nonlinear seismic responses of container crane including the contact problem between wheels and rails. J. Press. Vessel Technol. 2004, 126, 59–65. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees Manual, Pacific Earthquake Engineering Research Center. 2009. Available online: http://opensees.berkeley.edu/OpenSees/manuals/usermanual/ (accessed on 4 August 2018).
- Kosbab, B.D.; Jacobs, L.D.; Desroches, R.; Leon, R.T. Analysis and testing of container cranes under earthquake loads. In Proceedings of the Technical Council on Lifeline Earthquake Engineering Conference (TCLEE) 2009, Oakland, CA, USA, 28 June–1 July 2009; Volume 357, pp. 842–852. [Google Scholar] [CrossRef]
- Soderberg, E.; Jordan, M. Dockside Ship-to-Shore Cranes: Seismic Risk and Recommended Design Criteria; Liftech Consult Inc.: Oakland, CA, USA, 2007. [Google Scholar]
- Technical Note of NILIM. Study on the Seismic Performance-Based Design Methods for Container Cranes (Part 3). No.563. 2010. Available online: http://www.nilim.go.jp/english/documents (accessed on 8 July 2018).
- Tran, Q.H.; Huh, J.; Nguyen, V.B.; Haldar, A.; Kang, C.; Hwang, K.M. Comparative Study of Nonlinear Static and Time History Analyses of Typical Korean STS Container Cranes. Adv. Civ. Eng. 2018, 2176894. [Google Scholar] [CrossRef]
- Tran, Q.H.; Huh, J.; Nguyen, V.B.; Kang, C.; Ahn, J.-H.; Park, I.J. Sensitivity Analysis for Ship-to-Shore Container Crane Design. Appl. Sci. 2018, 8, 1667. [Google Scholar] [CrossRef]
- Muthukumar, S.; DesRoches, R. A Hertz contact model with non-linear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 2006, 35, 811–828. [Google Scholar] [CrossRef]
- Maison, B.F.; Kasai, K. Dynamics of pounding when two buildings collide. Earthq. Eng. Struct. Dyn. 1992, 21, 771–786. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A. Pounding of buildings in series during earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
- Park, Y.J.; Wen, Y.K.; Ang, A.H. Random vibration of hysteretic systems under bi-directional ground motions. Earthq. Eng. Struct. Dyn. 1986, 14, 543–557. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C. Nonlinear Dynamic Analysis of 3-D-Base-Isolated Structures. J. Struct. Eng. 1991, 117, 2035–2054. [Google Scholar] [CrossRef]
- Kosbab, B.D. Seismic Performance Evaluation of Port Container Cranes Allowed to Uplift; Georgia Institute of Technology: Atlanta, GA, USA, 2010. [Google Scholar]
- Jaradat, O.; Ph, D.; Pe, D.; Asce, M.; Lai, C. Crane-wharf Interaction Nonlinear Time-History Analysis for Pier E Wharf at the Port of Long Beach. In Proceedings of the Port 2013 ASCE, Seattle, WA, USA, 25–28 August 2013; pp. 1255–1264. [Google Scholar] [CrossRef]
- SAP2000. Linear and Nonlinear Static and Dynamic Analysis and Design of 3D Structures: Basic Analysis Reference Manual; CSI: Berkeyley, CA, USA, 2006. [Google Scholar]
- Edward, L.W. Three-Dimensional Static and Dynamic Analysis of Structures: A Physical Approach with Emphasis on Earthquake Engineering; CSI: Berkeley, CA, USA, 2002. [Google Scholar]
- ASCE/SEI 41. Seismic Evaluation and Retrofit of Existing Buildings; American Society of Civil Engineering: Reston, VA, USA, 2013. [Google Scholar]
- Chopra, A.K. Dynamics of Structures-Theory and Application to Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Huh, J.; Tran, Q.H.; Haldar, A.; Park, I.; Ahn, J.-H. Seismic Vulnerability Assessment of a Shallow Two-Story Underground RC Box Structure. Appl. Sci. 2017, 7, 735. [Google Scholar] [CrossRef]
- PIANC. Seismic Design Guidelines for Port Structures; A.A. Balkema: Leiden, The Netherlands, 2001. [Google Scholar]
- Suzuki, K. Earthquake Damage to Industrial Facilities and Development of Seismic and Vibration Control Technology. J. Syst. Des. Dyn. 2008, 2, 2–11. [Google Scholar] [CrossRef]
- Huh, J.; Haldar, A.; Yim, S. Effect of Uncertainty in Frequency Content and Strong Motion Duration on Structural Seismic Risks. Int. J. Syst. Eng. 2012, 2, 25–37. [Google Scholar]
- Architectural Institute of Korea. Korean Design Standard; Architectural Institute of Korea: Seoul, Korea, 2016. [Google Scholar]
- Jacobs, L.D. Shake Table Experiments for the Determination of the Seismic Response of Jumbo Container Cranes; Georgia Institute of Technology: Atlanta, GA, USA, 2010. [Google Scholar]







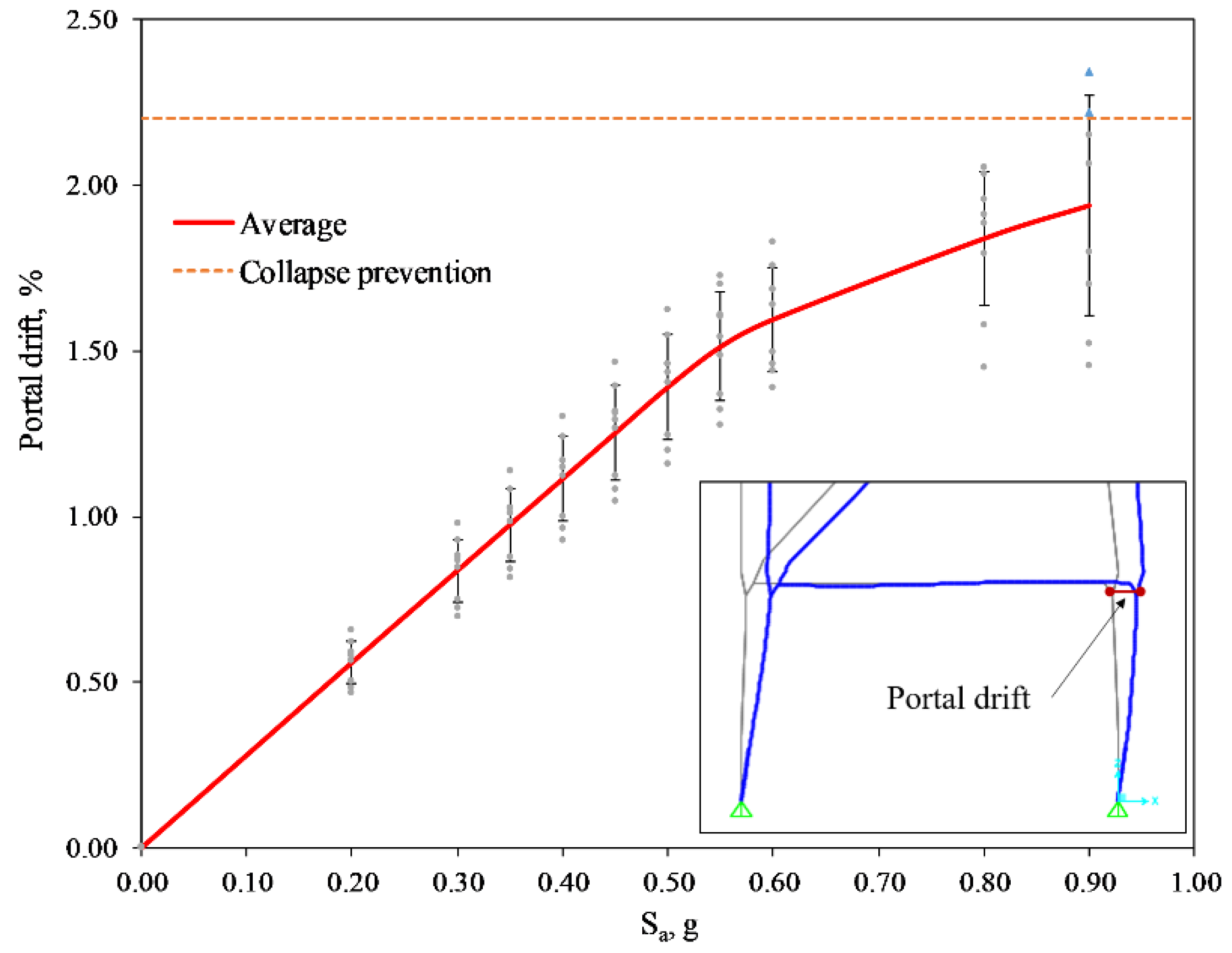




| Elements | Immediate Occupancy (IO) | Life Safety (LS) | Collapse Prevention (CP) |
|---|---|---|---|
| For vertical elements of steel moment frame (i.e., a portal column of the crane) | Minor local yielding at a few places. No fractures. Minor buckling or observable permanent distortion of members. | Hinges form. Local buckling of some beam elements. Severe joint distortion, but shear connections remain intact. A few elements may experience partial fracture. | Extensive distortion of beams and column panels. Many fractures at moment connections, but shear connections remain intact. |
| Overall damage | Light | Moderate | Severe |
| No. (GM) | Earthquake | Year | Station Name | Mag. | Rrup (km) | PGA (g) | Sao (g) (T = 1.35 s) |
|---|---|---|---|---|---|---|---|
| 1 | Imperial Valley-02 | 1940 | Elcentro Array #09 | 6.95 | 6.09 | 0.28 | 0.23 |
| 2 | Imperial Valley-06 | 1979 | Elcentro Array #06 | 6.53 | 1.35 | 0.45 | 0.39 |
| 3 | Landers | 1992 | Barstow | 7.28 | 34.86 | 0.13 | 0.11 |
| 4 | Landers | 1992 | Yermo Fire Station | 7.28 | 23.62 | 0.24 | 0.53 |
| 5 | Loma Prieta | 1989 | Gilroy-Gavilan Coll. | 6.93 | 9.96 | 0.36 | 0.23 |
| 6 | Northridge-01 | 1994 | Newhall-Fire Stn. | 6.69 | 5.92 | 0.58 | 0.68 |
| 7 | Northridge-01 | 1994 | Rinaldi Receiving Stn. | 6.69 | 6.50 | 0.87 | 1.22 |
| 8 | Northridge-01 | 1994 | Sylmar-Converter Stn. | 6.69 | 5.35 | 0.62 | 0.80 |
| 9 | Kobe_Japan | 1995 | KJMA | 6.90 | 0.96 | 0.83 | 0.92 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huh, J.; Nguyen, V.B.; Tran, Q.H.; Ahn, J.-H.; Kang, C. Effects of Boundary Condition Models on the Seismic Responses of a Container Crane. Appl. Sci. 2019, 9, 241. https://doi.org/10.3390/app9020241
Huh J, Nguyen VB, Tran QH, Ahn J-H, Kang C. Effects of Boundary Condition Models on the Seismic Responses of a Container Crane. Applied Sciences. 2019; 9(2):241. https://doi.org/10.3390/app9020241
Chicago/Turabian StyleHuh, Jungwon, Van Bac Nguyen, Quang Huy Tran, Jin-Hee Ahn, and Choonghyun Kang. 2019. "Effects of Boundary Condition Models on the Seismic Responses of a Container Crane" Applied Sciences 9, no. 2: 241. https://doi.org/10.3390/app9020241
APA StyleHuh, J., Nguyen, V. B., Tran, Q. H., Ahn, J.-H., & Kang, C. (2019). Effects of Boundary Condition Models on the Seismic Responses of a Container Crane. Applied Sciences, 9(2), 241. https://doi.org/10.3390/app9020241






