Microscopic Multiple Fatigue Crack Simulation and Macroscopic Damage Evolution of Concrete Beam

Abstract

Microcracks in concrete can coalesce into larger cracks that further propagate under repetitive load cycles. Complex process of crack formation and growth are essentially involved in the failure mechanism of concrete. Understanding the crack formation and propagation is one of the core issues in fatigue damage evaluation of concrete materials and components. In this regard, a numerical model was formulated to simulate the thorough failure process, ranging from microcracks growth, crack coalescence, macrocrack formation and propagation, to the final rupture. This model is applied to simulate the fatigue rupture of three-point bending concrete beams at different stress levels. Numerical results are qualitatively consistent with the experimental observations published in literature. Furthermore, in the framework of damage mechanics, one damage variable is defined to reflect stiffness reduction caused by fatigue loading. S-N curve is subsequently computed and the macroscopic damage evolution of concrete beams are achieved. By employing the combined approaches of fracture mechanics and damage mechanics, made possible is the damage evolution of concrete beam as well as the microscopic multiple fatigue crack simulation. The proposed approach has the potential to be applied to the fatigue life assessment of materials and components at various scales in engineering practice.

1. Introduction

Fatigue problems are prevalent in the service life of concrete structures such as bridge slabs, highway pavements and offshore structures [1,2,3]. Concrete lies in the category of quasi-brittle material and it is microscopically heterogeneous. Combination of concrete and other materials are extensively applied in engineering practice [4,5,6]. A large number of flaws are inevitably created before the loading, which can be considerably attributed to the loss of concrete moisture [7]. Under repetitive fatigue load cycles, pre-existing flaws or microcracks in concrete can trigger the initiation, coalesce into larger cracks that further propagate, ultimately leading to the final rupture. The so-called fatigue damage accumulation is a progressive, permanent and localized internal changes in the concrete. Complex process of crack formation and growth are essentially involved in the failure mechanism of concrete. Understanding the crack formation and propagation is one of the core issues in fatigue damage evaluation of concrete materials and components. How crack progression throughout the fatigue life affects and causes the final failure modes remains to be clarified.

The approaches of damage mechanics and fracture mechanics are generally employed to model the progressive fatigue accumulation in concrete materials [8,9,10,11,12]. In the framework of damage mechanics, a damage variable is required to be defined. A physically reasonable damage evolution law needs to be formulated such that the progressive material degradation caused by microcrack initiation, coalescence and propagation is reflected through the process. Both the microcrack evolution and stiffness reduction simultaneously reflect the material deterioration, microscopically and macroscopically. It should be pointed out that, in the concepts of damage mechanics, it is assumed that there are no pre-existing microcracks or flaws in material specimens. Damage evolution is a continuous process that describes damage or strain localization and characterizes the fatigue behavior of concrete, though microcracks are randomly distributed in specimens.

A series of fatigue models have been formulated based on thermodynamics concepts in the framework of damage mechanics [13,14]. Progressive stiffness reduction is straightforwardly reflected in these models. Nevertheless, most of these models are empirical and lack of physical basis. Damage parameters are highly dependent on experimental data. In recent years, state-of-the-art experimental technology has been introduced to this field. By using industrial computed tomography (ICT) technology, spatial distribution of fatigue cracks within concrete is observed. Subsequently a macroscopic fatigue damage parameter D is subsequently defined based on the quantitative description method of the overall distribution of fatigue cracks in concrete [15]. This combined micro–macro approach can better characterize the evolution process of material fatigue damage of concrete under compression from the overall distribution of fatigue cracks. A refined engineering rule for the assessment of remaining fatigue life of concrete under compressive cyclic loading with varying amplitude is proposed in [16]. The proposed empirical rule is derived based on a combined numerical and experimental investigation of the loading sequence effect. The equivalent tensile strain rate is adopted to govern the fatigue damage evolution in the applied modeling approach. It is generally accepted that models derived from physical principles are relatively reliable compared to the empirical models. These physical laws include energy principles, dimensional analysis as well as similitude concepts. It is noteworthy, a fatigue model for plain concrete under variable amplitude loading is proposed in [17] by unifying the concepts of damage mechanics and fracture mechanics through an energy equivalence. The whole work is on the basis of thermodynamic framework using the principles of dimensional analysis and self-similarity. A closed form expression for dual dissipation potential is derived. A damage evolution law is further proposed to compute damage in the volume element subjected to fatigue loading. This proposed model incorporates the complex behavior of concrete under fatigue and provides a more rational method for fatigue life evaluation of concrete materials and components. Some other physically based constitutive modeling of concrete fatigue can be found in [9,14,18].

Fracture mechanics serves the ideal mechanistic tool for concrete fatigue damage evolution, considering the inherent microcracks and flaws in concrete. Fracture mechanics approach is also extensively applied to crack initiation, crack growth rate, crack density evolution and stiffness degradation in other materials such as composite laminates [19,20,21]. The fatigue models in fracture mechanics are mostly the empirical Paris type equation, in which the crack growth rate with respect to number of fatigue load cycles is correlated to the stress intensity factor range. Not surprisingly, the Paris law is empirically formulated on the basis of metallic fatigue. Efforts have been taken to modify the Paris law by introducing extra crack growth influencing parameters [22,23]. Based on previous models, a newly proposed fatigue crack propagation model for concrete beam incorporates the effect of loading frequency of applied load, loading history as well as size effect parameters. An analytical crack growth model is developed to predict fatigue behavior of quasi-brittle materials in [24]. Early work related to concrete fatigue implies that parameters in the classical power law are dependent on micro-structural size, crack size and size scale [23]. An improved crack propagation model for plain concrete under fatigue loading is derived in [25], considering the effect of critical energy dissipation in fatigue. The so-called fatigue fracture energy is able to capture the observed size effect in concrete fatigue. The model is analytical and influence of fracture process zone is incorporated in the proposed formulation. An irreversible cohesive zone model for interface fatigue crack growth simulation is developed in [26]. The improved CZM is physically based and the traction–separation behavior does not follow a predefined approach. This proposed model for the computational simulation of FCG provides a crucial step in the direction of mechanistic mode developments in the area of fatigue crack growth. A predictive cohesive modeling framework for corrosion fatigue is proposed in [27]. These CZMs could also offer reference for concrete fatigue modeling.

In recent years, it is noteworthy that efforts are particularly being devoted to both microscopic and macroscopic aspects [28,29,30]. A microplane constitutive damage model is developed in [28]. The proposed model is able to describe both the fatigue crack growth and the nonlinear triaxial damage behavior of concrete. A discrete element modeling approach for fatigue damage growth in cemented materials are developed in [29]. The model formulation is based on coupling damage mechanics and plasticity theory and combining with a fatigue damage evolution law to describe the degrading response of cemented materials subjected to cyclic loading. Global fatigue damage response as well as microstructural effects could be reflected. A physical stochastic damage model for concrete subjected fatigue loading is formulated in [30]. It could be put in the framework of mesoscopic stochastic fracture models that are capable of reflecting the general nonlinearity and randomness in the mechanical behavior of concrete. It is fair to say, our work is motivated by the aforementioned efforts.

In this context, the purpose of approaches related to damage or fracture mechanics is to develop effective models that are able to reflect the progressive material degradation under fatigue loading. It shall be pointed out that the model is stipulated to pure concrete materials, the internal longitudinal and transverse reinforcements with related effects [4,5,6] are not considered in the present work. Based on these proposed models, attempts have been particularly made to the numerical simulation of fatigue [18,31]. The advantage of implementing a developed fatigue model in available finite element codes is that both constitutive equations and interface models can be included in the numerical simulation. The fatigue and mechanical behaviors of concrete materials and components are predicted through the numerical implementation in commercial FE software. A numerical procedure is developed to simulate crack propagation behaviors at the concrete aggregate-matrix interface in [31]. It shall be pointed out that, modeling of single aggregate-matrix interface crack is studied. Based on the conclusions in [31], it is assumed that interface crack can be mapped into idealized crack along the main axis of aggregate to solve the multiple crack coalescence and propagation in concrete. This leads to the work described in [32]. On the basis of these work, microscopic multiple fatigue crack simulation and macroscopic damage evolution of concrete beam subjected to cyclic loads is investigated in the present work. We are mainly focused on the fatigue damage analysis microscopically and macroscopically. In this regard, the aim of the present work is to define a damage variable that reflect the fatigue evolution of concrete specimens, on the basis of the multiple crack simulation in concrete beams.

The work presented in this paper is structured as follows: described in Section 2 are the numerical model for multiple crack simulation and fatigue crack growth law. Numerical modeling of three-point bending beams are presented in Section 3. Macroscopic fatigue damage analysis is discussed in Section 4. The main conclusions are summarized in Section 5.

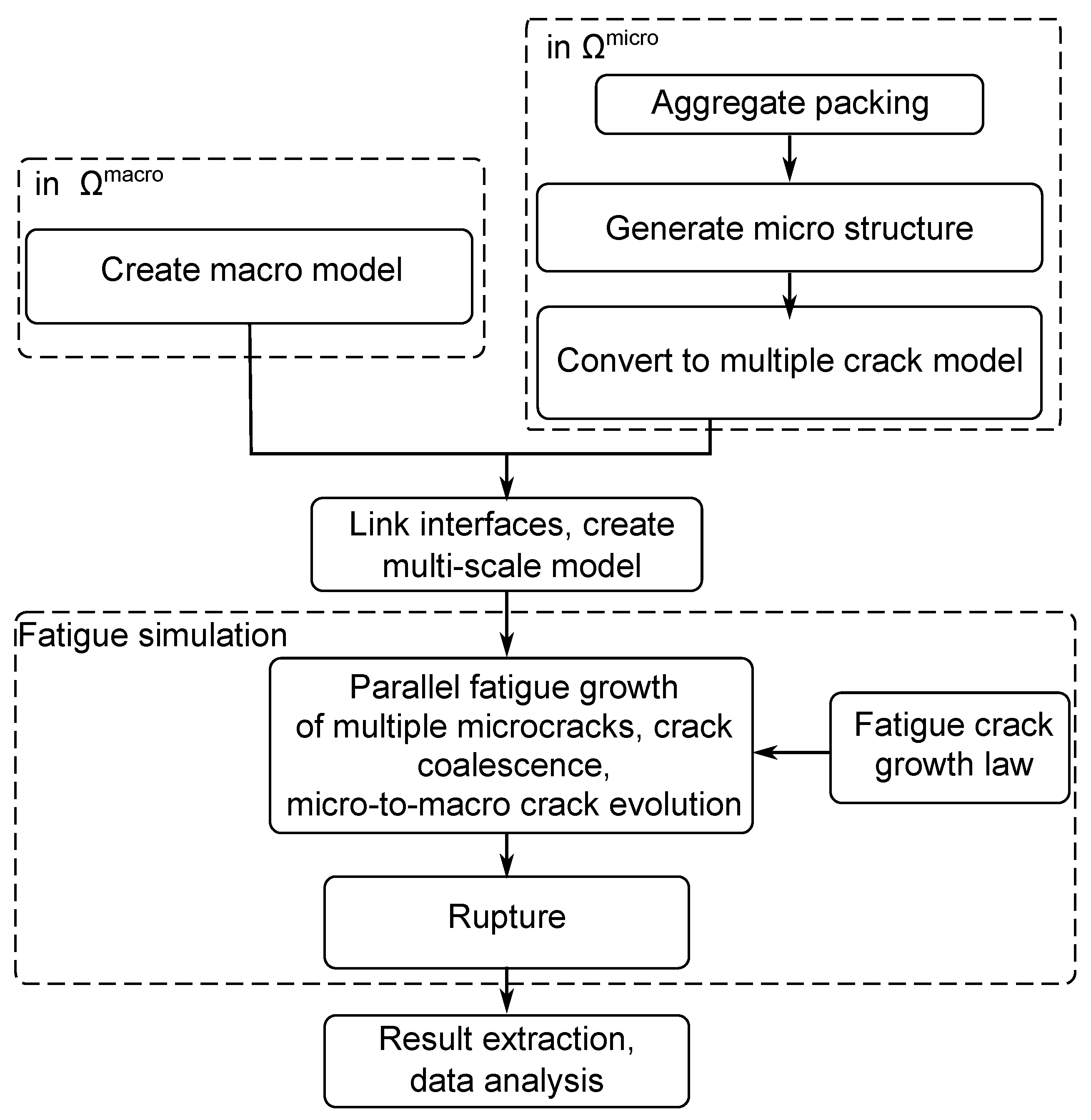
2. Microscopic Multiple Crack Simulation and Fatigue Crack Growth Law

At early age, initial microcracks usually emerge at the interface of cement paste and aggregate due to the natural shrinkage combined with other factors at the time of curing. The crack could propagate along the interface or penetrate into matrix or aggregate. In our previous work [31], modeling of one crack propagation in concrete is made possible (Figure 1). The multiple-phase structure of concrete material could be simplified as a continuum with multiple microcracks. Here we are mainly focused on simulation of multiple cracks as well as their parallel growths under fatigue loads. Figure 2 shows an example of the multiple crack model for concrete material.

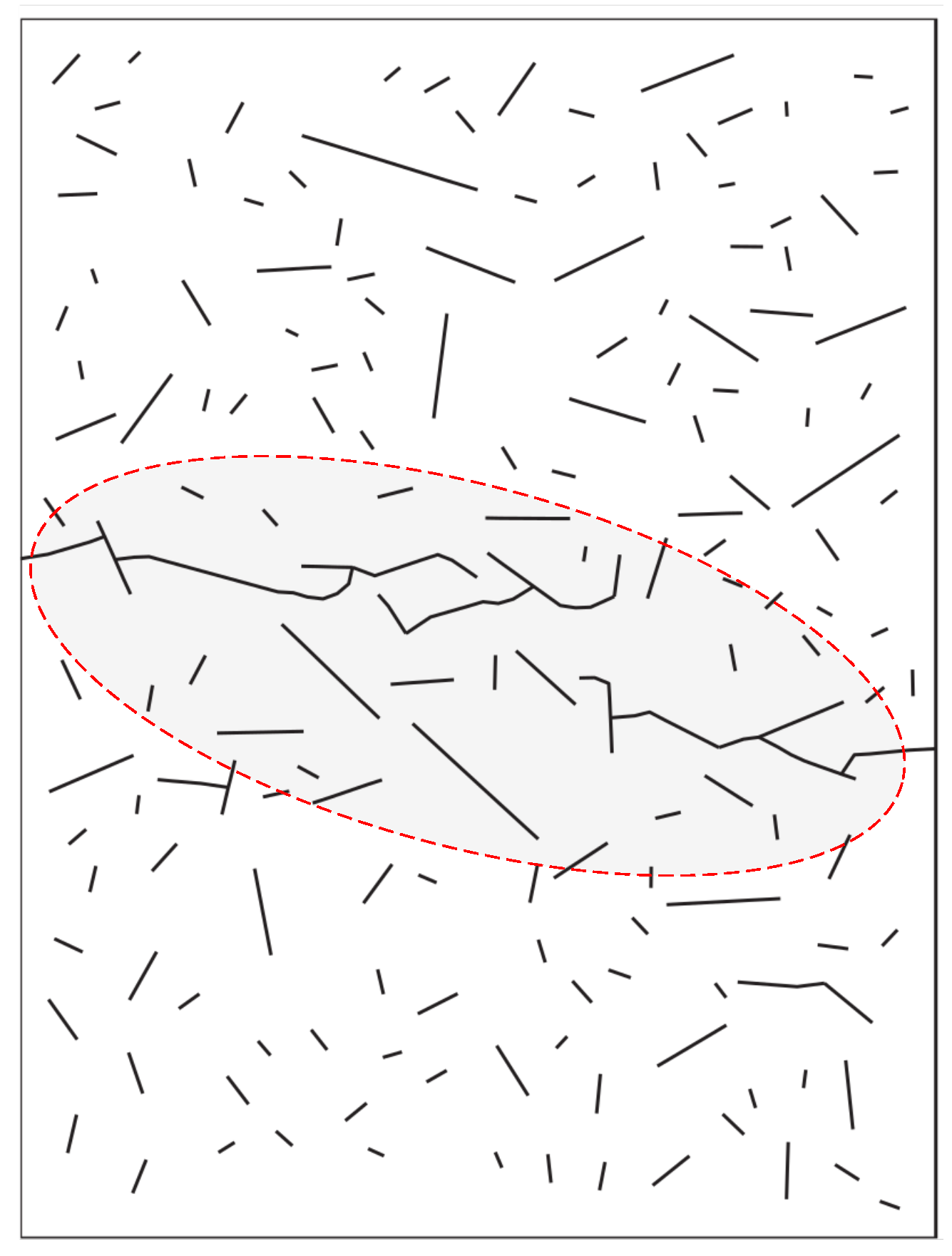
2.1. Modeling of Multiple Crack Growth

When a number of microcracks start to propagate simultaneously, induced by external fatigue load, the morphology of crack linking with each other may be very complex. However, it could be decomposed into three basic modes. As shown in Figure 3a, the two endpoints of Crack 1 and 2 meet together such that the two cracks merge into a single crack. Figure 3b shows Crack 4 is growing intersecting with Crack 3. In this situation, stress singularity at the intersected endpoint of Crack 4 vanishes—this crack tip will stop growing. Therefore, the situation of Figure 3c will not happen in the present work, though it could be simulated as well.

In the present study, a program has been developed comprehensively to achieve all crack growing situations, including detecting and treating crack merging and intersecting, multiple crack growth, and detecting boundary edges [32]. Presented in the highlighted area of Figure 2 is a relatively complicated situation of crack growth and multiple crack linking. It could be seen that the method could successfully simulate the concurrent growth of microcracks, crack coalescence, the formulation and growth of macrocracks, and the final rupture. Details of the approach can be found in [31,32]. On the basis of the formulated multiple crack simulation, we are mainly focused on the fatigue crack growth in concrete materials.

2.2. Fatigue Crack Growth Law

The fatigue crack propagation law is formulated by Paris and Erdogan based on experiments [33], which points out the relationship between stress intensity factor and crack growth rate, namely

$$\frac{da}{dN}=C{\left(\mathsf{\Delta }K\right)}^m.$$

(1)

Here $da/dN$ refers to the crack growth rate. a is the current crack length, and $\mathsf{\Delta }K$ is the incremental stress intensity factor. C and m are the empirical fatigue constants obtained from material tests. In this paper, a modified Paris law is introduced to govern the growth behavior of microcracks. The whole crack growth process is divided into three stages as displayed in Figure 4.

• In the low rate zone (Stage I) $\mathsf{\Delta }K<\mathsf{\Delta }{K}_{\mathrm{th},1}$, the crack is set not to propagate because the rate is very low. The fatigue threshold is chosen as

  $$\mathsf{\Delta }{K}_{\mathrm{th}1,J}=0.2K_{\mathrm{C},J}.$$

  (2)
• In the medium rate zone (Stage II) $\mathsf{\Delta }K>\mathsf{\Delta }{K}_{\mathrm{th},1}$ and $\mathsf{\Delta }K<\mathsf{\Delta }{K}_{\mathrm{th},2}$, the crack growth follows the Paris law [33].

  $$\frac{d{a}_J}{dN}=C{\left(\mathsf{\Delta }{K}_J\right)}^m.$$

  (3)

  According to the experiments, the value of m for concrete is generally between 1.0 and 2.5. In order to make the crack growth rate lies between ${10}^{-5}$ $\mathrm{mm}/\mathrm{c}$ and ${10}^{-2}$ $\mathrm{mm}/\mathrm{c}$ [12,34], the empirical parameters C and m are adopted as $C={10}^{-8}$, $m=1.5$.
• In the high rate zone (Stage III) $\mathsf{\Delta }K>\mathsf{\Delta }{K}_{\mathrm{th},2}$, the crack will quickly propagate in an unstable fashion, finally lead to rupture. For the convenience of numerical simulation, here in this zone, the growth rate is practically set to be $1.2\times {10}^{-3}$ $\mathrm{mm}/\mathrm{c}$. Also, the 2nd fatigue threshold $\mathsf{\Delta }{K}_{\mathrm{th},2}$ is set to be

  $$\mathsf{\Delta }{K}_{\mathrm{th}2,J}=0.8K_{\mathrm{C},J}.$$

  (4)

Microcracks subjected to repetitive load, start to propagate, though advancement of some cracks can be ignored. Subsequently, these cracks may coalesce into several macrocracks and finally reach to the stage of final rupture. In the actual computing process, one ‘computational step’ is not equal to one ‘load cycle step’. Since the crack shows a ‘significant’ growth only after the load has been repeated for a certain number of cycles, $\mathsf{\Delta }a$-controlled rather than N-controlled strategy is used here. In each step, marked by superscript i, the growth length of the crack that has the highest rate, assuming to be the ${\beta }^i-\mathrm{th}$ crack, is controlled to be $\mathsf{\Delta }{a}^i$. The number of load cycles $\mathsf{\Delta }{N}^i$ is determined by the following formula

$$\mathsf{\Delta }{N}^i=\frac{\mathsf{\Delta }{a}^i}{C{\left(\mathsf{\Delta }{K}_{\beta }\right)}^m}.$$

(5)

Then, incremental lengths for all cracks in this step could be calculated as

$$\mathsf{\Delta }{a}_J^{\left(i\right)}=C{\left(\mathsf{\Delta }{K}_J^{\left(i\right)}\right)}^m\mathsf{\Delta }{N}^{\left(i\right)}.$$

(6)

Summing up to get the total fatigue life

$$N=\sum \mathsf{\Delta }{N}^i$$

(7)

Displayed in Figure 5 is the flowchart of numerical algorithm for multiple fatigue crack simulation. It shall be emphasized that both macroscopic and microscopic models are created such that a multi-scale model is further created via interface linking. Fatigue crack growth law is subsequently adopted to study the multiple microcrack growth, coalescence and macrocrack formation. After the final rupture is reached, result extraction and data analysis is made possible.

3. Fatigue Modeling of Three-Point Bending Beams

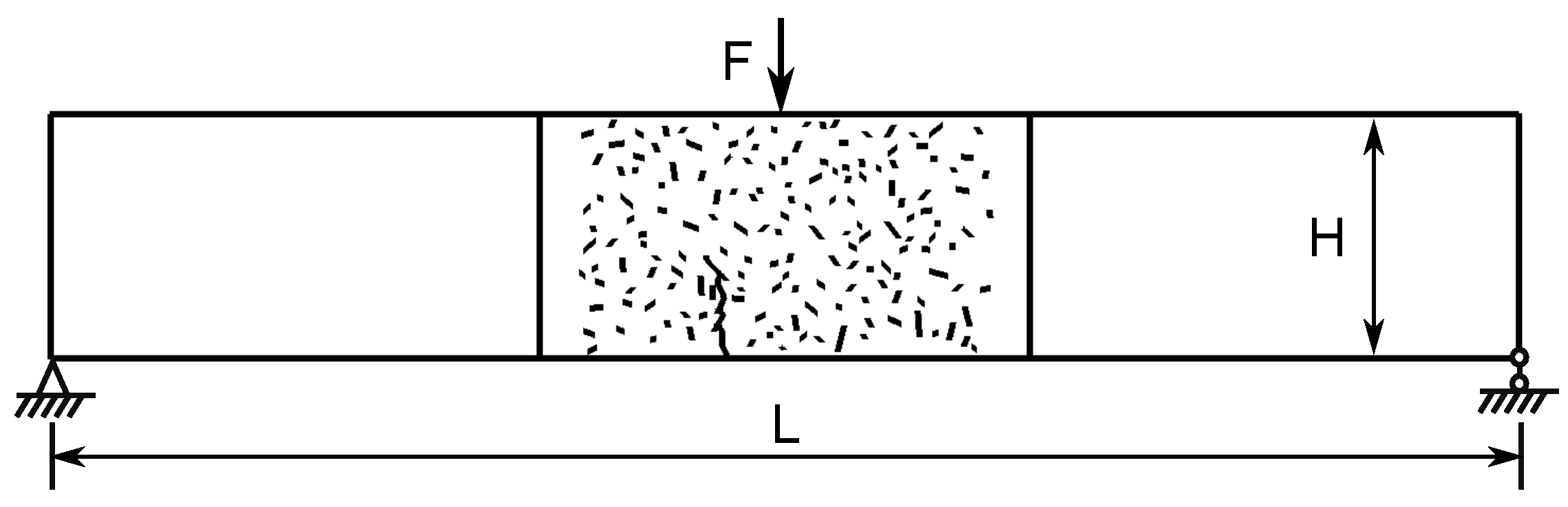
3.1. Three-Point Bending Beam Model

Beam is an important object in the study of concrete fatigue. Liner elastic constitution law is adopted for concrete. The model discussed in this paper is a three-point bending beam with a length of L, height of H and thickness of T. A concentrated force F is applied at the mid-span point, refer to Figure 6.

In order to improve the computational efficiency, the whole model is divided into two areas, the macro-scale area ${\mathsf{\Omega }}^{\mathrm{Macro}}$(side area) and the micro-scale area ${\mathsf{\Omega }}^{\mathrm{Micro}}$ (middle area). The difference between the two regions is: (1) The macro-scale region is considered as homogeneous material, while the micro-scale region is heterogeneous, meaning that this area contains randomly distributed microcracks, (2) the typical element size d of the two regions is different, $d^{\mathrm{Macro}}$ is usually about 10 to 40 times of $d^{\mathrm{Micro}}$. The element size of middle area is usually about 0.2–0.4 mm. Eight-node quadrilateral elements are subsequently generated.

In order to accurately simulate the stress field at the crack tip and to obtain stress intensity factor in the microscale area, singular elements needs to be added at crack tips, as shown in the Figure 7d. On the interface between these two regions, the connections are made by forcing the displacements to be equal. On the interface, the nodes of the coarse mesh are the master nodes, and the nodes of the fine mesh are the slave nodes. That is to say, for any microscopic node $A\in \partial {\mathsf{\Omega }}^{\mathrm{Micro}}$ locating at $\mathbf{x}$, its displacement $u^{\mathrm{Micro}}$ is forced to be

$$u^{\mathrm{Micro}}\left(\mathbf{x}\right)=\sum _i{N}_i^{\mathrm{Macro}}\left(\mathbf{x}\right)u_i^{\mathrm{Macro}}.$$

(8)

Figure 8 shows a stress contour of a bending concrete beam at the stage of fatigue rupture. It could be seen that in a global sense, the numerical results agree with the corresponding conclusion from classical beam theory. Moreover, the stress level may fluctuate in the local area, which can be attributed to the microscopic heterogeneity in concrete material.

3.2. Case Design

As shown in Figure 6, beam height $H=200$ mm, length $L=$ 800 mm, The concentrated sinusoidal loading is located at the middle span, and the loading frequency is 10 Hz. The parameter

$$R=F_{\min }/F_{\max }$$

is chosen to be constant 0.1, where $F_{\min }$ and $F_{\max }$ denote the maximum and minimum force per cycle, respectively. Considering that

$$R=\frac{F_{\min }}{F_{\max }}=\frac{K_{J,\min }}{K_{J,\max }},$$

(9)

We have

$$\mathsf{\Delta }{K}_J=K_{J,\max }(1-R).$$

(10)

That is to say, in each step, we can simply apply $F_{\max }$ on the beam to get $\mathsf{\Delta }{K}_J$ at all crack tips. Also, stress level S is introduced as

$$S=\frac{F_{\max }}{F_{\mathrm{u}}}.$$

(11)

Here $F_{\mathrm{u}}$ is the bending capacity of this beam. For three-point bending case, $F_{\mathrm{u}}$ could be estimated as 100 N via the formula

$$F_{\mathrm{u}}={\sigma }_{\mathrm{u}}\frac{2T·H^2}{3L},$$

(12)

where ${\sigma }_{\mathrm{u}}$ is the tensile strength of concrete. In this paper, the value of S is tuned from 0.1 to 0.9, to investigate the influence of fatigue stress ratio.

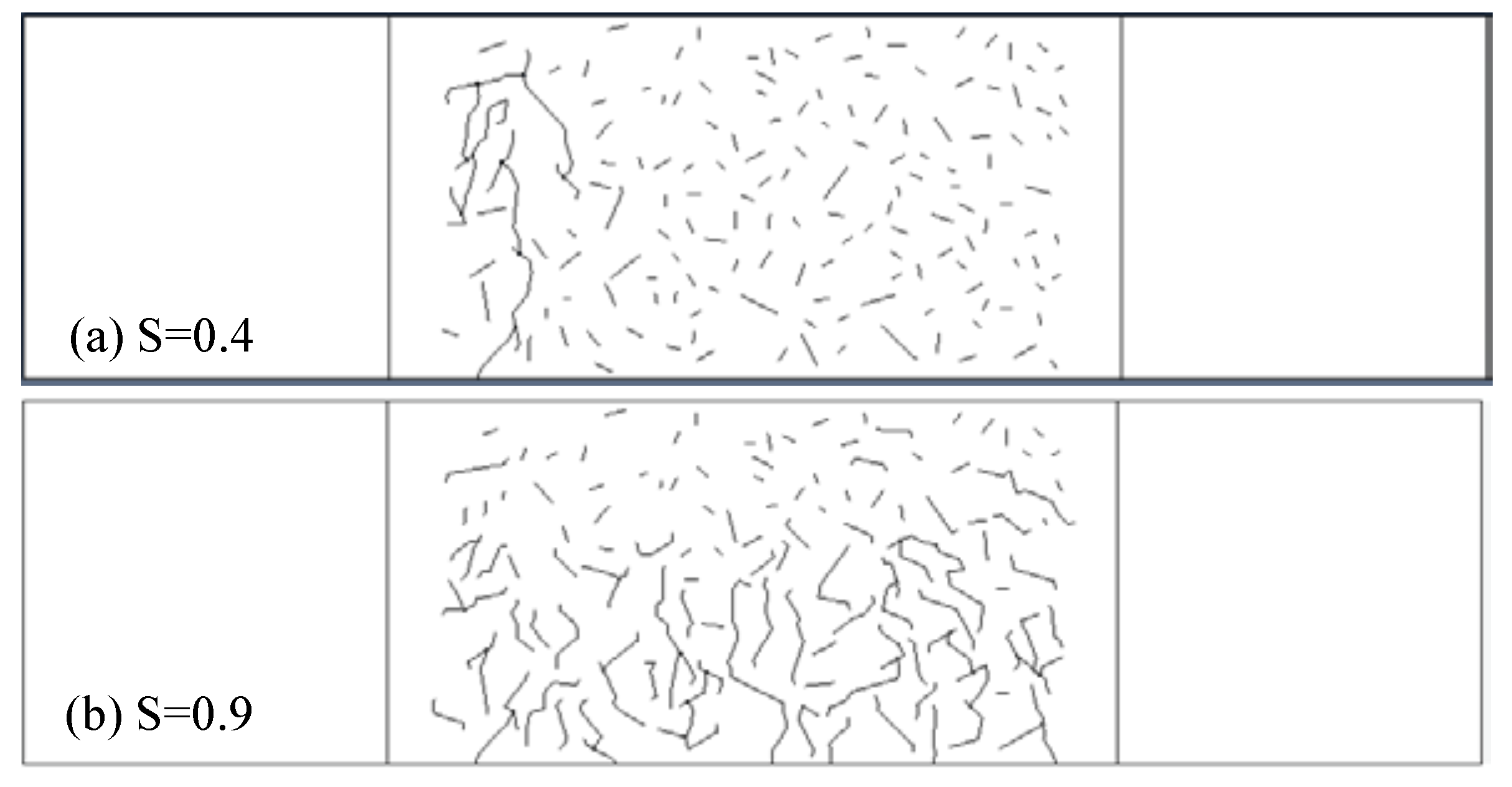
3.3. Fatigue Failure Analysis

In order to perform fatigue failure analysis, it shall be defined that the ultimate fatigue load is reached once the nominal stiffness of the beam is only 5% left. The so-called macroscopic mechanical behaviors are substantially influenced by microscopic fatigue crack growth. A cycle-jump technique is employed to model load cycles such that the computational cost can be saved. In the simulations of regular cyclic loading scenarios with the same loading range, a cycle can be adopted to reduce the computational cost. As an example, the results at the stress level $S=0.4$ are shown here. The three-point bending concrete beam is ruptured after 42,000 load cycles. Figure 9 shows crack propagation diagrams of the whole failure process, where $N_f$ is the fatigue life of this specimen.

There are naturally a large number of distributed microscopic cracks in concrete, usually occurring on the mortar-aggregate interfaces during cement hydration process. Under the fatigue load, microcracks in tensile zone of the beam start to stably grow at a medium rate (Stage II) according to Paris law, as shown in Figure 9a,b. As the number of fatigue load increases, crack coalescence initially takes place at the lower left corner of the specimen. Localized damage subsequently appears. It shall be pointed out that, crack coalescence does not necessarily occur in the designated area. The localized damage at the lower left corner of the specimen here is a reflection of random distribution of microcracks in concrete. To be able to describe this stochastic behavior is the strongest point of our algorithm. Once macrocrack appears, fatigue crack growth start to accelerate (but still in a stable fashion), gradually entering into Stage III, as shown in Figure 9c,d. The formation of macrocrack can be firstly seen in Figure 9c. Its further propagation will lead to final beam rupture. It should be noted that at this stage, cracks in other areas still grow at a low or medium rate. At later period of fatigue rupture, the neutral axis gradually moves up, the macrocrack on the left side propagates at a high rate, and the localized damage (on the upper left side) increases dramatically, which eventually leads to the rupture of beam, as shown in Figure 9e.

It is noteworthy that the unsymmetrical pattern of crack formation and propagation is clearly displayed in the middle area of concrete beam. It is reflective of the microscopically stochastic phenomenon of crack distribution. This is the strong point that our proposed model is able to achieve.

3.4. Influence of Stress Level on Fatigue Behaviors

Figure 10 shows different failure patterns under various stress levels, where (a) and (b) represent the final crack configurations at low stress level ($S=0.4$) and high stress level ($S=0.9$), respectively.

It could be observed that under low fatigue stress level, a relatively smaller number of microcracks propagate during the failure process. Rupture of the beam is mainly caused by one macrocrack, so the damage is highly localized. While in high fatigue stress situation, it could be seen that a relatively larger number of cracks have been propagating, thus macrocracks appear in large quantities. In rupture state, macrocracks scatter over the entire area. Calculated failure modes are basically consistent with the observed ones in literature [35], which could verify the effectiveness of the numerical model. In the experimental observation, macrocracks firstly emerge at certain local areas. Further crack progression will lead to final failure. It shall be emphasized that the experimental observation phenomenologically agrees with our numerical results. Quantitative agreement is limited.

4. Fatigue Damage Analysis of Concrete Beams

Numerical experiments are executed under different fatigue stress levels varying from $S=0.1$ to $S=0.9$, from which the fatigue life could be extracted for each stress level. Made possible is the S-N curve that is for engineering reference. Furthermore, since the whole fatigue response has been recorded, macroscopic damage evolution could also be quantitatively analyzed.

4.1. Fatigue Life and S-N Curve

Table 1. Stress level of load and corresponding fatigue life.

No.	S	${\mathit{F}}_{\mathbf{max}}$ (N)	${\mathit{N}}_{\mathbf{f}}$ (${10}^3$)
1	0.9	90	3
2	0.8	80	5
3	0.7	70	10
4	0.6	60	25
5	0.5	50	36
6	0.4	40	42
7	0.3	30	66
8	0.2	20	122
9	0.1	10	201

lists the calculated results of the numerical experiments. It shows that when the stress level S of the fatigue load decreases from 0.9 to 0.1, the fatigue life of specimen gradually increases from 3000 to 201,000 cycles, refer to Figure 11.

S-N curve could also be plotted by fitting above data using the classical S-N exponential formula. Note each point represents the fatigue life under designated stress level.

$$N_{\mathrm{f}}=\alpha exp(-\beta S)$$

(13)

Here we have $\alpha =3.56\times {10}^5$ and $\beta =5.12$.

4.2. Macroscopic Damage Analysis

Though S-N curve is enough for engineering use to estimate remaining life, it has some limits when it comes to evaluating the current performance state of structure. This is because fatigue life estimation based on S-N curve has an implicit assumption that the fatigue damage is linearly accumulated. In fact, the fatigue damage evolution is a nonlinear process. The period from microcracks propagation and coalescence to the formation of macroscopic cracks is relatively longer, while the speed from the initiation of macrocracks to the final rupture is relatively fast. In this sense, damage evolution based fatigue evaluation is required. According to Lemaitre’s concept of damage variable [36], damage is related to stiffness reduction [37,38].

$$D=1-\frac{\tilde{K}}{K_0}$$

(14)

Here, D is the damage variable, $K_0$ denotes the effective stiffness in defect-free state, and $\tilde{K}$ is the stiffness in damaged state. Obviously, the larger D grows, especially near 1, the closer material or structure is to the failure state. For three-point bending beams, effective stiffness could be defined as

$$\tilde{K}=\frac{F}{d}.$$

(15)

Here, F and d are mid-span force and displacement respectively, which could be extracted from calculated database. In defect-free or damage-free status, $d_0$ could be obtained as

$$d_0=\frac{F{L}^3}{48EI},$$

(16)

where E is the initial Young’s modulus of concrete.

Curves of damage evolution at different stress levels are plotted in Figure 12. It can be observed that the fatigue damage evolution of concrete can be roughly divided into three stages. When the cycle ratio $n/N_f$ is less than 0.2, the damage value is relatively small, and the damage evolution rate is also slow. Growth rate of most microcracks fall in zone I. Crack coalescence has not occurred yet. With the increase of load cycles, damage evolution enters into a stable stage that the value of damage increases linearly with the number of load cycles. In this period, microscopic crack growth rate may vary from area to area (some areas in zone II, some still in zone I). Microcracks begin to link with others, gradually forming macroscopic cracks (crack coalescence). When cycle ratio reaches 0.8, structure enters into an unstable crack growth stage. Macroscopic cracks continue to propagate forward, merging small or microcracks along the rupture path. Correspondingly, the value of damage rapidly approaches the value of 1, finally leading to the fracture of beams.

5. Conclusions

The numerical model developed in this paper is directly based on microscopic mechanism of concrete fatigue. Thus it can simulate the fatigue growth of multiple microcracks in concrete, as well as the macroscopic damage evolution. The numerical method is applied to three-point bending beams. Results clearly show that, no matter from macroscopic or microscopic view, fatigue rupture of beams endures three stages: (1) Microcrack growth and coalescence, (2) the formulation of macrocracks and stable fatigue damage evolution, and (3) unstable crack growth and the final fracture of concrete beam.

It is also observed from the simulation that different stress levels of fatigue load can lead to different failure patterns. At low stress level, the rupture of beam is mainly caused by one (or several) macrocrack and damage is highly localized. For high fatigue stress situation, macrocracks appear in large quantities, mostly scattering over the entire area. The computed results are consistent with experimental observation in published literature.

The numerical model could be used to calculate S-N curve. The macroscopic damage evolution of concrete beams is achieved. Based on the results of damage evolution, structural fatigue assessment is also made possible.

Although the present work is about plain concrete, the method can also be applied to other types of concretes, such as high-performance concrete or fiber reinforce concrete, or even masonry materials and structures, as long as the fatigue failure is mainly caused by the growth of microcracks. Last but not least, it shall be pointed out that the numerical modeling is currently stipulated to 2D problems. Computational cost will be substantially added once it comes to 3D. Computational efficiency shall be further improved in our forthcoming work.