3.1. Methodology for Estimating Alkali Ions in the Concrete Pore Solution
The chemical compositions of the seven common Portland cements are shown in
Table 1. Clinker phases were calculated by using Bogue equations are shown in
Table 2. According to Escalante-Garcia et al. [
11], estimated Ca/Si ratios from QXDA, TMBC, and EDS are similar but higher than the Ca/Si ratio obtained by using Bogue equations. Thus, it can be assessed that the results that are obtained using the Bogue calculation showed lower Ca/Si ratios, since the alite predicted content in the cement were lower than the actual one [
11].
Table 2 also shows the clinker phase composition assumed by Taylor in his work [
8]. This is a very rough estimation that is only applicable for the cement, for which the chemical composition is not available. Therefore, the present estimation method takes into account the cement chemical composition, in order to get a reliable estimation of the pore solution alkalinity.
It is evident that the main clinker phase, C3S, assumed by Taylor, was moderately reduced compared to that calculated in the present work. This is due to the higher amount of alite present in the modern Portland clinkers. Then, it is recommended that the calculated values of the clinker phase compositions for each cement.
The liquid phase contains several ions, where the alkali ions, K
+ and Na
+, and hydroxyl, and OH
− are usually the most dominant ions [
13,
14] in the pore solution. Both of them, K
+ and Na
+, are the most abundant cations in the pore solution, and the charge is mainly balanced by the hydroxyl ions.
Also, the alkalis released from the aggregates could increase the hydroxyl ion concentrations in the concrete [
15,
16]. In particular, the content of the alkali released is enhanced by the high alkalinity of the solution [
15]. Also, for the concrete affected by ASR, alkalis are released with the accompanying dissolution of silicate anions [
15]. Both are balanced with alkali metal ions. Also, aggregates may bind alkalis to some extent, which changes the pore solution alkalinity.
Lothenbach et al. [
17] have proposed a thermodynamic model to study the effects of composition and temperature on the pore solution. They found that with longer ages of hydration, the ion concentrations in the pore solutions are similar at all temperatures, in general. However, the concentrations of sulfate and aluminum increased at high temperature. This fact leads to the promotion of ettringite solubility, which results in a decrease of the hydroxide ions in the pore solution. Nevertheless, the Portland cement pore solution was oversaturated with regard to ettringite, probably due to the low Al/Ca and Al/sulfate ratio, which undermines the precipitation process of ettringite [
17].
Table 3 shows the water-soluble alkalis, as determined by the method described in
Section 2.3. According to Taylor [
8], it is assumed that all of the water-soluble alkalis in cement are alkali cations that are present as sulfates (
Table 3). Taylor proposed an assumed amount of 35% of the total weight of Na
2O in the cement, present as a sulfate, and an amount of 70% of the total weight of K
2O in the cement, present as sulfate, when the proportions are unknown. However, in this paper, an average of 53% of the total weight of Na
2O was Na
2O present as a sulfate in the cement, whereas 97% of the total weight of K
2O was K
2O present as a sulfate in the cement (
Table 4). The high variability with regard to the proportion of the soluble alkali cations against the total alkali cations suggests that it will be necessary, in the new proposed method, to use experimentally determined results.
Another source of error can be found in the testing method, because it is assumed that all the water-soluble alkali in the cement, mainly sulfates, will be dissolved. However, it could be possible that not all of the water-soluble alkalis in the cement were dissolved [
18]. Then, the real amount of alkalis present as sulfates could be even higher. According to Taylor [
8], most of the potassium normally is present as potassium sulfate whereas sodium was not the case.
Table 4 shows that sodium is bounded in cement paste hydrates in a higher extension than potassium, in agreement with other authors [
16,
19]. Whereas Taylor proposed that only about 70% of the potassium is water-soluble, in this research, almost all of the potassium is water-soluble. Also, he proposed a procedure for determining the alkali binding capacities of hydrated Portland cement paste.
Table 5 gives the fractional distribution of the total non-sulfate Na
2O and K
2O that are assumed to occur in the main clinker phases, which have been considered in this work.
The contents of Na
2O and K
2O in each of the major phases were then calculated (
Table 6) by using the fractional distribution that was proposed by Taylor, and given in
Table 5.
Table 6 shows the total non-reactive alkalis that are calculated by subtracting the measured total alkalis content from the measured water-soluble alkalis, as well as the assumed distribution to occur in the main clinker phases.
Dalziel and Gutteridge [
19] proposed an empirical formula (Equation (5)) to express the rates of reaction of alite, belite, aluminate, and ferrite. In this function, F is the fraction of the major clinker phases reacted at time T, in days, and k
1, k
2, and k
3 are constants, as shown in
Table 7.
Equation (5) was then used in the present work to obtain the fractions that were reacted for each clinker phase, C
3S, C
2S, C
3A, and C
4AF, bound water, and Ca in C-S-H and AF
m phases, at time T (in days) replacing the set of constants that are given in
Table 7.
Figure 1 illustrates the fractions reacted for the C
3S, C
2S, C
3A, and C
4AF clinker phases, bound water, and Ca uptake in the C-S-H and AF
m phases over time, as calculated with Equation (5).
Then, the fractions reacted for each clinker phase at 28 days was multiplied by the weight of Na
2O or K
2O in the phase, to obtain the weight of Na
2O or K
2O that was released, respectively.
Table 8 presents the results obtained. The mass of Na
2O or K
2O that was released from the major clinker phases was added to that present as sulfates (
Table 3), and the total alkalis present in the pore solution after 28 days are shown in
Table 9, expressed as in units of millimoles.
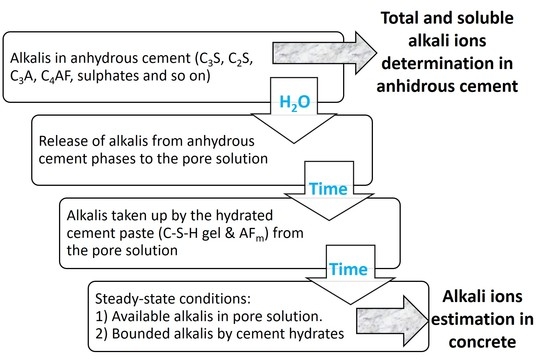
Finally,
Figure 2 summarizes the procedure proposed in the present paper to estimate the alkali ion concentrations in the cement pore solution, which is a reliable method for use in engineered barriers for waste confinement design.
3.1.1. Volume of the Pore Solution
First, the volume of the bound water was calculated, multiplying 31.6 by the quantity F as in Equation (5), with k
1, k
2, and k
3 constants (shown in
Table 7) of 0.25, 0.69, 0.90, respectively. For 28-days, the F-value was 0.793. Finally, the volume of the pore solution was calculated, subtracting the volume of the bound water from (100 × water–cement). The free water amount of the cement paste has very little influence on the determination of the free alkali metal ions when the water extraction method is used [
20]. Therefore, determining this parameter was not necessary.
3.1.2. Amount of Calcium Present in the C-S-H and AFm Phases
The amount of Ca present in the C-S-H and AF
m phases was also calculated by Equation (5), with k
1, k
2, and k
3 constant values (shown in
Table 7) of 0.25, 0.56, 0.90, respectively. After 28 days, the F-value was 0.721.
The amount of alkali ions taken up by the C-S-H and AFm phases depends on the amounts present, and the alkali-binding capacities of the mentioned hydration products. Knowledge of the alkali-binding capacities of such hydration productions will thus be useful when developing methods for predicting alkali and hydroxyl concentrations in the pore solution.
The alkali concentrations used by Hong and Glasser [
21,
22] for determining the alkali binding capacity were between 1 and 300 mmol/L for the C–S–H gel, and between 15 and 300 mmol/L for the C–A–S–H gel. However, the distribution ratio in real hydrated cement pastes could be significantly different from that obtained in synthetic pastes.
3.1.3. Na+ and K+ Concentrations in the Pore Solution
An alkali partition procedure was proposed, according to which part of the alkali ions are bound in the hydration products, also called C-S-H gel and AF
m phases and the others remain in the pore solution. From the mass balance, the quantity of the alkali cations released from the cement, m
released, is equal to that which is contained in the pore solution, mpore solution, plus that which is taken up by the hydration products, m
taken up (Equation (7)):
The amount in solution is equal to the alkali concentration, [Na
+] or [K
+], which is assumed to be uniform, is multiplied by the volume of solution, V. The amount of Na
+ or K
+ that is taken up by the cement hydration products is assumed to be proportional to the amount of such hydration products, and also proportional to the Na
+ or K
+ concentration in solution. Therefore, their concentrations in the pore solution and in the hydration products were calculated by using Equations (8) and (9), respectively:
where P is the amount of the hydration product that is able to take up alkali ions, divided by the same amount at complete hydration. Therefore, P is dimensionless. The constant b is named as the “binding factor” by Taylor [
8]. Combining Equations (7)–(9), we obtain Equation (10) and (11).
The “binding factor”, b, is equal to 31.0 cm
3 for Na
+ and 20.0 cm
3 for K
+, and it can be defined as an equivalent volume of pore solution. P is the quantity F that is obtained from Equation (5), equal to 0.721 at after 28 days. The volume of the pore solution, V, was calculated in
Section 3.1, and it is equal to 24.93 cm
3.
Finally, the amount in solution is equal to the alkali concentration, [Na
+ or K
+] at 28 days, which is shown in
Table 10.
Kawabata and Yamada [
23] developed a model to estimate the pore solution alkalinity. They found that a reduction in pore solution alkalinity is the key factor for reducing ASR expansion. Also, they reported on the effect of the Ca/Si ratio, and the amount of C-S-H gel on the alkali uptake. The effect of the coal fly ash on the Portland cement paste is the formation of a higher amount of C-S-H gel, with a lower Ca/Si ratio. On the contrary, granulated blast-furnace slag leads to a higher amount of C-S-H gel, with a similar Ca/Si ratio than the plain Portland cement. Thus, the higher amount of C-S-H gel is, the higher alkali metal ions uptake. However, they can be released from the C-S-H gel in the long-term [
23].
3.3. Relationship between the Water-Soluble Alkalis and the Major Clinker Phases
Figure 3 shows the relationship between the water-soluble alkalis obtained, following the procedure detailed in
Section 2.3 (an extraction time of less than 30 min) and the C
3S. It is clear that sodium uptake was preferred. Also, it was found that the concentrations of both Na
+ and K
+ in the solution apparently decreased with increasing C
3S content in the clinker, particularly for K
+. Therefore, the less alkali ions that are available for the pore solution, because more alkali ions are bound in the C–S–H gel. Also, C
3S hydration consumes less water than C
2S hydration, leaving more water available for the pore solution, resulting in a dilution of the alkali ions [
18].
Bach et al. [
26] found that the fraction of potassium uptake by low-pH cements is more than three times higher than that of sodium, disagreeing with the results shown in
Figure 3. This significant difference was explained by the smaller solvated ionic radius of potassium, and because potassium ions can enter the C-S-H gel interlayer to compensate for the negative charges [
26]. They also suggested that C-(A)-S-H is the phase that is mainly involved in the alkali retention by an effect of charge compensation. In addition, they reported a clear correlation between the dissolved alkali and alkali retention by C-S-H gel. In contrast, L’Hôpital et al. [
27] did not find any difference between sodium and potassium uptake. They observed that the alkali uptake depends on the Ca/Si ratio in C-S-H and C-A-S-H gels. Thus, the lower the Ca/Si ratio is, the greater the uptake of alkali metal ions.
Different behaviors of C–S–H gel concerning the binding of Na
+ and K
+ are observed in
Figure 3, where the effects of the alkali types in cement on the alkalinity of the pore solution is observed. The C–S–H gel binds less K
+ than Na
+, particularly at high concentrations, and more alkali ions remain in the solution [
16].
Figure 4 shows the soluble alkali concentrations in the pore solution of hydrated Portland cement paste as a function of the amount of C
3S, C
2S, C
3S + C
2S, and CaO/SiO
2 ratio in the clinkers.
According to various national regulations and standards, the total alkali content in cement is regulated as Na2Oequivalent. Therefore, the alkali types are not distinguished, and little attention is paid to the different types of alkalis, though the resultant alkalinity of the pore solution is quite different. Thus, the influence of mineral composition on the alkali concentrations was investigated using updated methods in this study. A water–cement ratio of 0.5 was considered. The C3S content in the clinker ranged from 57.18% to 77.93%, while the C2S content ranged from 4.81% to 17.92%, accordingly. These totaled 76% of the clinker content. The C3A and C4AF contents in the clinker ranged from 2.42% to 11%, and from 0.67% to 13.10%, respectively.
Figure 5 shows the relationship between the water-soluble alkalis of anhydrous cement and the water-soluble alkalis of hydrated cement paste after 28 days. In the case of the sodium ions, the trend was clearly linear (r
2 = 0.98); whereas in the case of potassium, this was less evident. From the analysis water-solubility data for alkalis, it can be concluded that sodium was significantly better bonded into the hydrated cement paste than potassium, as reported in the literature [
8]. However, the large size of the solvated sodium ion hinders its uptake by interlayer sites of the C-S-H gel [
26]. Alkali cations compete with calcium cations to compensate for the surface negative charge of the C-S-H gel. Bivalent cations present a higher electrostatic interaction; therefore, high amounts of calcium cations can hinder alkali uptake [
28]. On the contrary, the pH increases at high alkali concentrations, and this enhances silanol site de-protonation, leading to a more negatively charged C-S-H gel surface. In addition, the high pH induces a lower calcium concentration in equilibrium with the C-S-H gel. Both occurrences cause an increase in alkali metal binding [
28].
Some authors found an increase in alkali metal uptake in the presence of C-A-S-H gels, which was attributed to SiO
2 substitution by AlO
2−, and the need for the uptake of more positive cations, to maintain charge equilibrium [
22]. On the contrary, some studies observed less alkali metal uptake in the C-A-S-H gels than in the C-S-H gels [
29], while other studies found no significant difference in the systems, with or without aluminum [
26].
Brouwers and Van Eijk [
30] investigated the alkali binding capacities of hydrated Portland cement pastes following the same method proposed by Taylor [
8], but they used a computer model to predict the amount of alkali ions released by the cement hydration. They also proposed that the C–S–H gel is the only hydration product that is able to bind alkalis, instead of the relative fraction of C–S–H and AF
m phases that are formed in the paste. Currently, it is considered that the alkali metal uptake by AF
m is much lower than that of the C-S-H gel. Given that, most researchers have focused on alkali uptake by the C-S-H gel. They also suggest that the constant values of alkali distribution ratios imply that the alkali-binding capacity of C–S–H gel is linearly proportional to the alkali concentrations in the pore solution; this was verified for Na
+, but not for K
+ [
31]. Therefore, Chen and Browers [
31] found a linear relationship between the molar concentration of Na
+ in the C-S-H gel, and its concentration in the pore solution, with a proportionality constant of 0.45. The distribution ratio in cm
3/g found by other authors was 0.39 [
8,
21]. In the present work, such a constant is 1.6. On the contrary, they did not find a similar relationship in the case of K
+, and then, they proposed a non-linear relationship that is similar to a Freundlich isotherm, between the molar concentration of K
+ in the C-S-H gel, and the molar concentration of K
+ in the pore solution. In the present work, neither a linear relationship was found. Nevertheless, a good relationship was found between the total K
2O and K
2O/SiO
2 ratios (
Figure 6). SiO
2 is determined by X-ray fluorescence (XRF) in the Portland cement. It was found that the total K
2O of the paste correlated well with the K
2O/SiO
2 ratio; increasing the total K
2O in the clinker appeared to increase the overall K
2O/SiO
2 ratio.
Finally, the numerical prediction was compared with water-soluble alkali determination, as determined in the pastes after 28 days.