Design and Kinematic Control of the Cable-Driven Hyper-Redundant Manipulator for Potential Underwater Applications
Abstract
:1. Introduction
2. Mechanical Design of CDHRM
2.1. Overall Design of CDHRM
2.2. Manipulator Design
2.3. Driving Subsystem Design
3. Kinematic Analysis of CDHRM
3.1. Multilevel Mapping Relationships of CDHRM
3.2. Cable-Joint Kinematics
3.3. Joint-End Kinematics
4. Kinematic Control of a CDHRM
5. Experiment
5.1. Prototype
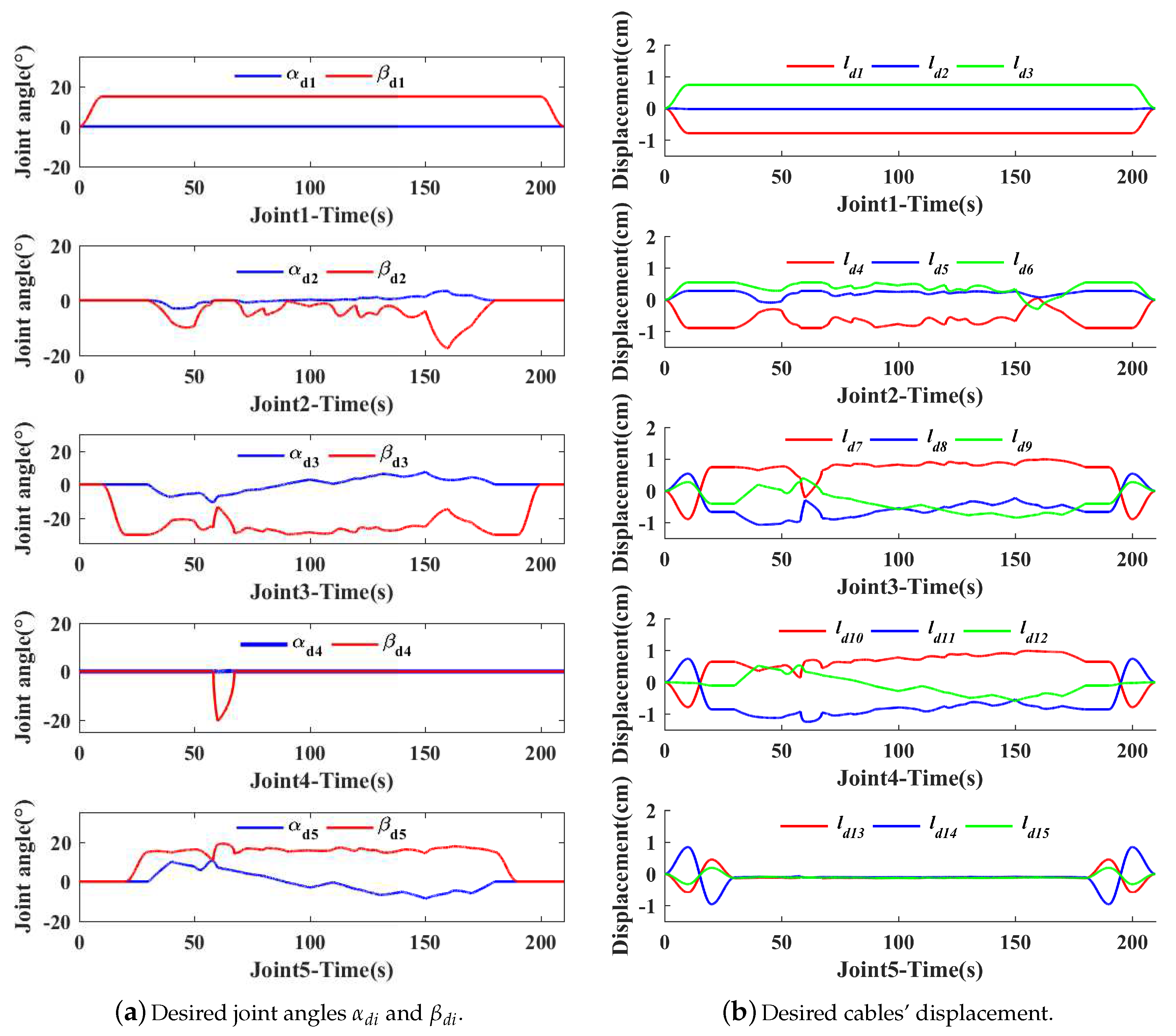
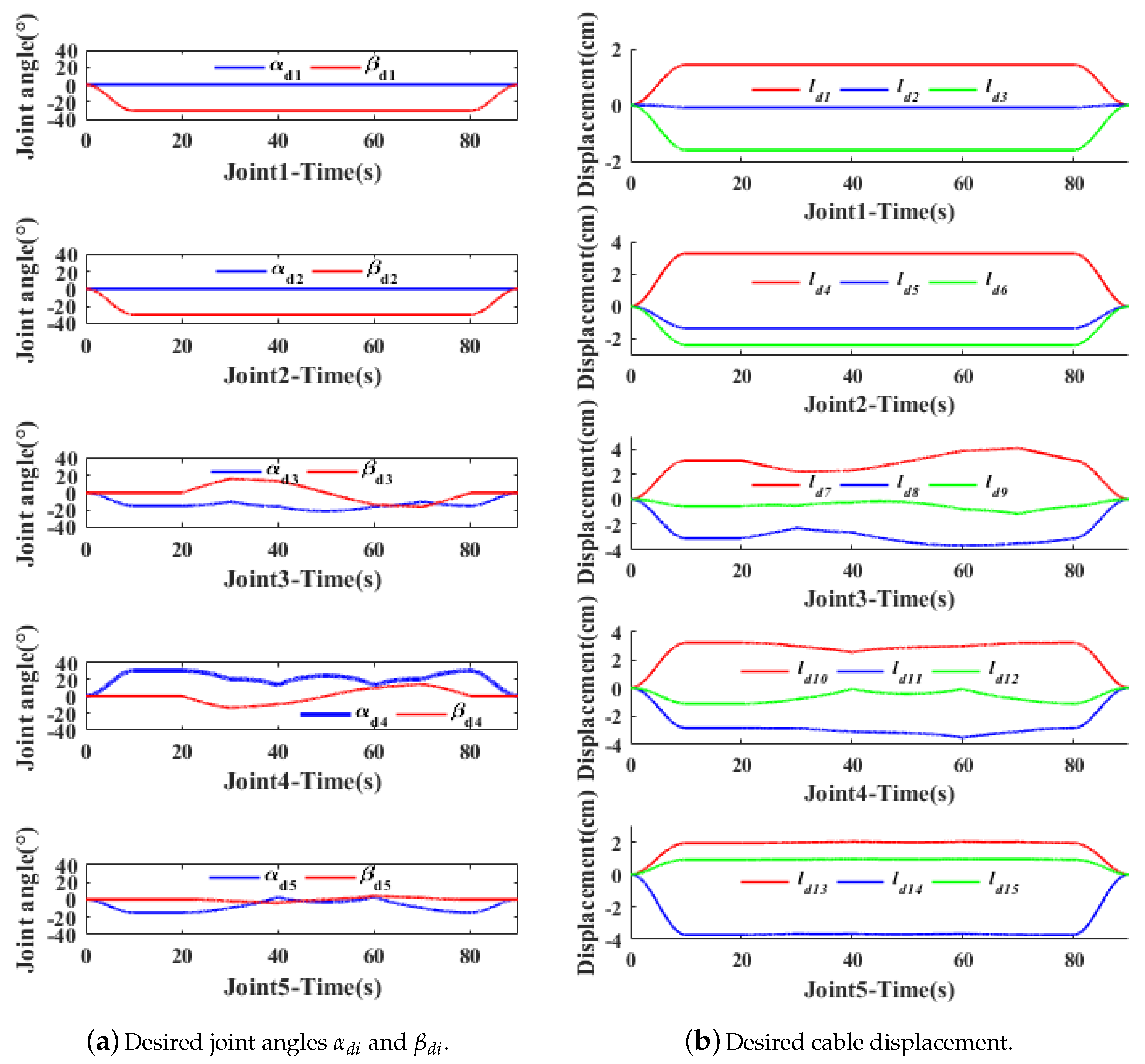
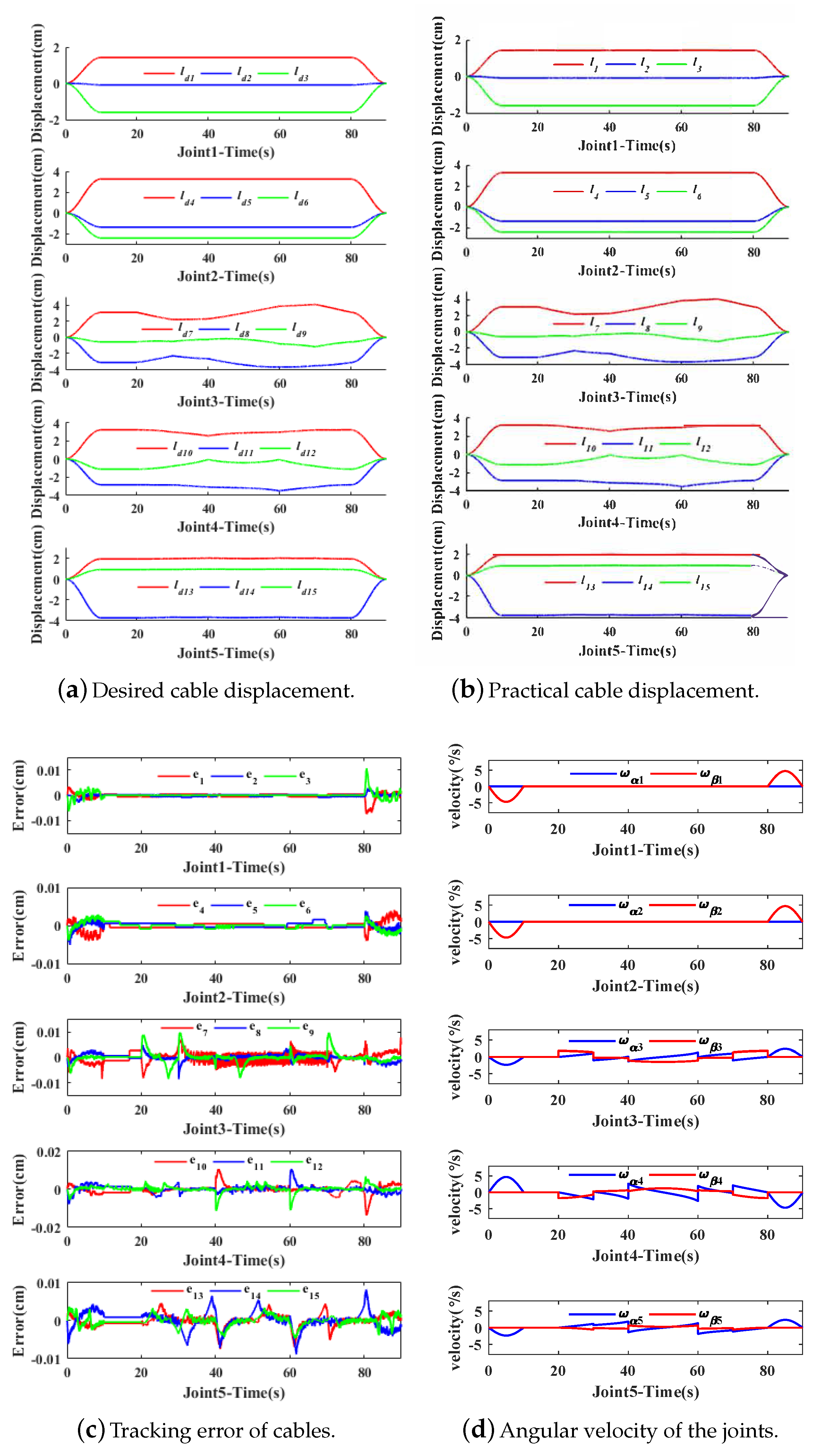
5.2. Experiment of Writing on a White Board
5.3. Experiment in the Underwater Environment
- SET1: Writing without load
- SET2: Writing with load
- SET3: Grasping objects
5.3.1. Experiment of SET1 in the Underwater Environment
5.3.2. Experiment of SET2 in the Underwater Environment
5.3.3. Experiment of SET3 in the Underwater Environment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, P.; Bose, N.; Chen, K.; Chen, K.; Xu, Y. Development and optimization of dual-mode propellers for renewable energy. Renew. Energy 2018, 119, 566–576. [Google Scholar] [CrossRef]
- Brito, M.P.; Lewis, R.S.; Bose, N. Gwyn Griffiths Adaptive Autonomous Underwater Vehicles: An Assessment of Their Effectiveness for Oceanographic Applications. IEEE Trans. Eng. Manag. 2018, 66, 98–111. [Google Scholar] [CrossRef]
- Lewis, R.; Bose, N.; Lewis, S.; King, P.; Walker, D.; Devillers, R.; Ridgley, N.; Husain, T.; Munroe, J.; Vardy, A. MERLIN—A decade of large AUV experience at Memorial University of Newfoundland. In Proceedings of the 2016 IEEE/OES Autonomous Underwater Vehicles (AUV), Tokyo, Japan, 6–9 November 2016. [Google Scholar]
- Alexander, P.; Duncan, A.; Bose, N.; Wilkes, D.; Lewis, R.; Souza, P. Noise characterisation of the Aurora Australis while stationary in Antarctic sea ice. Ocean Eng. 2014, 82, 52–64. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, F.; Chen, J.; Ju, F.; Chen, B. A new adaptive time-delay control scheme for cable-driven manipulators. IEEE Trans. Ind. Inf. 2018. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, B.; Wang, Q. Accurate motion control of linear motors with adaptive robust compensation of nonlinear electromagnetic field effect. IEEE/ASME Trans. Mechatron. 2013, 18, 1122–1129. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Yan, F.; Zhu, K.; Chen, B. Adaptive super-twisting fractional-order nonsingular terminal sliding mode control of cable-driven manipulators. ISA Trans. 2019, 86, 163–180. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, B.; Wang, Q. μ-synthesis based adaptive robust control of linear motor driven stages with high-frequency dynamics: A case study. IEEE/ASME Trans. Mechatron. 2015, 20, 1482–1490. [Google Scholar] [CrossRef]
- Yuan, M.; Chen, Z.; Yao, B.; Zhu, X. Time optimal contouring control of industrial biaxial gantry: A high-efficient analytical solution of trajectory planning. IEEE/ASME Trans. Mechatron. 2017, 22, 247–257. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, Y.J.; Gu, J. Integrated Adaptive Robust Control for Multilateral Teleoperation Systems under Arbitrary Time Delays. Int. J. Robust Nonlinear Control. 2016, 26, 2708–2728. [Google Scholar] [CrossRef]
- Sun, W.; Liu, Y.; Gao, H. Constrained sampled-data ARC for a class of cascaded nonlinear systems with applications to motor-servo systems. IEEE Trans. Ind. Inform. 2019, 15, 766–776. [Google Scholar] [CrossRef]
- Wang, Y.; Li, B.; Yan, F.; Chen, B. Practical adaptive fractional-order nonsingular terminal sliding mode control for a cable-driven manipulator. Int. J. Robust Nonlinear Control. 2019, 29, 1396–1417. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, J.; Liu, Z. Two-time-scale redesign for anti-lock braking systems of ground vehicles. IEEE Trans. Ind. Electron. 2019, 66, 4577–4586. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Yang, C.; Yao, B. Adaptive fuzzy backstepping control for stable nonlinear bilateral teleoperation manipulators with enhanced transparency performance. IEEE Trans. Ind. Electron. 2019. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W. Active disturbance rejection adaptive control of hydraulic servo systems. IEEE Trans. Ind. Electron. 2017, 64, 8023–8032. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W.; Jiao, Z. RISE-Based Adaptive Control of Hydraulic Systems with Asymptotic Tracking. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1524–1531. [Google Scholar] [CrossRef]
- Li, C.; Li, C.; Chen, Z.; Yao, B. Advanced synchronization control of a dual-linear-motor-driven gantry with rotational dynamics. IEEE Trans. Ind. Electron. 2018, 65, 7526–7535. [Google Scholar] [CrossRef]
- Barbalata, C.; Dunnigan, M.W.; Petillot, Y. Coupled and Decoupled Force/Motion Controllers for an Underwater Vehicle-Manipulator System. J. Mar. Sci. Eng. 2018, 6, 96. [Google Scholar] [CrossRef]
- Barbieri, L.; Bruno, F.; Gallo, A.; Muzzupappa, M.; Russo, M.L. Design, prototyping and testing of a modular small-sized underwater robotic arm controlled through a Master-Slave approach. Ocean Eng. 2018, 158, 253–262. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Dalvand, M.M.; Nahavandi, S.; Howe, R.D. An Analytical Loading Model for n-Tendon Continuum Robots. IEEE Trans. Robot. 2018, 34, 1215–1225. [Google Scholar] [CrossRef]
- Jia, H.; Huang, Z.; Fei, Z.; Dyson, P.J.; Zheng, Z.; Wang, X. Bilayered Polyurethane/Dipole-dipole and H-bonding Interaction Reinforced Hydrogels as Thermo-responsive Soft Manipulators. J. Mater. Chem. B 2017, 5, 8193–8199. [Google Scholar] [CrossRef]
- Camarillo, D.B.; Carlson, C.R.; Salisbury, J.K. Configuration Tracking for Continuum Manipulators with Coupled Tendon Drive. IEEE Trans. Robot. 2009, 25, 798–808. [Google Scholar] [CrossRef]
- Navarro-Alarcon, D.; Yip, H.M.; Wang, Z.; Zhong, F.; Liu, Y.-H.; Zhang, T.; Li, P. Automatic 3-D Manipulation of Soft Objects by Robotic Arms With an Adaptive Deformation Model. IEEE Trans. Robot. 2016, 32, 429–441. [Google Scholar] [CrossRef]
- Choi, D.; Yi, B.; Kim, W. Design of a spring backbone micro endoscope. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1815–1821. [Google Scholar]
- Ning, K.; Woergoetter, F. A Novel Concept for Building a Hyper-Redundant Chain Robot. IEEE Trans. Robot. 2009, 25, 1237–1248. [Google Scholar] [CrossRef]
- Hu, H.; Wang, P.; Zhao, B.; Li, M.; Sun, L. Design of a novel snake-like robotic colonoscope. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009; pp. 1957–1961. [Google Scholar]
- Walker, I.D.; Hannan, M.W. A novel ’elephant’s trunk’ robot. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Atlanta, GA, USA, 19–23 September 1999; pp. 410–415. [Google Scholar]
- Lau, D.; Oetomo, D.; Halgamuge, S.K. Inverse Dynamics of Multilink Cable-Driven Manipulators with the Consideration of Joint Interaction Forces and Moments. IEEE Trans. Robot. 2015, 31, 479–488. [Google Scholar] [CrossRef]
- Roy, R.; Wang, L.; Simaan, N. Modeling and Estimation of Friction, Extension, and Coupling Effects in Multisegment Continuum Robots. IEEE/ASME Trans. Mechatron. 2017, 22, 909–920. [Google Scholar] [CrossRef]
- Xu, D.; Li, E.; Liang, Z. Kinematics and statics analysis of a novel cable-driven snake arm robot. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 439–444. [Google Scholar]
- Lau, D.; Oetomo, D.; Halgamuge, S.K. Generalized Modeling of Multilink Cable-Driven Manipulators with Arbitrary Routing Using the Cable-Routing Matrix. IEEE Trans. Robot. 2013, 29, 1102–1113. [Google Scholar] [CrossRef]
- Hassan, M.; Khajepour, A. Analysis of Bounded Cable Tensions in Cable-Actuated Parallel Manipulators. IEEE Trans. Robot. 2011, 27, 891–900. [Google Scholar] [CrossRef]
- Hannan, M.W.; Walker, I.D. Analysis and initial experiments for a novel elephant’s trunk robot. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2000), Takamatsu, Japan, 31 October–5 November 2000; pp. 330–337. [Google Scholar]
- Hannan, M.W.; Walker, I.D. Kinematics and the implementation of an elephant’s trunk manipulator and other continuum style robots. J. Robot. Syst. 2003, 20, 45–63. [Google Scholar] [CrossRef]
- McMahan, W.; Jones, B.A.; Walker, I.D. Design and implementation of a multi-section continuum robot: Air-Octor. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, ALT, Cancda, 2–6 August 2005; pp. 2578–2585. [Google Scholar]
- Gravagne, I.A.; Walker, I.D. On the kinematics of remotely-actuated continuum robots. In Proceedings of the 2000 ICRA—Millennium Conference—IEEE International Conference on Robotics and Automation. Symposia Proceedings, San Francisco, CA, USA, 24–28 April 2000; Volume 3, pp. 2544–2550. [Google Scholar]
- Gravagne, I.A.; Walker, I.D. Kinematic transformations for remotely-actuated planar continuum robots. In Proceedings of the 2000 ICRA—Millennium Conference—IEEE International Conference on Robotics and Automation. Symposia Proceedings, San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 19–26. [Google Scholar]
- Wooten, M.; Frazelle, C.; Walker, I.D.; Kapadia, A.; Lee, J.H. Exploration and Inspection with Vine-Inspired Continuum Robots. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1–5. [Google Scholar]
- Ning, K.; Woergoetter, F. A DOF state controllable driving shared solution for building a hyper-redundant chain robot. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 5880–5885. [Google Scholar]
- Ning, K.; Woergoetter, F. To Paint What Is Seen: A System Implementation of a Novel Conceptual Hyper-Redundant Chain Robot with Monocular Vision. In Proceedings of the ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics), Munich, Germany, 7–9 June 2010; pp. 1–6. [Google Scholar]
- Ning, K.; Woergoetter, F. Control System Development for a Novel Wire-Driven Hyper-Redundant Chain Robot, 3D-Trunk. IEEE/ASME Trans. Mechatron. 2012, 17, 949–959. [Google Scholar] [CrossRef]
- Simaan, N. Snake-Like Units Using Flexible Backbones and Actuation Redundancy for Enhanced Miniaturization. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3012–3017. [Google Scholar]
- Xu, K.; Simaan, N. Analytic Formulation for Kinematics, Statics, and Shape Restoration of Multibackbone Continuum Robots Via Elliptic Integrals. ASME J. Mechan. Robot. 2009, 2, 011006. [Google Scholar] [CrossRef]
- Yoon, H.; Yi, B. A 4-DOF flexible continuum robot using a spring backbone. In Proceedings of the 2009 International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 1249–1254. [Google Scholar]
- Buckingham, R.; Graham, A. Reaching the unreachable snake arm robots. In Proceedings of the International Symposium of Robotics, Siena, Italy, 19–22 October 2003; Available online: www.ocrobotics.com (accessed on 14 March 2019).
- Chenguang, L.; Mingyuan, Z.; Jianyong, L.; Long, W. Design of a portable snake-like search and rescue apparatus used in the gap. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 676–679. [Google Scholar]
- Moses, M.S.; Murphy, R.J.; Kutzer, M.D.M.; Armand, M. Modeling Cable and Guide Channel Interaction in a High-Strength Cable-Driven Continuum Manipulator. IEEE/ASME Trans. Mechatron. 2015, 20, 2876–2889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, W.; Mu, Z.; Liu, T.; Liang, B. A modified modal method for solving the mission-oriented inverse kinematics of hyper-redundant space manipulators for on-orbit servicing. Acta Astronaut. 2017, 139, 54–66. [Google Scholar] [CrossRef]
- Xu, W.; Liu, T.; Li, Y. Kinematics, Dynamics, and Control of a Cable-Driven Hyper-Redundant Manipulator. IEEE/ASME Trans. Mechatron. 2018, 23, 1693–1704. [Google Scholar] [CrossRef]
- Tang, L.; Wang, J.G.; Zheng, Y.; Gu, G.; Zhu, L.; Zhu, X. Design of a cable-driven hyper-redundant robot with experimental validation. Int. J. Adv. Robot. Syst. 2018, 14, 1–12. [Google Scholar] [CrossRef]

















| Symbol | Property | Value |
|---|---|---|
| R | Radius of tubular structure | 33.8 mm |
| D | Distance from the tubular structure to universal joint | 12 mm |
| H | Length of tubular structure | 106 mm |
| N | Number of joints | 5 |
| Equipment | Equipment Model | Quantity |
|---|---|---|
| Actuators | Maxon EC-max 30 | 15 |
| Gears | Planetary Gearhead GP 32 C | 15 |
| Data acquisition device | Quanser QPID | 1 |
| Serve controller | ESCON 50/5 409510 | 15 |
| Linear magnetic encoder | LM10 | 15 |
| RMSE of l (Figure 9b) | RMSE of l (Figure 12b) | RMSE of l (Figure 14c) | RMSE of l (Figure 16c) | |
|---|---|---|---|---|
| Joint1 | 7.45 | 8.22 | 9.86 | 9.87 |
| Joint2 | 21.65 | 9.87 | 9.25 | 9.01 |
| Joint3 | 54.68 | 15.84 | 18.96 | 14.71 |
| Joint4 | 47.20 | 19.95 | 20.19 | 16.90 |
| Joint5 | 16.56 | 17.84 | 17.97 | 13.93 |
| Load | End-Effector Velocity | End-Effector Acceleration | Tracking Performance | |
|---|---|---|---|---|
| CDHRM in paper [50] | 2.5 kg | ≥0.25 m/s | ≥0.05 m/s | ≤10% (Cable tention) |
| CDHRM in paper [51] | 0.5 kg | ≤0.016 m/s | \ | ≤2% (End trajectory) |
| CDHRM in this paper | 0.5 kg | ≤0.086 m/s | ≤0.43 m/s | ≤0.011% (Cable length) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Zhang, Y.; Huang, F.; Li, J.; Chen, Z.; Song, W.; Zhu, S.; Gu, J. Design and Kinematic Control of the Cable-Driven Hyper-Redundant Manipulator for Potential Underwater Applications. Appl. Sci. 2019, 9, 1142. https://doi.org/10.3390/app9061142
Tang J, Zhang Y, Huang F, Li J, Chen Z, Song W, Zhu S, Gu J. Design and Kinematic Control of the Cable-Driven Hyper-Redundant Manipulator for Potential Underwater Applications. Applied Sciences. 2019; 9(6):1142. https://doi.org/10.3390/app9061142
Chicago/Turabian StyleTang, Jianzhong, Yougong Zhang, Fanghao Huang, Jianpeng Li, Zheng Chen, Wei Song, Shiqiang Zhu, and Jason Gu. 2019. "Design and Kinematic Control of the Cable-Driven Hyper-Redundant Manipulator for Potential Underwater Applications" Applied Sciences 9, no. 6: 1142. https://doi.org/10.3390/app9061142





