Analysis and Design of A PMQR-Type Repetitive Control Scheme for Grid-Connected H6 Inverters
Abstract
:1. Introduction
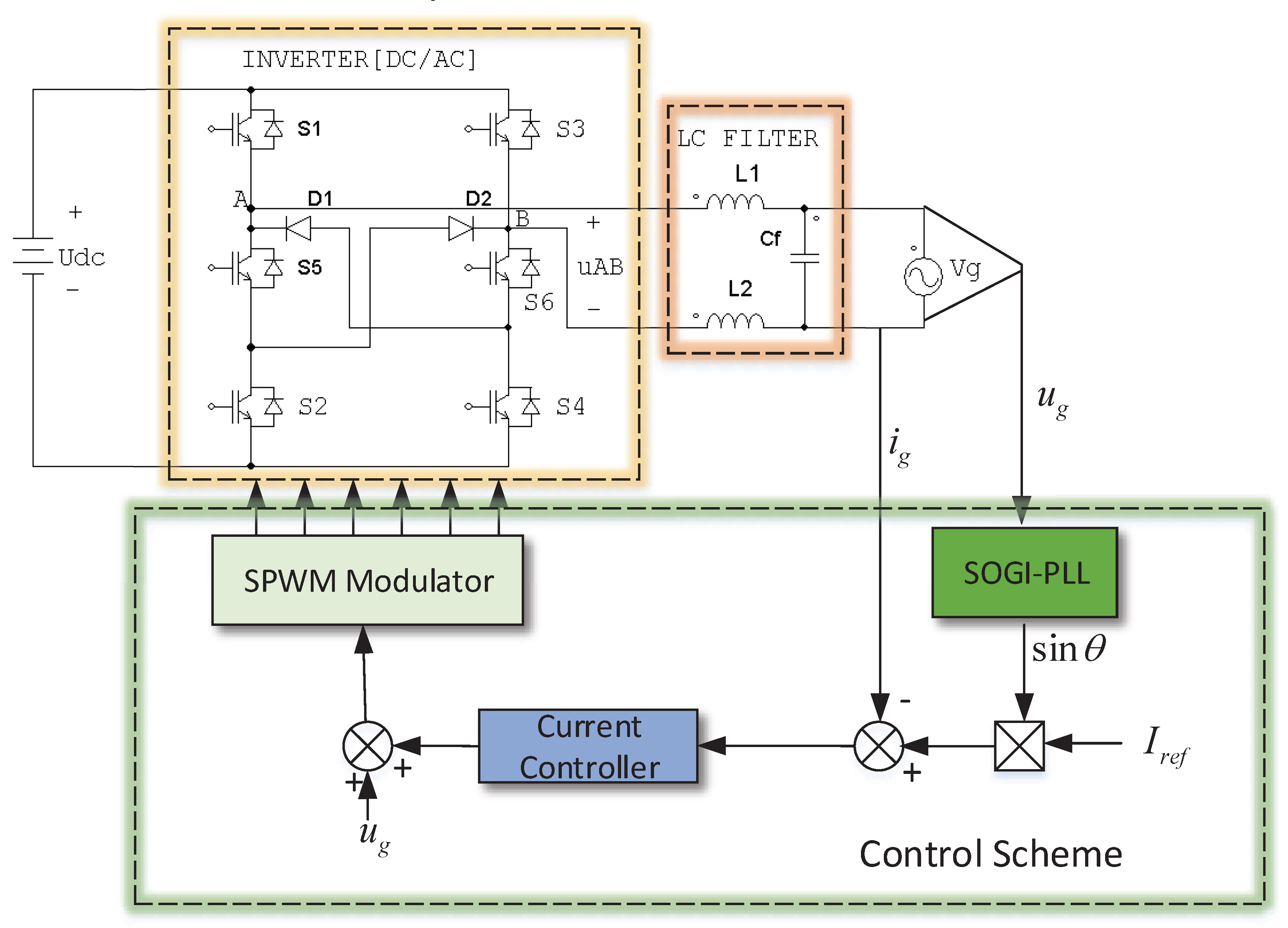
2. Description of the System
3. Analysis and Design of the PMQR-Type RC Scheme
3.1. Modelling of the Single-Phase Grid-Tied H6 Inverter
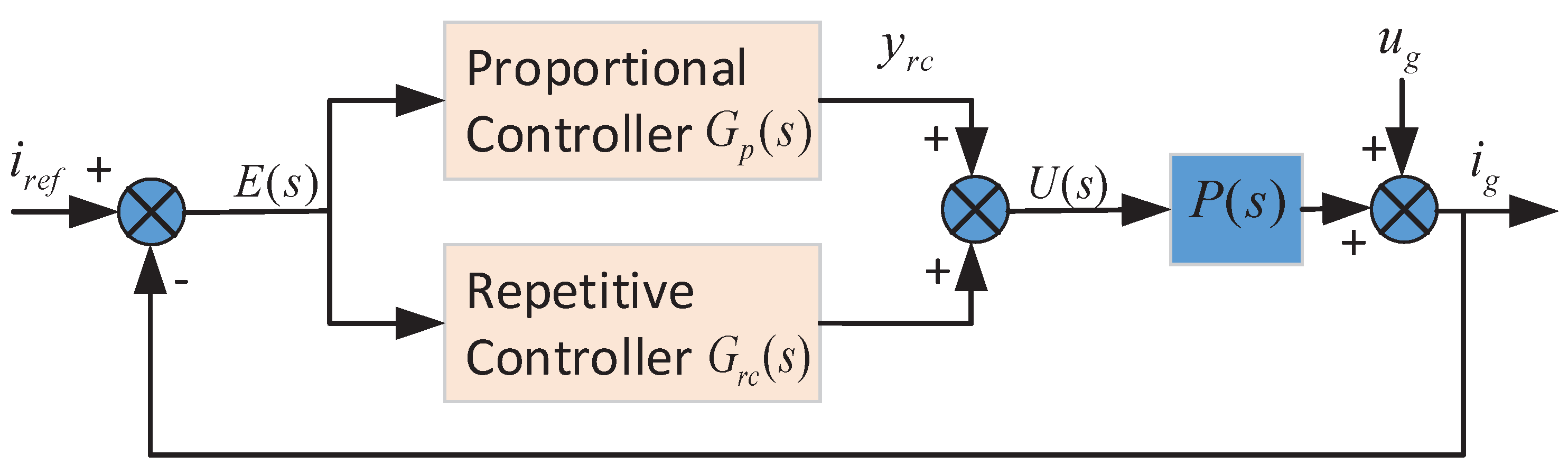
3.2. Control System Configuration
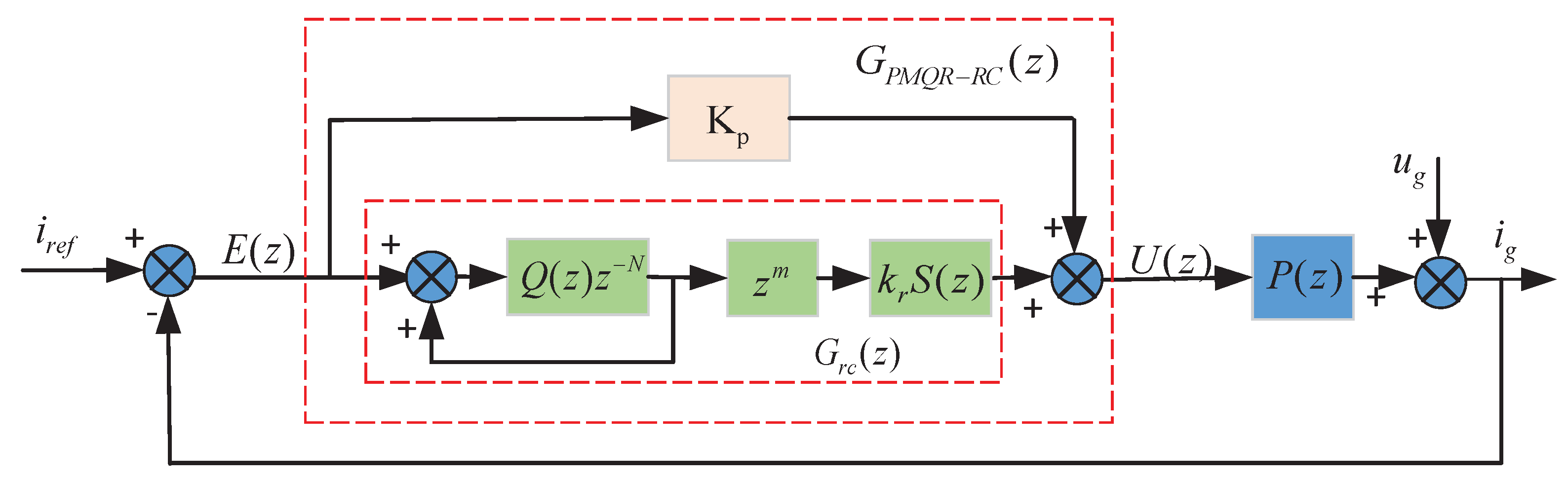
3.3. PMQR-Type RC Scheme Design
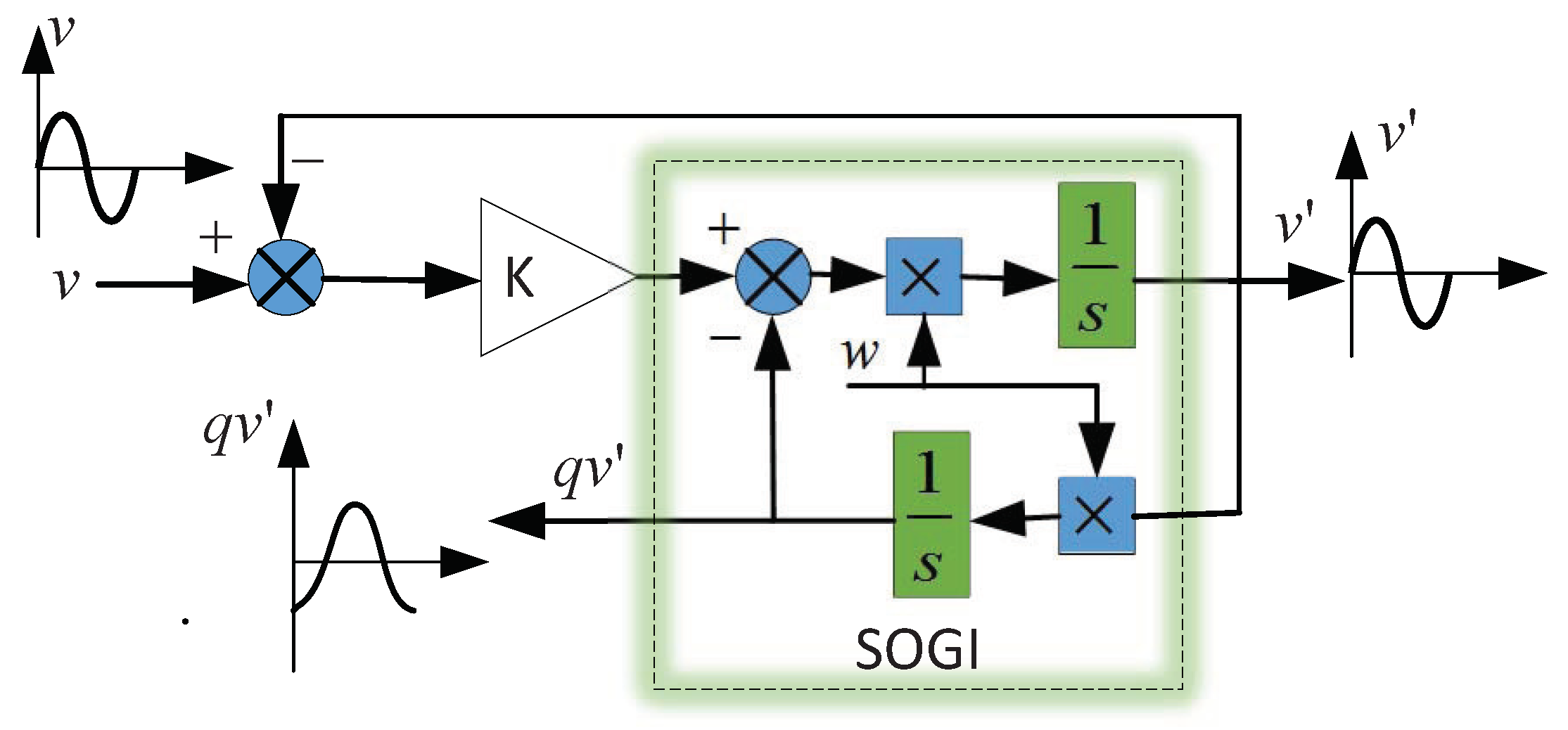
3.4. SOGI-PLL Design
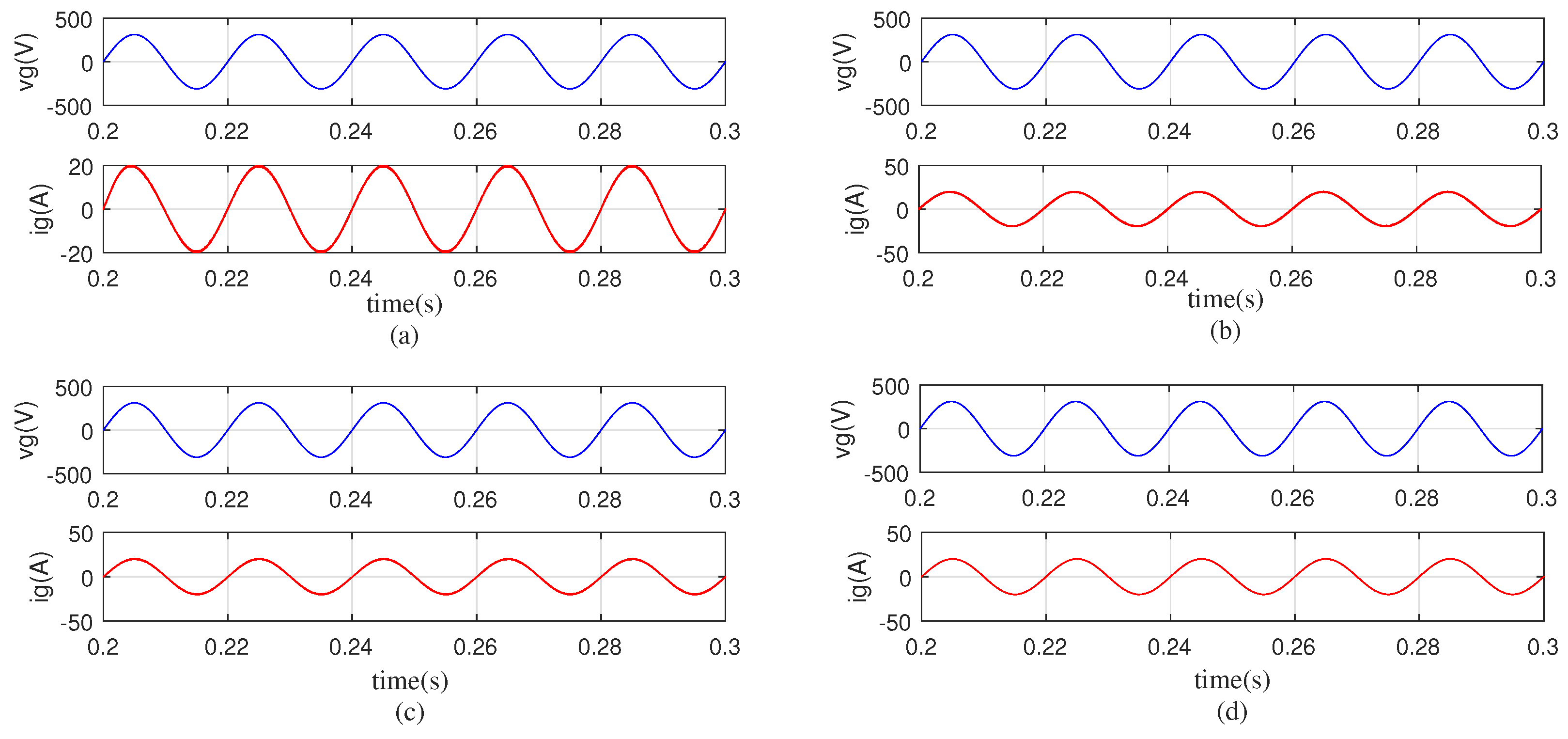
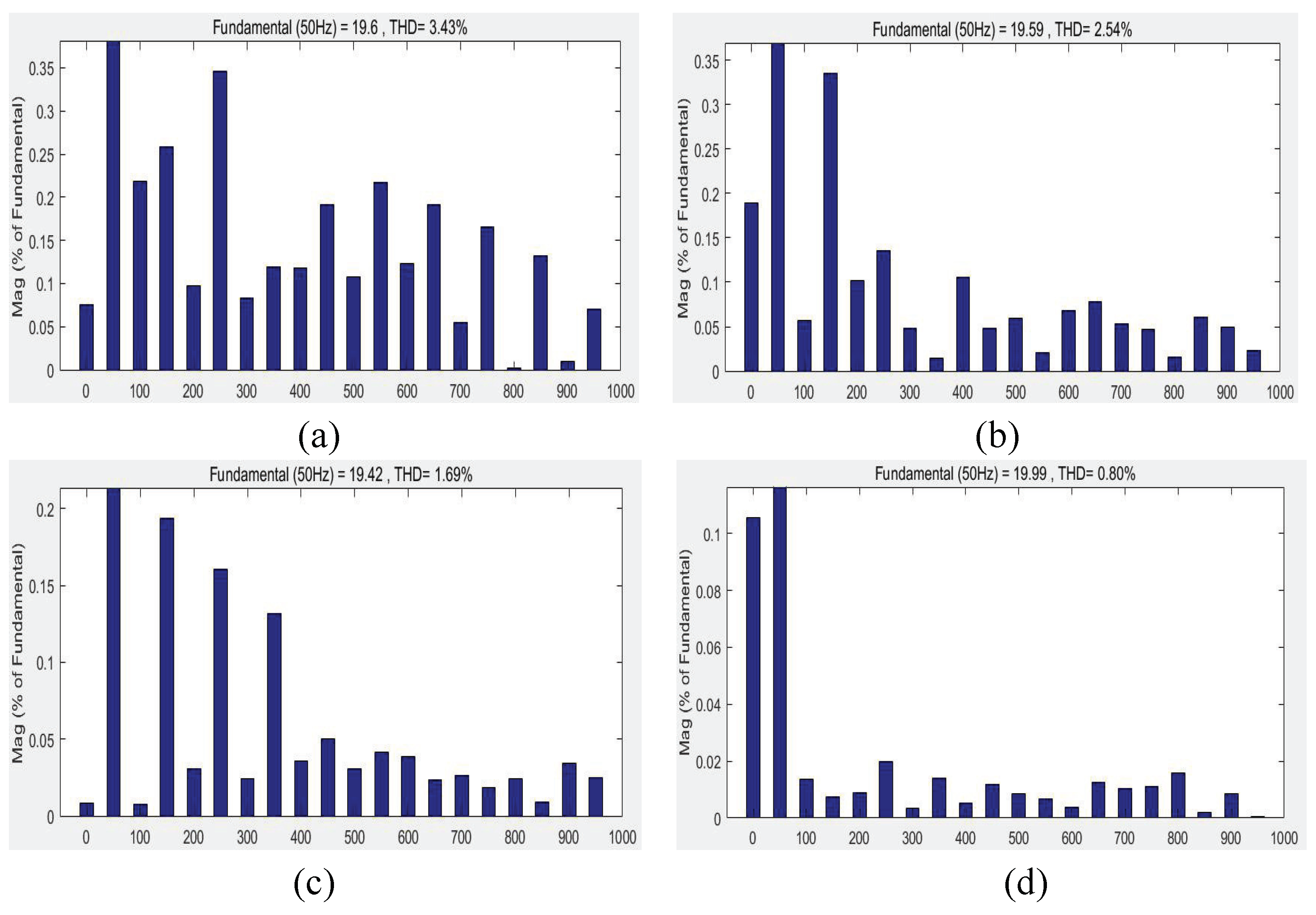
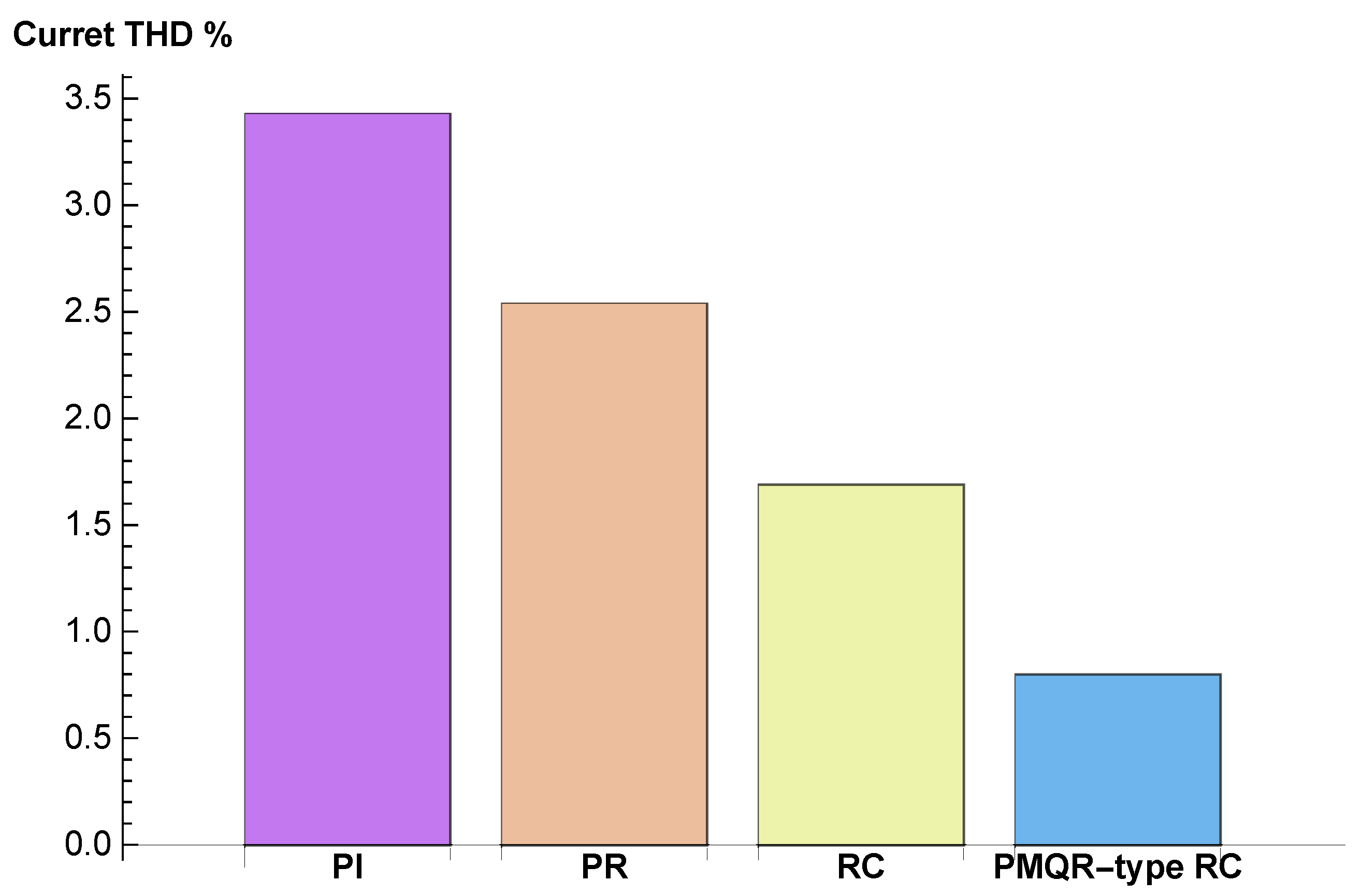
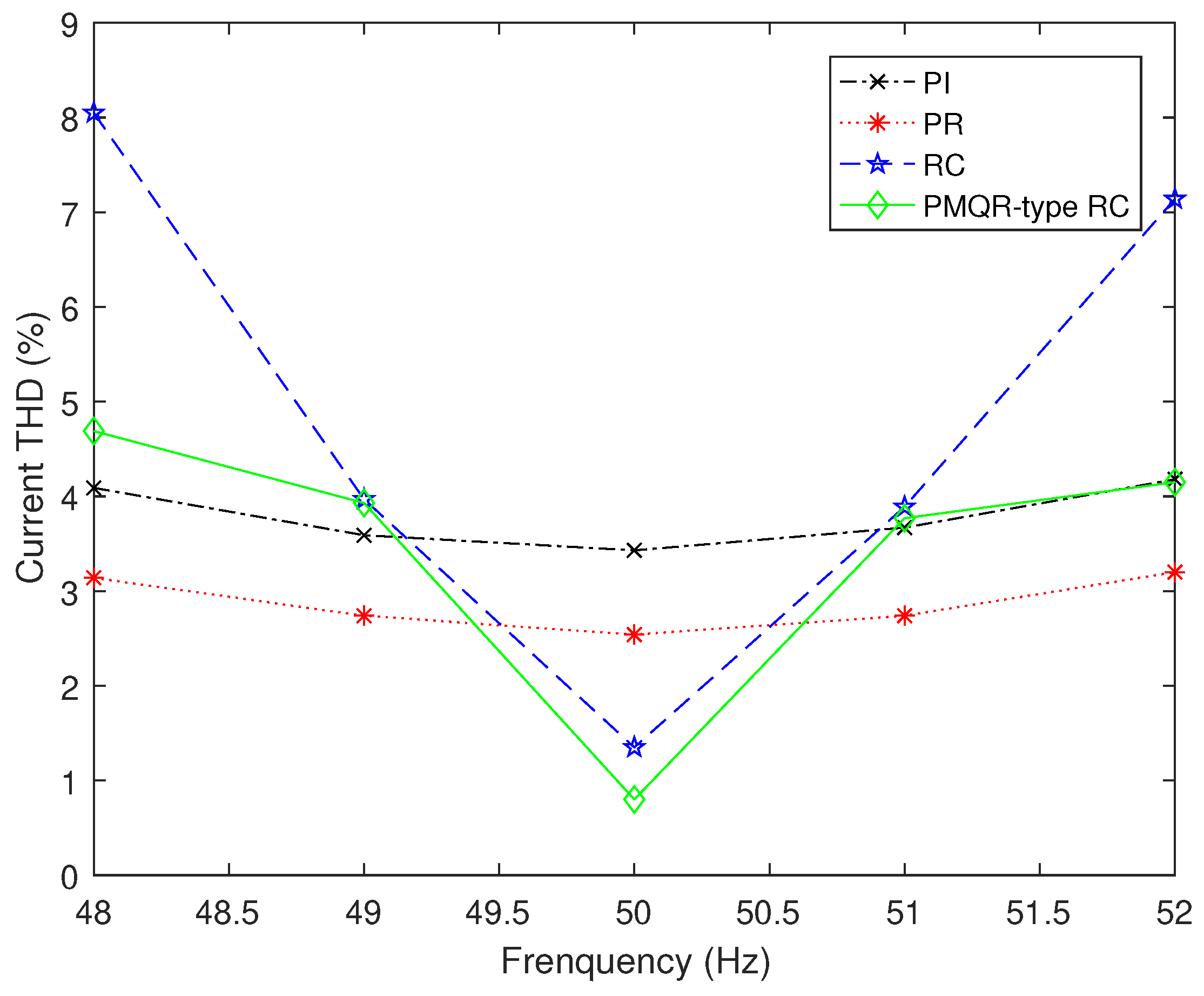
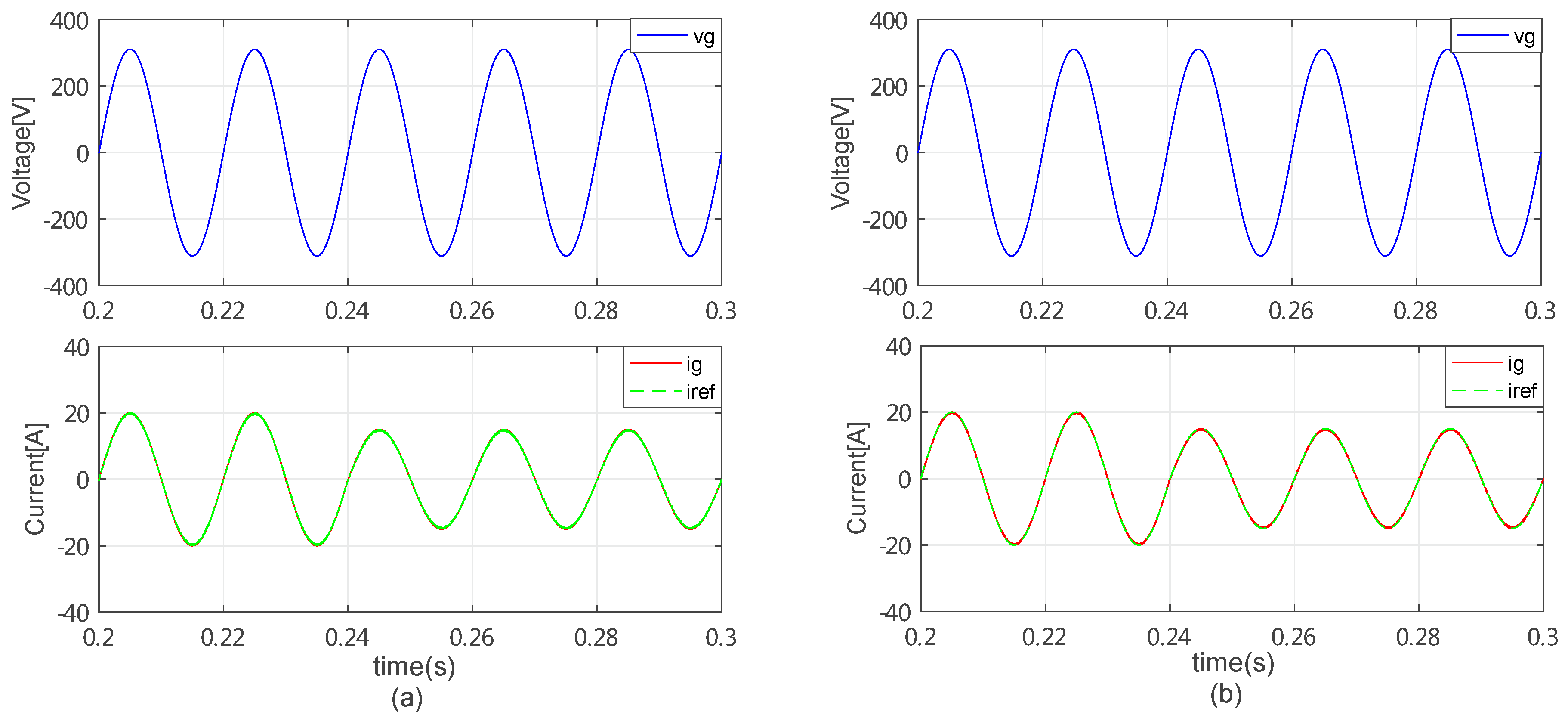
4. Simulation Results and Analysis
4.1. Controller Design
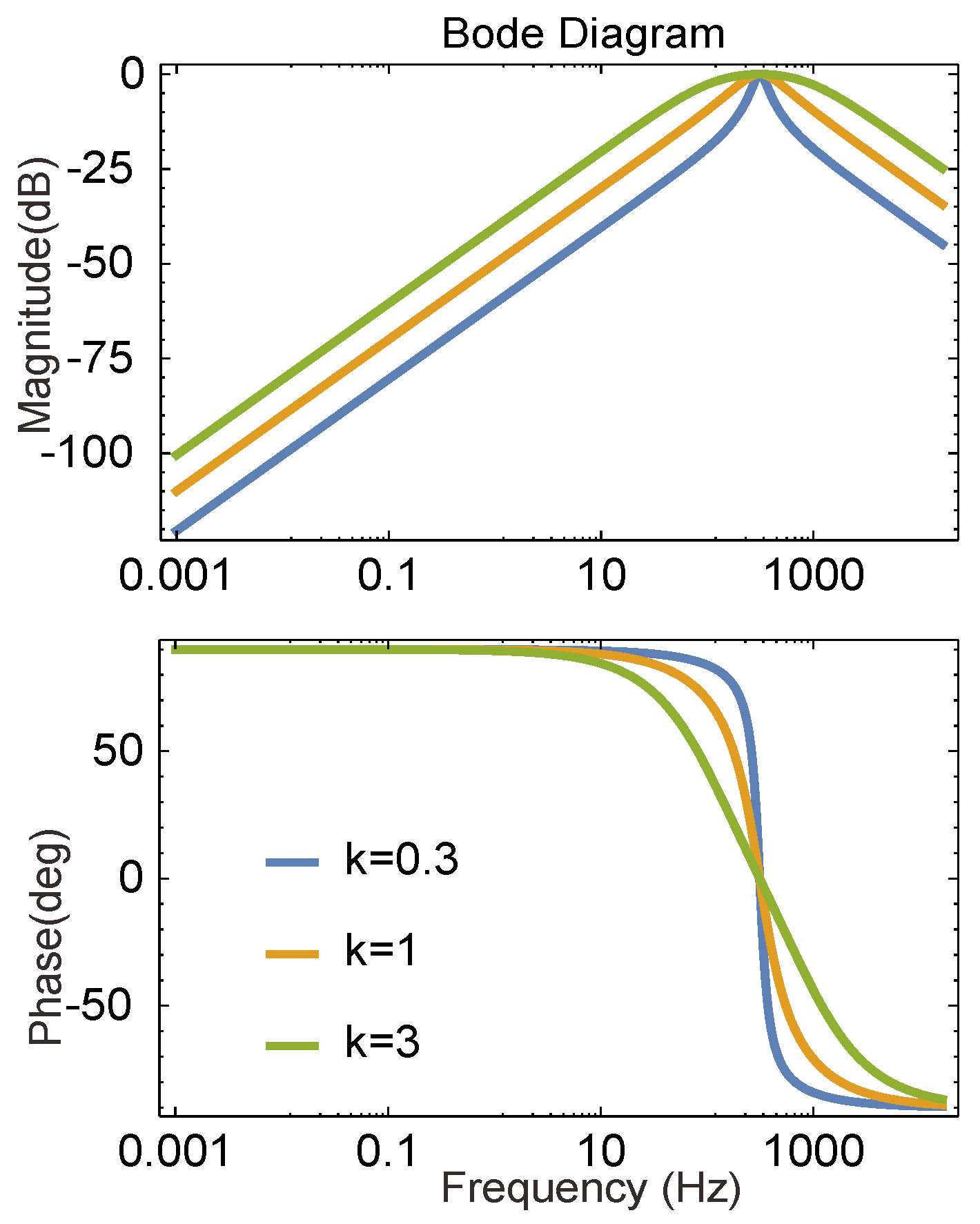
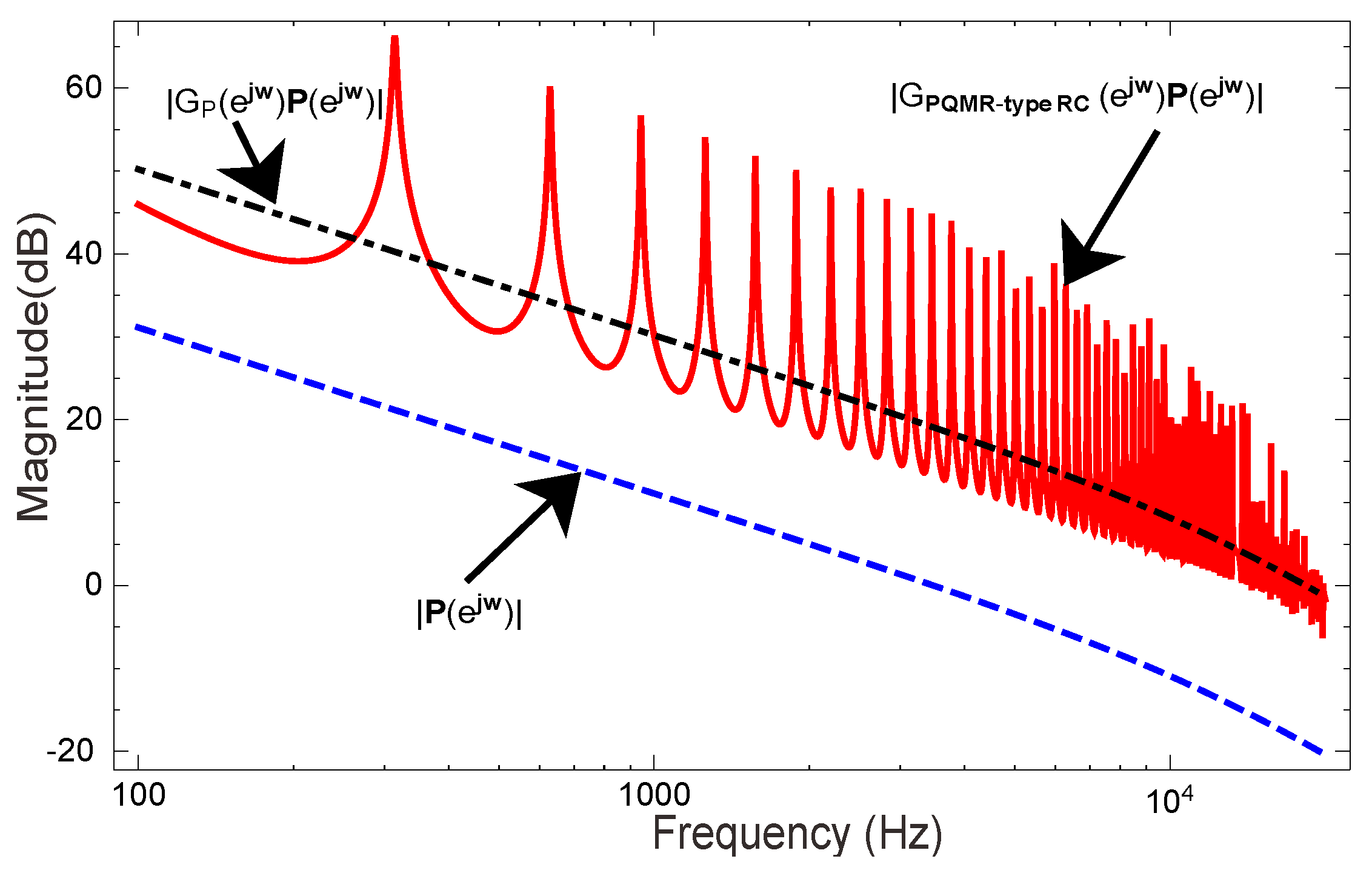
4.1.1. The Proportional Gain
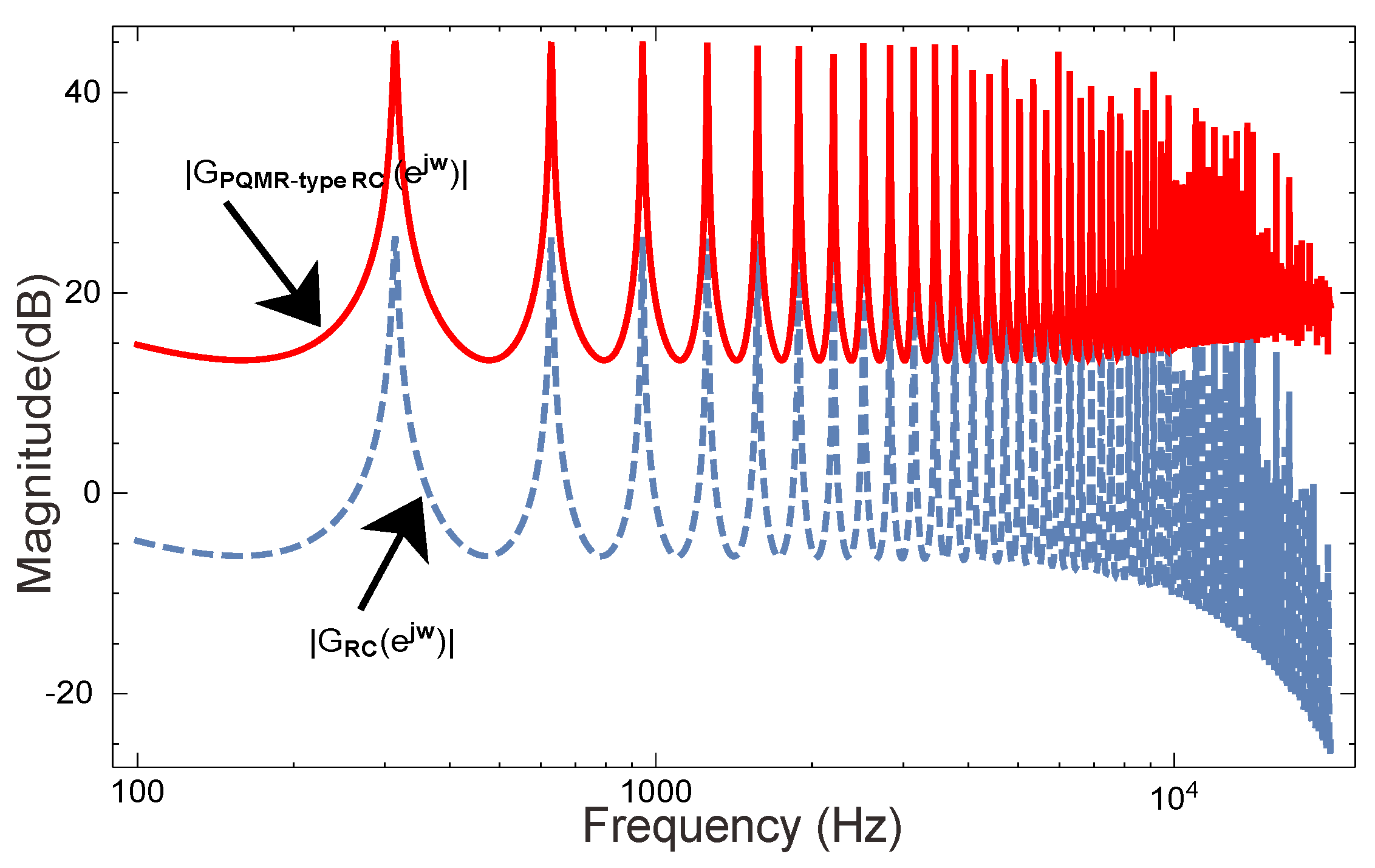
4.1.2. The Internal Model
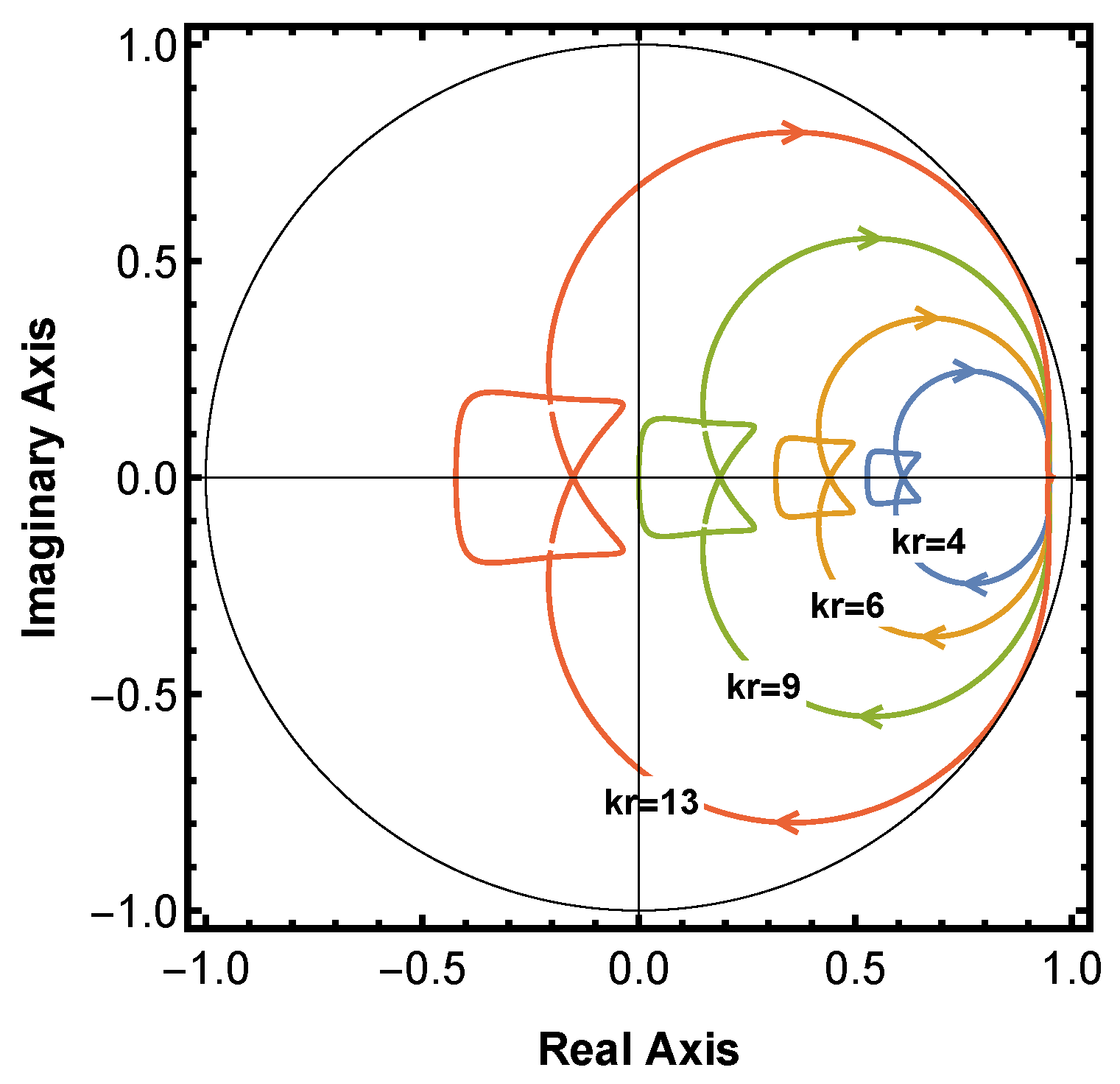
4.1.3. The Magnitude Compensator
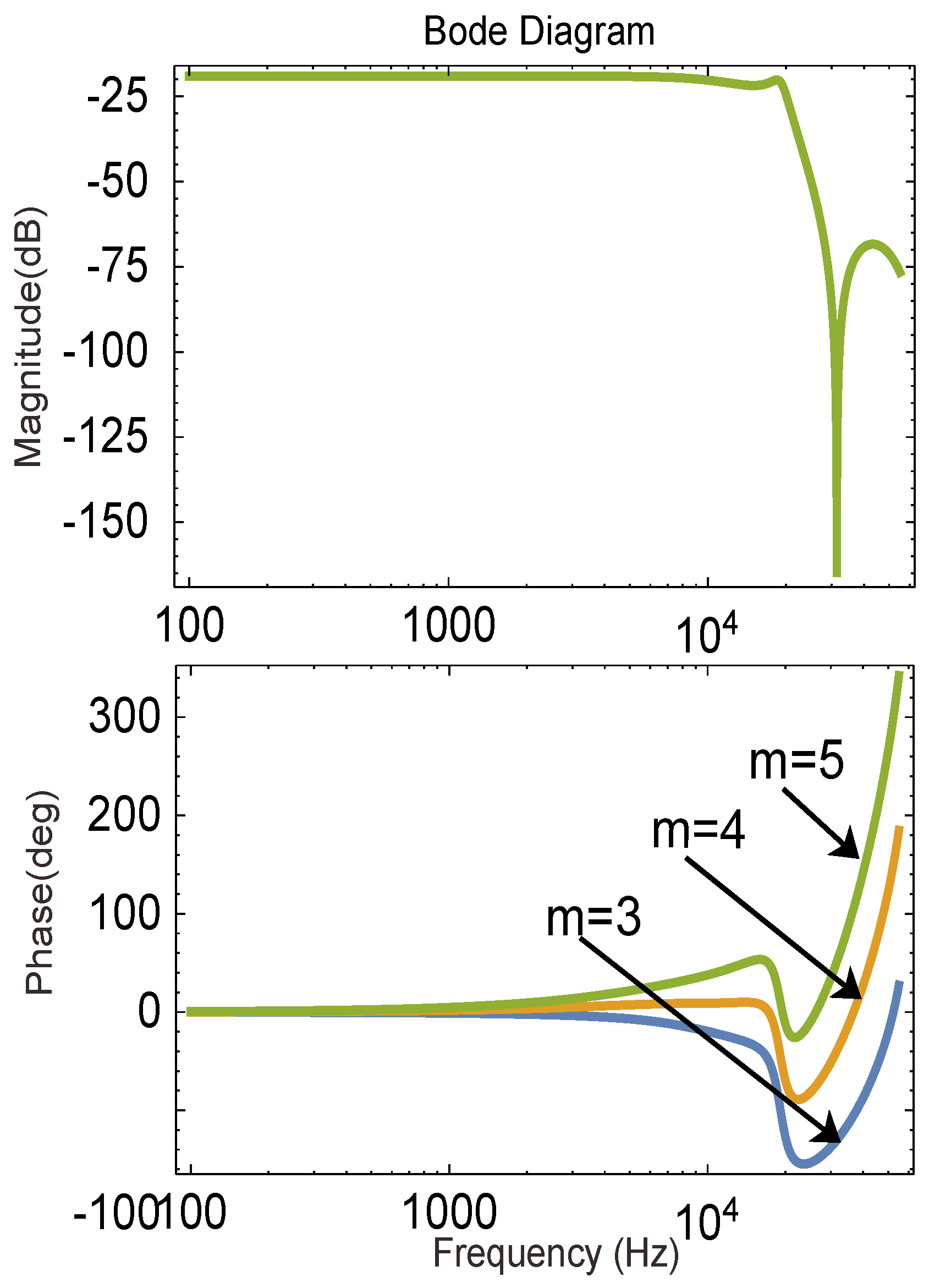
4.1.4. The Phase Advance Compensator
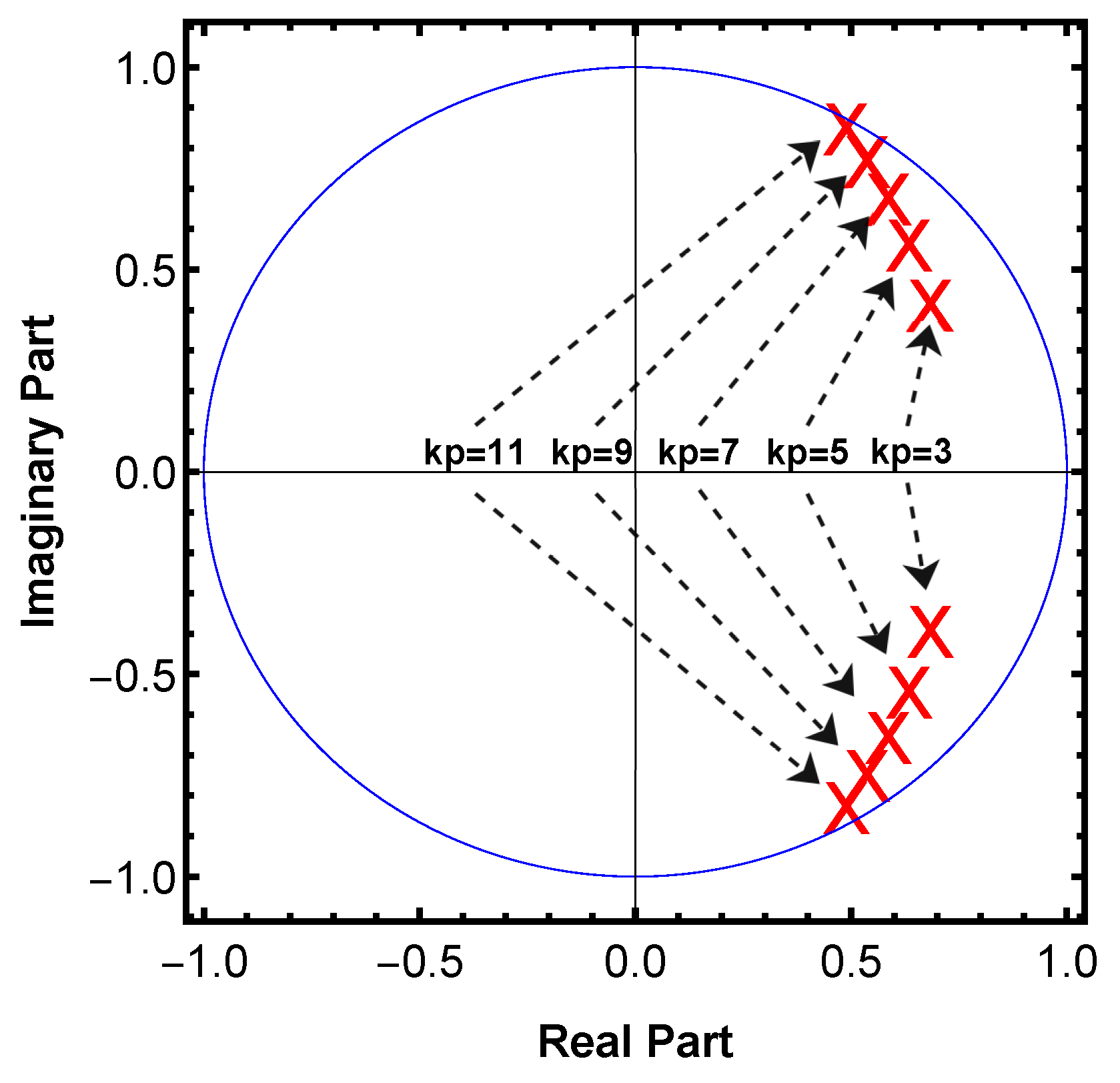
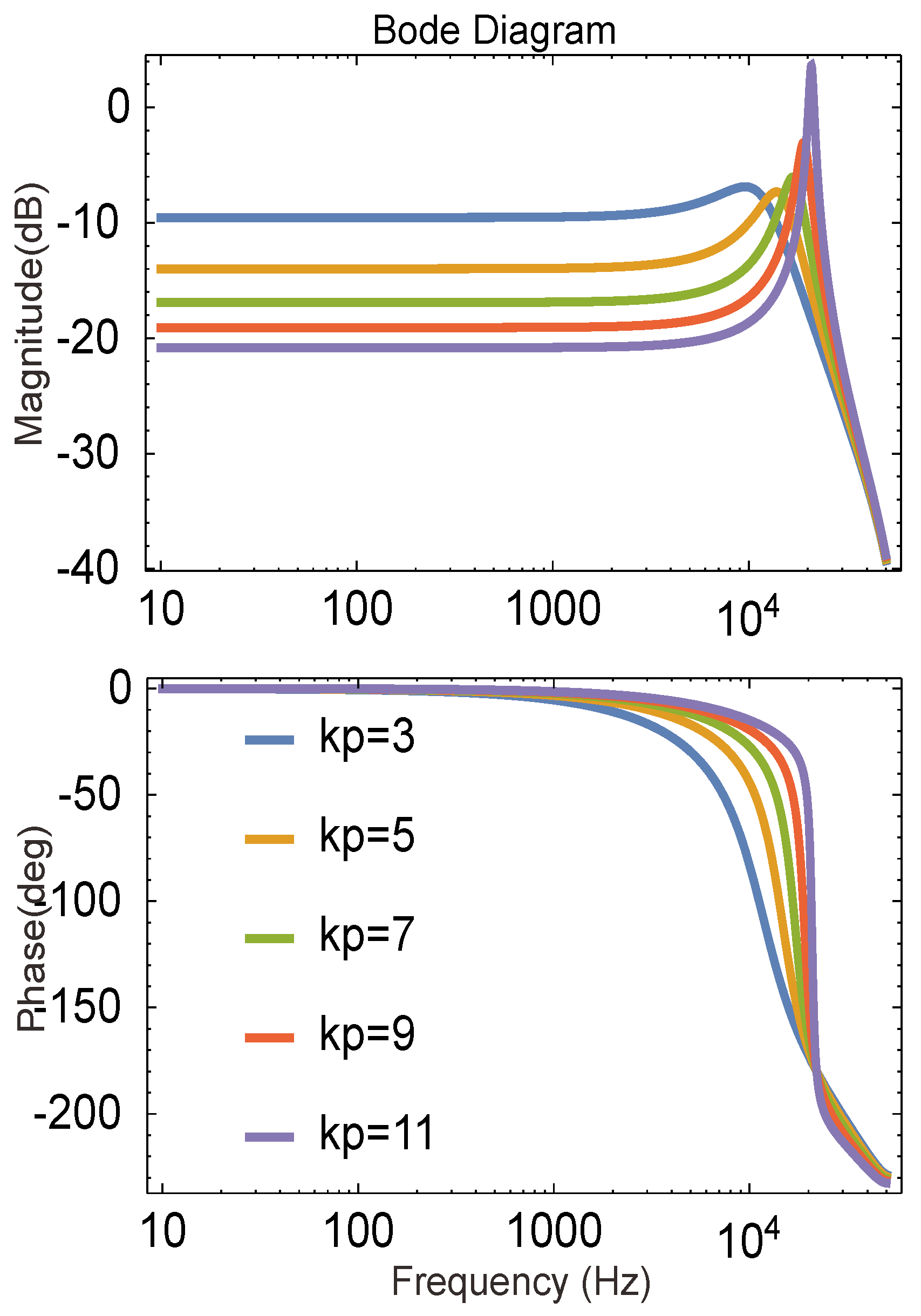
4.1.5. The Repetitive Gain
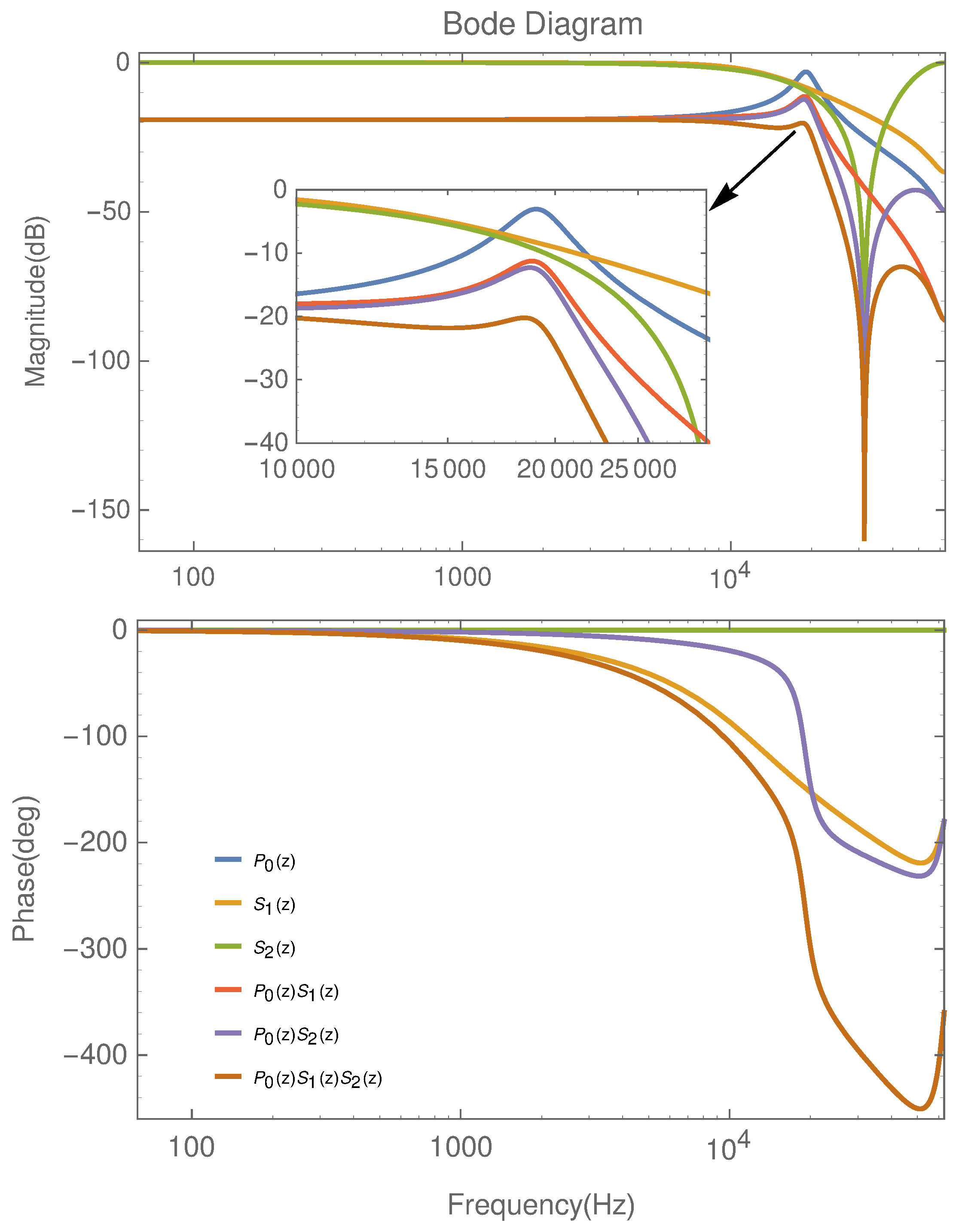
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adefarati, T.; Bansal, R. Integration of renewable distributed generators into the distribution system: A review. IET Renew. Power Gener. 2016, 10, 873–884. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, J.; Qian, Z. An improved repetitive control scheme for grid-connected inverter with frequency-adaptive capability. IEEE Trans. Ind. Electron. 2013, 60, 814–823. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F. Limitations of voltage-oriented pi current control of grid-connected pwm rectifiers with lcl filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc.-Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Rashed, M.; Klumpner, C.; Asher, G. Repetitive and resonant control for a single-phase grid-connected hybrid cascaded multilevel converter. IEEE Trans. Power Electron. 2013, 28, 2224–2234. [Google Scholar] [CrossRef]
- Lopez, O.; Teodorescu, R.; Freijedo, F.; DovalGandoy, J. Leakage current evaluation of a singlephase transformerless pv inverter connected to the grid. In Proceedings of the APEC 2007-Twenty Second Annual IEEE Applied Power Electronics Conference, Anaheim, CA, USA, 25 February–1 March 2007; pp. 907–912. [Google Scholar]
- Ahmad, Z.; Singh, S. Single phase transformerless inverter topology with reduced leakage current for grid connected photovoltaic system. Electr. Power Syst. Res. 2018, 154, 193–203. [Google Scholar] [CrossRef]
- Islam, M.; Mekhilef, S.; Hasan, M. Single phase transformerless inverter topologies for grid-tied photovoltaic system: A review. Renew. Sustain. Energy Rev. 2015, 45, 69–86. [Google Scholar] [CrossRef]
- Yu, W.; Lai, J.-S.; Qian, H.; Hutchens, C. High-efficiency mosfet inverter with h6-type configuration for photovoltaic nonisolated ac-module applications. IEEE Trans. Power Electron. 2011, 26, 1253–1260. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; Xing, Y.; Xing, M. H6 transformerless full-bridge pv grid-tied inverters. IEEE Trans. Power Electron. 2014, 29, 1229–1238. [Google Scholar] [CrossRef]
- Panda, A.; Pathak, M.; Srivastava, S. A single phase photovoltaic inverter control for grid connected system. Sadhana 2016, 41, 15–30. [Google Scholar] [CrossRef]
- Chatterjee, A.; Mohanty, K. Current control strategies for single phase grid integrated inverters for photovoltaic applications—A review. Renew. Sustain. Energy Rev. 2018, 92, 554–569. [Google Scholar] [CrossRef]
- Hassaine, L.; Lias, E.; Quintero, J.; Salas, V. Overview of power inverter topologies and control structures for grid connected photovoltaic systems. Renew. Sustain. Energy Rev. 2014, 30, 796–807. [Google Scholar] [CrossRef]
- Yang, S.; Lei, Q.; Peng, F.; Qian, Z. A robust control scheme for grid-connected voltage-source inverters. IEEE Trans. Ind. Electron. 2011, 58, 202–212. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, D.; Yuan, T.; Liu, Z.; Yu, J. A novel control strategy for grid-connected inverter based on iterative calculation of structural parameters. Energies 2018, 11, 3306. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple harmonics control for three-phase grid converter systems with the use of pi-res current controller in a rotating frame. IEEE Trans. Power Electron. 2006, 21, 836–841. [Google Scholar] [CrossRef]
- Schiesser, M.; Wasterlain, S.; Marchesoni, M.; Carpita, M. A simplified design strategy for multi-resonant current control of a grid-connected voltage source inverter with an lcl filter. Energies 2018, 11, 609. [Google Scholar] [CrossRef]
- Yepes, A.G.; Freijedo, F.D.; López, O.; Doval-Gandoy, J. High-performance digital resonant controllers implemented with two integrators. IEEE Trans. Power Electron. 2011, 26, 563–576. [Google Scholar] [CrossRef]
- Pan, Z.; Dong, F.; Zhao, J.; Wang, L.; Wang, H.; Feng, Y. Combined resonant controller and two-degree-of-freedom pid controller for pmslm current harmonics suppression. IEEE Trans. Ind. Electron. 2018, 65, 7558–7568. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, Y. A pimr-type repetitive control for a grid-tied inverter: Structure, analysis, and design. IEEE Trans. Power Electron. 2018, 33, 2730–2739. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Wang, P.; Tang, Y.; Choo, F.H. Mitigation of dc and harmonic currents generated by voltage measurement errors and grid voltage distortions in transformerless grid-connected inverters. IEEE Trans. Energy Convers. 2018, 33, 801–813. [Google Scholar] [CrossRef]
- Gao, Y.-G.; Jiang, F.-Y.; Song, J.-C.; Zheng, L.-J.; Tian, F.-Y.; Geng, P.-L. A novel dual closed-loop control scheme based on repetitive control for grid-connected inverters with an lcl filter. ISA Trans. 2018, 74, 194–208. [Google Scholar] [CrossRef]
- De, D.; Ramanarayanan, V. A proportional + multiresonant controller for three-phase four-wire high-frequency link inverter. IEEE Trans. Power Electron. 2010, 4, 899–906. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- He, L.; Zhang, K.; Xiong, J.; Fan, S. A repetitive control scheme for harmonic suppression of circulating current in modular multilevel converters. IEEE Trans. Power Electron. 2014, 30, 471–481. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, D.; Zhou, K.; Wang, Y. Linear phase lead compensation repetitive control of a cvcf pwm inverter. IEEE Trans. Ind. Electron. 2008, 55, 1595–1602. [Google Scholar] [CrossRef]
- Han, Y.; Luo, M.; Zhao, X.; Guerrero, J.M.; Xu, L. Comparative performance evaluation of orthogonal-signal-generators-based single-phase pll algorithms—A survey. IEEE Trans. Power Electron. 2016, 31, 3932–3944. [Google Scholar] [CrossRef]
- Özdemir, A.; Yazici, I.; Vural, C. Fast and robust software-based digital phase-locked loop for power electronics applications. IET Gener. Trans. Distrib. 2013, 7, 1435–1441. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. A nonadaptive window-based pll for single-phase applications. IEEE Trans. Power Electron. 2018, 33, 24–31. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vidal, A.; Yepes, A.G.; Doval-Gandoy, J.; Freijedo, F.D. Small-signal modeling, stability analysis and design optimization of single-phase delay-based plls. IEEE Trans. Power Electron. 2016, 31, 3517–3527. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Y.; Tian, Y.; Wang, L. Phase-locked loop research of grid-connected inverter based on impedance analysis. Energies 2018, 11, 3077. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D.; Guerrero, J.M. Dynamics assessment of advanced single-phase pll structures. IEEE Trans. Ind. Electron. 2013, 60, 2167–2177. [Google Scholar] [CrossRef]





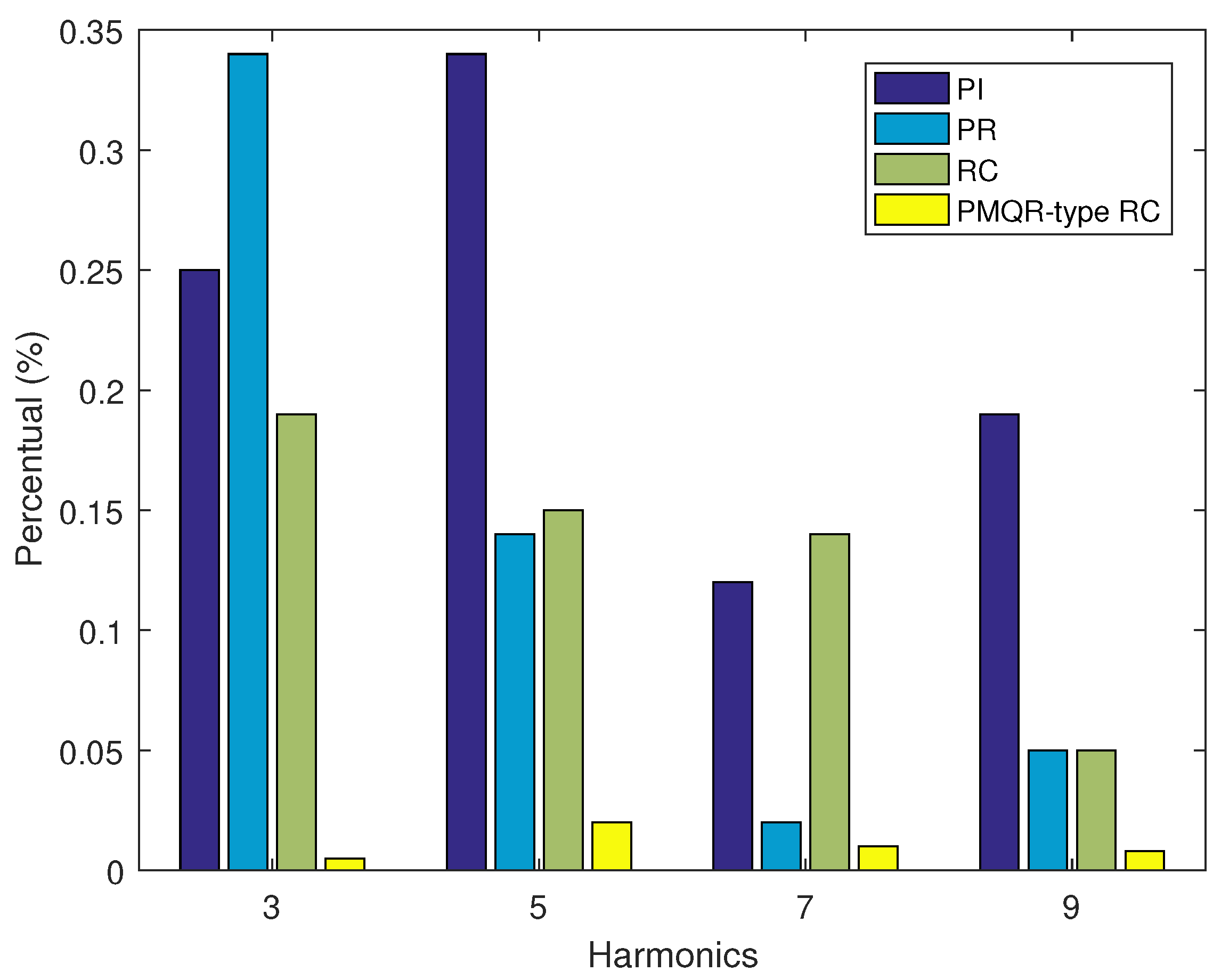
| Symbol | Description | Values |
|---|---|---|
| grid voltage | 220 V | |
| ideal grid voltage frequency | 50 Hz | |
| DC bus voltage | 360 V | |
| sampling frequency | 20 kHz | |
| filter inductor | mH | |
| filter capacitor | 4 F | |
| R | ESR | 0.1 |
| P | output power | 3 kW |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Liu, P.; Xu, S.; Liu, S. Analysis and Design of A PMQR-Type Repetitive Control Scheme for Grid-Connected H6 Inverters. Appl. Sci. 2019, 9, 1198. https://doi.org/10.3390/app9061198
Yang X, Liu P, Xu S, Liu S. Analysis and Design of A PMQR-Type Repetitive Control Scheme for Grid-Connected H6 Inverters. Applied Sciences. 2019; 9(6):1198. https://doi.org/10.3390/app9061198
Chicago/Turabian StyleYang, Xiaohui, Peiyun Liu, Shaoping Xu, and Shichao Liu. 2019. "Analysis and Design of A PMQR-Type Repetitive Control Scheme for Grid-Connected H6 Inverters" Applied Sciences 9, no. 6: 1198. https://doi.org/10.3390/app9061198





