Evidence-Theory-Based Robust Optimization and Its Application in Micro-Electromechanical Systems
Abstract
:Featured Application
Abstract
1. Introduction
2. Robustness Analysis Using Evidence Theory
3. Formulation of the EBRO Model
4. The Proposed Algorithm
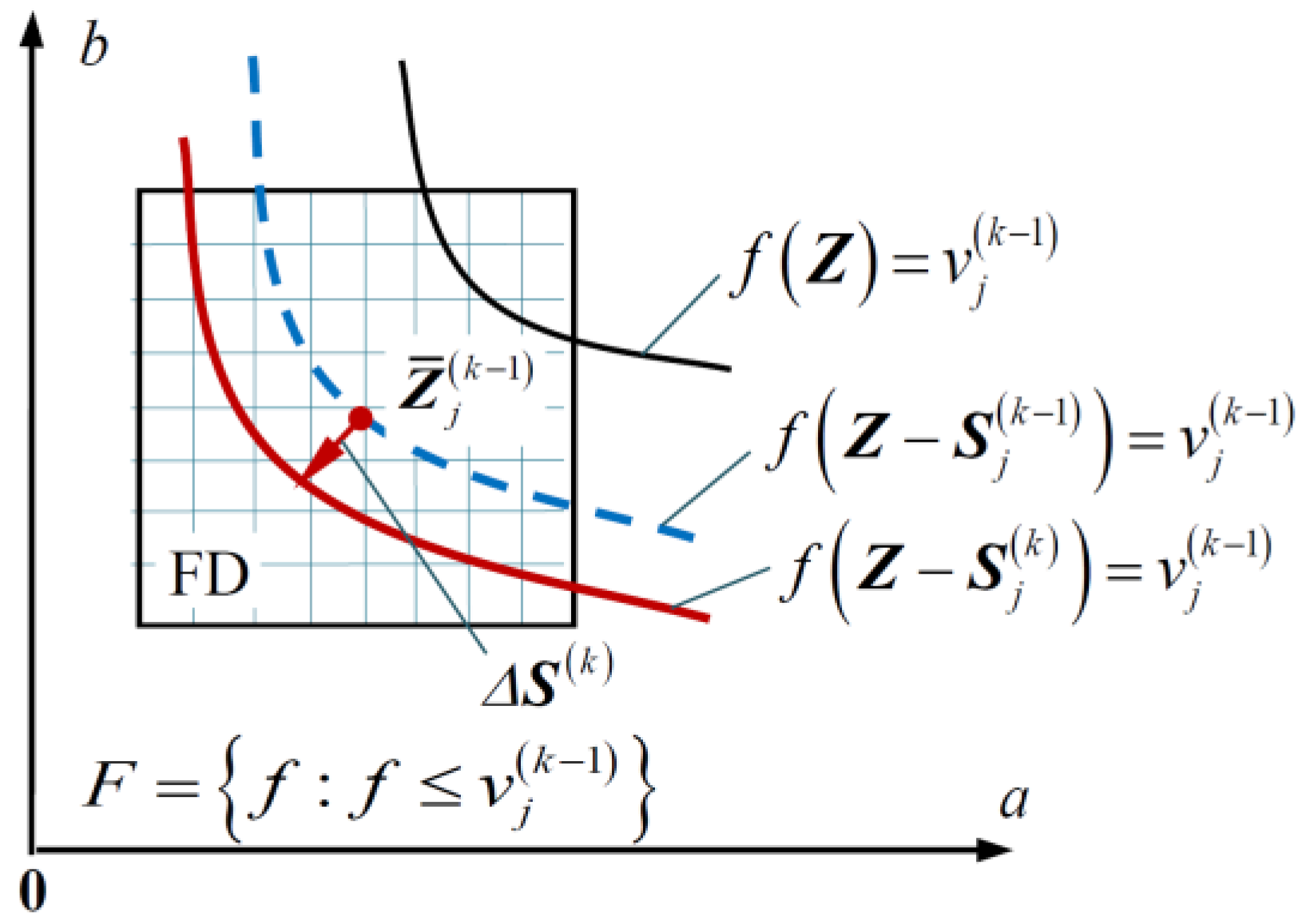
4.1. Decomposition into Sub-Problems
4.2. Iteration Framework
5. Application Discussion
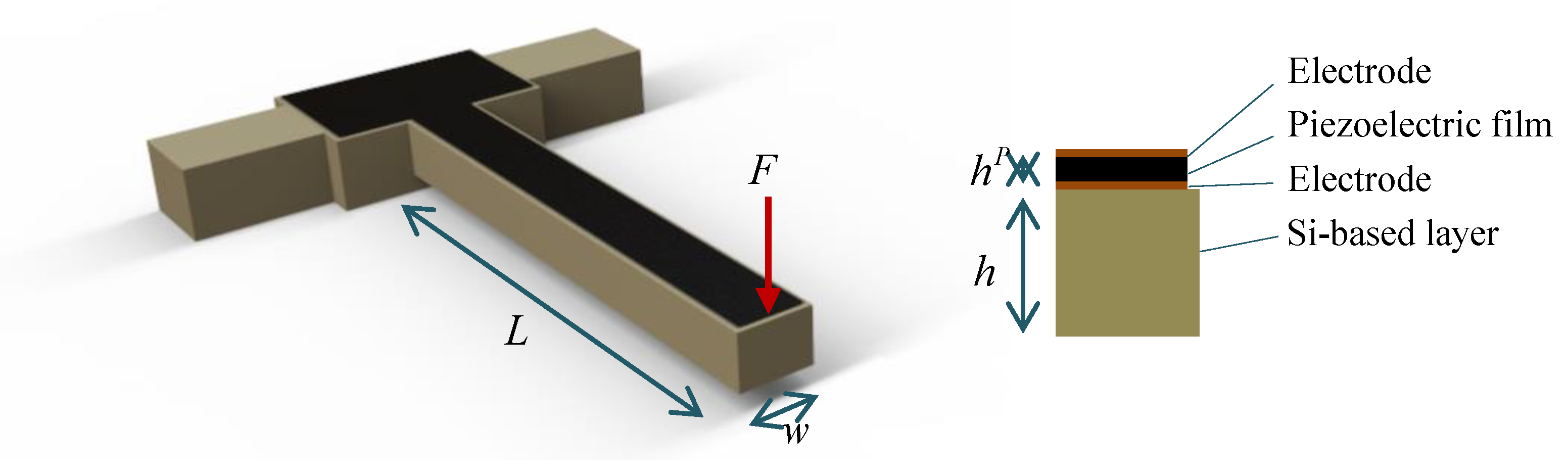
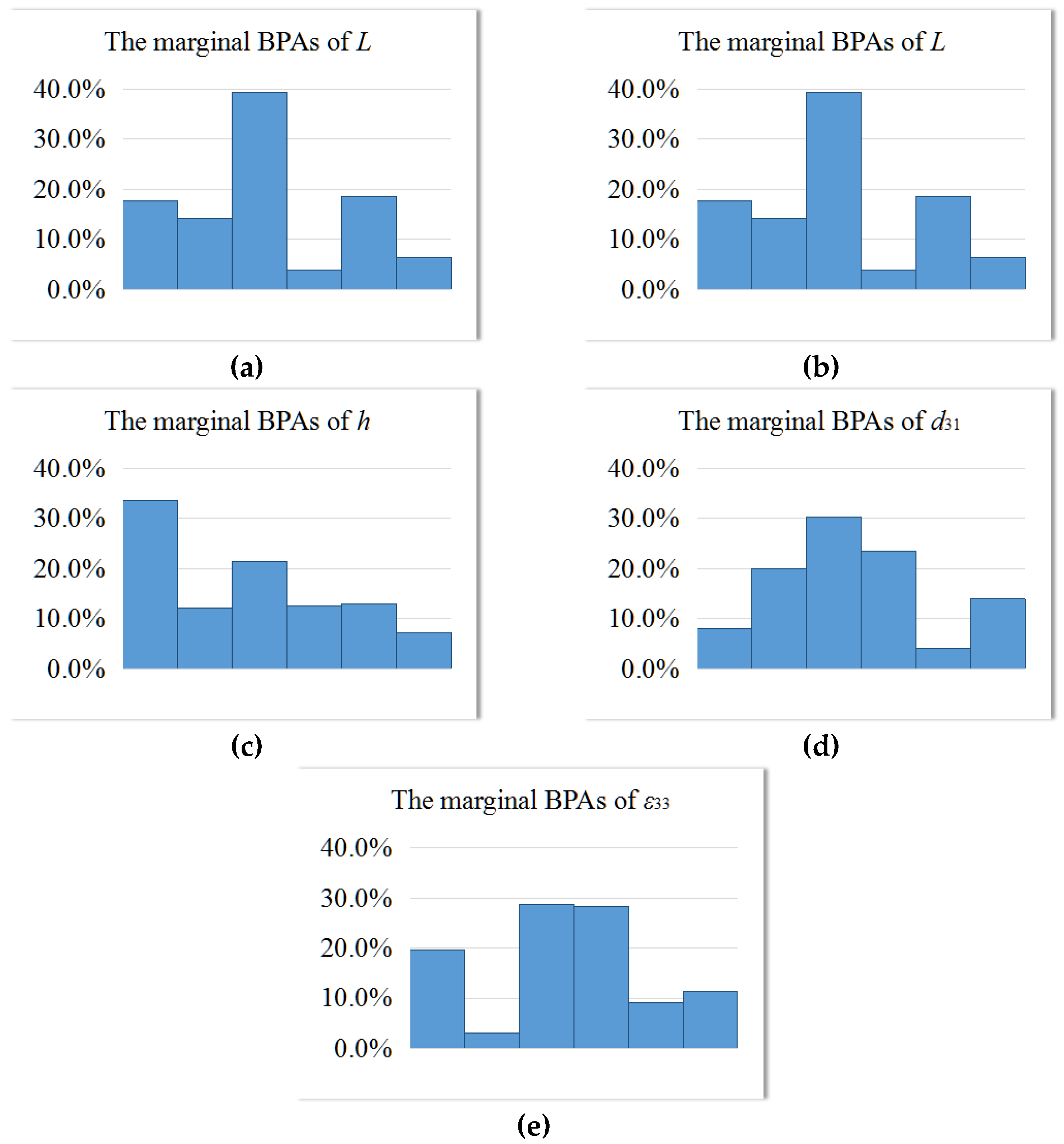
5.1. A Micro-Force Sensor
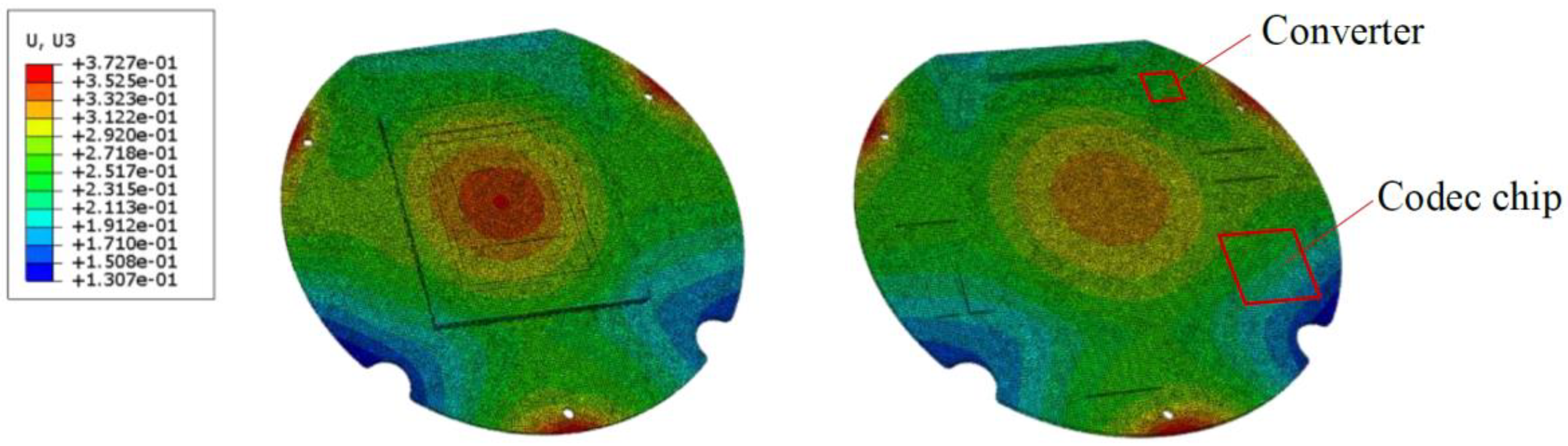
5.2. An Ultra-Low-Noise Image Sensor
5.3. A Capacitive Accelerometer
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Taguchi, G.; Phadke, M.S. Quality Control, Robust Design, and the Taguchi Method. In Quality Engineering through Design Optimization; Springer: Berlin, Germany, 1989; pp. 77–96. [Google Scholar]
- Beyer, H.G.; Sendhoff, B. Robust optimization—A comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar]
- Fowlkes, W.Y.; Creveling, C.M.; Derimiggio, J. Engineering Methods for Robust Product Design: Using Taguchi Methods in Technology and Product Development; Addison-Wesley: Reading, MA, USA; Bosten, MA, USA, 1995; pp. 121–123. [Google Scholar]
- Gu, X.; Sun, G.; Li, G.; Mao, L.; Li, Q. A comparative study on multiobjective reliable and robust optimization for crashworthiness design of vehicle structure. Struct. Multidiscip. Optim. 2013, 48, 669–684. [Google Scholar] [CrossRef]
- Yao, W.; Chen, X.; Luo, W.; van Tooren, M.; Guo, J. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Prog. Aerosp. Sci. 2011, 47, 450–479. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef] [Green Version]
- Hoffman, F.O.; Hammonds, J.S. Propagation of uncertainty in risk assessments: The need to distinguish between uncertainty due to lack of knowledge and uncertainty due to variability. Risk Anal. 1994, 14, 707–712. [Google Scholar] [CrossRef] [PubMed]
- Grubbs, F. An introduction to probability theory and its applications. Technometrics 1958, 9, 342. [Google Scholar] [CrossRef]
- Gao, W.; Chen, J.J.; Sahraee, S. Reliability-based optimization of trusses with random parameters under dynamic loads. Comput. Mech. 2011, 47, 627–640. [Google Scholar]
- Haldar, A.; Mahadevan, S.; Haldar, A.; Mahadevan, S. Probability, reliability and statistical methods in engineering design (haldar, mahadevan). Bautechnik 2013, 77, 379. [Google Scholar]
- Chen, W.; Wiecek, M.M.; Zhang, J. Quality utility—A compromise programming approach to robust design. J. Mech. Des. 1999, 121, 179–187. [Google Scholar] [CrossRef]
- Lee, K.H.; Park, G.J. Robust optimization considering tolerances of design variables. Comput. Struct. 2001, 79, 77–86. [Google Scholar] [CrossRef]
- Zheng, J.; Luo, Z.; Jiang, C.; Gao, J. Robust topology optimization for concurrent design of dynamic structures under hybrid uncertainties. Mech. Syst. Signal. Process. 2018, 120, 540–559. [Google Scholar] [CrossRef]
- Tzvieli, A. Possibility theory: An approach to computerized processing of uncertainty. J. Assoc. Inf. Sci. Technol. 1990, 41, 153–154. [Google Scholar] [CrossRef]
- Georgescu, I. Possibility Theory and the Risk; Springer: Berlin, Germany, 2012. [Google Scholar]
- Gupta, M.M. Fuzzy set theory and its applications. Fuzzy Sets Syst. 1992, 47, 396–397. [Google Scholar] [CrossRef]
- Sun, B.; Ma, W.; Zhao, H. Decision-theoretic rough fuzzy set model and application. Inf. Sci. 2014, 283, 180–196. [Google Scholar] [CrossRef]
- Elishakoff, I.; Colombi, P. Combination of probabilistic and convex models of uncertainty when scarce knowledge is present on acoustic excitation parameters. Comput. Methods Appl. Mech. Eng. 1993, 104, 187–209. [Google Scholar] [CrossRef]
- Ni, B.Y.; Jiang, C.; Huang, Z.L. Discussions on non-probabilistic convex modelling for uncertain problems. Appl. Math. Model. 2018, 59, 54–85. [Google Scholar] [CrossRef] [Green Version]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NY, USA, 1976. [Google Scholar]
- Caselton, W.F.; Luo, W. Decision making with imprecise probabilities: Dempster-shafer theory and application. Water Resour. Res. 1992, 28, 3071–3083. [Google Scholar] [CrossRef]
- Du, X. Uncertainty analysis with probability and evidence theories. In Proceedings of the 2006 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006. [Google Scholar]
- Vasile, M. Robust mission design through evidence theory and multiagent collaborative search. Ann. N. Y. Acad. Sci. 2005, 1065, 152–173. [Google Scholar] [CrossRef]
- Croisard, N.; Vasile, M.; Kemble, S.; Radice, G. Preliminary space mission design under uncertainty. Acta Astronaut. 2010, 66, 654–664. [Google Scholar] [CrossRef] [Green Version]
- Zuiani, F.; Vasile, M.; Gibbings, A. Evidence-based robust design of deflection actions for near Earth objects. Celest. Mech. Dyn. Astron. 2012, 114, 107–136. [Google Scholar] [CrossRef] [Green Version]
- Hou, L.; Pirzada, A.; Cai, Y.; Ma, H. Robust design optimization using integrated evidence computation—With application to Orbital Debris Removal. In Proceedings of the IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015. [Google Scholar]
- Sentz, K.; Ferson, S. Combination of Evidence in Dempster-Shafer Theory; Sandia National Laboratories: Albuquerque, NM, USA, 2002; Volume 4015.
- Jiang, C.; Zhang, W.; Han, X.; Ni, B.Y.; Song, L.J. A vine-copula-based reliability analysis method for structures with multidimensional correlation. J. Mech. Des. 2015, 137, 061405. [Google Scholar] [CrossRef]
- Dong, W.; Shah, H.C. Vertex method for computing functions of fuzzy variables. Fuzzy Sets Syst. 1987, 24, 65–78. [Google Scholar] [CrossRef]
- Jin, Y.; Branke, J. Evolutionary optimization in uncertain environments—A survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Park, G.J.; Lee, T.H.; Lee, K.H.; Hwang, K.H. Robust design: An overview. AIAA J. 2006, 44, 181–191. [Google Scholar] [CrossRef]
- Huang, Z.L.; Jiang, C.; Zhang, Z.; Fang, T.; Han, X. A decoupling approach for evidence-theory-based reliability design optimization. Struct. Multidiscip. Optim. 2017, 56, 647–661. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, C.; Wang, G.G.; Han, X. First and second order approximate reliability analysis methods using evidence theory. Reliab. Eng. Syst. Saf. 2015, 137, 40–49. [Google Scholar] [CrossRef]
- Breitung, K. Probability approximations by log likelihood maximization. J. Eng. Mech. 1991, 117, 457–477. [Google Scholar] [CrossRef]
- Du, X.; Chen, W. Sequential optimization and reliability assessment method for efficient probabilistic design. J. Mech. Des. 2002, 126, 871–880. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons: Somerset, NJ, USA, 2013; pp. 127–156. [Google Scholar]
- Coultate, J.K.; Fox, C.H.J.; Mcwilliam, S.; Malvern, A.R. Application of optimal and robust design methods to a MEMS accelerometer. Sens. Actuators A Phys. 2008, 142, 88–96. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Kouravand, S. Robust design of a bimetallic micro thermal sensor using taguchi method. J. Optim. Theory Appl. 2013, 157, 188–198. [Google Scholar] [CrossRef]
- Li, F.; Liu, J.; Wen, G.; Rong, J. Extending sora method for reliability-based design optimization using probability and convex set mixed models. Struct. Multidiscip. Optim. 2008, 59, 1–17. [Google Scholar] [CrossRef]
- Fishman, G. Monte Carlo: Concepts, Algorithms, and Application; Springer Science & Business Media: Berlin, Germany, 2013; pp. 493–583. [Google Scholar]
- Smits, J.G.; Dalke, S.I.; Cooney, T.K. The constituent equations of piezoelectric bimorphs. Sens. Actuators A Phys. 1991, 28, 41–61. [Google Scholar] [CrossRef]
- Fossum, E.R.; Hondongwa, D.B. A review of the pinned photodiode for CCD and CMOS image sensors. IEEE J. Electron. Devices Soc. 2014, 2, 33–43. [Google Scholar] [CrossRef]
- Benmessaoud, M.; Nasreddine, M.M. Optimization of MEMS capacitive accelerometer. Microsyst. Technol. 2013, 19, 713–720. [Google Scholar] [CrossRef] [Green Version]




| Results | ||||||
| Proposed method | (mm) | 0.937, 0.086, 0.072 | 0.937, 0.086, 0.072 | 0.937, 0.086, 0.072 | 0.937, 0.086, 0.072 | 0.937, 0.086, 0.072 |
| 22.1 mV, 80.4% | 20.0 mV, 85.3% | 18.2 mV, 90.6% | 15.7 mV, 95.5% | 9.6 mV, 99.9% | ||
| Reference solution | 22.4 mV, 80.0% | 20.0 mV, 85.3% | 18.5 mV, 90.0% | 16.1 mV, 95.0% | 9.6 mV, 99.9% | |
| Xi, i = 1, 2, 3 (mm) | P1 (W) | P2 (W) | |||
|---|---|---|---|---|---|
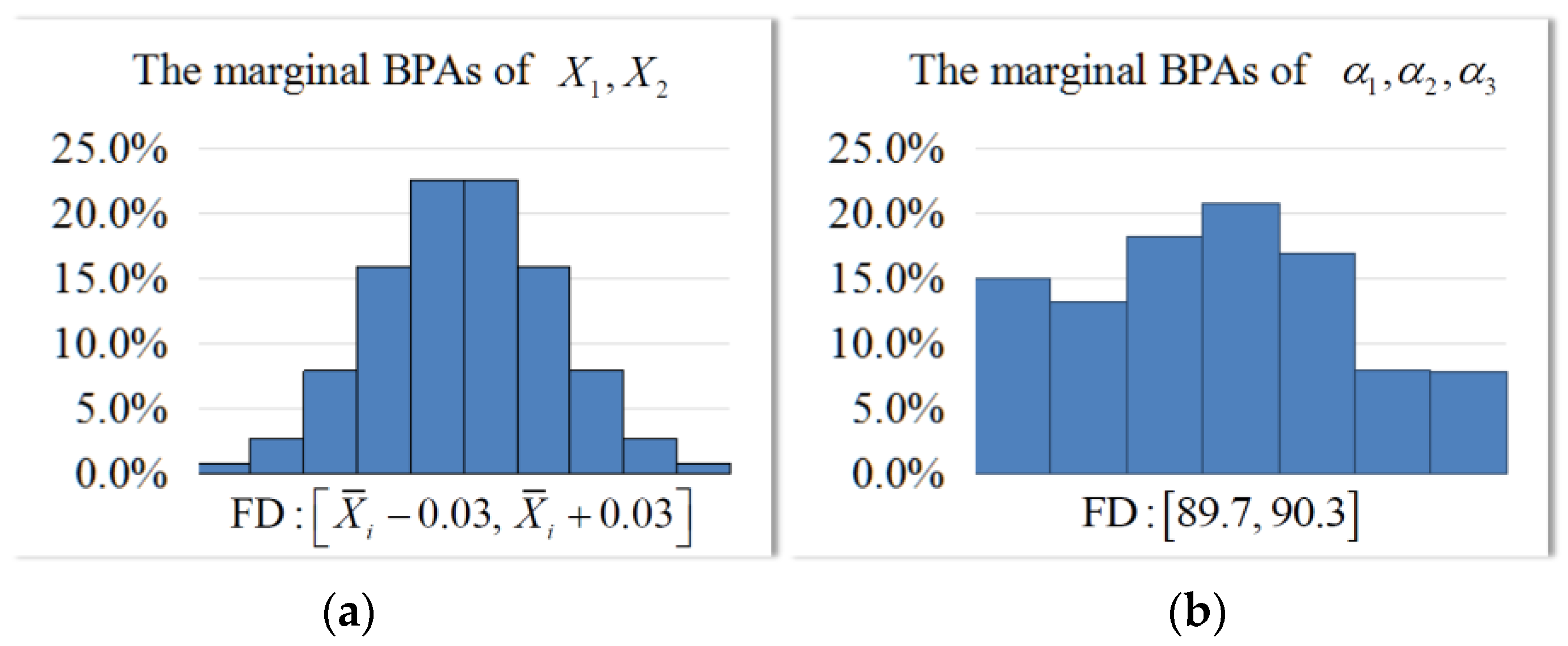
| Subinterval | BPA | Subinterval | BPA | Subinterval | BPA |
| 6.7% | 37.5% | 6.5% | |||
| 24.2% | 17.6% | 23.8% | |||
| 38.3% | 5.4% | 32.2% | |||
| 24.2% | 19.1% | 12.5% | |||
| 6.7% | 20.4% | 24.9% | |||
| Results | Case 1:2 Dimensions | Case 2:3 Dimensions | Case 3:5 Dimensions | |
|---|---|---|---|---|
| Proposed method | 128 | 142 | 198 | |
| Iterations | 3 | 4 | 4 | |
| (mm) | (0.200, 0.185, 0.000) (0.200, 0.186, 0.000) (0.200, 0.188, 0.000) | (0.200, 0.185, 0.000) (0.200, 0.186, 0.000) (0.200, 0.187, 0.000) | (0.200, 0.187, 0.000) (0.200, 0.188, 0.000) (0.200, 0.190, 0.000) | |
| (1.35 μm, 85.1%) (1.70 μm, 96.5%) (2.00 μm, 100.0%) | (1.41 μm, 85.8%) (1.55 μm, 96.4%) (1.65 μm, 100.0%) | (1.74 μm, 86.4%) (2.06 μm, 96.1%) (2.62 μm, 100.0%) | ||
| Reference solution | (1.35 μm, 85.1%) (1.69 μm, 95.5%) (2.00 μm, 100.0%) | (1.41 μm, 85.8%) (1.55 μm, 96.4%) (1.65 μm, 100.0%) | (1.71 μm, 85.8%) (2.02 μm, 95.4%) (2.56 μm, 99.9%) | |
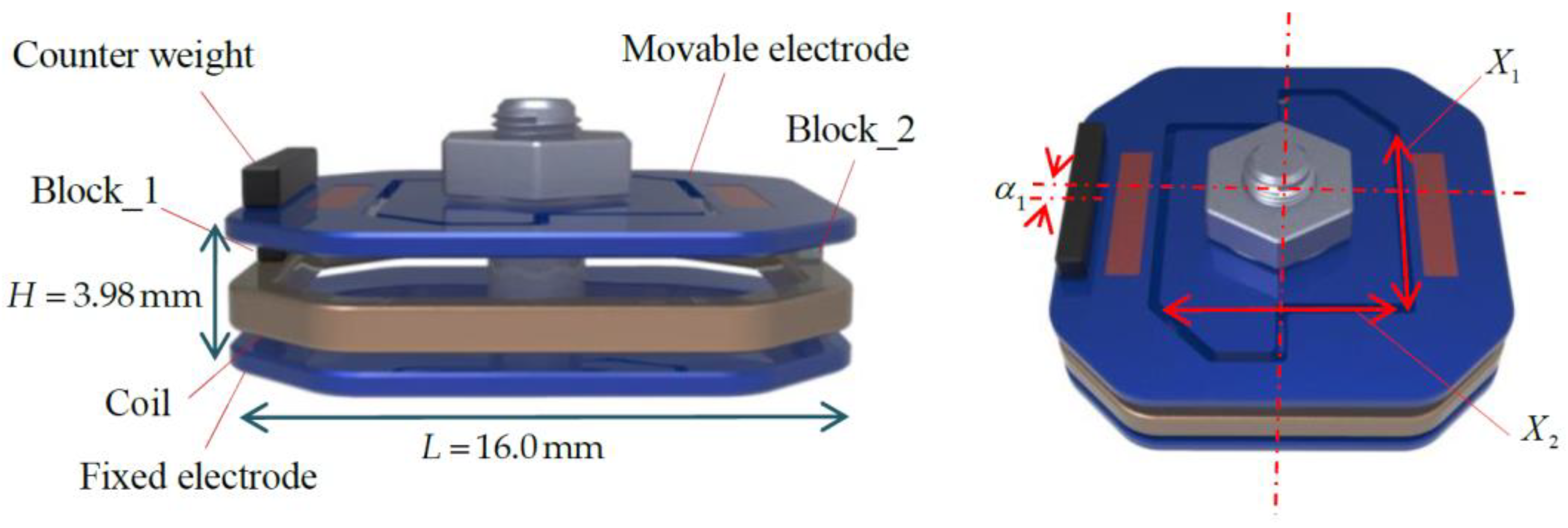
| Part | Fixed Electrode | Movable Electrode | Coil | Counter Weight | Block 1 | Block 2 |
|---|---|---|---|---|---|---|
| Material | Silicon | Silicon | Copper | Wolfram | Wolfram | Aluminium |
| Results | Proposed Method | Reference Solution |
|---|---|---|
| (mm) | (9.0661, 8.9042) (9.0659, 8.9040) (9.0657, 8.9038) (9.0653, 8.9035) (9.0653, 8.9035) (9.0653, 8.9035) | (9.0661, 8.9042) (9.0660, 8.9040) (9.0657, 8.9039) (9.0654, 8.9036) (9.0648, 8.9031) (9.0644, 8.9028) |
| (0.244 μm, 81.8%) (0.302 μm, 86.3%) (0.350 μm, 90.8%) (0.449 μm, 96.1%) (0.607 μm, 99.4%) (0.776 μm, 100.0%) | (0.244 μm, 81.8%) (0.279 μm, 85.2%) (0.338 μm, 90.1%) (0.424 μm, 95.5%) (0.594 μm, 99.2%) (0.733 μm, 99.9%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Xu, J.; Yang, T.; Li, F.; Deng, S. Evidence-Theory-Based Robust Optimization and Its Application in Micro-Electromechanical Systems. Appl. Sci. 2019, 9, 1457. https://doi.org/10.3390/app9071457
Huang Z, Xu J, Yang T, Li F, Deng S. Evidence-Theory-Based Robust Optimization and Its Application in Micro-Electromechanical Systems. Applied Sciences. 2019; 9(7):1457. https://doi.org/10.3390/app9071457
Chicago/Turabian StyleHuang, Zhiliang, Jiaqi Xu, Tongguang Yang, Fangyi Li, and Shuguang Deng. 2019. "Evidence-Theory-Based Robust Optimization and Its Application in Micro-Electromechanical Systems" Applied Sciences 9, no. 7: 1457. https://doi.org/10.3390/app9071457





