Mass Transport through Nanostructured Membranes: Towards a Predictive Tool
Abstract
:1. Introduction
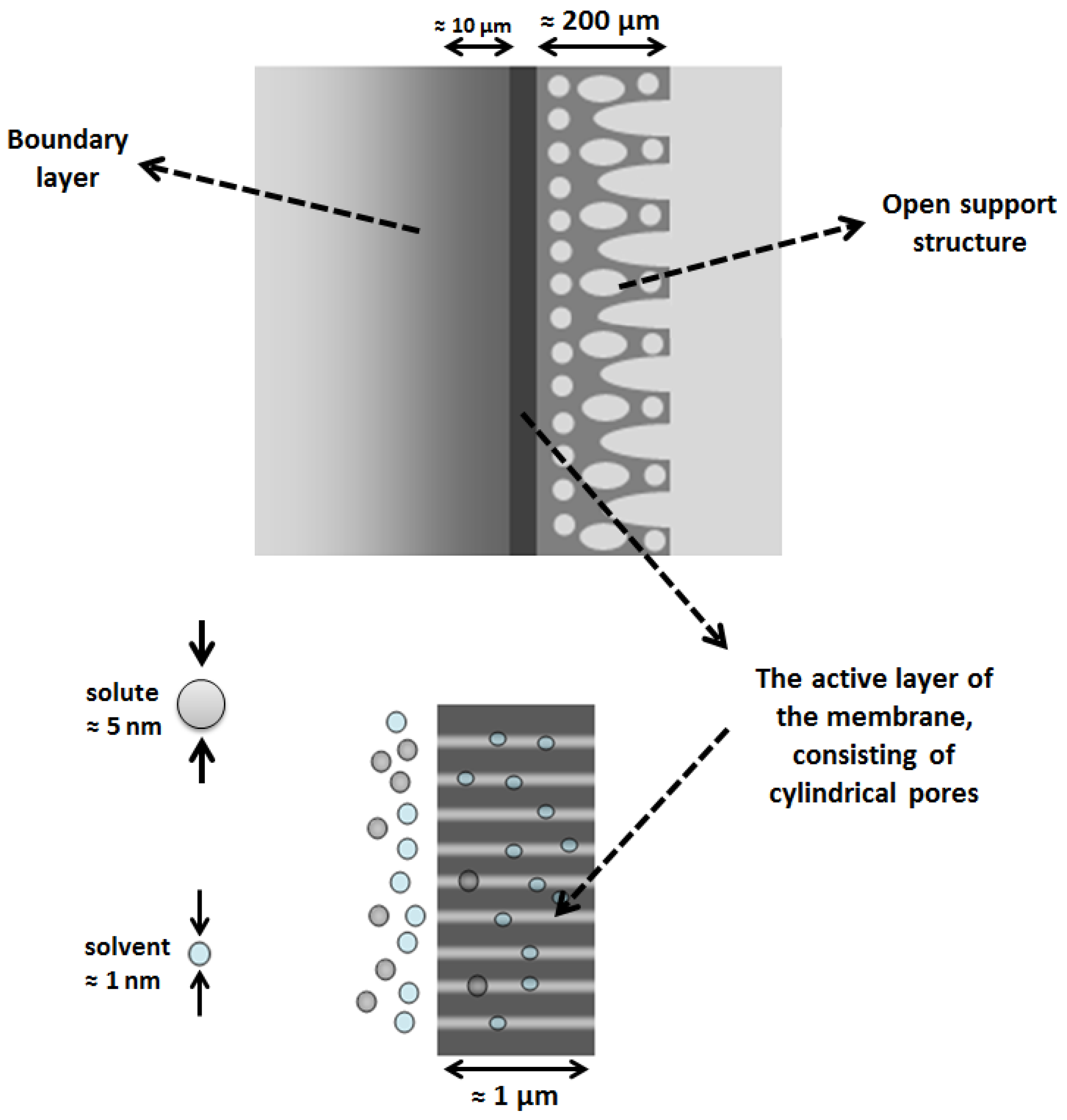
2. Modeling Approach
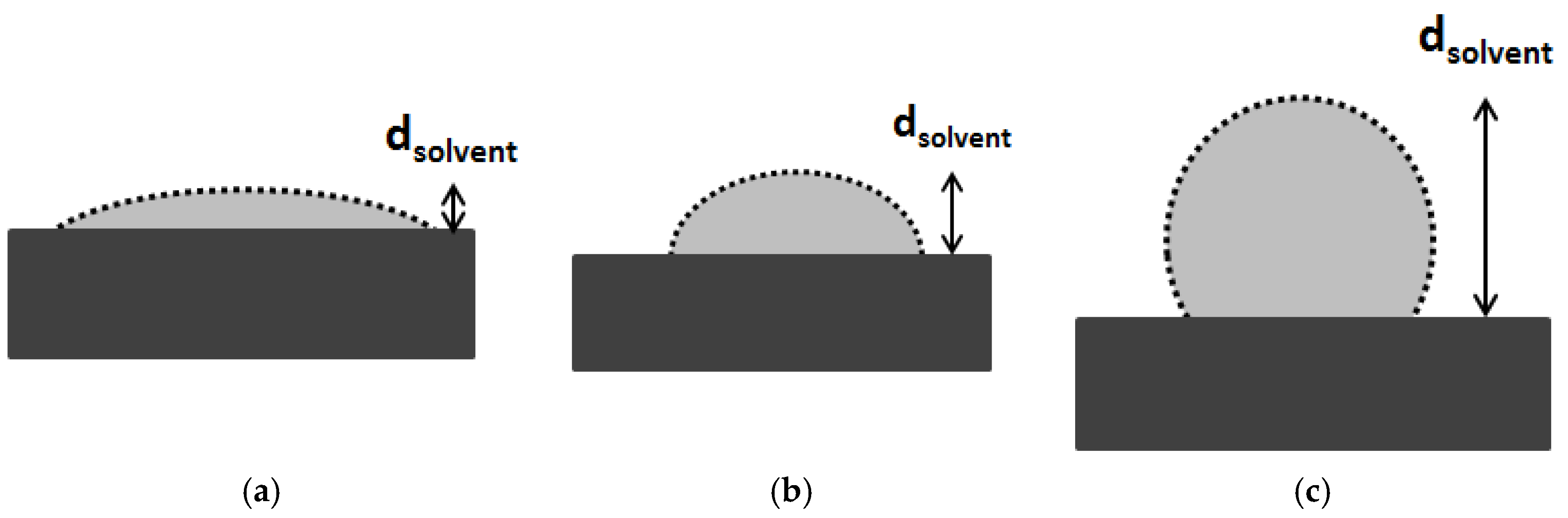
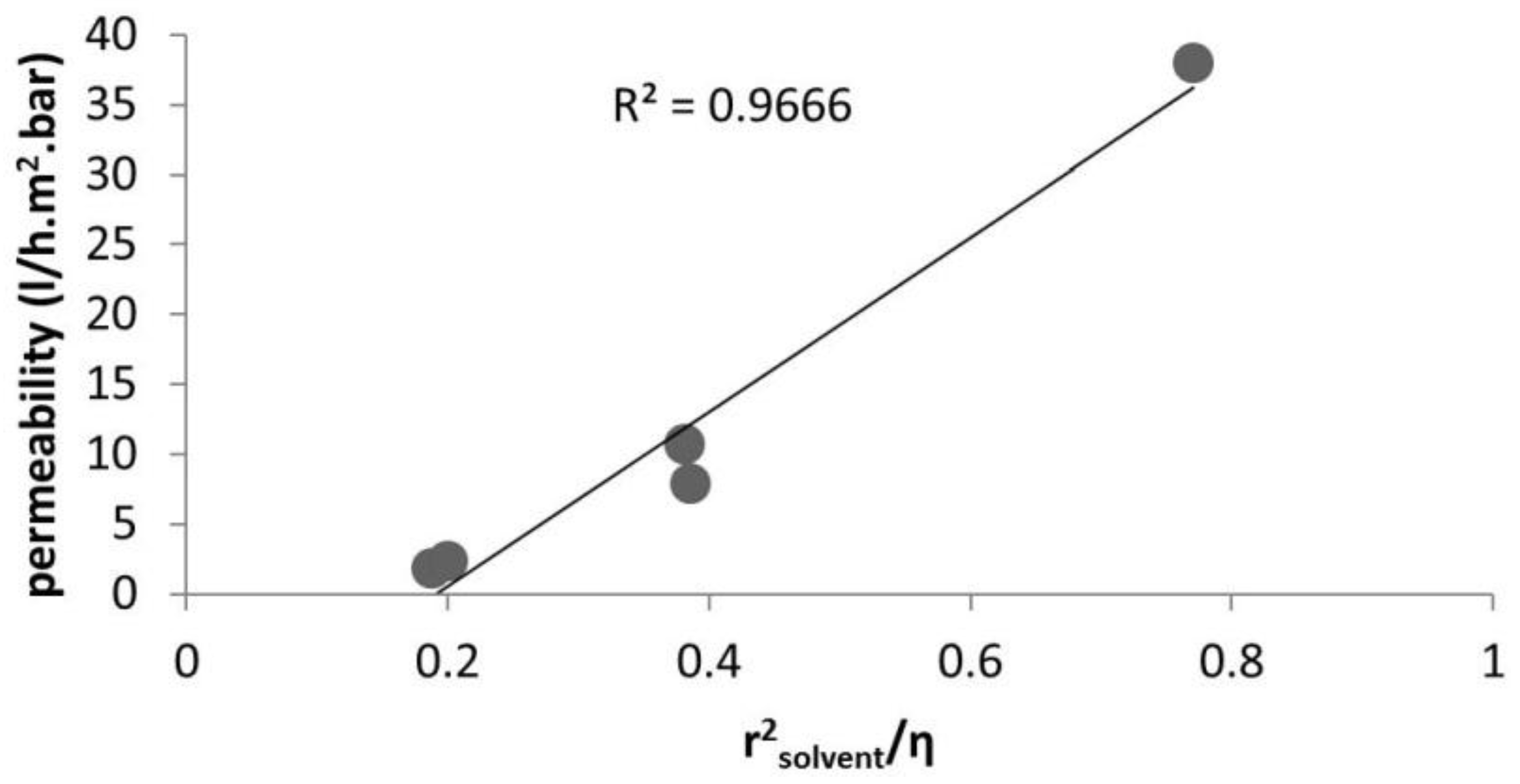
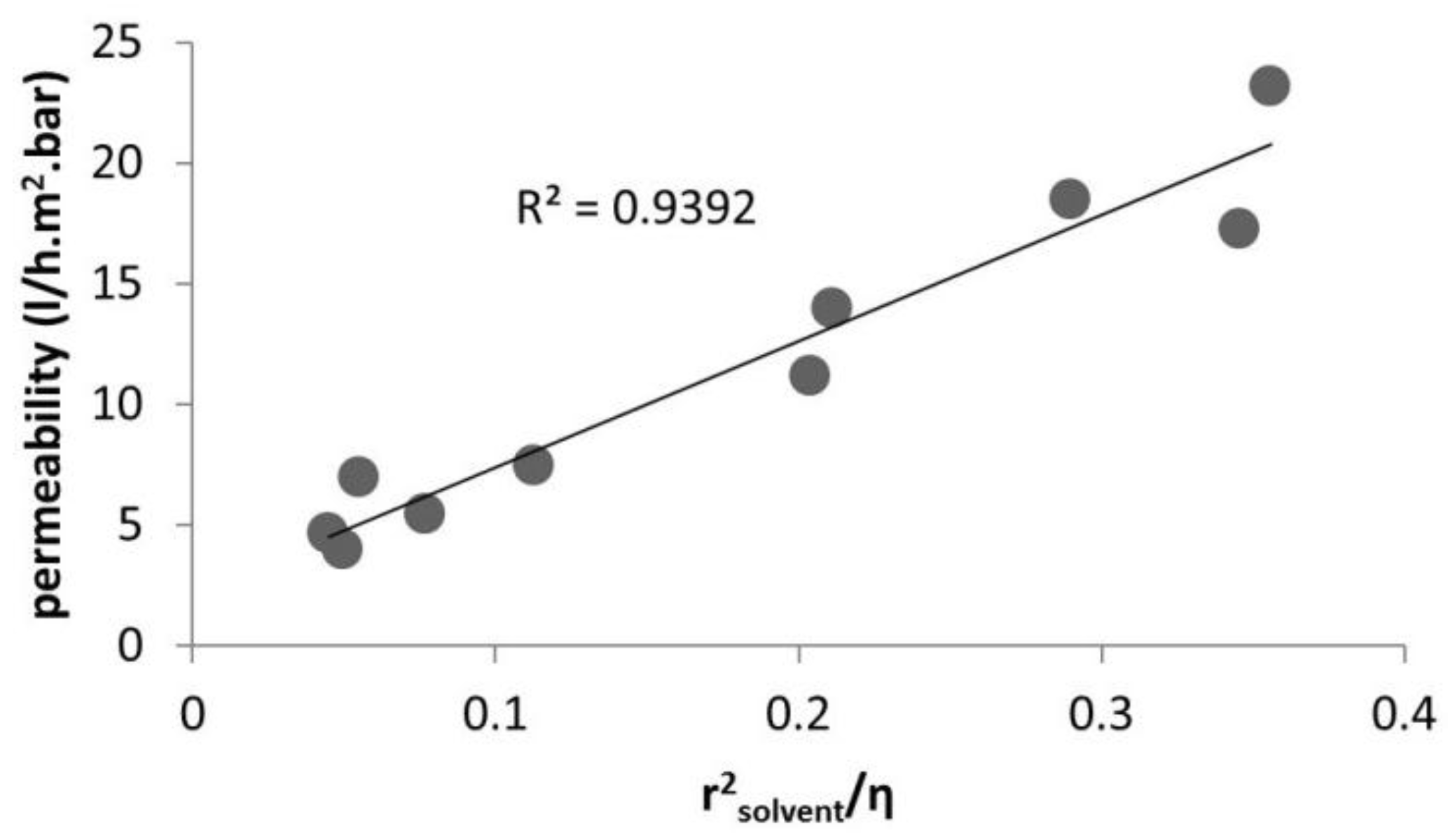
2.1. Solvent Transport inside Pores
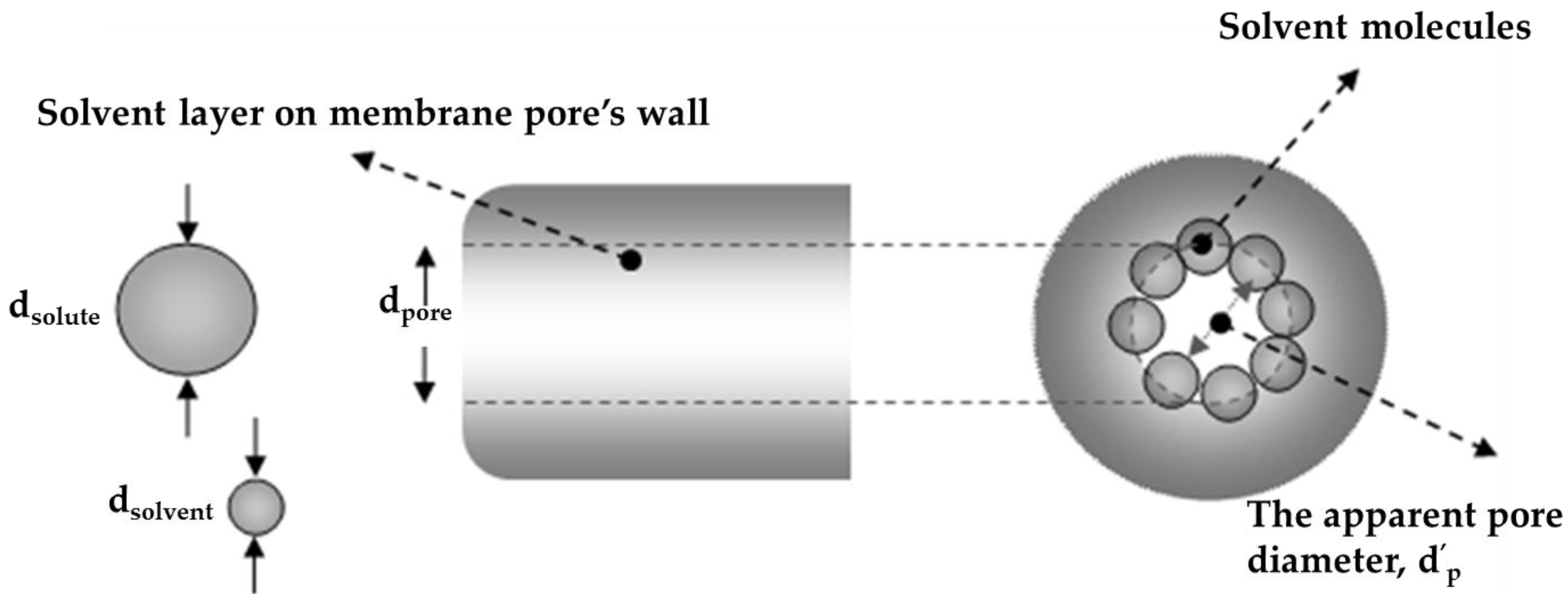
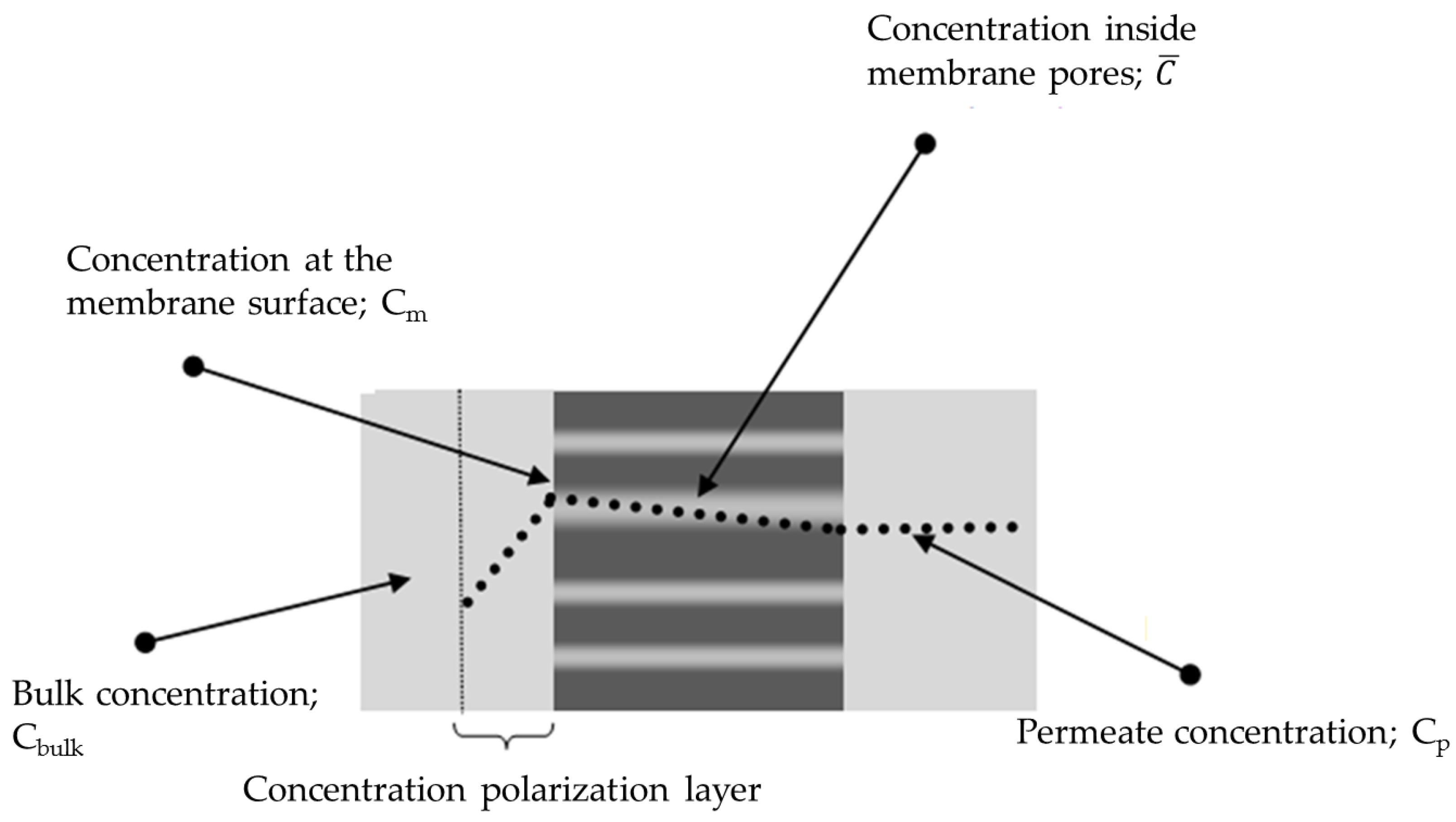
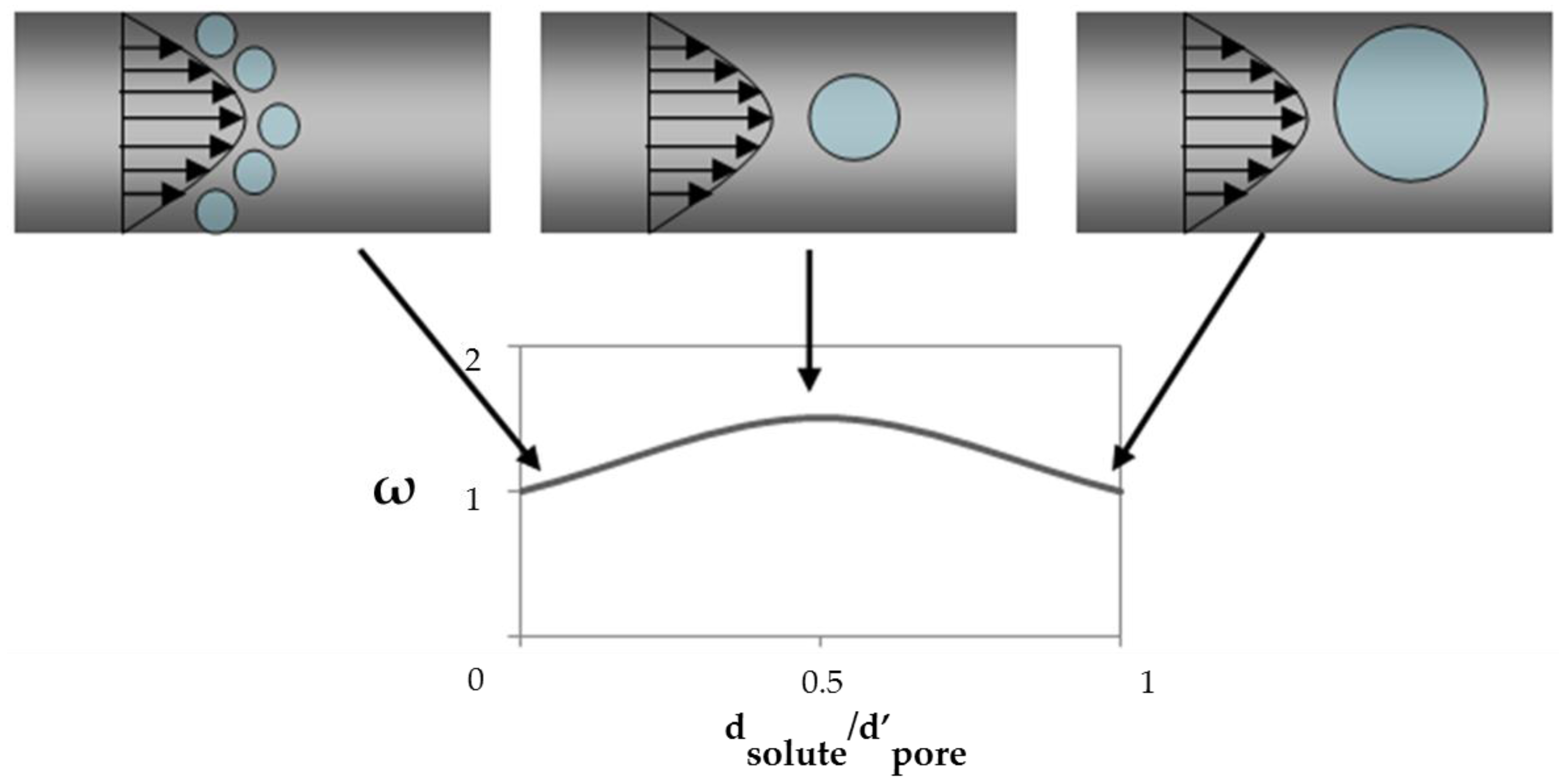
2.2. Solute Transport inside Pores
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Priske, M.; Lazar, M.; Schnitzer, C.; Baumgarten, G. Recent applications of organic solvent nanofiltration. Chem. Ing. Tech. 2016, 88, 39–49. [Google Scholar] [CrossRef]
- Buonomenna, M.; Bae, J. Organic solvent nanofiltration in pharmaceutical industry. Sep. Purif. Rev. 2015, 44, 157–182. [Google Scholar] [CrossRef]
- Kim, J.F.; Székely, G.; Valtcheva, I.B.; Livingston, A.G. Increasing the sustainability of membrane processes through cascade approach and solvent recovery—Pharmaceutical purification case study. Green Chem. 2014, 16, 133–145. [Google Scholar] [CrossRef]
- Szekely, G.; Jimenez-Solomon, M.F.; Marchetti, P.; Kim, J.F.; Livingston, A.G. Sustainability assessment of organic solvent nanofiltration: From fabrication to application. Green Chem. 2014, 16, 4440–4473. [Google Scholar] [CrossRef]
- Sourirajan, S. Separation of Hydrocarbon Liquids by Flow under Pressure through Porous Membranes; National Research Council of Canada Ottawa (Ontario) division of Applied Chemistry: Ottawa, ON, Canada, 1964.
- Bhanushali, D.; Bhattacharyya, D. Advances in solvent-resistant nanofiltration membranes. Adv. Membr. Technol. 2003, 984, 159–177. [Google Scholar] [CrossRef]
- Bhanushali, D.; Kloos, S.; Bhattacharyya, D. Solute transport in solvent-resistant nanofiltration membranes for non-aqueous systems: Experimental results and the role of solute-solvent coupling. J. Membr. Sci. 2002, 208, 343–359. [Google Scholar] [CrossRef]
- Darvishmanesh, S.; Degreve, J.; van der Bruggen, B. Mechanisms of solute rejection in solvent resistant nanofiltration: The effect of solvent on solute rejection. Phys. Chem. Chem. Phys. 2010, 12, 13333–13342. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M.F.J.; Bach, S.; Ebert, K. A transport model for organophilic nanofiltration. J. Membr. Sci. 2006, 286, 60–68. [Google Scholar] [CrossRef]
- Ebert, K.; Koll, J.; Dijkstra, M.F.J.; Eggers, M. Fundamental studies on the performance of a hydrophobic solvent stable membrane in non-aqueous solutions. J. Membr. Sci. 2006, 285, 75–80. [Google Scholar] [CrossRef]
- Vanherck, K.; Cano-Odena, A.; Koeckelberghs, G.; Dedroog, T.; Vankelecom, I. A simplified diamine crosslinking method for pi nanofiltration membranes. J. Membr. Sci. 2010, 353, 135–143. [Google Scholar] [CrossRef]
- Vanherck, K.; Vandezande, P.; Aldea, S.O.; Vankelecom, I.F.J. Cross-linked polyimide membranes for solvent resistant nanofiltration in aprotic solvents. J. Membr. Sci. 2008, 320, 468–476. [Google Scholar] [CrossRef]
- Machado, D.R.; Hasson, D.; Semiat, R. Effect of solvent properties on permeate flow through nanofiltration membranes. Part I: Investigation of parameters affecting solvent flux. J. Membr. Sci. 1999, 163, 93–102. [Google Scholar] [CrossRef]
- Bhanushali, D.; Kloos, S.; Kurth, C.; Bhattacharyya, D. Performance of solvent-resistant membranes for non-aqueous systems: Solvent permeation results and modeling. J. Membr. Sci. 2001, 189, 1–21. [Google Scholar] [CrossRef]
- Yang, X.J.; Livingston, A.G.; Freitas dos Santos, L. Experimental observations of nanofiltration with organic solvents. J. Membr. Sci. 2001, 190, 45–55. [Google Scholar] [CrossRef]
- White, L.S. Transport properties of a polyimide solvent resistant nanofiltration membrane. J. Membr. Sci. 2002, 205, 191–202. [Google Scholar] [CrossRef]
- Van der Bruggen, B.; Geens, J.; Vandecasteele, C. Influence of organic solvents on the performance of polymeric nanofiltration membranes. Sep. Sci. Technol. 2002, 37, 783–797. [Google Scholar] [CrossRef]
- Vankelecom, I.F.J.; de Smet, K.; Gevers, L.E.M.; Livingston, A.; Nair, D.; Aerts, S.; Kuypers, S.; Jacobs, P.A. Physico-chemical interpretation of the SRNF transport mechanism for solvents through dense silicone membranes. J. Membr. Sci. 2004, 231, 99–108. [Google Scholar] [CrossRef]
- Robinson, J.P.; Tarleton, E.S.; Millington, C.R.; Nijmeijer, A. Solvent flux through dense polymeric nanofiltration membranes. J. Membr. Sci. 2004, 230, 29–37. [Google Scholar] [CrossRef]
- Silva, P.; Han, S.; Livingston, A.G. Solvent transport in organic solvent nanofiltration membranes. J. Membr. Sci. 2005, 262, 49–59. [Google Scholar] [CrossRef]
- Geens, J.; van der Bruggen, B.; Vandecasteele, C. Transport model for solvent permeation through nanofiltration membranes. Sep. Purif. Technol. 2006, 48, 255–263. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, Q. Effect of membrane pretreatment on performance of solvent resistant nanofiltration membranes in methanol solutions. J. Membr. Sci. 2006, 280, 195–201. [Google Scholar] [CrossRef]
- Darvishmanesh, S.; Buekenhoudt, A.; Degrève, J.; van der Bruggen, B. General model for prediction of solvent permeation through organic and inorganic solvent resistant nanofiltration membranes. J. Membr. Sci. 2009, 334, 43–49. [Google Scholar] [CrossRef]
- Othman, R.; Mohammad, A.W.; Ismail, M.; Salimon, J. Application of polymeric solvent resistant nanofiltration membranes for biodiesel production. J. Membr. Sci. 2010, 348, 287–297. [Google Scholar] [CrossRef]
- Whu, J.A.; Baltzis, B.C.; Sirkar, K.K. Nanofiltration studies of larger organic microsolutes in methanol solutions. J. Membr. Sci. 2000, 170, 159–172. [Google Scholar] [CrossRef]
- Van der Bruggen, B.; Geens, J.; Vandecasteele, C. Fluxes and rejections for nanofiltration with solvent stable polymeric membranes in water, ethanol and n-Hexane. Chem. Eng. Sci. 2002, 57, 2511–2518. [Google Scholar] [CrossRef]
- Geens, J.; Hillen, A.; Bettens, B.; van der Bruggen, B.; Vandecasteele, C. Solute transport in nonaqueous nanofiltration: Effect of membrane material. J. Chem. Technol. Biotechnol. 2005, 80, 1371–1377. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, Q. A comparison of nanofiltration with aqueous and organic solvents. J. Membr. Sci. 2006, 279, 453–458. [Google Scholar] [CrossRef]
- Tarleton, E.S.; Robinson, J.P.; Millington, C.R.; Nijmeijer, A.; Taylor, M.L. The influence of polarity on flux and rejection behaviour in solvent resistant nanofiltration—Experimental observations. J. Membr. Sci. 2006, 278, 318–327. [Google Scholar] [CrossRef]
- Veríssimo, S.M.; Silva, P.; Livingston, A.G. Membrane separations|nanofiltration in organic liquids. In Encyclopedia of Separation Science; Ian, D.W., Ed.; Academic Press: Oxford, UK, 2007; pp. 1–8. [Google Scholar]
- Zheng, F.; Li, C.; Yuan, Q.; Vriesekoop, F. Influence of molecular shape on the retention of small molecules by solvent resistant nanofiltration (SRNF) membranes: A suitable molecular size parameter. J. Membr. Sci. 2008, 318, 114–122. [Google Scholar] [CrossRef]
- Tarleton, E.S.; Robinson, J.P.; Low, J.S. Nanofiltration: A technology for selective solute removal from fuels and solvents. Chem. Eng. Res. Des. 2009, 87, 271–279. [Google Scholar] [CrossRef]
- Valadez-Blanco, R.; Livingston, A.G. Solute molecular transport through polyimide asymmetric organic solvent nanofiltration (OSN) membranes and the effect of membrane-formation parameters on mass transfer. J. Membr. Sci. 2009, 326, 332–342. [Google Scholar] [CrossRef]
- Nguyen, Q.; Bendjama, Z.; Clément, R.; Ping, Z. Poly(dimethylsiloxane) crosslinked in different conditions part I. Sorption properties in water–ethyl acetate mixtures. Phys. Chem. Chem. Phys. 1999, 1, 2761–2766. [Google Scholar] [CrossRef]
- Lencki, R.W.; Williams, S. Effect of nonaqueous solvents on the flux behavior of ultrafiltration membranes. J. Membr. Sci. 1995, 101, 43–51. [Google Scholar] [CrossRef]
- Darvishmanesh, S.; Degrève, J.; van der Bruggen, B. Physicochemical characterization of transport in nanosized membrane structures. ChemPhysChem 2010, 11, 404–411. [Google Scholar] [CrossRef] [PubMed]
- Darvishmanesh, S.; Degrève, J.; van der Bruggen, B. Comparison of pressure driven transport of ethanol/n-Hexane mixtures through dense and microporous membranes. Chem. Eng. Sci. 2009, 64, 3914–3927. [Google Scholar] [CrossRef]
- Nguyen, Q.; Bendjama, Z.; Clément, R.; Ping, Z. Poly(dimethylsiloxane) crosslinked in different conditions. Part II. Pervaporation of water–ethyl acetate mixtures. Phys. Chem. Chem. Phys. 2000, 2, 395–400. [Google Scholar] [CrossRef]
- Darvishmanesh, S.; Buekenhoudt, A.; Degrève, J.; van der Bruggen, B. Coupled series-parallel resistance model for transport of solvent through inorganic nanofiltration membranes. Sep. Purif. Technol. 2009, 70, 46–52. [Google Scholar] [CrossRef]
- Toshinori Tsuru, H.K.; Yoshioka, T.; Asaeda, M. Permeation of nonaqueous solution through organic/inorganic hybrid nanoporous membranes. AIChE J. 2004, 50, 1080–1087. [Google Scholar] [CrossRef]
- Barrett, A.M. 1-carbamoylalkyl phenoxy-3-amino-2-propanols. U.S. Patent 3663607 A, 16 May 1972. [Google Scholar]
- Tsuru, T.; Sudou, T.; Kawahara, S.-I.; Yoshioka, T.; Asaeda, M. Permeation of liquids through inorganic nanofiltration membranes. J. Colloid Interface Sci. 2000, 228, 292–296. [Google Scholar] [CrossRef] [PubMed]
- Tsuru, T.; Miyawaki, M.; Kondo, H.; Yoshioka, T.; Asaeda, M. Inorganic porous membranes for nanofiltration of nonaqueous solutions. Sep. Purif. Technol. 2003, 32, 105–109. [Google Scholar] [CrossRef]
- Dias, C.R.; Rosa, M.J.; de Pinho, M.N. Structure of water in asymmetric cellulose ester membranes—And ATR-FTIR study. J. Membr. Sci. 1998, 138, 259–267. [Google Scholar] [CrossRef]
- Bowen, W.R.; Welfoot, J.S. Modelling the performance of membrane nanofiltration—Critical assessment and model development. Chem. Eng. Sci. 2002, 57, 1121–1137. [Google Scholar] [CrossRef]
- Guizard, C.; Ayral, A.; Julbe, A. Potentiality of organic solvents filtration with ceramic membranes. A comparison with polymer membranes. Desalination 2002, 147, 275–280. [Google Scholar] [CrossRef]
- Froimowitz, M. Hyperchem: A software package for computational chemistry and molecular modeling. Biotechniques 1993, 14, 1010–1013. [Google Scholar] [PubMed]
- Dobrak, A.; Verrecht, B.; van den Dungen, H.; Buekenhoudt, A.; Vankelecom, I.F.J.; van der Bruggen, B. Solvent flux behavior and rejection characteristics of hydrophilic and hydrophobic mesoporous and microporous TiO2 and ZrO2 membranes. J. Membr. Sci. 2010, 346, 344–352. [Google Scholar] [CrossRef]
- Buekenhoudt, A. Application of Ceramic nf Membrane in Production of Peptide Api’s; Imperial College London: London, UK, 2010. [Google Scholar]
- Koops, G.H.; Yamada, S.; Nakao, S.I. Separation of linear hydrocarbons and carboxylic acids from ethanol and hexane solutions by reverse osmosis. J. Membr. Sci. 2001, 189, 241–254. [Google Scholar] [CrossRef]
- Geens, J.; Peeters, K.; van der Bruggen, B.; Vandecasteele, C. Polymeric nanofiltration of binary water-alcohol mixtures: Influence of feed composition and membrane properties on permeability and rejection. J. Membr. Sci. 2005, 255, 255–264. [Google Scholar] [CrossRef]
- Bowen, W.R.; Julian, S.W. Modelling the performance of nanofiltration membranes. In Nanofiltration: Principles and Applications; Schäfer, A.I., Fane, A.G., Waite, T.D., Eds.; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Krishna, R.; Wesselingh, J.A. The maxwell-stefan approach to mass transfer. Chem. Eng. Sci. 1997, 52, 861–911. [Google Scholar] [CrossRef]

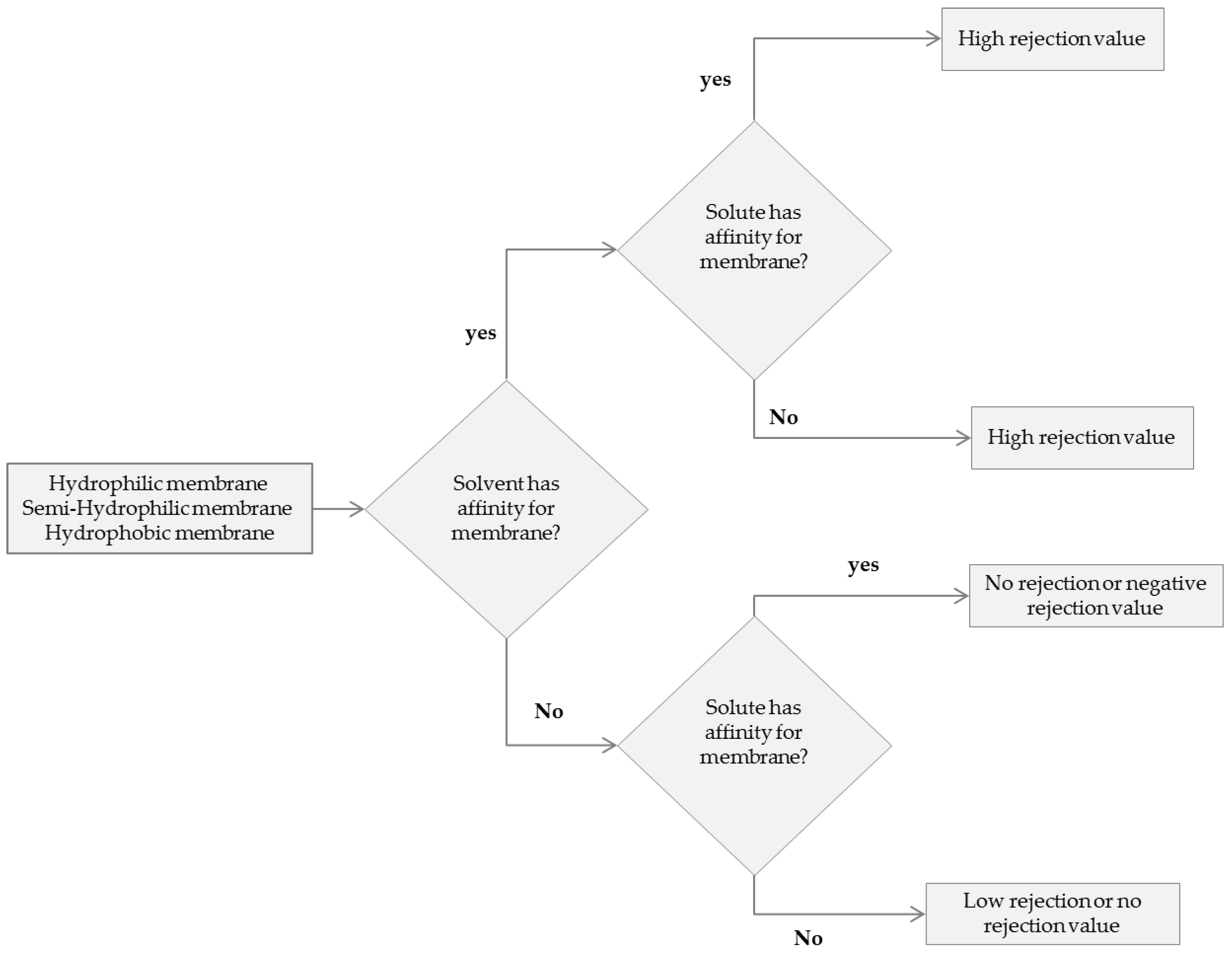
| High Affinity | Good Affinity | Moderate Affinity | No Affinity |
|---|---|---|---|
| 0.001 | 0.01 | 0.1 | 1 |
| Membrane | Pore Radius of Membrane (nm) | Solvent | Solvent Molecule Diameter (nm) | Correction Factor ψ | ψ Solvent Molecule Diameter (nm) | Permeability L/h·m2·bar |
|---|---|---|---|---|---|---|
| ZrO2 | 0.35 | Ethanol | 0.34 | 0.01 | 0.0034 | 10.3 |
| Heptane | 0.57 | 1 | 0.57 | 2.5 | ||
| Toluene | 0.5 | 1 | 0.5 | 1.3 | ||
| 0.25 | Ethanol | 0.34 | 0.01 | 0.0034 | 4.9 | |
| Heptane | 0.57 | 1 | 0.57 | 0.9 | ||
| Toluene | 0.5 | 1 | 0.5 | 0.2 | ||
| TiO2 | 0.25 | Ethanol | 0.34 | 0.1 | 0.034 | 1 |
| Heptane | 0.57 | 1 | 0.57 | 0.2 | ||
| toluene | 0.5 | 1 | 0.5 | <0.1 |
| Pore Radius of Membrane (nm) | Solvent | Solvent Molecule Diameter (nm) | Correction Factor ψ | ψ Solvent Molecule Diameter (nm) | Permeability L/h·m2·bar |
|---|---|---|---|---|---|
| 0.6 | methanol | 0.27 | 0.1 | 0.02 | 7.9 |
| ethanol | 0.34 | 0.1 | 0.0225 | 1.8 | |
| 0.8 | methanol | 0.27 | 0.1 | 0.02 | 38 |
| ethanol | 0.34 | 0.1 | 0.0225 | 10.7 | |
| iso-propanol | 0.39 | 0.1 | 0.0255 | 2.27 |
| Solvent | Solvent Molecule Diameter (nm) | Correction Factor ψ | ψ Solvent Molecule Diameter (nm) | Permeability L/h·m2·bar |
|---|---|---|---|---|
| Methanol | 0.27 | 0.01 | 0.0027 | 23.2 |
| Ethanol | 0.34 | 0.1 | 0.034 | 7.5 |
| Iso-propanol | 0.39 | 0.1 | 0.039 | 7 |
| Ethyl actetate | 0.71 | 0.1 | 0.071 | 11.2 |
| THF | 0.59 | 1 | 0.59 | 4 |
| Heptane | 0.57 | 1 | 0.57 | 5.5 |
| Dichloromethane | 0.36 | 0.1 | 0.036 | 11.1 |
| Acetonitrile | 0.37 | 0.1 | 0.037 | 17.3 |
| Toluene | 0.5 | 1 | 0.5 | 4.7 |
| Water | 0.21 | 0.01 | 0.0021 | 23.2 |
| Membrane | Average Pore Size | MWCO | Solute | Solute Diameter | Solvent Name | Solvent Molecule Diameter (nm) | ψ × Solvent Molecule Diameter (nm) | k | α | ω | Cin | Cout | Calculated Rejection Value | Experimental Rejection Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TiO2 | 0.9 | 275 | Brilliant blue | 0.58 | Ethanol | 0.34 | 0.034 | 0.001 | 0.8 | 1.00 | 3 | 0.00 | 0.999 | 0.991 |
| TiO2 | 0.9 | 275 | Bromothymol blue | 0.49 | Ethanol | 0.34 | 0.034 | 0.317 | 0.4 | 1.00 | 3 | 0.95 | 0.683 | 0.670 |
| TiO2 | 0.9 | 275 | Bromothymol blue | 0.49 | Toluene | 0.50 | 0.500 | 0.023 | 0.4 | 1.00 | 3 | 0.07 | 0.977 | 0.993 |
| TiO2 | 1.2 | 650 | Brilliant blue | 0.58 | Ethanol | 0.34 | 0.034 | 0.051 | 0.8 | 1.01 | 3 | 0.15 | 0.946 | 0.955 |
| TiO2 | 1.2 | 650 | Bromothymol blue | 0.49 | Ethanol | 0.34 | 0.034 | 0.349 | 0.5 | 1.01 | 3 | 1.05 | 0.548 | 0.555 |
| ZrO2 | 1.2 | 600 | Brilliant blue | 0.58 | Ethanol | 0.34 | 0.003 | 0.254 | 0.5 | 1.06 | 3 | 0.76 | 0.741 | 0.700 |
| ZrO2 | 1.2 | 600 | Bromothymol blue | 0.49 | Ethanol | 0.34 | 0.003 | 0.625 | 0.25 | 1.06 | 3 | 1.88 | 0.205 | 0.165 |
| ZrO2 | 1.2 | 600 | Bromothymol blue | 0.49 | Toluene | 0.50 | 0.500 | 0.588 | 0.25 | 1.26 | 3 | 1.76 | 0.339 | 0.360 |
| Solvent Name | k | α | ω | Cin | Cout | Calculated Rejection Value | Experimental Rejection Value |
|---|---|---|---|---|---|---|---|
| methanol | 0.58 | 0.2 | 1.000 | 3.00 | 1.73 | 0.42 | 0.38 |
| ethanol | 0.77 | 0.1 | 1.000 | 3.00 | 2.30 | 0.23 | 0.22 |
| isopropanol | 0.76 | 0.1 | 1.000 | 3.00 | 2.29 | 0.24 | 0.21 |
| ethyl acetate | 0.55 | 0.2 | 1.000 | 3.00 | 1.64 | 0.45 | 0.51 |
| THF | 0.23 | 0.15 | 1.000 | 3.00 | 0.68 | 0.77 | 0.78 |
| heptane | 0.45 | 0.1 | 1.000 | 3.00 | 1.36 | 0.55 | 0.38 |
| toluene | 0.21 | 0.2 | 1.000 | 3.00 | 0.63 | 0.79 | 0.80 |
| methanol | 0.58 | 0.2 | 1.000 | 3.00 | 1.73 | 0.42 | 0.38 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darvishmanesh, S.; Van der Bruggen, B. Mass Transport through Nanostructured Membranes: Towards a Predictive Tool. Membranes 2016, 6, 49. https://doi.org/10.3390/membranes6040049
Darvishmanesh S, Van der Bruggen B. Mass Transport through Nanostructured Membranes: Towards a Predictive Tool. Membranes. 2016; 6(4):49. https://doi.org/10.3390/membranes6040049
Chicago/Turabian StyleDarvishmanesh, Siavash, and Bart Van der Bruggen. 2016. "Mass Transport through Nanostructured Membranes: Towards a Predictive Tool" Membranes 6, no. 4: 49. https://doi.org/10.3390/membranes6040049
APA StyleDarvishmanesh, S., & Van der Bruggen, B. (2016). Mass Transport through Nanostructured Membranes: Towards a Predictive Tool. Membranes, 6(4), 49. https://doi.org/10.3390/membranes6040049






