MicroRNA-222 Regulates Melanoma Plasticity
Abstract
:1. Introduction
2. Results
2.1. Overshoot in the Mean-Field Model
2.2. Inhibition of Phenotypic Switching
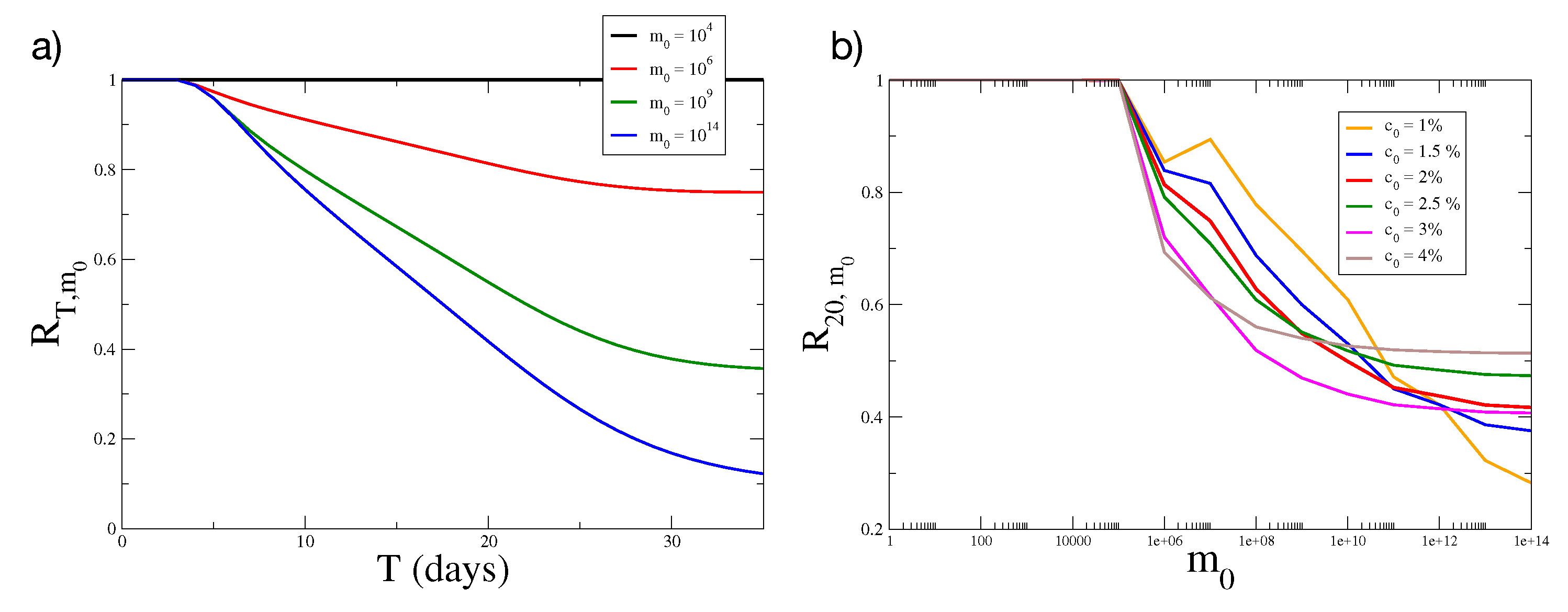
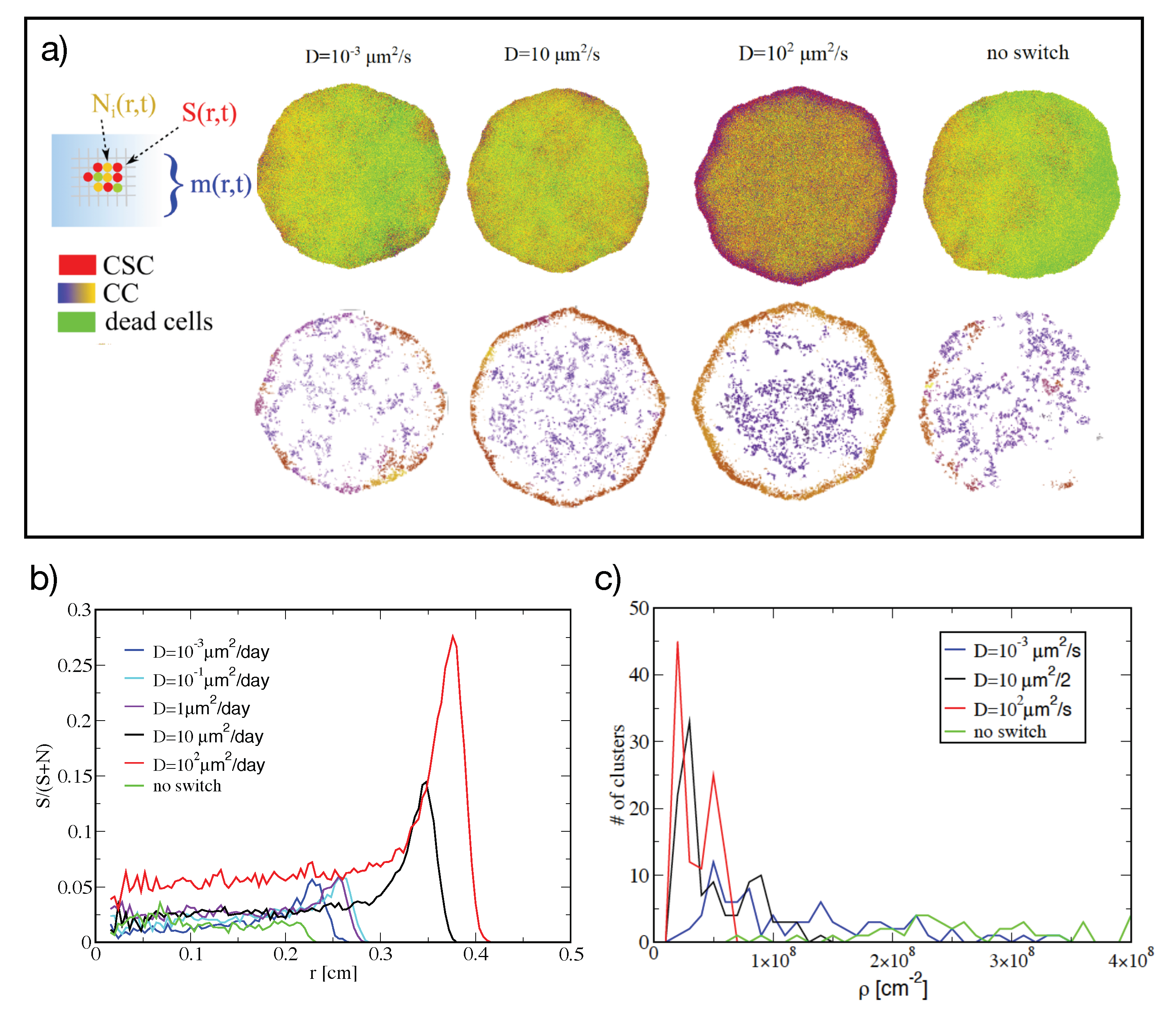
2.3. Simulations of Tumor Growth in Two Dimensions
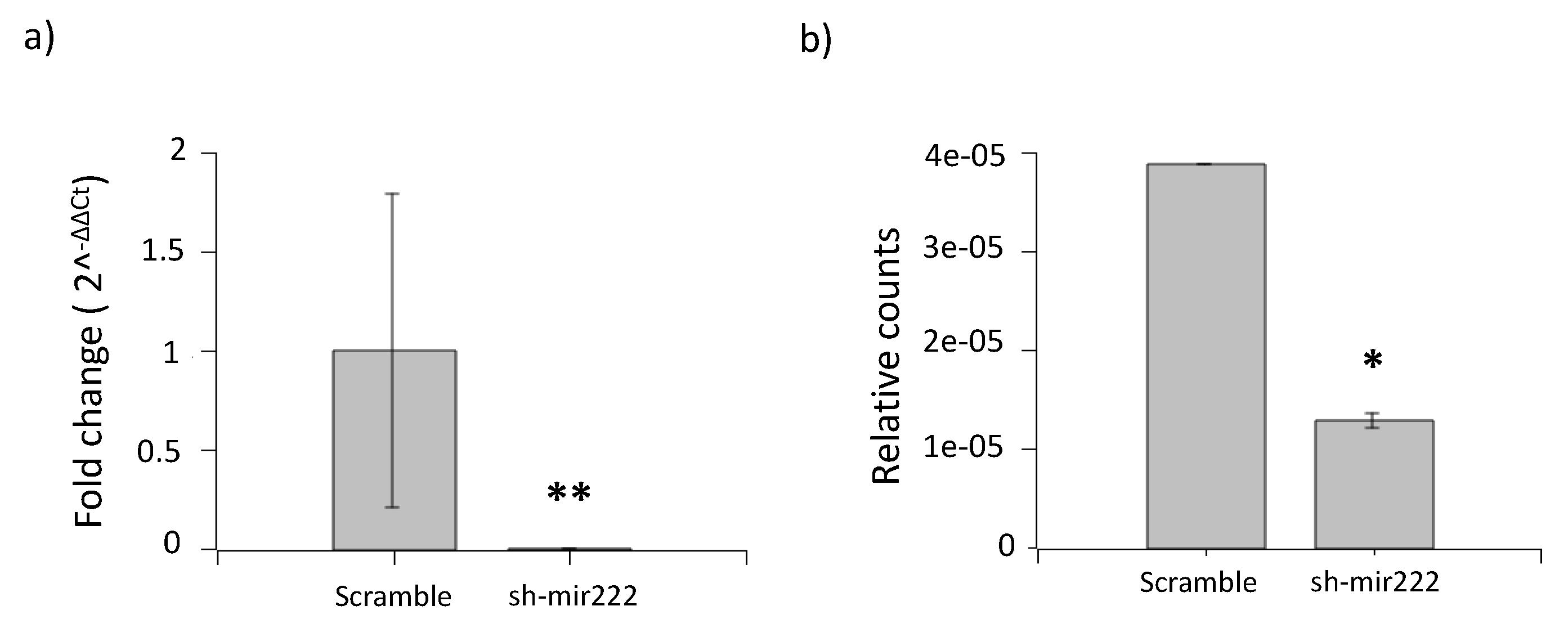
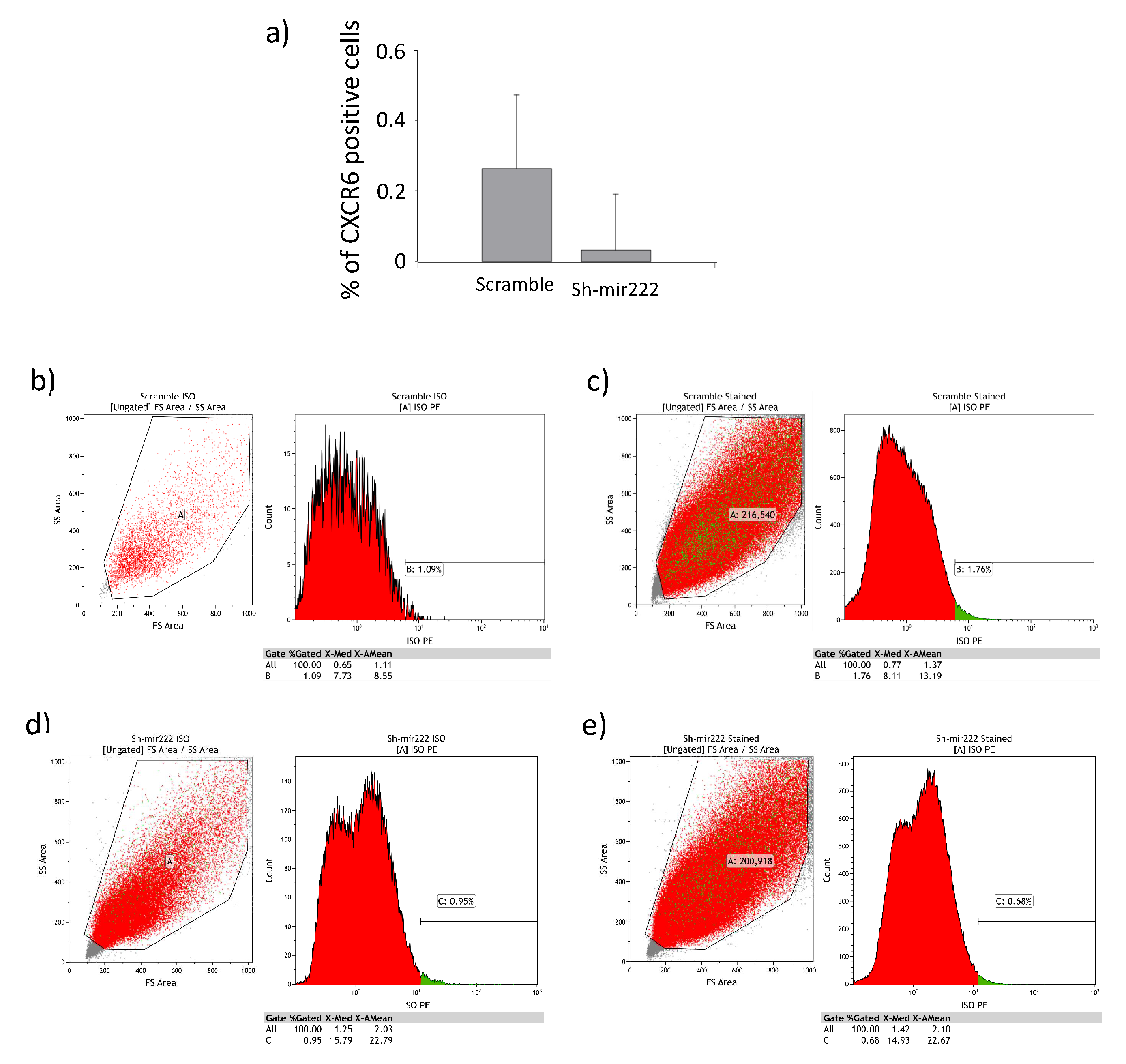
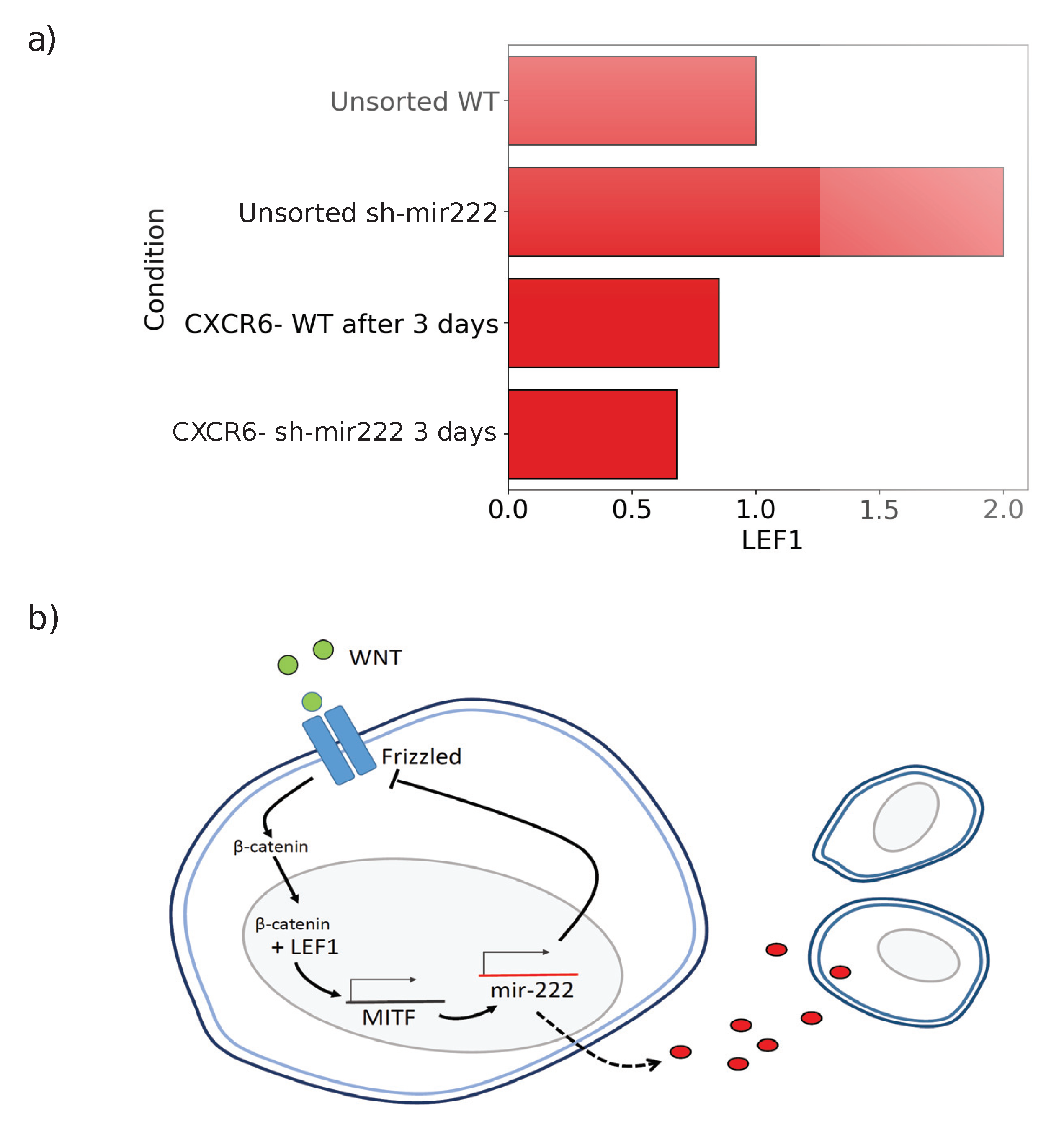
2.4. Impact of hsa-mir222-5p on Phenotopic Switching
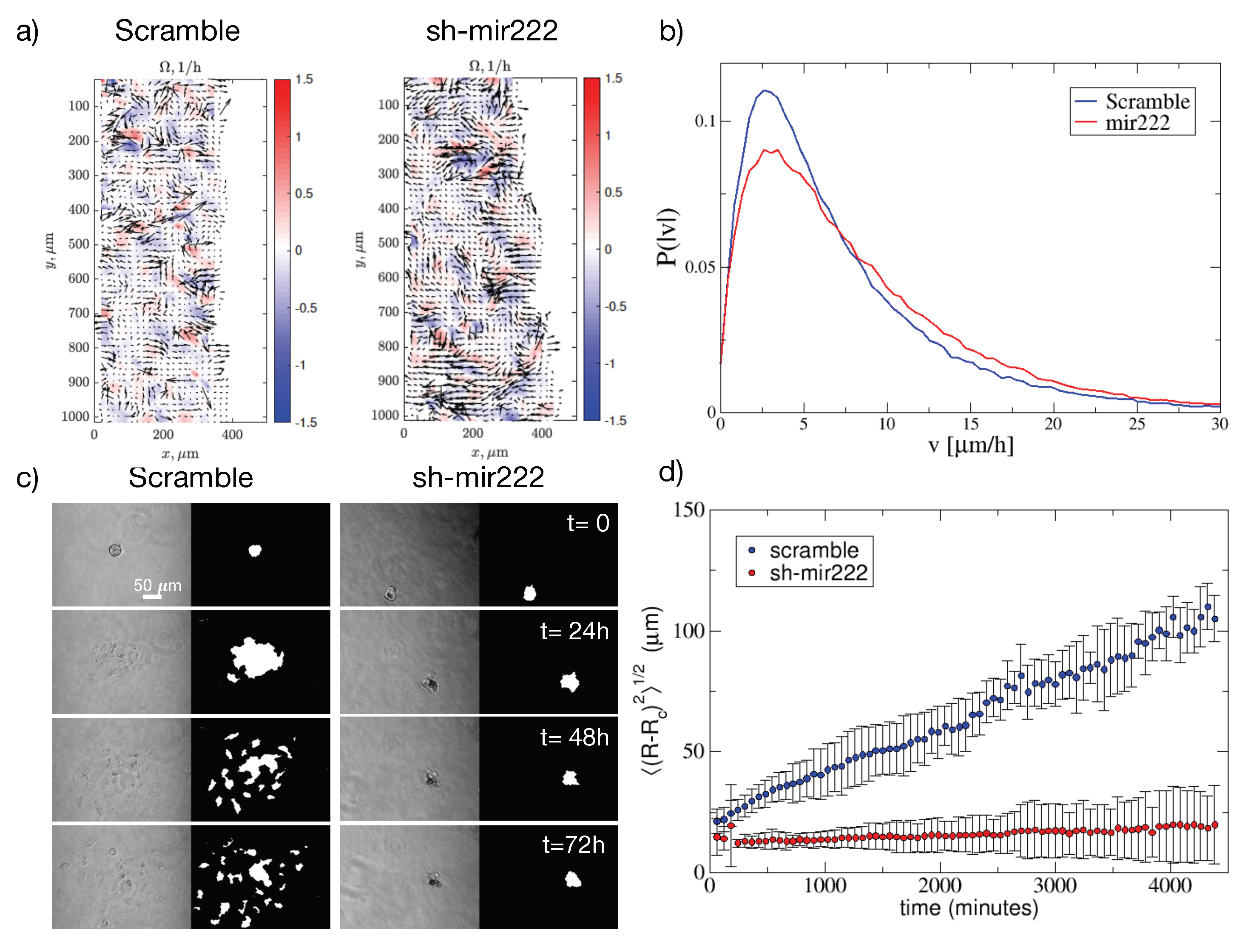
2.5. Impact of hsa-mir222-5p on Cell Migration
3. Discussion
4. Materials and Methods
4.1. The Computational Model
4.2. Cell Culture
4.3. Conditioned Media
4.4. FACS Analysis
4.5. Sponge Lentiviral Plasmids and Plasmid Amplification, Virus Production and Infection, Isolation and Detection of miRNAs
4.6. miRNA Analysis by miRCURY LNA Universal RT miRNA PCR
4.7. Isolation and Detection of miRNAs
4.8. miRNA Analysis
4.9. miRNA Differential Expression Analysis
4.10. miRNAs Expression in Conditioned Media
4.11. Migration Assay
4.12. PIV Analysis
4.13. Spheroids Culture, Collagen Invasion Assay and Image Analysis
4.14. Statistical Analysis
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CSC | Cancer stem cell |
| CC | Cancer cell |
| SC | Stem cell |
| sh-miR222 | Sponge miR222 |
Appendix A
Is the Mean-Field Model a Minimal Model?
Appendix B
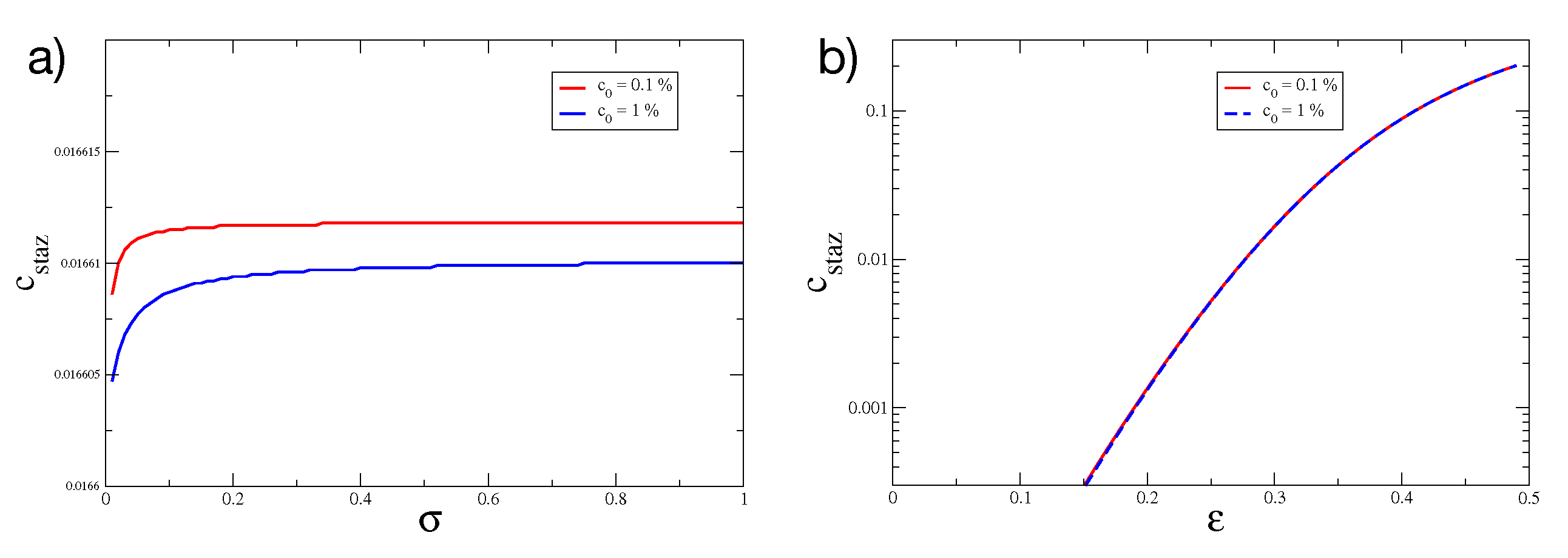
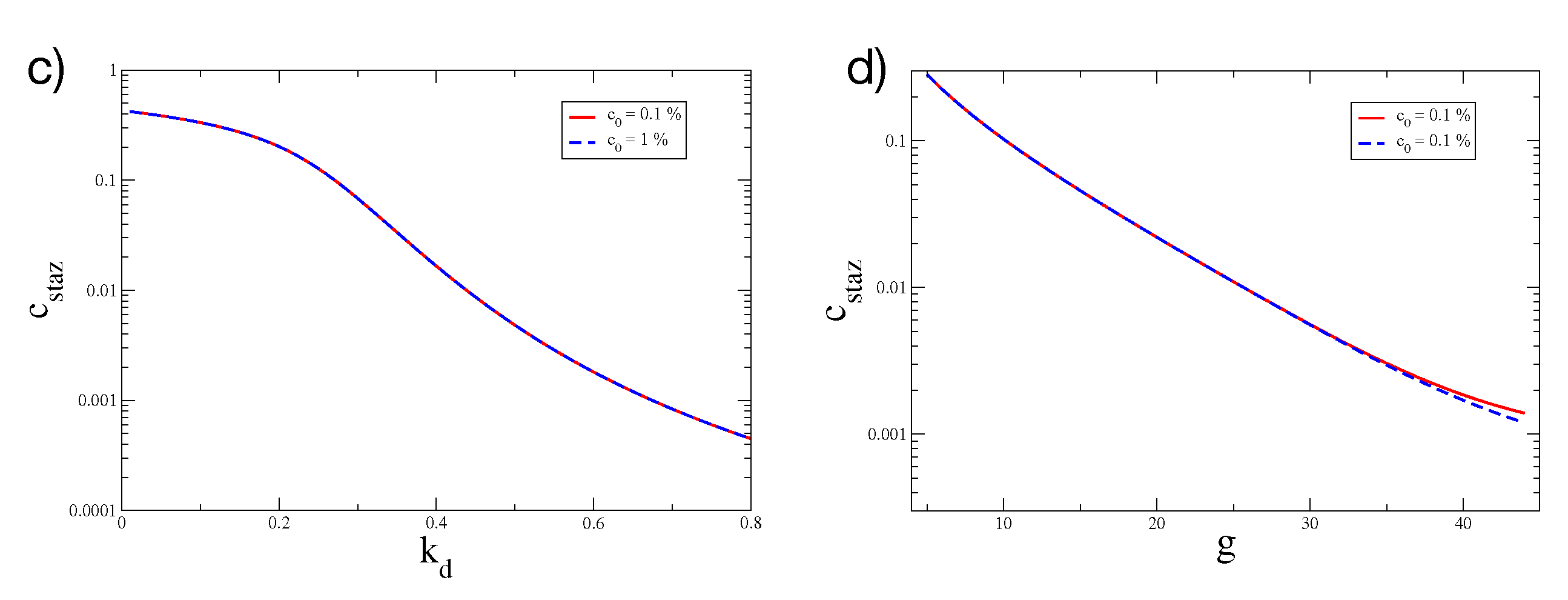


| Coefficient | Value | Cellular/Molecular Process |
|---|---|---|
| 300.0 (day · V) | rate of production of signal molecule concentration m by CSCs | |
| 4.0 day | rate of decay of signal molecules concentration m | |
| 0.22 day | rate of switching of CCs | |
| 0.4 day | rate of symmetric division of CSC into 2 CSCs | |
| 0.1 day | rate of symmetric division of CSC into 2 CCs | |
| 0.2 day | rate of asymmetric division of CSC into 1 CC and 1 CSC | |
| 0.4 day | rate of symmetric division of CC into 2 CCs | |
| 0.4 day | death rate of senescent (last generation) CCs | |
| 600,000 | threshold of Hill’s inhibition function | |
| 4 | exponent of Hill’s inhibition function | |
| g | 20 | number of generations to senescence of CCs |
| 4 (days) | time delay associated to the switching-regulation process |
| Pimer | Sequence |
|---|---|
| Foward | CATGGTCCTGCTGGAGTTCGTG |
| Reverse | CATAGCGTAAAAGGAGCAACA |
Appendix C
Supplementary Video Captions
- Video S1. Time-lapse of the growth of a 3D spheroid in a collagen network for scramble IgR39 cells. We digitize the images to quantify the area occupied by cells as described in the Materials and Methods section.
- Video S2. Time-lapse of the growth of a 3D spheroid in a collagen network for sh-mir222 IgR39 cells. We digitize the images to quantify the area occupied by cells as described in the Materials and Methods section.
References
- Sellerio, A.L.; Ciusani, E.; Ben-Moshe, N.B.; Coco, S.; Piccinini, A.; Myers, C.R.; Sethna, J.P.; Giampietro, C.; Zapperi, S.; Porta, C.A.M.L. Overshoot during phenotypic switching of cancer cell populations. Sci. Rep. 2015, 5, 15464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- La Porta, C.A.M.; Zapperi, S. Complexity in cancer stem cells and tumor evolution: Toward precision medicine. Semin. Cancer Biol. 2017, 44, 3–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tetteh, P.W.; Basak, O.; Farin, H.F.; Wiebrands, K.; Kretzschmar, K.; Begthel, H.; van den Born, M.; Korving, J.; de Sauvage, F.; van Es, J.H.; et al. Replacement of Lost Lgr5-Positive Stem Cells through Plasticity of Their Enterocyte-Lineage Daughters. Cell Stem Cell 2016, 18, 203–213. [Google Scholar] [CrossRef] [PubMed]
- Leushacke, M.; Tan, S.H.; Wong, A.; Swathi, Y.; Hajamohideen, A.; Tan, L.T.; Goh, J.; Wong, E.; Denil, S.L.I.J.; Murakami, K.; et al. Lgr5-expressing chief cells drive epithelial regeneration and cancer in the oxyntic stomach. Nat. Cell Biol. 2017, 19, 774–786. [Google Scholar] [CrossRef]
- Stange, D.E. Intestinal stem cells. Dig. Dis. 2013, 31, 293–298. [Google Scholar] [CrossRef]
- Blanpain, C.; Lowry, W.E.; Geoghegan, A.; Polak, L.; Fuchs, E. Self-renewal, multipotency, and the existence of two cell populations within an epithelial stem cell niche. Cell 2004, 118, 635–648. [Google Scholar] [CrossRef]
- Claudinot, S.; Nicolas, M.; Oshima, H.; Rochat, A.; Barrandon, Y. Long-term renewal of hair follicles from clonogenic multipotent stem cells. Proc. Natl. Acad. Sci. USA 2005, 102, 14677–14682. [Google Scholar] [CrossRef] [Green Version]
- Enderling, H. Cancer stem cells: Small subpopulation or evolving fraction. Integr. Biol. 2015, 7, 14. [Google Scholar] [CrossRef] [Green Version]
- Morgner, J.; Ghatak, S.; Jakobi, T.; Dieterich, C.; Aumailley, M.; Wickström, S.A. Integrin-linked kinase regulates the niche of quiescent epidermal stem cells. Nat. Commun. 2015, 6, 8198. [Google Scholar] [CrossRef] [Green Version]
- Hoeck, J.D.; Biehs, B.; Kurtova, A.V.; Kljavin, N.M.; de Sousa E Melo, F.; Alicke, B.; Koeppen, H.; Modrusan, Z.; Piskol, R.; de Sauvage, F.J. Stem cell plasticity enables hair regeneration following Lgr5+ cell loss. Nat. Cell Biol. 2017, 19, 666–676. [Google Scholar] [CrossRef]
- Hsu, Y.C.; Pasolli, H.A.; Fuchs, E. Dynamics between stem cells, niche, and progeny in the hair follicle. Cell 2011, 144, 92–105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Es, J.H.; Sato, T.; van de Wetering, M.; Lyubimova, A.; Yee Nee, A.N.; Gregorieff, A.; Sasaki, N.; Zeinstra, L.; van den Born, M.; Korving, J.; et al. Dll1+ secretory progenitor cells revert to stem cells upon crypt damage. Nat. Cell Biol. 2012, 14, 1099–1104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bocci, F.; Gearhart-Serna, L.; Boareto, M.; Ribeiro, M.; Ben-Jacob, E.; Devi, G.R.; Levine, H.; Onuchic, J.N.; Jolly, M.K. Toward understanding cancer stem cell heterogeneity in the tumor microenvironment. Proc. Natl. Acad. Sci. USA 2019, 116, 148–157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, S.; Kulkarni, R.; Sen, S. Cell motility and ECM proteolysis regulate tumor growth and tumor relapse by altering the fraction of cancer stem cells and their spatial scattering. Phys. Biol. 2016, 13, 036001. [Google Scholar] [CrossRef] [Green Version]
- Nam, A.; Mohanty, A.; Bhattacharya, S.; Kotnala, S.; Achuthan, S.; Hari, K.; Nathan, A.; Rangarajan, G.; Massarelli, E.; Levine, H.; et al. Suppressing chemoresistance in lung cancer via dynamic phenotypic switching and intermittent therapy. bioRxiv 2020. [Google Scholar] [CrossRef]
- Ahmed, N.; Escalona, R.; Leung, D.; Chan, E.; Kannourakis, G. Tumour microenvironment and metabolic plasticity in cancer and cancer stem cells: Perspectives on metabolic and immune regulatory signatures in chemoresistant ovarian cancer stem cells. Semin. Cancer Biol. 2018, 53, 265–281. [Google Scholar] [CrossRef]
- Taghizadeh, R.; Noh, M.; Huh, Y.H.; Ciusani, E.; Sigalotti, L.; Maio, M.; Arosio, B.; Nicotra, M.R.; Natali, P.; Sherley, J.L.; et al. CXCR6, a newly defined biomarker of tissue-specific stem cell asymmetric self-renewal, identifies more aggressive human melanoma cancer stem cells. PLoS ONE 2010, 5, e15183. [Google Scholar] [CrossRef]
- Leder, K.; Holland, E.C.; Michor, F. The Therapeutic Implications of Plasticity of the Cancer Stem Cell Phenotype. PLoS ONE 2010, 5, e14366. [Google Scholar] [CrossRef] [Green Version]
- Turner, C.; Kohandel, M. Investigating the link between epithelial-mesenchymal transition and the cancer stem cell phenotype: A mathematical approach. J. Theor. Biol. 2010, 265, 329–335. [Google Scholar] [CrossRef]
- Gupta, P.B.A. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell 2011, 146, 633–644. [Google Scholar] [CrossRef] [Green Version]
- Beretta, E.C.V.M.V. Mathematical Modelling of Cancer Stem Cells Population Behavior. Math. Model. Nat. Phenom. 2012, 7, 279–305. [Google Scholar] [CrossRef] [Green Version]
- Tonekaboni, S.A.; Dhawan, A.; Kohandel, M. Mathematical modelling of plasticity and phenotype switching in cancer cell populations. Math. Biosci. 2016, 283, 30–37. [Google Scholar] [CrossRef] [PubMed]
- La Porta, C.A.M.; Zapperi, S.; Sethna, J.P. Senescent cells in growing tumors: Population dynamics and cancer stem cells. PLoS Comput. Biol. 2012, 8, e1002316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Tzedakis, G.; Tzamali, E.; Marias, K.; Sakkalis, V. The Importance of Neighborhood Scheme Selection in Agent-based Tumor Growth Modeling. Cancer Inform. 2015, 14, 67–81. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, A.; Laio, A. Machine learning Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [Green Version]
- La Porta, C.A.M.; Zapperi, S. Explaining the dynamics of tumor aggressiveness: At the crossroads between biology, artificial intelligence and complex systems. Semin. Cancer Biol. 2018, 53, 42–47. [Google Scholar] [CrossRef] [Green Version]
- Friedl, P.; Wolf, K. Tumour-cell invasion and migration: Diversity and escape mechanisms. Nat. Rev. Cancer 2003, 3, 362–374. [Google Scholar] [CrossRef]
- Felicetti, F.; De Feo, A.; Coscia, C.; Puglisi, R.; Pedini, F.; Pasquini, L.; Bellenghi, M.; Errico, M.C.; Pagani, E.; Carè, A. Exosome-mediated transfer of miR-222 is sufficient to increase tumor malignancy in melanoma. J. Transl. Med. 2016, 14, 56. [Google Scholar] [CrossRef] [Green Version]
- Ozsolak, F.; Poling, L.L.; Wang, Z.; Liu, H.; Liu, X.S.; Roeder, R.G.; Zhang, X.; Song, J.S.; Fisher, D.E. Chromatin structure analyses identify miRNA promoters. Genes Dev. 2008, 22, 3172–3183. [Google Scholar] [CrossRef] [Green Version]
- Chung, H.K.; Chen, Y.; Rao, J.N.; Liu, L.; Xiao, L.; Turner, D.J.; Yang, P.; Gorospe, M.; Wang, J.Y. Transgenic expression of miR-222 disrupts intestinal epithelial regeneration by targeting multiple genes including Frizzled-7. Mol. Med. 2015, 21, 676–687. [Google Scholar] [CrossRef] [PubMed]
- Phesse, T.; Flanagan, D.; Vincan, E. Frizzled7: A promising Achilles’ heel for targeting the Wnt receptor complex to treat cancer. Cancers 2016, 8, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sottoriva, A.; Verhoeff, J.J.; Borovski, T.; McWeeney, S.K.; Naumov, L.; Medema, J.P.; Sloot, P.M.; Vermeulen, L. Cancer stem cell tumor model reveals invasive morphology and increased phenotypical heterogeneity. Cancer Res. 2010, 70, 46–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borovski, S.K.M.; Naumov, L.; Medema, J.P.; Sloot, P.M.; Vermeulen, L. Cancer Stem Cell Driven Tumor Growth Promotes Invasive Morphology. Cancer Stem Cell Niche Place Be. Ph.D. Thesis, University of Amsterdam, UvA Digital Academic Repository, Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zapperi, S.; La Porta, C.A.M. Do cancer cells undergo phenotypic switching? the case for imperfect cancer stem cell markers. Sci. Rep. 2012, 2, 441. [Google Scholar] [CrossRef] [Green Version]
- Ashkenazi, R.; Gentry, S.N.; Tl, J. Pathways to tumorigenesis-modeling mutation acquisition in stem cells and their progeny. Neoplasia 2008, 10, 1170–1182. [Google Scholar] [CrossRef] [Green Version]
- Kingston, R.E.; Chen, C.A.; Rose, J.K. Calcium phosphate transfection. Curr. Protoc. Mol. Biol. 2003, 63. [Google Scholar] [CrossRef]
- Wingett, S.W.; Andrews, S. FastQ Screen: A tool for multi-genome mapping and quality control. F1000Res 2018, 7, 1338. [Google Scholar] [CrossRef]
- Langmead, B.; Trapnell, C.; Pop, M.; Salzberg, S.L. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009, 10, R25. [Google Scholar] [CrossRef] [Green Version]
- Kozomara, A.; Griffiths-Jones, S. miRBase: Annotating high confidence microRNAs using deep sequencing data. Nucleic Acids Res. 2014, 42, D68–D73. [Google Scholar] [CrossRef] [Green Version]
- Friedländer, M.R.; Mackowiak, S.D.; Li, N.; Chen, W.; Rajewsky, N. miRDeep2 accurately identifies known and hundreds of novel microRNA genes in seven animal clades. Nucleic Acids Res. 2012, 40, 37–52. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E. PIVlab–Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2. [Google Scholar] [CrossRef] [Green Version]
- Chepizhko, O.; Giampietro, C.; Mastrapasqua, E.; Nourazar, M.; Ascagni, M.; Sugni, M.; Fascio, U.; Leggio, L.; Malinverno, C.; Scita, G.; et al. Bursts of activity in collective cell migration. Proc. Natl. Acad. Sci. USA 2016, 113, 11408–11413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehmann, S.; Te Boekhorst, V.; Odenthal, J.; Bianchi, R.; van Helvert, S.; Ikenberg, K.; Ilina, O.; Stoma, S.; Xandry, J.; Jiang, L.; et al. Hypoxia Induces a HIF-1-Dependent Transition from Collective-to-Amoeboid Dissemination in Epithelial Cancer Cells. Curr. Biol. 2017, 27, 392–400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robinson, M.D.; McCarthy, D.J.; Smyth, G.K. edgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 2010, 26, 139–140. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lionetti, M.C.; Cola, F.; Chepizhko, O.; Fumagalli, M.R.; Font-Clos, F.; Ravasio, R.; Minucci, S.; Canzano, P.; Camera, M.; Tiana, G.; et al. MicroRNA-222 Regulates Melanoma Plasticity. J. Clin. Med. 2020, 9, 2573. https://doi.org/10.3390/jcm9082573
Lionetti MC, Cola F, Chepizhko O, Fumagalli MR, Font-Clos F, Ravasio R, Minucci S, Canzano P, Camera M, Tiana G, et al. MicroRNA-222 Regulates Melanoma Plasticity. Journal of Clinical Medicine. 2020; 9(8):2573. https://doi.org/10.3390/jcm9082573
Chicago/Turabian StyleLionetti, Maria Chiara, Filippo Cola, Oleksandr Chepizhko, Maria Rita Fumagalli, Francesc Font-Clos, Roberto Ravasio, Saverio Minucci, Paola Canzano, Marina Camera, Guido Tiana, and et al. 2020. "MicroRNA-222 Regulates Melanoma Plasticity" Journal of Clinical Medicine 9, no. 8: 2573. https://doi.org/10.3390/jcm9082573





