Numerical Simulation Study of the Horizontal Submerged Jet Based on the Wray–Agarwal Turbulence Model
Abstract
:1. Introduction
2. Modeling and Numerical Methods
2.1. Model Building
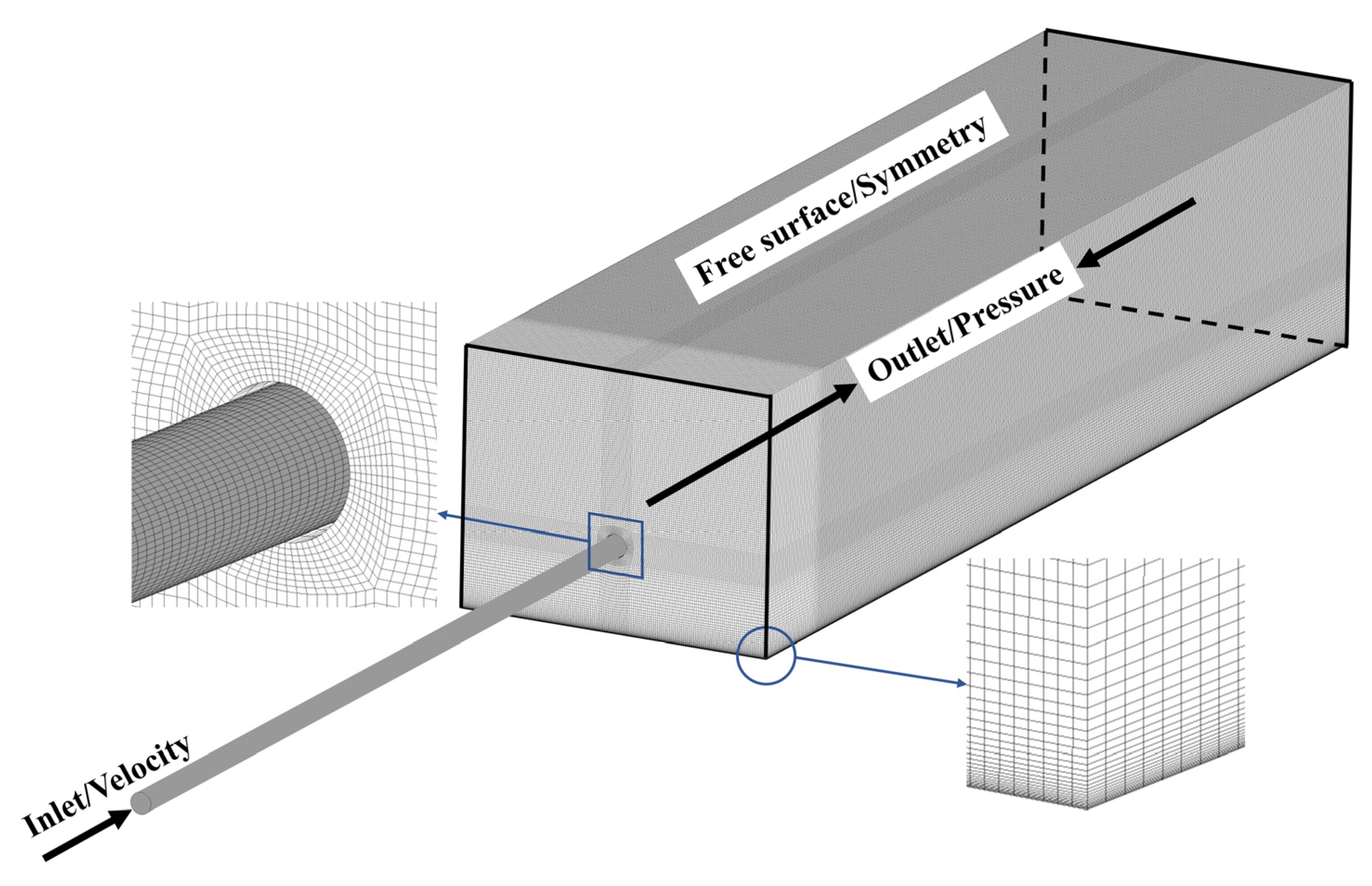
2.2. Numerical Methods and Boundary Conditions
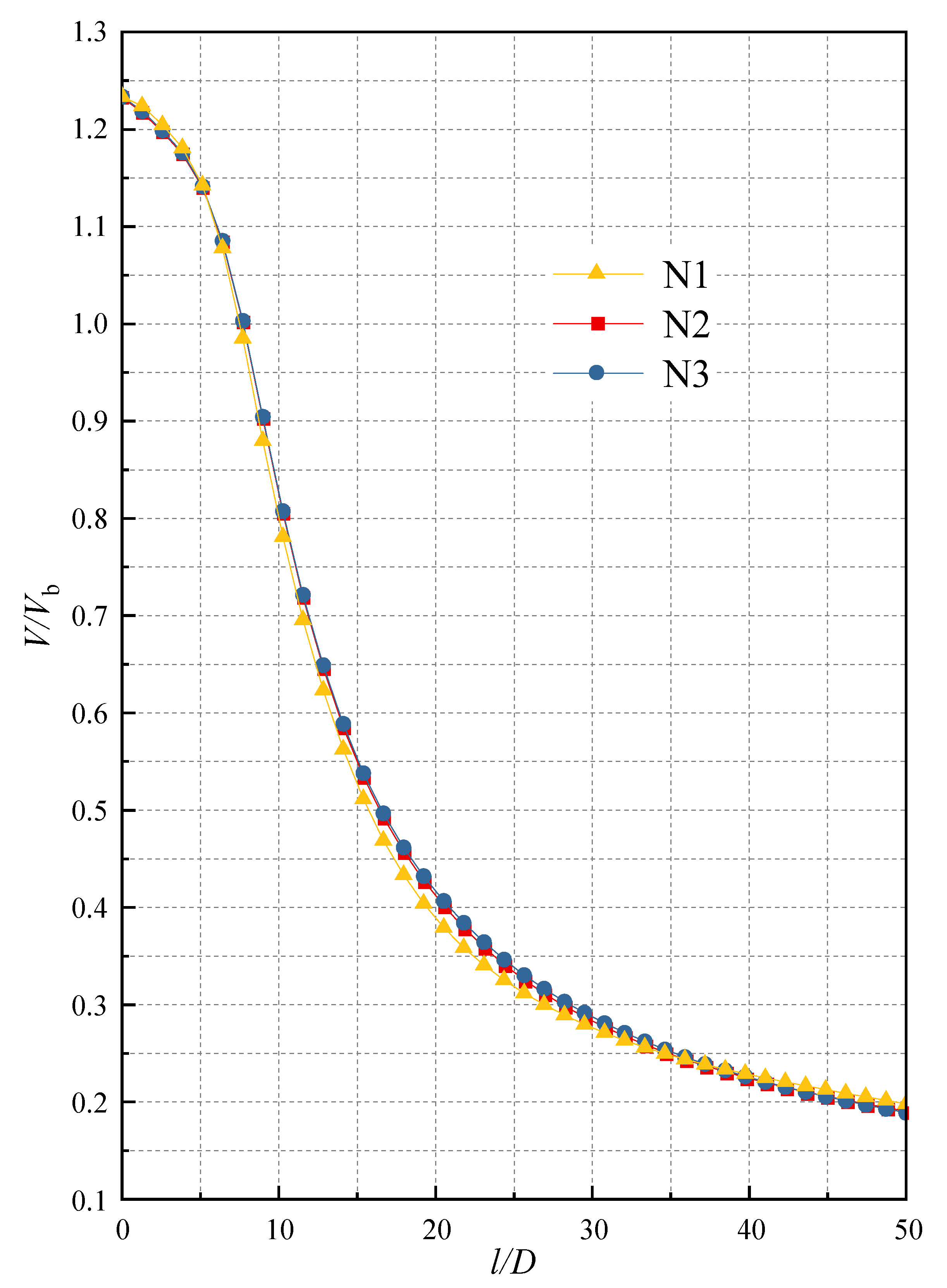
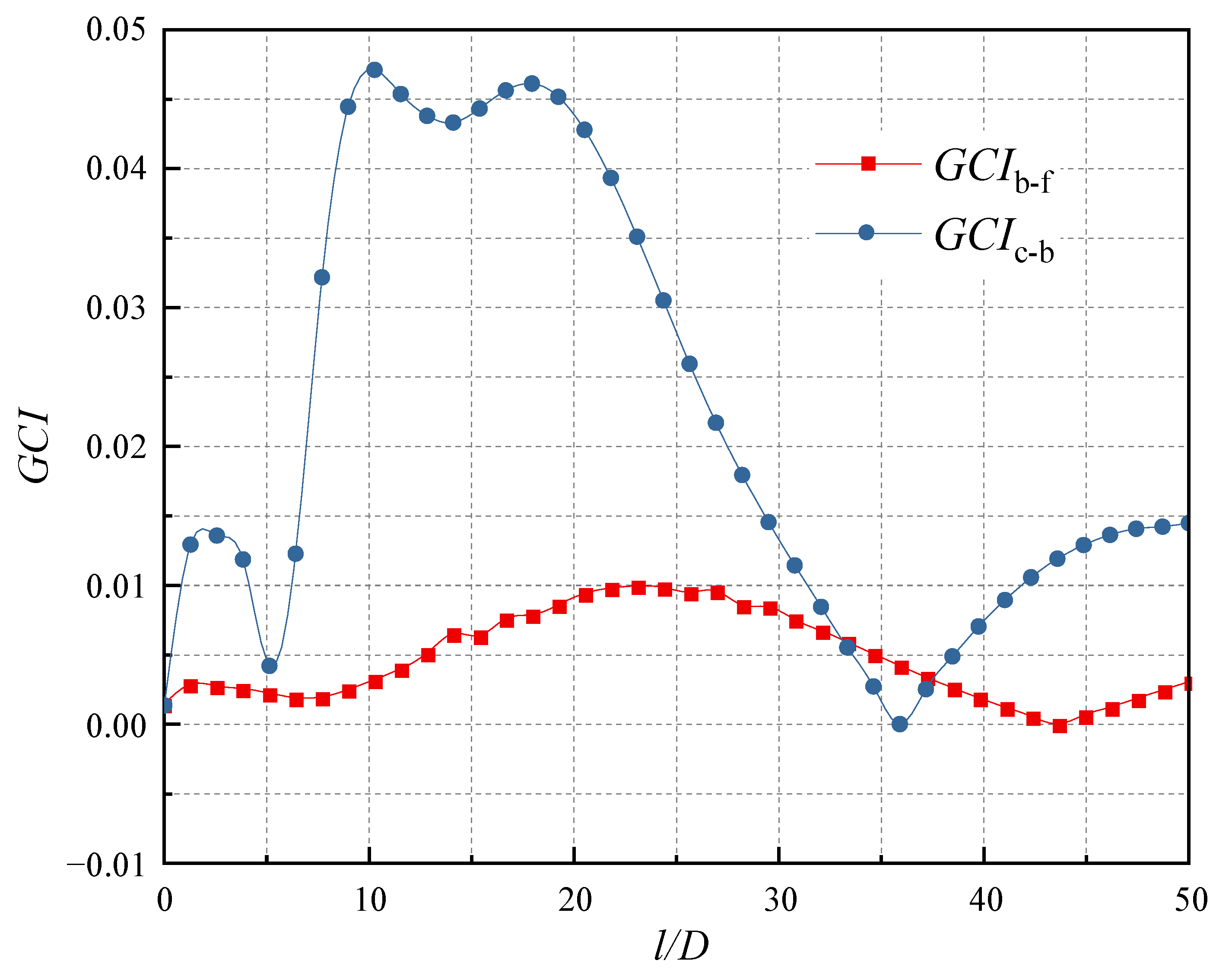
2.3. Grid-Independence Analysis
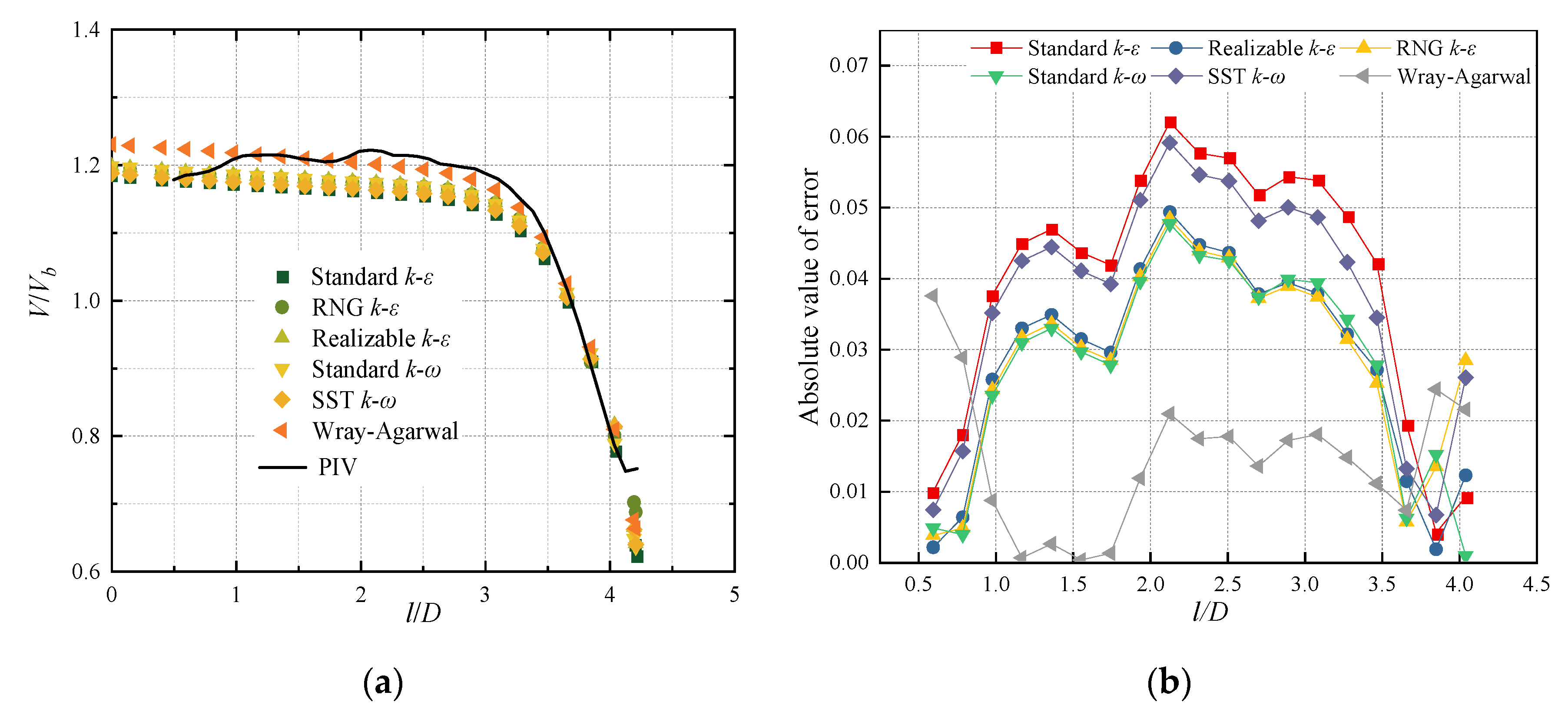
2.4. Turbulence Model Validation
3. Results and Discussion
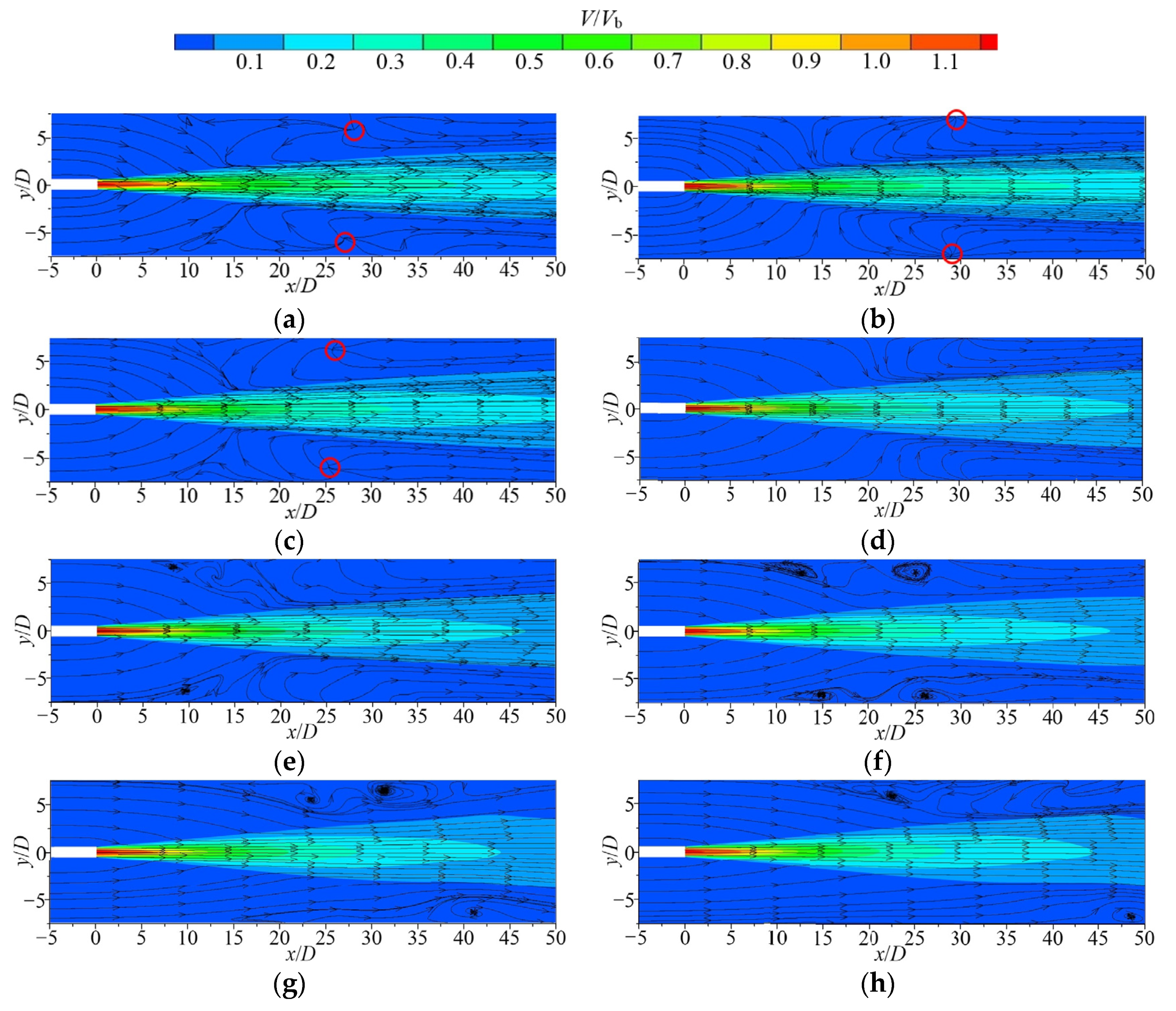
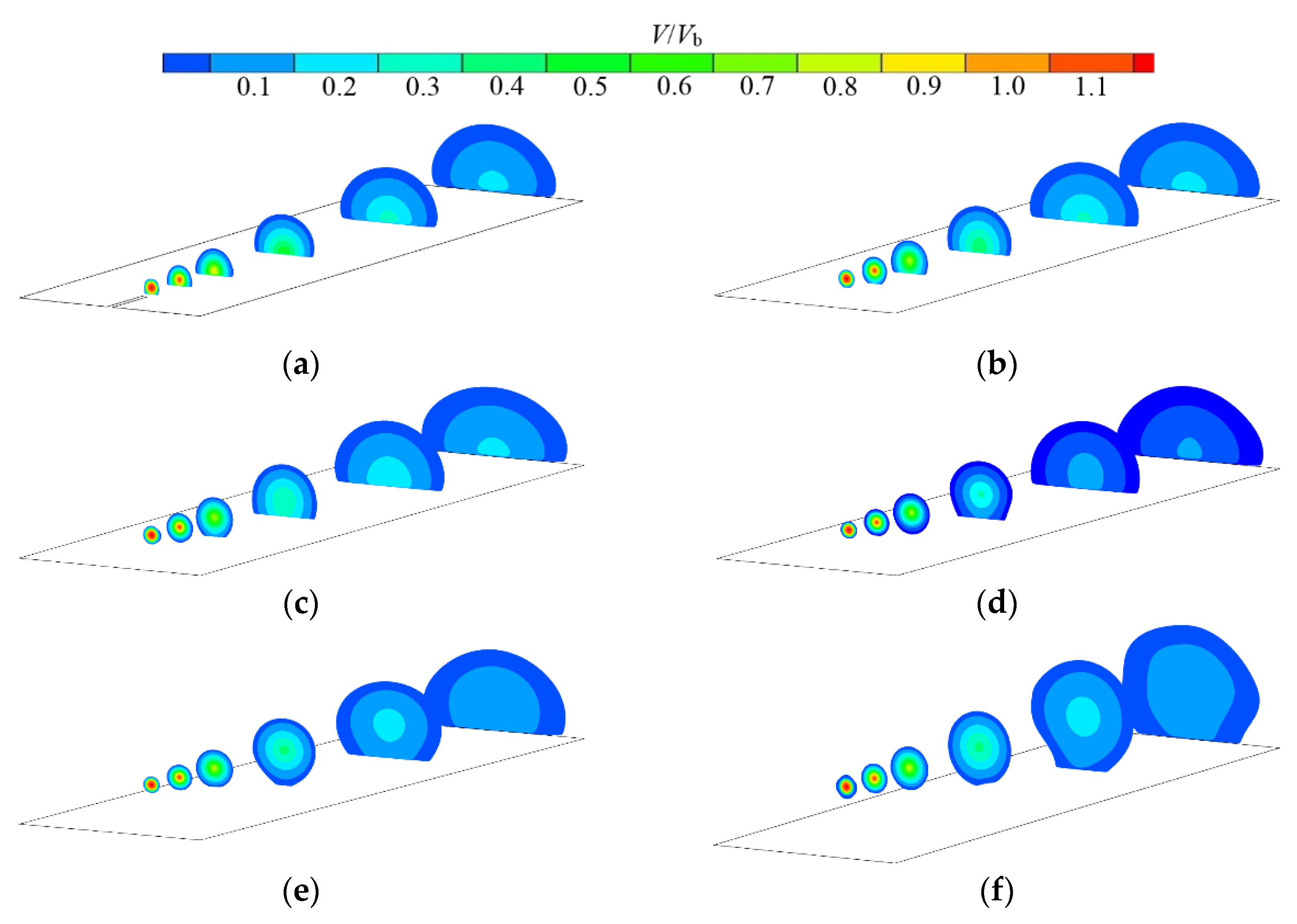
3.1. Flow Field Analysis
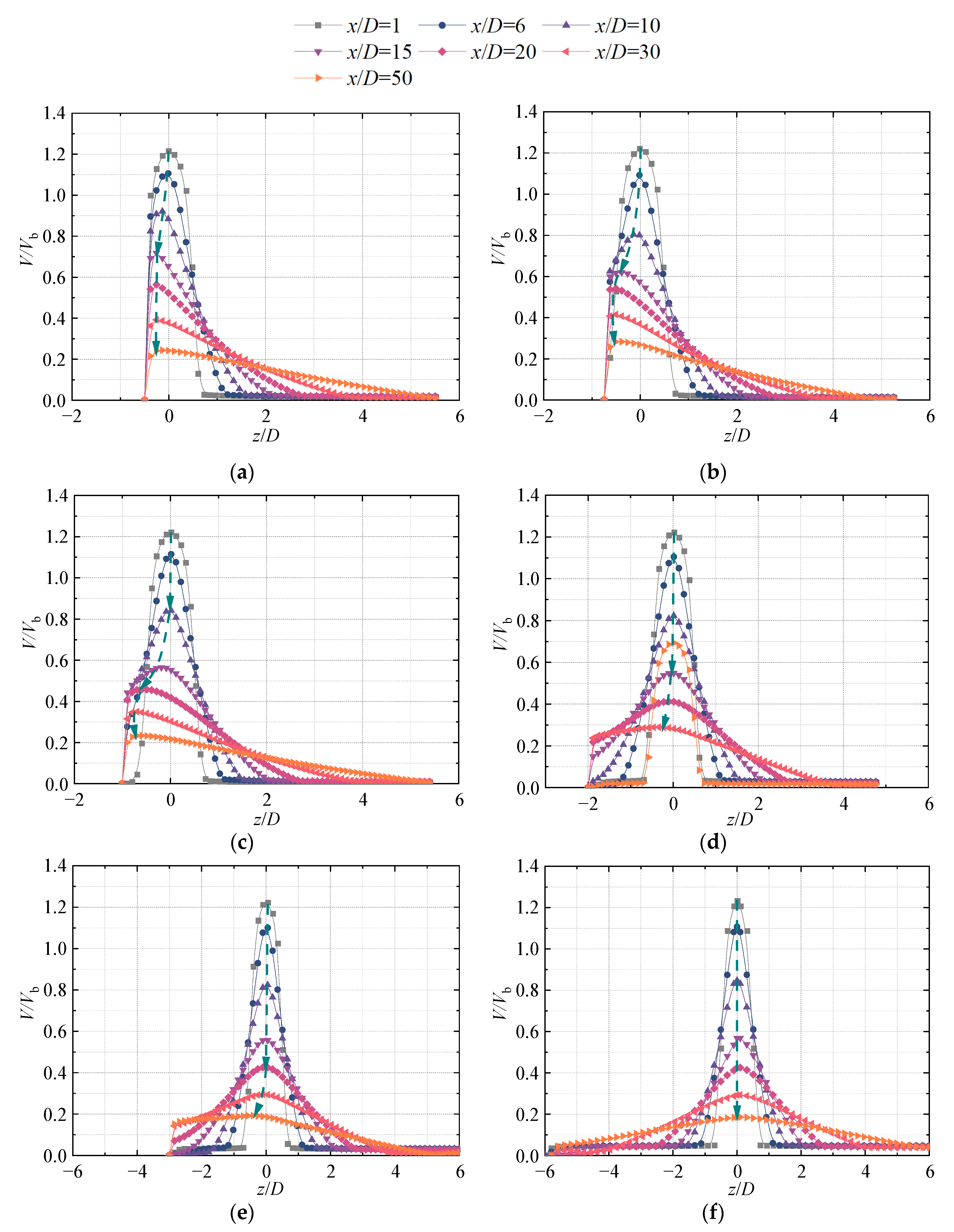
3.2. Jet Velocity Distribution in the Near-Wall Region
4. Conclusions
- (1)
- The jet horizontal height H/D has a large effect on the flow field structure of HSJ. When H/D is small, the unsteady structure in the jet flow field is dominated by vortexes, and the distribution is more regular, all starting generation around x/D = 30. In the meantime, the vortex structure in the flow field has a clear boundary and is insensitive to the variation of H/D. In addition, significant wall-attached vortexes are generated on both sides of the flow field. In the +y direction, the wall-attached vortexes gradually develop. They are also observed to gradually move in the +x direction as H/D increases.
- (2)
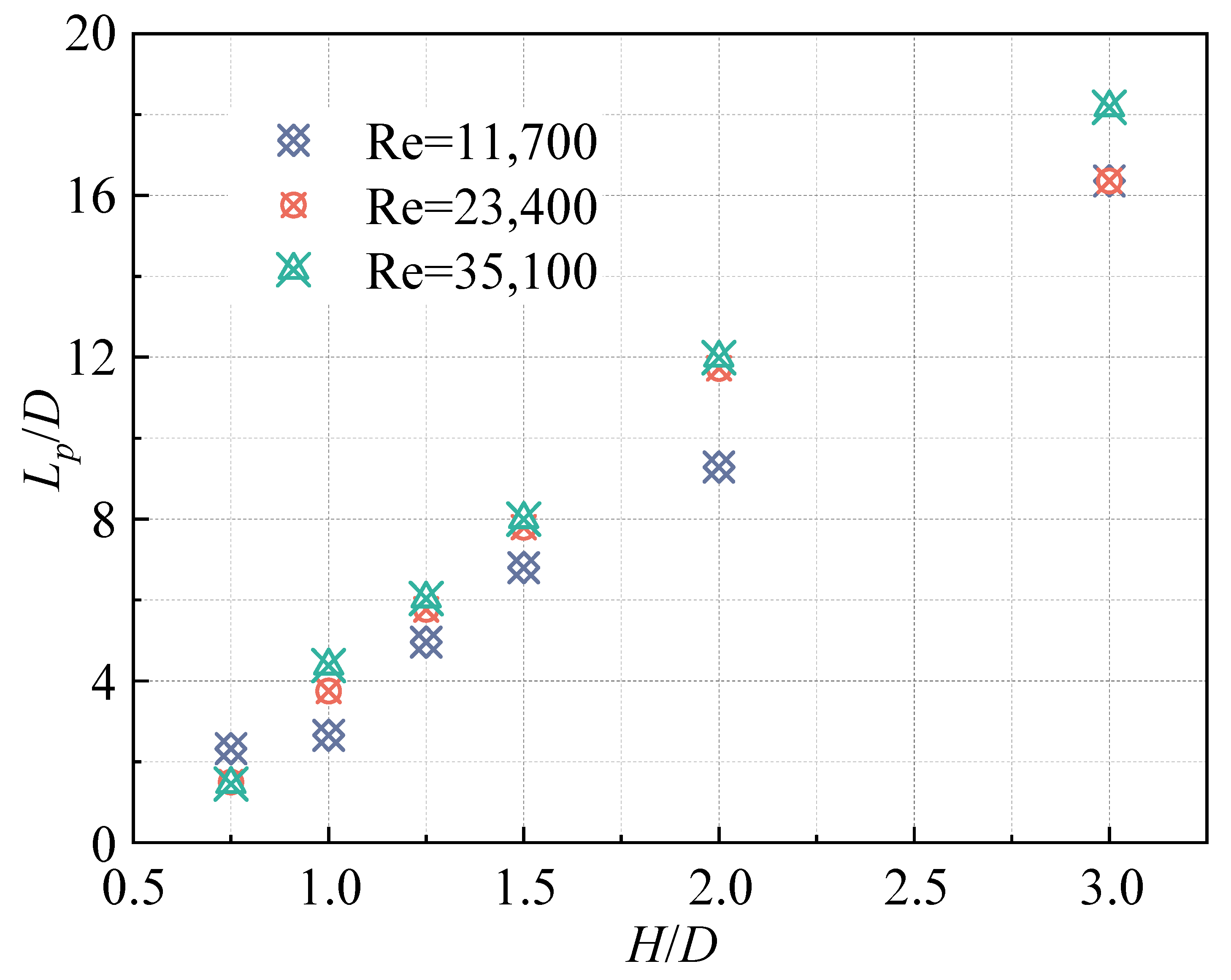
- The distance between the JCP and the jet pipe outlet increases linearly with the increase in the incidence height H/D, but the distribution pattern of the JCP gradually becomes relatively independent of the Reynolds number with the increase in the jet Reynolds number.
- (3)
- The velocity distribution of the jet axial velocity under different incidence heights H/D has very high similarity, and all of them have obvious velocity inflection points at x = 10D. The horizontal inundation jet is divided into two zones; in zone I, the velocity drops sharply, while in zone II, the drop of axial velocity slows down. In addition, when H/D is small, its axial speed is significantly higher than in other working conditions, up to 1.29 times. It can be seen that the wall attachment effect of the jet and the boundary layer effect generated at the bottom of the fluid domain have a certain role in maintaining the velocity of the jet near the wall. The flow velocity of the main stream of the jet near the wall is obviously large. This phenomenon disappears with the increase in H/D. In addition, this velocity retention effect is most significant at H/D = 1.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, Z. Impinging Jets; China Ocean Press: Beijing, China, 1997. [Google Scholar]
- Rouse, H. Cavitation in the mixing zone of a submerged jet. La Houille Blanche 1953, 1, 9–19. [Google Scholar] [CrossRef]
- Law, H.S. Numerical prediction of the flow field due to a confined laminar two-dimensional submerged jet. Comput. Fluids 1984, 12, 199–215. [Google Scholar] [CrossRef]
- Wen, Q.; Kim, H.D.; Liu, Y.; Kim, K.C. Dynamic structures of a submerged jet interacting with a free surface. Exp. Therm. Fluid Sci. 2014, 57, 396–406. [Google Scholar] [CrossRef]
- Liu, H.; Kang, C.; Zhang, W.; Zhang, T. Flow structures and cavitation in submerged waterjet at high jet pressure. Exp. Therm. Fluid Sci. 2017, 88, 504–512. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Shi, W.; Zhang, W.; El-Emam, A.M. Numerical Investigation of a High-Pressure Submerged Jet Using a Cavitation Model Considering Effects of Shear Stress. Processes 2019, 7, 541. [Google Scholar] [CrossRef]
- Ma, J.; Song, Y.; Zhou, P.; Cheng, W.; Chu, S. A mathematical approach to submerged horizontal buoyant jet trajectory and a criterion for jet flow patterns. Exp. Therm. Fluid Sci. 2018, 92, 409–419. [Google Scholar] [CrossRef]
- Yang, H.C. Horizontal two-phase jet behavior with an annular nozzle ejector in the water tank. J. Vis. 2015, 18, 359–367. [Google Scholar] [CrossRef]
- Xi, B.; Wang, C.; Xi, W.; Liu, Y.; Wang, H.; Yang, Y. Experimental investigation on the water hammer characteristic of stalling fluid in eccentric casing-tubing annulus. Energy 2022, 253, 124113. [Google Scholar] [CrossRef]
- Shao, D.; Huang, D.; Jiang, B.; Law, A.W.K. Flow patterns and mixing characteristics of horizontal buoyant jets at low and moderate Reynolds numbers. Int. J. Heat Mass Transf. 2017, 105, 831–846. [Google Scholar] [CrossRef]
- Chatterjee, S.S.; Ghosh, S.N.; Chatterjee, M. Local scour due to submerged horizontal jet. J. Hydraul. Eng. 1994, 120, 973–992. [Google Scholar] [CrossRef]
- Chiew, Y.M.; Lim, S.Y. Local scour by a deeply submerged horizontal circular jet. J. Hydraul. Eng. 1996, 122, 529–532. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent Fault Diagnosis of Hydraulic Piston Pump Based on Deep Learning and Bayesian Optimization. ISA Trans. 2022, in press. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Tang, S.; Wang, R.; Su, H.; Wang, C. Acoustic Signal-based Fault Detection of Hydraulic Piston Pump using a Particle Swarm Optimization Enhancement CNN. Appl. Acoust. 2022, 192, 108718. [Google Scholar] [CrossRef]
- Abdelaziz, S.; Bui, M.D.; Rutschmann, P. Numerical simulation of scour development due to submerged horizontal jet. River Flow 2010, 2010, 1597–1604. [Google Scholar]
- Li, H.; Zheng, T.; Dai, L.; Chen, X. Theoretical Research on New Energy Dissipation Type of Multi-horizontal Submerged Jets. Water Resour. Power 2010, 20, 74–76+166. [Google Scholar]
- Li, W.; Zhang, W.; Shi, W.; Yang, Y.; Cao, W. Experiment study on cavitation cloud evolution law of cavitation jet of convergent-divergent nozzle. J. Irrig. Drain. Eng. 2020, 38, 547–552. [Google Scholar]
- Kan, B.; Gao, Y.; Xu, S.; Ding, J. Numerical simulation of flow field characteristics of pressure controllable pipe with microporous walls. J. Irrig. Drain. Eng. 2020, 38, 183–187. [Google Scholar]
- Qi, M.; Wang, L.; Chen, Q.; Zhao, J.; Ju, Y.; Fu, Q. Numerical simulation of cavitating jet in dual chamber self-oscillation pulse nozzle. J. Irrig. Drain. Eng. 2020, 38, 457–461. [Google Scholar]
- Jiang, H.; Yan, H.; Xiao, Z.; Cheng, L.; Liu, H. Numerical simulation of hydraulic characteristics of three-side inlet of vertical shaft inlet channel of horizontal pumping station. J. Irrig. Drain. Eng. 2021, 39, 1008–1013. [Google Scholar]
- Shi, G.; Yao, X.; Wang, S.; Li, H. Analysis of stress and strain of multiphase pump blade considering medium viscosity. J. Irrig. Drain. Eng. 2020, 38, 991–996. [Google Scholar]
- Zhang, H.; Zheng, Y.; Zhang, Z.; Kan, K.; Mo, X. Influence of placement angle of sewage mixer on its hydraulic characteristics. J. Irrig. Drain. Eng. 2021, 39, 483–487. [Google Scholar]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the impeller blade with a slot structure on the centrifugal pump performance. Energies 2020, 13, 1628. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, Z. Analysis of internal flow characteristics of marine water-jet propulsion. J. Irrig. Drain. Eng. 2022, 40, 55–61. [Google Scholar]
- Quan, H.; Cheng, J.; Peng, G. Effect of screw centrifugal inducer on mechanical characteristics of vortex pump. Drain. Irrig. Mach. Eng. 2021, 39, 345–350. [Google Scholar]
- Roache, P.J. A method for uniform reporting of grid refinement studies. ASME-Publ.-Fed 1993, 158, 109. [Google Scholar] [CrossRef]
- Khayrullina, A.; van Hooff, T.; Blocken, B.; van Heijst, G. Validation of steady RANS modelling of isothermal plane turbulent impinging jets at moderate Reynolds numbers. Eur. J. Mech. B/Fluids 2019, 75, 228–243. [Google Scholar] [CrossRef]
- Liu, H.; Liu, M.; Bai, Y.; Du, H.; Dong, L. Grid convergence based on GCI for centrifugal pump. J. Jiangsu Univ. Nat. Sci. Ed. 2014, 35, 279–283. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 7. [Google Scholar]
- Ying, J.; Yu, X.; He, W.; Zhang, J. Volume of fluid model-based flow pattern in forebay of pump station and combined rectification scheme. J. Irrig. Drain. Eng. 2020, 38, 476–480. [Google Scholar]
- Feng, L.; Xu, R.; Feng, J. Numerical simulation of flow and heat transfer characteristics in helical pipe. J. Irrig. Drain. Eng. 2020, 38, 697–701. [Google Scholar]
- Wray, T.J.; Agarwal, R.K. Low-Reynolds-number one-equation turbulence model based on k-ω closure. AIAA J. 2015, 53, 2216–2227. [Google Scholar] [CrossRef]
- Han, X.; Rahman, M.; Agarwal, R.K. Development and Application of Wall-Distance-Free Wray-Agarwal Turbulence Model (WA2018). In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0593. [Google Scholar]
- Hu, B.; Wang, H.; Liu, J.; Zhu, Y.; Wang, C.; Ge, J.; Zhang, Y. A Numerical Study of a Submerged Water Jet Impinging on a Stationary Wall. J. Mar. Sci. Eng. 2022, 10, 228. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, H.; Liu, J.; Wang, C.; Ge, J.; Zhu, Y.; Chen, X.; Hu, B. Flow Characteristics of Oblique Submerged Impinging Jet at Various Impinging Heights. J. Mar. Sci. Eng. 2022, 10, 399. [Google Scholar] [CrossRef]
- Xu, W.; Wang, C.; Zhang, L.; Ge, J.; Zhang, D.; Gao, Z. Numerical study of continuous jet impinging on a rotating wall based on Wray–Agarwal turbulence model. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 433. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Shi, W.; Lu, W.; Tan, S.K.; Zhou, L. Experimental investigation on impingement of a submerged circular water jet at varying impinging angles and Reynolds numbers. Exp. Therm. Fluid Sci. 2017, 89, 189–198. [Google Scholar] [CrossRef]
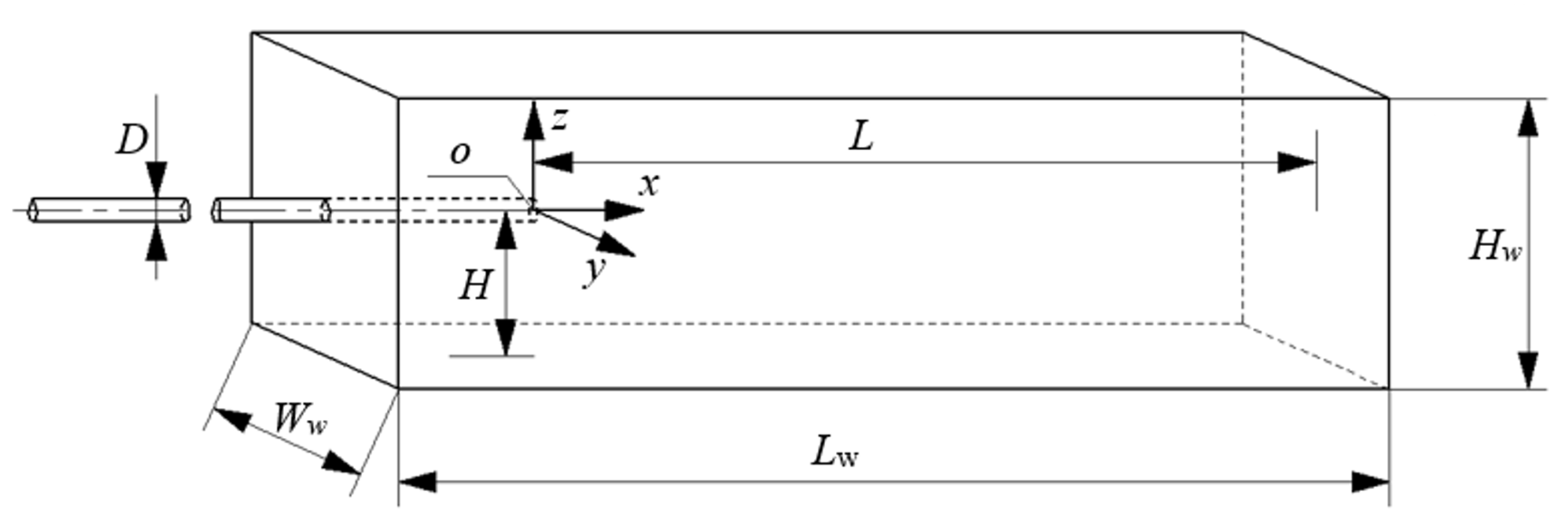







| Abbreviations | Meaning | Dimensionless Length | Actual Length |
|---|---|---|---|
| H | Vertical distance of the horizontal jet axis from the bottom | - | - |
| L | Vertical distance of the horizontal jet outlet from the right wall | - | - |
| Lj | Length of jet pipe | 50 D | 1000 mm |
| Lw | Length of sink | 55 D | 1100 mm |
| Ww | Width of sink | 15 D | 300 mm |
| Hw | Height of sink | 12 D | 240 mm |
| Case | N1 | N2 | N3 |
|---|---|---|---|
| Number of grids | 2,504,627 | 4,258,458 | 7,308,570 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Wang, C.; Wang, H.; Yu, Q.; Liu, J.; Zhu, Y.; Ge, J.; Chen, X.; Yang, Y. Numerical Simulation Study of the Horizontal Submerged Jet Based on the Wray–Agarwal Turbulence Model. J. Mar. Sci. Eng. 2022, 10, 1217. https://doi.org/10.3390/jmse10091217
Hu B, Wang C, Wang H, Yu Q, Liu J, Zhu Y, Ge J, Chen X, Yang Y. Numerical Simulation Study of the Horizontal Submerged Jet Based on the Wray–Agarwal Turbulence Model. Journal of Marine Science and Engineering. 2022; 10(9):1217. https://doi.org/10.3390/jmse10091217
Chicago/Turabian StyleHu, Bo, Chuan Wang, Hui Wang, Qian Yu, Jinhua Liu, Yong Zhu, Jie Ge, Xinxin Chen, and Yang Yang. 2022. "Numerical Simulation Study of the Horizontal Submerged Jet Based on the Wray–Agarwal Turbulence Model" Journal of Marine Science and Engineering 10, no. 9: 1217. https://doi.org/10.3390/jmse10091217





