Water Properties and Diffusive Convection in the Canada Basin
Abstract
:1. Introduction
2. Observational Data and Methods
2.1. Observational Data
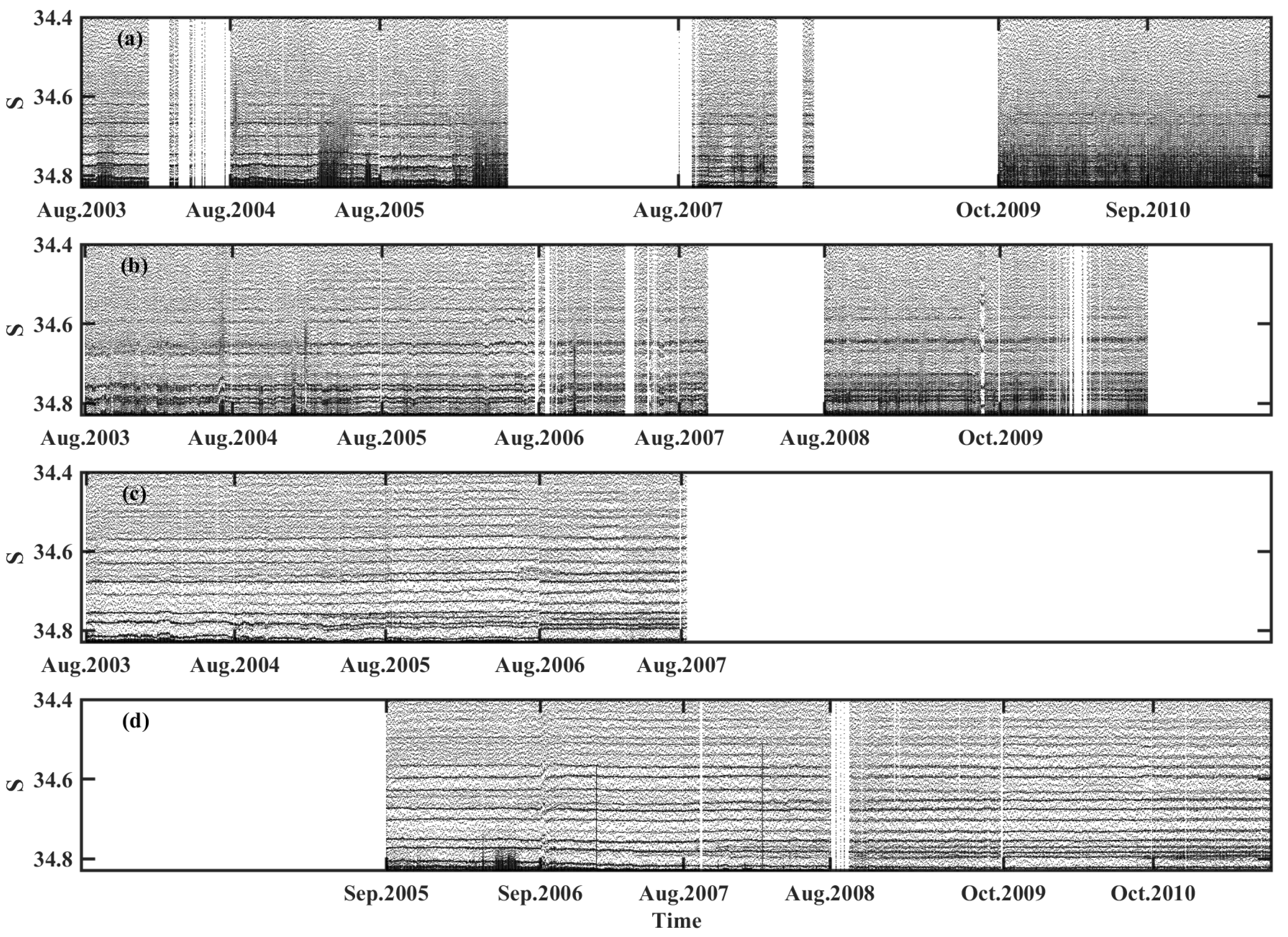
2.2. Typical Hydrographic Profile
2.3. Identification of the DC Staircase
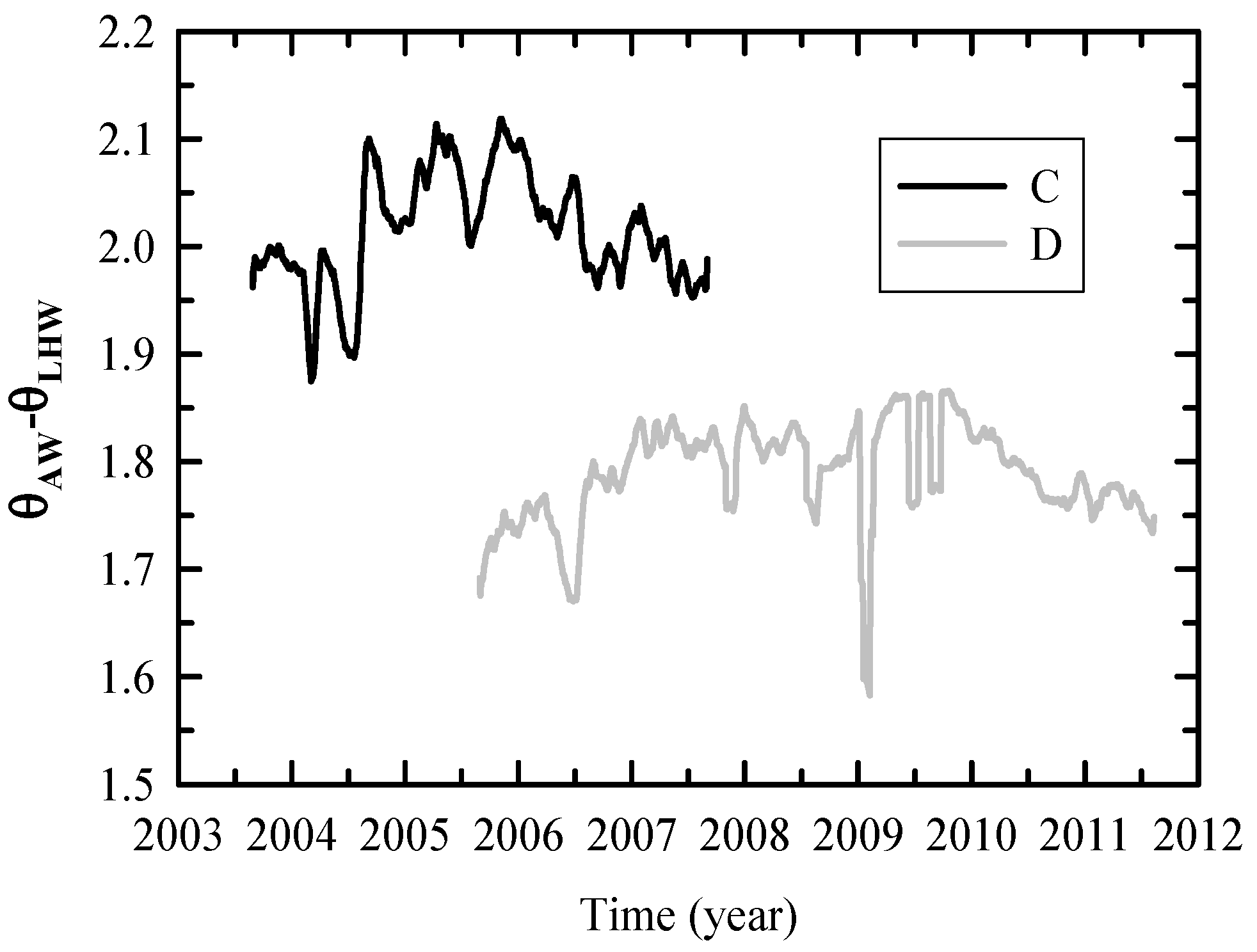
3. Variation in the Characteristics of AW and LHW
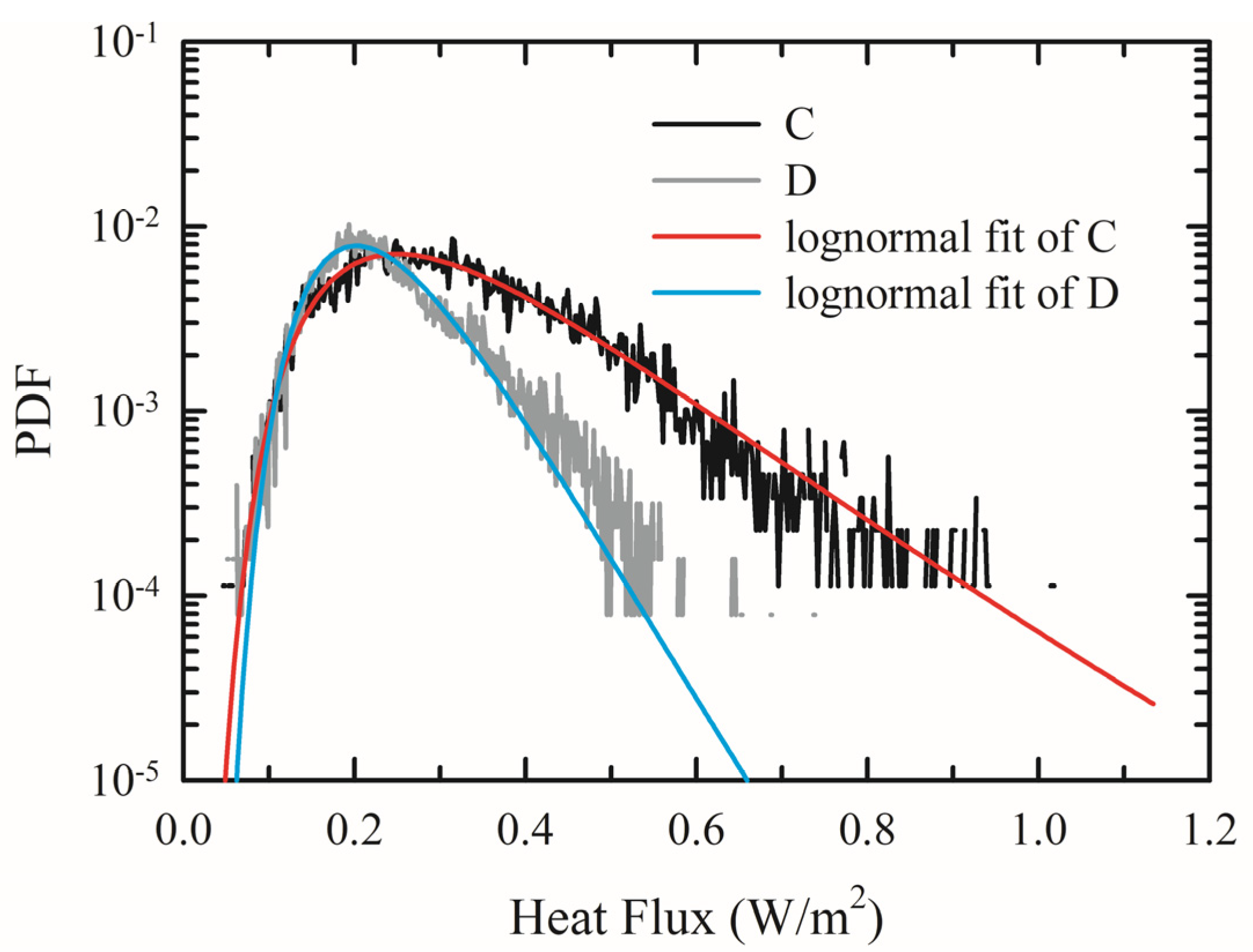
4. DC Staircase and Vertical Heat Transport
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turner, J.S. Double-diffusive phenomena. Annu. Rev. Fluid Mech. 1974, 6, 37–54. [Google Scholar] [CrossRef]
- Huppert, H.E.; Turner, J.S. Double-diffusive convection. J. Fluid Mech. 1981, 106, 299–329. [Google Scholar] [CrossRef]
- Kelley, D.E.; Fernando, H.J.S.; Gargett, A.E.; Tanny, J.; Özsoy, E. The diffusive regime of double-diffusive convection. Prog. Oceanogr. 2003, 56, 461–481. [Google Scholar] [CrossRef]
- van der Boog, C.G.; Dijkstra, H.A.; Pietrzak, J.D.; Katsman, C.A. Double-diffusive mixing makes a small contribution to the global Ocean circulation. Commun. Earth Environ. 2021, 2, 46. [Google Scholar] [CrossRef]
- McLaughlin, F.A.; Carmack, E.C.; Macdonald, R.W.; Melling, H.; Swift, J.; Wheeler, P.; Sherr, B.; Sherr, E. The joint roles of Pacific and Atlantic-origin waters in the Canada Basin, 1997–1998. Deep Sea Res. Part I Oceanogr. Res. Pap. 2004, 51, 107–128. [Google Scholar] [CrossRef]
- Turner, J.S. The Melting of Ice in the Arctic Ocean: The Influence of Double-Diffusive transport of heat from below. J. Phys. Oceanogr. 2010, 40, 249–256. [Google Scholar] [CrossRef]
- Rudels, B.; Jones, E.P.; Schauer, U.; Eriksson, P. Atlantic sources of the Arctic Ocean surface and halocline waters. Polar Res. 2004, 23, 181–208. [Google Scholar] [CrossRef]
- Toole, J.M.; Timmermans, M.L.; Perovich, D.K.; Krishfield, R.A.; Proshutinsky, A.; Richter-Menge, J.A. Influences of the ocean surface mixed layer and thermohaline stratification on Arctic Sea ice in the central Canada Basin. J. Geophys. Res. Ocean. 2010, 115, C10. [Google Scholar] [CrossRef]
- Qu, L.; Song, X.L.; Zhou, S.Q. Temporal evolution of mooring-based observations of double diffusive staircases in the southeast Canada Basin. Acta Oceanol. Sin. 2015, 37, 21–29. (In Chinese) [Google Scholar] [CrossRef]
- Shibley, N.C.; Timmermans, M.-L. The formation of double-diffusive layers in a weakly turbulent environment. J. Geophys. Res. Ocean. 2019, 124, 1445–1458. [Google Scholar] [CrossRef]
- Dosser, H.V.; Chanona, M.; Waterman, S.; Shibley, N.C.; Timmermans, M.-L. Changes in internal wave-driven mixing across the Arctic Ocean: Finescale estimates from an 18-year pan-Arctic record. Geophys. Res. Lett. 2021, 48, e2020GL091747. [Google Scholar] [CrossRef]
- Ménesguen, C.; Lique, C.; Caspar-Cohen, Z. Density staircases are disappearing in the Canada Basin of the Arctic Ocean. J. Geophys. Res. Ocean. 2022, 127, e2022JC018877. [Google Scholar] [CrossRef]
- McLaughlin, F.A.; Carmack, E.C.; Williams, W.J.; Zimmermann, S.; Shimada, K.; Itoh, M. Joint effects of boundary currents and thermohaline intrusions on the warming of Atlantic water in the Canada Basin, 1993-2007. J. Geophys. Res. 2009, 114, C00A12. [Google Scholar] [CrossRef]
- Bebieva, Y.; Timmermans, M.-L. Double-diffusive layering in the Canada basin: An explanation of along-layer temperature and salinity gradients. J. Geophys. Res. Ocean. 2019, 124, 723–735. [Google Scholar] [CrossRef]
- Ainslie, K. Formation and Destruction of Arctic Thermohaline Staircases; Naval Postgraduate School: Monterey, CA, USA, 2021. [Google Scholar]
- Carmack, E.C.; Macdonald, R.W.; Perkin, R.G.; McLaughlin, F.A.; Pearson, R.J. Evidence for warming of Atlantic water in the southern Canadian Basin of the Arctic Ocean: Results from the Larsen-93 expedition. Geophys. Res. Lett. 1995, 22, 1061–1064. [Google Scholar] [CrossRef]
- Polyakov, I.V.; Pnyushkov, A.V.; Rember, R.; Ivanov, V.V.; Lenn, Y.-D.; Padman, L.; Carmack, E.C. Mooring-Based Observations of Double-Diffusive Staircases over the Laptev Sea Slope. J. Phys. Oceanogr. 2012, 42, 95–109. [Google Scholar] [CrossRef]
- Lique, C.; Guthrie, J.D.; Steele, M.; Proshutinsky, A.; Morison, J.H.; Krishfield, R. Diffusive vertical heat flux in the Canada Basin of the Arctic Ocean inferred from moored instruments. J. Geophys. Res. Ocean. 2014, 119, 496–508. [Google Scholar] [CrossRef]
- Shibley, N.C.; Timmermans, M.-L. The Beaufort Gyre’s diffusive staircase: Finescale signatures of Gyre-scale transport. Geophys. Res. Lett. 2022, 49, e2022GL098621. [Google Scholar] [CrossRef]
- Ruddick, B.; Gargett, A.E. Oceanic double-infusion: Introduction. Prog. Oceanogr. 2003, 56, 381–393. [Google Scholar]
- Zhao, Q.; Zhao, J.P. Distribution of double-diffusive staircase structure and heat flux in the Canadian Basin. Adv. Earth Sci. 2011, 26, 193–201. (In Chinese) [Google Scholar]
- Padman, L.; Dillon, T.M. Thermal microstructure and internal waves in the Canada Basin diffusive staircase. Deep Sea Res. Part A Oceanogr. Res. Pap. 1989, 36, 531–542. [Google Scholar] [CrossRef]
- Padman, L.; Dillon, T.M. Vertical heat fluxes through the Beaufort Sea thermohaline staircase. J. Geophys. Res. Ocean. 1987, 92, 10799–10806. [Google Scholar] [CrossRef]
- Song, X.L.; Zhou, S.Q.; Fer, I. Analysis of the double-diffusive heat flux in the upper Arctic Ocean. Acta Oceanol. Sin. 2014, 36, 65–71. (In Chinese) [Google Scholar] [CrossRef]
- Itoh, M.; Carmack, E.; Shimada, K.; McLaughlin, F.; Nishino, S.; Zimmermann, S. Formation and spreading of Eurasian source oxygen-rich halocline water into the Canadian Basin in the Arctic Ocean. Geophys. Res. Lett. 2007, 34, 8. [Google Scholar] [CrossRef]
- Kikuchi, T.; Hatakeyama, K.; Morison, J.H. Distribution of convective lower halocline water in the eastern Arctic Ocean. J. Geophys. Res. Ocean. 2004, 109, C12. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Xia, K.Q. Spatially correlated temperature fluctuations in turbulent convection. Phys. Rev. E 2001, 63, 046308. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.Q.; Lu, Y.Z. Characterization of double diffusive convection steps and heat budget in the deep Arctic Ocean. J. Geophys. Res. Ocean. 2013, 118, 6672–6686. [Google Scholar] [CrossRef]
- Guo, S.X.; Zhou, S.Q.; Cen, X.R.; Qu, L.; Lu, Y.Z.; Sun, L.; Shang, X.D. The effect of cell tilting on turbulent thermal convection in a rectangular cell. J. Fluid Mech. 2015, 762, 273–287. [Google Scholar] [CrossRef]
- Guo, S.X.; Zhou, S.Q.; Qu, L.; Cen, X.R.; Lu, Y.Z. Evolution and statistics of thermal plumes in tilted turbulent convection. Int. J. Heat Mass Transf. 2017, 111, 933–942. [Google Scholar] [CrossRef]
- Bourgain, P.; Gascard, J.C. The Arctic Ocean halocline and its interannual variability from 1997 to 2008. Deep Sea Res. Part I Oceanogr. Res. Pap. 2011, 58, 745–756. [Google Scholar] [CrossRef]
- Lu, Y.Z.; Guo, S.X.; Zhou, S.Q.; Song, X.L.; Huang, P.Q. Identification of thermohaline sheet and its spatial structure in the Canada Basin. J. Phys. Oceanogr. 2022, 52, 2773–2787. [Google Scholar] [CrossRef]
- Proshutinsky, A.; Krishfield, R.; Timmermans, M.L.; Toole, J.; Carmack, E.; McLaughlin, F.; Williams, W.J.; Zimmermann, S.; Itoh, M.; Shimada, K. Beaufort Gyre freshwater reservoir: State and variability from observations. J. Geophys. Res. Ocean. 2009, 114, C1. [Google Scholar] [CrossRef]
- Zhao, M.; Timmermans, M.L. Vertical scales and dynamics of eddies in the Arctic Ocean’s Canada Basin. J. Geophys. Res. Ocean. 2015, 120, 8195–8209. [Google Scholar] [CrossRef]
- Li, J.; Pickart, R.S.; Lin, P.; Bahr, F.; Arrigo, K.R.; Juranek, L.; Yang, X. The Atlantic water boundary current in the Chukchi Borderland and southern Canada Basin. J. Geophys. Res. Ocean. 2020, 125, e2020JC016197. [Google Scholar] [CrossRef]
- Jackson, J.M.; Allen, S.E.; Carmack, E.C.; McLaughlin, F.A. Suspended particles in the Canada Basin from optical and bottle data, 2003–2008. Ocean. Sci. Discuss. 2010, 7, 1017–1057. [Google Scholar] [CrossRef]
- Yang, J.Y. The seasonal variability of the Arctic Ocean Ekman transport and its role in the mixed layer heat and salt fluxes. J. Clim. 2006, 19, 5366–5387. [Google Scholar] [CrossRef]
- Kelley, D.E. Fluxes through diffusive staircases: A new formulation. J. Geophys. Res. 1990, 95, 3365–3371. [Google Scholar] [CrossRef]
- Guo, S.X.; Zhou, S.Q.; Qu, L.; Lu, Y.Z. Laboratory experiments on diffusive convection layer thickness and its oceanographic implications. J. Geophys. Res. Ocean. 2016, 121, 7517–7529. [Google Scholar] [CrossRef]
- Guo, S.X.; Cen, X.R.; Zhou, S.Q. New parametrization for heat transport through diffusive convection interface. J. Geophys. Res. Ocean. 2018, 123, 1327–1338. [Google Scholar] [CrossRef]
- Guo, S.X.; Zhou, S.Q.; Cen, X.R.; Zhou, S.Q. Evolution of Staircase Structures in Diffusive Convection. J. Vis. Exp. 2018, 139, e58316. [Google Scholar]
- Merryfield, W.J. Origin of thermohaline staircases. J. Phys. Oceanogr. 2000, 30, 1046–1068. [Google Scholar] [CrossRef]
- Inoue, R.; Yamazaki, H.; Wolk, F.; Kono, T.; Yoshida, J. An Estimation of Buoyancy Flux for a Mixture of Turbulence and Double Diffusion. J. Phys. Oceanogr. 2007, 37, 611–624. [Google Scholar] [CrossRef]
- Timmermans, M.-L.; Toole, J.; Proshutinsky, A.; Krishfield, R.; Plueddemann, A. Eddies in the Canada Basin, Arctic Ocean, observed from ice-tethered profilers. J. Phys. Oceanogr. 2008, 38, 133–145. [Google Scholar] [CrossRef]
- Castaing, B.; Gunaratne, G.; Heslot, F.; Kadanoff, L.; Libchaber, A.; Thomae, S.; Wu, X.-Z.; Zaleski, S.; Zanetti, G. Scaling of hard thermal turbulence in Rayleigh-Benard convection. J. Fluid Mech. 1989, 204, 1–30. [Google Scholar] [CrossRef]
- Gurvich, A.S.; Yaglom, A.M. Breakdown of eddies and probability distributions for small-scale turbulence. Phys. Fluids 1967, 10, S59. [Google Scholar] [CrossRef]
- Siggia, E.B. High Rayleigh number convection. Annu. Rev. Fluid Mech. 1994, 26, 137–168. [Google Scholar] [CrossRef]
- Shibley, N.C.; Timmermans, M.-L.; Carpenter, J.R.; Toole, J.M. Spatial variability of the Arctic Ocean’s double-diffusive staircase. J. Geophys. Res. Ocean. 2017, 122, 980–994. [Google Scholar] [CrossRef]
- Polyakov, I.V.; Rippeth, T.P.; Fer, I.; Baumann, T.M.; Carmack, E.C.; Ivanov, V.V.; Janout, M.; Padman, L.; Pnyushkov, A.V.; Rember, R. Intensification of near-surface currents and shear in the Eastern Arctic Ocean. Geophys. Res. Lett. 2020, 47, e2020GL089469. [Google Scholar] [CrossRef]
- Fer, I.; Skogseth, R.; Geyer, F. Internal waves and mixing in the marginal ice zone near the Yermak Plateau. J. Phys. Oceanogr. 2010, 40, 1613–1630. [Google Scholar] [CrossRef]
- Rippeth, T.P.; Lincoln, B.J.; Lenn, Y.-D.; Green, J.M.; Sundfjord, A.; Bacon, S. Tide-mediated warming of Arctic halocline by Atlantic heat fluxes over rough topography. Nat. Geosci. 2015, 8, 191–194. [Google Scholar] [CrossRef]
- Timmermans, M.L.; Toole, J.; Krishfield, R.; Winsor, P. Ice-Tethered Profiler observations of the double-diffusive staircase in the Canada Basin thermocline. J. Geophys. Res. Ocean. 2008, 113, C1. [Google Scholar] [CrossRef]
- Manley, T.O.; Hunkins, K. Mesoscale eddies of the Arctic Ocean. J. Geophys. Res. 1985, 90, 4911–4930. [Google Scholar] [CrossRef]
- Rainville, L.; Winsor, P. Mixing across the Arctic Ocean: Microstructure observations during the Beringia 2005 Expedition. Geophys. Res. Lett. 2008, 35, L08606. [Google Scholar] [CrossRef]
- Fer, I. Weak vertical diffusion allows maintenance of cold halocline in the central Arctic. Atmos. Ocean. Sci. Lett. 2009, 2, 148–152. [Google Scholar] [CrossRef]
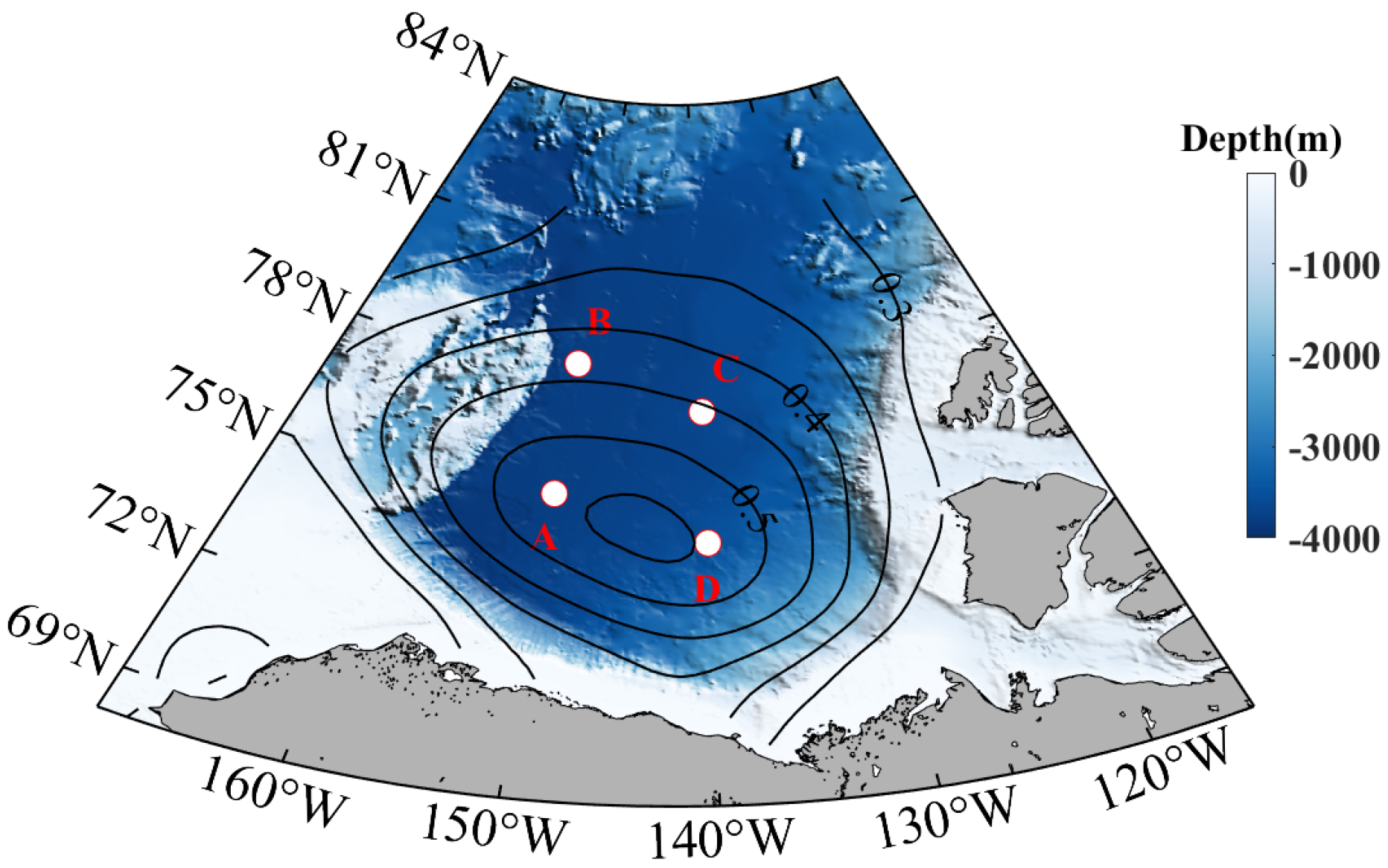





| MMP Data | A | B | C | D |
|---|---|---|---|---|
| Location | 75° N, 150° W | 78° N, 150° W | 77° N, 140° W | 74° N, 140° W |
| Time | August 2003–June 2006 August 2007–July 2008 October 2009–July 2011 | August 2003–September 2010 | August 2003–August 2008 | August 2005–August 2011 |
| Profile number | 1578 | 1967 | 1296 | 1896 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, L.; Guo, S.; Zhou, S.; Lu, Y.; Zhu, M.; Cen, X.; Li, D.; Zhou, W.; Xu, T.; Sun, M.; et al. Water Properties and Diffusive Convection in the Canada Basin. J. Mar. Sci. Eng. 2024, 12, 290. https://doi.org/10.3390/jmse12020290
Qu L, Guo S, Zhou S, Lu Y, Zhu M, Cen X, Li D, Zhou W, Xu T, Sun M, et al. Water Properties and Diffusive Convection in the Canada Basin. Journal of Marine Science and Engineering. 2024; 12(2):290. https://doi.org/10.3390/jmse12020290
Chicago/Turabian StyleQu, Ling, Shuangxi Guo, Shengqi Zhou, Yuanzheng Lu, Mingquan Zhu, Xianrong Cen, Di Li, Wei Zhou, Tao Xu, Miao Sun, and et al. 2024. "Water Properties and Diffusive Convection in the Canada Basin" Journal of Marine Science and Engineering 12, no. 2: 290. https://doi.org/10.3390/jmse12020290







