Mechanism of Speed Loss Reduction and Propulsion Efficiency Improvement of ONR Tumblehome with Active-Controlled Stern Flaps in Resonance Waves
Abstract
:1. Introduction
2. CFD Method and Control Model
2.1. RANS Equations
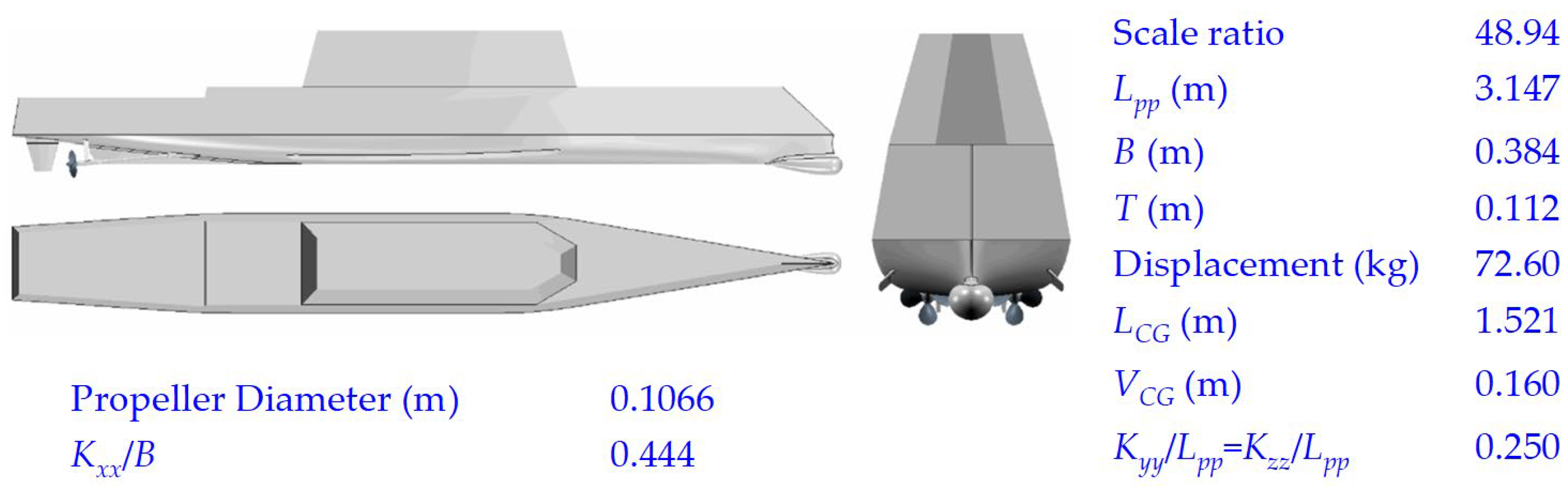
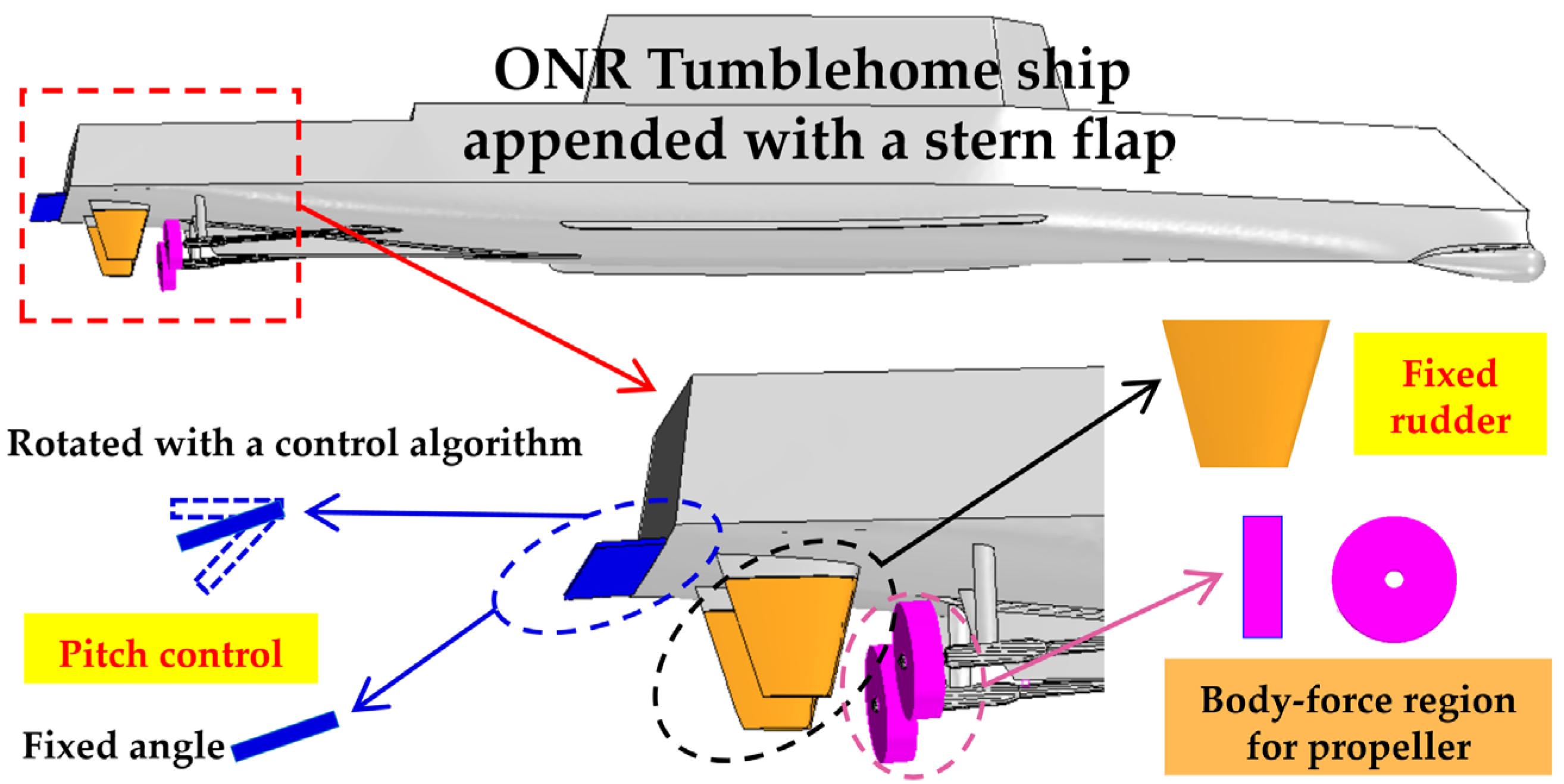
2.2. ONR Tumblehome Ship and Control Model
2.2.1. Propulsion Model
2.2.2. Speed Control Strategy
2.2.3. Pitch and Heave Control Strategy
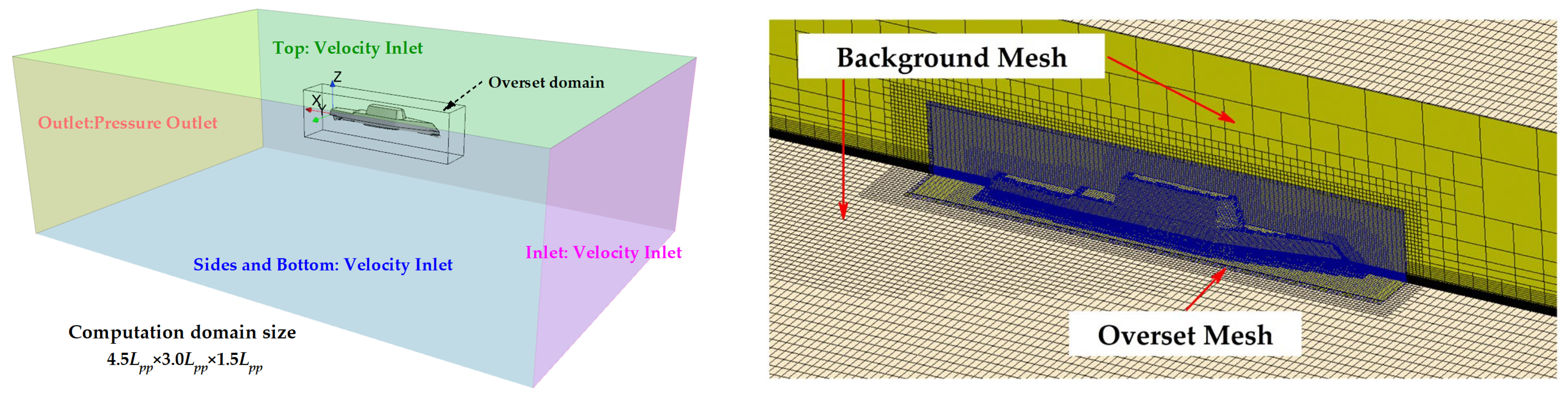
3. Free-Running CFD Model and Validation
3.1. Self-Propulsion of the ONRT Ship Model in Calm Water
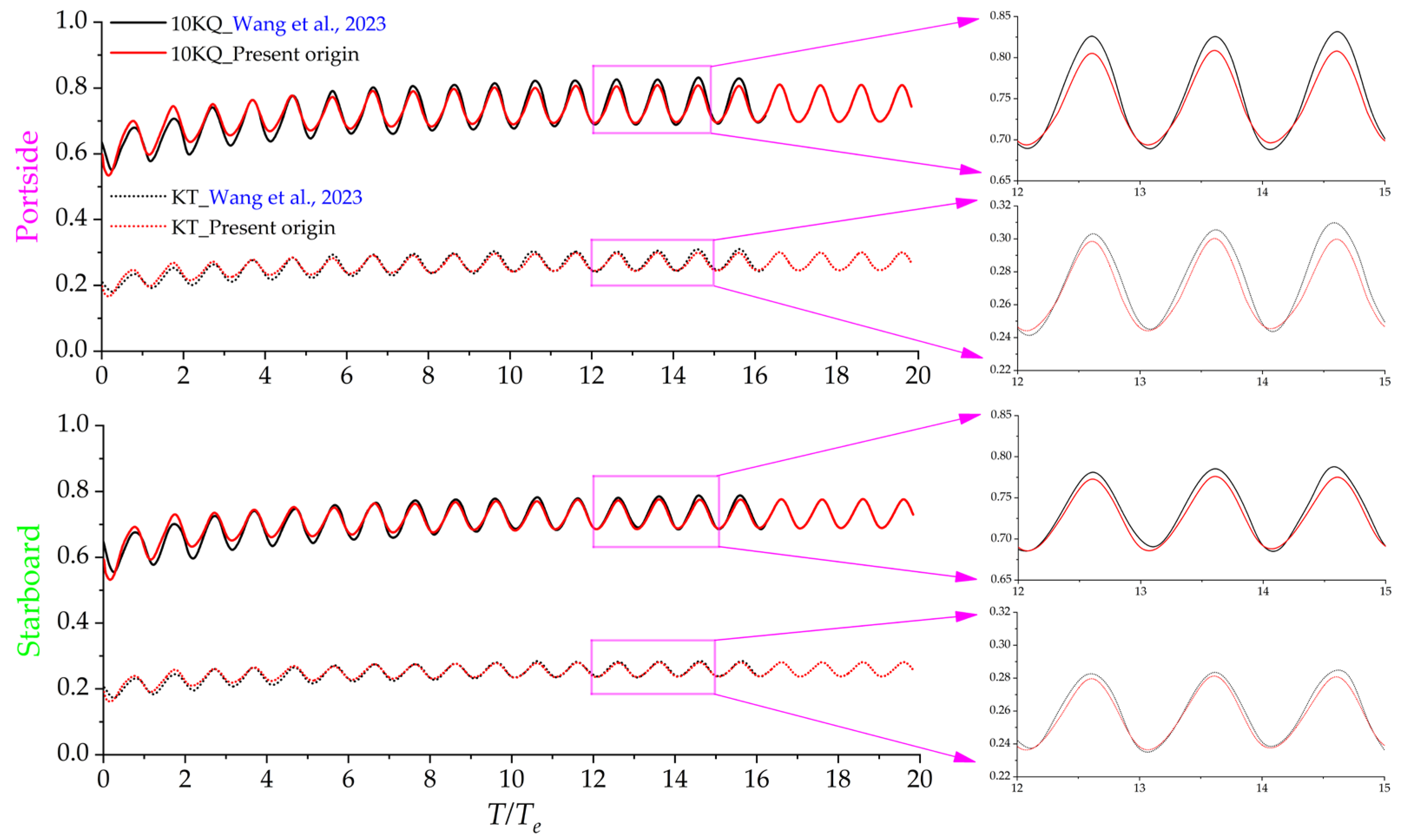
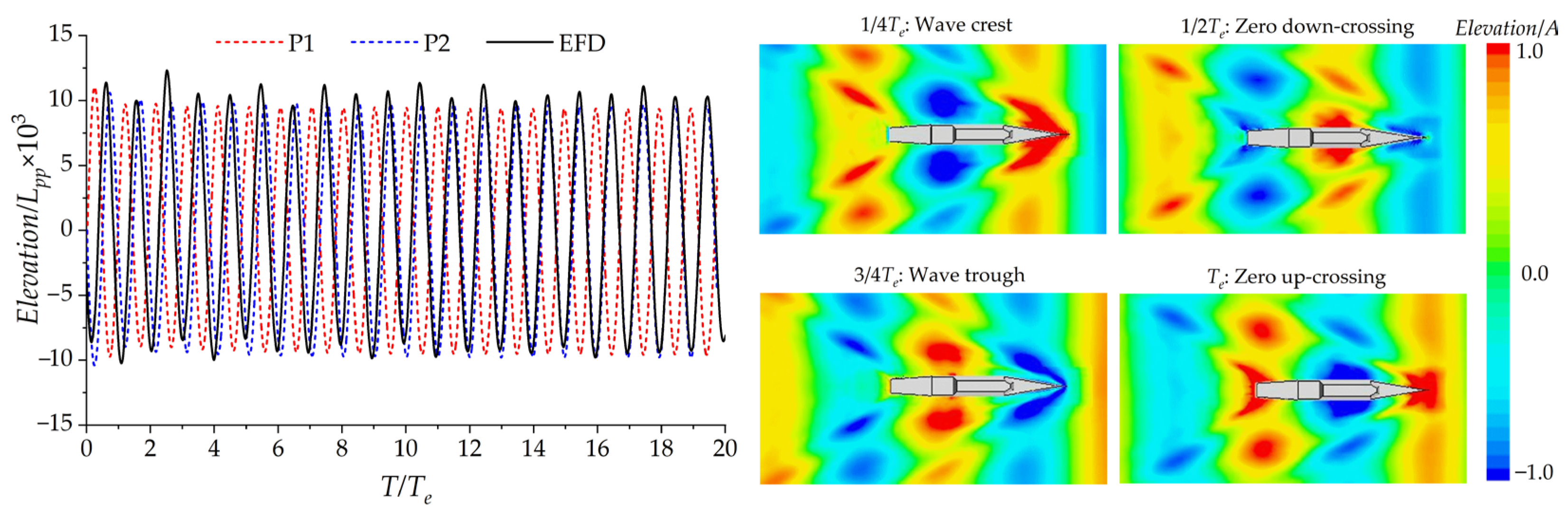
3.2. Free-Running ONRT Ship Model in Resonance Wave
4. Effect of Active-Controlled Stern Flaps on ONRT in Resonance Waves
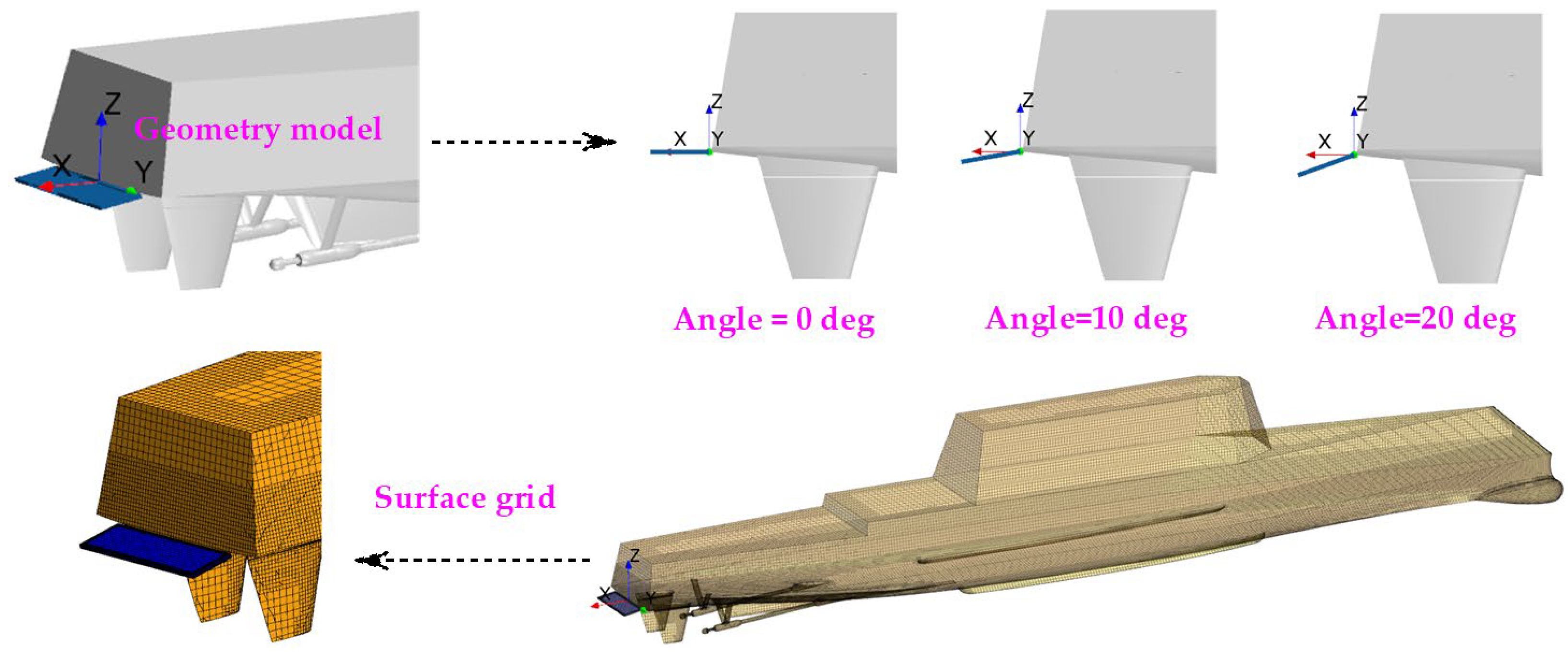
4.1. Computational Model with Active Stern Flaps
4.2. Research Schemes
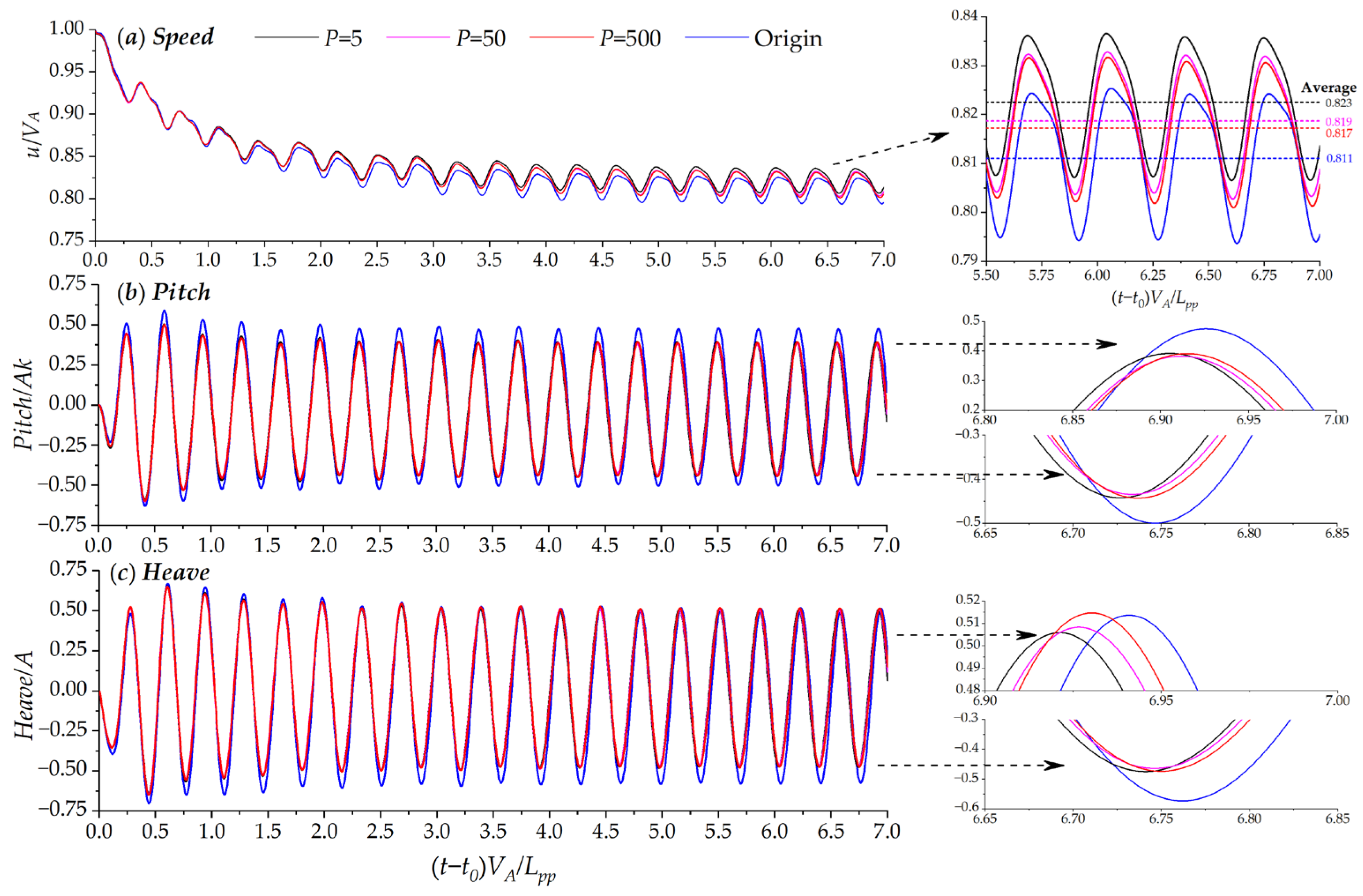
- Effect of different P coefficients of the stern flap controller;
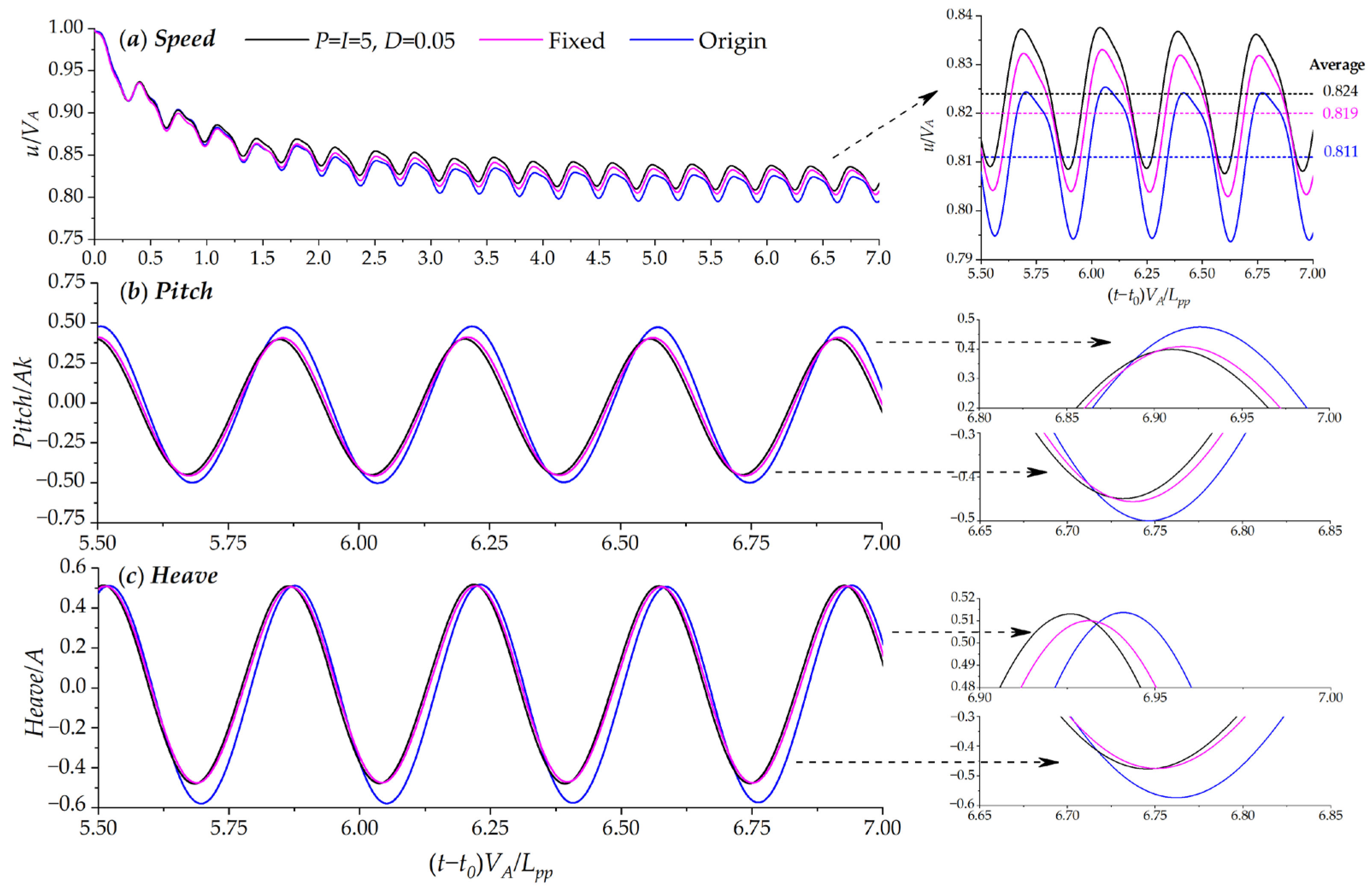
- Effect of different combinations of PID coefficients of the stern flap controller;
- Comparison of the fixed stern flap angle and the PID controller.
4.3. Effects of P Coefficients on the Stern Flap Controller
4.4. Effects of PID Coefficient Combination on the Stern Flap Controller
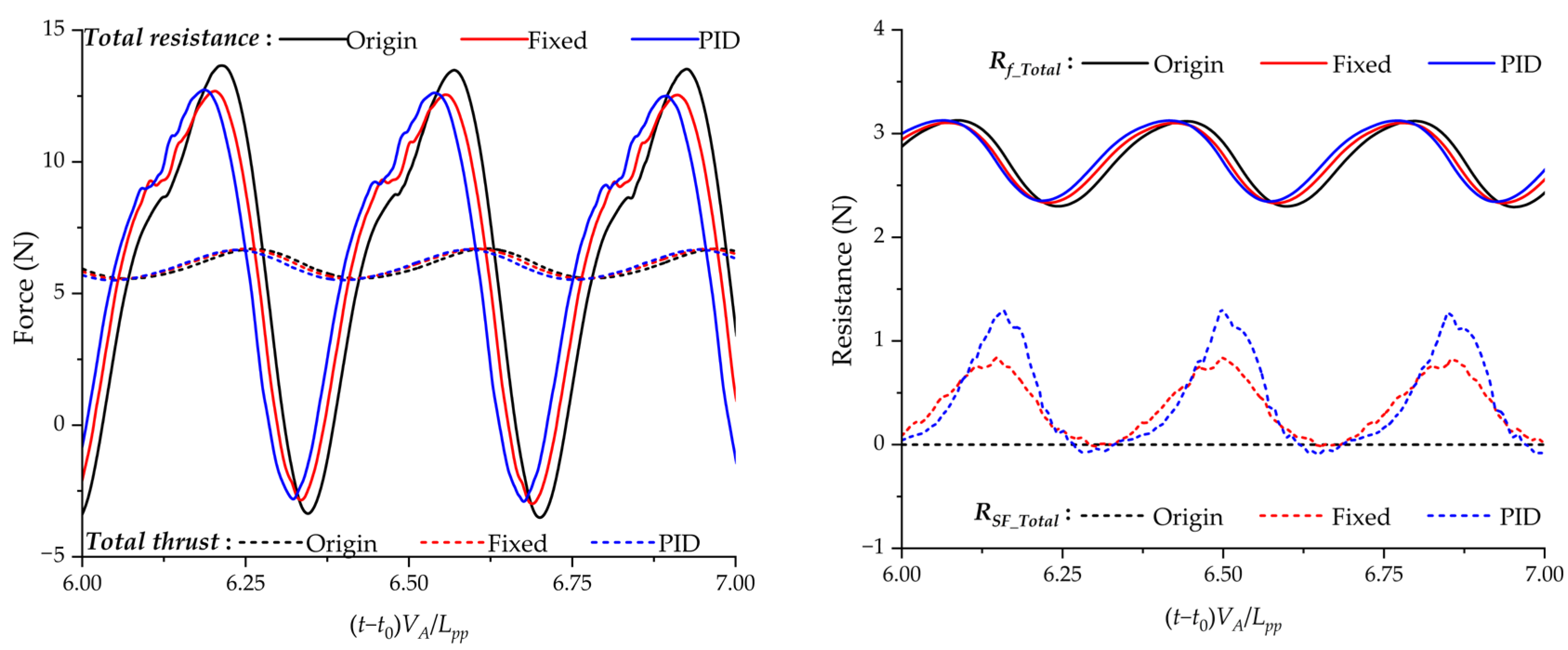
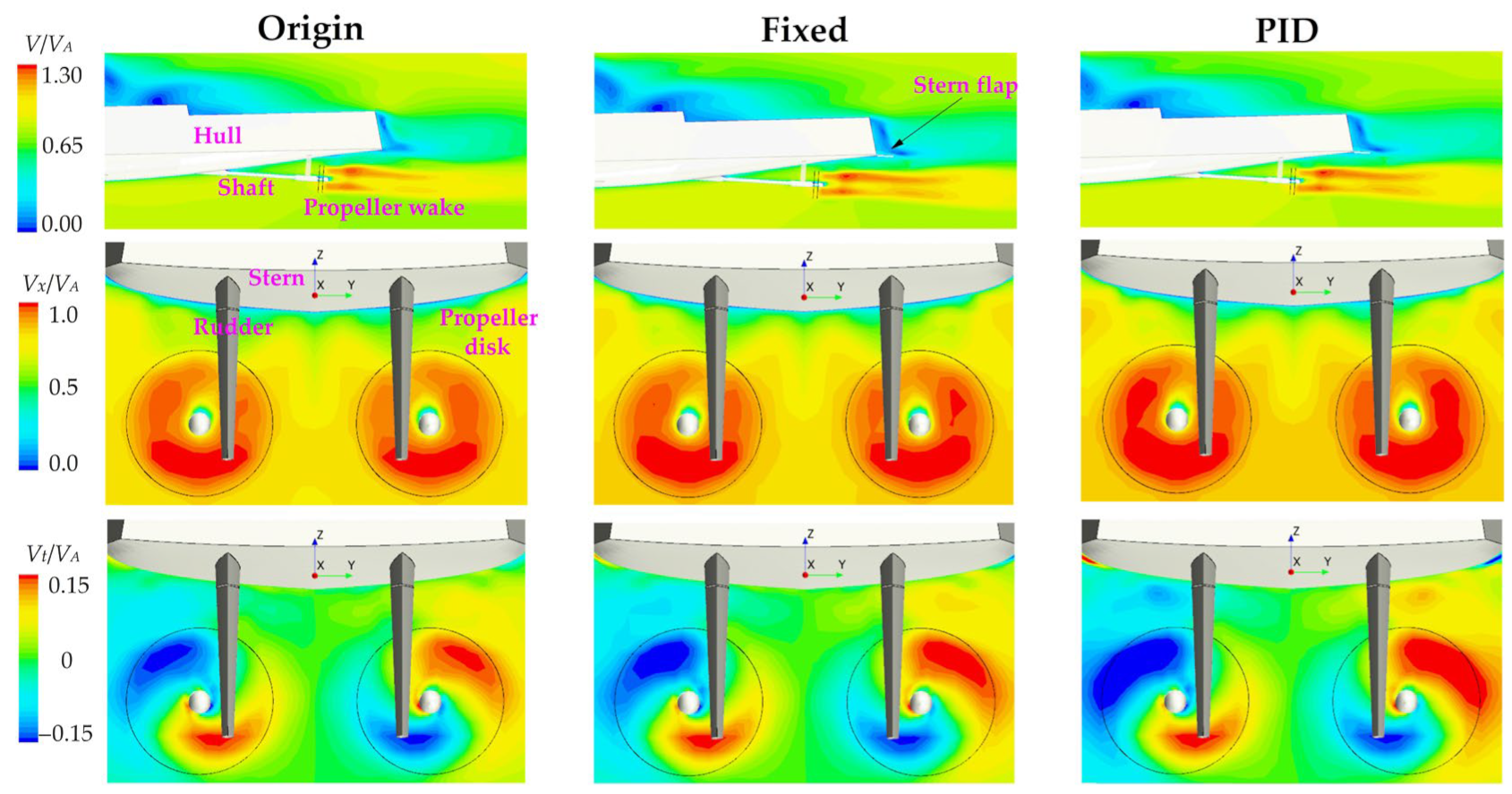
4.5. Mechanism of the Performance Improving of the Active Stern Flap and Discussions
5. Conclusions
- (1)
- Dimensionless speed and motion attitudes result from different single P coefficients, and PID coefficients show that the control coefficient of P = I = 5, D = 0.05 shows comprehensive advantages, where the speed loss is reduced by 6.9% and propulsion efficiency is promoted by 1.4% compared with the original ONRT vessel without the stern flap.
- (2)
- The 10 deg fixed flap installation suppress the heave and pitch motion variations of ONRT, resulting in a resistance decrease in global effects caused by the reduction in motion amplitude. The local effects of the stern flap–propeller–stern interaction, which blocks the stern flow field, lead to the local resistance increment. The overall influence of the global and local effects brings an average speed loss reduction of 4.2% and an average propulsive efficiency improvement of 1.0%.
- (3)
- Furthermore, the stern flap controlled by the PID strategy exhibits similar average attitudes compared to the fixed flap. This indicates that the global effect of attitude on resistance is nearly the same for the two cases. Through further suppressing at the stern trim state and releasing at the bow trim state of the stern flap by the PID controller, the resistance increment of the local effect is weakened. As a result, the average speed loss decreases by an additional 2.7%, and the average propulsive efficiency improves by 0.4% compared with the ONRT vessel with a 10° fixed stern flap.
- (4)
- The present work preliminary researched the active-controlled stern flap on the navigation performance effect and mechanism on the ONRT vessel in resonance waves and relatively low Fr. However, the numerical results between different models show relatively small differences, which may be related to the ship type, considered model, and traveling condition, especially the speed. Further research on different stern appendages, higher speeds, and wave conditions could be meaningful for the promotion of navigation performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grigoropopulos, G.J.; Loukakis, T.A. Effect of wedges on the calm water resistance of planing hulls. In Proceedings of the First International Conference on Marine Industry, Varna, Bulgaria, 2–7 June 1996. [Google Scholar]
- Grigoropopulos, G.J. The use of spray rails and wedges in fast monohulls. In Proceedings of the 4th International Conference on High Speed Marine Vehicles (HSMV ’97), Naples, Italy, 21–23 March 1997. [Google Scholar]
- Cusanelli, D.S.; O’Connell, L. US Coast Guard Island Class 110 WPB: Stern flap evaluation and selection (Model 5526). In Hydromechanics Directorate Report, 1999; NSWCCD: Potomac, MD, USA, 1999. [Google Scholar]
- Pogorzelski, D.; Adamos, E.G. Energy saving alternatives for U.S. Coast Guard (USCG) boats. In Hydromechanics Directorate Report, 2001; NSWCCD: Potomac, MD, USA, 2001. [Google Scholar]
- Cusanelli, D.S.; Barry, C.D. Stern flap performance on 110 ft patrol boat WPB 1345 STATEN ISLAND. In Hydromechanics Directorate Report, 2002; NSWCCD: Potomac, MD, USA, 2002. [Google Scholar]
- Cusanelli, D.S. Hydrodynamic and supportive structure for gated ship sterns: Amphibious ship stern flap. J. Ship Prod. Des. 2012, 28, 182–190. [Google Scholar] [CrossRef]
- Blackburn, W.K. Otter: An Optimized Transit Tool and Easy Reference; Naval Postgraduate School: Monterey, CA, USA, 2016. [Google Scholar]
- Cusanelli, D.S.; Chesnakas, C.J. Joint High Speed Sealift (JHSS) Baseline Shaft & Strut (BSS) Model 5653-3: Series 2, Propeller Disk LDV Wake Survey; and Series 3, Stock Propeller Powering and Stern Flap Evaluation Experiments; Report; NSWCCD: Potomac, MD, USA, 2007. [Google Scholar]
- O’Rourke, R. Navy Ship Propulsion Technologies: Options for Reducing Oil Use-Background for Congress; Report, 2016; University of North Texas Libraries, UNT Digital Library, UNT Libraries Government Documents Department: Washington, DC, USA, 2016; Available online: https://digital.library.unt.edu/ark:/67531/metacrs9419/ (accessed on 11 May 2024).
- Maki, A.; Arai, J.; Tsutsumoto, T.; Suzuki, K.; Miyauchi, Y. Fundamental research on resistance reduction of surface combatants due to stern flaps. J. Mar. Sci. Technol. 2016, 21, 344–358. [Google Scholar] [CrossRef]
- Jadmiko, E.; Arief, I.S.; Arif, L. Comparison of stern wedge and stern flap on fast monohull vessel resistance. Int. J. Mar. Eng. Innov. Res. 2018, 3, 41–49. [Google Scholar] [CrossRef]
- Song, K.W.; Guo, C.Y.; Wang, C.; Sun, C.; Li, P.; Wang, W. Numerical analysis of the effects of stern flaps on ship resistance and propulsion performance. Ocean Eng. 2019, 193, 106621. [Google Scholar] [CrossRef]
- Song, K.W.; Guo, C.Y.; Wang, C.; Sun, C.; Li, P.; Zhong, R.F. Experimental and numerical study on the scale effect of stern flap on ship resistance and flow field. Ships Offshore Struct. 2020, 15, 981–997. [Google Scholar]
- Zou, J.; Lu, S.; Jiang, Y.; Sun, H.; Li, Z. Experimental and numerical research on the influence of stern flap mounting angle on double-stepped planing hull hydrodynamic performance. J. Mar. Sci. Eng. 2019, 7, 346. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.N.; Shang, Y.C. Stern flap–waterjet–hull interactions and mechanism: A case of waterjet-propelled trimaran with stern flap. J. Offshore Mech. Arct. Eng. 2020, 142, 021203. [Google Scholar] [CrossRef]
- Li, Y.; Li, A.; Gong, J.; Fu, Z.; Dai, K. Numerical investigation on added resistance and motions of a high-speed trimaran equipped with T-foil and stern flap in regular head and oblique waves for varying wave steepness. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 451. [Google Scholar] [CrossRef]
- Budiarto, U.; Samuel, S.; Wijaya, A.A.; Yulianti, S.; Kiryanto, K.; Iqbal, M. Stern flap application on planing hulls to improve resistance. Int. J. Eng. 2022, 35, 2313–2320. [Google Scholar] [CrossRef]
- Tripathi, S.; Vijayakumar, R. Numerical and experimental study of stern flaps impact on resistance and propulsion of high–speed displacement ships. Ocean Eng. 2024, 292, 116483. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, H.; Wei, Y.; Zhang, Y.; Shang, Y.; Zhang, J. Active longitudinal motion control of waterjet-propelled trimaran in random waves using direct CFD approach integrated with auto-control algorithm. Ocean Eng. 2023, 286, 115586. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhao, W.W.; Wan, D.C. Free maneuvering simulation of ONR tumblehome using overset grid method in naoe-FOAM-SJTU solver. In Proceedings of the 31st Symposium on Naval Hydrodynamics, Monterey, CA, USA, 11–16 September 2016. [Google Scholar]
- Zhang, L.; Wei, Y.; Deng, Y.; Yin, H.; Zhang, Y.; Shang, Y.; Zhang, J. A comparative investigation of fixed and free-running CFD self-propulsion models on a waterjet-propelled trimaran. Ocean Eng. 2021, 232, 109081. [Google Scholar] [CrossRef]
- Carrica, P.M.; Mofidi, A.; Eloot, K.; Delefortrie, G. Direct simulation and experimental study of zigzag maneuver of KCS in shallow water. Ocean Eng. 2016, 112, 117–133. [Google Scholar] [CrossRef]
- Bakica, A.; Vladimir, N.; Malenica, Š.; Im, H. Numerical procedure for Pre-Swirl Stator structural integrity evaluation. Ocean Eng. 2022, 258, 111698. [Google Scholar] [CrossRef]
- Obwogi, E.O.; Shen, N.; Su, Y. The design and energy saving effect prediction of rudder-bulb-fin device based on CFD and model test. Appl. Ocean. Res. 2021, 114, 102814. [Google Scholar] [CrossRef]
- Bakica, A.; Malenica, Š.; Vladimir, N.; Senjanović, I. Hydroelastic analysis of Pre-Swirl Stator. Mar. Struct. 2022, 85, 103267. [Google Scholar] [CrossRef]
- Kim, J.; Choi, J.; Choi, B.; Chung, S.; Seo, H. Development of energy-saving devices for a full slow-speed ship through improving propulsion performance. Int. J. Nav. Archit. Ocean. Eng. 2015, 7, 390–398. [Google Scholar] [CrossRef]
- Shang, Y.C.; Horrillo, J.J. Numerical simulation and hydrodynamic performance predicting of 2 two-dimensional hydrofoils in tandem configuration. J. Mar. Sci. Eng. 2021, 9, 462. [Google Scholar] [CrossRef]
- Shang, Y.C.; Nikolaos, I.X. Numerical analysis of hydrodynamic performance of FX-83-W hydrofoil current turbine. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017. [Google Scholar]
- Yao, H.L.; Wang, L.J.; Zhang, H.X.; Liu, Y. Wake physics of two-dimensional flapping-hydrofoil turbines. Phys. Fluids 2023, 35, 105104. [Google Scholar] [CrossRef]
- Gong, J.; Li, Y.; Jiang, F.; Fu, Z. Prediction of turn and zigzag maneuvers with the hydrodynamic derivatives obtained by SQCM. Ocean Eng. 2024, 304, 117812. [Google Scholar] [CrossRef]
- IIHR. ONR tumblehome free-running test data for CFD workshop Tokyo 2015. In Proceedings of the Tokyo 2015 a Workshop on CFD in Ship Hydrodynamics, Tokyo, Japan, 2–4 December 2015. [Google Scholar]
- ITTC. ITTC-Recommended Procedures and Guidelines: Practical Guidelines for Ship Self-Propulsion CFD; ITTC: Copenhagen, Denmark, 2014. [Google Scholar]
- Feng, D.; Yu, J.; He, R.; Zhang, Z.; Wang, X. Improved body force propulsion model for ship propeller simulation. Appl. Ocean. Res. 2020, 104, 102328. [Google Scholar] [CrossRef]
- Kim, D.; Tezdogan, T.; Incecik, A. Hydrodynamic analysis of ship manoeuvrability in shallow water using high-fidelity URANS computations. Appl. Ocean Res. 2022, 123, 103176. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.N.; Shang, Y.C. A practical direct URANS CFD approach for the speed loss and propulsion performance evaluation in short-crested irregular head waves. Ocean Eng. 2021, 219, 108287. [Google Scholar] [CrossRef]
- Roy, J.; Heintzelman, C.; Roberts, S. Estimation of numerical error for 3D inviscid flows on Cartesian grids. In Proceedings of the 45th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Hosseini, H.S. CFD Prediction of Ship Capsize: Parametric Rolling, Broaching, Surf-Riding, and Periodic Motions; University of Iowa: Iowa, IA, USA, 2009. [Google Scholar]
- Aram, S.; Kim, S.E. A numerical study of added resistance, speed loss and added power of a surface ship in regular head waves using coupled URANS and rigid-body motion equations. In Proceedings of the VII International Conference on Computational Methods in Marine Engineering, CIMNE, Nantes, France, 15–17 May 2017; pp. 960–974. [Google Scholar]
- Wang, S.; Kim, B.S.; Zhu, Z.; Kim, Y. Numerical course-keeping tests of ONR tumblehome in waves with different rudder control strategies. Ocean Eng. 2023, 269, 113584. [Google Scholar] [CrossRef]





| Grid Uncertainty | Grid Density | Grids Number | CFD | EXP | Error | rg | RG | PG | UG (%D) |
|---|---|---|---|---|---|---|---|---|---|
| Propeller revolution (RPS) | Coarse | 1.0 M | 9.55 | 8.97 | 6.47% | 1.2 | 0.727 | 0.873 | 4.06 |
| Medium | 1.8 M | 9.44 | 5.24% | ||||||
| Fine | 3.1 M | 9.36 | 4.35% | ||||||
| Total resistance (N) | Coarse | 1.0 M | 4.72 | 4.54 | 3.96% | 1.2 | 0.714 | 0.923 | 4.59 |
| Medium | 1.8 M | 4.65 | 2.42% | ||||||
| Fine | 3.1 M | 4.60 | 1.32% |
| Controller | Speed | Resistance (N) | Propulsion Efficiency | Motions | |||||||||
| Mean u/VA | Speed Loss | Speed Loss Reduction | Mean Rx | Mean Rf | Mean RSF | Rx Reduction | Eta_P | Diff | Eta_S | Diff | Max Heave/A | Max Pitch/Ak | |
| Origin | 0.811 | 0.189 | - | 6.13 | 2.73 | 0.00 | - | 0.515 | - | 0.504 | - | 0.58 | 0.50 |
| Fixed | 0.819 | 0.181 | −4.2% | 6.09 | 2.72 | 0.33 | −0.7% | 0.521 | 1.1% | 0.509 | 0.9% | 0.51 | 0.45 |
| PID | 0.824 | 0.176 | −6.9% | 6.07 | 2.75 | 0.38 | −0.9% | 0.522 | 1.4% | 0.511 | 1.4% | 0.51 | 0.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Du, C.; Ni, Y.; Shang, Y.; Zhang, J. Mechanism of Speed Loss Reduction and Propulsion Efficiency Improvement of ONR Tumblehome with Active-Controlled Stern Flaps in Resonance Waves. J. Mar. Sci. Eng. 2024, 12, 822. https://doi.org/10.3390/jmse12050822
Zhang L, Du C, Ni Y, Shang Y, Zhang J. Mechanism of Speed Loss Reduction and Propulsion Efficiency Improvement of ONR Tumblehome with Active-Controlled Stern Flaps in Resonance Waves. Journal of Marine Science and Engineering. 2024; 12(5):822. https://doi.org/10.3390/jmse12050822
Chicago/Turabian StyleZhang, Lei, Chuanshun Du, Yongsen Ni, Yuchen Shang, and Jianing Zhang. 2024. "Mechanism of Speed Loss Reduction and Propulsion Efficiency Improvement of ONR Tumblehome with Active-Controlled Stern Flaps in Resonance Waves" Journal of Marine Science and Engineering 12, no. 5: 822. https://doi.org/10.3390/jmse12050822






