Inherent Addiction Mechanisms in Video Games’ Gacha

Abstract

Gacha games, particularly those using Free-to-Play (F2P) models, have become increasingly popular yet controversial due to their addictive mechanics, often likened to gambling. This study investigates the inherent addictive mechanisms of Gacha games, focusing on Genshin Impact, a leading title in the genre. We analyze the interplay between reward frequency, game attractiveness, and player addiction using the Game Refinement theory and the Motion in Mind framework. Our analysis identifies a critical threshold at approximately 55 pulls per rare item ($N\approx 55$), with a corresponding gravity-in-mind value of 7.4. Beyond this point, the system exhibits gambling-like dynamics, as indicated by Game Refinement and Motion in Mind metrics. This threshold was measured using empirical gacha data collected from Genshin Impact players and analyzed through theoretical models. While not claiming direct causal evidence of player behavior change, the results highlight a measurable boundary where structural design risks fostering addiction-like compulsion. The study contributes theoretical insights with ethical implications for game design, by identifying critical thresholds in reward frequency and game dynamics that mark the shift toward gambling-like reinforcement. The methodologies, including quantitative analysis and empirical data, ensure robust results contributing to responsible digital entertainment discourse.

1. Introduction

Video games have become a mainstream form of entertainment thanks to digital platforms. Over the years, game monetization and marketing have evolved from traditional Pay-to-Play (P2P) to Free-to-Play (F2P) models. As such, developers need to adapt to meet the demands of the growing player base while looking for new sources of income to sustain their development operations. Micro-transactions and subscriptions were the primary sources of income. Recently, live service games monetize by periodically adding new content to maintain player retention [1].

Developers increasingly use randomized or stochastic monetization methods, such as loot boxes and Gacha systems [2], to generate revenue across various video game genres. Interestingly, over half of mobile games and around 30% of desktop games employ these methods instead of traditional static pricing [3]. In Japan, “Gachapon” machines are widely used to dispense random small capsule toys and collectibles [4]. These machines are commonly found in convenience stores, toy stores, and arcades and typically cost JPY 200–300 per attempt. They offer exclusive or limited-edition items, making them popular for tourists seeking souvenirs. The Gachapon industry in Japan generates over JPY 100 billion in revenue [5].

Gacha games (also known as loot boxes in Western games) [6] is a popular and profitable gaming feature that randomly distributes virtual items such as characters, weapons, and equipment. Players can enhance their gaming experience by using in-game currency or real money to make micro-transactions for these items. Early digital Gacha games lacked proper documentation. The first mobile Gacha games, Dragon Collection, appeared in 2010 with randomized virtual items [6]. They were less advanced than current versions. The Gacha mechanism was applied to F2P games where players could earn in-game currency or points. This condition tempted players to spend real money to obtain items more quickly.

Games with Gacha systems are like gambling and can lead to overspending due to the uncertainty of item rewards [7]. Addiction, financial struggles, and strained relationships are commonly associated with gambling and lotteries [8,9]. In addition, these activities can fuel organized crime and money laundering [10,11]. Despite government efforts to regulate them, the allure of a big win remains, creating a complex issue [12]. Gacha rewards have no real-world value, but addiction to these games is still a noteworthy issue. Recent news reported a teenager who spent over USD 20,000 in six weeks on Genshin Impact [13,14].

Genshin Impact is a widely enjoyed F2P game that has generated an impressive $4 billion in revenue since its launch in September of 2020 [15]. Players can obtain items of varying rarity (1 to 5 stars) through in-game accomplishments or purchasing gems. Regular updates are provided to players every six weeks, ensuring that the live service game always has fresh content [16]. Revenue for the game is generated through microtransactions and battle passes.

A central feature of Gacha systems is the “pity system.” This mechanism ensures that after a fixed number of unsuccessful attempts (pulls), the player is guaranteed to receive a high-rarity reward (e.g., a 5-star character or weapon). In Genshin Impact, for example, if a player does not obtain a 5-star item within 89 pulls, the 90th pull is guaranteed to produce one. The “pity system” is designed to balance frustration by limiting the maximum streak of failures. However, while it provides certainty in the long run, it also extends the average number of required pulls, thereby reinforcing prolonged engagement and sustaining spending behaviors.

Many popular Gacha games employ a “pity system” that ensures players receive rewards after several attempts [2]. This feature allowed players to exchange in-game resources for the highest-rarity character [17] or guarantee high-quality character after some number of attempts [18]. However, relying solely on the pity system in Gacha games is risky as players often save up their pity to increase their chances, and could also backfire as it does not always work out and can result in wasted resources (i.e., pity farming). Research suggests that pathological gamblers may commit offenses to fund their addiction [19]. Gacha games have a “pity system” that curbs excessive losses. Compared to F2P games, Gacha games offer more significant initial rewards but slow game progression later on. Addiction to gambling and Gacha games differs from psychological addictions posed by drug addiction [20]. Gamblers are motivated by the prospect of winning money, while Gacha rewards hold no value beyond the game.

In this study, the term addiction is used in a behavioral sense rather than as a clinical diagnosis. Specifically, we define it as a compulsive engagement with Gacha mechanics that manifests in excessive play time, overspending, or a persistent inability to disengage despite negative consequences. This framing is consistent with prior work that links gambling-like systems, lotteries, and loot boxes to problematic play behaviors [8,9,20]. While not equated with clinical gambling disorder, such behaviors raise important concerns for ethical game design and regulation.

Several theories have been associated with gambling and addiction, especially in the context of the Gacha system or Gacha games. For instance, according to exposure theory [21], the availability of gambling can be linked to addiction. As live service games use simulated gambling as a monetization strategy, it normalizes the act of gambling without spending money and affects players’ perception of winning and gambling [22]. Fear of Missing Out (FoMO) is social anxiety caused by feeling left out of rewarding experiences [23], leading to a lack of sleep, emotional tension, and dependence on social media [24]. Gacha games often have multiple Gacha banners, including permanent and time-limited ones, which induces FoMO effect on players [25]. For instance, Diablo Immortal caused FoMO by offering time-limited items without clear information on availability [26].

A “completionist” is driven by reward motivation, hoarding mentality, and irrational fears [27]. Completing tasks gives players satisfaction and achievement rewards, which drives them to complete the game for bragging rights and perceived superiority. Hoard mentality is when people struggle to part with possessions, accumulating items regardless of their worth [28,29]. Meanwhile, the irrational fears stemming from the FoMO often drive gamers to pursue completionism, striving for total completeness and symmetry before ending their playing session [27]. In the context of the Gacha game, players were driven to collect items rather than using them [30], upgrading [18,31], and completing the total collections [32], which can be very costly to maintain.

Finally, Gacha also presents a unique appeal according to the Prospect theory [33,34] and Discounting theory [35]. As Prospect theory involves subjective evaluation of people when evaluating risks, Gacha players often keep buying to get rare items at reasonable cost [2]. The time-limited debut of certain rare items of the Gacha game caused people to spend money now rather than later due to the opportunity cost described by the discounting theory. This condition can also be compounded with the completionist and FoMO mentality.

Our study employs two theoretical frameworks that are particularly suited to analyzing the addictive qualities of Gacha mechanics. Game Refinement Theory (GRT) is a mathematical framework that models the balance between challenge and uncertainty in gameplay, typically expressed through formulas capturing game progress, success probability, and player engagement dynamics. It has been applied across board games, sports, and digital games to quantify how uncertainty drives excitement and sustained engagement.

Complementing this, the Motion in Mind (MiM) framework conceptualizes player cognition as a dynamic process where decision-making is continuously shaped by reward anticipation and feedback. Originating from behavioral psychology and refined through computational modeling, MiM provides a lens for understanding how repeated probabilistic rewards—such as those in Gacha systems—stimulate cognitive effort and risk-reward evaluation, potentially fostering addictive play patterns.

By combining these two frameworks, the paper bridge structural measures of gameplay uncertainty with cognitive-behavioral insights, thereby offering a comprehensive analytic basis for examining the addictive potential of Gacha systems. The primary goal of this study is to identify and quantify the threshold at which engaging Gacha mechanics shift into gambling-like experiences. Specifically, the study aims to

• Examine how reward frequency influences game attractiveness and player retention in Gacha systems.
• Investigate the role of the ‘pity system’ in shaping player behavior and its contribution to addiction mechanisms.
• Compare Genshin Impact’s Gacha design with other popular titles to evaluate the ethical implications of different pity systems.

Meanwhile, the following research hypotheses were created:

H1: 

A higher reward frequency (lower number of attempts) correlates with increased attractiveness and stronger player engagement.

H2: 

The pity system significantly alters the Game Refinement (GR) and Addictive (AD) measures, creating conditions closer to gambling thresholds.

H3: 

Variations in pity counter thresholds across games are systematically related to probability design and price per attempt.

2. Research Background

2.1. Background of Gacha in Genshin Impact

According to a report by Sensor Tower’s latest data, “Genshin Impact” is one of the most successful mobile games ever, having earned more than 4 billion USD by 2023 [15]. The game was developed by HoYoverse [36], a Chinese video game development company, and was released in September 2020. “Genshin Impact” is a free-to-play open-world action role-playing game that can be played on multiple platforms, including mobile devices, PCs, and gaming consoles. The game’s success can be attributed to its immersive gameplay, stunning visuals, and a storyline that keeps players engaged.

Items in Genshin Impact are categorized by rarity, ranging from 1-star to 5-star, with 5-star being the rarest. Characters and weapons are obtainable through the Gacha system, where players will use in-game currency to roll and see which items they receive. The currency used to play the Gacha is called gems, and it is obtainable by playing the game or purchasing it from the store. Most stronger characters and weapons are usually 5-star rarity and are only obtainable through the Gacha system. Hence, collecting gems is vital in increasing the combat strength of the players and helping them progress further in the game. The Gacha has been very lucrative to the developers, with many crediting the Gacha as the reason behind Genshin Impact’s success [37].

Genshin Impact follows the live service model, where update patches are released every six weeks [16]. These patches usually contain new characters, weapons, events, exploration areas, and story progression. As the game follows the F2P model, monetization is focused on the micro-transaction of various items, such as gems for the Gacha, character or weapon enhancement materials, and skins. There are also subscriptions to a daily pass for gems and a battle pass, which rewards players with items based on their achievements in the game.

The Gacha system in Genshin Impact is called “Wish,” it involves the player spending 160 gems to gamble to obtain a rare character or weapon with rarity ranging from 3-star to 5-star. The higher the number of stars, the more powerful the character or the weapon. 5-star characters and weapons are only obtainable through the Gacha, and the odds of obtaining one 5-star character are infinitesimally small at 0.6% while 5-star weapons are at 0.7% [38,39].

Genshin Impact has three different Gacha types: Character Event Wish, Weapon Event Wish, and Permanent Wish. Players use the terminology “banner” to refer to different Gacha. Two banners are time-limited, whereas the featured item in the Gacha is only available for three weeks. The permanent wish is the least popular Gacha banner, as the contents within this banner will always be available, making it less of a priority for players.

To participate in the Gacha, players must use gems that can be obtained by playing the game daily or during events. However, the rate at which gems are earned is slow, so players must collect and save them to play the Gacha. Since 5-star characters and weapons are often only available for a limited time, it can be difficult for players to acquire the necessary gems quickly. Consequently, some players purchase gems directly from the in-game store using real money. Buying the most expensive bundle (USD 99.99) is the most worthwhile in terms of money spent per gem (USD 0.012 per gem vs USD 0.016 per gem in the cheapest bundle). Each attempt at the Gacha can be estimated to cost about USD 2 as it takes 160 gems for one go.

On average, we expect it would take about 166.7 attempts to obtain one 5-star character as the odds of receiving one is 0.6%. Hence, players must spend about USD 333 to obtain just one 5-star character. However, it could be possible that a player would be extremely unlucky and not obtain any 5-star characters even after spending all that money. Therefore, Granblue Fantasy introduced the “pity system” in 2016 to guarantee the reward if the player is exceptionally unlucky [2]. The pity system immensely helped create a ceiling price for the Gacha and has been quickly adopted by most Gacha games today, with the specific parameters of the system being tweaked slightly for each game.

The pity system in Genshin Impact is designed so players will always obtain a 5-star item if they have not received one until the previously set cut-off point. For example, the character banners have their pity counter set at 90, where players will always obtain a 5-star item if they have yet to obtain one after 89 attempts at the Gacha. On the other hand, weapons have a pity counter slightly lower at 80. In the worst-case scenario, the pity system helped lower the price of obtaining a 5-star character from the previously mentioned 333 USD to only 180 USD.

To effectively control their expenses and determine their current pity status in a Gacha game, players must keep track of their previous Gacha attempts. Although the game provides a Gacha history, it only displays the past six months’ history. Since Genshin Impact was launched in September 2020, many records for earlier Gacha attempts are no longer accessible. Therefore, many players use external apps to record their Gacha spending and outcomes.

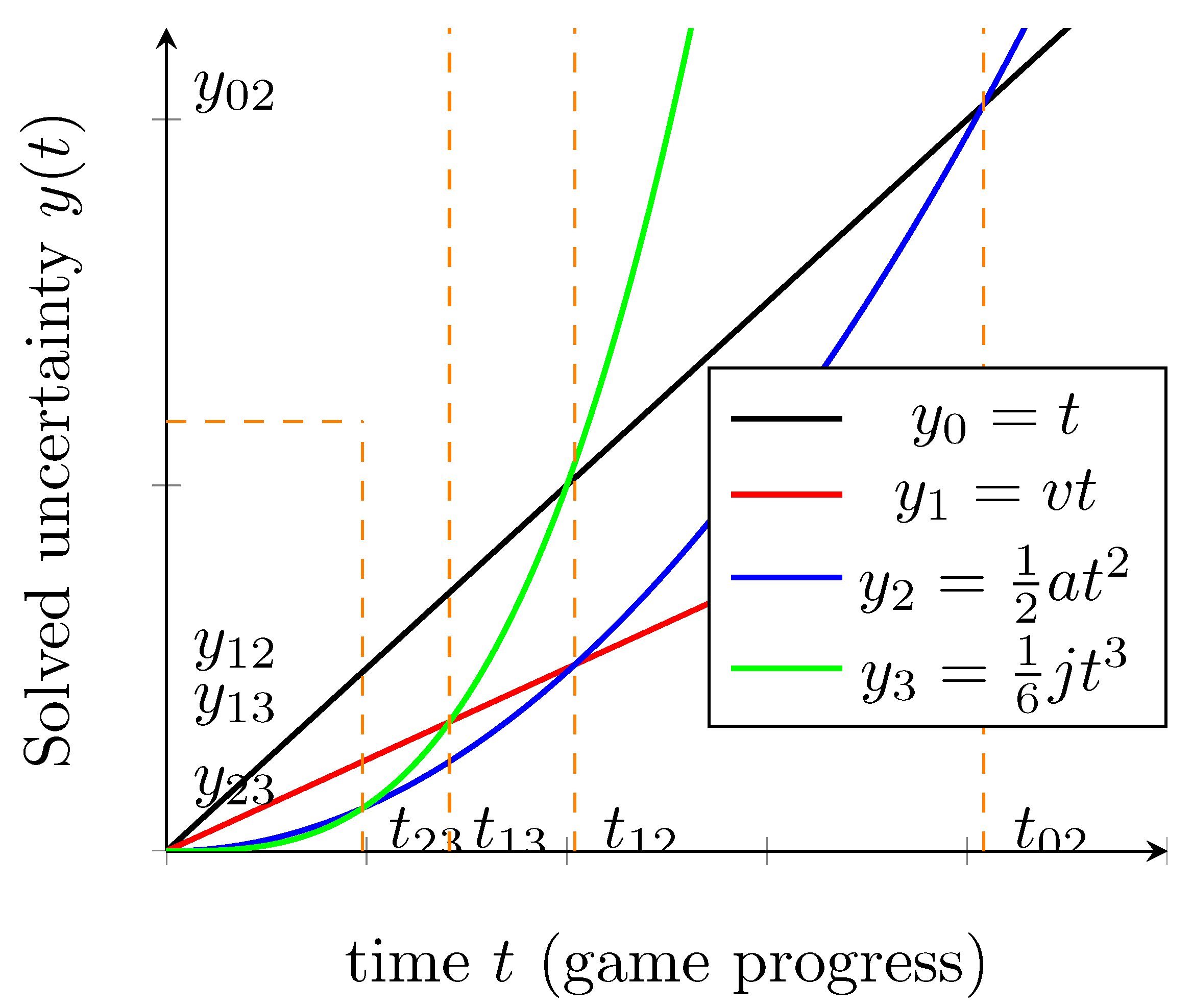
2.2. Motion in Mind

Game refinement (GR) theory is a theory proposed by Iida et al. [40], and it focuses on the sophistication and the uncertainty of the outcome of a game, which in turn increases the attractiveness of a game. This theory is not used to calculate winning strategies but to see the quality of the game and the amount of entertainment it can provide.

GR theory proposes the $GR$ measure, a metric derived from the game progress model, to identify the deterministic and stochastic aspects of the game. Based on previous works on the application of game refinement theory on various games, it was found that an ideal game has a $GR$ value within the range of $GR\in [0.07,0.08]$, which is dubbed the “comfortable” zone. The “comfortable” zone was identified based on shared game patterns that were enjoyable and attractive to players of both beginner and advanced skill levels [41].

We adopt Game Refinement (GR) Theory and Reinforcement Theory as the primary analytical frameworks for this study due to their suitability in capturing both the structural sophistication of games and the psychological reinforcement mechanisms underpinning player engagement.

GR Theory has been successfully applied in prior research to board games, sports, and digital environments to evaluate entertainment quality by quantifying uncertainty and sophistication in gameplay progression [40]. More recently, Gao et al. demonstrated that GR metrics can identify addictive tendencies in competitive and stochastic games, highlighting the overlap between entertainment and potential compulsion [42,43]. This makes GR particularly relevant for analyzing Gacha systems, where unpredictability and reward timing are central to player engagement.

Reinforcement Theory, especially the variable-ratio reinforcement schedule first established by Skinner [44], is well-recognized in behavioral psychology as the mechanism underlying gambling and lottery addiction. The unpredictable reward pattern in Gacha closely mirrors this reinforcement schedule, sustaining persistent player engagement even in the face of frequent losses.

By combining these two frameworks, we capture both sides of the phenomenon:

• The quantitative structure of Gacha systems (via GR and Motion-in-Mind metrics such as velocity, acceleration, and jerk).
• The psychological reinforcement mechanisms (via variable-ratio reinforcement) that explain why players continue engaging despite uncertain outcomes.

The core tenets of Game Refinement Theory (GRT) rest on the assumption that the enjoyment of games derives from a balance between skill and uncertainty. GRT models this through mathematical measures that capture the pace of progress toward a goal and the level of unpredictability embedded in the system. Games are considered most engaging when they provide a moderate level of uncertainty—neither fully predictable nor entirely random—thus maintaining tension and excitement throughout play. This balance explains why games with either too much determinism (no challenge) or too much randomness (no agency) tend to lose entertainment value.

In contrast, the core tenets of the Motion in Mind (MiM) framework emphasize the cognitive and psychological processes of the player as they engage with uncertain reward structures. MiM posits that the mind experiences gameplay as a series of dynamic changes—akin to physical motion—characterized by measures such as velocity (rate of reward acquisition), acceleration (changes in reward pacing), and jerk (sudden shifts in outcome). These variables are theorized to map onto the psychological experience of anticipation, surprise, and compulsion. The framework suggests that when acceleration and jerk intensify without sufficient player control, the gameplay experience moves closer to compulsive, addiction-like behavior.

Together, these frameworks establish that both the structural design of games (captured by GRT) and the cognitive dynamics of player experience (captured by MiM) are essential to understanding how Gacha mechanics can cross the threshold from entertainment to addiction. With this rationale established, we now present the specific formulas and metrics derived from these theories that enable the quantitative evaluation of Gacha mechanics.

The formula for measuring $GR$ differs depending on the type of the game being analyzed. In the domain of board games, the branching factor and depth of the game are used to denote the average number of possible moves and game length, expressed as B and D, respectively. In score-based games like soccer, the total goals (G) and the total attempts at goals (T) are used to evaluate $GR$. Equation (1) shows the formula for assessing $GR$.

$$GR={\displaystyle \frac{\sqrt{B}}{D}}={\displaystyle \frac{\sqrt{2G}}{T}}=\sqrt{a}$$

(1)

There may be instances where two teams have the same $GR$ value but feel entirely different while attempting to score. This can be explained by the change in mind’s acceleration throughout the game, denoted using jerk j. Jerk represents the change in informational acceleration (the magnitude of thrills, the tendency of obtaining attractiveness, and related to game addiction), which is linked to an addictive-like event due to the tendency of motivation retention thus, denoted as $AD$ value [43]. The “comfortable” zone for $AD$ is within the range of $AD\in [0.045,0.06]$. The $AD$ value is evaluated differently depending on the type of the game. Equation (2) shows the formula to assess $AD$.

$$AD={\displaystyle \frac{\sqrt[3]{3B}}{D}}={\displaystyle \frac{\sqrt[3]{6G}}{T}}=\sqrt[3]{j}$$

(2)

According to the game progress model, we can express the rate of solving uncertainty as velocity v while the magnitude of challenge or resistance the player faces during the game as mass m. In the current context, v is generally the rate of solving uncertainty, whereas m implies the difficulty of solving such uncertainty ($m=1-v$) [45]. Velocity can also be expressed as a scoring-based game’s winning rate or scoring rate. Equation (3) shows the formula for evaluating velocity v for both board and scoring-based games.

$$v={\displaystyle \frac{B}{2D}}={\displaystyle \frac{G}{T}}=1-m$$

(3)

Reinforcement theory is a psychological principle proposed by [44], suggesting that action is shaped by its consequence, and the behaviors can be shaped through reinforcement, punishment, and extinction [46]. There are four notable types of reinforcement schedules: continuous, partial, fixed-ratio, and variable-ratio reinforcement. For this research, we will only focus on the variable-ratio reinforcement schedule. The variable-ratio schedule perfectly explains lottery, gambling, and Gacha games, where reinforcement (reward) is given after an unpredictable or random number of responses. The variable-ratio reinforcement schedule helps maintain player interest as the regular small wins help to disguise the losses suffered previously [47], leading to addiction.

In variable-ratio schedules, the parameter N shows the average reward frequency, where $1<N\in \mathbb{R}$. In the context of a game, winning the game corresponds to obtaining a reward [48]. As such, N can be expressed as the inverse of the winning rate v. In the context of Gacha games, we can assume that a player “wins” when they successfully obtain the rare item from the Gacha. For example, obtaining a 5-star character from Genshin Impact can be assumed as a “win,” where the reward frequency $N=90$ in the worst-case scenario due to the pity system.

Although there is a limit to how much G-force humans can physically feel, our minds might experience a different type of gravity when playing games. This “gravity in mind” or “gravity of play” is a subjective feeling of G-force caused by the acceleration of the game’s progress. We conjecture that this feeling can be approximated by the ratio of gravity of play over the gravity in mind, which can be approximated by the square root of the reward frequency (represented as $\sqrt{N}$).

The motions in mind can be expressed using velocity, acceleration, and jerk, where each metric shows the amount of solved uncertainty throughout the game’s progress. We show, in Figure 1, the trend and intersections of two lines and two curves depicting the distance $y_0$, velocity $y_1$, acceleration $y_2$ and jerk $y_3$ in our mind throughout the progress of a game. Acceleration and jerk are given as in Equation (4) and Equation (5), respectively.

$$y_2={\displaystyle \frac{1}{2}}{a}_0{t}^2\mathrm{with}{a}_0=G{R}^2$$

(4)

$$y_3={\displaystyle \frac{1}{6}}j{t}^3\mathrm{with}j=A{D}^3$$

(5)

Gao et al. [43] observed that competitive games are most entertaining and addictive when the levels of GR and AD are equal, which can be expressed as the intersection between lines $y_2$ and $y_3$ from Figure 1. The cross point between $y_2$ and $y_3$ is given by $t_{23}=3{\displaystyle \frac{a_0}{j}}$. A new gravity of play is produced by the jerk in mind ($y_3$ curve), and the certainty can expressed as Equation (6).

$$y_{23}\left(t_{23}\right)={\displaystyle \frac{9}{2}}{\varphi }^6\mathrm{where}\varphi ={\displaystyle \frac{GR}{AD}}$$

(6)

A new thing, characterized by its velocity, is created by a mixture of the gravity in mind ($y_2$ curve) and jerk in mind ($y_3$ curve), producing the gravity of play.

$$y=vt\mathrm{with}v={\displaystyle \frac{y_{23}}{t_{23}}}$$

(7)

$$N=v^{-1}={\displaystyle \frac{t_{23}}{y_{23}}}={\displaystyle \frac{2}{9}}{\displaystyle \frac{t_{23}}{{\varphi }^6}}={\displaystyle \frac{2}{3}}{\displaystyle \frac{G{R}^{-1}}{{\varphi }^3}}$$

(8)

Assuming $GR={\displaystyle \frac{1}{12}}$, we obtain Equation (9). Let $\psi$ be the magnitude of gravity, the ratio of gravity of play over gravity in mind, given by Equation (10). Applying Equations (9) and (10), we obtain Equation (11). Finally, we can simplify it as Equation (12).

$$N\simeq {\left({\displaystyle \frac{2}{\varphi }}\right)}^3$$

(9)

$$\psi ={\displaystyle \frac{a}{a_0}}={\displaystyle \frac{2}{t_{13}}}{\displaystyle \frac{T}{2}}={\displaystyle \frac{T}{t_{13}}}$$

(10)

$${\psi }^2\simeq {\left({\displaystyle \frac{2}{\varphi }}\right)}^3\simeq N$$

(11)

$${\displaystyle \frac{a}{a_0}}\simeq \sqrt{N}$$

(12)

Conjecture 1 

(magnitude of gravity). The level of gravity of play, denoted as g, is connected to the frequency of obtaining rewards. Specifically, g is approximately equal to the square root of the reward frequency, denoted as $\sqrt{N}$. Humans can handle higher levels of gravity of play without experiencing any uncomfortable or nauseous sensations, and there is currently no known upper limit to this tolerance.

Players often play a game several times to gain confidence and certainty in their skills and the outcome. This ensures that the game is replayable and that the player will want to play it again. We conjecture that the number of attempts needed for a player to become confident in the game’s outcome can be estimated by dividing the total game length $y_{02}$ with the optimal game length $y_{23}$, as shown in Equation (13).

$${\displaystyle \frac{y_{02}}{y_{23}}}={\displaystyle \frac{4}{9a{\varphi }^6}}$$

(13)

By assuming $GR={\displaystyle \frac{1}{12}}$, we can further simplify Equation (13) to be expressed only in terms of $\varphi$ as shown in Equation (14). The value of $\varphi$ shows how many times a game should be repeated for the players to obtain confidence in the outcome. Stochastic games such as lottery and gambling have a lower $\varphi$, which would make the player repeat the game hundreds or thousands of times, while educational games should ensure that $1\le \varphi \le 2$ do not bore the players. Educational games often exclude stochastic elements, making repetitions boring due to their predictable outcome. Hence, balancing $GR$ and $AD$ is crucial in designing an ideal game.

$${\displaystyle \frac{y_{02}}{y_{23}}}\simeq {\displaystyle \frac{64}{{\varphi }^6}}={\left({\displaystyle \frac{2}{\varphi }}\right)}^6\approx N^2$$

(14)

Conjecture 2 

(outcome approximation). The number of play attempts required for obtaining confidence in the outcome of the game can be estimated using ${\left({\displaystyle \frac{2}{\varphi }}\right)}^6$, where it is approximately the square of the reward frequency, $N^2$.

In the context of Gacha mechanics, these two frameworks are applied directly to the structure and outcomes of player draws. Game Refinement Theory (GR) is operationalized by treating the acquisition of a rare character or item (e.g., a 5-star pull) as a ‘goal,’ while each Gacha attempt represents a ‘trial.’ The probability of success and the total number of required pulls (T) are used to compute GR values. A higher T (as seen in extended pity cycles) lowers the GR, signaling reduced entertainment value and a shift toward frustration and compulsion.

The Motion in Mind (MiM) framework extends this analysis by mapping gameplay dynamics onto cognitive ‘motion.’ Reward pacing in Gacha where outcomes can accelerate (e.g., sudden early pulls) or decelerate (long dry streaks before pity triggers), which is modeled through velocity, acceleration, and jerk. For instance, a sudden win early in the pity cycle represents high positive jerk, producing excitement, while long streaks without success amplify negative acceleration, fostering compulsion to continue pulling.

By combining these approaches, our analysis links the structural metrics of Gacha systems (via GR theory) with the psychological experience of reinforcement (via MiM). This dual application enables us to identify quantitative thresholds, such as when reward frequency exceeds ≈55 attempts that mark the transition from engaging play into gambling-like risk.

3. Data Collection and Analysis

Data collection for this research was done using Genshin Wish Export (available on https://github.com/biuuu/genshin-wish-export, 10 September 2025), an open-source application created by the player community to record and visualize Gacha history. The dataset covers 12 active players, spanning a collection period from October 2021 to March 2023. In total, we analyzed 7087 Gacha pulls, of which 4632 were Character Event Wishes, 1793 were Weapon Event Wishes, and 662 were Permanent Wishes (see

Table 1. Summary of Gacha wish history recorded from player.

Banner	Wish Events
Type	Character	Weapon	Permanent
Pulls Made	4632	1793	662
Pity counter	90	80	90
5-star	75 (1.6%)	35 (2.0%)	11 (1.7%)
4-star	608 (13.1%)	267 (14.9%)	81 (12.2%)
3-star	3949 (85.3%)	1491 (83.2%)	570 (86.1%)
Average N	61.5	51.11	57.1

). While this sample provides sufficient depth for exploratory analysis, it does not include detailed demographic information such as age, gender, or geographic region, which limits its representativeness. We therefore frame this dataset as a case study sample rather than a population-level dataset, using it to test theoretical frameworks rather than to generalize across all players.

The tool provides raw CSV files of Gacha attempts, including banner type, rarity of outcome, and timestamp. Preprocessing involved removing duplicate entries, aligning pity counters across banners, and validating totals against in-game history. For statistical analysis, we used Python 3.10 with NumPy and Pandas (https://www.python.org/downloads/release/python-3100/, 10 September 2025) for data handling, and SciPy for multiple linear regression and correlation analysis. Figures were generated using Matplotlib (https://matplotlib.org/), 10 September 2025, while descriptive tables were collected in Microsoft Excel.

This study focuses on the Character Event Wish banner for three reasons. First, it is the most popular banner, accounting for the majority of pulls in our dataset (65%). Second, it has the highest addictive potential because it features limited-time characters, introducing urgency and scarcity that strongly influence player behavior. Third, the pity system for Character Event Wishes is relatively standardized across events, making it a consistent basis for comparative analysis. By contrast, the Permanent and Weapon banners are less frequently used and have different pity rules, making them less central to understanding the mechanisms of compulsion.

While the dataset does not capture the full breadth of Genshin Impact’s global player base, it provides a sufficient and reliable sample for exploratory analysis of reward frequency patterns and the role of the pity system in shaping addictive tendencies. We explicitly note this as a limitation in scope, and we frame our analysis as theory-driven rather than population-representative.

Importantly, the analysis connects directly with our research goals. Specifically:

• To examine how reward frequency (H1) relates to game attractiveness and addictive potential, and
• To assess how the pity system (H2) shifts the balance between engaging gameplay and gambling-like mechanics.

By situating the dataset within these hypotheses, the analysis moves beyond pure numerical metrics and grounds the results in the central research question: how inherent design choices in Gacha systems contribute to player addiction.

The motion-in-mind measures were used to analyze the game’s progress to understand its entertainment value. In a Gacha game, “winning” could be generalized as the moment the player receives the rare item (reward). Hence, the reward frequency N for Genshin Impact would be the number of attempts required to obtain the 5-star item, which is the highest rarity in the game. In Genshin Impact, the probability of obtaining a 5-star character is 0.6%. In the worst-case scenario, players will obtain one 5-star character after 90 attempts at the Gacha. On average, it takes ≈61.50 attempts to obtain a 5-star character from Genshin Impact’s Gacha feature. The luckiest moment for the player in Table 1 was just five attempts, while the unluckiest needed 83 attempts (refer

Table 2. Motion-in-mind measures for average, luckiest, unluckiest, and worst-case based on Gacha history.

	G	T	v	m	GR	AD
Average	1	61.50	0.016	0.984	0.023	0.030
Luckiest	1	5.00	0.200	0.800	0.283	0.363
Unluckiest	1	83.00	0.012	0.988	0.017	0.022
Best-case	1	1	1	0	1.41	1.817
Worst-case	1	90.00	0.011	0.989	0.016	0.020

G: Goal; T: Total attempts; v: Velocity; m: Mass; $GR$: Game’s refinement measure; $AD$: Game’s addictive measure.

).

Table 2 shows that luck influences $GR$, $AD$, and v values, indicating the player’s success. The minimum velocity is $v=0.011$, and the maximum is $v=1$, indicating that the player never loses thanks to the implementation of the pity system. This could explain the reason behind the addiction to Gacha.

To ensure data quality, duplicate entries were removed, pity counter sequences were cross-verified against in-game logs, and totals were checked for consistency with banner histories. This process reduced the likelihood of recording errors introduced by the export tool.

Nonetheless, potential limitations and biases remain. First, the use of Genshin Wish Export, while widely adopted and validated by the player community, may still produce minor discrepancies compared to official logs. Second, the dataset represents a convenience sample of 12 players who voluntarily provided data, which introduces possible self-selection bias. These limitations constrain the generalizability of findings and are acknowledged in Section 4.4.

3.1. Practical Interpretation of the Results

While the quantitative metrics (GR, AD, velocity, mass) provide a scientific lens, their broader implications can be summarized for practitioners and policymakers as follows:

• Reward Frequency (N): On average, players in Genshin Impact required ≈61 attempts to obtain a 5-star character. This places the game beyond the hypothesized safe threshold ($N\approx 55$), indicating gambling-like risk.
• Addictive Measure (AD): Values fell below the ‘comfortable’ range (0.045–0.06), suggesting that the design encourages repeated attempts before satisfaction is achieved, heightening risk of compulsive play.
• Impact of the Pity System: While the pity counter guarantees eventual rewards, it also locks players into extended play cycles, effectively delaying gratification in a way consistent with variable-ratio reinforcement.

These findings suggest that game designers should carefully calibrate pity thresholds to avoid reward frequencies above ≈55, which we identify as the critical boundary between engaging play and gambling-like compulsion. For policy makers, our results demonstrate that monitoring pity system design and reward frequency is as important as regulating loot box odds disclosure. For mental health practitioners, the results underscore the psychological risks posed by extended reward cycles that mimic gambling reinforcement.

3.2. Theoretical Interpretation of the Results

In the motion-in-mind framework, game difficulty or challenge is represented by mass m and success rate by velocity v. In Gacha games, $m\le v$ only when obtaining a single 5-star character from one attempt ($m=0,v=1$) or two attempts ($m=v=0.5$). In all other cases, m is significantly larger than v, making winning in Gacha games an ordeal due to the low odds of obtaining a 5-star character.

The ideal zone for the $AD$ measure is where $AD\in [0.045,0.06]$, where the total number of attempts for the Gacha in the Genshin Impact within the range of $T\in [30,40]$ to be most attractive. Lowering the 5-star pity from 90 to 40 would achieve this. However, a complex decision could affect the game’s economy. For instance, pulling one Gacha is about $1.98 (It costs about $100 to purchase 8080 gems, and it takes 160 gems to pull one Gacha), which can add up to a whopping $178.22 in the worst-case scenario. Reducing the pity from 90 to 40 may cut the cost to $79.21, but it could make the 5-star characters feel less valuable to players.

Gao stated that people should feel exceedingly engaged and addicted when $GR=AD$ [42]. This condition is caused by the fact that the GR sophisticated zone can entertain the player, and the high AD value is associated with the feeling of surprise and unpredictability. The ratio between $GR$ and $AD$ can also be expressed as $\varphi$ (see (15)), which can be calculated using (1) and (2). In Gacha games, G represents the number of 5-star characters obtained, while T represents the total attempts required and can also be equated to the reward frequency N. Subsequently, $\varphi$ will always be a constant value when analyzing Gacha games without influencing the number of attempts T as the T cancels out during the division of $GR$ and $AD$. Hence, a Gacha game with $T=5$ value still has the same $\varphi$ as a game with $T=55$ or $T=200$. Hence, we conjectured that $\varphi =0.78$ is an ideal peak for Gacha games.

$$\varphi ={\displaystyle \frac{GR}{AD}}={\displaystyle \frac{\sqrt{2}}{\sqrt[3]{6}}}=0.78$$

(15)

When $\varphi \le 1$, games exhibit a higher degree of randomness and unpredictability, characterized by a larger $AD$ compared to the $GR$ measure. In this context, $\varphi$ represents a measure of predictability and control within the game mechanics. Gacha games and other games of chance are designed with a lower $\varphi$ to emphasize their inherent unpredictability and the element of surprise for players. This low $\varphi$ value reflects a system where random events significantly influence outcomes rather than player skill or strategy.

In Gacha games, players often spend real or virtual currency to receive a randomized reward, ranging from common items to rare and highly coveted ones. The unpredictability is a key factor in their appeal, as it creates a sense of excitement and anticipation with each purchase or pull. This randomness can lead to significant variance in player experience and satisfaction, as some players may receive valuable items quickly while others may not, driving repeated engagement (addiction) and spending in hopes of achieving better outcomes.

Furthermore, the low $\varphi$ in these games can lead to heightened emotional responses, both positive and negative. The thrill of unexpectedly receiving a rare item can be exhilarating, while the frustration of continuous common rewards can drive players to spend more in pursuit of desired items. This dynamic is designed to enhance player retention and monetization, leveraging the psychological impacts of chance and variability.

Figure 2 shows the trend of the reward frequency N (number of attempts) over all the Gacha attempts recorded in Table 1. The number of attempts required varies over each subsequent character obtained with a random up-and-down motion. Each point on the graph shows that it took N attempts to obtain that 5-star character. For example, we can observe from Figure 2 that the first 5-star is obtained after 83 attempts, while the next 5-star is obtained after 75 attempts. A lower N value signifies that the player was really lucky. This randomness creates a roller-coaster effect within players, making the game feel more engaging and entertaining to players. Perhaps the reasons for enjoying Gacha are similar to that of a roller coaster.

Previous research on roller coasters from 1976 to 2016 showed the evolution from focusing purely on thrill into focusing on an exciting ride experience [49]. The key to a roller coaster’s design is to ensure the highest safety under high speed by regulating its height, velocity, and acceleration, ensuring that riders can withstand it. The ever-changing acceleration and forces trigger our body’s fight or flight responses, releasing adrenaline or dopamine, causing people to feel excitement and enjoyment from a roller coaster ride [50,51].

The value of N can indicate whether players are lucky or unlucky in the game. A lower N suggests players are lucky, while a higher N suggests unlucky. The pattern from Figure 2 shows that the game purposely gives specific periods of luck (lucky phases) to entice the player and a cooling down period to allow the player to take a breather before the next burst of luck. Players are never always lucky and never constantly unlucky, creating a sense of unpredictability and anticipation when playing the Gacha. Giving players too many 5 stars would cause them to feel less valuable while giving too little would frustrate them. Hence, developers should thoroughly experiment with the pity and odds of Gacha to ensure maximum player engagement.

The pity mechanism of Gacha games will also increase player retention. Players who know they will soon obtain a 5-star item will log in and play the game daily to ensure they earn sufficient gems for attempting the Gacha. Live service games prioritize ensuring player retention by implementing various mechanics such as daily quests, daily login rewards, and other limited-time event rewards that are only obtainable if players check in to the game often.

Gacha is a purely stochastic game, as players do not need any skills. It is possible to generalize that “skill” in Gacha games would be the number of resources (money) the player is willing to spend. Players who spend significant money in the game are often known as “whale” players [52]. A whale player who spends thousands of dollars would obtain more 5 stars than other players as they can attempt the Gacha more often. However, the average number of attempts to obtain a 5-star rating does not vary much, as we know that Gacha games implement some mechanism to ensure players are never constantly lucky.

The frequency of lucky phases should be adjusted to increase players’ emotional attachment to rare items. It is crucial that these phases don’t happen too frequently or infrequently. By doing so, players will assign a greater personal value to these items, resulting in a more meaningful connection with the game.

4. Discussion

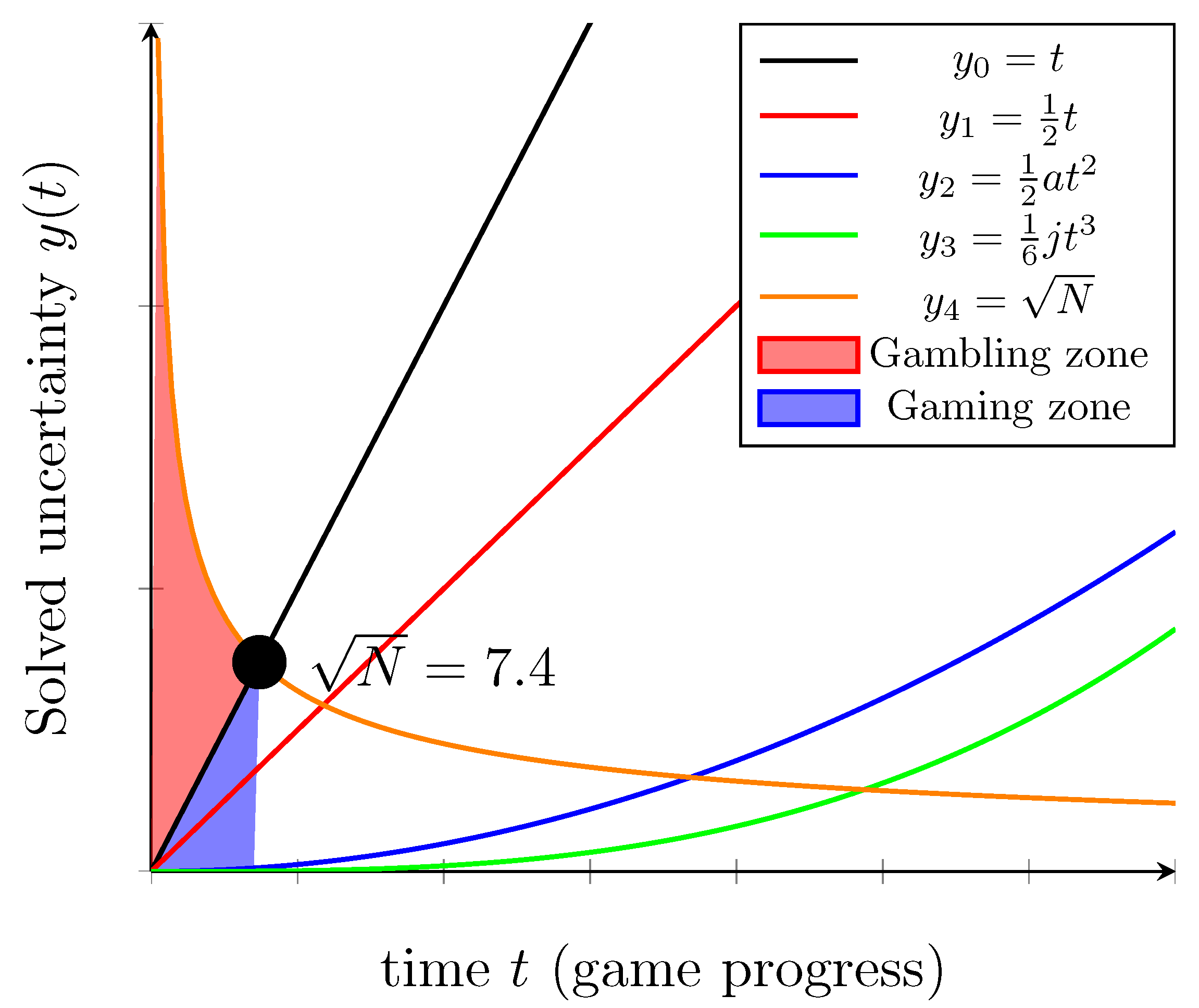
4.1. Border Between Gaming and Gambling

The rise of Gacha games in the mainstream has blurred the distinction between gambling and gaming, making it critical to establish a measurable boundary. Our approach integrates Game Refinement (GR) and Motion-in-Mind metrics to estimate where a game crosses from engaging uncertainty into gambling-like risk.

Based on Conjecture 1, we can estimate the gravity in mind using the root of reward frequency $\sqrt{N}$. Gambling and lotteries have high reward frequencies due to the complete stochastic nature of the games. Although the value of the reward is high, games of gambling in nature would have higher gravity in mind due to the scarcity of wins. Hence, we can hypothesize that stochastic games would have a higher gravity in mind, while games requiring player skills result in a lower gravity in mind.

By re-purposing Figure 1, we could plot the gravity in mind to examine the exact border between gambling and gaming. Motion in mind states that game velocity (success rate) can range between 0 and 1 due to the zero-sum assumption, as shown in Equation (3). Zero-sum games reflect the perception that another party’s losses necessarily offset one party’s gains, and both parties have all the relevant information to make decisions. However, the true odds in certain gambling and lotteries are often hidden or explained vaguely, making it difficult for players to make informed decisions. Hence, we assume that gambling-inspired games and lotteries are not zero-sum games, and thus, their velocity would not be between zero and one.

Line $y_0=t$ from Figure 1 could also be expressed as $y_0=vt$, where $v=1$. As this would be the limit for the velocity, the intersection between $y_0$ and gravity in mind $y_4$ as shown in Equation (16) would give us the border between gambling and gaming. Figure 3 shows the intersection of $y_0$ and gravity in mind $y_4$, depicting the border between gambling and gaming.

$$y_4=\sqrt{N}\mathrm{where}N={\displaystyle \frac{T}{t}}\mathrm{and}T={\displaystyle \frac{2}{a}}$$

(16)

The border between gambling and gaming as shown in Figure 3 can be expressed as $y_{04}$ which is the cross point between lines $y_0$ and $y_4$, expressed in Equation (17). Assuming that $GR=0.07$, we conjecture that a game is considered gambling when the gravity in mind $g\ge 7.4$ or reward frequency $N\ge 54.76$.

$$y_{04}=\sqrt[3]{{\displaystyle \frac{2}{a}}}$$

(17)

Conjecture 3. 

The border between gambling and gaming can be estimated using $\sqrt[3]{{\displaystyle \frac{2}{a}}}$. A game located within the $GR$ zone of 0.07 and 0.08 can be considered gambling if the gravity in mind $g\ge 7.4$ or reward frequency $N\ge 55$.

Conceptually, this boundary is important because it allows us to test H1 (reward frequency as a driver of engagement) and H2 (pity system’s role in shifting addictive thresholds). Rather than being absolute cut-offs, the thresholds we calculate should be understood as heuristic indicators of when randomness dominates over skill or player agency.

Based on our combined model, we conjecture that a game enters gambling territory (or critical threshold) as the point where reward frequency and gravity-in-mind values cross into ranges previously associated with gambling. Specifically, when $N\ge 55$ or $g\ge 7.4$, the Gacha system begins to operate less like a game of skill and more like a system of chance-driven compulsion. These values were obtained from empirical data (∼7000 pulls) and serve as heuristic markers derived from GR and Motion in Mind theory. These values correspond to conditions where unpredictability overwhelms skill, and player motivation risks becoming compulsive. For reference, Genshin Impact records an average $N=61.5$ and $g=7.8$, placing it above this threshold. Importantly, these thresholds are structural indicators, not direct measures of psychological change. They signal conditions under which addictive reinforcement is most likely, a proposition that requires validation in future behavioral studies.

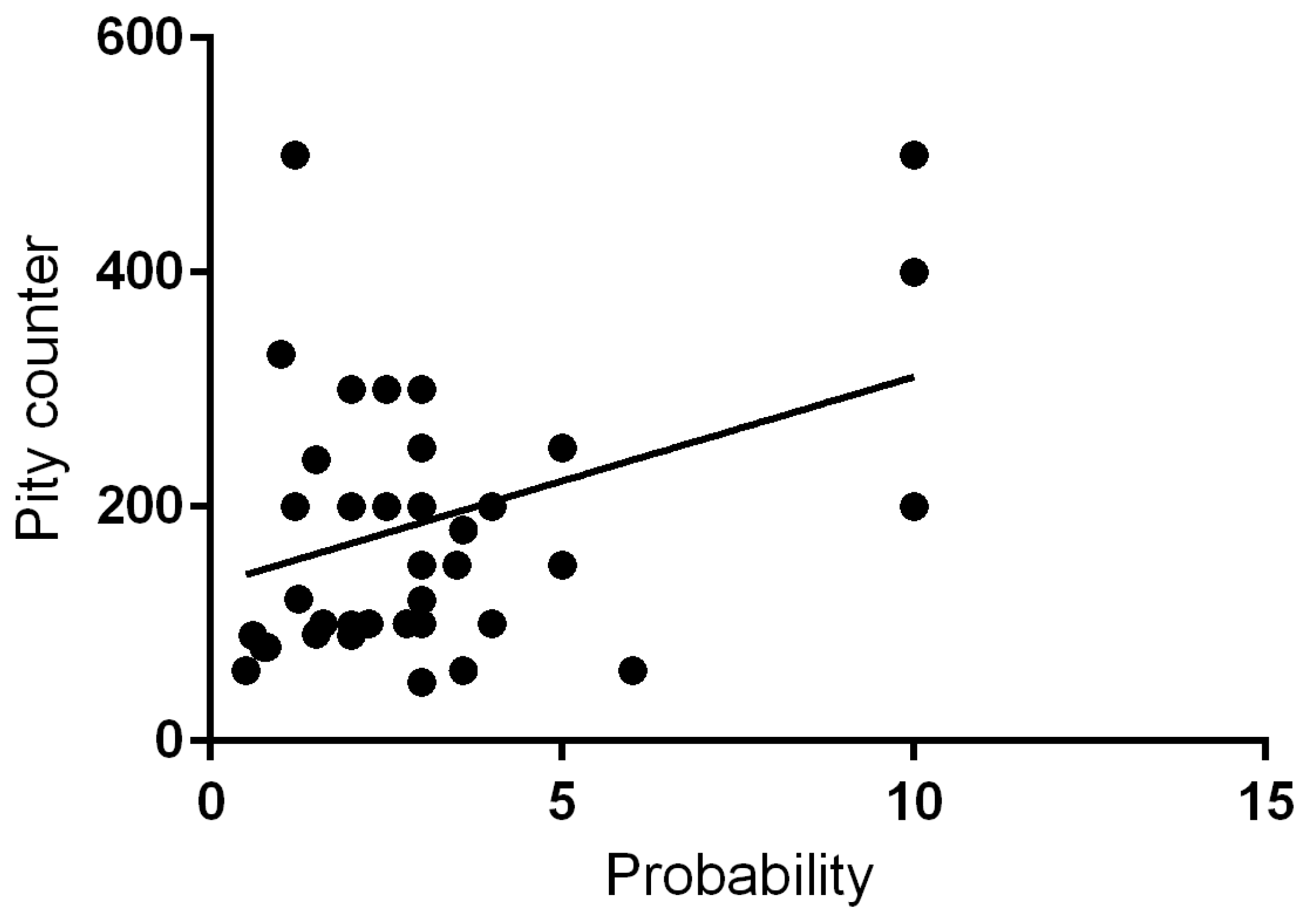
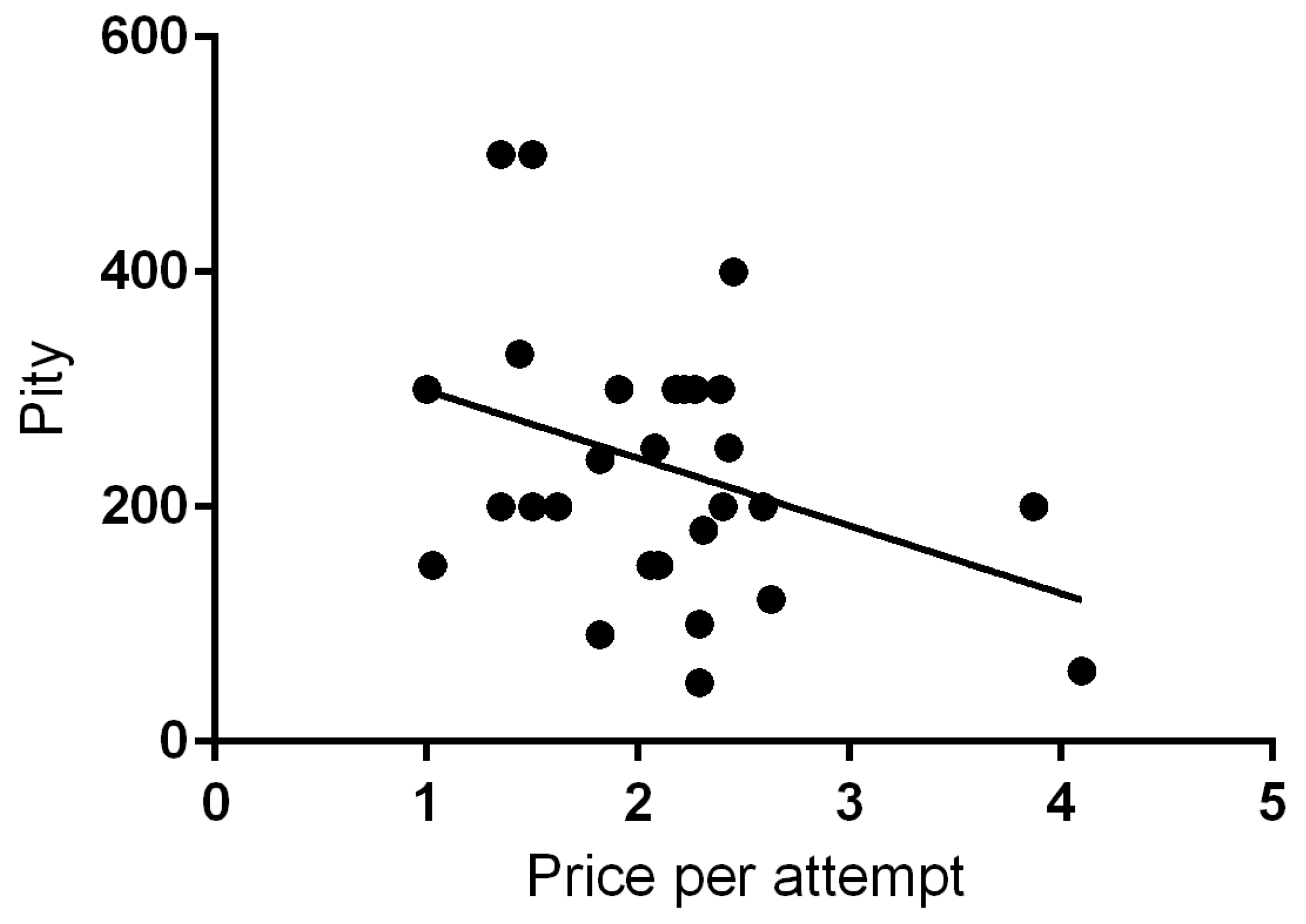
4.2. Comparing the Pity of Various Other Gacha Games

The multiple linear regression model shows that mass (m) and acceleration (a) are significant predictors of addictive measure (AD), which suggests a moderate relationship between structural game metrics and addictive potential. However, it should be noted that this result is exploratory, constrained by the limited dataset size (7000 pulls across 12 players). Weak correlations with other variables suggest that important behavioral and demographic factors—such as player spending patterns, session duration, and psychological traits—were not captured in the current dataset.

Thus, the results should be interpreted as illustrative rather than definitive. The findings support the view that GR and Motion-in-Mind metrics are meaningful indicators but must be combined with richer behavioral variables to achieve stronger explanatory capacity. This limitation is acknowledged in Section 4.4, where we recommend future studies with larger datasets and broader predictor sets to refine the analysis.

It should also be noted that given the small sample size, some of the classical assumptions of linear regression (e.g., normal distribution of residuals, homoscedasticity, absence of multicollinearity) may not be fully satisfied. Potential violations could bias coefficient estimates, inflate error terms, or weaken the interpretability of relationships. Therefore, the regression results should be treated as illustrative patterns rather than statistically robust predictions.

The probability of obtaining the rarest item from a Gacha is often relatively low, making it difficult to obtain it in a reasonable number of attempts. The pity system acts as a safety net for players by providing a guaranteed shot at obtaining them. Some games have a pity system that increases the probability of obtaining rare items after several unsuccessful attempts. For example, Genshin Impact pities 90, where players are guaranteed to receive the highest rarity item (5-star) if they have yet to obtain one. Several games achieve this by gradually increasing the probability of obtaining the item until it reaches 100%, while other games instantly increase the likelihood to 100%.

For example, Alchemy Stars has a base probability of 2% to obtain a 6-star item. After 50 unsuccessful attempts, the probability will gradually increase by 2.5%, achieving 100% odds on the 90th attempt [53]. On the other hand, the developers of Genshin Impact did not reveal how they increased the probabilities of the item. Still, many users speculated that the game has a hidden mechanism that boosts the probability after 70 unsuccessful attempts. This was dubbed as the soft-pity system by online forum users, with many documenting how most players obtain their 5-star item between 70 to 80 attempts.

Other games implement a pity called the “spark” system. This was first introduced by Granblue Fantasy back in 2016 [2], where players obtained an item called spark when they attempted the Gacha. Players can then exchange this accumulated spark to claim the item with the highest rarity directly from the Gacha. The pity counter for these games is denoted by the number of sparks needed to exchange for the item. In the case of Granblue Fantasy, players needed 300 sparks to exchange for the item from the shop. Hence, the pity for Granblue Fantasy is listed as 300.

Games that utilize the spark system often have their pity counter much higher than other games. This is because the probability of obtaining the item is usually much higher. However, the problem arises when multiple items of high rarity are available. Let us look at an example case where the probability of obtaining one 5-star item is 10%, and there is a total of 50 different 5-star items in that Gacha. A player who wants a specific item out of the 50 available will have to battle two odds: the 10% odds of obtaining the 5-star item and the 1/50 odds of receiving the item they wanted, making the probability insanely small at 1/500.

The spark system was introduced before the probability-altering pity system. Many players preferred the latter version of pity as it feels less overwhelming due to its lower pity counter. However, both systems are still widely used in popular Gacha games today. The table below shows several popular Gacha games categorized by their pity system.

Games that utilize the spark system often have their pity counter much higher than other games. This is because the probability of obtaining the item is usually much higher. However, the problem arises when multiple items of high rarity are available. Let us look at an example case where the probability of obtaining one 5-star item is 10%, and there is a total of 50 different 5-star items in that Gacha. A player who wants a specific item out of the 50 available must battle two odds: the 1/10 odds of obtaining the 5-star item and the 1/50 odds of receiving the item they wanted, making the probability tiny at 1/500.

The spark system was introduced before the probability-altering pity system, offering players a choice in their gaming experience. Many players found the latter version of pity more manageable, as it features a lower pity counter. However, both systems continue to be widely used in popular Gacha games today, giving players the power to choose the gaming experience that suits them best.

Table 3. Summary of probability, price per attempt, pity counter, and pity type of various Gacha games.

Game	Probability in %	Price in USD	Pity Counter
Alchemy Stars ★	2.00	2.86	90
Arknights ★	2.00	1.80	99
Bang Dream ★	3.00	2.27	50
Cookie Run: Kingdom (Epic) ★	2.80	1.92	100
Dragalia Lost ★	4.00	2.29	100
Dragalia Lost Gala ★	6.00	2.29	60
Fire Emblem Heroes ★	3.00	2.14	120
Genshin Impact ★	0.60	1.98	90
Girls Frontline: Neural Cloud ★	3.60	2.31	60
Honkai Impact 3rd ★	2.25	3.46	100
Honkai Star Rail ★	0.60	1.98	90
Tears of Themis ★	1.60	2.23	100
Tower of Fantasy ★	0.75	1.93	80
Wuthering Waves ★	0.80	1.98	80
Azur Lane †	1.20	1.35	200
Counter:Side †	3.50	1.03	150
Dangeki Bunko: Crossing Void †	1.50	1.82	91
Epic Seven †	1.25	2.63	121
Fate/Grand Order †	1.00	1.44	330
Girls Frontline: Neural Cloud †	3.60	2.31	180
Punishing Gray Raven †	0.50	4.10	60
Alice Fiction ‡	2.50	2.40	200
Azur Lane ‡	1.20	1.35	500
Bang Dream ‡	3.00	2.27	300
Blue Archive ‡	3.00	1.62	200
Dangeki Bunko: Crossing Void ‡	1.50	1.82	240
Dissidia Final Fantasy ‡	5.00	2.06	150
Dragon Ball Z: Dokkan Battle ‡	10.00	1.50	500
Dragon Ball Z: Dokkan Battle ‡ v2	10.00	1.50	200
Granblue Fantasy ‡	3.00	1.00	300
Guardian Tales ‡	2.00	1.91	300
Hatsune Miku Colorful Stage Free ‡	3.00	2.29	100
Hatsune Miku Colorful Stage Paid ‡	3.00	2.29	50
Idolmaster Cinderella Girls Starlight Stage ‡	3.00	2.22	300
Idolmaster Million Live ‡	3.00	2.22	300
Idolmaster Shiny Colors ‡	2.00	2.39	300
Love Live School Idol Festival 2 ‡	3.00	2.08	250
Love Live SIF Allstars ‡	5.00	2.43	250
Nier Reincarnation ‡	2.00	2.59	200
Nikke ‡	4.00	3.87	200
Pokemon Masters EX ‡	10.00	2.45	400
Princess Connect! Re:Dive ‡	2.50	2.18	300
SinoAlice ‡	3.00	2.10	150

^★: pity increasing probability; ^†: pity increasing probability for specific item; ^‡: spark system.

categorizes several popular Gacha games based on their pity system, the probability of obtaining the highest rarity item, and the price per attempt.

It can be observed that the pity counter is generally higher when the probability is high. Conversely, the pity counter is set lower when it is more difficult to obtain the character. This ensures that players have a safety net when playing the Gacha, where they will eventually win if they are incredibly unlucky. However, it also ensures that players do not win too often, as it will reduce the perceived value of the Gacha to players due to the over-saturation of high-rarity characters.

Gacha games that increase the probability of the items can guarantee the players obtain a specific or a random rare item. In Table 3, we can observe that the games that increase the probability of guaranteeing a particular item have a significantly higher pity than those that guarantee a random item. This strategic design of the pity system by developers is intriguing, as it ensures that players do not obtain the items too easily, thereby maintaining its subjective value towards the player.

We feel that the probability and price of the Gacha contribute to how the pity counter is set. We used multi-linear correlation analysis to find the probability correlation between the pity and the price.

Results of the multiple linear regression indicated that there was a weak collective significant effect between the probability, price per attempt, and pity counter, $\left(F\right(1,41)=5.75,$ $p=0.021,R^2=0.12,R_{adj}^2=0.1)$. The overall regression is right-tailed, $F(1,41)=5.75$, p-value = 0.021. Since p-value < $\alpha$ (0.05), we reject the $H_0$. Price was ignored as it is not a significant predictor for pity and was excluded from the model. The R-square ($R^2$) equals 0.123, meaning the probability explains 12.3% of the pity variance. The adjusted R-square equals 0.102. The coefficient of multiple correlation (R) equals 0.351. This means there is a weak correlation between the predicted and observed data.

We conjecture that the pity counter for a Gacha game can be predicted using the best-fit line equation, shown in Equation (18). Figure 4 shows the scatter plot of the pity against the probability of all Gacha games listed in Table 3. It can inferred that Gacha game developers decide on the pity counter based on the success rate of obtaining the highest rarity character. The Equation (18) considers games with all types of pity. It would be necessary to consider each kind of pity separately to give a more accurate equation for predicting the pity counter.

$$Pity=133.1+17.78\left(Probability\right)$$

(18)

We believe that the pity type, which increases the probability of a specific item, cannot be compared with those that guarantee a random rare item. The certainty guaranteed a particular item makes it comparable to the spark pity type. Hence, the pity type that increases the probability of a specific item will be analyzed together with the spark type. The multiple linear regression results indicated a weak collective non-significant effect between the probability, price per attempt, and pity counter for Gacha games with increasing probability.

The overall regression is right-tailed, $F(1,12)=1.11$, p-value = 0.312. Since p-value > $\alpha$ (0.05), we accept the $H_0$. Price was ignored as it is less significant as a predictor for pity when compared to the probability. The R-square ($R^2$) equals 0.085, meaning the probability explains 8.5% of the pity variance. The adjusted R-square equals 0.009. The coefficient of multiple correlation (R) equals 0.192. This means there is a weak correlation between the predicted and observed data. Figure 5 shows the scatter plot of the pity against the probability of Gacha games with increasing probability pity listed in Table 3. The pity counter for this pity type can be predicted using the equation in Equation (19).

$$Pity=95.7-3.7\left(Probability\right)$$

(19)

Next, we analyzed the remaining two pity types together. The multiple linear regression results indicated a weak collective non-significant effect between the probability, price per attempt, and pity counter for Gacha games. The overall regression is right-tailed, $F(1,27)=3.83$, p-value = 0.061. Since p-value > $\alpha$ (0.05), we accept the $H_0$. Probability was ignored as it is a less significant predictor for pity than the price per attempt. The R-square ($R^2$) equals 0.124, meaning the probability explains 12.4% of the pity variance. The adjusted $R^2=0.09$ and the coefficient of multiple correlation $R=0.352$. This means there is a weak correlation between the predicted and observed data. Figure 6 shows the scatter plot of the pity against the price per attempt of Gacha games with specific item guarantee and spark pity system pity listed in Table 3. The pity counter for this pity type can be predicted using Equation (20).

$$Pity=356.9-57.6\left(\mathrm{Price}\mathrm{per}\mathrm{attempt}\right)$$

(20)

When comparing the three equations obtained from the linear regression, we found that two showed the significance of the probability towards the pity counter. In contrast, one showed that the price per attempt was more significant than the probability. The finding suggests that Gacha games with increasing probability of obtaining a random item have its pity at a maximum of 95.7 based on Equation (5) as the probability will always be greater than 0. On the other hand, Gacha games with spark pity types have their maximum pity at 356.9 based on Equation (6) as the price could not be negative. The overall comparison between all Gacha games showed that the pity counter should be at least 133.1 based on Equation (4).

Interestingly, the price per attempt is more significant for Gacha games with spark-type pity systems, as the pity counter is generally higher. Hence, developers should pay more attention to the price per attempt of Gacha games when the pity counter is higher to ensure players do not feel too frustrated. The ideal pity counter for a Gacha game should be based on the success rate. The ideal pity counter for a general Gacha game can be estimated using $133.1+127.78\left(\mathrm{Probability}\right)$. When focusing only on Gacha games with increasing probability of obtaining a random rare item, the pity counter can be estimated using $95.7-3.7\left(\mathrm{Probability}\right)$. The pity counter for Gacha games with sparks systems then can be predicted using $356.9-57.6\left(\mathrm{Price}\mathrm{per}\mathrm{attempt}\right)$. Although the price per attempt is important in maintaining the game’s economy, it is not too significant in deciding the pity counter of the game with a lower pity counter.

To create a fair environment for players, developers of Gacha games should ensure that the price of each attempt is regulated following the pity system and the probability of obtaining the rare items. For a Gacha with a higher pity counter, say 300, the cost of each attempt should be cheaper than Genshin Impact (USD 2) if the probability is kept at 0.6%, as the total price for the worst-case scenario would be too expensive otherwise.

A Gacha game would be most exciting if the pity counter were between 30 and 40. However, the pity formula obtained from linear regression does not match, as the pity of most of the games analyzed appears to be much higher than expected. We believe the pity counter was intentionally higher to maximize player retention over entertainment. A higher pity would ensure that players would play and grind the game longer to collect sufficient resources or spend money to attempt the Gacha. Both options benefit developers as they help increase the game’s longevity. In 2022, Dragalia Lost shut down its servers, with many speculating that the game’s revenue was the main reason behind its decline [54]. Many users online felt that the Gacha from the game was too generous to players, reducing the need for players to spend money on the game. Hence, the pity formula we proposed can be considered ideal in the eyes of the developers, not the players.

4.3. Significance of the Number of Attempts $\eta$

Although the regression results lack strong statistical significance, the qualitative interpretation aligns well with the broader discussion of when gaming converges with gambling. The observed relationships suggest that addiction risk escalates when the mass of attempts grows disproportionately, and when acceleration reflects rapid intensification of player effort without corresponding reward. These dynamics reinforce the theoretical thresholds discussed earlier (e.g., $N\ge 55$, $g\ge 7.4$), where uncertainty overwhelms engagement and shifts into compulsion.

In other words, while the regression models are not predictive, they conceptually support the argument that Gacha mechanics, through their structural design, can create reinforcement loops that mirror gambling. This synthesis of quantitative indicators (GR thresholds) and qualitative patterns (regression relationships) strengthens the case for considering Gacha systems as potential risk factors for behavioral addiction

A game is engaging when the outcome is unpredictable in a fair game scenario. As the act of playing a game is equated to solving the uncertainty of its outcome, it would be necessary in some cases for the player to make several attempts at the game to receive sufficient confidence for the outcome. Hence, it is also essential to consider the number of attempts made and their significance throughout the game. Consider a notion of the potential reinforcement energy ($PRE$) as a measurement of objectivity of the outcome of the thing of a given event; the number of attempts is characterized by its velocity v (where $N=1/v$), is defined as a function of the number of trials $\eta$, which is determined by Equation (21).

$$PRE=\eta T/N^2$$

(21)

As conjectured in Conjecture 1, the magnitude of gravity of play gives us an extraordinary feeling in space with larger gravity compared to the magnitude we were previously comfortable with. Likewise, we may feel comfort by the standard gravity in mind, denoted as $a_0$, whereas extraordinary by the different (uncomfortable or larger) degree of gravity in mind, denoted as a. Then, the magnitude of extraordinary experience ($MEE$) can be defined as the ratio of extraordinary gravity in mind over the standard one, determined by Equation (22).

$$MEE={\displaystyle \frac{a}{a_0}}=\sqrt{N}$$

(22)

Figure 7 illustrates the $PRE$ and $MEE$, focusing on the cross points between the different lines for $PRE$ where $\eta$ is 1, N and $N/100$, respectively. The highlighted region shows the intersections for the $GR$ zone between the $[0.07,0.08]$ ranges.

The three cross points between $MEE$ and $PRE$ signify three different scenarios of games:

• When $\eta =N$, it signifies that the game has to be played N times in order to be confident of the outcome of the game. This is apparent in games of chance, where if the probability of winning the game is 1% ($v=0.01,N=100$), it would take 100 attempts on average to ensure that you win once. Gacha games implement this where players have to attempt the Gacha for N times until they reach the pity and obtain the rare item, where $N=61.5$ based on the data collected in Table 1. Hence, games with $N>45$ require at least N attempts to ensure players’ engagement toward the outcome of the game.
• $\eta =1$ shows the cross point between $PRE$ and $MEE$ happens when $N\approx 10$. Previous work showed how imperfect information games like Mahjong and Doudizhu have their reward frequencies at 8 and 9, respectively [42]. This cross point shows the scenario of imperfect information games that incorporate chance and skill, contrasting to games of pure chance, as shown in the previous cross point where $N>45$. Hence, players often time only need to play games with $N\approx 10$ once to be fully engaged and confident throughout the outcome of the game.
• The final cross point shows the scenario for perfect information games like Chess and Go where $N\approx 2$. These games are more skill-oriented and have less influence by chance compared to the previously listed games. However, to achieve this cross point, players would need to play the game $1/100$ times ($1\%$ of the game progress), which is harder to imagine compared to the previous two cases. We conjecture that grand-master-level players often can predict the outcome of a game based on the opening moves. As such, we feel that $\eta =1/100$ signifies the opening moves of a game in a perfect information skill-based game.

4.4. Limitations and Assumptions

This study is exploratory in nature, and several limitations must be acknowledged:

• Dataset Representativeness: The dataset, while substantial (7000 pulls across 12 players), does not cover the full Genshin Impact player population. It is used primarily to test the theoretical framework rather than to provide population-level statistics.
• Use of External Tools: Data was collected using the community-built Genshin Wish Export tool. Although widely adopted and validated by players, it is not an official data source. Minor discrepancies may exist between exported logs and in-game histories.
• Assumptions in Theoretical Frameworks: The application of Game Refinement (GR) Theory and Reinforcement Theory assumes that game addiction mechanisms can be approximated by structural uncertainty and reinforcement schedules. While these frameworks are established in game studies and psychology, they simplify complex player behaviors and may not capture all motivational factors.
• Assumptions of regression: With a limited dataset, some regression assumptions (e.g., residual normality, homoscedasticity, independence) may be violated. Such violations could affect coefficient stability and reduce the reliability of statistical significance. The analysis therefore remains exploratory, highlighting possible structural relationships rather than definitive predictive models.
• Threshold Values: The thresholds identified for distinguishing gaming from gambling (e.g., $N\ge 55$, $g\ge 7.4$) are derived from a specific dataset and theoretical modeling. They should be interpreted as heuristic indicators rather than universal constants across all Gacha games.
• Regression Analysis: The multiple linear regression results should be interpreted cautiously, as the dataset size limits statistical power. Future work should validate these results with larger, more diverse samples and potentially include variables such as player demographics, session length, and in-game spending.

Despite these limitations, the study provides a valuable foundation for understanding how reward frequency and pity systems shape addictive mechanics in Gacha games. Future work should expand datasets across regions, integrate demographic information, and refine theoretical thresholds with larger-scale empirical validation.

4.5. Ethical Design and Policy Implications

The results of this study highlight several ways in which Gacha systems can be designed and regulated more responsibly. One of the most important insights concerns reward frequency. Our analysis suggests that when the number of attempts required for a rare reward exceeds roughly 55, the experience begins to shift from engaging uncertainty into gambling-like risk. From a design perspective, developers should therefore calibrate pity systems to maintain reward cycles below this threshold, ensuring that players remain entertained without being driven into compulsion.

Transparency also emerges as a critical ethical consideration. Current industry practice often requires developers to disclose pull probabilities, yet this information alone does not reflect the actual player experience of pity systems and extended reward cycles. More meaningful disclosure would include effective reward frequencies and pity thresholds, allowing players to make informed decisions about their spending and play. Such measures would strengthen consumer trust while reducing the risk of misleading perceptions of rarity.

Policy makers likewise have a role to play in safeguarding players from excessive engagement. One possible avenue is the introduction of spending safeguards, such as caps on allowable purchases within a fixed time frame or the implementation of cool-down periods when players exceed certain pull counts without success. These measures, similar to those in responsible gambling, can help mitigate overspending driven by variable-ratio reinforcement schedules. Age-appropriate restrictions may also be necessary, as the resemblance between Gacha mechanics and gambling suggests that younger players are particularly vulnerable.

Finally, game interfaces themselves can be designed to encourage healthier patterns of engagement. Simple interventions such as real-time notifications, warnings after a large number of unsuccessful pulls, or reminders of spending can nudge players toward reflection and more responsible decision-making. By integrating such mechanisms, designers can create systems that remain profitable and engaging while respecting the well-being of their users.

An additional ethical concern relates to the socioeconomic consequences of whale spending behavior. In many Gacha systems, revenue models depend heavily on a small fraction of players who spend excessively to secure rare rewards. While this practice sustains profitability for developers, it poses significant risks, particularly when spending far exceeds reasonable discretionary income. The study’s findings, which highlight extended reinforcement cycles and high reward thresholds, suggest that whales are effectively subsidizing the free-to-play ecosystem at the cost of potential financial harm.

Addressing this imbalance requires the introduction of player protection mechanisms similar to those employed in gambling regulation. For instance, spending caps or affordability checks could be integrated into Gacha platforms to prevent players from making financially damaging purchases. Developers might also introduce voluntary tools such as spending dashboards, alerts, or self-imposed limits, allowing players greater control over their behavior. Policy makers, in turn, may consider mandating reporting requirements or independent oversight to ensure transparency in revenue concentration and its social implications.

By recognizing whale spending as both a business model and a potential source of socioeconomic harm, the study underscores the importance of balancing profitability with player welfare. Integrating protection mechanisms into game design not only aligns with ethical principles but also contributes to sustainable industry practices that do not disproportionately rely on a vulnerable minority of players.

To illustrate, our findings suggest that Genshin Impact’s current pity system (90 pulls for a guaranteed 5-star) results in an average reward frequency of 61 pulls, exceeding the proposed safe threshold of 55. An ethically informed adjustment could lower the hard pity to 70–75 pulls, thereby reducing extended losing streaks while still maintaining challenge and excitement.

Similarly, rather than only disclosing base probabilities, the game could present players with a transparent breakdown of effective reward cycles, making it clearer how pity affects outcomes over time. Finally, soft interventions such as reminders after long losing streaks or spending dashboards could provide nudges toward healthier engagement. These examples are not prescriptive design mandates but rather illustrative applications of how our threshold-based insights can inform more ethical design choices.

5. Conclusions

This paper analyzed the reward frequency in the Gacha mechanics of Genshin Impact, revealing that it took an average of 61.5 attempts to obtain a 5-star character. Based on these findings, the threshold between games of chance and gambling was identified at around $N=55$, facilitating a more apparent distinction between the two. We believe understanding this boundary can be instrumental in designing optimal experiences for Gacha players, significantly enhancing their engagement with their audience. By carefully calibrating the balance between reward frequency and emotional impact, game developers can create a more satisfying and compelling experience for all players.

An ideal Gacha game can be designed using the linear regression formula derived from comparing various popular Gacha games currently on the market. Our analysis suggests that the pity counter for a Gacha game with increasing probability should be around 90, while spark-type pity games should have their pity around 350. We also observed that the importance of price increases significantly when the pity counter is higher, indicating that customers place greater emphasis on cost as they approach a guaranteed reward or outcome.

Additionally, games were categorized based on their reward frequency by analyzing the intersection points between potential reinforcement energy $PRE$ and the magnitude of extraordinary experience $MEE$ concerning the number of attempts made $\eta$. The findings from this study have given some insights into why some games could have tendencies for addiction. The number of attempts for a game is an important concept to consider as games like Gacha are short duration but become addictive after $\eta$ number of attempts. The border between games and gambling would help create a more ethical environment for video games in the future and better rate curate games for people of all ages.

Beyond theoretical contributions, this study offers practical implications for different stakeholders:

• For game developers, our results provide quantitative thresholds (e.g., reward frequency $N\approx 55$) that can guide ethical design of pity systems, ensuring games remain engaging without tipping into gambling-like risk.
• For policymakers, the findings highlight that regulation should not only require odds disclosure but also consider pity system design, which plays a central role in sustaining addictive reinforcement cycles.
• For practitioners in psychology and education, the insights demonstrate how variable-ratio reinforcement in digital games parallels gambling mechanisms, underlining the need for preventive interventions and awareness campaigns.

These applications show how the study can inform responsible digital entertainment practices, bridging the gap between computational metrics and societal impact

Future works could focus on adjusting the probabilities of obtaining different rarity levels or modifying the pity counter thresholds to study how these alterations affect player behavior, emotional responses, and overall satisfaction. More games could also be analyzed to verify and solidify the boundary between gaming and gambling. Although demonstrated with Genshin Impact, the proposed framework is not restricted to this title. It can be applied to other Gacha-based games to evaluate whether their mechanics cross into gambling-like design.

Also, future studies should extend this analysis across multiple games (e.g., Fate/Grand Order, Fire Emblem Heroes, Honkai: Star Rail) to refine thresholds and test the framework’s universality. Some future work should validate these thresholds beyond Genshin through a multi-title telemetry study, pre-registered lab experiments manipulating reward frequency (N), and industry A/B tests of pity and protection features, complemented by longitudinal and cross-cultural cohorts to determine whether the proposed boundaries are universal or context-dependent.