An Effective and Robust Single Image Dehazing Method Using the Dark Channel Prior
Abstract
:1. Introduction
2. Related Work
2.1. Atmospheric Scattering Model
2.2. Analysis of DCP Limitations
3. Single Image Dehazing Method
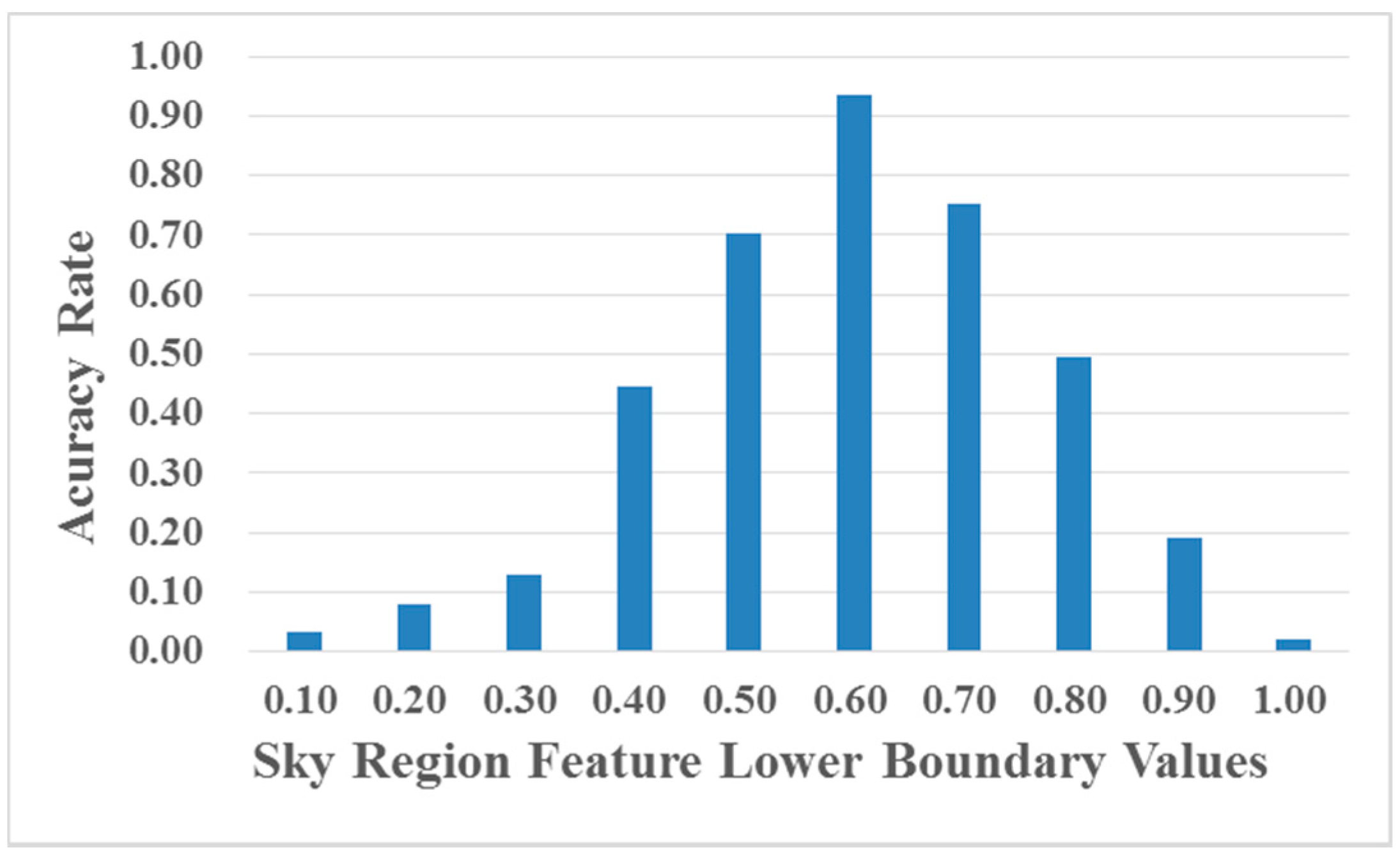
3.1. Sky Region Detection via Scene Segmentation
3.2. Improved Global Atmospheric Light Estimation Method
3.3. Multi-Scale Transmission Map Fusion Method
3.4. The Adaptive Sky Region Transmission Correction Method
3.5. The Transmission Map Refinement via GTV
4. Experimental Results
4.1. Transmission Estimation Comparison
4.2. Qualitative Comparison
4.3. Quantitative Comparison
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Narasimhan, S.G.; Nayar, S.K. Contrast restoration of weather degraded images. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 713–724. [Google Scholar] [CrossRef]
- Narasimhan, S.G.; Nayar, S.K. Vision and the atmosphere. Int. J. Comput. Vis. 2002, 48, 233–254. [Google Scholar] [CrossRef]
- Nayar, S.K.; Narasimhan, S.G. Chromatic framework for vision in bad weather. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head, SC, USA, 13–15 June 2000; pp. 598–605. [Google Scholar]
- Tan, R.T. Visibility in bad weather from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Fattal, R. Single image dehazing. ACM Trans Graph. 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Zhu, Q.; Mai, J.; Shao, L. A fast single image haze removal algorithm using color attenuation prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar] [PubMed]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 33, 2341–2353. [Google Scholar]
- Ju, M.Y.; Gu, Z.F.; Zhang, D.Y. Single image haze removal based on the improved atmospheric scattering model. Neurocomputing 2017. [Google Scholar] [CrossRef]
- Meng, G.; Wang, Y.; Duan, J.; Xiang, S. Efficient image dehazing with boundary constraint and contextual regularization. In Proceedings of the IEEE Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 617–624. [Google Scholar]
- Tarel, J.P.; Hautiere, N. Fast visibility restoration from a single color or gray level image. In Proceedings of the IEEE Conference on Computer Vision, Kyoto, Japan, 29–30 September 2009; pp. 2201–2208. [Google Scholar]
- Ju, M.; Zhang, D.; Wang, X. Single image dehazing via an improved atmospheric scattering model. Vis. Comput. 2016, 1–13. [Google Scholar] [CrossRef]
- Xiao, C.; Gan, J. Fast image dehazing using guided joint bilateral filter. Vis. Comput. 2012, 28, 713–721. [Google Scholar] [CrossRef]
- Xie, B.; Guo, F.; Cai, Z. Improved single image dehazing using dark channel prior and multi-scale retinex. In Proceedings of the IEEE Conference on Intelligent System Design and Engineering Application, Changsha, China, 13–14 October 2010; pp. 848–851. [Google Scholar]
- Yu, J.; Xiao, C.; Li, D. Physics-based fast single image fog removal. Acta Autom. Sin. 2010, 37, 1048–1052. [Google Scholar]
- Zhang, D.Y.; Ju, M.Y.; Wang, X.M. A fast image daze removal algorithm using dark channel prior. Chin. J. Electron. 2015, 43, 1437–1443. [Google Scholar]
- Ju, M.Y.; Zhang, D.Y.; Ji, Y.T. Image haze removal algorithm based on haze thickness estimation. Acta Autom. Sin. 2016, 42, 1367–1379. [Google Scholar]
- Choi, L.K.; You, J.; Bovik, A.C. Referenceless prediction of perceptual fog density and perceptual image defogging. IEEE Trans. Image Process. 2015, 24, 3888–3901. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.B.; He, N.; Zhang, L.L.; Lu, K. Single image dehazing with a physical model and dark channel prior. Neurocomputing 2015, 149, 718–728. [Google Scholar] [CrossRef]
- Yeh, C.H.; Kang, L.W.; Lee, M.S; Lin, C.Y. Haze effect removal from image via haze density estimation in optical model. Opt. Express 2013, 21, 27127–27141. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.F.; Ju, M.Y.; Zhang, D.Y. A single image dehazing method using average saturation prior. Math. Probl. Eng. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Li, B.; Wang, S.; Zheng, J.; Zheng, L. Single image haze removal using content-adaptive dark channel and post enhancement. IET Comput. Vis. 2014, 8, 131–140. [Google Scholar] [CrossRef]
- Galdran, A.; Vazquez-Corral, J.; Pardo, D.; Bertalmio, M. Fusion-based variational image dehazing. IEEE Signal Process. Lett. 2017, 24, 151–155. [Google Scholar] [CrossRef]
- Galdran, A.; Vazquez-Corral, J.; Pardo, D.; Bertalmío, M. A variational framework for single image dehazing. In Presented at the Proceedings of the European Conference on Computer Vision, Heidelberg, Germany, 20 March 2014; pp. 259–270. [Google Scholar]
- Yoon, I.; Jeong, S.; Jeong, J.; Seo, D.; Paik, J. Wavelength-Adaptive Dehazing Using Histogram Merging-Based Classification for UAV Images. Sensors 2015, 15, 6633–6651. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Riaz, I.; Piao, J.; Shin, H. Real-time single image dehazing using block-to-pixel interpolation and adaptive dark channel prior. IET Image Process. 2015, 9, 725–734. [Google Scholar] [CrossRef]
- He, K.M.; Sun, J.; Tang, X.O. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Long, J.; Tang, W.; Zhang, C. Single image dehazing in inhomogeneous atmosphere. Optik 2014, 125, 3868–3875. [Google Scholar] [CrossRef]
- Li, Y.; Miao, Q.; Song, J.; Quan, Y.; Li, W. Single image haze removal based on haze physical characteristics and adaptive sky region detection. Neurocomputing 2015, 182, 221–234. [Google Scholar] [CrossRef]
- Reynolds, D.A.; Quatieri, T.F.; Dunn, R.B. Speaker verification using adapted Gaussian mixture models. Digit. Signal Process. 2000, 10, 19–41. [Google Scholar] [CrossRef]
- Yu, F.; Qing, C.M.; Xu, X.M.; Cai, B.L. Image and video dehazing using view-based cluster segmentation. In Proceedings of the IEEE Conference on Visual Communications and Image Processing, Chengdu, China, 27–30 November 2016; pp. 1–4. [Google Scholar]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 532–550. [Google Scholar] [CrossRef] [PubMed]
- Sulami, M.; Glatzer, I.; Fattal, R.; Werman, M. Automatic recovery of the atmospheric light in hazy images. In Proceedings of the IEEE Conference on Computational Photography, Santa Clara, CA, USA, 2–4 May 2014; pp. 1–11. [Google Scholar]
- Shwartz, S.; Namer, E.; Schechner, Y.Y. Blind haze separation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 17–22 June 2006; pp. 1984–1991. [Google Scholar]
- Wang, S.; Li, B.; Zheng, J. Parameter-adaptive nighttime image enhancement with multi-scale decomposition. IET Comput. Vis. 2016, 10, 425–432. [Google Scholar] [CrossRef]
- Burt, P.J.; Adelson, E.H. The Laplacian pyramid as a compact image code. IEEE Trans. Commun. 1983, 31, 532–540. [Google Scholar] [CrossRef]
- Ancuti, C.O.; Ancuti, C. Single image dehazing by multi-scale fusion. IEEE Trans. Image Process. 2013, 22, 3271–3282. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Hautière, N.; Tarel, J.P.; Aubert, D.; Dumont, E. Blind contrast enhancement assessment by gradient ratioing at visible edges. Image Anal. Stereol. 2008, 27, 87–95. [Google Scholar] [CrossRef]














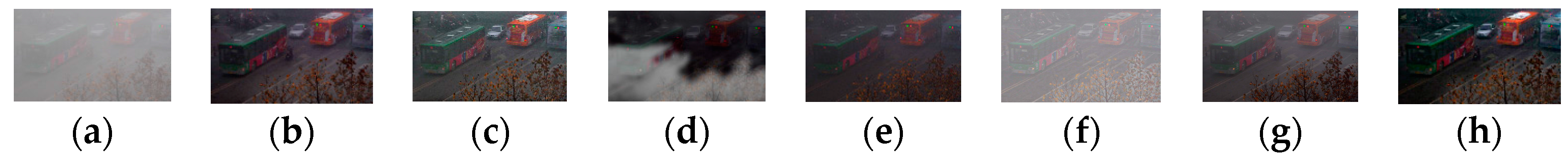


| SSIM | He et al.’s [7] | Meng et al.’s [9] | Ancuti et al.’s [36] | Yu et al.’s [25] | Tarel et al.’s [10] | Choi et al.’s [17] | Ours |
|---|---|---|---|---|---|---|---|
| Figure 14 | 0.7283 | 0.3502 | 0.4503 | 0.3109 | 0.3097 | 0.6123 | 0.7694 |
| Figure 15 | 0.5365 | 0.6203 | 0.5284 | 0.5686 | 0.7307 | 0.6993 | 0.3625 |
| Figure 16 | 0.7491 | 0.6986 | 0.3744 | 0.4900 | 0.6768 | 0.7963 | 0.7638 |
| Figure 17 | 0.8220 | 0.7778 | 0.2211 | 0.7296 | 0.8580 | 0.6413 | 0.8801 |
| He et al.’s [7] | Meng et al.’s [9] | Ancuti et al.’s [36] | Yu et al.’s [25] | Tarel et al.’s [10] | Choi et al.’s [17] | Ours | |
|---|---|---|---|---|---|---|---|
| Figure 14 | 1.6311 | 4.5341 | 3.3588 | 3.4462 | 3.8793 | 1.9113 | 3.9868 |
| Figure 15 | 3.7015 | 4.2383 | 2.9231 | 2.0669 | 2.8428 | 2.2243 | 5.2784 |
| Figure 16 | 1.7584 | 2.7013 | 1.9429 | 1.2296 | 1.8631 | 1.4586 | 2.8840 |
| Figure 17 | 1.5584 | 1.7493 | 2.2455 | 1.4611 | 1.5466 | 1.9429 | 1.6909 |
| e | He et al.’s [7] | Meng et al.’s [9] | Ancuti et al.’s [36] | Yu et al.’s [25] | Tarel et al.’s [10] | Choi et al.’s [17] | Ours |
|---|---|---|---|---|---|---|---|
| Figure 14 | 2.3328 | 1.8269 | 1.4599 | 2.4607 | 2.3789 | 2.4253 | 2.5318 |
| Figure 15 | 53.0796 | 50.0129 | 20.0974 | 35.5132 | 28.6893 | 20.3140 | 53.3612 |
| Figure 16 | 0.0454 | 0.3872 | 0.0046 | 0.1907 | 0.5697 | 0.0850 | 0.2417 |
| Figure 17 | 0.3377 | 0.4775 | 0.3751 | 0.6067 | 0.2177 | 0.3825 | 0.4171 |
| FADE | He et al.’s [7] | Meng et al.’s [9] | Ancuti et al.’s [36] | Yu et al.’s [25] | Tarel et al.’s [10] | Choi et al.’s [17] | Ours |
|---|---|---|---|---|---|---|---|
| Figure 14 | 0.3437 | 0.3589 | 0.4964 | 0.2763 | 0.3158 | 0.2651 | 0.2299 |
| Figure 15 | 0.7070 | 0.7728 | 1.2817 | 0.9385 | 1.7907 | 1.2396 | 0.3767 |
| Figure 16 | 0.3113 | 0.2887 | 0.4049 | 0.2802 | 0.4291 | 0.4792 | 0.2468 |
| Figure 17 | 0.2411 | 0.2190 | 0.2203 | 0.1861 | 0.4108 | 0.2584 | 0.2057 |
| Time Consumption | He et al.’s [7] | Meng et al.’s [9] | Ancuti et al.’s [36] | Yu et al.’s [25] | Tarel et al.’s [10] | Choi et al.’s [17] | Ours |
|---|---|---|---|---|---|---|---|
| Figure 14 | 1.36 | 4.02 | 2.23 | 1.29 | 7.60 | 18.50 | 0.88 |
| Figure 15 | 0.94 | 5.16 | 2.48 | 0.82 | 19.00 | 24.91 | 0.79 |
| Figure 16 | 0.84 | 2.18 | 1.69 | 0.69 | 1.55 | 7.13 | 0.81 |
| Figure 17 | 0.96 | 3.33 | 2.08 | 0.74 | 7.38 | 15.26 | 0.83 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.; Ju, M.; Gu, Z.; Wang, S. An Effective and Robust Single Image Dehazing Method Using the Dark Channel Prior. Information 2017, 8, 57. https://doi.org/10.3390/info8020057
Yuan X, Ju M, Gu Z, Wang S. An Effective and Robust Single Image Dehazing Method Using the Dark Channel Prior. Information. 2017; 8(2):57. https://doi.org/10.3390/info8020057
Chicago/Turabian StyleYuan, Xiaoyan, Mingye Ju, Zhenfei Gu, and Shuwang Wang. 2017. "An Effective and Robust Single Image Dehazing Method Using the Dark Channel Prior" Information 8, no. 2: 57. https://doi.org/10.3390/info8020057





