Circular Thermodynamics of Organisms and Sustainable Systems

Abstract

A circular thermodynamics of organisms and sustainable systems is presented based on dynamic closures in nested space-time domains that enable the system to approach the ideal of zero entropy production simultaneously at equilibrium and far from equilibrium conditions.

1. Introduction

The circular thermodynamics of organisms and sustainable systems has been developed in three successive editions of The Rainbow and the Worm, The Physics of Organisms [1] and elsewhere (especially [2,3]). The basic argument of this review article goes as follows.

(1)

A comparison of information processing in current supercomputers and the human brain reveals the enormous density and efficiency of reactions in the living system that most likely involves quantum coherence.

(2)

The organism as a whole captures, stores, and mobilizes energy in a perfectly coordinated and super-efficient way, while maintaining its organization (homeostasis); these key features require a special thermodynamic explanation that dovetails with quantum coherence.

(3)

Energy is mobilized predominantly in cycles manifesting as biological rhythms with cycling times ranging from split seconds to minutes, hours, days, and years that are nevertheless coupled together. Cycles confer both dynamic stability and autonomy to the system. They also enable the activities to be coupled together, so that energy yielding processes can transfer energy directly to those requiring energy. Thermodynamically, no net entropy is generated in the case of perfect cycles; hence, the system can maintain its organization.

(4)

The organism has a nested dynamical structure, with activities spanning a wide range of characteristic space-time scales. The nested space-time structure partitions the organism into a hierarchy of systems within systems defined by the extent of equilibration of thermal energies. Thus, energies thermalized or equilibrated within a smaller space-time will still be out of equilibrium in the larger system encompassing the first, and hence capable of doing work. It is that which enables the organism to simultaneously achieve the most efficient equilibrium and non-equilibrium energy transfer.

(5)

The organism’s nested dynamical structure also optimizes the kinetics of energy mobilization. For example, biochemical reactions depend strictly on local concentrations of reactants, which are very high, as their extent of equilibration is typically at nanometer dimensions.

(6)

The space-time differentiation of the living system is directly proportional to its energy storage capacity or energy residence time, which is also proportional to the material residence time; in ecosystem/sustainable system terms, these translate to biodiversity, biomass, or productivity.

(7)

In the ideal—approached most closely by the healthy mature organism and the healthy mature ecosystem—an overall internal conservation of energy and compensation of entropy (ΣΔS = 0) is achieved. In this state of balance, the system organization is maintained and dissipation minimized; i.e., the entropy exported to the environment also approaches zero, ΣΔS ≥ 0. Internal entropy compensation (and energy conservation) implies that there is free variation in microscopic states within the macroscopic system; i.e., the internal microscopic detailed balance at every point of classical steady state theory is violated.

(8)

The above considerations give rise to the prediction that a sustainable system maximizes cyclic, non-dissipative flows while minimizing dissipative flows, i.e., it tends towards minimum entropy production.

(9)

Some applications of the theory are presented to show how it disposes of major myths such as: sustainable systems mean no growth at all; a constant carrying capacity defines a plot of land; and the equation of energy with money.

2. The Computer versus the Brain

Scientists are attempting to put the human brain into a supercomputer. They propose to map all of the ~100 billion neurons in the human brain and their ~100 trillion connections (synapses) and then simulate it with the fastest supercomputer available.

There are fundamental reasons why the much touted European Human Brain Project and its U.S. counterpart, Brain Activity Map, will not achieve their goal. The precise connections between neurons in the brain vary from one individual to another, even between identical twins; memory is not stored in synapses, and above all, brains/minds do not work like a classical computer [4]; it could act more like a still theoretical quantum computer, though I have serious doubts as to whether a quantum computer can ever be practically implemented [5]. There is also a technical bottleneck most relevant to the thermodynamic argument presented here; the supercomputer cannot cope with the waste heat generated by the processing operations required to simulate the brain [6]. This is where the brain excels.

The human brain, about 1.2 L in volume, has an estimated memory of 3.5 × 10¹⁵ bytes, operates at a speed of 2.2 petaflops (10¹⁵ operations per second), and consumes 20 W in power. In comparison, the world’s fastest supercomputer in June 2011 was Fujitsu’s K computer the size of a small warehouse, has a memory of 30 × 10¹⁵ bytes, operates at a speed of 8.2 petaflops, and consumes 12.6 MW [7]. A year later, K computer was ousted as the world’s fastest computer by the American IBM Sequoia, a Blue Gene/Q supercomputer performing at 16.325 petaflops using 123% more Central Processing Unit (CPU) processors and consumes only 7.9 MW, 37% less than the K computer [8]. However, China’s Tianhe-2 (Milkyway-2) has now overtaken the U.S. supercomputer by performing twice as fast, at 30.7 petaflops [9], and the race is continuing apace.

The vast amount of power consumed by current computers generates a great deal of heat that has to be carried away by bulky cooling systems that consume yet more power. The human brain is a clear winner by far in terms of size and power consumption. The functional density (flops/L) in current computers is 10¹⁰ compared to 10¹⁴ in the brain; current computers carries out ~10⁷ operations per Joule of energy consumed, while the brain does 10¹⁴ operations for the same amount of energy [6].

The human brain is 2% of the body’s volume and consumes 20% of its total energy demand; but it is fantastically energy efficient. It can achieve 7 orders of magnitude more computing for each Joule of energy consumed, while also performing in parallel all the activities required for keeping the brain cells alive. That is one reason I have proposed that organisms are quantum coherent [1]. The other main reason is, in 1992, we discovered in my laboratory that all living organisms display dynamic liquid crystalline interference (rainbow) colors under the polarizing light microscope [10,11,12]. The fact that living moving organisms, with all their molecules churning round transforming energy could still display colors typical of liquid crystals is evidence that living organisms are coherent (organized) to a high degree, right down to the alignment and motions of the macromolecules—and associated living water [13] in their tissues and cells—and it is coherent energy that is being mobilized and transformed in organisms [1,14]. Specifically, organisms are powered by quantum molecular machines that transform and transfer energy at close to 100% efficiency, which is why the brain can do 10¹⁴ operations per second in processing information and, at a conservative guess, another 10¹¹ metabolic reactions per second to keep the cells alive. Such density of function cannot be achieved classically, and requires quantum coherence of a high order (close to zero energy dissipation). Consequently, it also calls for a thermodynamics that dovetails with quantum coherence, and that is what I shall present here.

3. Thermodynamics of Living Systems

The thermodynamics of living systems was formulated over a period of some 16 years, most fully detailed in successive editions of The Rainbow and the Worm, the Physics of Organisms [1]. I shall recapitulate the main results and bring this work up to date.

The first thing to take note is that organisms do not make their living by heat transfer. Instead, they are isothermal systems (Morowitz [15]) dependent on the direct transfer of molecular energy, by proteins and other macromolecules acting as “molecular energy machines” (more specifically, quantum molecular energy machines). For isothermal processes, the change in Gibbs free energy ΔG (thermodynamic potential at constant temperature and pressure) is,

ΔG = ΔH − TΔS

(1)

where ΔH is the change in enthalpy (heat content), T is the temperature in deg K. and ΔS the change in entropy.

Thermodynamic efficiency requires that ΔS approaches 0 (least dissipation) and ΔH = 0; or ΔG approaches 0 via entropy-enthalpy compensation, i.e., entropy and enthalpy changes cancelling each other out [1,16].

The organism as a whole keeps far away from thermodynamic equilibrium (in the classical sense), but how does it free itself from “all the entropy it cannot help producing while alive?” was the question that Schrödinger asked [17]). That is also my point of departure for the thermodynamics of living systems.

The pre-requisite for a system to keep away from thermodynamic equilibrium—the state of maximum entropy or death by another name—is to be capable of capturing energy and material from the environment to develop, grow and recreate itself from moment to moment during its life time, and also to reproduce and provide for future generations, all part and parcel of sustainability.

The organism has solved the problem of sustainability over billions of years of evolution. It has an obviously nested physical structure. Our body is enclosed and protected by a rather tough skin, but we can exchange energy and material with the outside, as we need to, we eat, breathe and excrete. Within the body, there are organs, tissues and cells, each with a certain degree of autonomy and closure. Within the cells, there are numerous intracellular compartments that operate more or less autonomously from the rest of the cell. And within each compartment, there are molecular complexes doing different things: transcribing genes, making proteins and extracting energy from our food, etc., all working within confines of nanometre dimensions (nanospaces). More importantly, the activities in all those compartments, from the microscopic to the macroscopic are perfectly orchestrated, which is why the organism looks like a dynamic liquid crystal display, as explained earlier.

It can be questioned whether physical closure is necessary, at least as far as the sustainable system is concerned; more important than physical closure is dynamic closure, which enables the organism to store as much energy and material as possible, and to use the energy and material most efficiently, i.e., with the least waste and dissipation.

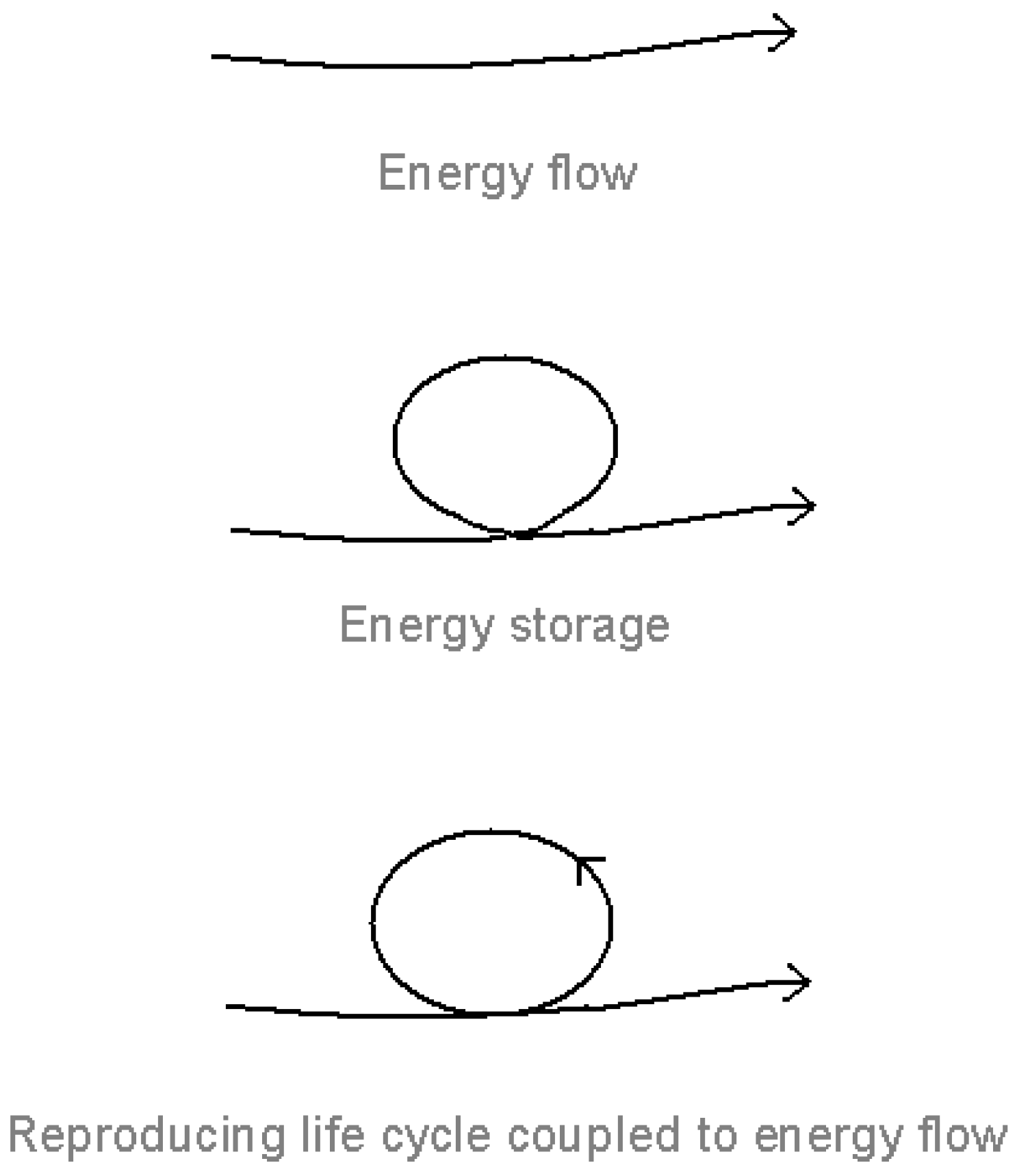
Figure 1. Energy flow, energy storage and the reproducing life-cycle [1].

Figure 1. Energy flow, energy storage and the reproducing life-cycle [1].

The key to understanding the thermodynamics of the living system is not so much energy flow (stressed by many commentators, for example, Prigogine [18], Morowitz [15], and Ulanowicz [19]) as energy capture and storage under energy flow (Figure 1). Energy flow is of no consequence unless the energy is trapped and stored within the system, where it is mobilized to give a self-maintaining, self-reproducing life cycle coupled to the energy flow. (By energy, I include material flow, which enables the energy to be stored and mobilized.)

My approach diverges significantly from the framework established by earlier applications of thermodynamics to ecology as described in detail in [3]. For example, stored energy, as I shall define it more precisely, is distinct from exergy as widely used by ecologists, and also from free energy as defined by chemists and physicists (Equation (1)). It is stored energy being mobilized in a non-classical steady state (as will be made clear) that characterizes living organisms and sustainable systems.

4. Cycles Make Sense

The perfect coordination (organization) of the organism depends on how the captured energy is mobilized within the organism. It is actually mobilized in cycles, or more precisely, quasi-limit cycles, which can be regarded as dynamic boxes; and they come in all sizes, from the very fast to the very slow, from the global to the most local.

Cycles provide the dynamic closure that’s absolutely necessary for life, much more so than physical closure.

Biologists have long puzzled over why biological activities are predominantly rhythmic or cyclic, and much effort has gone into identifying the center of control, and more recently to identifying master genes that control biological rhythms, to no avail.

The organism is full of cycles (as is the earth, for that matter), possibly because cycles make thermodynamic sense; Morowitz [15] has proven an important theorem that a flow of energy from a source to a sink in a system at steady state will lead to at least one cycle, so there is definitely a deeper reason why cycles tend to form under energy flow. (Intuitively, I suspect energy storage is important; it is like water forming eddies flowing through a pool, a consequence of the conservation of momentum.) Cycles mean returning repeatedly to the same states, and no entropy is generated in perfect cycles according to classical thermodynamics. In other words, the system as a whole remains organized and no waste heat is produced; free energy change is zero because the energy has not been degraded into thermal energy. Cycles give dynamic stability as well as autonomy to the organism; and this applies as well in ecosystems [19].

Cycles also enable the activities to be coupled, or linked together, so that those yielding energy can transfer the energy directly to those requiring energy, and the direction can be reversed when the need arises. This is implicit in Onsager’s reciprocity relationship [20], which shows how symmetrical coupling of processes (through forces and flows) can arise naturally in a system under energy flow at equilibrium or near equilibrium, as pointed out since the first edition of Rainbow Worm [1]. These symmetrical, reciprocal relationships are most important for sustaining the system. Our metabolism is organized precisely in that way: closing cycles and linking up, with pathways that readily reverses the direction of energy and material flows.

Figure 2 is a diagram representing the nested cycles that span all space-time scales, the totality of which make up the life cycle of the organism (see 2nd and 3rd editions of [1]). I proposed that the life cycle has a self-similar fractal structure (simply because natural processes are known to be predominantly fractal [21], and in my view, fractal mathematics is the only tractable way to describe complex organic space-time). Therefore, if you magnify each cycle, you will see smaller cycles within, looking much the same as the whole. Fractal dynamics are the hallmarks of natural processes and are especially fit for the organization of living systems, as we shall see.

Figure 2. The life cycle of the organism consists of a self-similar fractal structure of cycles turning within cycles [1].

Figure 2. The life cycle of the organism consists of a self-similar fractal structure of cycles turning within cycles [1].

The complex nested dynamical space-time structure of the organism is the secret of sustainability. It maximizes the efficiency and rapidity of energy mobilization, and the degree of space-time differentiation is directly correlated with the amount of energy stored.

5. Redefining the Second Law for Living Systems

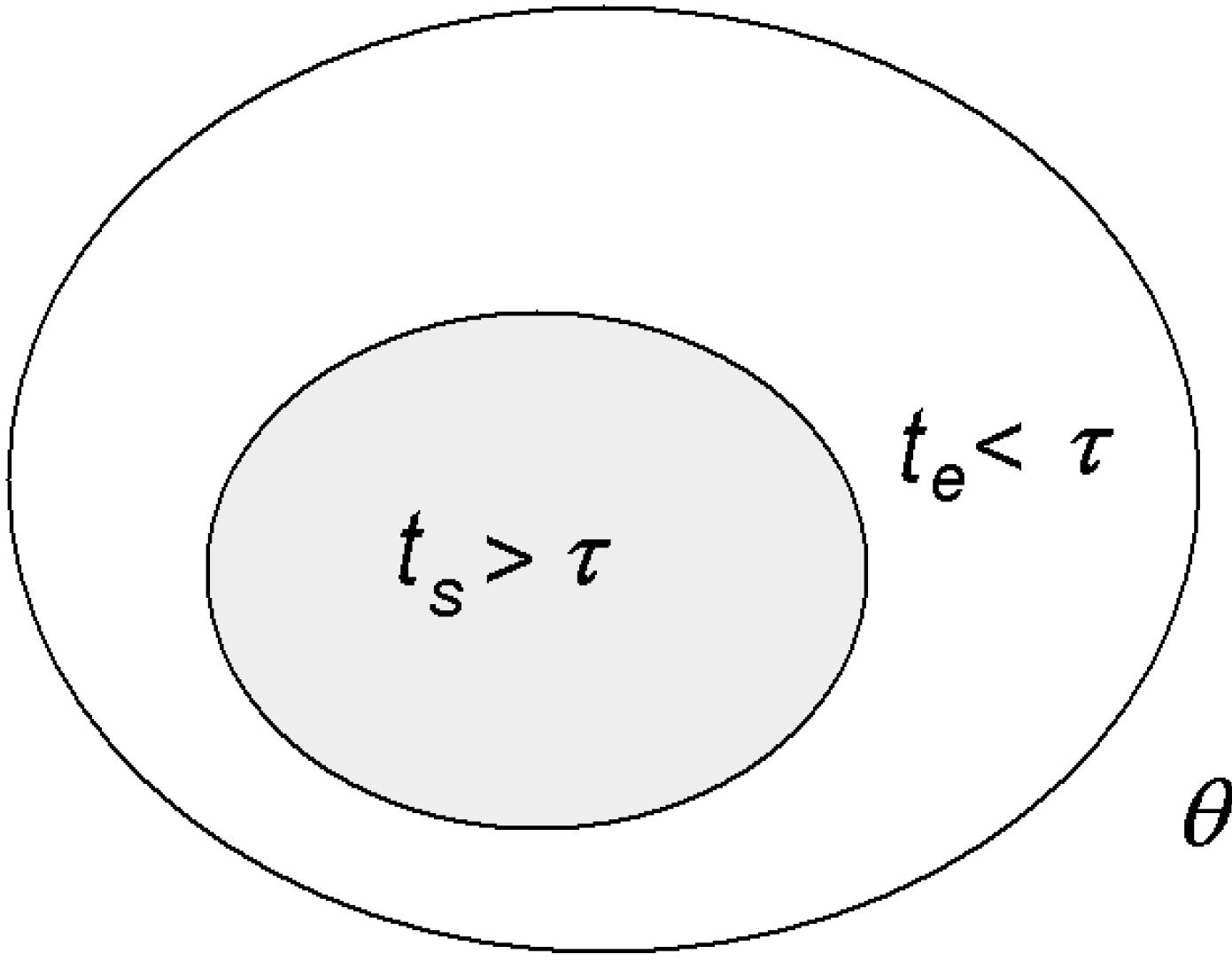
Physiologist Colin McClare [22] made an important contribution towards reformulating thermodynamics so that it can apply to living systems, especially to energy transfer between molecules, which is what happens in living systems. He proposed that in a system defined by some macroscopic parameter, such as temperature, θ, its energies can be separated into two categories: stored (coherent) energies that remain in a non-equilibrium state within a characteristic time, τ, and thermal (random) energies that exchange with each other and reach equilibrium (or equilibrate) in a time less than τ (Figure 3).

Figure 3. Stored vs. thermal energy [1].

Figure 3. Stored vs. thermal energy [1].

McClare introduced time structure into systems, with the very important consequence that there are now two ways to mobilize energy efficiently with entropy change approaching zero: very slowly with respect to τ, so it is reversible at every point; or very rapidly with respect to τ, so that the energy remains stored (in a coherent or non-degraded form) as it is mobilized.

For a process with characteristic timescale of 10⁻¹⁰ s, a millisecond is an eternity, so a “slow” process need not be very slow at all from our point of view to be energy efficient. Most enzyme reactions in the living system therefore could be occurring at or near thermodynamic equilibrium.

On the other hand, resonant energy transfer is an example of a very fast process occurring in <10⁻¹⁴ s, so the energy remains stored as it is transferred. Resonant energy transfer is also very important for living systems. Resonance interactions coordinate reactions in different parts of the cell and the organism. Resonating molecules attract one another, and there is indeed evidence that proteins, nucleic acids and other molecules find one another by resonating to the same electromagnetic frequencies [23], and not by random collision in aqueous solution as represented in conventional biochemistry and enzymology (see [1,13]). For one thing, the cell is an extremely crowded and organized environment for molecules.

McClare [22] proposed that, “Useful work is only done by a molecular system when one form of stored energy is converted into another”. In other words, thermalized energies cannot be used to do work, and thermalized energy cannot be converted into stored energy. This proposal raised obvious objections, as critics pointed out, automobiles do run on thermalized energy from burning petrol, so the proposal is not correct for automobiles and cannot be correct for molecular systems, if molecular systems do not violate the Second Law of thermodynamics.

McClare’s proposal was incomplete, and I completed his proposal as follows [1,16]: “Useful work is only done by a molecular system when one form of stored energy is converted into another in the same system.” The additional phrase “in the same system” effectively defines a “system” by the extent to which thermal energies equilibrate within a characteristic space-time. This also generalizes McClare’s characteristic time of processes to characteristic space-time of processes.

In the case of the automobile and other similar contraptions, the hot gases expand against a constraint, the piston, which, in taking up the thermalized energy, does work against the system external to the combustion chamber.

Figure 4. A nested hierarchy of space-times in which equilibrium and non-equilibrium canco-exist [1].

Figure 4. A nested hierarchy of space-times in which equilibrium and non-equilibrium canco-exist [1].

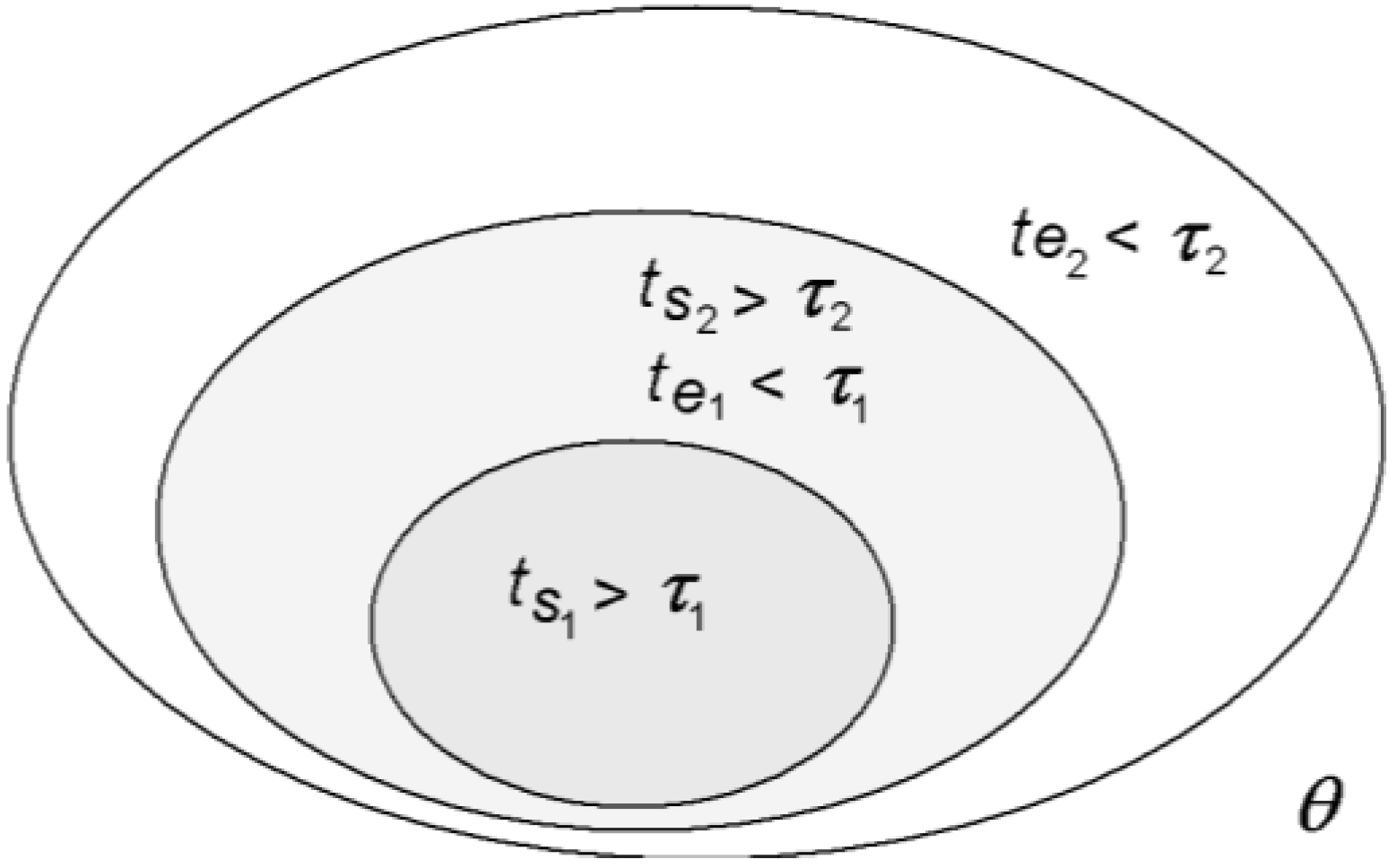
This definition of a system is crucial for the nested space-time structure of the organism. As the organism is partitioned into a hierarchy of systems within systems within systems defined by equilibration space-times, energies thermalized or equilibrated within a smaller space-time (system) will still be out of equilibrium in the larger system encompassing the first (Figure 4). So, even though the organism as a whole is far from thermodynamic equilibrium, its space-time differentiation nevertheless allows for a hierarchy of local near-equilibrium regimes to be maintained within.

Stored energy, like exergy and free energy, refers to energy available for doing useful work, it is coherent energy. But stored energy is explicitly defined with respect to a characteristic space-time, and is hence a real property of systems rather than a pseudo-property (see [3]).

The nested space-time structure in organisms optimizes thermodynamic efficiency by allowing the organism to simultaneously exploit equilibrium (very slow) and non-equilibrium (very fast) energy transfers with minimum dissipation, always with reference to the characteristic times of the processes involved as described above. It also optimizes the rapidity of energy mobilization. Biochemical reactions depend strictly on local concentrations of reactants, which could be enormously high, depending on their extent of equilibration. Cell biologists are beginning to take seriously the view that the cell approaches the solid-state, or more accurately, a liquid crystalline state, where nothing is freely diffusible, and even the cell water is organized into polarized multi-layers [1,13,14] as first proposed by Gilbert Ling [24]. Typically, molecular interactions occur within nanospaces both inside and outside cells. The nanospace defines the local system for molecular energy machines in the extent of equilibration (Figure 3, Figure 4).

Another point to note is that the greater the space-time differentiation, the more the amount of coherent energy effectively stored within the system. Because the activities are all coupled together, the energy residence time depends on how many activities there are within the system.

Finally, I conjectured that the fractal space-time structure in the organism allows activities at all scales to remain distinct and independent, and yet poised for energy exchange with one another. In other words, energies in different space-time domains are separately mobilized, and nevertheless able to spread from any point to the entire system, or conversely to converge from all over the system to any point whenever and wherever required [1,2,25]. However, it was only in 2009 that I suddenly got an inkling of why that might be the case.

As we were about to watch Simon McBurney’s A Disappearing Number performed by the company Complicité at the National Theatre in London, a beautiful play (as it turned out) created around the Indian mathematical sensation Srinivasa Ramanujan, I asked Peter Saunders, my husband and mathematical adviser for more than 35 years, if all irrational numbers were arbitrarily close to rational numbers, and he said yes. My guess was that living fractals are associated with irrational numbers such as the golden mean, and cannot enter into resonance; which is why the activities can remain distinct. However, the fractals are also close to harmonics that do resonate, so phase coupling and energy transfer through resonance is readily achieved by sliding from fractals to harmonics. Sliding from fractals to harmonics may coincide with the threshold for percolation in which local connects with global. Panchelyuga and Panchelyuga [26] recently considered resonance and fractals and the distribution of rational versus irrational numbers on the real numbers set and their relevance for physical systems, though without relating to the hypothesis presented here.

Cell biologists have independently proposed that the cytoplasm can be described as a percolation cluster or a random fractal [27]. A percolation cluster is an ensemble of sites that become globally connected beyond a percolation threshold (see Chapter 18 of [13] for more details).

There is also abundant evidence that fractal dynamics characterize the healthy heart rhythm, which reflects the constant intercommunication between the heart and all other parts of the body [28]. Real time monitoring shows how the heart rhythm can change abruptly, and how positive emotions such as love and appreciation can make the heart beat in synchrony with the pulse and respiratory rhythms, possibly through sliding from fractals to harmonic resonance on a macroscopic scale [29].

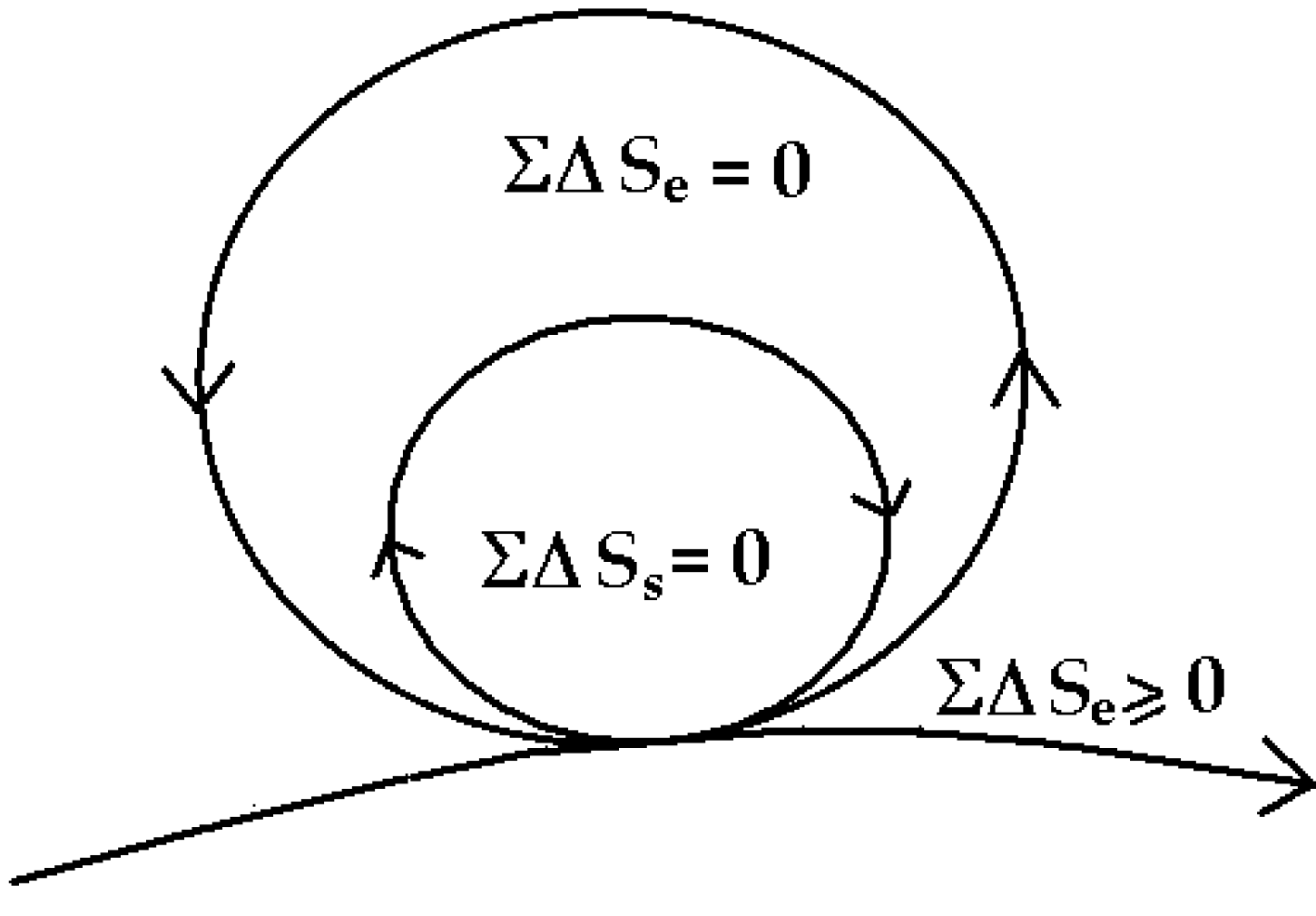
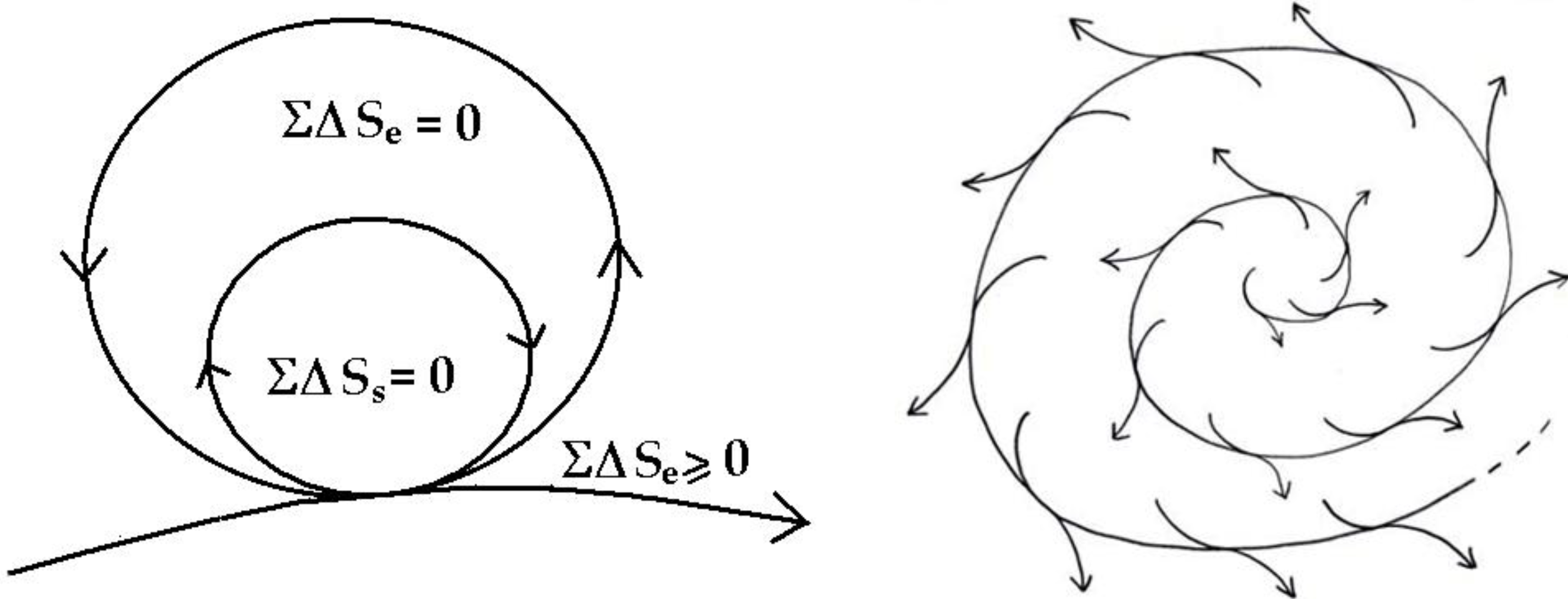
6. The “Zero-Entropy” Ideal

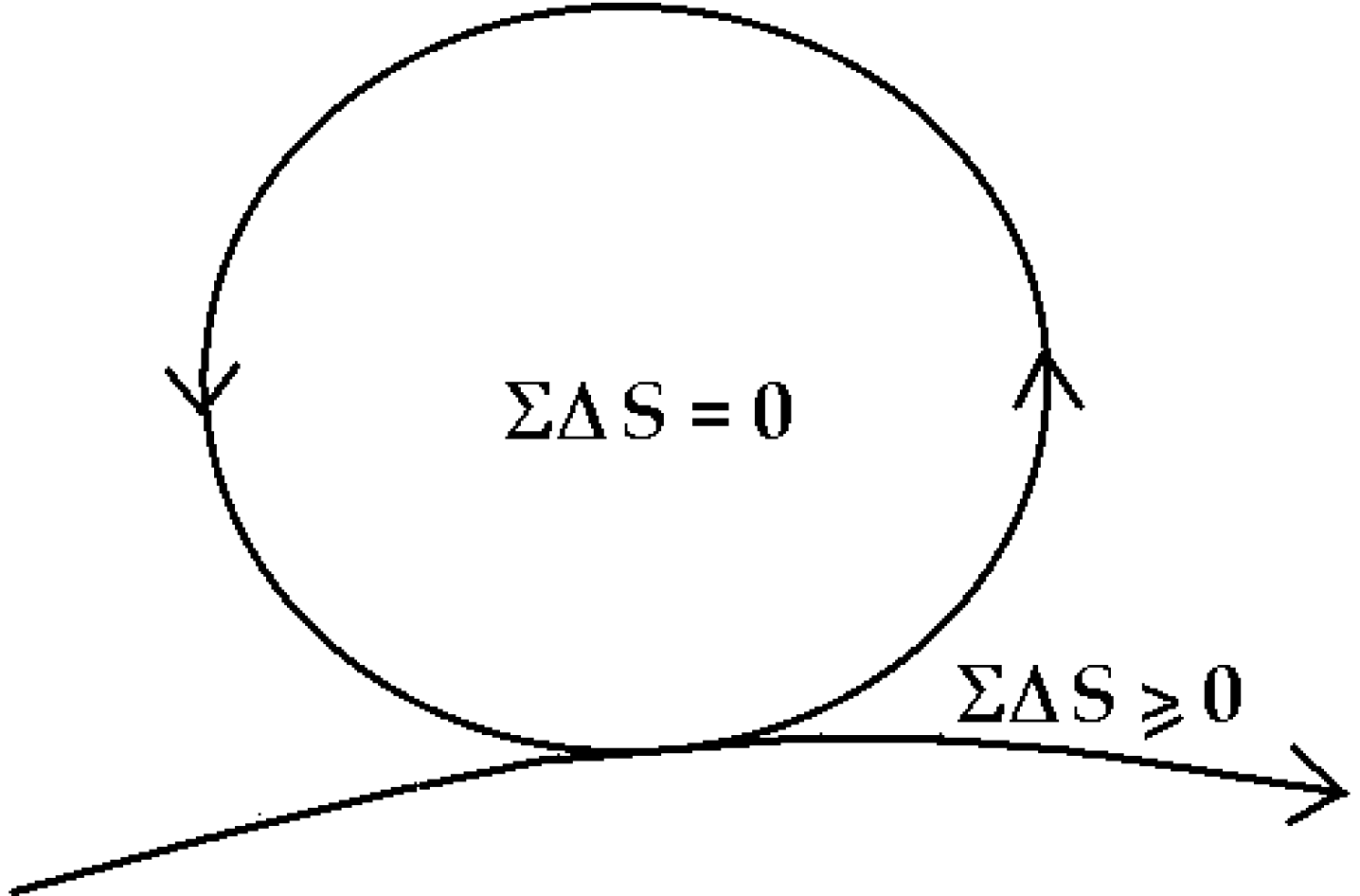
The healthy mature organism as well as the healthy mature ecosystem as defined by Odum [30] approaches an ideal dynamic balance of zero-entropy production (Figure 5). The simple equation ΣΔS = 0 inside the cycle, says there is an overall internal conservation of energy and compensation of entropy so that the system organization is maintained and dissipation reduced to zero—while the necessary dissipation exported to the outside, is also minimized, ΣΔS ≥ 0. Readers will note that this zero-entropy ideal is also the ideal quantum coherent state [1]. I emphasize ideal, because the ideal system will never age and never die, whereas real organisms and ecosystems slowly age and eventually die, basically because real organisms interact with the environment and decohere before re-establishing coherence as an asymptotically stable state [1].

Figure 5. Zero-entropy model of the ideal organism and sustainable system [1].

Figure 5. Zero-entropy model of the ideal organism and sustainable system [1].

Internal entropy compensation and energy conservation implies that positive entropy generated somewhere is compensated by negative entropy (or decrease in entropy) elsewhere within the organism over a finite time. This is just what Schrödinger [17] had tried to represent with the term “negentropy”. This is possible only if the internal microscopic detailed balance at every point of classical steady state theory is violated.

Denbigh [31] defined the “steady state” as one in which “the macroscopic parameters such as temperature, pressure and composition, have time-independent values at every point of the system, despite the occurrence of a dissipative process”. This is far too restriction for any real process, which always takes place in finite time and finite volume. Instead, I proposed [1] to define the living system in homeostasis as a “dynamic equilibrium in which the macroscopic parameters, such as temperature, pressure and composition have time-independent values despite the occurrence of dissipative processes”. The omission of the phrase “at every point of the system” is important and significant.

Microscopic homogeneity is not necessary for the formulation of any thermodynamic state, as the thermodynamic parameters are macroscopic entities quite independent of the microscopic interpretations. Like the principle of microscopic reversibility, it is extraneous to the phenomenological laws of thermodynamics, as Denbigh himself had convincingly argued [31].

It is the organized space-time heterogeneity within the living system that allows for the necessary “free” variation of the microscopic states within the macroscopic thermodynamic constraints. Thus, stability criteria that apply to the system as a whole need not be satisfied; or stronger yet, cannot be satisfied in every individual space-time element for all times.

The tendency to conserve coherent energy and compensate for entropy production within the system will result in the minimum entropy being exported to the outside. Intuitively, one can see that if the system were maximally efficient, then it would also produce the least dissipation. This is the basis for Prigogine’s minimum entropy production principle (see [18]), which, in the present case, applies to conditions both near and far from thermodynamic equilibrium.

From the outside, it might appear that the system is “maximally dissipative” in terms of having “degraded” the energy gradient most effectively [32,33,34]. But this misses the coherent energy stored non-degraded within the system, and stored energy is also embodied in matter within the system, i.e., biomass.

7. Sustainable Systems as Organisms and Diagnostic Signs of Sustainability

Based on the circular thermodynamics of organisms, I have suggested diagnostic criteria of sustainability or health that depend on the tendency of a sustainable system to maximize non-dissipative cyclic flows of energy and minimizing dissipative flows [25].

Maximizing non-dissipative cyclic flows will increase the following: energy storage capacity, which translates into carrying capacity or biomass; the number of cycles in the system; the efficiency of energy use; space-time differentiation, which translates into biodiversity; balanced flows of resources and energy; reciprocal coupling of processes. The minimization of dissipation will result in reducing entropy production (towards zero).

These diagnostic criteria are interlinked, so once one is identified, the others are likely to follow. Some support for these criteria is that they are similar to those Schneider and Kay [32] have identified for mature, established ecosystems [25]. Data collected for carbon-energy flows in two aquatic marsh ecosystems next to a large power-generating facility in the Crystal River in Florida showed that the “stressed” system, exposed to hot water coming out of the nuclear power station, which increased the temperature by 6 °C, captured 20% less energy, made 20% less efficient use of the energy captured, had 50% fewer cycles and 34% less biomass than the control.

Schneider and Kay [32] also drew attention to some interesting measurements made by Luvall and Holbo [35] with a NASA thermal infrared multispectral scanner from the air, which assess energy budgets of terrestrial landscapes. They found that the more developed the ecosystem, the colder its surface temperature. This is consistent with the maximization of energy storage capacity and the minimization of dissipation, as the system develops towards the zero-entropy ideal; rather than it being more effective at degrading the energy gradient, as interpreted by Schneider and Kay [32].

Another indication of the energy efficiency and potential increase in carrying capacity of sustainable systems is provided by a comparison of 25 rice cultivation system [25,36], of which 8 were pre-industrial in terms of low fossil fuel input (2–4%) and high labor input (35–78%), 10 were semi-industrial with moderate to high fossil fuel input (23–93%) and low to moderate labor input (4–46%) and seven were full industrial with 95% fossil fuel input and extremely low labor input of 0.04–0.2%. The total output per hectare (in gigajoules) in the pre-industrial fell into a low (2.4 to 9.9) and a high-output (149.3 to 166.9) subgroup, with the former one-twentieth to one-fifth of the full industrial average. However, the output of the high subgroup was two to three times the full-industrial systems. The yields of semi-industrial systems were more homogeneous, with an average of 51.75 GJ, while the yields of full-industrial systems, even more uniform, averaged 65.66 GJ.

When the ratio of total energetic output to total input was calculated, the pre-industrial low yielding systems ranged between 6.9 and 11.5, whiles figures for the high output system registered from 15.3 to 29.2. Semi-industrial systems gave ratios of 2.1 to 9.7, whereas the ratios of full-industrial systems were not much better than unity. These figures illustrate the law of diminishing returns: there seems to be a plateau of output per hectare around 70–80 GJ regardless of the total input, which is only exceeded in the three high-yielding pre-industrial systems of Yunnan, China. Intensifying energy input led to a drop in efficiency, particularly sharp as input approaches the output ceiling, which appeared to conform to the notion of a uniform carrying capacity. But this is highly misleading, as the carrying capacity depends on how the land is organized for production, in particular, soil fertility, as already suggested by the Yunnan rice production systems.

Another interesting study compared the whole of Danish agriculture from 1936 to 1990, during which, mechanization and chemical inputs in fertilizers and pesticides increased 20-fold, the average farm size more than doubled from 15.7 ha to 35.1 ha, and average crop yields for human food rose from 10 GJ/ha to 21.7 GJ/ha [37]. However, total energy input increased 8-fold over the period, from 2.6 GJ/ha to 21.1 GJ/ha; consequently, the energy output/input ratio fell from 3.9 to 1.0.

In both examples, the energy output/input ratio gives a good indication of sustainability and energy efficiency. Industrial monoculture not only pollutes the environment with its chemical and fossil fuel inputs, it harms the complex ecosystem of the soil that plays an essential role in nutrient recycling, water retention, as well as disease control, effectively putting a ceiling on agricultural productivity. In contrast, all forms of low-input sustainable agriculture depend on working with and within the circular economy of nature with maximum use of internal inputs, biological pest control, composting, green manure and farmyard manure (see [38] for a comprehensive report on the subject). There are more ways to approach the zero-entropy ideal of the organism and sustainable system. I shall begin with a conceptual example.

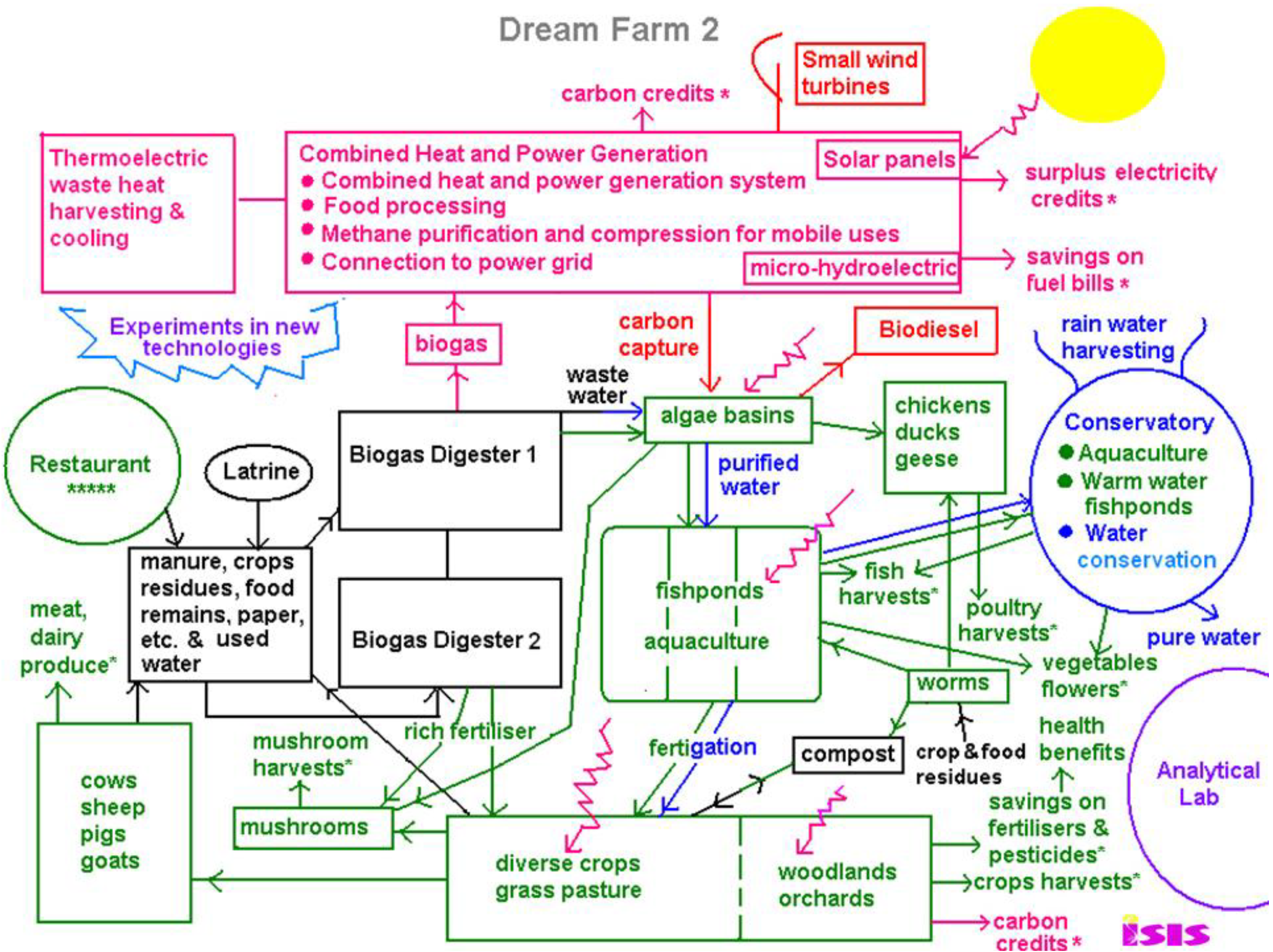
8. Dream Farm 2

Some time ago, I proposed the concept of an integrated food and energy self-sufficient farm based on the circular thermodynamics of organisms; one of the most recent versions is given in Figure 6 [39]. Anaerobic digestion recycles plant, livestock, food and human wastes into biogas fuel and agricultural nutrients, and other green energies at small to micro-scale are also incorporated, such as solar, wind, microhydroelectric, as appropriate. Combined heat and power generation provides heating for buildings and thermoelectric waste heat harvesting and cooling could be incorporated for maximum energy recycling. Surplus electricity could be used for charging batteries for energy storage, as well as electric cars, tractors, computers, mobile phones etc. This mix of energies ensures a reliable supply, and can reduce energy use by at least 30% through exploiting ‘waste’ heat from power generation, use of heat pumps, and preventing energy loss in long distance distribution and transmission.

Figure 6. Dream Farm 2 based on the zero-entropy ideal of the organism [39].

Figure 6. Dream Farm 2 based on the zero-entropy ideal of the organism [39].

The diagram is color-coded. Pink is for energy, green for agricultural produce, blue is for water conservation and flood control, black is waste in the ordinary sense of the word, which soon gets recycled and converted into food and energy resources. Purple is for education and research into new science and technologies. It is estimated to save 44% of energy consumption, only counting anaerobic digestion. With the addition the other renewables, there would be more than enough energy for the entire farm, (while also compensating substantially if not completely for carbon emissions) (see Table 1, estimated for China [39]).

Table 1. Green potential of Dream Farm 2 if adopted nationally for China [39].

	CO2e savings	(%National)	Energy savings	(%National)
Organic agriculture	955.1 Mt	(12.69%)	2.608 EJ	(3.61%)
Anaerobic digestion	586.0 Mt	(7.79%)	7.470 EJ	(10.35%)
Energy savings local gen.	1,287.1 Mt	(17.10%)	21.660 EJ	(30.00%)
Total	2,828.2 Mt	(37.58%)	31.738 EJ	(43.96%)

Table 1. Green potential of Dream Farm 2 if adopted nationally for China [39].

	CO2e savings	(%National)	Energy savings	(%National)
Organic agriculture	955.1 Mt	(12.69%)	2.608 EJ	(3.61%)
Anaerobic digestion	586.0 Mt	(7.79%)	7.470 EJ	(10.35%)
Energy savings local gen.	1,287.1 Mt	(17.10%)	21.660 EJ	(30.00%)
Total	2,828.2 Mt	(37.58%)	31.738 EJ	(43.96%)

Dream Farm 2 would be an excellent project for a university or a research institute because engineers, architects, scientists, artists, medical doctors, sociologists, economists and business can all work together across the disciplines to realize the circular, zero-entropy model in design, energy flow, architecture, marketing, etc., while providing opportunities for education, research and innovation.

A more modest version of the scheme would be particularly suitable for providing off-grid energy (as well as sanitation in anaerobic digestion toilets) to isolated communities in developing countries [39]. Modern electronic lighting, mobile phones and other household equipment have low power requirements, and are ideally served by the local renewable energies available. Indeed, small anaerobic digesters, solar lanterns, and solar panels are already improving the lives of millions in isolated parts of China and Africa.

On the other hand, Dream Farm 2 can also be scaled up for a local community, say for visionary science, which includes everyone whom the research will benefit. There would be housing, childcare centers, restaurants, shops, theatre, concert hall, art gallery, a university, a high school, primary school, and a community bank.

9. Productivity, Carrying Capacity & Biodiversity

Dream Farm 2 illustrates how it is possible to have sustainable growth and development. Too many critics of the dominant paradigm think that the only alternative to unsustainable growth is to have no growth at all.

The minimum entropy exported to the environment is important, as the system depends on environmental input, hence, entropy exported to the environment will simply mean diminished environmental input. This can be made more explicit by enclosing the system within the immediate environment of the system as in Figure 7.

The ecological environment surrounding the system is now explicitly represented also as a zero-entropy cycle. Once again, that this is a fractal diagram, the environment surrounding the system is exporting to a larger ecological domain, and this kind of embedding can go on, ultimately to the entire earth. In addition, each cycle is of course made up of many smaller cycles within (see Figure 2) all working by reciprocity and cooperation. This principle is well illustrated in sustainable integrated farming.

Figure 7. The coupled flows of system and ecological cycles in a sustainable system [1].

Figure 7. The coupled flows of system and ecological cycles in a sustainable system [1].

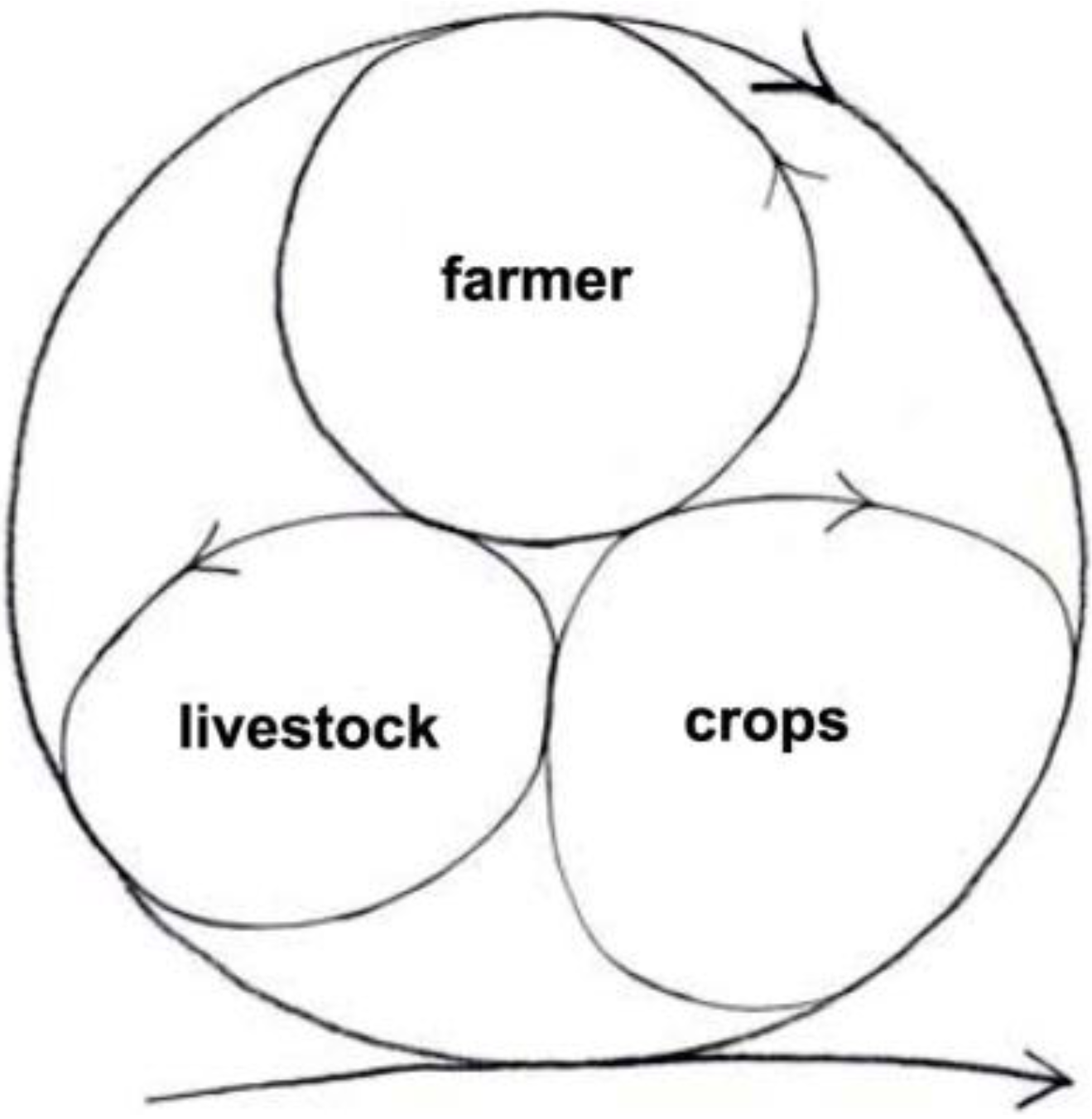
The minimum integrated farm has the farmer, livestock and crops (Figure 8). The farmer prepares the ground to sow the seeds for the crops to grow that feed the livestock and the farmer; the livestock returns manure to feed the crops. Very little is wasted or exported to the environment. In fact, a high proportion of the resources are recycled and kept inside the system. The system stores energy as well as material resources such as carbon. The extra carbon is sequestered in the soil as the soil improves, and in the standing biomass of crops and livestock.

More importantly, the farm can perpetuate itself like that quite successfully and sustainably, or it can grow by engaging more cycles, units of devolved autonomy that help one another do better. (In analogy with the organism, it will develop a more complex space-time differentiation, and grow bigger.)

Figure 8. The minimum integrated sustainable farm [48].

Figure 8. The minimum integrated sustainable farm [48].

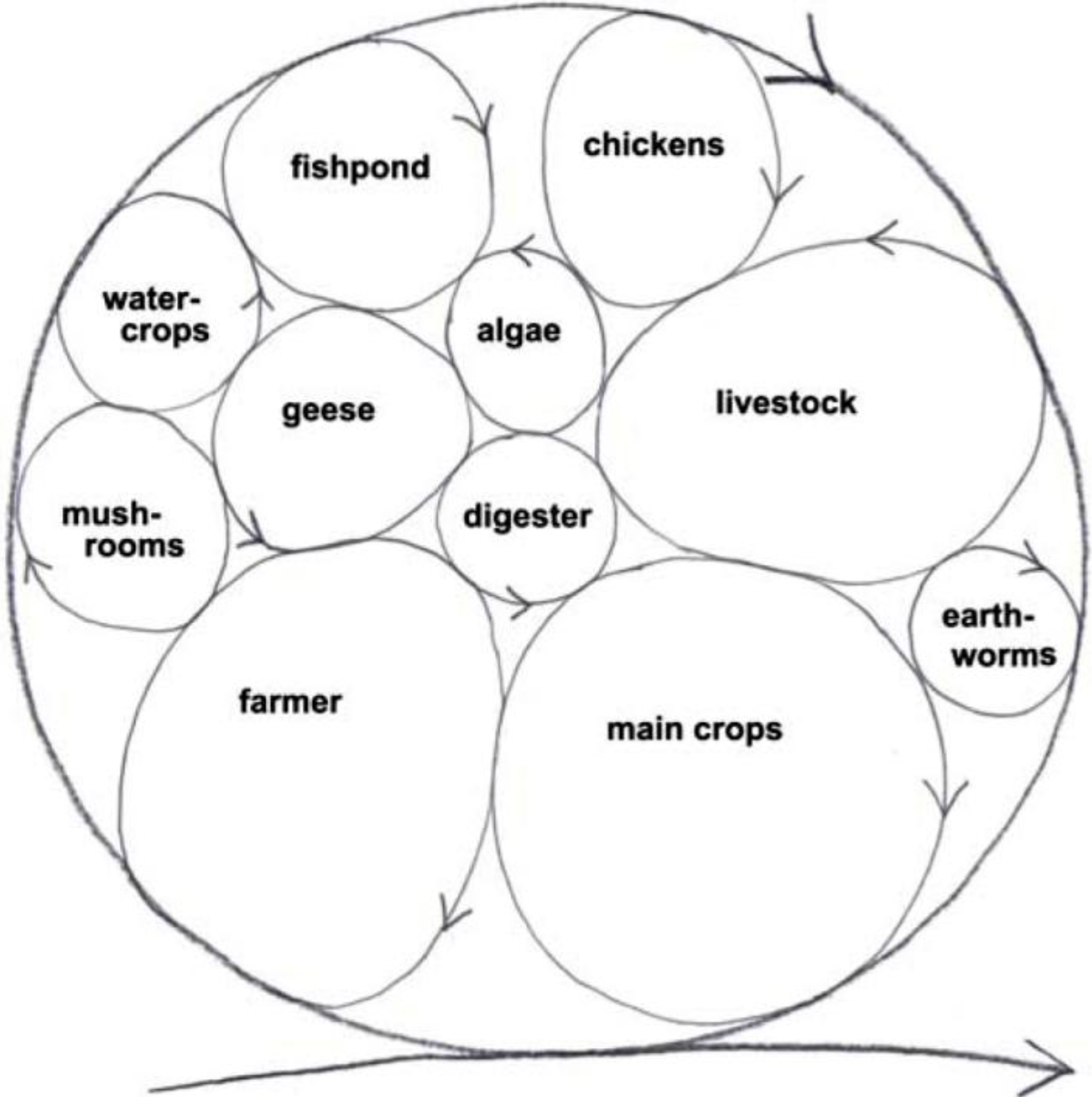
In the old paradigm, organisms are predominantly seen to compete for resources and for space. However, we’ve got three space dimensions and the time dimension too. We’ve got space-time that can be filled up more thickly with life cycles of different sizes that occupy different space-times. So you can add fish, algae, poultry, worms, mushrooms, etc., turning the ‘waste’ from one cycle to resource for another (Figure 9).

Figure 9. Sustainable system develops and grows by incorporating more life cycles within the system, the wastes from one cycle is resource for another [48].

Figure 9. Sustainable system develops and grows by incorporating more life cycles within the system, the wastes from one cycle is resource for another [48].

The more lifecycles incorporated, the more energy and standing biomass are stored within the system, the greater the productivity of the farm and more farmers and farm workers supported. Chinese farmers have perfected the circular economy over the past two thousand years especially in the Pearl River Delta of southeast China [40]. Crops, livestock and silkworms are grown on the dykes, some overhanging the ponds, where up to five species of carp are fed on the wastes; the water and pond mud are used to fertilize the crops. Variants of such dyke-pond systems supported 17 people per ha in the 1980s, a carrying capacity at least ten times the average of industrial farming, and two to three times the world average. It disposes of another myth: that a constant carrying capacity exists for a given piece of land.

Productivity and biodiversity always go together in a sustainable system, as generations of farmers have known, and recent academic researchers have rediscovered. The different life cycles are essentially holding the energy for the benefit of the whole system, and by way of reciprocity, recycling the energy within the system. Once it is recognized that coherent energy is stored within the system, it follows that energy can be recycled, contrary to the conventional wisdom that regards only materials as capable of being recycled.

That is exactly what happens in a naturally biodiverse ecosystem: organisms maximize the reciprocal, symbiotic relationships that ultimately benefit all the species; and biodiverse systems have been shown time and again to be more productive than monoculture cropping [41].

Physiologists have long observed that the sizes (body weights) B of animals scale allometrically with basal (resting) metabolic rate M:

B = B₀M^α

(2)

where B₀ and α are constants. This has remained a mystery until Geoffrey West, James Brown and Brian Enquist derived the scaling relationship from first principles, showing that it stems from the fractal structure of organisms, especially of circulatory and transport networks that are optimized for maximum exchange surface, minimum transport distances and times, and minimum dissipation [42]. This is certainly in line with the circular thermodynamics zero-entropy ideal model of organisms and sustainable systems proposed here [43].

10. Circular Thermodynamics and Green Living Economy

Thermodynamics is the science of material and energy transformation, the circular thermodynamics of organisms is therefore none other than living economy: the transformation of energy and materials that enable organisms including human beings to survive and thrive.

It is of interest that “circular economy” is in Chinese mainstream discourse [44]; and is actually adopted as a national policy, albeit only in the manufacturing and service sectors; they had neglected to include agriculture [45], the primary production for all economies. Circular economy is also entering the mainstream in the world at large, as championed by Ellen MacArthur, who has started the “Circular Economy 100” for the business world [46], so it is all the more important to understand what circular economy is all about.

There is a world of difference between circular integrated farming and the linear input-out industrial agriculture. It is also the difference between zero-entropy circular economy that some of us aspire to, and the dominant economy of infinite competitive growth and maximum dissipation (entropy generation). I contrast the two in Figure 10.

The dominant linear input-output system grows relentlessly, swallowing up the earth’s resources, laying waste to everything in its path, like a hurricane. There is no closed cycle to hold resources within, to build up stable organized social or ecological structures. That’s the essence of our “boom and bust” economy.

Figure 10. The zero-entropy circular economy patterned after and integrated with the circular economy of nature (left) versus the dominant economic model of infinite unsustainable growth that swallows up the earth’s resources and exports massive amounts of wastes and entropy (right).

Figure 10. The zero-entropy circular economy patterned after and integrated with the circular economy of nature (left) versus the dominant economic model of infinite unsustainable growth that swallows up the earth’s resources and exports massive amounts of wastes and entropy (right).

The zero entropy circular economy, on the other hand, is embedded within and integrated with the circular economy of the natural ecosystem. It builds up space-time structures within to store and mobilize renewable energy and materials through values added in various ways to the primary productivity from sunlight and photosynthesis.

As argued earlier, the fractal structure of the circular economy (see Figure 2) ensures that all space-times are bridged, and is optimized for capturing, storing, and mobilizing resources efficiently and rapidly while conferring local autonomy on all scales. It also maximizes diversity: numerous small entities scaling up to very few large ones. Old mature forests tend towards this ideal “all size” distribution [47] and are more productive and diverse. It could be that a distribution supporting the greatest diversity is also the most equitable, and makes the most efficient use and mobilization of resources; but this hypothesis needs to be thoroughly examined and tested.

Another key feature (already mentioned) is that activities requiring energy or material are coupled to those that generate them; and the giving and taking can be reversed as the need arises. In other words, the system maximizes symbiosis, reciprocity and cooperation. It is fair and just reciprocal exchange of materials and energy that maintains and ensures the survival of the whole. Perhaps this is the biggest lesson for the commercial sector that has hitherto operated on exploitation and competition.

This raises the question on the medium of exchange. In human economy, money has become the medium of exchange for goods and services, replacing trust and goodwill. Goods and services have their obvious counterparts in living systems as materials and energy. But what is the equivalent of money in living systems? Is there such a thing?

11. Energy in Living Systems versus Money in Human Economy

Energy in living systems is all too often equated with money in economy, and vice versa. This has misled generations of biologists and economists alike. As we have seen, living energy transactions are always tied to real interactions and exchanges between molecules with minimum dissipation. For money to be equivalent to energy, it too, has to be tied to exchanges in real goods and services. Unfortunately, money has become more and more decoupled from real goods and services, and hence more like entropy than energy. It becomes entropy in unequal exchanges when the price paid is too low, as in exploitative labor or between currencies that are grossly overvalued on the side of the purchaser. The money market is especially entropic [25,44,48], because it is not based on any real-valued goods or services; furthermore, it artificially inflates the purchasing power of the rich, leading to greater exploitation of environmental resources. This becomes more explicit when the medium for energy exchange in the living system is considered.

The medium of exchange in the living system is adenosine triphosphate (ATP), which many cell biologists and biochemists too, have equated with money. It is the universal energy transducer in living organisms, so much so that its concentration in cells is maintained constant as far as possible by a reserve molecule creatine phosphate, which is allowed to deplete, and its sole function appears to be to keep the supply of ATP constant. ATP has a very special role in maintaining the living state (see [13]).

ATP itself is synthesized using energy from food stuffs or from sunlight, and never from nothing. In other words, ATP, the medium of exchange of goods and services in the living system is never decoupled from material and energy cycles, and that is where the analogy to money ends, at least in the current economic system.

In our current human economy, money is being created electronically practically out of nothing, without limit or control; or worse, out of toxic debt and debt pyramids [49]. It has become completely decoupled from real goods and services, and generates real entropy in Earth’s ecosystem (and contributing to global warming) when used for overconsumption and exploitation of natural resources. That is ultimately the reason why we need to “shut down Wall Street” [50] in favor of restoring the real high street economy.

Contrary to what many economists assume, an economy that genuinely supports livelihood is not just about the flow of money; it is about people making a living transforming and exchanging materials and energy, and is therefore closely aligned with thermodynamics. Money is the means for the exchange of real goods and services, and not the end of economy. It must never be decoupled from the value of real goods and services. Major disasters like the current financial crisis come about because money has been created without control, and because people mistake the means for the end.

The circular thermodynamics of the living state—the science of energy and material transformation in living organisms and sustainable systems—gives ample support to the following features of a truly green economy [44].

• The green economy is a renewable, closed-loop resource use model that includes agriculture, the energy, construction, manufacturing, and service industries, as well as finance. It is a complete way of life
• Like nature, the truly green economy maximizes diversity, reciprocity, symbiosis, cooperation and equity; greed and inequity are unsustainable
• A truly green economy is embedded within nature’s economy
• It regards nature as the ultimate source of wealth, of “natural capital” [51], which must be regenerated and indeed, increased, in order to feed all sectors of the human economy.

12. Conclusions

I have presented a circular thermodynamics of organisms and sustainable systems based on dynamic closures in nested space-time domains that enable the system to approach the ideal of zero entropy production simultaneously at equilibrium and far from equilibrium conditions.

A sustainable system, like an organism, maximizes cyclic, non-dissipative flows while minimizing dissipative flows, i.e., it tends towards minimum entropy production. Activities yielding energy are directly coupled to those requiring energy and the direction can be reversed as the need arises. This dynamic space-time differentiation is based on symbiosis, cooperation and reciprocity. It also explains why biodiverse systems are more resilient and productive.

As a model of sustainable systems, it disposes of some major myths in ecology and economy. For example, the carrying capacity of a piece of land is not a constant; it depends on how it is organized for production. Similarly, a sustainable system does not mean one without growth. On the contrary, it can easily grow by engaging more cycles. Finally, it exposes the weaknesses of the dominant economic model of unlimited competitive growth based on money decoupled from real value of goods and services.