Subsecond Tsunamis and Delays in Decentralized Electronic Systems
Abstract
:1. Introduction
2. Background
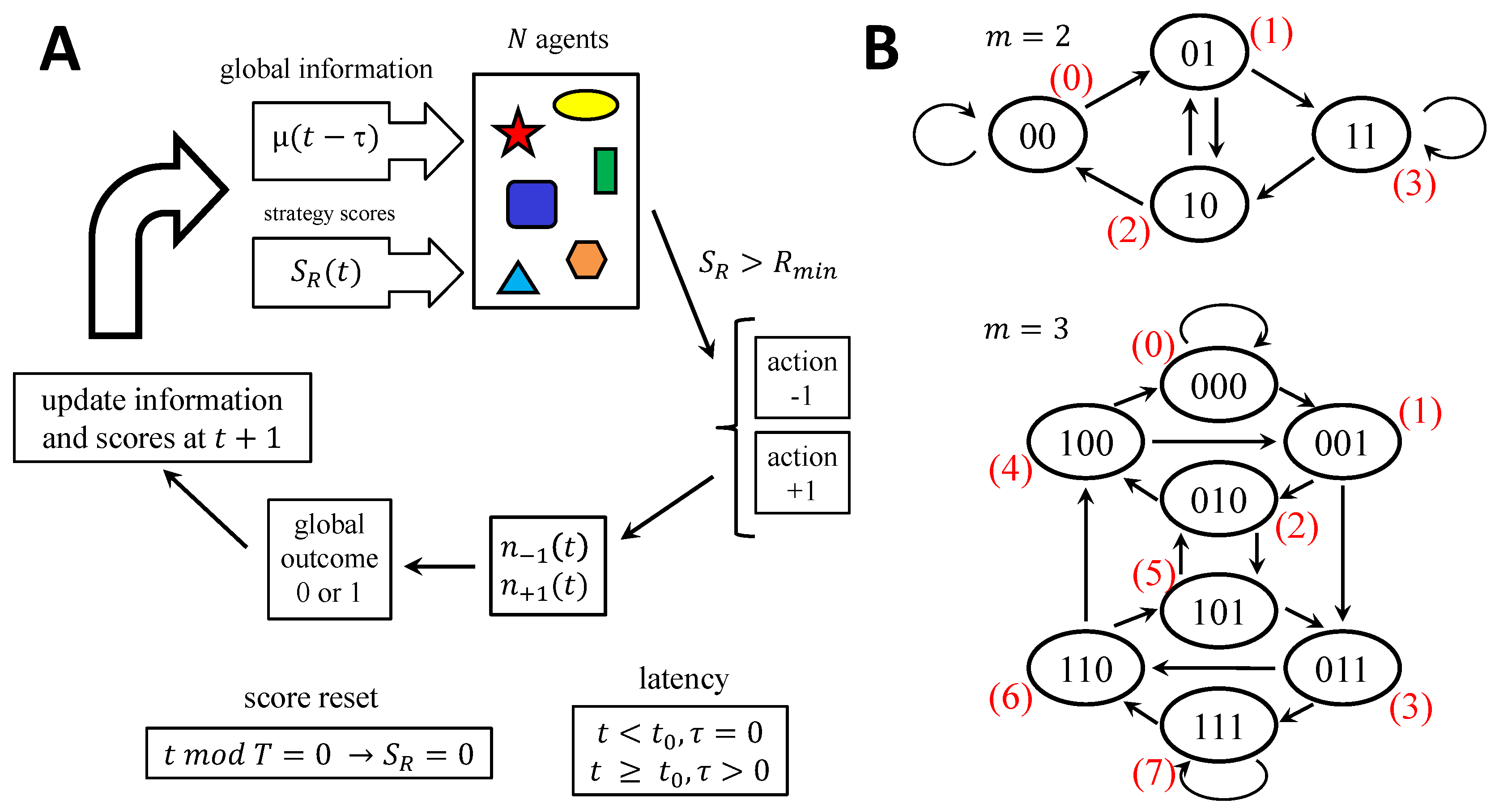
3. Model
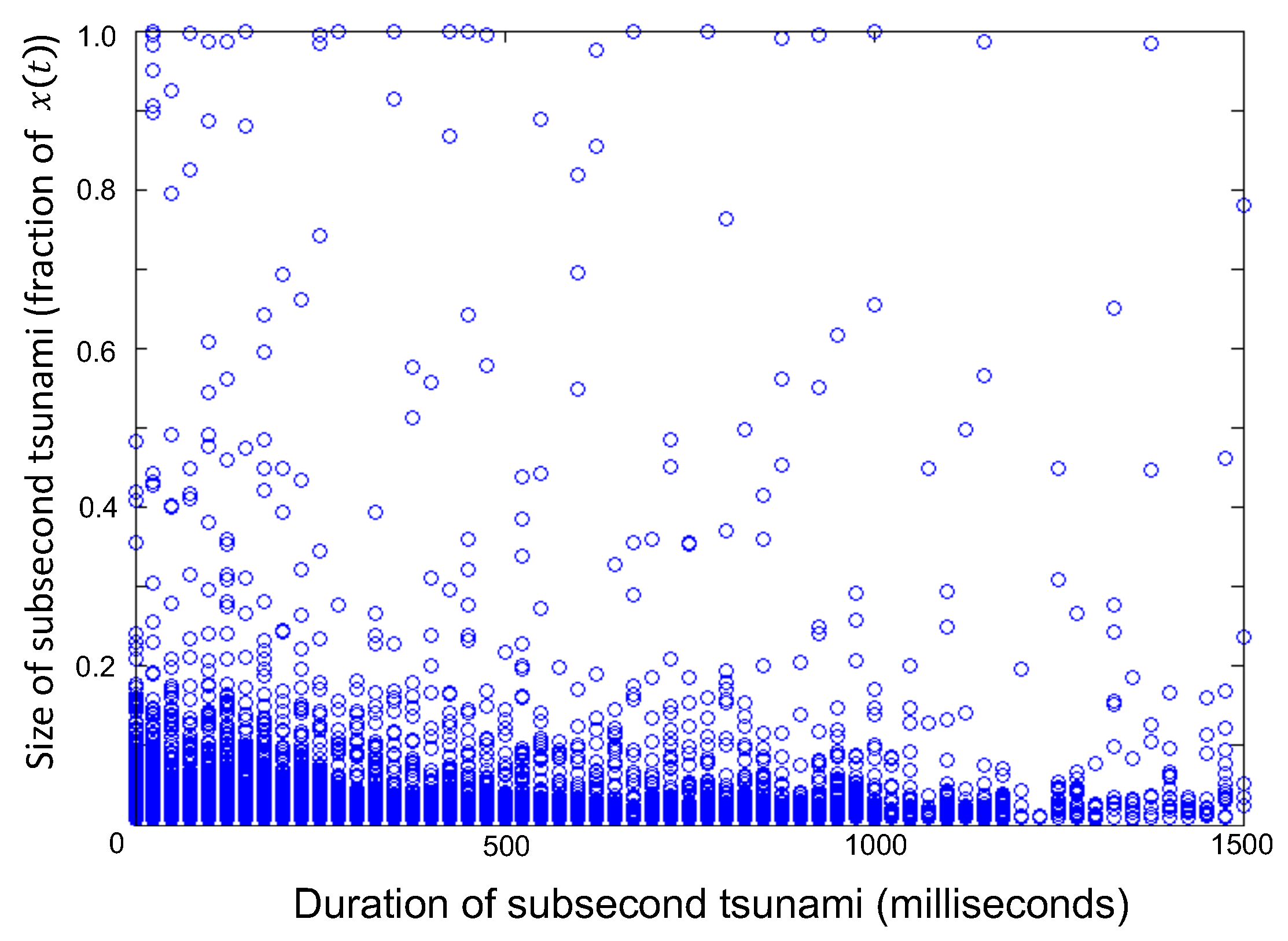
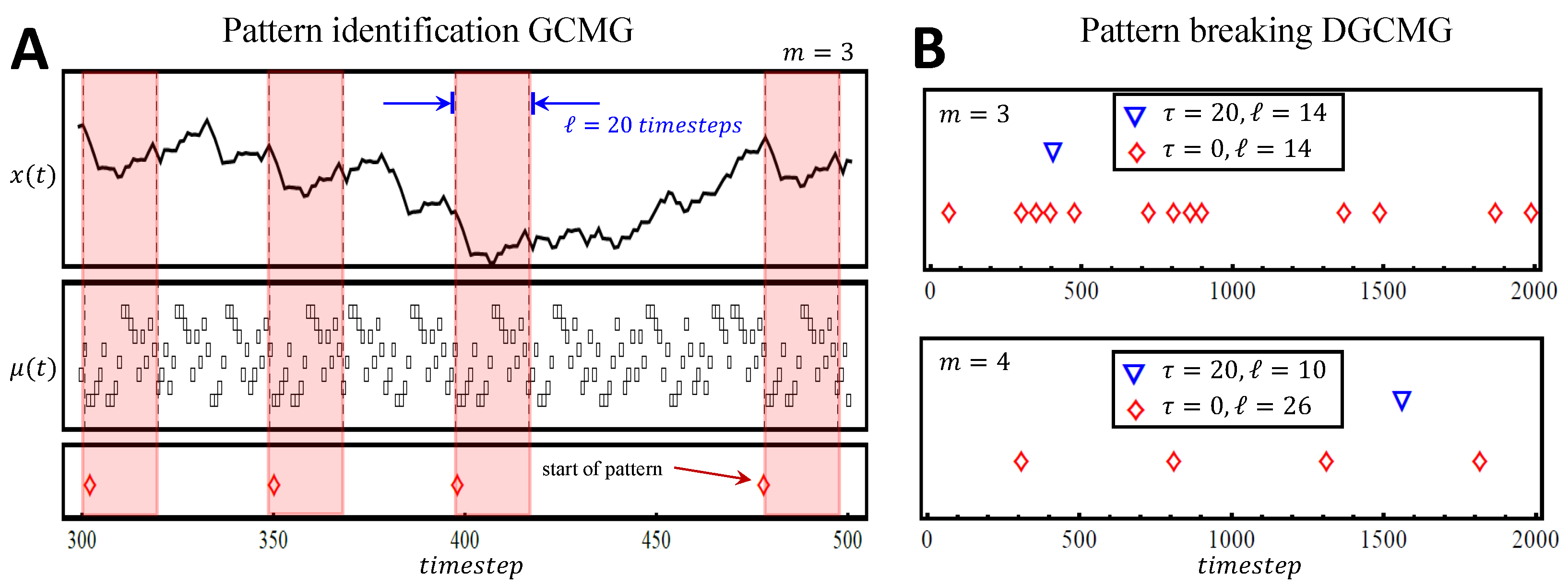
4. Results: Simulation
5. Results: Analytics
5.1. Crowding
5.2. GCMG Nodal Weighting Analysis
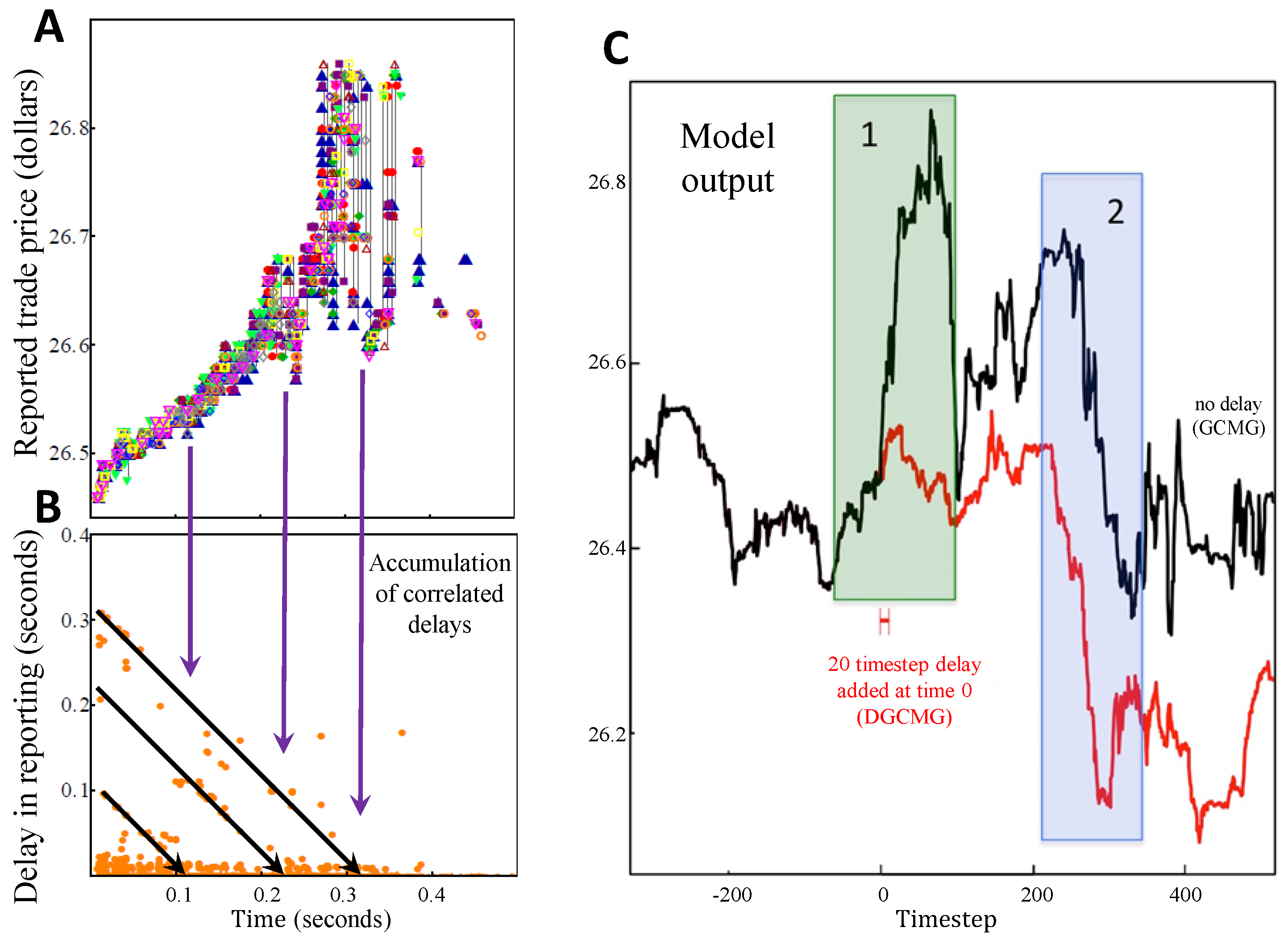
5.3. DGCMG Impact of Delays
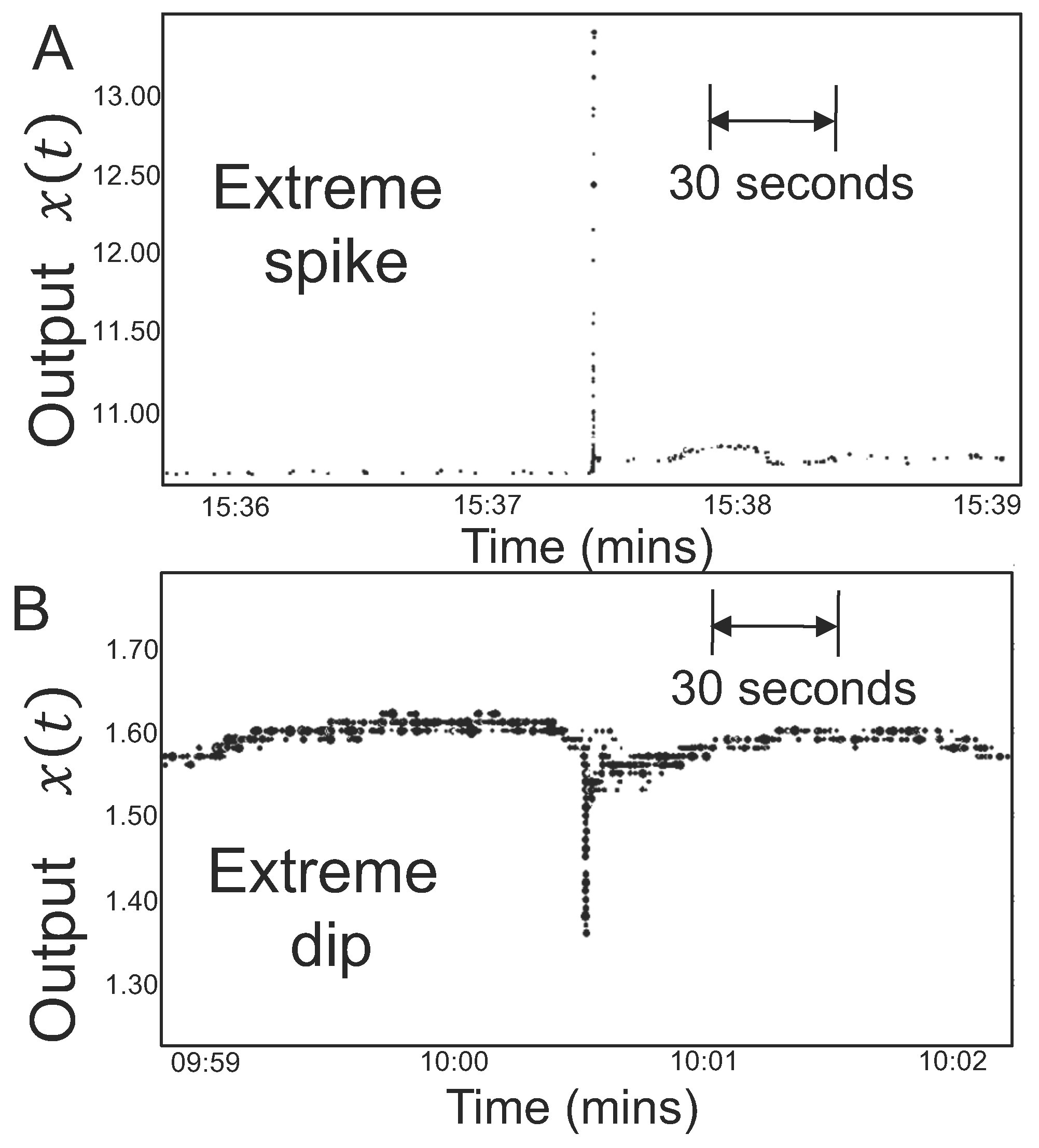
6. Results: Real World Data
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Edward, A.L. The Past, Present and Future of Cyber-Physical Systems: A Focus on Models. Sensors 2015, 15, 4837–4869. [Google Scholar]
- Loiseau, P.; Schwartz, G.A.; Musacchio, J.; Amin, S.; Sastry, S.S. Incentive mechanisms for internet congestion management. IEEE/ACM Trans. Netw. 2014, 22, 647–661. [Google Scholar] [CrossRef]
- Lee, E.A. Computing Foundations and Practice for Cyber-Physical Systems: A Preliminary Report; Technical Report UCB/EECS-2007-72; University of California: Berkeley, CA, USA, 2007. [Google Scholar]
- Rajkumar, R. A cyber-physical future. Proc. IEEE 2012, 100, 1309–1312. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, Y.Y.; Zhou, X.S.; Liang, D.F. Approach for cyber-physical system simulation modeling. J. Syst. Simul. 2014, 3, 631. [Google Scholar]
- Liu, Y.; Peng, Y.; Wang, B.; Yao, S.; Liu, Z. Review on Cyber-physical Systems. IEEE/CAA J. Autom. Sin. 2017, 4, 27–40. [Google Scholar]
- Konstantakopoulos, I.C.; Ratliff, L.; Jin, M.; Spanos, C.; Sastry, S.S. Smart Building Energy Efficiency via Social Game: A Robust Utility Learning Framework for Closing the Loop. In Proceedings of the 1st International Workshop on Science of Smart City Operations and Platforms Engineering (SCOPE) (ACM/IEEE CPSWeek), Vienna, Austria, 12–14 April 2016. [Google Scholar]
- Calderone, D.; Mazumdar, E.; Ratliff, L.; Sastry, S.S. Understanding the Impact of Parking on Urban Mobility via Routing Games on Queue Flow Networks. In Proceedings of the IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016. [Google Scholar]
- Zebulum, R.S.; Pacheco, M.A.C.; Vellasco, M.M. Evolutionary Electronics; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Conway, B. Wall Street’s Need For Trading Speed: The Nanosecond Age. Available online: http://blogs.wsj.com/marketbeat/2011/06/14/wall-streets-need-for-trading-speed-the-nanosecond-age/ (accessed on 1 October 2017).
- Pappalardo, J. New Transatlantic Cable Built to Shave 5 Milliseconds off Stock Trades. Available online: http://www.popularmechanics.com/technology/engineering/infrastructure/a-transatlantic-cableto-shave-5-milliseconds-off-stock-trades (accessed on 1 October 2017).
- Lewis, M. Flash Boys: A Wall Street Revolt; W.W. Norton & Company: New York, NY, USA, 2014. [Google Scholar]
- McCoy, K. IEX Exchange Readies for Mainstream Debut. 18 August 2016. Available online: http://tabbforum.com/news/iex-exchange-readies-for-mainstream-debut?utm_campaign=d19dc21bc0-UA-12160392-1&utm_medium=email&utm_source=TabbFORUM%20Alerts&utm_term=0_29f4b8f8f1-d19dc21bc0-278278873 (accessed on 18 August 2016).
- Johnson, N.F.; Zhao, G.; Hunsader, E.; Qi, H.; Johnson, N.; Meng, J.; Tivnan, B. Abrupt rise of new machine ecology beyond human response time. Sci. Rep. 2013, 3, 2627. [Google Scholar] [CrossRef] [PubMed]
- Manrique, P.D.; Zheng, M.; Restrepo, D.D.J.; Hui, P.M.; Johnson, N.F. Impact of delayed information in sub-second complex systems. Results Phys. 2017, 7, 3024–3030. [Google Scholar] [CrossRef]
- Johnson, N.F. Simply Complexity; Oneworld: Oxford, UK, 2009. [Google Scholar]
- U.S. Commodity Futures Trading Commission. Findings Regarding the Market Events of 6 May 2010. Available online: http://www.sec.gov/news/studies/2010/marketevents-report.pdf (accessed on 1 October 2017).
- Krafcik, J. Say Hello to Waymo: What’s Next for Google’s Self-Driving Car Project. Available online: https://medium.com/waymo/say-hello-to-waymo-whats-next-for-google-s-self-driving-car-project-b854578b24ee.mrpkjhhm9 (accessed on 22 February 2016).
- Uber to Introduce Self-Driving Cars within Weeks. Available online: http://www.bbc.com/news/technology-37117831. (accessed on 18 August 2016).
- Kramer, D. White House Encourages Adoption of Drones. Phys. Today 2016. Available online: http://scitation.aip.org/content/aip/magazine/physicstoday/news/10.1063/PT.5.1080?utm_source=Physics%20Today&utm_medium=email&utm_campaign=7427978_The%20week%20in%20Physics%208\T1\textendash12%20August&dm_i=1Y69,4F7GQ,E1O09U,GA27B,1 (accessed on 9 August 2016).
- Vespignani, A. Predicting the behavior of techno-social systems. Science 2009, 325, 425–428. [Google Scholar] [CrossRef] [PubMed]
- Eagleman, D. How does the timing of neural signals map onto the timing of perception? In Space and Time in Perception and Action; Nijhawan, R., Ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Johnson, N.F.; Hart, M.; Hui, P.M.; Zheng, D. Trader dynamics in a model market. Int. J. Theor. Appl. Financ. 2000, 3, 443. [Google Scholar] [CrossRef]
- Johnson, N.F.; Jefferies, P.; Hui, P.M. Financial Market Complexity; Jefferies, P., Phil, D., Eds.; Oxford University Press: Oxford, UK, 2003; Chapter 4. [Google Scholar]
- Jefferies, P.; Lamper, D.; Johnson, N.F. Anatomy of extreme events in a complex adaptive system. Phys. A Stat. Mech. Appl. 2003, 318, 592–600. [Google Scholar] [CrossRef]
- Johnson, N.F.; Hui, P.M. Crowd-anticrowd theory of dynamical behavior in competitive, multi-agent autonomous systems and networks. J. Comput. Intell. Electron. Syst. 2015, 3, 256–277. [Google Scholar] [CrossRef]
- Moro, E. The Minority Game: An Introductory Guide. Available online: http://arxiv.org/pdf/cond-mat/0402651.pdf (accessed on 1 October 2017).
- Challet, D.; Chessa, A.; Marsili, A.; Chang, Y.C. From Minority Games to Real Markets. Quant. Financ. 2001, 1, 168–176. [Google Scholar] [CrossRef]
- Jefferies, P.; Hart, M.; Johnson, N.F. Deterministic dynamics in the minority game. Phys. Rev. E 2002, 65, 016105. [Google Scholar] [CrossRef] [PubMed]
- Choe, S.C.; Johnson, N.F.; Hui, P.M. Error-driven global transition in a competitive population on a network. Phys. Rev. E 2004, 70, 055101. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Yang, G.; Wang, W.; Chen, Y.; Huang, J.; Ohashi, H.; Stanley, H.E. Herd behavior in a complex adaptive system. Proc. Natl. Acad. Sci. USA 2011, 108, 15058. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; An, K.N.; Yang, G.; Huang, J.P. Contrarian behavior in a complex adaptive system. Phys. Rev. E 2013, 87, 012809. [Google Scholar] [CrossRef] [PubMed]
- Helbing, D. Dynamic Decision Behavior and Optimal Guidance Through Information Services: Models and Experiments. In Human Behaviour and Traffic Networks; Schreckenberg, M., Selten, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; p. 47. [Google Scholar]
- Cartlidge, J.; Szostek, C.; De Luca, M.; Cliff, D. Too fast, too furious. In Proceedings of the 4th International Conference on Agents & Artificial Intelligence, Vilamoura, Portugal, 6–8 February 2012. [Google Scholar]
- Johnson, N.F. To slow or not? Challenges in subsecond networks. Science 2017, 355, 801–802. [Google Scholar] [CrossRef] [PubMed]
- Johnson, N.F.; Tivnan, B. Mechanistic origin of dragon-kings in a population of competing agents. Eur. Phys. J. Spec. Top. 2012, 205, 65–78. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manrique, P.D.; Zheng, M.; Cao, Z.; Johnson Restrepo, D.D.; Hui, P.M.; Johnson, N.F. Subsecond Tsunamis and Delays in Decentralized Electronic Systems. Electronics 2017, 6, 80. https://doi.org/10.3390/electronics6040080
Manrique PD, Zheng M, Cao Z, Johnson Restrepo DD, Hui PM, Johnson NF. Subsecond Tsunamis and Delays in Decentralized Electronic Systems. Electronics. 2017; 6(4):80. https://doi.org/10.3390/electronics6040080
Chicago/Turabian StyleManrique, Pedro D., Minzhang Zheng, Zhenfeng Cao, David Dylan Johnson Restrepo, Pak Ming Hui, and Neil F. Johnson. 2017. "Subsecond Tsunamis and Delays in Decentralized Electronic Systems" Electronics 6, no. 4: 80. https://doi.org/10.3390/electronics6040080



