Theoretical Tools for Relativistic Gravimetry, Gradiometry and Chronometric Geodesy and Application to a Parameterized Post-Newtonian Metric
Abstract
:1. Introduction
2. Review of Past Work in Relativistic Gravimetry, Gradiometry and Chronometric Geodesy
2.1. Chronometric Geodesy
2.2. The Chronometric Geoid
“The relativistic geoid is the surface where precise clocks run with the same speed and the surface is nearest to mean sea level”
2.3. Gravimetry and Gradiometry
3. Theoretical Tools of Relativistic Geodesy
3.1. Notations and Conventions
3.2. The Local Frame
The Proper Reference Frame
- On the observer world line, the temporal coordinate of the proper reference frame is equal to the proper time τ of the observer, and the spatial coordinates are constant.
- At first order in the new coordinates , we want to recover the metric of an accelerated and rotating observer in special relativity [44].
The Fermi Normal Frame
3.3. Geodesic Equation in the Local Frame
3.3.1. Gravimetric Observables
3.3.2. Gradiometric Observables
3.4. Clock Frequency Comparisons and Syntonization
4. Application to a Stationary PPN Metric Tensor
4.1. PPN Metric of an Isolated, Axisymmetric Rotating Body
4.2. Clock Observables
4.3. Gravimetry Observables
4.4. Gradiometry Observables
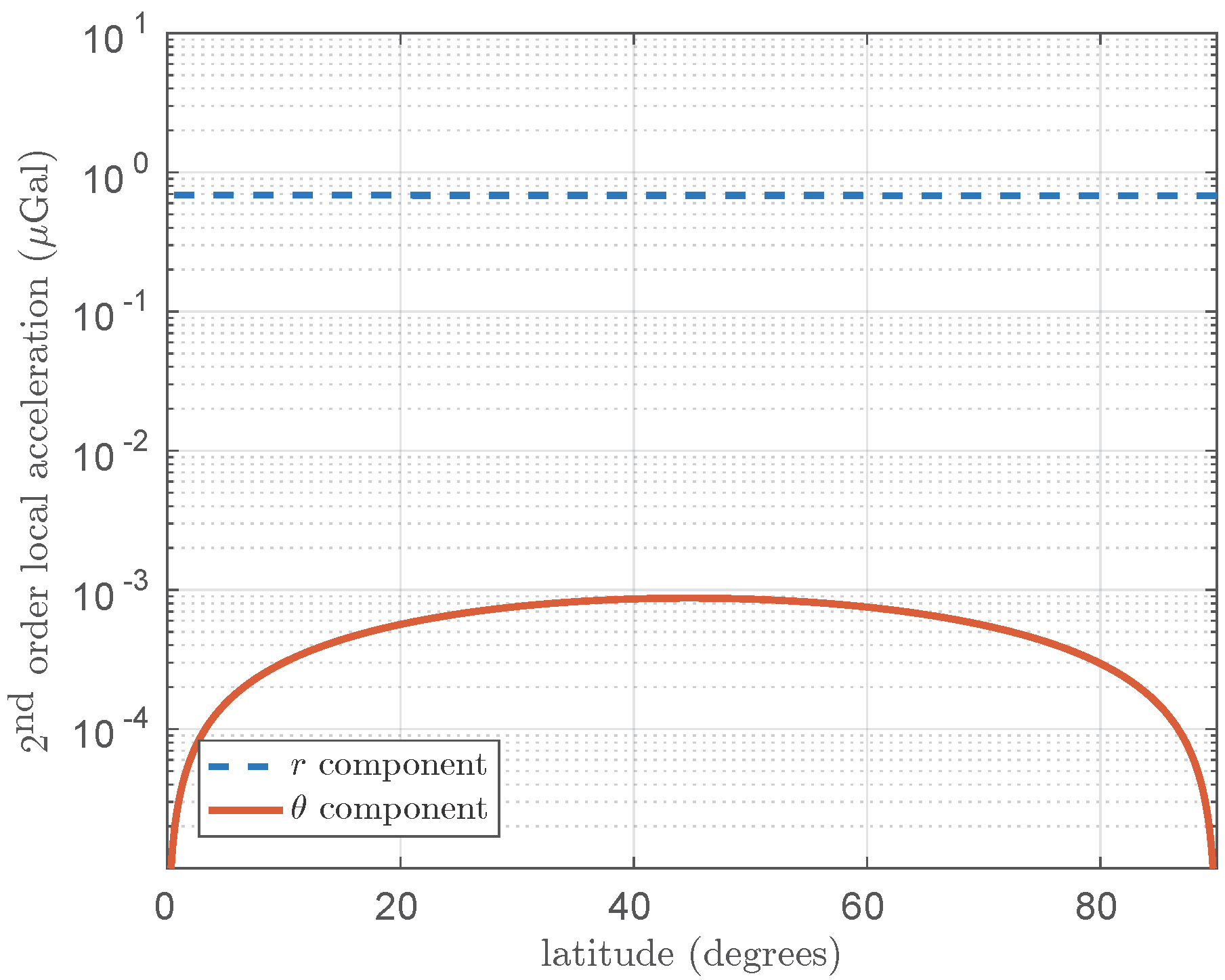
5. Orders of Magnitudes
6. Conclusions
- differences between the chronometric geoid and the Newtonian geoid are of order 2 mm;
- post-Newtonian corrections for gravimeters are below or just at the level of current accuracy of the best absolute gravimeters, which is about 1 μGal;
- post-Newtonian corrections for gradiometers are below current accuracy, a few E, but could be measurable by integrating for a long time.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cacciapuoti, L.; Salomon, C. Space Clocks and Fundamental Tests: The ACES Experiment. Eur. Phys. J. Spec. Top. 2009, 172, 57–68. [Google Scholar] [CrossRef]
- Koller, S.B.; Grotti, J.; Vogt, S.; Al-Masoudi, A.; Dörscher, S.; Häfner, S.; Sterr, U.; Lisdat, C. Transportable Optical Lattice Clock with 7 × 10−17 Uncertainty. Phys. Rev. Lett. 2017, 118, 073601. [Google Scholar] [CrossRef] [PubMed]
- Delva, P.; Lodewyck, J. Atomic Clocks: New Prospects in Metrology and Geodesy. Acta Futura 2013, 7, 67–78. [Google Scholar]
- Flury, J. Relativistic Geodesy. J. Phys. Conf. Ser. 2016, 723, 012051. [Google Scholar] [CrossRef]
- Denker, H.; Timmen, L.; Voigt, C.; Weyers, S.; Peik, E.; Margolis, H.S.; Delva, P.; Wolf, P.; Petit, G. Geodetic methods to determine the relativistic redshift at the level of 10−18 in the context of international timescales—A review and practical results. J. Geod. 2017, in press. [Google Scholar]
- Müller, J.; Soffel, M.; Klioner, S.A. Geodesy and Relativity. J. Geod. 2007, 82, 133–145. [Google Scholar] [CrossRef]
- Soffel, M.; Kopeikin, S.; Han, W.B. Advanced Relativistic VLBI Model for Geodesy. J. Geod. 2016, 1–19. [Google Scholar] [CrossRef]
- Will, C.M. Relativistic Gravity in the Solar System. II. Anisotropy in the Newtonian Gravitational Constant. Astrophys. J. 1971, 169, 141–155. [Google Scholar] [CrossRef]
- Will, C.M. Theoretical Frameworks for Testing Relativistic Gravity. II. Parametrized Post-Newtonian Hydrodynamics, and the Nordtvedt Effect. Astrophys. J. 1971, 163, 611–628. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- Vermeer, M. Chronometric Levelling; Technical Report; Finnish Geodetic Institute: Helsinki, Finland, 1983. [Google Scholar]
- Margolis, H.; Godun, R.; Gill, P.; Johnson, L.; Shemar, S.; Whibberley, P.; Calonico, D.; Levi, F.; Lorini, L.; Pizzocaro, M.; et al. International Timescales with Optical Clocks (ITOC). In Proceedings of the 2013 Joint European Frequency and Time Forum International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 21–25 July 2013; pp. 908–911.
- Petit, G.; Wolf, P.; Delva, P. Atomic Time, Clocks, and Clock Comparisons in Relativistic Spacetime: A Review. In Frontiers in Relativistic Celestial Mechanics—Volume 2: Applications and Experiments; Kopeikin, S.M., Ed.; De Gruyter Studies in Mathematical Physics; De Gruyter: Berlin, Germany, 2014; pp. 249–279. [Google Scholar]
- Brumberg, V.A.; Groten, E. On Determination of Heights by Using Terrestrial Clocks and GPS Signals. J. Geod. 2002, 76, 49–54. [Google Scholar] [CrossRef]
- Bondarescu, R.; Bondarescu, M.; Hetényi, G.; Boschi, L.; Jetzer, P.; Balakrishna, J. Geophysical Applicability of Atomic Clocks: Direct Continental Geoid Mapping. Geophys. J. Int. 2012, 191, 78–82. [Google Scholar] [CrossRef]
- Chou, C.W.; Hume, D.B.; Rosenband, T.; Wineland, D.J. Optical Clocks and Relativity. Science 2010, 329, 1630–1633. [Google Scholar] [CrossRef] [PubMed]
- Lion, G.; Panet, I.; Wolf, P.; Guerlin, C.; Bize, S.; Delva, P. Determination of a High Spatial Resolution Geopotential Model Using Atomic Clock Comparisons. J. Geod. 2017, 1–15. [Google Scholar] [CrossRef]
- Bjerhammar, A. On a Relativistic Geodesy. Bull. Geod. 1985, 59, 207–220. [Google Scholar] [CrossRef]
- Bjerhammar, A. Relativistic Geodesy; Technical Report NON118 NGS36; National Oceanic and Atmospheric Administration (NOAA): Silver Spring, MD, USA, 1986.
- Soffel, M.; Herold, H.; Ruder, H.; Schneider, M. Relativistic Theory of Gravimetric Measurements and Definition of the Geoid. Manuscr. Geod. 1988, 13, 143–146. [Google Scholar]
- Soffel, M.H. Relativity in Astrometry, Celestial Mechanics, and Geodesy; Springer: New York, NY, USA, 1989. [Google Scholar]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Kopejkin, S.M. Relativistic Manifestations of Gravitational Fields in Gravimetry and Geodesy. Manuscr. Geod. 1991, 16, 301–312. [Google Scholar]
- Kopeikin, S.M.; Efroimsky, M.; Kaplan, G. Relativistic Celestial Mechanics of the Solar System; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Kopeikin, S.M.; Mazurova, E.M.; Karpik, A.P. Towards an Exact Relativistic Theory of Earth’s Geoid Undulation. Phys. Lett. A 2015, 379, 1555–1562. [Google Scholar] [CrossRef]
- Kopeikin, S.M.; Han, W.; Mazurova, E. Post-Newtonian Reference Ellipsoid for Relativistic Geodesy. Phys. Rev. D 2016, 93, 044069. [Google Scholar] [CrossRef]
- Kopeikin, S.M. Reference Ellipsoid and Geoid in Chronometric Geodesy. Front. Astron. Space Sci. 2016, 3, 5. [Google Scholar] [CrossRef]
- Iorio, L. On the Impossibility of Measuring the General Relativistic Part of the Terrestrial Acceleration of Gravity with Superconducting Gravimeters. Geophys. J. Int. 2006, 167, 567–569. [Google Scholar] [CrossRef]
- Mashhoon, B.; Theiss, D.S. Relativistic Tidal Forces and the Possibility of Measuring Them. Phys. Rev. Lett. 1982, 49, 1542–1545. [Google Scholar] [CrossRef]
- Theiss, D.S. A General Relativistic Effect of a Rotating Spherical Mass and the Possibility of Measuring It in a Space Experiment. Phys. Lett. A 1985, 109, 19–22. [Google Scholar] [CrossRef]
- Mashhoon, B.; Paik, H.J.; Will, C.M. Detection of the Gravitomagnetic Field Using an Orbiting Superconducting Gravity Gradiometer. Theoretical Principles. Phys. Rev. D 1989, 39, 2825–2838. [Google Scholar] [CrossRef]
- Li, X.Q.; Shao, M.X.; Paik, H.J.; Huang, Y.C.; Song, T.X.; Bian, X. Effects of Satellite Positioning Errors and Earth’s Multipole Moments in the Detection of the Gravitomagnetic Field with an Orbiting Gravity Gradiometer. Gen. Relativ. Gravit. 2014, 46, 1–14. [Google Scholar] [CrossRef]
- Xu, P.; Paik, H.J. First-Order Post-Newtonian Analysis of the Relativistic Tidal Effects for Satellite Gradiometry and the Mashhoon-Theiss Anomaly. Phys. Rev. D 2016, 93, 044057. [Google Scholar] [CrossRef]
- Bini, D.; Mashhoon, B. Relativistic Gravity Gradiometry. Phys. Rev. D 2016, 94, 124009. [Google Scholar] [CrossRef]
- Qiang, L.E.; Xu, P. Testing Chern-Simons Modified Gravity with Orbiting Superconductive Gravity Gradiometers: The Non-Dynamical Formulation. Gen. Relativ. Gravit. 2015, 47, 1–15. [Google Scholar] [CrossRef]
- Qiang, L.E.; Xu, P. Probing the Post-Newtonian Physics of Semi-Conservative Metric Theories through Secular Tidal Effects in Satellite Gradiometry Missions. Int. J. Mod. Phys. D 2016, 25, 1650070. [Google Scholar] [CrossRef]
- Soffel, M.; Klioner, S.A.; Petit, G.; Wolf, P.; Kopeikin, S.M.; Bretagnon, P.; Brumberg, V.A.; Capitaine, N.; Damour, T.; Fukushima, T.; et al. The IAU 2000 Resolutions for Astrometry, Celestial Mechanics, and Metrology in the Relativistic Framework: Explanatory Supplement. Astron. J. 2003, 126, 2687–2706. [Google Scholar] [CrossRef]
- Fukushima, T. The Fermi Coordinate System in the Post-Newtonian Framework. Celest. Mech. 1988, 44, 61–75. [Google Scholar] [CrossRef]
- Ashby, N.; Bertotti, B. Relativistic Perturbations of an Earth Satellite. Phys. Rev. Lett. 1984, 52, 485–488. [Google Scholar] [CrossRef]
- Ashby, N.; Bertotti, B. Relativistic Effects in Local Inertial Frames. Phys. Rev. D 1986, 34, 2246–2259. [Google Scholar] [CrossRef]
- Kostić, U.; Horvat, M.; Gomboc, A. Relativistic Positioning System in Perturbed Spacetime. Class. Quantum Gravity 2015, 32, 215004. [Google Scholar] [CrossRef]
- De Felice, F.; Bini, D. Classical Measurements in Curved Space-Times; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: New York, NY, USA, 1973. [Google Scholar]
- Delva, P.; Angonin, M.C. Extended Fermi Coordinates. Gen. Relativ. Gravit. 2012, 44, 1–19. [Google Scholar] [CrossRef]
- Kopejkin, S.M. Celestial Coordinate Reference Systems in Curved Space-Time. Celest. Mech. 1988, 44, 87–115. [Google Scholar] [CrossRef]
- Damour, T.; Soffel, M.; Xu, C. General-Relativistic Celestial Mechanics. I. Method and Definition of Reference Systems. Phys. Rev. D 1991, 43, 3273–3307. [Google Scholar] [CrossRef]
- Brumberg, V.A.; Kopejkin, S.M. Relativistic Reference Systems and Motion of Test Bodies in the Vicinity of the Earth. Nuovo Cimento 1989, 103, 63–98. [Google Scholar] [CrossRef]
- Li, W.Q.; Ni, W.T. Coupled Inertial and Gravitational Effects in the Proper Reference Frame of an Accelerated, Rotating Observer. J. Math. Phys. 1979, 20, 1473–1480. [Google Scholar] [CrossRef]
- Blanchet, L.; Salomon, C.; Teyssandier, P.; Wolf, P. Relativistic Theory for Time and Frequency Transfer to Order. Astron. Astrophys. 2001, 370, 320–329. [Google Scholar] [CrossRef]
- Linet, B.; Teyssandier, P. Time transfer and frequency shift to the order 1/c4 in the field of an axisymmetric rotating body. Phys. Rev. D 2002, 66, 024045. [Google Scholar] [CrossRef]
- Geršl, J.; Delva, P.; Wolf, P. Relativistic Corrections for Time and Frequency Transfer in Optical Fibres. Metrologia 2015, 52, 552. [Google Scholar] [CrossRef]
- Sánchez, L. Towards a Vertical Datum Standardisation under the Umbrella of Global Geodetic Observing System. J. Geod. Sci. 2012, 2, 325–342. [Google Scholar] [CrossRef]
- Burša, M.; Kenyon, S.; Kouba, J.; Šíma, Z.; Vatrt, V.; Vítek, V.; Vojtíšková, M. The Geopotential Value W0 for Specifying the Relativistic Atomic Time Scale and a Global Vertical Reference System. J. Geod. 2006, 81, 103–110. [Google Scholar] [CrossRef]
- Dayoub, N.; Edwards, S.J.; Moore, P. The Gauss–Listing Geopotential Value W0 and Its Rate from Altimetric Mean Sea Level and GRACE. J. Geod. 2012, 86, 681–694. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. Sea Level Projections to AD2500 with a New Generation of Climate Change Scenarios. Glob. Planet. Chang. 2012, 80–81, 14–20. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A Test of General Relativity Using Radio Links with the Cassini Spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic Effects and Dark Matter in the Solar System from Observations of Planets and Spacecraft. Mon. Not. R. Astron. Soc. 2013, 432, 3431–3437. [Google Scholar] [CrossRef]
- Iorio, L. Constraining the preferred frame α1, α2 parameters from Solar System planetary precessions. Int. J. Mod. Phys. D 2013, 23, 1450006. [Google Scholar] [CrossRef]
- Debono, I.; Smoot, G.F. General Relativity and Cosmology: Unsolved Questions and Future Directions. Universe 2016, 2, 23. [Google Scholar] [CrossRef]
- Soffel, M.; Frutos, F. On the Usefulness of Relativistic Space-Times for the Description of the Earth’s Gravitational Field. J. Geod. 2016, 90, 1345–1357. [Google Scholar] [CrossRef]
- Iorio, L.; Lichtenegger, H.I.M.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense-Thirring Effect in the Solar System. Astrophys. Space Sci. 2010, 331, 351–395. [Google Scholar] [CrossRef]
- Renzetti, G. History of the Attempts to Measure Orbital Frame-Dragging with Artificial Satellites. Open Phys. 2013, 11, 531–544. [Google Scholar] [CrossRef]
- Ciufolini, I.; Wheeler, J.A. Gravitation and Inertia; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Angonin, M.C.; Tourrenc, P.; Delva, P. Cold Atom Interferometer in a Satellite: Orders of Magnitude of the Tidal Effect. Appl. Phys. B 2006, 84, 579–584. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Muhlfelder, B.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Silbergleit, A.S.; Acworth, E.B.; Adams, M.; Adler, R.; Bencze, W.J.; et al. The Gravity Probe B Test of General Relativity. Class. Quantum Gravity 2015, 32, 224001. [Google Scholar] [CrossRef]
- Iorio, L. An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense-Thirring Effect with Satellite Laser Ranging. Space Sci. Rev. 2009, 148, 363–381. [Google Scholar] [CrossRef]
- Renzetti, G. First Results from LARES: An Analysis. New Astron. 2013, 23–24, 63–66. [Google Scholar] [CrossRef]
- Paik, H.J. Detection of the Gravitomagnetic Field Using an Orbiting Superconducting Gravity Gradiometer: Principle and Experimental Considerations. Gen. Relativ. Gravit. 2008, 40, 907–919. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delva, P.; Geršl, J. Theoretical Tools for Relativistic Gravimetry, Gradiometry and Chronometric Geodesy and Application to a Parameterized Post-Newtonian Metric. Universe 2017, 3, 24. https://doi.org/10.3390/universe3010024
Delva P, Geršl J. Theoretical Tools for Relativistic Gravimetry, Gradiometry and Chronometric Geodesy and Application to a Parameterized Post-Newtonian Metric. Universe. 2017; 3(1):24. https://doi.org/10.3390/universe3010024
Chicago/Turabian StyleDelva, Pacôme, and Jan Geršl. 2017. "Theoretical Tools for Relativistic Gravimetry, Gradiometry and Chronometric Geodesy and Application to a Parameterized Post-Newtonian Metric" Universe 3, no. 1: 24. https://doi.org/10.3390/universe3010024




