AdS/CFT in Fractional Dimension and Higher-Spins at One Loop
Abstract
:1. Introduction
2. Higher-Spin Partition Function in Fractional Dimensions
2.1. Integer Dimensions
2.2. Fractional Dimensions
2.3. Volume of Hyperbolic Space
2.4. Non-Minimal Type-A
2.5. Minimal Type-A
2.6. Matching Free Vector Model
2.7. Matching Critical Vector Model
3. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. From Intermediate to Final Form
Appendix B. Modified Zeta Function
Appendix B.1. Zeta
Appendix B.2. Deficit
Appendix B.2.1. d = 3
Appendix B.2.2. d = 5
References
- Maldacena, J.M. The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from non-critical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Polyakov, A.M. AdS dual of the critical O(N) vector model. Phys. Lett. B 2002, 550, 213–219. [Google Scholar] [CrossRef]
- Brezin, E.; Wallace, D.J.; Wilson, K. Feynman-graph expansion for the equation of state near the critical point. Phys. Rev. B 1973, 7, 232–239. [Google Scholar] [CrossRef]
- Wilson, K.G.; Kogut, J.B. The Renormalization group and the epsilon expansion. Phys. Rep. 1974, 12, 75–200. [Google Scholar] [CrossRef]
- Sundborg, B. Stringy gravity, interacting tensionless strings and massless higher spins. Nucl. Phys. Proc. Suppl. 2001, 102, 113–119. [Google Scholar] [CrossRef]
- Sezgin, E.; Sundell, P. Massless higher spins and holography. Nucl. Phys. 2002, B644, 303–370. [Google Scholar] [CrossRef]
- Sezgin, E.; Sundell, P. Holography in 4D (super) higher spin theories and a test via cubic scalar couplings. J. High Energy Phys. 2005, 2005, 044. [Google Scholar] [CrossRef]
- Leigh, R.G.; Petkou, A.C. Holography of the N = 1 higher spin theory on AdS(4). J. High Energy Phys. 2003, 2003, 011. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R. Interpolating between a and F. J. High Energy Phys. 2015, 2015, 117. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R. One Loop Tests of Higher Spin AdS/CFT. J. High Energy Phys. 2013, 2013, 068. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Safdi, B.R. Higher Spin AdSd+1/CFTd at One Loop. Phys. Rev. D 2014, 89, 084004. [Google Scholar] [CrossRef]
- Vasiliev, A.N.; Pismak, Y.M.; Khonkonen, Y.R. Simple Method of Calculating the Critical Indices in the 1/N Expansion. Theor. Math. Phys. 1981, 46, 104–113. [Google Scholar] [CrossRef]
- Lang, K.; Ruhl, W. The Critical O(N) sigma model at dimensions 2 < d < 4: Fusion coefficients and anomalous dimensions. Nucl. Phys. B 1993, 400, 597–623. [Google Scholar]
- Petkou, A. Conserved currents, consistency relations and operator product expansions in the conformally invariant O(N) vector model. Ann. Phys. 1996, 249, 180–221. [Google Scholar] [CrossRef]
- Moshe, M.; Zinn-Justin, J. Quantum field theory in the large N limit: A Review. Phys. Rep. 2003, 385, 69–228. [Google Scholar] [CrossRef]
- El-Showk, S.; Paulos, M.; Poland, D.; Rychkov, S.; Simmons-Duffin, D.; Vichi, A. Conformal Field Theories in Fractional Dimensions. Phys. Rev. Lett. 2014, 112, 141601. [Google Scholar] [CrossRef] [PubMed]
- Fei, L.; Giombi, S.; Klebanov, I.R. Critical O(N) models in 6-ϵ dimensions. Phys. Rev. D 2014, 90, 025018. [Google Scholar] [CrossRef]
- Mati, P. Critical scaling in the large-N O(N) model in higher dimensions and its possible connection to quantum gravity. Phys. Rev. D 2016, 94, 065025. [Google Scholar] [CrossRef]
- Zamolodchikov, A.B. Irreversibility of the Flux of the Renormalization Group in a 2D Field Theory. JETP Lett. 1986, 43, 730–732. [Google Scholar]
- Cardy, J.L. Is There a c Theorem in Four-Dimensions? Phys. Lett. B 1988, 215, 749–752. [Google Scholar] [CrossRef]
- Komargodski, Z.; Schwimmer, A. On Renormalization Group Flows in Four Dimensions. J. High Energy Phys. 2011, 2011, 099. [Google Scholar] [CrossRef]
- Myers, R.C.; Sinha, A. Seeing a c-theorem with holography. Phys. Rev. D 2010, 82, 046006. [Google Scholar] [CrossRef]
- Jafferis, D.L.; Klebanov, I.R.; Pufu, S.S.; Safdi, B.R. Towards the F-Theorem: N = 2 Field Theories on the Three-Sphere. J. High Energy Phys. 2011, 2011, 102. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Pufu, S.S.; Safdi, B.R. F-Theorem without Supersymmetry. J. High Energy Phys. 2011, 2011, 038. [Google Scholar] [CrossRef]
- Casini, H.; Huerta, M.; Myers, R.C. Towards a derivation of holographic entanglement entropy. J. High Energy Phys. 2011, 2011, 036. [Google Scholar] [CrossRef]
- Casini, H.; Huerta, M. On the RG running of the entanglement entropy of a circle. Phys. Rev. D 2012, 85, 125016. [Google Scholar] [CrossRef]
- Affleck, I.; Ludwig, A.W.W. Universal noninteger ‘ground state degeneracy’ in critical quantum systems. Phys. Rev. Lett. 1991, 67, 161–164. [Google Scholar] [CrossRef] [PubMed]
- Gubser, S.S.; Klebanov, I.R. A Universal result on central charges in the presence of double trace deformations. Nucl. Phys. B 2003, 656, 23–36. [Google Scholar] [CrossRef]
- Diaz, D.E.; Dorn, H. Partition functions and double-trace deformations in AdS/CFT. J. High Energy Phys. 2007, 2007, 046. [Google Scholar] [CrossRef]
- Allais, A. Double-trace deformations, holography and the c-conjecture. J. High Energy Phys. 2010, 2010, 040. [Google Scholar] [CrossRef]
- Aros, R.; Diaz, D.E. Determinant and Weyl anomaly of Dirac operator: A holographic derivation. J. Phys. A 2012, 45, 125401. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Tseytlin, A.A. Partition Functions and Casimir Energies in Higher Spin AdSd+1/CFTd. Phys. Rev. D 2014, 90, 024048. [Google Scholar] [CrossRef]
- Beccaria, M.; Tseytlin, A.A. Higher spins in AdS5 at one loop: Vacuum energy, boundary conformal anomalies and AdS/CFT. J. High Energy Phys. 2014, 2014, 114. [Google Scholar] [CrossRef]
- Beccaria, M.; Bekaert, X.; Tseytlin, A.A. Partition function of free conformal higher spin theory. J. High Energy Phys. 2014, 2014, 113. [Google Scholar] [CrossRef] [Green Version]
- Beccaria, M.; Tseytlin, A.A. Vectorial AdS5/CFT4 duality for spin-one boundary theory. J. Phys. A 2014, 47, 492001. [Google Scholar] [CrossRef]
- Beccaria, M.; Macorini, G.; Tseytlin, A.A. Supergravity one-loop corrections on AdS7 and AdS3, higher spins and AdS/CFT. Nucl. Phys. B 2015, 892, 211–238. [Google Scholar] [CrossRef] [Green Version]
- Basile, T.; Bekaert, X.; Boulanger, N. Flato-Fronsdal theorem for higher-order singletons. J. High Energy Phys. 2014, 2014, 131. [Google Scholar] [CrossRef]
- Beccaria, M.; Tseytlin, A.A. On higher spin partition functions. J. Phys. A 2015, 48, 275401. [Google Scholar] [CrossRef]
- Beccaria, M.; Tseytlin, A.A. Iterating free-field AdS/CFT: Higher spin partition function relations. J. Phys. A 2016, 49, 295401. [Google Scholar] [CrossRef]
- Bae, J.-B.; Joung, E.; Lal, S. One-loop test of free SU(N) adjoint model holography. J. High Energy Phys. 2016, 2016, 061. [Google Scholar] [CrossRef]
- Bae, J.-B.; Joung, E.; Lal, S. On the Holography of Free Yang-Mills. J. High Energy Phys. 2016, 2016, 074. [Google Scholar] [CrossRef]
- Pang, Y.; Sezgin, E.; Zhu, Y. One Loop Tests of Supersymmetric Higher Spin AdS4/CFT3. Phys. Rev. D 2017, 95, 026008. [Google Scholar] [CrossRef]
- Günaydin, M.; Skvortsov, E.D.; Tran, T. Exceptional F(4) higher-spin theory in AdS6 at one-loop and other tests of duality. J. High Energy Phys. 2016, 2016, 168. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Tan, Z. M. The ABC of Higher-Spin AdS/CFT. arXiv 2006, arXiv:1608.07611. [Google Scholar]
- Bae, J.-B.; Joung, E.; Lal, S. A note on vectorial AdS5/CFT4 duality for spin-j boundary theory. J. High Energy Phys. 2016, 2016, 077. [Google Scholar] [CrossRef]
- Brust, C.; Hinterbichler, K. Partially Massless Higher-Spin Theory II: One-Loop Effective Actions. J. High Energy Phys. 2017, 2017, 126. [Google Scholar] [CrossRef]
- Maldacena, J.; Zhiboedov, A. Constraining Conformal Field Theories with A Higher Spin Symmetry. arXiv 2011, arXiv:1112.1016. [Google Scholar]
- Alba, V.; Diab, K. Constraining conformal field theories with a higher spin symmetry in d = 4. arXiv 2013, arXiv:1307.8092. [Google Scholar]
- Boulanger, N.; Ponomarev, D.; Skvortsov, E.; Taronna, M. On the uniqueness of higher-spin symmetries in AdS and CFT. arXiv 2013, arXiv:1307.8092. [Google Scholar]
- Stanev, Y.S. Constraining conformal field theory with higher spin symmetry in four dimensions. Nucl. Phys. 2013, B876, 651–666. [Google Scholar] [CrossRef]
- Alba, V.; Diab, K. Constraining conformal field theories with a higher spin symmetry in d > 3 dimensions. arXiv 2015, arXiv:1510.02535. [Google Scholar]
- Dowker, J.S.; Critchley, R. Effective Lagrangian and Energy Momentum Tensor in de Sitter Space. Phys. Rev. D 1976, 13, 3224–3232. [Google Scholar] [CrossRef]
- Hawking, S.W. Zeta Function Regularization of Path Integrals in Curved Space-Time. Commun. Math. Phys. 1977, 55, 133–148. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Nonlinear equations for symmetric massless higher spin fields in (A)dS(d). Phys. Lett. B 2003, 567, 139–151. [Google Scholar] [CrossRef]
- Camporesi, R.; Higuchi, A. Spectral functions and zeta functions in hyperbolic spaces. J. Math. Phys. 1994, 35, 4217–4246. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Tarnopolsky, G. Conformal QEDd, F-Theorem and the ϵ Expansion. J. Phys. A 2016, 49, 135403. [Google Scholar] [CrossRef]
- Brust, C.; Hinterbichler, K. Free □k scalar conformal field theory. J. High Energy Phys. 2017, 2017, 066. [Google Scholar] [CrossRef]
- Giombi, S.; Yin, X. Higher Spin Gauge Theory and Holography: The Three-Point Functions. J. High Energy Phys. 2010, 2010, 115. [Google Scholar] [CrossRef]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Towards holographic higher-spin interactions: Four-point functions and higher-spin exchange. J. High Energy Phys. 2015, 2015, 170. [Google Scholar] [CrossRef]
- Skvortsov, E.D. On (Un)Broken Higher-Spin Symmetry in Vector Models. In Proceedings of the International Workshop on Higher Spin Gauge Theories, Singapore, 4–6 November 2015; 2017; pp. 103–137. [Google Scholar]
- Muta, T.; Popovic, D.S. Anomalous Dimensions of Composite Operators in the Gross-Neveu Model in Two + Epsilon Dimensions. Prog. Theor. Phys. 1977, 57, 1705–1719. [Google Scholar] [CrossRef]
- Giombi, S.; Gurucharan, V.; Kirilin, V.; Prakash, S.; Skvortsov, E. On the Higher-Spin Spectrum in Large N Chern-Simons Vector Models. J. High Energy Phys. 2017, 2017, 058. [Google Scholar] [CrossRef]
- Giombi, S.; Kirilin, V. Anomalous dimensions in CFT with weakly broken higher spin symmetry. J. High Energy Phys. 2016, 2016, 068. [Google Scholar] [CrossRef]
- Giombi, S.; Kirilin, V.; Skvortsov, E. Notes on Spinning Operators in Fermionic CFT. J. High Energy Phys. 2017, 2017, 041. [Google Scholar] [CrossRef]
- Manashov, A.N.; Skvortsov, E.D. Higher-spin currents in the Gross-Neveu model at 1/n2. J. High Energy Phys. 2017, 2017, 132. [Google Scholar] [CrossRef]
- Manashov, A.N.; Skvortsov, E.D.; Strohmaier, M. Higher spin currents in the critical O(N) vector model at 1/N2. arXiv 2017, arXiv:1706.09256. [Google Scholar]
- Braun, V.M.; Manashov, A.N. Evolution equations beyond one loop from conformal symmetry. Eur. Phys. J. C 2013, 73, 2544. [Google Scholar] [CrossRef]
- Derkachov, S.E.; Gracey, J.A.; Manashov, A.N. Four loop anomalous dimensions of gradient operators in ϕ4 theory. Eur. Phys. J. C 1998, 2, 569–579. [Google Scholar]
- Camporesi, R.; Higuchi, A. Arbitrary spin effective potentials in anti-de Sitter space-time. Phys. Rev. D 1993, 47, 3339–3344. [Google Scholar] [CrossRef]
| 1. | |
| 2. | The second term in the brackets is to subtract the ghosts. |
| 3. | One can represent the spectral zeta-function as a differential operator acting on some seed function that has enough parameters to produce . Character is an example of such a function [42,47], which is also indispensable for taking tensor products. The characters are however difficult to define in non-integer dimension. |
| 4. | For a more detailed discussion see [57]. |
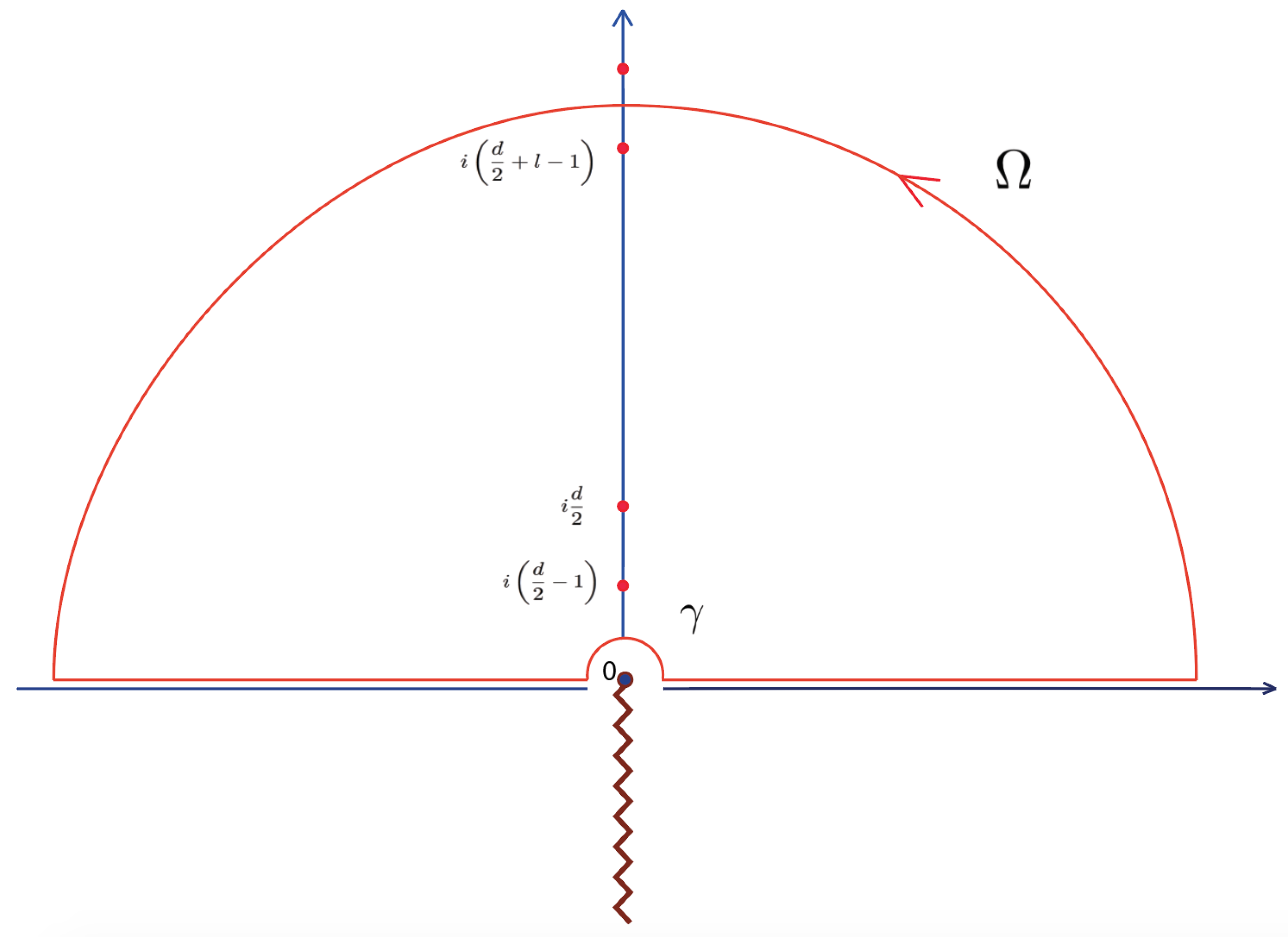
| 5. | The contour is the reflection image of Figure 1 around the real axis. |
| 6. | Recall that . |
| 7. | We refer to it as intermediate as the integral is divergent and requires regularization. |
| 8. | The deficit at order z is just the leftover of without the part including in [45]. This allows us to conclude that the modified zeta function works well for arbitrary dimension since is irrelevant at one loop. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skvortsov, E.; Tran, T. AdS/CFT in Fractional Dimension and Higher-Spins at One Loop. Universe 2017, 3, 61. https://doi.org/10.3390/universe3030061
Skvortsov E, Tran T. AdS/CFT in Fractional Dimension and Higher-Spins at One Loop. Universe. 2017; 3(3):61. https://doi.org/10.3390/universe3030061
Chicago/Turabian StyleSkvortsov, Evgeny, and Tung Tran. 2017. "AdS/CFT in Fractional Dimension and Higher-Spins at One Loop" Universe 3, no. 3: 61. https://doi.org/10.3390/universe3030061



