Cavity Optomechanics with Ultra Cold Atoms in Synthetic Abelian and Non-Abelian Gauge Field
Abstract
:1. Introduction

2. Cavity Optomechanics with Cold Atoms
2.1. Introduction to Cavity Optomechanics
2.1.1. Classical Treatment
2.1.2. Quantum Treatment
2.1.3. Two Level Atom in a Single Mode Cavity
2.1.4. Ultracold Atoms in a Cavity
3. Ultracold Atoms in Abelian and Non-Abelian Gauge Field
3.1. Abelian Gauge Field
3.2. Neutral Cold Atoms in Synthetic Abelian Gauge Field: Rotating Ultracold Condensate

3.3. Geometric Phase in Quantum Mechanics and the Related Gauge Fields
3.4. Ultracold Atoms in Non Abelian Gauge Field

3.4.1. Geometrically Created Non-Abelian Gauge Field
3.5. Synthetic Spin-Orbit Coupling for Ultracold Atomic Gases: Case of Non Abelian Gauge Field
3.6. Principle of Spin Orbit Coupling in Ultracold Bosonic Systems: NIST Method
4. Cavity Optomechanics of Ultracold Fermions in a Synthetic Gauge Field
4.1. Formalism

4.2. The Shubnikov de Hass Oscillation

5. Dynamically Created Spin-Orbit Coupling inside a Cavity
5.1. Synthetic SO Coupling in Ring-Cavity
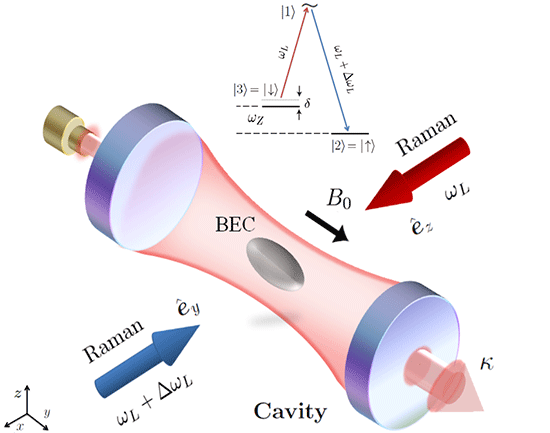
6. Cavity Mediated Spin-Orbit Coupling
7. Spin-Orbit Coupled Ultracold Bosons in a Cavity
7.1. Formalism
7.2. Non-Interacting Limit



7.3. Interaction and Magnetic Order

| Order | |
|---|---|
| zAFM | 0 |
| Stripe | |
| VX | |
| 3-Spiral | |
| 4-Spiral | |
| zFM |


8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lebedew, P. Untersuchungen über die Drucjkäfte des Litches. Ann. Phys. 1901, 311, 433–458. [Google Scholar] [CrossRef]
- Nichols, E.F.; Hull, G.F. A Preliminary Communication on the Pressure of Heat and Light Radiation. Phys. Rev. 1901, 13, 307–320. [Google Scholar] [CrossRef]
- Marquardt, F.; Girvin, S.M. Trend: Optomechanics. Physics 2009, 2, 40. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity Optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Meystre, P.; Schwab, K. Cavity Quantum Optomechanics. Phys. Today 2012, 65, 29–35. [Google Scholar] [CrossRef]
- Meystre, P. A short walk through quantum optomechanics. Ann. Phys. 2013, 525, 215–233. [Google Scholar] [CrossRef]
- Marquardt, F. Quantum Optomechanics. In Quantum Machines: Measurement and Control of Engineered Quantum Systems; Devoret, M., Huard, B., Schoelkopf, R., Cugliandolo, L.F., Eds.; Oxford University Press Canada: Don Mills, ON, Canada, 2014. [Google Scholar]
- Stamper-Kurn, D.M. Cavity Optomechanics with cold atoms. In Cavity Optomechanics; Aspelmeyer, M., Kippenberg, T., Marquardt, F., Eds.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Shore, B.W.; Knight, P.L. The Jaynes-Cummings Model. J. Mod. Opt. 1993, 40, 1195–1238. [Google Scholar] [CrossRef]
- Storey, P.; Collett, A.; Walls, D. Measurement-Induced diffraction and Interference of Atoms. Phys. Rev. Lett. 1992, 68, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Tavis, M.; Cummings, F.W. Exact solution for an N-molecule-Radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379–384. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Pethick, C.J.; Smith, H. Bose Einstein Condensation in Dilute Gases, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Murch, K.W.; Moore, K.L.; Gupta, S.; Stamper-Kurn, D.M. Observation of quantum-measurement backaction with an ultracold atomic gas. Nat. Phys. 2008, 4, 561–564. [Google Scholar] [CrossRef]
- Gupta, S.; Moore, K.L.; Murch, K.W.; Stamper-Kurn, D.M. Cavity Nonlinear Optics at Low Photon Numbers from Collective Atomic Motion. Phys. Rev. Lett. 2007, 99, 213601. [Google Scholar] [CrossRef] [PubMed]
- Purdy, T.P.; Brooks, D.W.C.; Botter, T.; Brahms, N.; Ma, Z.-Y.; Stamper-Kurn, D.M. Tunable Cavity Optomechanics with Ultracold Atoms. Phys. Rev. Lett. 2010, 105, 133602. [Google Scholar] [CrossRef] [PubMed]
- Brennecke, F.; Ritter, S.; Donner, T.; Esslinger, T. Cavity Optomechanics with a Bose Einstein Condensate. Science 2008, 322, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Mekhov, I.B.; Maschler, C.; Ritsch, H. Probing quantum phases of ultracold atoms in optical lattices by transmission spectra in cavity quantum electrodynamics. Nat. Phys. 2007, 3, 319–323. [Google Scholar] [CrossRef]
- Maschler, C.; Mekhov, I.B.; Ritsch, H. Ultracold atoms in optical lattices generated by quantized light fields. Eur. Phys. J. D 2008, 46, 545–560. [Google Scholar] [CrossRef]
- Ritsch, H.; Domokos, P.; Bernnecke, F.; Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 2013, 85, 553–601. [Google Scholar] [CrossRef]
- Elliott, T.J.; Mazzucchi, G.; Kozlowski, W.; Caballero-Benitez, S.F.; Mekhov, I.B. Probing and Manipulating Fermionic and Bosonic Quantum Gases with Quantum Light. Atoms 2015, 3, 392–406. [Google Scholar] [CrossRef]
- Agarwala, A.; Nath, M.; Lugani, J.; Thyagarajan, K.; Ghosh, S. Fock-space exploration by angle-resolved transmission through a quantum diffraction grating of cold atoms in an optical lattice. Phys. Rev. A 2012, 85, 063606. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, K.; Goldbaum, D.S.; Bhattacharya, M.; Meystre, P. Bistable Mott-insulator-to-superfluid phase transition in cavity optomechanics. Phys. Rev. A 2009, 80, 011801. [Google Scholar] [CrossRef]
- Larson, J.; Damski, B.; Morigi, G.; Lewenstein, M. Mott-Insulator States of Ultracold Atoms in Optical Resonators. Phys. Rev. Lett. 2008, 100, 05040. [Google Scholar] [CrossRef] [PubMed]
- Kanamoto, R.; Meystre, P. Optomechanics of a Quantum-Degenerate Fermi Gas. Phys. Rev. Lett. 2010, 104, 063601. [Google Scholar] [CrossRef] [PubMed]
- Dalibard, J.; Gerbier, F.; Juzeliunas, G.; Ohberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523–1543. [Google Scholar] [CrossRef]
- Ghosh, S.; Sachdeva, R. Synthetic Gauge Fields for Ultra Cold Atoms: A Primer. J. Indian Inst. Sci. 2014, 94, 217–232. [Google Scholar]
- Spielman, I. B. Raman processes and effective gauge potentials. Phys. Rev. A. 2009, 79, 063613. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Naschimbene, S. Quantum simulations with ultracold quantum gases. Nat. Phys. Insight 2012, 8, 267–276. [Google Scholar] [CrossRef]
- Larson, J.; Levin, S. Effective Abelian and Non-Abelian Gauge Potentials in Cavity QED. Phys. Rev. Lett. 2009, 103, 013602. [Google Scholar] [CrossRef] [PubMed]
- Mivehvar, F.; Feder, D.L. Synthetic spin-orbit interactions and magnetic fields in ring-cavity QED. Phys. Rev. A 2014, 89, 013803. [Google Scholar] [CrossRef]
- Dong, L.; Zhou, L.; Wu, B.; Ramachandhran, B.; Pu, H. Cavity-assisted dynamical spin-orbit coupling in cold atoms. Phys. Rev. A 2014, 89, 011602(R). [Google Scholar] [CrossRef]
- Padhi, B.; Ghosh, S. Cavity Optomechanics with Synthetic Landau Levels of Ultracold Fermi Gas. Phys. Rev. Lett. 2013, 111, 043603. [Google Scholar] [CrossRef] [PubMed]
- Padhi, B.; Ghosh, S. Spin-orbit-coupled Bose-Einstein condensates in a cavity: Route to magnetic phases through cavity transmission. Phys. Rev. A 2014, 90, 023627. [Google Scholar] [CrossRef]
- Law, C.K. Effective Hamiltonian for the radiation in a cavity with a moving mirror and a time-varying dielectric medium. Phys. Rev. A 1994, 49, 433–437. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.; Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Vidal, S.F. Ultracold Atoms in Optical Cavity. Ph.D. Thesis, Universitat Autonoma de Barcelona, Barcelona, Spain, 2010. [Google Scholar]
- Ludwig, M.; Kubala, B.; Marquardt, F. The optomechanical stability in the quantum regime. New J. Phys. 2008, 10, 095013. [Google Scholar] [CrossRef]
- Maschler, C.; Ritsch, H. Cold Atom Dynamics in a Quantum Optical Lattice Potential. Phys. Rev. Lett. 2005, 95, 260401. [Google Scholar] [CrossRef] [PubMed]
- Pitaevski, L.; Stringari, S. Bose-Einstein Condensation; Clarendon Press: Oxford, UK, 2003. [Google Scholar]
- Berry, M.V. Quantal Phase Factors Accompanying Adiabatic Changes. Proc. R. Soc. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Shapere, A.; Wilczek, F. Geometric Phases in Physics; World Scientific: Singapore, 1989. [Google Scholar]
- Pancharatnam, S. Genneralized theory of interference, and its applications Part I. Coherent pencils. Proc. Ind. Acad. Sci 1956, 44, 247–262. [Google Scholar]
- Mead, C.A.; Truhler, D.G. On the determination of Born-Oppenheimer nuclear motion wave functions including complications due to coniccal intersection and identical nuclei. J. Chem. Phys. 1979, 70, 2284–2296. [Google Scholar] [CrossRef]
- Jackiw, R. Berry’s phase-topological ideas from atomic, molecular and optical physics. Comments At. Mol. Phys. 1988, 21, 71. [Google Scholar]
- Fetter, A.L.; Svidzinsky, A.A. Vortices in a trapped dilute Bose-Einstein condensate. J. Phys. Condens. Matter 2001, 13, R135. [Google Scholar] [CrossRef]
- Ghosh, S. Vortices in Atomic Bose-Einstein Condensates: An Introduction. Ph. Transit. 2004, 77, 625–676. [Google Scholar] [CrossRef]
- Madison, K.W.; Chevy, F.; Wohlleben, W.; Dalibard, J. Vortex Formation in a Stirred Bose-Einstein Condensate. Phys. Rev. Lett. 2000, 84, 806–809. [Google Scholar] [CrossRef] [PubMed]
- Abo-Shaeer, J.R.; Raman, C.; Vogels, J.M.; Ketterle, W. Observation of Vortex Lattices in Bose-Einstein Condensates. Science 2001, 292, 476–479. [Google Scholar] [CrossRef] [PubMed]
- Engels, P.; Coddington, I.; Haljan, P.; Schweikhard, V.; Cornell, E. Observation of Long-Lived Vortex Aggregates in Rapidly Rotating Bose-Einstein Condensates. Phys. Rev. Lett. 2003, 90, 170405. [Google Scholar] [CrossRef] [PubMed]
- Aftalion, A.; Blanck, X.; Dalibard, J. Vortex patterns in a fast rotating Bose-Einstein condensate. Phys. Rev. A 2005, 71, 023611. [Google Scholar] [CrossRef]
- Fetter, A.L. Rotating trapped Bose-Einstein condensates. Rev. Mod. Phys. 2009, 81, 647–691. [Google Scholar] [CrossRef]
- Cooper, N.R. Rapidly Rotating Atomic Gases. Adv. Phys. 2008, 57, 539–616. [Google Scholar] [CrossRef]
- Shankar, R. Principles of Quantum Mechanics; Springer: Berlin, Germany, 2007; Chapter 21. [Google Scholar]
- Lin, Y.-J.; Jimenez-Garcia, K.; Spielman, I.B. Spin-orbit-coupled Bose-Einstein condensates. Nature 2011, 471, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-J.; Compton, R.L.; Jiménez-García, K.; Porto, J.V.; Spielman, I.B. Synthetic magnetic fields for ultracold neutral atoms. Nature 2009, 462, 628–632. [Google Scholar] [CrossRef] [PubMed]
- Sinitsyn, N.A.; Hankiewicz, E.M.; Teizer, W.; Sinova, J. Spin Hall and spin-diagonal conductivity in the presence of Rashba and Dresselhaus spin-orbit coupling. Phys. Rev. B 2004, 70, 081312(R). [Google Scholar] [CrossRef]
- Hassan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Estienne, B.; Hakker, S.M.; Schoutens, K. Particles in non-Abelian gauge potentials: Landau problem and insertion of non-Abelian flux. New J. Phys. 2011, 13, 045012. [Google Scholar] [CrossRef]
- Zhai, H. Spin-Orbit Coupled Quantum Gases. Int. J. Mod. Phys. B 2011, 26, 1230001. [Google Scholar] [CrossRef]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar] [CrossRef]
- Westfahl, H.; Castro-Neto, A.H.; Calderia, A.O. Landau level bosonization of a two-dimensional electron gas. Phys. Rev. B 1997, 55, R7347(R). [Google Scholar] [CrossRef]
- Sadowski, M.L.; Martinez, G.; Potemski, M.; Berger, C.; de Heer, W.A. Landau Level Spectroscopy of Ultrathin Graphite Layers. Phys. Rev. Lett. 2006, 97, 266405. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Cheng, J.; Jing, H.; Yi, S. Bose-Einstein Condensate with Cavity-Mediated Spin-Orbit Coupling. Phys. Rev. Lett. 2014, 112, 143007. [Google Scholar] [CrossRef] [PubMed]
- Mivehvar, F.; Feder, D.L. Enhanced stripe phases in spin-orbit-coupled Bose-Einstein condensates in ring cavities. Phys. Rev. A 2015, 92, 023611. [Google Scholar] [CrossRef]
- Goldman, N.; Kubasiak, A.; Gaspard, P.; Lewenstein, M. Ultracold atomic gases in non-abelian gauge potentials: The case of constant Wilson loop. Phys. Rev. A 2009, 79, 023624. [Google Scholar] [CrossRef]
- Bychkov, Y.A.; Rashba, E.I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C Solid State Phys. 1984, 17, 6039–6045. [Google Scholar] [CrossRef]
- Dresselhaus, G. Spin-Orbit Coupling Effects in Zinc Blende Structures. Phys. Rev. 1955, 100, 580–586. [Google Scholar] [CrossRef]
- Jaksch, D.; Bruder, C.; Cirac, J.I.; Gardiner, C.W.; Zoller, P. Cold Bosonic Atoms in Optical Lattices. Phys. Rev. Lett. 1998, 81, 3108–3111. [Google Scholar] [CrossRef]
- Brennecke, F.; Donner, T.; Ritter, S.; Bourdel, T.; Köhl, M.; Esslinger, T. Fast cavity-enhanced atom detection with low noise and high fidelity. Nature 2007, 450, 268–271. [Google Scholar] [CrossRef] [PubMed]
- Öttl, A.; Ritter, S.; Köhl, M.; Esslinger, T. Correlations and Counting Statistics of an Atom Laser. Phys. Rev. Lett. 2005, 95, 090404. [Google Scholar] [CrossRef] [PubMed]
- Slama, S.; Bux, S.; Krenz, G.; Zimmermann, C.; Courteille, P.W. Superradiant Rayleigh Scattering and Collective Atomic Recoil Lasing in a Ring Cavity. Phys. Rev. Lett. 2007, 98, 053603. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Quantum Theory of Solids; John Wiley & Sons: New York, NY, USA, 1963. [Google Scholar]
- Hofstadter, D.R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 1976, 14, 2239–2249. [Google Scholar] [CrossRef]
- Aidelsburger, M.; Atala, M.; Lohse, M.; Barreiro, J.T.; Paredes, B.; Bloch, I. Realization of the Hofstadter Hamiltonian with Ultracold Atoms in Optical Lattices. Phys. Rev. Lett. 2013, 111, 185301. [Google Scholar] [CrossRef] [PubMed]
- Miyake, H.; Siviloglou, G.A.; Kennedy, C.J.; Burton, W.C.; Ketterle, W. Realizing the Harper Hamiltonian with Laser-Assisted Tunneling in Optical Lattices. Phys. Rev. Lett. 2013, 111, 185302. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.P.; Kasevich, M.A. Macroscopic Quantum Interference from Atomic Tunnel Arrays. Science 1998, 282, 1686–1689. [Google Scholar] [CrossRef] [PubMed]
- Ibañez-Azpiroz, J.; Eiguren, A.; Bergara, A.; Pettini, G.; Modugno, M. Self-consistent tight-binding description of Dirac points moving and merging in two-dimensional optical lattices. Phys. Rev. A 2013, 88, 033631. [Google Scholar] [CrossRef]
- Ashhab, S.; Leggett, A.J. Bose-Einstein condensation of spin-1/2 atoms with conserved total spin. Phys. Rev. A 2003, 68, 063612. [Google Scholar] [CrossRef]
- Zhu, S.-L.; Wang, B.; Duan, L.-M. Simulation and Detection of Dirac Fermions with Cold Atoms in an Optical Lattice. Phys. Rev. Lett. 2007, 98, 260402. [Google Scholar] [CrossRef] [PubMed]
- Prasanna-Venkatesh, B.; Larson, J.; O’Dell, D.H.J. Band structure loops and multistability in Cavity QED. Phys. Rev. A 2011, 83, 063606. [Google Scholar] [CrossRef]
- Montambaux, G.; Piéchon, F.; Fuchs, J.-N.; Goerbig, M.O. Merging of Dirac points in a two-dimensional crystal. Phys. Rev. B 2009, 80, 153412. [Google Scholar] [CrossRef]
- Lim, L.-K.; Fuchs, J.N.; Montambaux, G. Bloch-Zener Oscillations across a Merging Transition of Dirac Points. Phys. Rev. Lett. 2012, 108, 175303. [Google Scholar] [CrossRef] [PubMed]
- Gomes, K.K.; Mar, W.; Ko, W.; Guinea, F.; Manoharan, H.C. Designer Dirac fermions and topological phases in molecular graphene. Nature 2012, 483, 306–310. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wu, B. Bose-Einstein Condensate in a Honeycomb Optical Lattice: Fingerprint of Superfluidity at the Dirac Point. Phys. Rev. Lett. 2011, 107, 06530. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Fu, L. Interaction-induced merging of Dirac points in non-Abelian optical lattices. Phys. Rev. A 2013, 87, 053612. [Google Scholar] [CrossRef]
- Altman, E.; Hofstetter, W.; Demler, E.; Lukin, M.D. Phase diagram of two-component bosons on an optical lattice. New J. Phys. 2003, 5, 113. [Google Scholar] [CrossRef]
- Kuklov, A.B.; Svistunov, B.V. Counterflow Superfluidity of Two-Species Ultracold Atoms in a Commensurate Optical Lattice. Phys. Rev. Lett. 2003, 90, 100401. [Google Scholar] [CrossRef] [PubMed]
- Kuklov, A.; Prokofév, N.; Svistunov, B. Commensurate Two-Component Bosons in an Optical Lattice: Ground State Phase Diagram. Phys. Rev. Lett. 2004, 92, 050402. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.-M.; Demler, E.; Lukin, M.D. Controlling Spin Exchange Interactions of Ultracold Atoms in Optical Lattices. Phys. Rev. Lett. 2003, 91, 090402. [Google Scholar] [CrossRef] [PubMed]
- Cole, W.S.; Zhang, S.; Paramekanti, A.; Trivedi, N. Bose-Hubbard Models with Synthetic Spin-Orbit Coupling: Mott Insulators, Spin Textures, and Superfluidity. Phys. Rev. Lett. 2012, 109, 085302. [Google Scholar] [CrossRef] [PubMed]
- Mandal, S.; Saha, K.; Sengupta, K. Superfluid-insulator transition of two-species bosons with spin-orbit coupling. Phys. Rev. B 2012, 86, 155101. [Google Scholar] [CrossRef]
- Radić, J.; di Ciolo, A.; Sun, K.; Galitski, V. Exotic Quantum Spin Models in Spin-Orbit-Coupled Mott Insulators. Phys. Rev. Lett. 2012, 109, 085303. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Zhou, X.; Wu, C. Magnetic phases of bosons with synthetic spin-orbit coupling in optical lattices. Phys. Rev. A 2012, 85, 061605(R). [Google Scholar] [CrossRef]
- Dzyaloshinskii, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Fisher, M.P.A.; Weichman, P.B.; Grinstein, G.; Fisher, D.S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 1989, 40, 546–570. [Google Scholar] [CrossRef]
- Meystre, P.; Sargent, M., III. Elements of Quantum Optics, 3rd ed.; Springer (India) Pvt. Ltd.: New Delhi, India, 2009. [Google Scholar]
- Isacsson, A.; Cha, M.-C.; Sengupta, K.; Girvin, S.M. Superfluid-insulator transitions of two-species bosons in an optical lattice. Phys. Rev. B 2005, 72, 184507. [Google Scholar] [CrossRef]
- Galitski, V.; Spielman, I.B. Spin-orbit coupling in quantum gases. Nature 2008, 494, 49–54. [Google Scholar] [CrossRef] [PubMed]
- Corcovilos, T.A.; Baur, S.K.; Hitchcock, J.M.; Mueller, E.J.; Hulet, R.G. Detecting antiferromagnetism of atoms in an optical lattice via optical Bragg scattering. Phys. Rev. A 2010, 81, 013415. [Google Scholar] [CrossRef]
- Altman, E.; Demler, E.; Lukin, M.D. Probing many-body states of ultracold atoms via noise correlations. Phys. Rev. A 2004, 70, 013603. [Google Scholar] [CrossRef]
- Higbie, J.M.; Sadler, L.E.; Inouye, S.; Chikkatur, A.P.; Leslie, S.R.; Moore, K.L.; Savalli, V.; Stamper-Kurn, D.M. Direct Nondestructive Imaging of Magnetization in a Spin-1 Bose-Einstein Gas. Phys. Rev. Lett. 2005, 95, 050401. [Google Scholar] [CrossRef] [PubMed]
- Nelson, N.D.; Li, X.; Weiss, D.S. Imaging single atoms in a three-dimensional array. Nat. Phys. 2007, 3, 556–560. [Google Scholar] [CrossRef]
- Münstermann, P.; Fischer, T.; Maunz, P.; Pinkse, P.W.H.; Rempe, G. Observation of Cavity-Mediated Long-Range Light Forces between Strongly Coupled Atoms. Phys. Rev. Lett. 2000, 84, 4068–4071. [Google Scholar] [CrossRef] [PubMed]
- Baumann, K.; Guerlin, C.; Brennecke, F.; Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 2010, 464, 1301–1306. [Google Scholar] [CrossRef] [PubMed]
- Grass, T.; Saha, K.; Sengupta, K.; Lewenstein, M. Quantum phase transition of ultracold bosons in the presence of a non-Abelian synthetic gauge field. Phys. Rev. A 2011, 84, 053632. [Google Scholar] [CrossRef]
- Brahms, N.; Botter, T.; Schreppler, S.; Brooks, D.W.C.; Stamper-Kurn, D.M. Optical Detection of the Quantization of Collective Atomic Motion. Phys. Rev. Lett. 2012, 108, 133601. [Google Scholar] [CrossRef] [PubMed]
- Domokos, P.; Ritsch, H. Collective Cooling and Self-Organization of Atoms in a Cavity. Phys. Rev. Lett. 2002, 89, 253003. [Google Scholar] [CrossRef] [PubMed]
- Asbóth, J.K.; Domokos, P.; Ritsch, H.; Vukics, A. Self-organization of atoms in a cavity field: Threshold, bistability, and scaling laws. Phys. Rev. A 2005, 72, 053417. [Google Scholar] [CrossRef]
- Strack, P.; Sachdev, S. Dicke Quantum Spin Glass of Atoms and Photons. Phys. Rev. Lett. 2011, 107, 277202. [Google Scholar] [CrossRef] [PubMed]
- Mekhov, I.B.; Maschler, C.; Ritsch, H. Light scattering from ultracold atoms in optical lattices as an optical probe of quantum statistics. Phys. Rev. A 2007, 76, 053618. [Google Scholar] [CrossRef]
- Mancini, M.; Pagano, G.; Cappellini, G.; Livi, L.; Rider, M.; Catani, J.; Sias, C.; Zoller, P.; Inguscio, M.; Dalmonte, M.; et al. Observation of chiral edge states with neutral fermions in synthetic Hall ribbons. 2015. arxiv:1502.02495v1. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padhi, B.; Ghosh, S. Cavity Optomechanics with Ultra Cold Atoms in Synthetic Abelian and Non-Abelian Gauge Field. Atoms 2016, 4, 1. https://doi.org/10.3390/atoms4010001
Padhi B, Ghosh S. Cavity Optomechanics with Ultra Cold Atoms in Synthetic Abelian and Non-Abelian Gauge Field. Atoms. 2016; 4(1):1. https://doi.org/10.3390/atoms4010001
Chicago/Turabian StylePadhi, Bikash, and Sankalpa Ghosh. 2016. "Cavity Optomechanics with Ultra Cold Atoms in Synthetic Abelian and Non-Abelian Gauge Field" Atoms 4, no. 1: 1. https://doi.org/10.3390/atoms4010001