Robotic Design Choice Overview Using Co-Simulation and Design Space Exploration

Abstract

Rapid robotic system development has created a demand for multi-disciplinary methods and tools to explore and compare design alternatives. In this paper, we present a collaborative modeling technique that combines discrete-event models of controller software with continuous-time models of physical robot components. The proposed co-modeling method utilizes the Vienna development method (VDM) and MATLAB for discrete-event modeling and 20-sim for continuous-time modeling. The model-based development of a mobile robot mink feeding system is used to illustrate the collaborative modeling method. Simulations are used to evaluate the robot model output response in relation to operational demands. An example of a load-carrying challenge in relation to the feeding robot is presented, and a design space is defined with candidate solutions in both the mechanical and software domains. Simulation results are analyzed using design space exploration (DSE), which evaluates candidate solutions in relation to preselected optimization criteria. The result of the analysis provides developers with an overview of the impacts of each candidate solution in the chosen design space. Based on this overview of solution impacts, the developers can select viable candidates for deployment and testing with the actual robot.

1. Introduction

The general goal of automatic robotic system development is to enable a robot to perform the desired tasks within the context of overall system requirements [1], and modeling and simulation are gradually being adopted as an integral part of the developmental process [2,3,4]. Modeling enables developers to explore hardware and software solutions before developing the actual component. In conjunction with simulation, it also enables the automatic evaluation of a much larger potential design space compared to a manual trial-and-error approach. The alternative approach to developing a robotic system involves time-intensive ad hoc trial-and-error testing to achieve a usable configuration of the physical system. One drawback of this approach is that developers may spend valuable time determining the optimal solution to some aspect of the system, only for such effort to show little impact on the overall desired outcome.

The primary challenge of the modeling and simulation approach is that knowledge of many complementary disciplines, such as electrical, mechanical, software and embedded systems engineering and signal processing, is required to determine viable solutions [5,6,7]. These disciplines have different cultures, tools and methodologies, which may prove to be an impediment to cross-disciplinary projects. In this paper, we propose a collaborative modeling approach known as co-modeling that enables the combination of models from different disciplines. Collaborative simulations, or co-simulations, allow developers to examine different aspects of a system to explore design alternatives. They utilize models to describe the different aspects of the robotic system.

The aim of the present study is the analysis of cross-disciplinary robotic design alternatives using co-simulation. This type of co-simulation-based analysis is known as a design space exploration (DSE) [8]. The co-model robot design is based on a mink feeding vehicle used in agricultural farming applications, as illustrated in Figure 1 and Figure 3. The co-modeling and co-simulation were accomplished by a combination of the Crescendo technology produced by the European Design Support and Tooling for Embedded Control Software (DESTECS) FP7 project [9,10] and a MATLAB extension.

Figure 1. Three-dimensional visualization of a co-simulated load-carrying robot dispensing mink fodder.

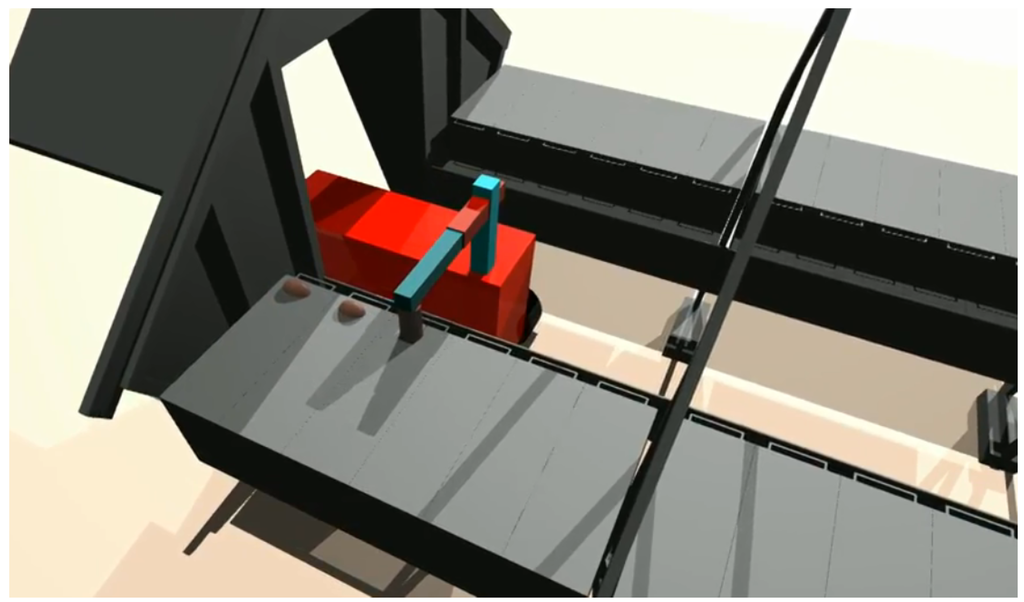
Figure 1. Three-dimensional visualization of a co-simulated load-carrying robot dispensing mink fodder.

In the Crescendo technology, DSE is used to select viable candidate sensor positions on an R2-G2P line-following robot with a fixed controller setup [11]. Co-simulations performed using other tools apart from Crescendo have also been documented. For example, the MODELISAR [12] project developed the Functional Mock-up Interface (FMI), which enables co-simulation and model exchange between different domain-specific simulation frameworks. The standard FMI can support MATLAB/Simulink, Modelica, Python and C/C++, among other tools. In the Integrated Tool Chain for Model-based Design of Cyber-Physical Systems (INTO-CPS) project [13], the Crescendo technology is taken further in an FMI setting [14].

Feeding robots used in animal husbandry have also been developed and documented. In [15], a static feeding system was used in combination with an RFID reader to dispense food to cows with the aid of an attached RFID tag. A mobile feeding platform was also used for outdoor piglet feeding in [16]. The pig-feeding robot was used to influence the behavioral pattern of the piglets to facilitate manure collection by daily changing of the feeding position in the field.

The remainder of the paper is organized as follows. Section 2 describes the co-modeling technologies utilized for coupling the Crescendo technology with MATLAB. Section 3 introduces the robotic design challenge of the mink feeding ground vehicle as a system boundary definition consisting of a problem area and modeling case. Section 4 describes the co-modeling of the developed vehicle, design exploration and evaluated simulation conditions. The domain-specific modeling methods applied to the robot and its environment are documented in Section 5. Section 6 describes the signal processing and control. Section 7 presents the results of the simulations and an overview of the candidate solutions. Section 8 discusses the simulation results and setups that are considered to be capable of ensuring the expected performance under the required conditions. Finally, concluding remarks are made in Section 9.

2. Co-Modeling Technologies

Co-modeling enables the modeling of system components using different developmental tools, as well as facilitating simultaneous co-simulation [9,17,18]. Co-modeling involves the combination of separate domain-specific models to create a complete model of the intended system by collaborative exchange of information between the utilized tools. The exchanged information comprises the simulation parameters, control signals and system events.

2.1. Crescendo Technology

The Crescendo technology enables modeling using different specialized tools [19]. It combines the discrete event (DE) modeling of a digital controller and the continuous time (CT) modeling of the plant/environment for the purpose of co-simulation. The Overture tool [20] and Vienna development method (VDM) [21,22] formalism are used for the DE modeling, and the 20-sim tool was used for the CT modeling. The 20-sim tool models multi-disciplinary dynamic systems, such as the combined mechanical, electrical and hydraulic systems [23]. VDM real time (VDM-RT) [24] is the dialect used for the Crescendo co-model, which is capable of describing real-time, asynchronous, distributed, object-oriented software systems. The Crescendo technology also provides different patterns for checking the fault tolerance of the co-models, so different kinds of design patterns are suggested for different situations [9].

The Crescendo co-simulation engine coordinates the 20-sim and VDM simulations by implementing a protocol for time-step synchronization between the tools. It is possible to support both event-triggered, as well as time-triggered synchronization between the two simulators. This is achieved by having a master-slave architecture where there is a master that controls the progress of time in the two individual simulators, so they exchange information whenever the discrete step side can take its smallest step, affecting the points that have an effect on the CT side (measured in nanoseconds). Crescendo binds the domain models together with a Crescendo contract and is responsible for the exchange of information between the tools. The overall semantics of this mechanism is formalized in [25], and a journal paper enhancement of this is under construction. The Crescendo contract contains the parameters and variables that the CT and DE developers require for the development of a combined model. Crescendo has a feature known as automated co-model analysis (ACA) that can be used for the DSE of a co-model [8]. ACA enables the testing of different system configurations by running all of the combinations chosen by a user. The system configurations comprise different combinations of the actuators, controllers, filters, platforms and sensors of the candidate systems in the design space that the developers intend to explore.

2.2. MATLAB Extension

We have extended the current Crescendo technology to the two-tool DE co-modeling solution illustrated in Figure 2. The DE side was constructed so that actions sent to the CT side are determined by VDM, and the sensory signal processing and sensor fusion are performed in MATLAB. MATLAB is well known for signal processing and sensor fusion [26,27]. VDM utilizes MATLAB as an extension to obtain a combined position estimate to input into the VDM controllers.

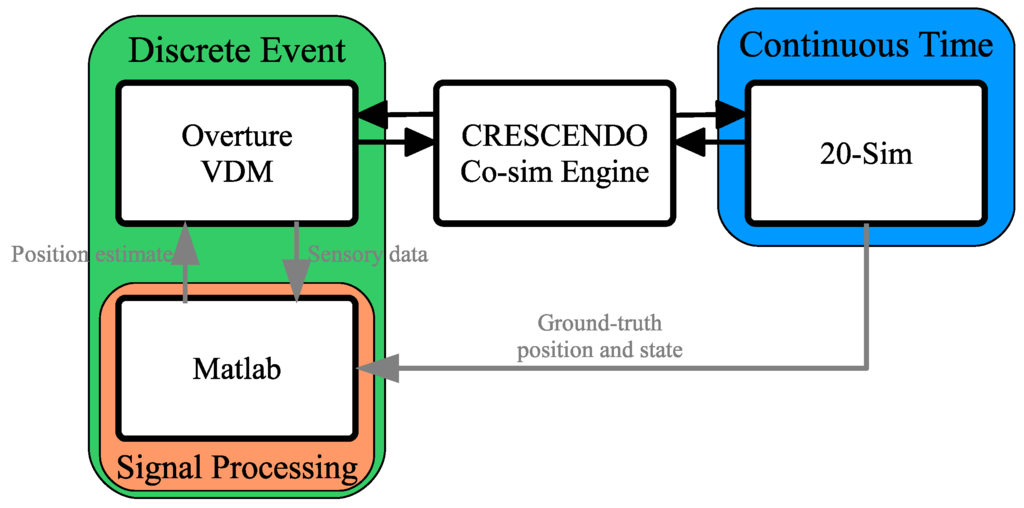
Figure 2. The Crescendo technology with a MATLAB extension to allow for signal processing development.

Figure 2. The Crescendo technology with a MATLAB extension to allow for signal processing development.

Providing a ground position and system state reference is a well-known method for evaluating sensor fusion precision [28,29]. The 20-sim model provides these ground-truth position and system state values to MATLAB for the evaluation of both the signal processing and overall intended system response. Because MATLAB is implemented as an extension interface, the time step synchronization of the overall model is kept intact without the need to change the co-simulation engine structure.

3. System Boundary Definition

3.1. Problem Area Definition

Identification tags, such as radio frequency identification (RFID) tags, have been used for the last decade to provide local and global positioning information about a vehicle [30,31,32]. RFID tags with known positions are placed along the vehicle’s path to provide fixed position references (landmarks). Using an a priori map of the identification tag locations, the vehicle is able to obtain absolute positioning estimates in relation to the soundings. Positioning estimates from the identification tags are provided to the vehicle when the tag is within the detection zone of the tag reader. Using sensory information from other sensor sources can be used to lower the number of RFID tags required. By combining the RFID tag locations with other on-board positioning sensors, for example wheel rotary encoders and an inertial measurement unit (IMU), the vehicle can continually update its current position estimate [33]. The allowable distance between identification tags is dependent on the required position accuracy and available data from other sensor sources.

When a wheel rotary encoder is used to estimate traveled distance, one normally assumes that the estimated effective radius $R_{ee}$ of the tire is known a priori. By measuring the tire rotational speed using a wheel rotary encoder, the vehicle computer can provide an estimate of the tire speed:

$$u_{w{e}_k}=R_{ee}{\omega }_w\approx R_{ee}\frac{2\pi G_k}{T_k{G}_n}$$

(1)

where ${\omega }_w$ is the wheel rotational speed, obtained from the sample time $T_k$ at the k-th interval, $G_k$ the count value of the encoder at the k-th interval and $G_n$ the encoder count per revolution. The relative tire wheel traveled distance can then be calculated using numeric integration.

In agriculture, load-carrying vehicles are used for tasks, such as spraying plants and dispensing animal fodder. The change in load affects the weight distribution of the vehicle and consequently tire compression. A load-carrying robotic vehicle provided with sensory information obtained from tire-mounted rotary encoders may over- or under-estimate current vehicle speed and position as a result of its tire compression. If the effective radius is compressed 0.01 m compared to expected conditions, it would, according to Equation (1), result in an estimate difference of 0.0628 m each revolution, not accounting for other influencing factors.

These estimation problems require cross-disciplinary analyses, because multiple factors affect the outcomes, and possible solutions can be found in different engineering disciplines. Here, we analyze the estimation problems by modeling a load-carrying robot used for dispensing mink fodder at predetermined locations along rows of cages. Feeding mink is a high precision task compared to other domestic animals in livestock production. The farmer chooses the amount of fodder each cage gets based on personal experience and knowledge about demands for mink gender, age and race. Based on feedback from mink-farmers, each mink cage is given a portion of fodder in the range of 80–300 g. In all cases of mink feeding, the total weight of the vehicle changes gradually throughout the feeding process. With vehicle fodder tanks able to transport loads of 500–2500 kg, a machine would theoretically be able to feed 1500–30,000 cages. Automatically placing the fodder at these specific areas requires an on-board localization system that is able to determine the current vehicle position. The co-model of the robot is evaluated based on the required overall system performances obtained using solutions from different disciplines.

Figure 3. Robotic Mink Feeding system mounted onto a manually operated vehicle. (Source: Picture of a Minkpapir A/S vehicle solution, Conpleks Innovation.)

Figure 3. Robotic Mink Feeding system mounted onto a manually operated vehicle. (Source: Picture of a Minkpapir A/S vehicle solution, Conpleks Innovation.)

3.2. System Configuration and Performance Demands

The chosen robot is a four-wheeled vehicle with front-wheel steering and rear-wheel drive equipped with differential gearing, as illustrated in Figure 3. The mink feeding ground vehicle is able to transport a maximum load $M_{l_{max}}$ of 600 kg. The robot receives sensory input from a vision system, an RFID tag reader, an IMU and rotary encoders installed on the back wheels and front wheel kingpins. The vision system is used to detect the entrance to the feeding area when the robot still is outside. The RFID tags are placed along the rows of mink cages to act as fixed location reference points, as illustrated in Figure 4. Fused sensory data are used to determine the current location and to enable the robot to perform its required actions in the environment. A feeder arm mounted on the robot is used to dispense the fodder on the cages (80 g) at the predetermined locations. When the robot moves into the feeding area, it stops to deploy the feeding arm and then begins the feeding procedure.

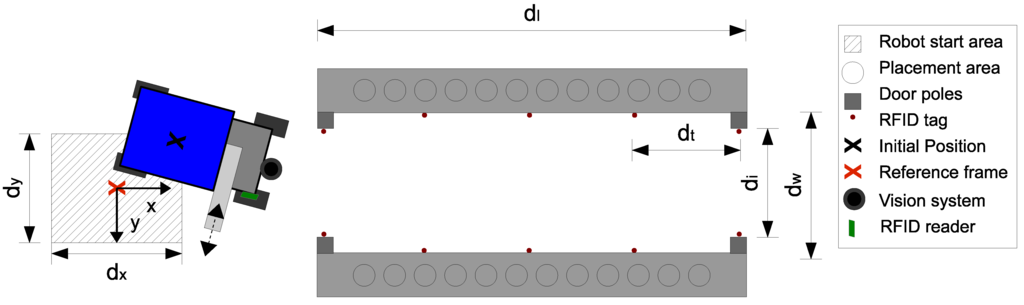
Figure 4. Sketch of the load-carrying feeding robot and the mink feeding area.

Figure 4. Sketch of the load-carrying feeding robot and the mink feeding area.

The system performance requirements define what the robot must achieve to be considered effective. The system performance required by the project stakeholders includes the following:

• Maximum vehicle speed of 0.25 m/s (conforming to ISO-10218 [34])
• No collisions with the surroundings, as laid out in Figure 4.
• The distance between the RFID tags $d_t$ should be between 0.3 and 20 m.
• Feeding with a precision of ±0.08 m inside the placement area.

It should be noted that the performance requirements are non-domain specific and focus on the overall performance of the robot. Here, the maximum distance between the RFID tags represents the length of the feeding area and sets the limit for the minimum number of tags. The lower limit for $d_t$ is chosen based on the length of the mink cages used in the co-modeling, resulting in one RFID tag for each cage.

3.3. Modeling Cases

The co-model describes the vehicle and its sensor, actuator, steering controller, feeding system and sensor fusion components. The goal was to achieve maximum distance between the RFID tags without compromising the pre-set system constraints. The question here was whether the loading of the vehicle should be accounted for by reducing the maximum compression of the tire, compensated for in the DE controller, or a combination of both approaches. The following DE controller conditions were applied:

• <Static> The estimated effective tire radius was considered to be the mean of the values for the unloaded and fully-loaded robot. This is based on the assumption that the mean value will produce the least overall error in the estimate.
• <Pre-calibration> A pre-measured estimate of the current rear tire wheel radius in relation to the transported load is used in the DE part of the co-model. The estimates of the effective radius were obtained through the MATLAB bridge and directly passed from 20-sim with an accuracy of ±0.001 m.
• <Estimator> The input data obtained by the vision sensor were used to estimate the current effective radius before entering the feeding area. This estimate was based on the distance traveled between the updates, with an accuracy of$-0.005m$.

Rather than simulating a single scenario, the test set in Table 1 evaluates the expected min-mean-max operational values used for DSE. The DSE was used to evaluate the configuration solutions in Table 1 in different development domains to account for the load-carrying effects. The operational values represent the expected range of transported loads, as well as the surface of the tire and initial robot position conditions. The initial position was of interest in this case because a human operator could place the robot at its starting point without the necessary accuracy. The models of the tire radius on the CT side vary between low and fully-loaded conditions. The tire surface friction is of interest here, since the vehicle will be stopping to deploy the feeding arm before starting the feeding process.

Table 1. Candidate solution sets used for the system evaluation and min-mean-max test set used for the design space exploration (DSE) of the feeding robot.

System Configurations		Min-Mean-Max Test Set
Rear Tire	Vehicle	Load Mass	Tire Surface	Initial Position
Radius Change	State Estimate		μ friction	$x_{init},y_{init},{\psi }_{init}$
0.001 m	<Static>	1% (6 kg)	0.3	$x_{init}=\{-0.5m,0m,0.5m\}$
0.02 m	<Pre-calibration>	50% (300 kg)	0.5	$y_{init}=\{-0.1m,0m,0.1m\}$
0.04 m	<Estimator>	100% (600 kg)	0.7	${\psi }_{init}=\{-{15}^{\circ },0^{\circ },{15}^{\circ }\}$

Table 1. Candidate solution sets used for the system evaluation and min-mean-max test set used for the design space exploration (DSE) of the feeding robot.

System Configurations		Min-Mean-Max Test Set
Rear Tire	Vehicle	Load Mass	Tire Surface	Initial Position
Radius Change	State Estimate		μ friction	$x_{init},y_{init},{\psi }_{init}$
0.001 m	<Static>	1% (6 kg)	0.3	$x_{init}=\{-0.5m,0m,0.5m\}$
0.02 m	<Pre-calibration>	50% (300 kg)	0.5	$y_{init}=\{-0.1m,0m,0.1m\}$
0.04 m	<Estimator>	100% (600 kg)	0.7	${\psi }_{init}=\{-{15}^{\circ },0^{\circ },{15}^{\circ }\}$

4. Co-Modeling

The co-modeling perspective of the robot includes a contract between the DE and CT models and the ACA specifications for a DSE using co-simulation. This contract represents the work template between the developers, and the ACA specifications are the concrete requirements of the stakeholder.

4.1. Crescendo Contract

The Crescendo contract in Table 2 defines the parameters and variables to be exchanged during the simulation. The shared design parameters are defined by the sdp keyword; the variables controlled by the CT side are defined by the monitored keyword; and the variables controlled by the DE side are defined by the controlled keyword. The parameters in the contract provide the communication variables that both the DE and CT developers require for the development of a combined model. Compared to reality, these variables are abstractions and only provide information for current co-model development.

Table 2. Crescendo contract.

	Name	Type	Parameter Symbol
sdp	Initial_Position	array	$[x_{init},y_{init},{\varphi }_{init}]$
sdp	Surface_Tyre	real	μ
sdp	Load_Mass	real	$m_{L_p}$
sdp	Tag_dist	real	$d_t$
controlled	Speed_out	real	$u_o$
controlled	Steering_Wheel_Angle	real	${\delta }_{f_o}$
controlled	Feeder_arm_pos	real	$y_{arm}$
controlled	Feeder_output	real	$p_o$
monitored	Vision	array	$[r_{s_1},{\theta }_{s_1},r_{s_2},{\theta }_{s_2},{\theta }_{s_e},d_{s_e}]$
monitored	RFID	array	$[ID,RSSI]$
monitored	IMU	real	${\dot{\psi }}_s$
monitored	Encoders_Back	array	$[{\omega }_{r{r}_s},{\omega }_{r{l}_s}]$
monitored	Encoder_Front	real	${\delta }_{f_s}$

Table 2. Crescendo contract.

	Name	Type	Parameter Symbol
sdp	Initial_Position	array	$[x_{init},y_{init},{\varphi }_{init}]$
sdp	Surface_Tyre	real	μ
sdp	Load_Mass	real	$m_{L_p}$
sdp	Tag_dist	real	$d_t$
controlled	Speed_out	real	$u_o$
controlled	Steering_Wheel_Angle	real	${\delta }_{f_o}$
controlled	Feeder_arm_pos	real	$y_{arm}$
controlled	Feeder_output	real	$p_o$
monitored	Vision	array	$[r_{s_1},{\theta }_{s_1},r_{s_2},{\theta }_{s_2},{\theta }_{s_e},d_{s_e}]$
monitored	RFID	array	$[ID,RSSI]$
monitored	IMU	real	${\dot{\psi }}_s$
monitored	Encoders_Back	array	$[{\omega }_{r{r}_s},{\omega }_{r{l}_s}]$
monitored	Encoder_Front	real	${\delta }_{f_s}$

In this co-model, the shared design parameters represent the values that developers should explore in terms of effect. Values $x_{init}$, $y_{init}$ and ${\varphi }_{init}$ define the starting position of the robot in the global coordinate frame, whereas $m_{L_p}$ and μ set the current operational parameters of the robot and its surroundings. Furthermore, $d_t$ is the factor to be increased while still achieving the system performance goals for each DSE candidate. The controlled variables are the input to the robot movement and the feeding arm. The input to the robot movement is transmitted to the drive motor and front wheel steering actuator, and the feeding arm transmits the desired arm position and current feeding output to the CT model. The monitored variables represent the sensory inputs to the DE side: vision, RFID, IMU and encoders. In the case of vision, the full image or laser scan is not transmitted for processing; rather, the processed input of the detected objects (e.g., the poles in illustrated in Figure 4) are transmitted when they are in view. When inside the feeding area, the vision system instead provides an estimate of vehicle orientation ${\theta }_{s_e}$ and distance to the side wall $d_{s_e}$. The IMU is also only represented by a single measurement value ${\dot{\psi }}_s$ that is rotated in the global frame, where the actual sensor might contain acceleration and rotation sensors for all three dimensions. The RFID reader provides tag identification data (ID) and a received signal strength indicator (RSSI) value when in range of an RFID tag.

4.2. Automatic Co-Model Analysis

To select the value of parameter $d_t$ for the ACA co-simulation, an output cost-function is defined. The result of each co-simulation is evaluated based on the rate of success for placing the fodder at the correct positions between two tags.

$$f_{d_t}=-\frac{b_{suc}^2}{b_{tot}}$$

(2)

where $b_{tot}$ is the total number of placement positions between two RFID-tags and $b_{suc}$ is the number of successful fodder placements. The output of the cost function ensures that the largest $d_t$ with the highest number of successful fodder placements is the minimum for the searchable range. In mathematics, by convention, optimization problems are usually stated in terms of minimization, thus the minus sign. ACA uses the golden section search method ([35] Chapter 7) in combination with the cost function in Equation (2) to determine the best candidate within the design space. Golden section search assumes that the cost function is a unimodal function, meaning that there is only a single local minimum.

Evaluation of each ACA run co-simulation is performed during the simulation or after the execution, as in post-processing, as illustrated in Figure 5. In-run co-simulation evaluation is based on readily available values, such as the CT-simulated robot speed and position in the global coordinate frame. The evaluation of a running co-simulation allows for a direct exit from the execution, instead of having to run an already failed scenario to its end.

The post-processing evaluation of an ACA co-simulation is based on the feeding output of the robot in its surroundings relative to the stakeholder requirements. Evaluating the feeding output requires information about the location of each food placement in the operational environment, and this significantly increases computation. By logging the types of failures that the co-simulation encounters, developers can order and rerun specific scenarios that are found to be relevant.

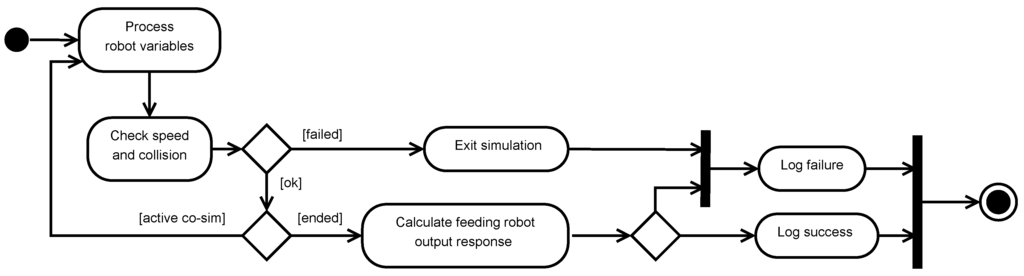
Figure 5. Activity diagram showing the evaluation of a co-simulation.

Figure 5. Activity diagram showing the evaluation of a co-simulation.

5. CT Modeling

The CT model describes the sensors, actuators, robot vehicle, environment and their interactions. The actuator output affects the robot movement and output response, which in turn affects the sensory responses. In the present study, vision and IMU sensors were modeled using known methods [36] that are not described in this paper.

5.1. Tire Modeling for Encoder Data

The wheel encoders provide inputs to the DE controller to control the drive speed and estimation of the current position. The data of the wheel encoders are based on rotational data obtained by a dynamic tire model that takes into consideration the vertical, lateral and longitudinal dynamics of the tire, as illustrated in Figure 6.

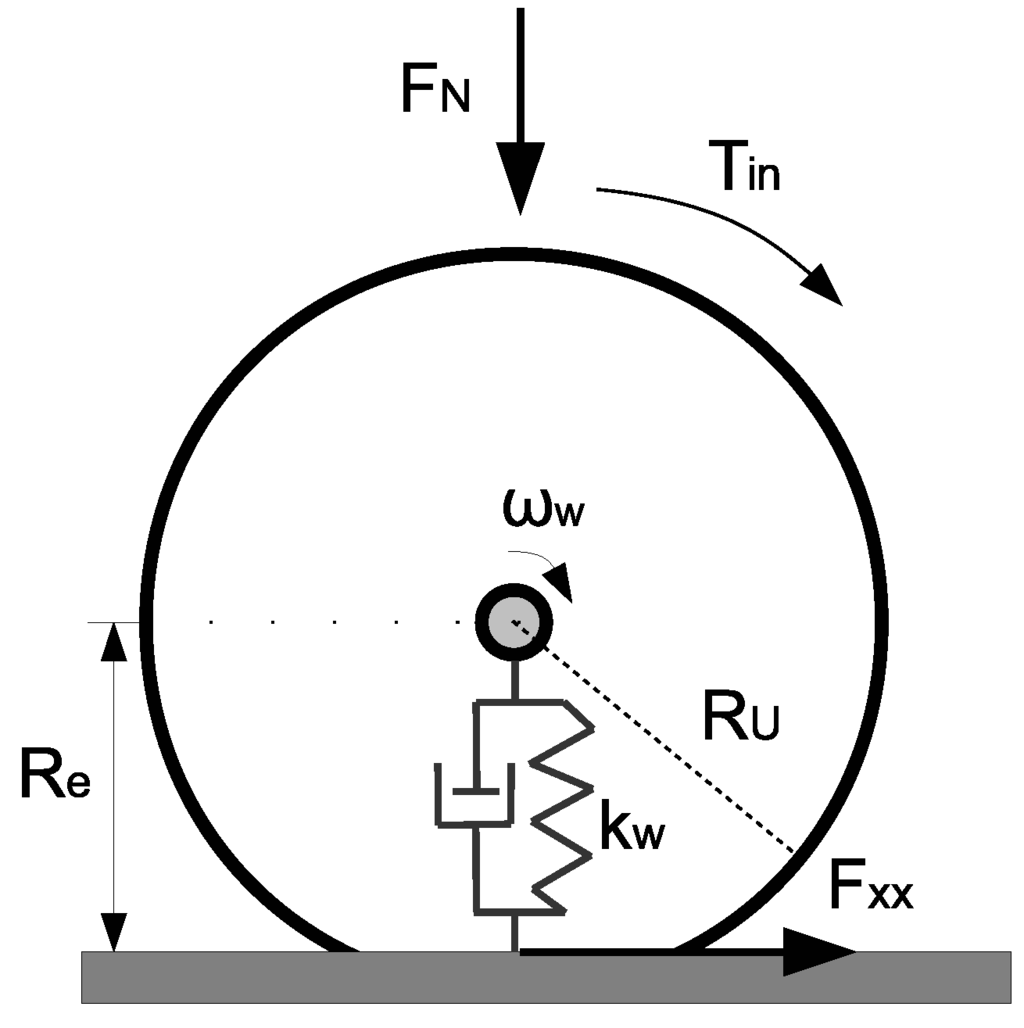
Figure 6. Forces in the longitudinal tyre model.

Figure 6. Forces in the longitudinal tyre model.

The tire model describes the rotational changes ${\dot{\omega }}_w$ and the effects of the steering along the feed area side wall, braking and wheel surface conditions. The longitudinal tire force $F_{x_w}$ includes the effects of acceleration and braking:

$$J_w\dot{{\omega }_w}=T_{in}-F_{x_w}{R}_e$$

(3)

where $J_w$ is the wheel moment of inertia, $T_{in}$ is the acceleration or braking torque and $R_e$ is the effective rolling radius (a compression of the unloaded radius $R_U$ based on the applied load $F_N$). Radius $R_e$ is modeled by a spring-damper system as follows:

$$R_e=R_U-F_N/k_w$$

(4)

Each tire’s $R_e$ value changes dynamically depending on the load forces applied by the robot. The $k_w$ factor represents the current tire stiffness applied in the DSE and is based on the expected compression rate.

Both empirical and analytical models have been developed to describe the generated lateral and longitudinal tire forces [37,38,39,40]. In the present implementation of the tire, the Fiala tire model was used to calculate the resultant lateral and longitudinal tire forces.

5.2. Vehicle Body Dynamics

The generated tire forces interact with the robot to produce the output response in the environment. The robot utilizes trapezoid steering, as illustrated in Figure 7a, which produces equal steering angles on the right and left sides, making the transformation the same for both sides [41].

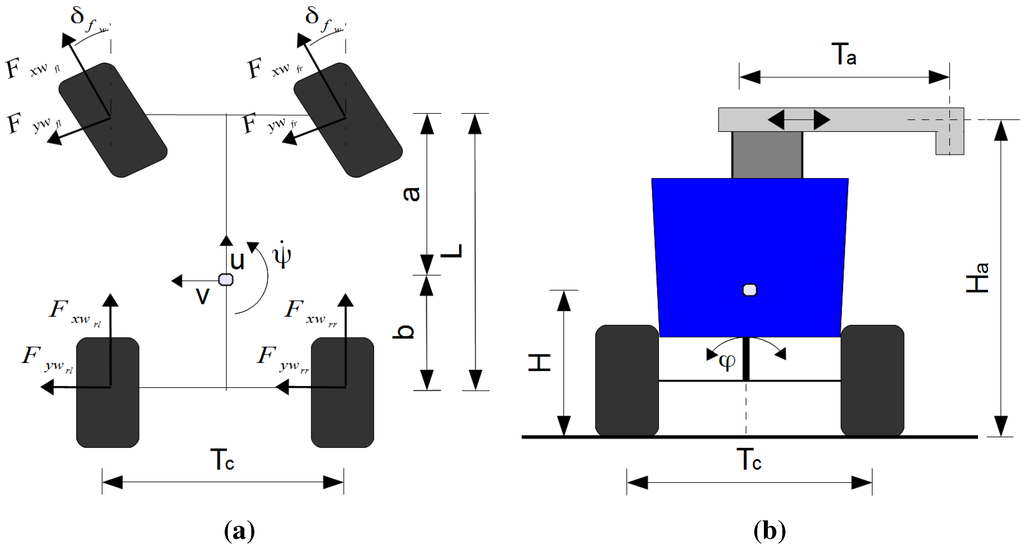
Figure 7. Free-body diagrams of the robot. (a) Forces in the x-y plane. (b) Forces in the y-z plane.

Figure 7. Free-body diagrams of the robot. (a) Forces in the x-y plane. (b) Forces in the y-z plane.

To take the front steer angle into consideration, the CT model rotates the front tire forces into the coordinate system of the robot vehicle. The CT side models the dynamic yaw ψ, pitch ϕ, lateral u and longitudinal v motion responses of the robot vehicle. The differential equations ([41] p.71) model the motion of the robot body.

Roll angle θ, H, a and b were treated as constant in each simulation, because the expected changes were assumed to be negligible and therefore only updated for each DSE case. The current total mass of the robot and load M was used to calculate the current values of a and b, which define the CGposition:

$$M=M_{vehicle}+M_{l_{max}}{m}_{L_p}$$

(5)

$$a=a_u+{\eta }_x{M}_{l_{max}}{m}_{L_p}$$

(6)

where $a_u$ and $b_u$ are respectively the longitudinal distances of the front and rear wheels of the unloaded robot from its CG, and ${\eta }_x$ is a constant, because the change in the CG was assumed to be linear within the load limits $[0,M_{l_{max}}]$. Likewise, M, a, b and the tire spring values were used to calculate ψ and H, with $H_U$ corresponding to the unloaded CG height.

5.3. RFID Tag Reader

An RFID reader has a zone in three-dimensional space (the detection zone) in which a specific type of tag is detectable [42]. To model the detection zone, an ellipsoid with its center at $(x_{dz},y_{dz},z_{dz})$ and a semi-principal axis of length $(r_1,r_2,r_3)$ was used to compare the RFID tag positions $(x_{tg},y_{tg},z_{tg})$, which were rotated into the coordinate frame of the reader to determine whether the tag was within range. An RFID reader is able to read a tag if the following Equation (7) is satisfied.

$$\left(\frac{{(x_{rf}-x_{tg})}^2}{r_1^2}+\frac{{(y_{rf}-y_{tg})}^2}{r_2^2}+\frac{{(z_{rf}-z_{tg})}^2}{r_3^2}\right)\le 1$$

(7)

The actual distance $d_{rf}$ is calculated using the global coordinates of the RFID reader $(x_{rf},y_{rf},z_{rf})$ and the RFID tag.

$$d_{rf}=\sqrt{{(x_{rf}-x_{tg})}^2+{(y_{rf}-y_{tg})}^2+{(z_{rf}-z_{tg})}^2}$$

(8)

The mathematical relationship between the RSSI value and actual distance $d_{rf}$ is as follows:

$$RSSI\left(d_{rf}\right)=\left\{\begin{array}{cc}\frac{K_{rf}}{d_{rf}}\hfill & \text{if}\frac{K_{rf}}{d_{rf}}\ge RSS{I}_{min}\hfill \\ RSS{I}_{min}\hfill & \text{if}\frac{K_{rf}}{d_{rf}}<RSS{I}_{min}\hfill \end{array}\right.$$

(9)

where $RSS{I}_{min}$ is the minimum value that the reader outputs to the DE side and $K_{rf}$ is a constant in the piece-wise function.

5.4. CT Setup

The CT parameters of the co-simulations for the intended DSE are documented in Table 3.

In the co-simulation, the CT side utilized a variable step-size ordinary differential equation (ODE) solver based on the Dormand–Prince method, a member of the Runge–Kutta family of ODE solvers. The ODE solver runs with a maximum step size of 1 kHz.

Table 3. Continuous time (CT) parameters used for the co-simulations.

Sub-System	Parameter Values
Environment	$d_l=$ 20 m, $d_w=$ 1.5 m, $d_i=$ 1.34 m,
	$d_x=$ 1 m, $d_y=$ 0.2 m
Vehicle body	$L=$ 2.1 m, $a_U=$ 1.2 m, $b_U=$ 0.9 m, $H_U=$ 0.55 m, $T_a=$ 0.65 m, $T_c=$ 0.74 m,
	$H_a=$ 1.2 m, $M_{vehicle}=$ 800 kg, $M_{l_{max}}=$ 600 kg, ${\eta }_x=5.83·{10}^{-4}\frac{m}{kg}$,
	${\eta }_y=1.33·{10}^{-4}\frac{m}{kg}$, $R_U=$ 0.3 m, $k_{w,0.04}=127,250\frac{N}{m}$,
	$k_{w,0.02}=254,500\frac{N}{m}$, $k_{w,0.001}=3,100,000\frac{N}{m}$
Sensors	$RSS{I}_{min}=$ 4, $K_{rf}=$ 0.12 m, $r_1=$ 0.16 m, $r_2=r_3=$ 0.12 m
	Encoder resolution = 13 bit, $r_{max}=$ 5 m, $r_{min}=$ 0.01 m, $r_{\sigma }=$ 0.005 m
	$\left|{\theta }_{max}\right|=\frac{\pi }{2}$, ${\theta }_{\sigma }=0.5^{\circ }$

Table 3. Continuous time (CT) parameters used for the co-simulations.

Sub-System	Parameter Values
Environment	$d_l=$ 20 m, $d_w=$ 1.5 m, $d_i=$ 1.34 m,
	$d_x=$ 1 m, $d_y=$ 0.2 m
Vehicle body	$L=$ 2.1 m, $a_U=$ 1.2 m, $b_U=$ 0.9 m, $H_U=$ 0.55 m, $T_a=$ 0.65 m, $T_c=$ 0.74 m,
	$H_a=$ 1.2 m, $M_{vehicle}=$ 800 kg, $M_{l_{max}}=$ 600 kg, ${\eta }_x=5.83·{10}^{-4}\frac{m}{kg}$,
	${\eta }_y=1.33·{10}^{-4}\frac{m}{kg}$, $R_U=$ 0.3 m, $k_{w,0.04}=127,250\frac{N}{m}$,
	$k_{w,0.02}=254,500\frac{N}{m}$, $k_{w,0.001}=3,100,000\frac{N}{m}$
Sensors	$RSS{I}_{min}=$ 4, $K_{rf}=$ 0.12 m, $r_1=$ 0.16 m, $r_2=r_3=$ 0.12 m
	Encoder resolution = 13 bit, $r_{max}=$ 5 m, $r_{min}=$ 0.01 m, $r_{\sigma }=$ 0.005 m
	$\left|{\theta }_{max}\right|=\frac{\pi }{2}$, ${\theta }_{\sigma }=0.5^{\circ }$

6. DE Modeling

6.1. Control

The robot controller consists of a steering controller that can follow a pre-determined path, and the feeding system is intended to place food at pre-selected positions. The steering controller steers the robot along the predetermined path, which is defined as a sequence of waypoints, utilizing the modal mode concept illustrated in Figure 8. The current modal controller mode is dependent on movement inside or outside the feeding area. The current waypoint determines the current mode and when the feeding arm is deployed.

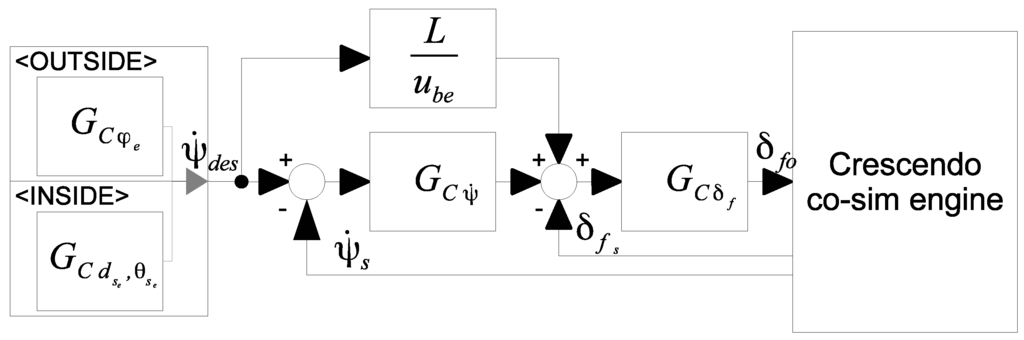
Figure 8. Block diagram of the modal steering controller.

Figure 8. Block diagram of the modal steering controller.

The feedforward response is based on the kinematic bicycle model where L is the length of the wheelbase and the estimated drive speed $u_{be}$ by the rear wheels of the robot. The drive speed of the robot at time interval k is calculated as:

$$u_{b{e}_k}=\frac{R_{ee}\left({\omega }_{r{l}_s}+{\omega }_{r{r}_s}\right)}{2}$$

(10)

where ${\omega }_{r{l}_s}$ and ${\omega }_{r{r}_s}$ are the sensory inputs of the left and right wheel encoders, respectively.

When the robot is moving into and out of the feeding area, the estimated heading error ${\psi }_e$ is the chosen steering concept. Inside the mink farm house, the robot needs to move along the cages in straight lines and to ensure that the feeding arms are held straight over the cages. Correct operation is ensured by maintaining a fixed distance from and orientation to the sides of the mink cages. The control law employed by [43,44], which is given by Equation (11), was chosen for inside operation. The robot rotational angle speed ${\dot{\psi }}_{des}$ was set to be proportional to the errors in distance $d_e$ and orientation ${\theta }_e$:

$$r_{des}=\left[\begin{array}{cc}{K}_{11}& 0\\ 0& K_{22}\end{array}\right]\left[\begin{array}{c}{d}_e\\ {\theta }_e\end{array}\right]$$

(11)

The controller parameter is tuned by the Ziegler–Nichols closed loop method. The parameter $K_{22}$ is determined first and tuned to diminish the angle error ${\theta }_e$. The procedure is then repeated for the $K_{11}$ parameter for the distance error $d_e$. When the robot moves outside the feeding area, the heading error ${\varphi }_e$ in relation to the predetermined path of the robot is selected as the steering concept. A classic PD controller is used to steer the robot outside the mink farm houses, based on the method described in [41].

When the robot moves into the feeding area, it stops to deploy the feeding arm system to the preselected position by updating $y_{arm}$. Robot movement cannot continue before the feeding arm system has been completely moved in or out when the robot is entering or exiting a mink farm house. The robot has a feed map in the form of a sequence of amounts and positions of fodder to place. The feeding arm system starts the feeding process using the output $p_o$ when the next position in the map is reached.

6.2. Sensor Fusion

The idea of sensor fusion is that more accurate estimates of a physical phenomenon can be obtained by combining different sensor data sources [45]. The combined sensor data can better accommodate uncertainty and noise in measurements [46]. The sensor fusion solution adopted in this study uses an extended Kalman filter (EKF) [36] to estimate the current position of the robot. The process is represented by the following velocity motion model:

$$f({\widehat{x}}_{k-1},{\mu }_k,0)=\left[\begin{array}{c}{x}_k\\ y_k\\ {\psi }_k\end{array}\right]=\left[\begin{array}{c}{x}_{k-1}\\ y_{k-1}\\ {\psi }_{k-1}\end{array}\right]+\left[\begin{array}{c}-\frac{u_{e_k}}{{\dot{\psi }}_{s_k}}\left(sin\left({\psi }_{k-1}\right)-sin({\psi }_{k-1}+{\dot{\psi }}_{s_k}{T}_k)\right)\\ \frac{u_{e_k}}{{\dot{\psi }}_{s_k}}\left(cos\left({\psi }_{k-1}\right)-cos({\psi }_{k-1}+{\dot{\psi }}_{s_k}{T}_k)\right)\\ {\dot{\psi }}_{s_k}{T}_k\end{array}\right]$$

(12)

The process input ${\mu }_k$ at interval k in time is used to predict the next state and is based on the monitored variables ${\dot{\varphi }}_s$, variables ${\omega }_{r{r}_s}$ and ${\omega }_{r{l}_s}$ obtained from the Crescendo contract. The value determined from ${\dot{\psi }}_s$ is passed directly to the EKF and represents the current ${\psi }_k$. ${\omega }_{r{r}_s}$ and ${\omega }_{r{l}_s}$ represent the back wheel encoder measurements used to estimate the current robot speed:

$$u_{e_k}=\frac{R_{ee}\left({\omega }_{r{l}_s}+{\omega }_{r{r}_s}\right)}{2}\left(\sqrt{1+\frac{4L^2{({\omega }_{r{l}_s}-{\omega }_{r{r}_s})}^2}{T_c^2{({\omega }_{r{l}_s}+{\omega }_{r{r}_s})}^2}}\right)$$

(13)

where $R_{ee}$ is the estimated effective tire radius used by the DE side and L and $T_c$ are respectively the length and width of the robot wheelbase. The square root part of Equation (13) is used to transpose the measurements to the chosen localization reference point.

The EKF utilizes an event-based correction stage that is dependent on the inputs from the vision system and RFID. The vision system provides updates when the door poles of the entrance and exit are in view and compares them against a pole landmark map. The chosen landmark coordinates $\left(m_{x,j},m_{y,j}\right)$ are converted into polar coordinates ($r,\theta$) to allow for direct comparison with the sensor input:

$$h_{visio{n}_{out}}(x_{k,j},0)=\left[\begin{array}{c}{r}_{k,j}\\ {\theta }_{k,j}\end{array}\right]=\left[\begin{array}{c}\sqrt{{(m_{x,j}-x_k)}^2+{(m_{y,j}-y_k)}^2}\\ arctan2(m_{y,j}-y_k,m_{x,j}-x_k)-{\psi }_k\end{array}\right]$$

(14)

where $(m_{x,j}$,$m_{y,j})$ is the position of the door pole in the local map and ($x_k$,$y_k$,${\psi }_k$) is the estimated position of the robot.

When the robot is moving inside the feeding area, the vision input can be used to update the vehicle orientation and distance to the side wall [47].

$$h_{visio{n}_{in}}(x_{k,j},0)=\left[\begin{array}{c}{d}_m\\ {\theta }_m\end{array}\right]=\left[\begin{array}{c}\frac{A_m{y}_k+B_m{x}_k+C_m}{\sqrt{A_m^2+B_m^2}}\\ arctan2(A_m,B_m)-{\psi }_k\end{array}\right]$$

(15)

where $A_m$, $B_m$ and $C_m$ are the parameters for the general form of the line equation representing the mapped position of the side wall. The sensory update does not provide the robot with information about its current position along the side wall, and therefore, position correction is needed.

The positions of the RFID tags can also be seen as points along the side wall ($m_{x,i},m_{y,i}$). When the RFID tag reader first detects the tag, we can use this to provide a position estimate ($\Delta x_{e,i},\Delta y_{e,i}$) relative to this tag by combining the detection event with input from the vision sensor. In these co-modeling scenarios, we assume it to be at the center of the detection zone (i.e., at zero), making the relative position measurement output correspond to the intersection point between the line (side wall) and ellipse (detection zone). The landmark related to the RFID tag is then:

$$h_{rfid}(x_{k,j},0)=\left[\begin{array}{c}\Delta x_{k,i}\\ \Delta y_{k,i}\end{array}\right]=\left[\begin{array}{c}{m}_{x,i}cos(-{\psi }_k)-m_{y,i}sin(-{\psi }_k)-x_k\\ m_{x,i}sin(-{\psi }_k)+m_{y,i}cos(-{\psi }_k)-y_k\end{array}\right]$$

(16)

The Jacobian matrices utilized in the EKF localization method are not presented in this paper, but can be calculated based on Equations (12) and (14)–(16).

7. Results

The result of the ACA is illustrated in Figure 9 using boxplots. In each boxplot, the central line marks the median; the edges of the box are the 25th and 75th percentiles; and the whiskers mark the two most extreme data points. A total of 12,028 co-simulations was run, for the 2187 scenarios in the min-mean-max test set from Table 1. Each system configuration boxplot represents the determined maximum RFID $d_t$ distance values for each scenario.

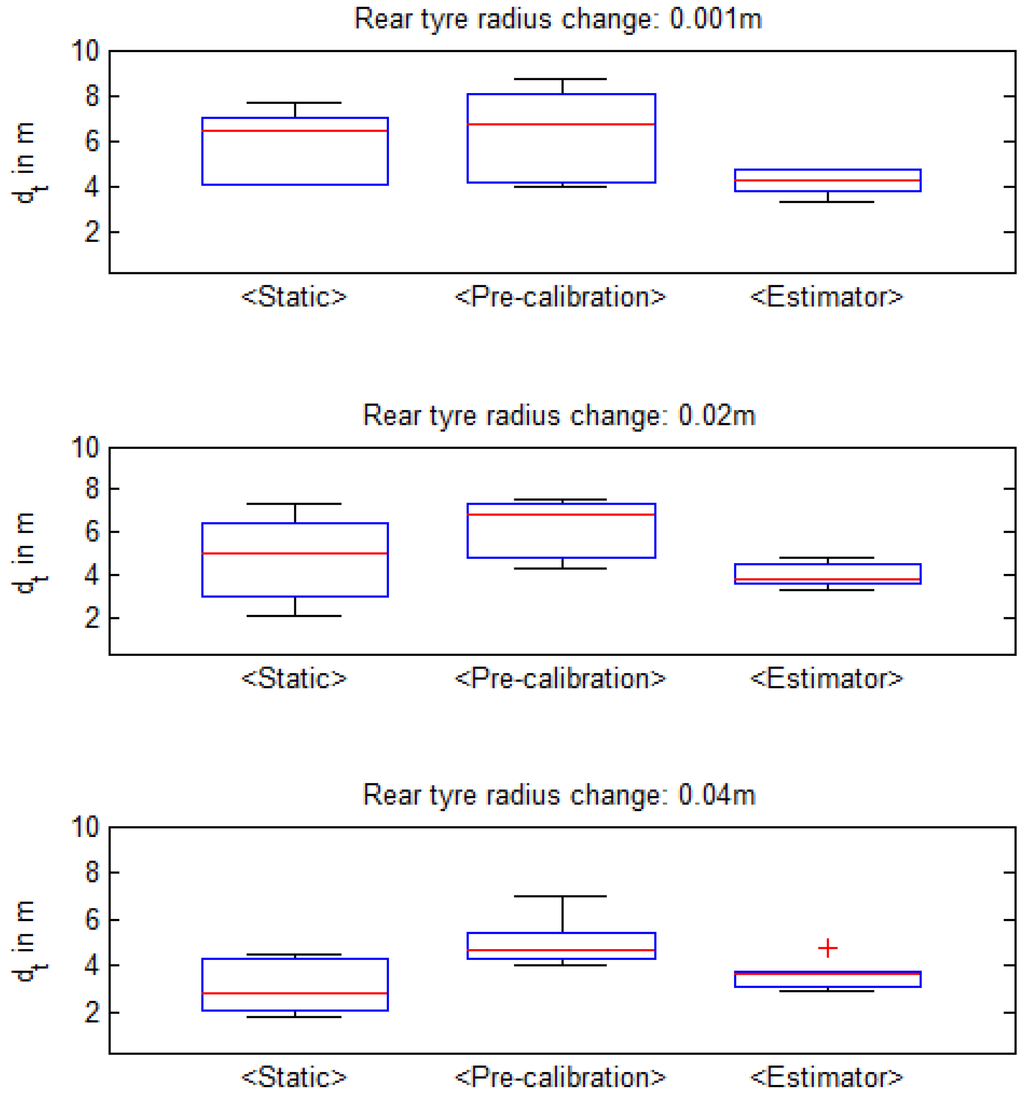
Figure 9. Result of the automated co-model analysis (ACA) run for the feeding farming co-model in terms of determined $d_t$, for the nine different system configurations in Table 1.

Figure 9. Result of the automated co-model analysis (ACA) run for the feeding farming co-model in terms of determined $d_t$, for the nine different system configurations in Table 1.

7.1. Selected Individual Results

Further information about the individual co-simulations can be gained by visualizing the response in terms of mink fodder placement. In Figure 10, Figure 11 and Figure 12, a select number of runs from the DSE performed are illustrated, representing both successful and failed scenarios. Only a section of the feeding area is shown to allow individual fodder placements to be seen.

Figure 10 illustrates some of the early co-simulation runs that were made before the final model was developed. Lessons learned from these failed co-simulations were used to improve the DE controller operating the robotic vehicle.

A successful and a failed co-simulation scenario are shown in Figure 11, to illustrate the different types of outcome from the DSE. The white rectangles on the side wall represent the placement of the RFID tags, illustrating their impact on the mink fodder placement.

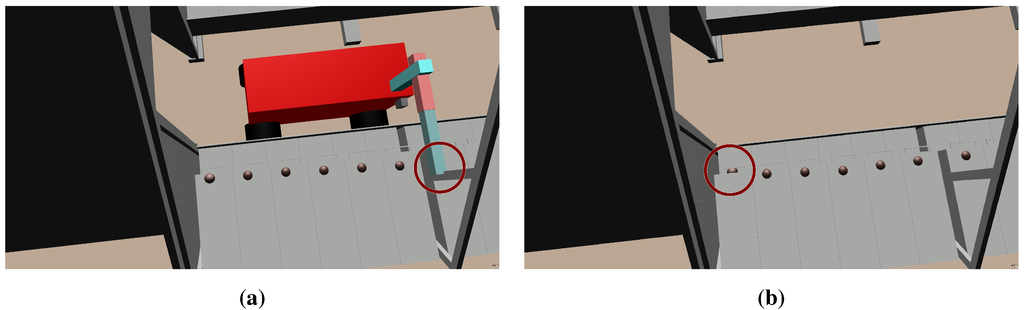
Figure 10. Failed co-simulation runs from the development process of the co-model. (a) Collision of the feeding arm with support beam. (b) Misplacement of fodder whenentering.

Figure 10. Failed co-simulation runs from the development process of the co-model. (a) Collision of the feeding arm with support beam. (b) Misplacement of fodder whenentering.

Figure 11. Selected visualisation examples of the co-simulations made using DSE. (a) Misplacement of mink fodder. (b) Successful placement of mink fodder.

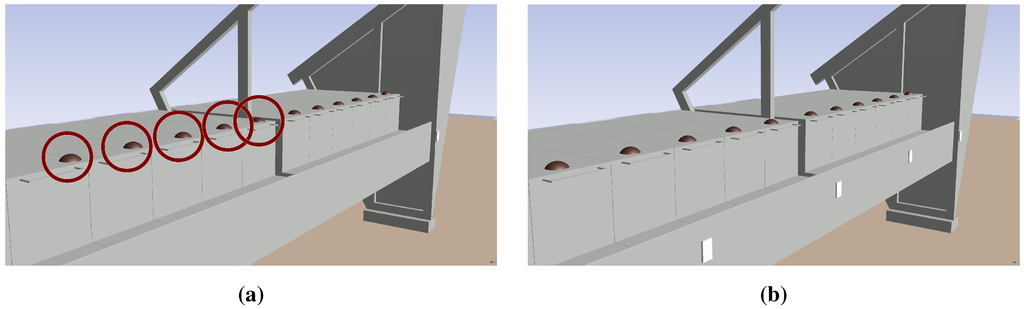
Figure 11. Selected visualisation examples of the co-simulations made using DSE. (a) Misplacement of mink fodder. (b) Successful placement of mink fodder.

Co-simulations can also differ for the same system configuration, but still provide acceptable outcomes. Figure 12 illustrates the influence that the transported load has on the placement of the mink fodder inside the feeding area.

Figure 12. The selected example DSE results illustrates the variation of the system configuration: vehicle state estimate = <Static> and rear tyre radius change of 0.04 m. (a) Fodder placement with a 1% load mass. (b) Fodder placement with a 100% load mass.

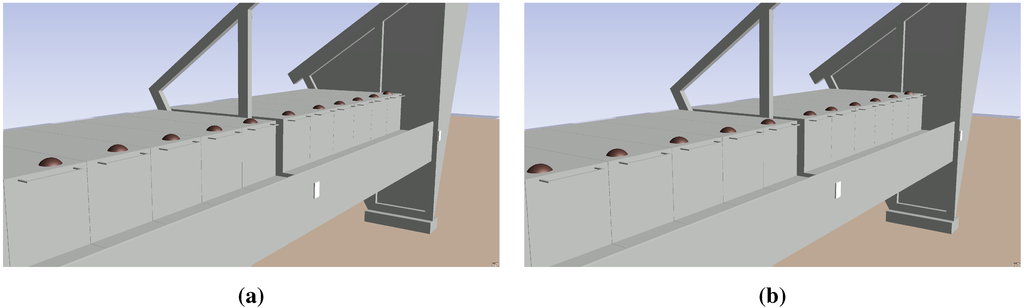
Figure 12. The selected example DSE results illustrates the variation of the system configuration: vehicle state estimate = <Static> and rear tyre radius change of 0.04 m. (a) Fodder placement with a 1% load mass. (b) Fodder placement with a 100% load mass.

8. Discussion

The results provide an overview of the candidate system configurations based on the estimated RFID tag distance. Developers can use the candidate overview to select configurations for testing on the an actual platform. The intention here is to provide the stakeholders in the project with an overview of the different candidate solutions.

From the box plots, it can be seen that the <Pre-calibration> method provides the best overall results for all tire solutions. This is to be expected since the value $R_{ee}$ used matches reality with a high degree of accuracy. The candidate with the best results in terms of largest overall $d_t$ for all co-simulation cases is not necessarily the one that will be chosen for implementation on the actual robot. Factors, such as material, development, implementation and maintenance costs, affect the final configuration selection. The 0.001-m tire compression solution requires adjustment by an operator before start-up. The pre-calibrated solution must be updated periodically to account for changes in the robot setup. The vision solution is calibrated for a specific set of farm configurations and requires adjustments for new conditions. Nevertheless, this overview provides a means of evaluating the external costs with respect to the expected distance between the RFID tag and affords a more educated configuration selection.

Based on the co-simulation result, approximately 300 h are required to perform the analysis on the actual platform, excluding the time spent fixing the starting position and that taken up by mistakes during the test. Note that the co-model can be reused to explore other aspects of this robotic system. One could, for example, extend the co-model with another feeding arm to provide feeding capabilities on both sides and redo a similar design analysis. The time saved by the co-modeling and ACA could be invested in other areas of the project. The overview obtained by ACA does not guarantee optimal solutions, but it does facilitate the analysis of multiple candidate solutions.

The results from the individual co-simulations run can be used to judge the overall fodder placement. Individual result evaluation was the approach that was taken when the co-model was developed as illustrated in Figure 10, to improve on the DE controller design. The possibility exists to re-evaluate individual failed candidate solutions, to determine if the new improvements that the developers come up with would yield a better result. Here, co-simulation would allow the developers to rapidly evaluate these new candidate solutions under the same min-mean-max test set, to compare against Figure 9. Based on the lessons learned from developing the described co-model, we see co-modeling and co-simulation, as well as suited development tools for future robotics projects.

A similar analysis could also be completely performed using MATLAB/Simulink, Gazebo or a comparable tool. We expect the result of the simulations using one of these tools to match if the co-model described in this paper in Section 5 and Section 6 were implemented. However, developers would need to understand and work collaboratively using a single tool, without the advantages of co-modeling and co-simulation using multiple domain-specific tools. In this article, we have illustrated that co-modeling and co-simulation provide the ability to analyze multi-disciplinary design problem, using tools from individual disciplines.

9. Concluding Remarks

The development of a robotic system that conforms to the overall system requirements is essential. In this paper, we described the concept of co-modeling and co-simulation as an approach to robot design. We also showed how co-simulation using DSE affords a cross-disciplinary overview of design candidates for a proposed robot. This was exemplified by the case study of a load-carrying robot for dispensing fodder. The cross-disciplinary DSE was used to determine the maximum distance between the RFID tags for each design candidate. An alternative trial-and-error approach to determine the best design candidate would normally require 300 h.

The co-modeling and co-simulation of the feeding robot was used to illustrate tool-decoupled development involving dynamic modeling, control and signal processing. Overture, 20-sim and MATLAB were all used to create a complete co-model of the robot in the proposed design approach, thereby allowing multi-disciplinary developers to utilize tools specific to their respective disciplines. The effects of the carried load, surface conditions and safety considerations were considered in evaluating the different candidate designs in this study. It is our belief that the combination of co-modeling and co-simulation with DSE can be used as a part of the development to analyze and compare design candidates in different domains.