A Geographical-Based Multi-Criteria Approach for Marine Energy Farm Planning
Abstract
:1. Introduction
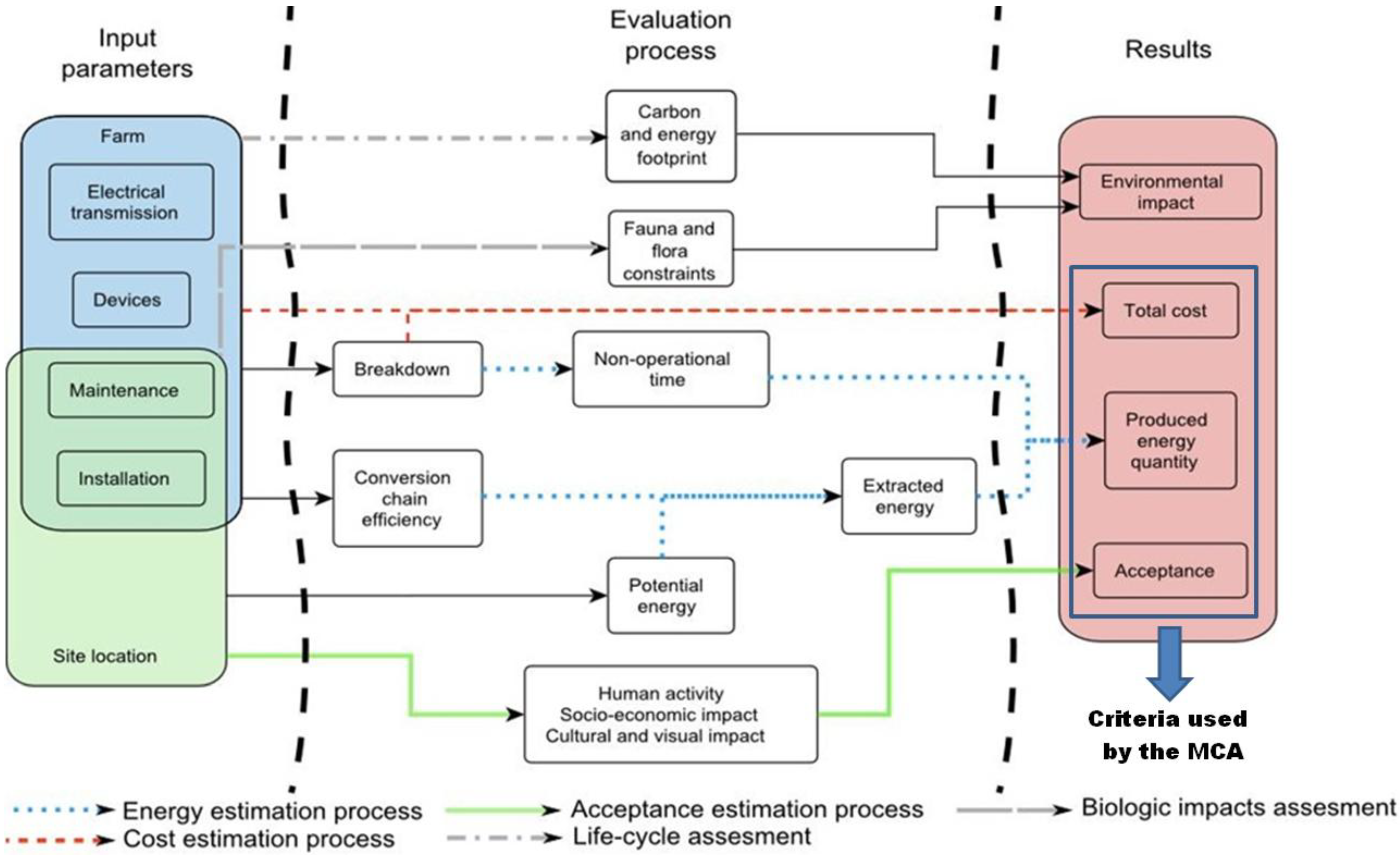
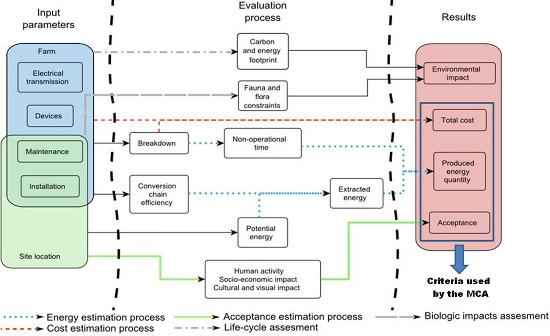
2. Methodology Principles
- -
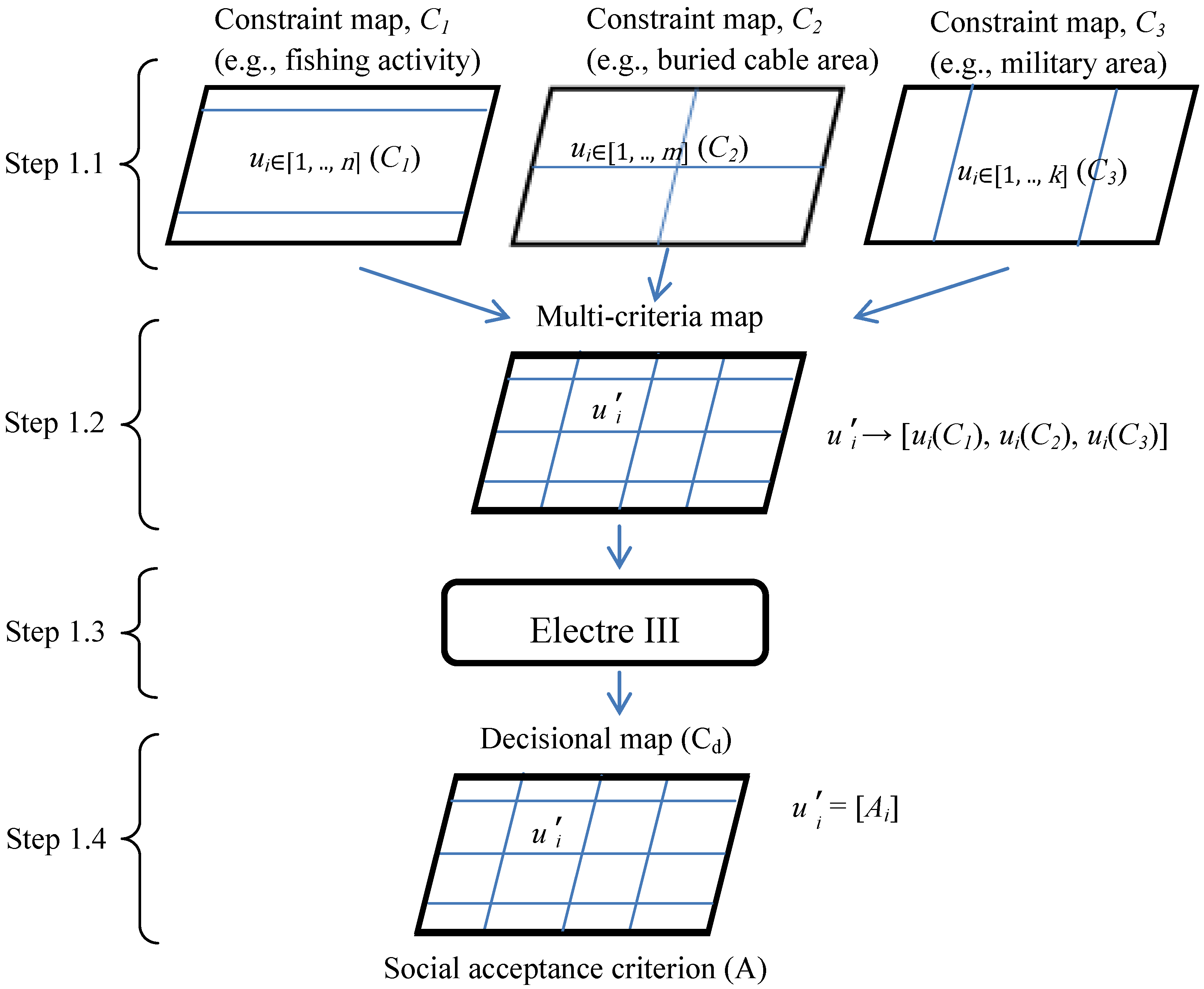
- Step 1.1: Generate a series of constraint maps. Each map represents a geographical area with a specific conflict source. Each constraints map is respectively divided into a number (n, m, k in Figure 3) of spatial units, ui, having an attribute, ai, describing the activities. With respect to the example presented in Figure 3, these maps are C1 for fishing area, C2 for buried cables and C3 for military activities and have n, m and k spatial units, respectively.C1 : [u1, …, un] → [a1, …, an]C2 : [u1, …, um] → [a1, …, am]C3 : [u1, …, uk] → [a1, …, ak]
- -
- Step 1.2: Derive the multi-criteria map. The generation of this intermediate map, Cm, is obtained by the overlay of constraint maps. This intermediate map is composed of a set of p spatial units uʹ1, …, uʹp. This means that each spatial unit, uʹi, is derived from the intersection of spatial units from C1 and C2 and C3 and is valued by three attributes a(C1), a(C2) and a(C3).Cm : [uʹ1, …, uʹi, …, uʹp] → [aʹ1, …, aʹi, …, aʹp] with uʹi → aʹi = {ai(C1), ai(C2), ai(C3)}
- -
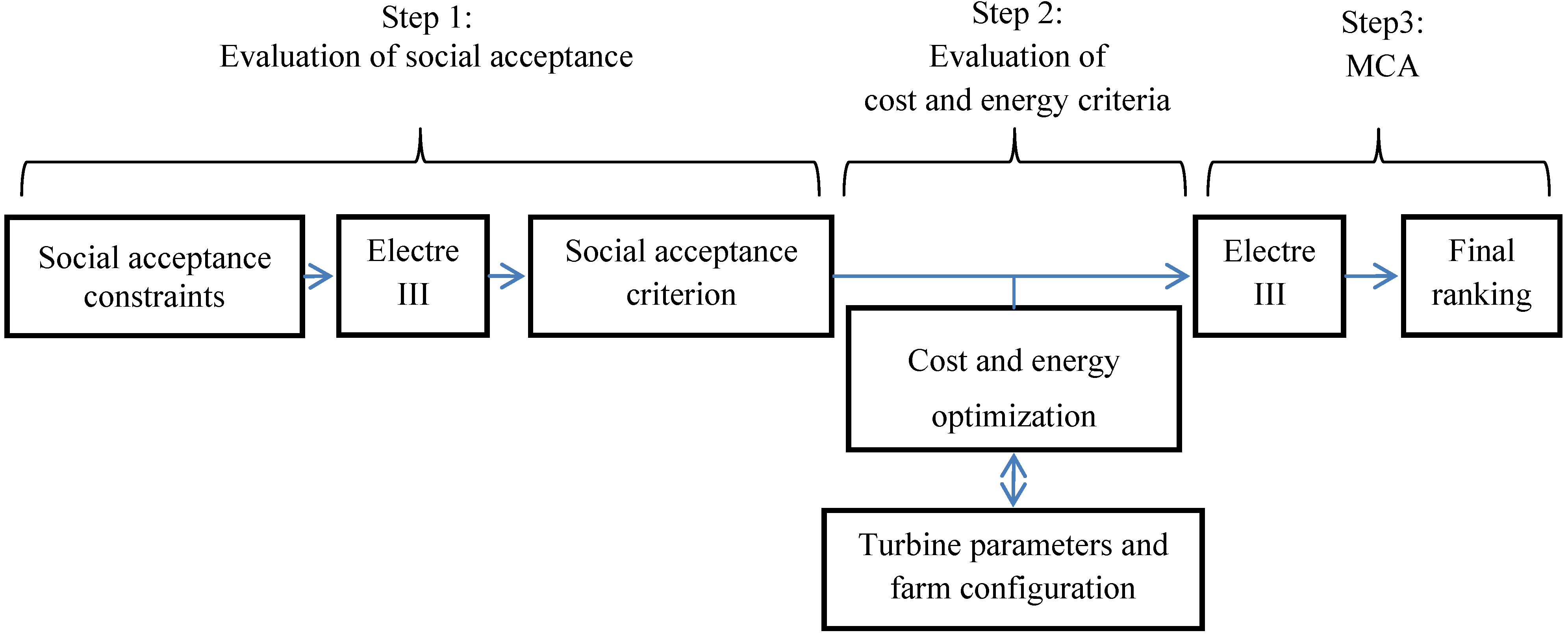
- Step 1.3: Apply the MCA method. The goal of this step is to reduce the dimension of uʹi to a single attribute, A, applying the aggregation method of Electre III.
- -
- Step 1.4: Generate the decision-based map. The p spatial unit, uʹ, of this final map, Cd, is the same as the multi-criteria map. However, each of these units has a single attribute. The unique value assigned to each spatial unit reflects the final social acceptance ranking of each sub-area.Cd : [uʹ1, …, uʹp] → [A1, …, Ap]
- -
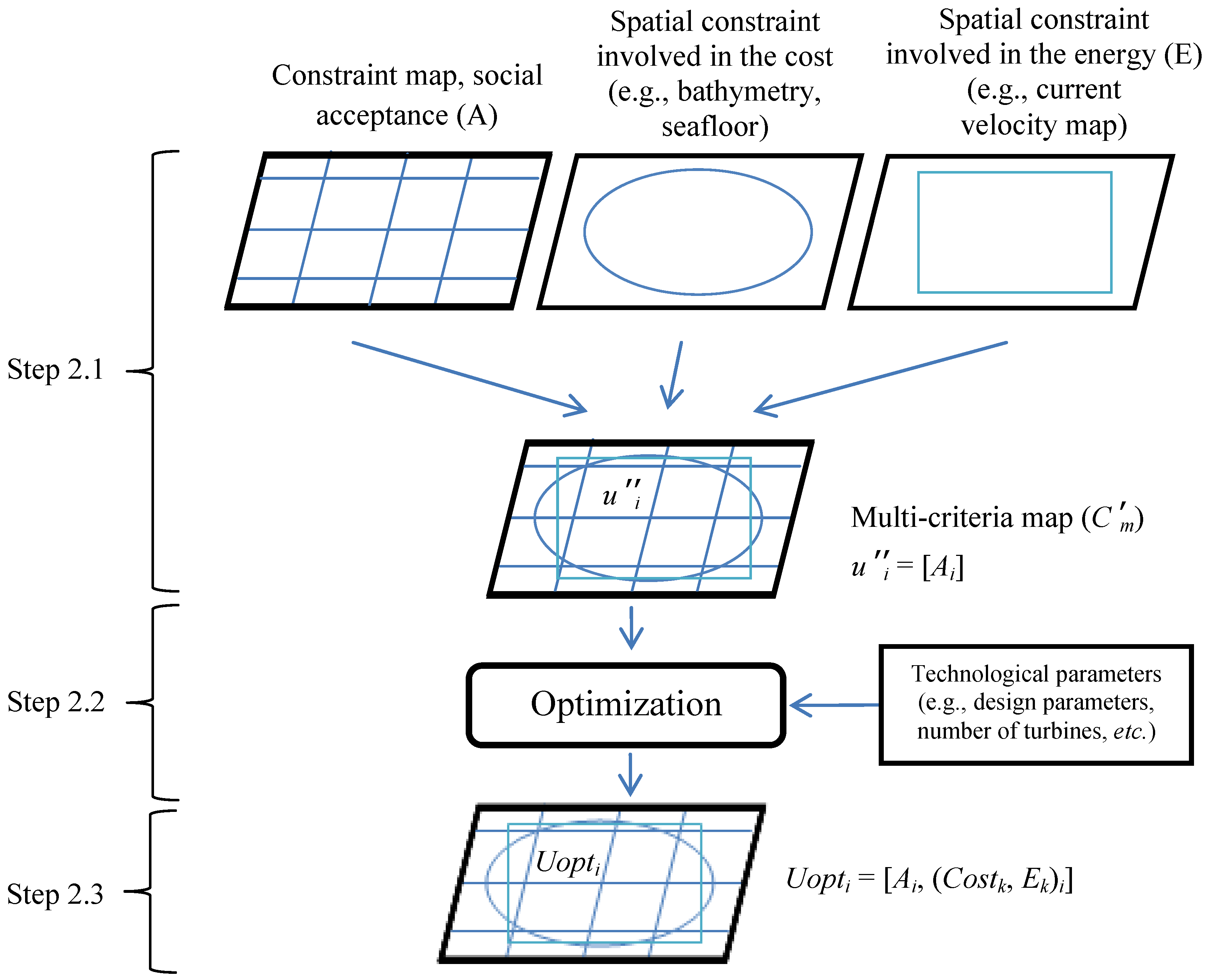
- Step 2.1: Generate a map (as Step 1.2) derived from an overlay of the social acceptance map with geographical constraints involved in the estimation of the cost and energy. The geographical maps considered here are the bathymetry, marine currents and seafloor geological characteristics. This derived map, Cʹm, is split into q spatial units, uʹʹ, having only one attribute: the value of social acceptability. This step generates a map of the study area segmented into homogeneous sub-areas. Values, such as the depth, are the parameters used in the appraisal of the cost.Cʹm : [uʹʹ1, …, uʹʹq] → [A1, … Aq]
- -
- Step 2.2: Optimize and evaluate the possible solutions using a genetic algorithm. For each spatial unit, uʹʹi, the optimization process searches, among all the possible configurations of the farm (number of machines, design choices, individual rating of the machines, etc.), for those that maximize the energy produced while minimizing the cost. The genetic algorithm is used to define a Pareto frontier that takes into account these two objectives. This Pareto frontier denotes the optimal solutions (i.e., solutions that minimize the cost for a set of given values of produced energy), as it exhibits a set of solutions that dominate the others (i.e., a solution, A, dominates a solution, B, if A is better than B regarding all dimensions considered). The optimal solutions exhibited by this Pareto frontier are ordered. This process provides the p best solutions for the cost-energy couple, (Costj=1, ... ,p, Ej=1, ... ,p) for each defined spatial unit (uʹʹi).
- -
- Step 2.3: Project the optimization solutions to each spatial unit of the multi-criteria map, Cʹm, as new attributes (cost and energy). Therefore, each spatial unit, Uopt, is characterized by three criteria. The social acceptance, A, and the p pairs of values related to the optimal cost and an energy corresponding to the optimal farm configurations, which have been found in the previous step.Cʹm : [uʹʹ1, …, uʹʹi, …,uʹʹq] with uʹʹi = Uopti → [Ai, (Costj=1, ... , p, Ej=1, ... , p)i]
3. Multi-Criteria Approach
3.1. Social Acceptance
3.2. Energy Assessment
- -
- vertical axis turbine;
- -
- horizontal axis turbine with yaw;
- -
- horizontal axis turbine without yaw.
- -
- three-stage gearbox with DFIG (double-fed induction generator),
- -
- direct drive with PMSG (permanent magnet synchronous generator).
3.3. Marine Farm System Cost
4. Case Study

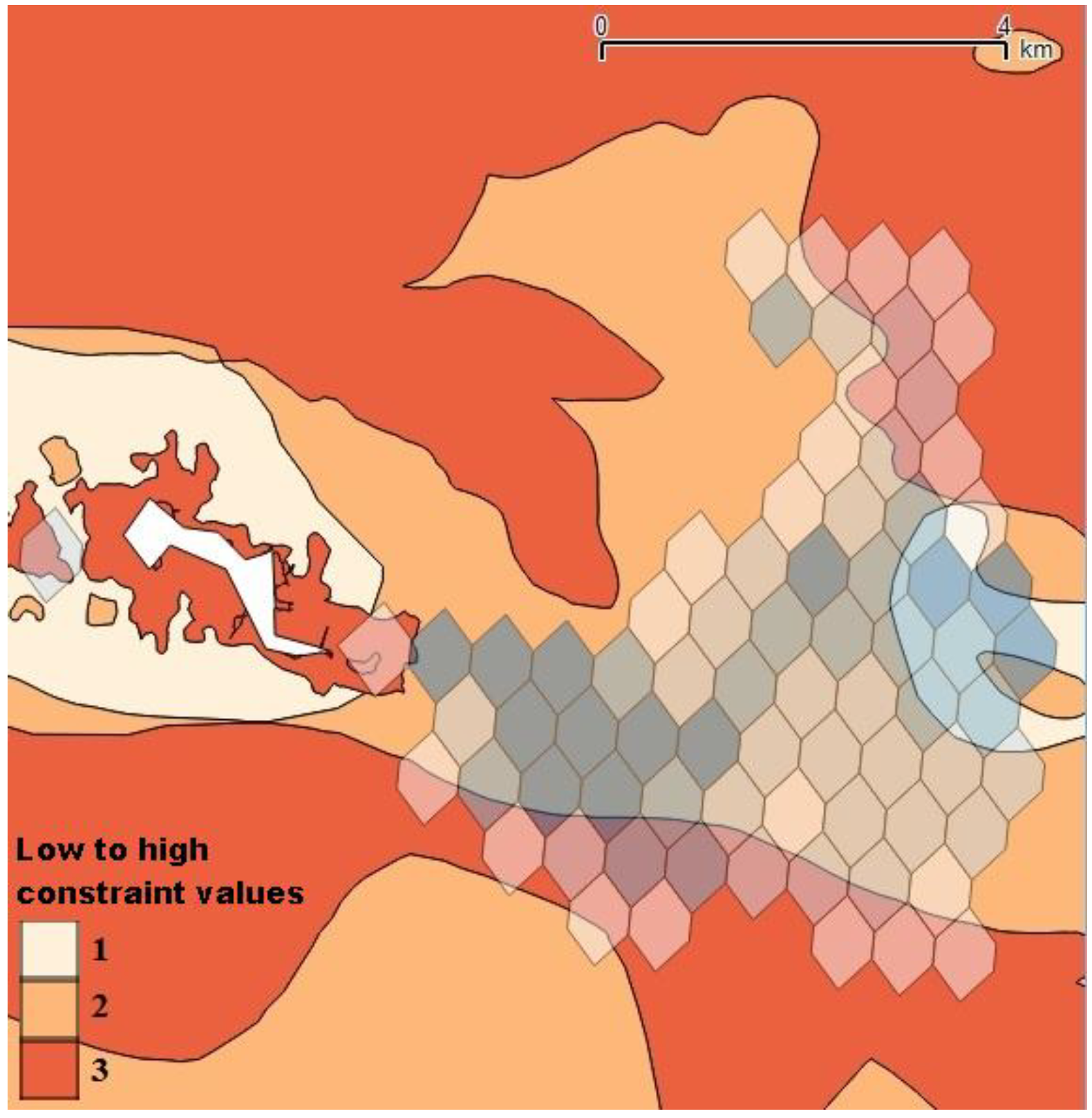
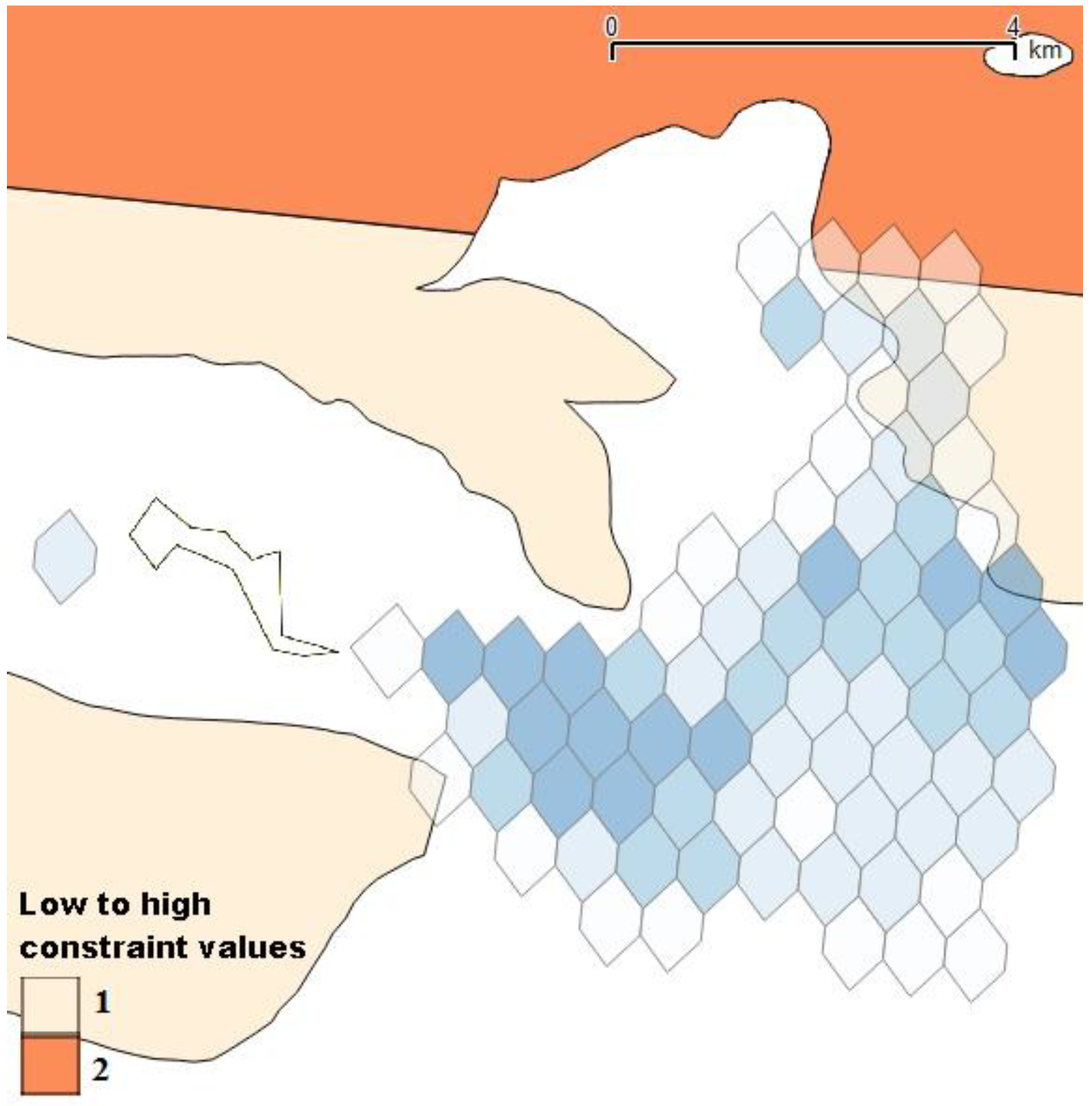
4.1. Social Acceptance Evaluation Using Electre III
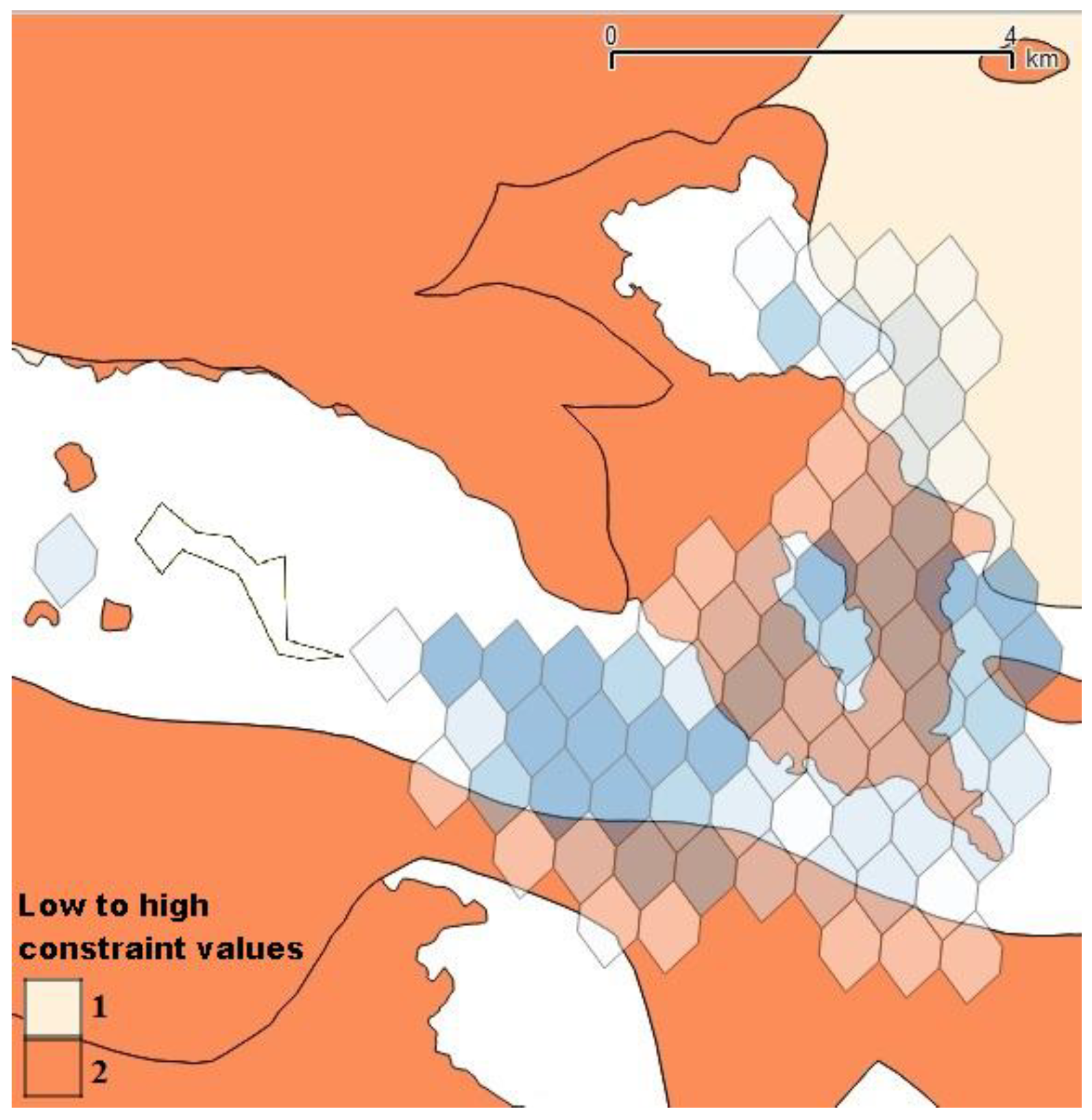

| Constraints | Weight (k) | Indifference Threshold (q) | Preference Threshold (p) | Veto Threshold (v) |
|---|---|---|---|---|
| Trawling/dredge | 3 | 0 | 1 | 3 |
| Nets | 2 | 0 | 1 | 3 |
| Floating lines | 1 | 0 | 1 | 3 |
| Ground lines | 2 | 0 | 1 | 3 |
4.2. Cost and Energy: Evaluation Using a Genetic Algorithm
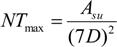
- -
- the turbine type (TT): VA or HA without yaw or HA + yaw
- -
- the rotor radius (R): 2.5 m to Rmax with a step of 0.5 m
- -
- the drive train configuration (DT): Direct-drive PMSG or DFIG + gearbox
- -
- the rating power (Pn) of DT: 0.1 to 3MW with a step of 0.1 MW
- -
- the number of turbines (NT) one to NTmax
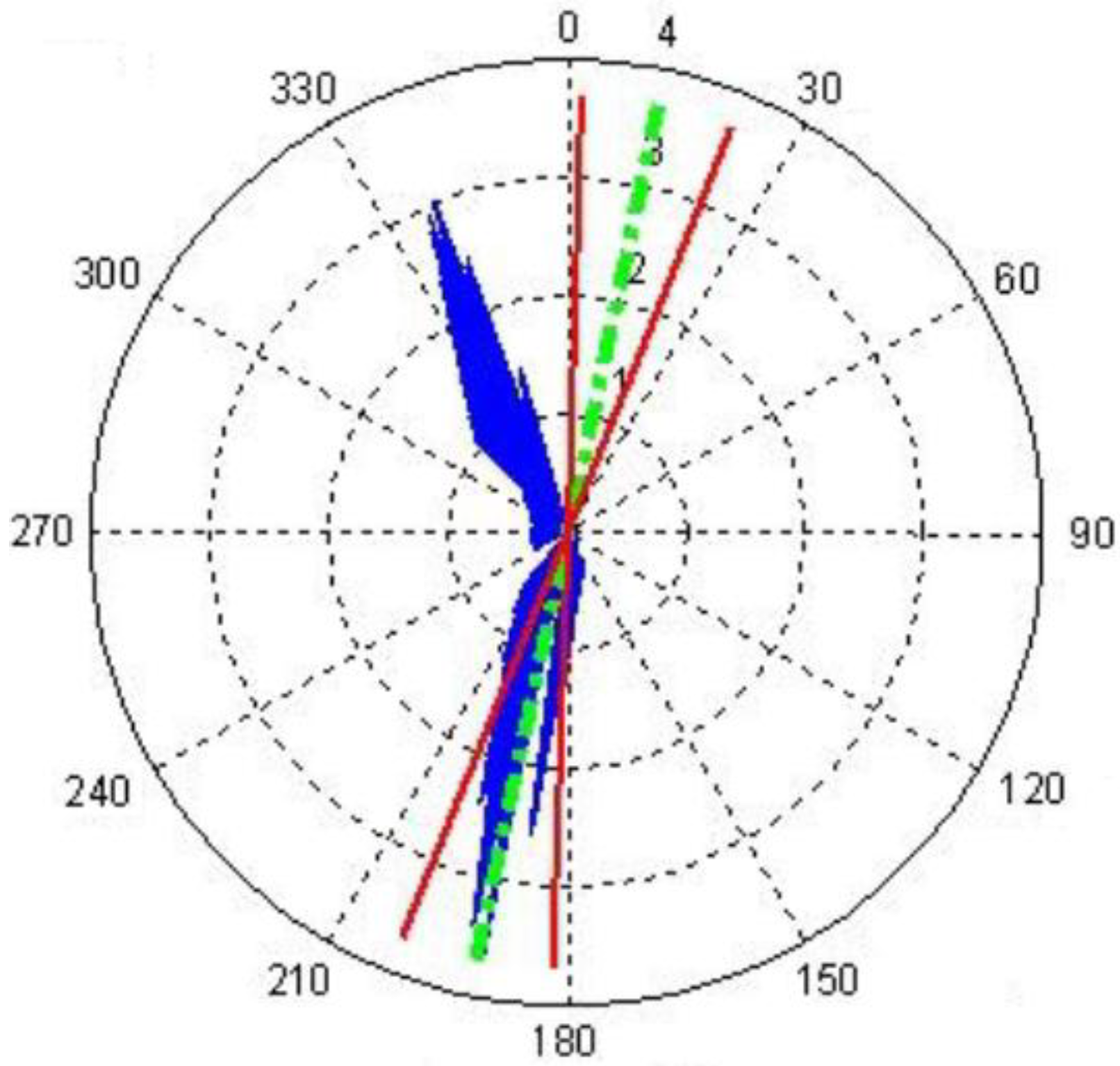
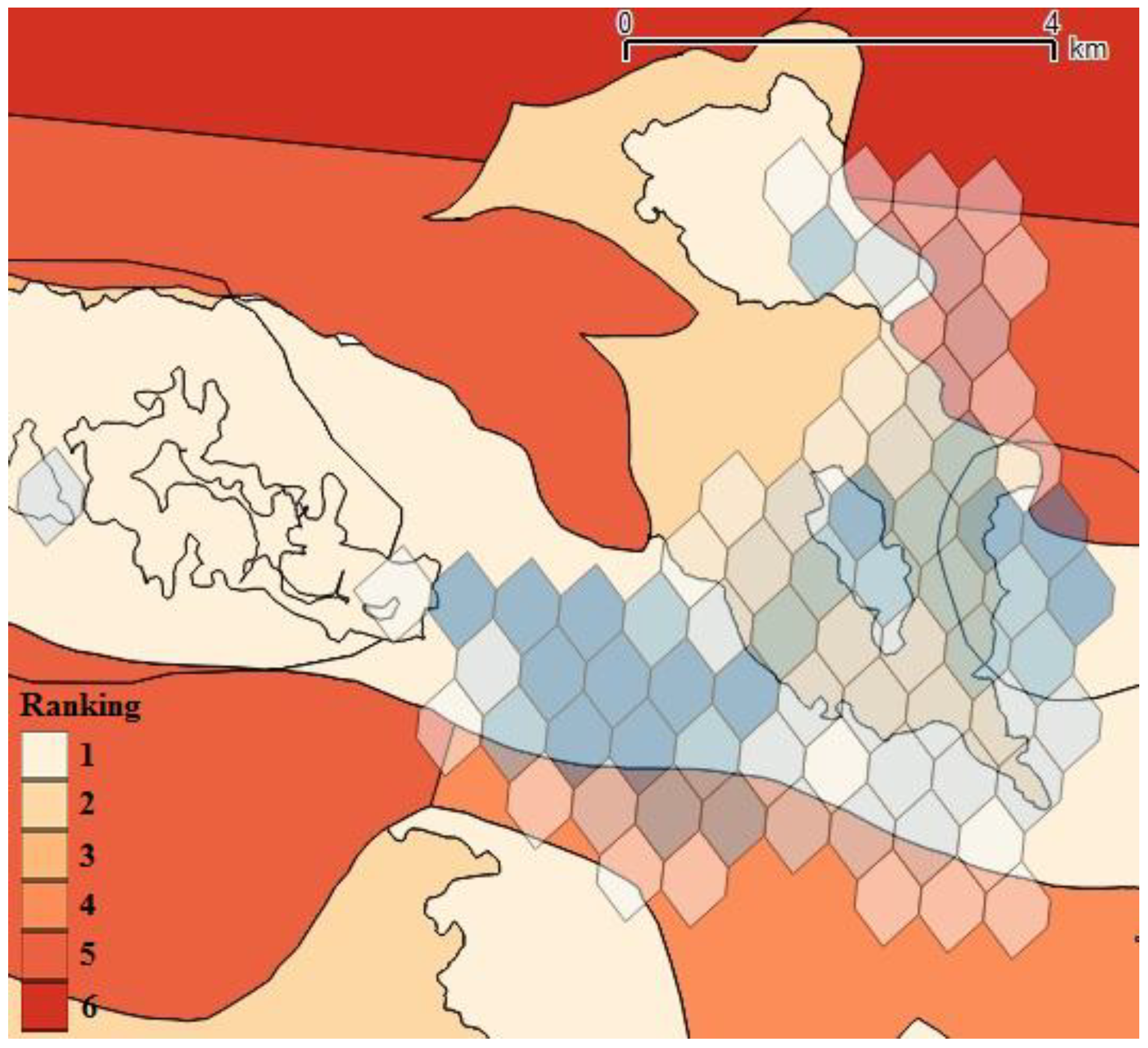
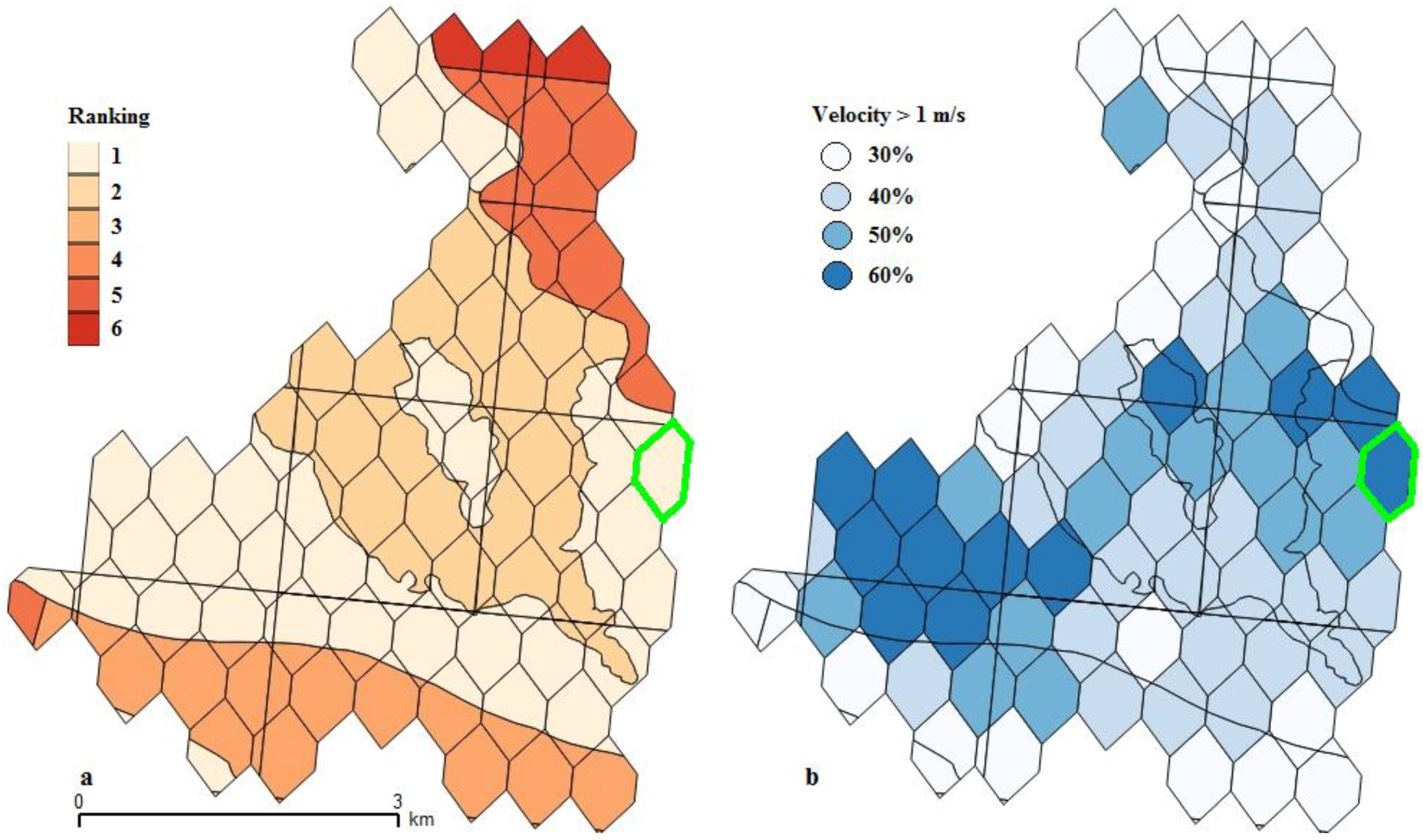
4.3. Final Ranking
| Alternatives | Energy (MWh/year) | Cost (M€) | Pn (MW) | R (m) | TT | NT | DT | €/MWh (20 years) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1068 | 5.7 | 0.3 | 7 | HA + yaw | 1 | PMSG | 267 |
| 2 | 1210 | 5.8 | 0.4 | 7 | HA + yaw | 1 | PMSG | 240 |
| 3 | 1469 | 6.2 | 1 | 7 | HA + yaw | 1 | PMSG | 211 |
| 4 | 1478 | 6.3 | 1.1 | 7 | HA + yaw | 1 | PMSG | 213 |
| 5 | 1493 | 6.4 | 1.4 | 7 | HA + yaw | 1 | PMSG | 214 |
| 6 | 1496 | 6.9 | 2.1 | 7 | HA + yaw | 1 | PMSG | 231 |
| 7 | 2137 | 8.3 | 0.3 | 7 | HA + yaw | 2 | PMSG | 194 |
| 8 | 2420 | 8.4 | 0.4 | 7 | HA + yaw | 2 | PMSG | 174 |
| 9 | 2956 | 9.3 | 1.1 | 7 | HA + yaw | 2 | PMSG | 157 |
| 10 | 2985 | 9.7 | 1.4 | 7 | HA + yaw | 2 | PMSG | 162 |
| 11 | 2993 | 10.2 | 1.8 | 7 | HA + yaw | 2 | PMSG | 170 |
| 12 | 3205 | 10.8 | 0.3 | 7 | HA + yaw | 3 | PMSG | 168 |
| 13 | 3630 | 11 | 0.4 | 7 | HA + yaw | 3 | PMSG | 152 |
| 14 | 4407 | 12.2 | 1 | 7 | HA + yaw | 3 | PMSG | 138 |
| 15 | 4433 | 12.4 | 1.1 | 7 | HA + yaw | 3 | PMSG | 140 |
| 16 | 4478 | 13 | 1.4 | 7 | HA + yaw | 3 | PMSG | 145 |
| 17 | 4489 | 13.8 | 1.8 | 7 | HA + yaw | 3 | PMSG | 154 |
| 18 | 8867 | 21.6 | 1.1 | 7 | HA + yaw | 6 | PMSG | 122 |
| Constraints | Weight (k) | Indifference Threshold (q) | Preference Threshold (p) | Veto Threshold (v) |
|---|---|---|---|---|
| Energy | 1 | 10 (MWh) | 300 (MWh) | 3000 (MWh) |
| Cost | 3 | 0 | 0.1 (M€) | 1 (M€) |
| Social acceptance | 1 | 0 | 1 | 3 |
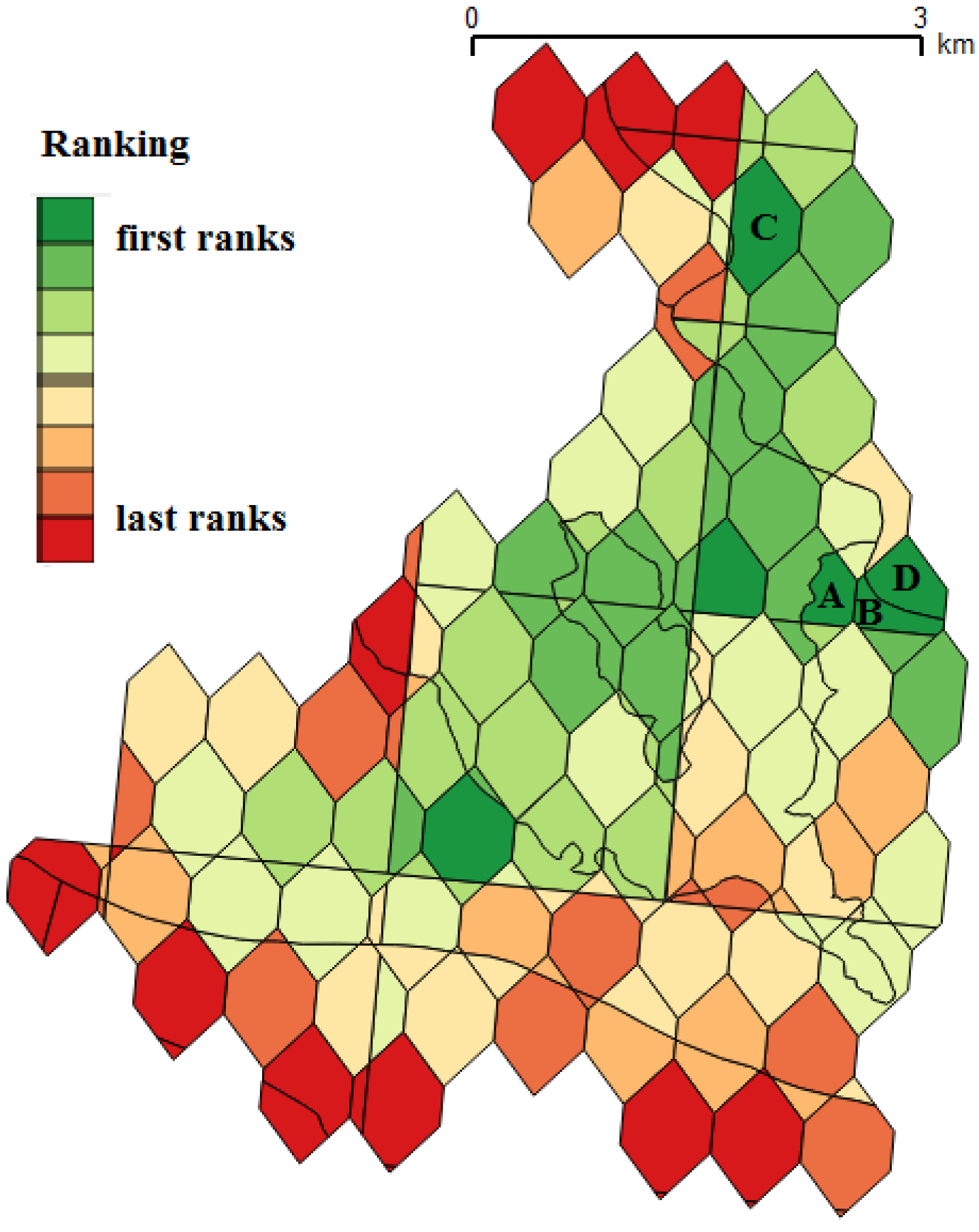
| Spatial Unit | Rank | Energy (MWh/year) | Cost (M€) | Pn (MW) | R (m) | TT | NT | NTmax | DT | €/MWh (20 years) |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 2710 | 6.3 | 0.5 | 11 | HA | 1 | 5 | PMSG | 116.2 |
| B | 3 | 2860 | 6.5 | 1.1 | 11 | HA + yaw | 1 | 4 | PMSG | 113. 6 |
| C | 6 | 7426 | 11.9 | 0.6 | 12 | HA | 3 | 10 | PMSG | 80.1 |
| D | 7 | 3221 | 7.3 | 2.1 | 11 | HA + yaw | 1 | 7 | PMSG | 113.3 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Multon, B. Marine Renewable Energy Handbook; Wiley-ISTE: Hoboken, NJ, USA, 2011. [Google Scholar]
- O’Sullivan, D.L.; Lewis, A.W. Generator selection and comparative performance in offshore oscillating water column ocean wave energy converters. IEEE Trans. Energy Convers. 2011, 26, 603–614. [Google Scholar] [CrossRef]
- Khan, M.J.; Bhuyan, G.; Iqbal, M.T.; Quaicoe, J.E. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Benelghali, S.; Benbouzid, M.E.H.; Charpentier, J.F. Marine Tidal Current Electric Power Generation Technology: State of the Art and Current Status. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC ’07), Antalya, Turkey, 3–5 May 2007.
- Roy, B. ELECTRE III: Un algorithme de classements fondé sur une représentation floue des préférences en présence de criteres multiples. Cahiers du CERO 1978, 20, 3–24. [Google Scholar]
- Beccali, M.; Cellura, M.; Mistretta, M. Decision-making in energy planning. Application of the electre method at regional level for the diffusion of renewable energy technology. Renew. Energy 2003, 13, 2063–2087. [Google Scholar]
- Barda, O.H.; Dupuis, J.; Lencioni, P. Multicriteria location of thermal power plants. Eur. J. Oper. Res. 1990, 45, 332–346. [Google Scholar] [CrossRef]
- Georgopoulou, E.; Lalas, D.; Papagiannakis, L. A multicriteria decision aid approach for energy: The case of renewable energy option. Eur. J. Oper. Res. 1997, 103, 38–54. [Google Scholar] [CrossRef]
- Rogers, M.; Bruen, M. Choosing realistic values of indifference, preference and veto thresholds for use with environmental criteria within ELECTRE. Eur. J. Oper. Res. 1998, 107, 542–551. [Google Scholar] [CrossRef]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar]
- Douvere, F. The importance of marine spatial planning in advancing ecosystem-based sea use management. Mar. Policy 2008, 32, 762–771. [Google Scholar]
- Ehler, C.; Douvere, F. Marine Spatial Planning, a Step-by-Step Approach towards Ecosystem-Based Management; Intergovernmental Oceanographic Commission and Man and the Biosphere Programme: Paris, France, 2009. [Google Scholar]
- Chakhar, S. Cartographie Décisionnelle Multicritère: Formalisation et Implémentation Informatique. Ph.D. Thesis, University of Paris Dauphine, Paris, France, 2006. [Google Scholar]
- Young, O.R.; Osherenko, G.; Ekstrom, J.; Crowder, L.B.; Ogden, J.; Wilson, J.A.; Day, J.C.; Douvere, F.; Ehler, C.N.; McLeod, K.L.; et al. Solving the crisis in ocean governance: Place-based management of marine ecosystems. Environ. Sci. Policy Sustain. Dev. 2007, 49, 20–32. [Google Scholar]
- Henderson, A. Offshore Wind Energy—Ready to Power a Sustainable Europe. EU Concerted Action on Offshore Wind Energy in Europe. 2001. Available online: http://www.offshorecenter.dk/log/bibliotek/offshore%20wind%20energy%20ready%20to%20power.PDF (accessed on 12 March 2014).
- Le Guyader, D. Modélisation des Activités Humaines en Mer Côtière. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2012. [Google Scholar]
- Benelghali, S.; Benbouzid, M.E.H.; Charpentier, J.F. Comparison of PMSG and DFIG for Marine Current Turbine Applications. In Proceedings of the 2010 XIX International Conference on Electrical Machines (ICEM); Rome, Italy: 6–8 September 2010.
- Suzuki, M. Numerical analysis of horizontal-axis wind turbine characteristics in yawed conditions. Open J. Fluid Dyn. 2012, 2, 331–336. [Google Scholar] [CrossRef]
- Gonzalez, J.S.; Payan, B.M.; Santos, J.R. An Improved Evolutive Algorithm for Large Offshore Wind Farm Optimum Turbines Layout. In Proceedings of the 2011 IEEE Trondheim PowerTech; Trondheim, Norway: 19–23 June 2011.
- Le Tixerant, M.; Gourmelon, F.; Tissot, C.; Brosset, D. Modelling of human activity development in coastal sea areas. J. Coast. Conserv. 2011, 15, 407–416. [Google Scholar] [CrossRef]
- Pham, D.T.; Pham, P.T.N. Artificial intelligence in engineering. Int. J. Mach. Tools Manuf. 1999, 39, 937–949. [Google Scholar] [CrossRef]
- Diveux, T.; Sebastian, P.; Bernard, D.; Puiggali, J.R.; Grandidier, J.Y. Horizontal axis wind turbine systems: Optimization using genetic algorithms. Wind Energy 2001, 4, 151–171. [Google Scholar] [CrossRef]
- Legrand, C. Assessment of Tidal Energy Resource: Marine Renewable Energy Guides; European Marine Energy Centre: London, UK, 2009. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Maslov, N.; Brosset, D.; Claramunt, C.; Charpentier, J.-F. A Geographical-Based Multi-Criteria Approach for Marine Energy Farm Planning. ISPRS Int. J. Geo-Inf. 2014, 3, 781-799. https://doi.org/10.3390/ijgi3020781
Maslov N, Brosset D, Claramunt C, Charpentier J-F. A Geographical-Based Multi-Criteria Approach for Marine Energy Farm Planning. ISPRS International Journal of Geo-Information. 2014; 3(2):781-799. https://doi.org/10.3390/ijgi3020781
Chicago/Turabian StyleMaslov, Nicolas, David Brosset, Christophe Claramunt, and Jean-Frédéric Charpentier. 2014. "A Geographical-Based Multi-Criteria Approach for Marine Energy Farm Planning" ISPRS International Journal of Geo-Information 3, no. 2: 781-799. https://doi.org/10.3390/ijgi3020781