Population Genetic Structure and Diversity of Cryptic Species of the Plant Genus Macrocarpaea (Gentianaceae) from the Tropical Andes
Abstract
:1. Introduction
2. Results
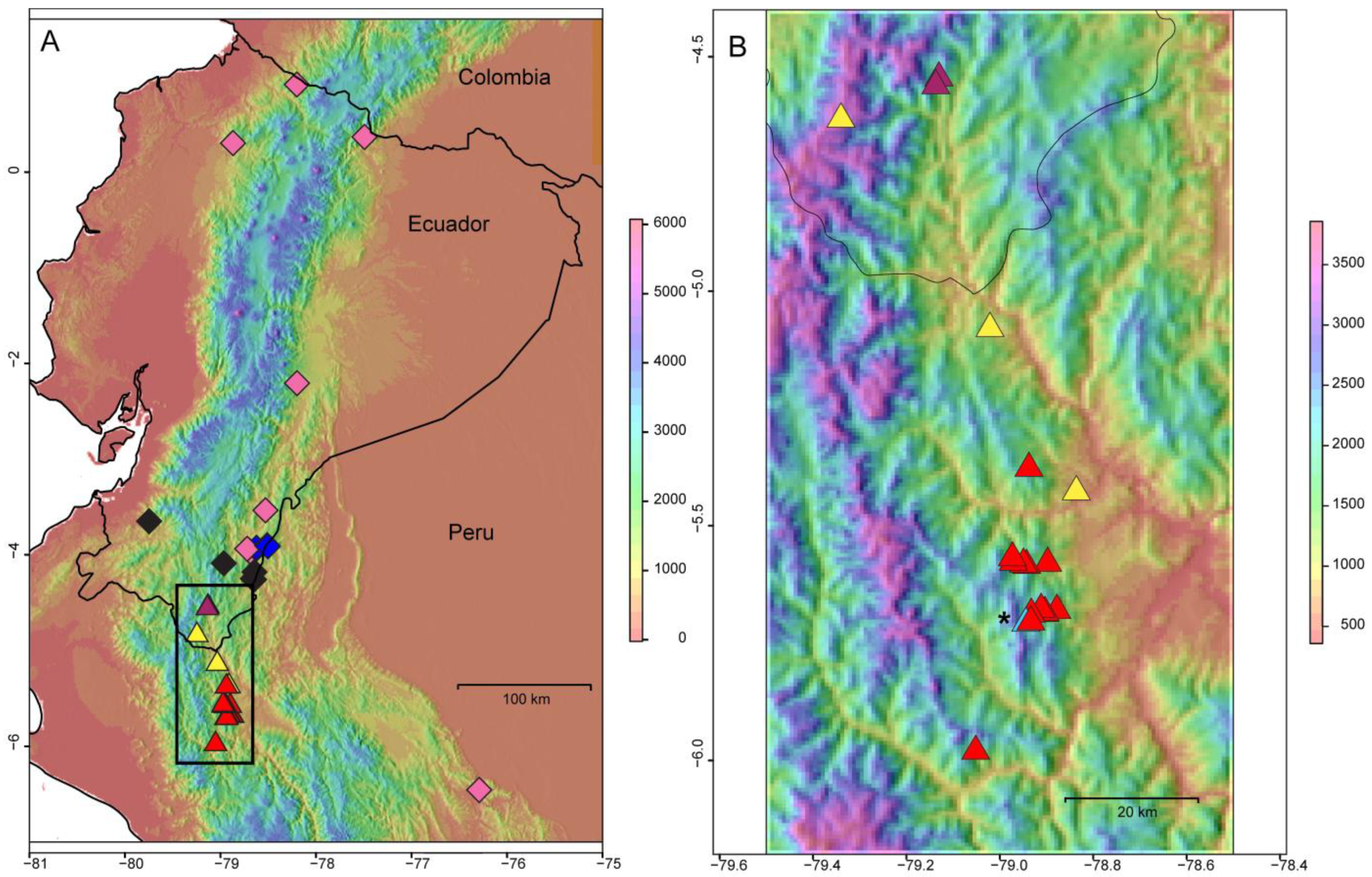
2.1. Population Structure
2.2. Descriptive Statistics of Diversity
2.3. Spatial Genetic Structure
3. Discussion
3.1. Deep Genetic Structure
3.2. The Concept of Species Inside the Species Complex
3.3. Differences in Gene Diversity and the Dry Refugia
3.4. Spatial Genetic Structure
3.5. Limitations and Alternative Explanations
4. Materials and Methods
4.1. Sampling
4.2. DNA Extraction and Genotyping
4.3. Population Structure
4.4. Descriptive Statistics
4.5. Spatial Genetic Structure
5. Conclusions
6. Simple Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a.s.l. | above sea level |
| AHZ | Amotape-Huancabamba zone |
| AFLP | amplified fragment length polymorphism genetic markers |
| AMOVA | analysis of molecular variance |
| LMF | lower montane forest |
| MMF | middle elevation montane forest |
| MRCA | most recent common ancestor |
| mya | million years ago |
| Myr | million years |
| NJ | neighbor-joining |
| PCO | Pleistocene climatic oscillations |
| SDTF | Seasonally dry tropical forests |
| SGS | spatial genetic structure |
| UFL | upper forest line |
| UMF | upper montane forest |
References
- Afzan, A.; Bréant, L.; Bellstedt, D.U.; Grant, J.R.; Queiroz, E.F.; Wolfender, J.-L.; Kissling, J. Can biochemical phenotype, obtained from herbarium samples, help taxonomic decisions?—A case study using Gentianaceae. TAXON 2019, 68, 771–782. [Google Scholar] [CrossRef]
- Baker, P.A.; Bush, M.; Fritz, S.; Rigsby, C.A.; Seltzer, G.; Silman, M. Last Glacial Maximum in an Andean cloud forest environment (Eastern Cordillera, Bolivia): Comment and Reply: COMMENT. Geology 2004, 31, e26–e27. [Google Scholar] [CrossRef]
- Bonin, A.; Bellemain, E.; Bronken Eidesen, P.; Pompanon, F.; Brochmann, C.; Taberlet, P. How to track and assess genotyping errors in population genetics studies. Mol. Ecol. 2004, 13, 3261–3273. [Google Scholar] [CrossRef] [PubMed]
- Brunschön, C.; Behling, H. Reconstruction and visualization of upper forest line and vegetation changes in the Andean depression region of southeastern Ecuador since the last glacial maximum—A multi-site synthesis. Rev. Palaeobot. Palynol. 2010, 163, 139–152. [Google Scholar] [CrossRef]
- Bush, M.B.; de Oliveira, P.E. The rise and fall of the Refugial Hypothesis of Amazonian speciation: A paleoecological perspective. Biota Neotrop. 2006, 6. [Google Scholar] [CrossRef]
- Colinvaux, P.A.; De Oliveira, P.E.; Bush, M.B. Amazonian and neotropical plant communities on glacial time-scales: The failure of the aridity and refuge hypotheses. Quat. Sci. Rev. 2000, 19, 141–169. [Google Scholar] [CrossRef]
- Collevatti, R.; Lima, J.S.; Soares, T.; Telles, M. Spatial genetic structure and life history traits in cerrado tree species: Inferences for conservation. Nat. Conserv. 2010, 8, 54–59. [Google Scholar] [CrossRef]
- Coulon, A.; Fitzpatrick, J.W.; Bowman, R.; Stith, B.M.; Makarewich, C.A.; Stenzler, L.M.; Lovette, I.J. Congruent population structure inferred from dispersal behaviour and intensive genetic surveys of the threatened Florida scrub-jay (Aphelocoma coerulescens). Mol. Ecol. 2008, 17, 1685–1701. [Google Scholar] [CrossRef]
- Crespi, E.J.; Rissler, L.J.; Browne, R.A. Testing Pleistocene refugia theory: Phylogeographical analysis of Desmognathus wrighti, a high-elevation salamander in the southern Appalachians. Mol. Ecol. 2003, 12, 969–984. [Google Scholar] [CrossRef]
- Dlugosch, K.M.; Parker, I.M. Founding events in species invasions: Genetic variation, adaptive evolution, and the role of multiple introductions. Mol. Ecol. 2008, 17, 431–449. [Google Scholar] [CrossRef]
- Durand, E.; Jay, F.; Gaggiotti, O.E.; François, O. Spatial inference of admixture proportions and secondary contact zones. Mol. Biol. Evol. 2009, 26, 1963–1973. [Google Scholar] [CrossRef] [PubMed]
- Earl, D.A.; von Holdt, B.M. STRUCTURE HARVESTER: A website and program for visualizing STRUCTURE output and implementing the Evanno method. Conserv. Genet. Resour. 2012, 4, 359–361. [Google Scholar] [CrossRef]
- Elias, M.; Joron, M.; Willmott, K.; Silva-Brandão, K.L.; Kaiser, V.; Arias, C.F.; Gomez Piñerez, L.M.; Uribe, S.; Brower, A.V.Z.; Freitas, A.V.L.; et al. Out of the Andes: Patterns of diversification in clearwing butterflies. Mol. Ecol. 2009, 18, 1716–1729. [Google Scholar] [CrossRef]
- Evanno, G.; Regnaut, S.; Goudet, J. Detecting the number of clusters of individuals using the software STRUCTURE: A simulation study. Mol. Ecol. 2005, 14, 2611–2620. [Google Scholar] [CrossRef] [PubMed]
- Excoffier, L.; Lischer, H.E.L. Arlequin suite ver 3.5: A new series of programs to perform population genetics analyses under Linux and Windows. Mol. Ecol. Resour. 2010, 10, 564–567. [Google Scholar] [CrossRef]
- Falush, D.; Stephens, M.; Pritchard, J.K. Inference of population structure using multilocus genotype data: Linked loci and correlated allele frequencies. Genetics 2003, 164, 1567–1587. [Google Scholar] [CrossRef]
- Felsenstein, J. PHYLIP (Phylogeny Inference Package) Version 3.6, Distributed by the Author; Department of Genome Sciences, University of Washington: Seattle, WA, USA, 2005. [Google Scholar]
- Fjeldså, J.; Bowie, R.C.K.; Rahbek, C. The role of mountain ranges in the diversification of birds. Annu. Rev. Ecol. Evol. Syst. 2012, 43, 249–265. [Google Scholar] [CrossRef]
- Flantua, S.G.A.; Hooghiemstra, H.; van Boxel, J.H.; Cabrera, M.; González-Carranza, Z.; González-Arango, C. Connectivity Dynamics since the Last Glacial Maximum in the Northern Andes: A Pollen-Driven Framework to Assess Potential Migration; St. Louis Missouri Botanical Garden Press: St. Louis, MO, USA, 2014. [Google Scholar]
- Fleming, T.H.; Geiselman, C.; Kress, W.J. The evolution of bat pollination: A phylogenetic perspective. Ann. Bot. 2009, 104, 1017–1043. [Google Scholar] [CrossRef]
- Gentry, A.H. Neotropical floristic diversity: Phytogeographical connections between Central and South America, Pleistocene climatic fluctuations, or an accident of the Andean ogrogeny? Ann. Mo. Bot. Gard. 1982, 69, 557–593. [Google Scholar] [CrossRef]
- Grant, J.R. A monographic revision of the neotropical genus Macrocarpaea (Gentianaceae) in Ecuador. In The Gentianaceae—Volume 1: Characterization and Ecology; Rybczyński, J.J., Davey, M.R., Mikuła, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014a; pp. 37–147. [Google Scholar] [CrossRef]
- Grant, J.R. De Macrocarpaeae Grisebach (Ex Gentianaceis) Speciebus novis XI: Five new species from the Andes of Ecuador and Colombia. Harvard Pap. Bot. 2014b, 19, 227–239. [Google Scholar] [CrossRef]
- Grant, J.R. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis IX: A Synopsis of the Genus in Bolivia. Harvard Pap. Bot. 2011, 16, 389–397. [Google Scholar] [CrossRef]
- Grant, J.R. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis VIII: Two new species from Ecuador. Harvard Pap. Bot. 2008, 13, 253–259. [Google Scholar] [CrossRef]
- Grant, J.R. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis VII: Four new species and two natural hybrids. Harvard Pap. Bot. 2007, 11, 129–139. [Google Scholar] [CrossRef]
- Grant, J.R. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis VI: Seed morphology, palynology, an infrageneric classification, and another twenty-three new species, largely from Colombia. Harvard Pap. Bot. 2005, 9, 305–342. [Google Scholar]
- Grant, J.R. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis V: Twenty-three new species largely from Peru, and typification of all species in the genus. Harvard Pap. Bot. 2004, 9, 11–49. [Google Scholar]
- Grant, J.R. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus Novis II: Typification of the Ruiz & Pavon names. Harvard Pap. Bot. 2003, 7, 423–436. [Google Scholar]
- Grant, J.R.; Struwe, L. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis III: Six new species of moon-gentians (Macrocarpaea, Gentianaceae: Helieae) from Parque Nacional Podocarpus, Ecuador. Harvard Pap. Bot. 2003, 8, 61–81. [Google Scholar]
- Grant, J.R.; Struwe, L. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus Novis I: An introduction to the genus Macrocarpaea and three new species from Colombia, Ecuador, and Guyana. Harvard Pap. Bot. 2001, 5, 489–498. [Google Scholar]
- Grant, J.R.; Trunz, V. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis X: A synopsis of the genus in Montane Atlantic Forests of Brazil. Harvard Pap. Bot. 2011, 16, 399–420. [Google Scholar] [CrossRef]
- Grant, J.R.; Vieu, J. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis XII: Three new species from the Andes of Peru. Harvard Pap. Bot. 2014, 19, 241–246. [Google Scholar] [CrossRef]
- Grant, J.R.; Weaver, R.E. De Macrocarpaeae Grisebach (ex Gentianaceis) Speciebus novis IV: Twelve new species of Macrocarpaea (Gentianaceae: Helieae) from Central and South America, and the first report of the presence of a stipule in the family. Harvard Pap. Bot. 2003, 8, 83–109. [Google Scholar]
- Hardy, O.J. Estimation of pairwise relatedness between individuals and characterization of isolation-by-distance processes using dominant genetic markers. Mol. Ecol. 2003, 12, 1577–1588. [Google Scholar] [CrossRef] [PubMed]
- Hardy, O.J.; Maggia, L.; Bandou, E.; Breyne, P.; Caron, H.; Chevallier, M.-H.; Doligez, A.; Dutech, C.; Kremer, A.; Latouche-Hallé, C.; et al. Fine-scale genetic structure and gene dispersal inferences in 10 neotropical tree species. Mol. Ecol. 2006, 15, 559–571. [Google Scholar] [CrossRef] [PubMed]
- Hardy, O.J.; Vekemans, X. SPAGeDi: A versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol. Ecol. Notes 2002, 2, 618–620. [Google Scholar] [CrossRef]
- Herrmann, D.; Poncet, B.N.; Manel, S.; Rioux, D.; Gielly, L.; Taberlet, P.; Gugerli, F. Selection criteria for scoring amplified fragment length polymorphisms (AFLPs) positively affect the reliability of population genetic parameter estimates. Genome 2010, 53, 302–310. [Google Scholar] [CrossRef]
- Hewitt, G.M. Genetic consequences of climatic oscillations in the Quaternary. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 2004, 359, 183–195. [Google Scholar] [CrossRef]
- Hewitt, G.M. Some genetic consequences of ice ages, and their role in divergence and speciation. Biol. J. Linn. Soc. 1996, 58, 247–276. [Google Scholar] [CrossRef]
- Hughes, C.; Eastwood, R. Island radiation on a continental scale: Exceptional rates of plant diversification after uplift of the Andes. PNAS 2006, 103, 10334–10339. [Google Scholar] [CrossRef]
- Hughes, C.E.; Atchison, G.W. The ubiquity of alpine plant radiations: From the Andes to the Hengduan Mountains. New Phytol. 2015, 207, 275–282. [Google Scholar] [CrossRef]
- Hutter, C.R.; Guayasamin, J.M.; Wiens, J.J. Explaining Andean megadiversity: The evolutionary and ecological causes of glassfrog elevational richness patterns. Ecol. Lett. 2013, 16, 1135–1144. [Google Scholar] [CrossRef]
- Knowles, L.L. Tests of Pleistocene speciation in montane grasshoppers (genus Melanoplus) from the Sky Islands of western North America. Evolution 2000, 54, 1337–1348. [Google Scholar] [CrossRef]
- Kopelman, N.M.; Mayzel, J.; Jakobsson, M.; Rosenberg, N.A.; Mayrose, I. Clumpak: A program for identifying clustering modes packaging population structure inferences across, K. Mol. Ecol. Resour. 2015, 15, 1179–1191. [Google Scholar] [CrossRef]
- Linder, H.P.; Rabosky, D.L.; Antonelli, A.; Wüest, R.O.; Ohlemüller, R. Disentangling the influence of climatic and geological changes on species radiations. J. Biogeogr. 2014, 41, 1313–1325. [Google Scholar] [CrossRef]
- Lynch, M.; Milligan, B.G. Analysis of population genetic structure with RAPD markers. Mol. Ecol. 1994, 3, 91–99. [Google Scholar] [CrossRef]
- Moritz, C.; Patton, J.L.; Schneider, C.J.; Smith, T.B. Diversification of rainforest faunas: An integrated molecular approach. Annu. Rev. Ecol. Syst. 2000, 31, 533–563. [Google Scholar] [CrossRef]
- Mourguiart, P.; Ledru, M.-P. Last Glacial Maximum in an Andean cloud forest environment (Eastern Cordillera, Bolivia). Geology 2003, 31, 195–198. [Google Scholar] [CrossRef]
- Murray, M.G.; Thompson, W.F. Rapid isolation of high molecular weight plant, D.N.A. Nucleic Acids Res. 1980, 8, 4321–4325. [Google Scholar] [CrossRef]
- Nybom, H. Comparison of different nuclear DNA markers for estimating intraspecific genetic diversity in plants. Mol. Ecol. 2004, 13, 1143–1155. [Google Scholar] [CrossRef]
- Orme, C.D.L.; Davies, R.G.; Burgess, M.; Eigenbrod, F.; Pickup, N.; Olson, V.A.; Webster, A.J.; Ding, T.-S.; Rasmussen, P.C.; Ridgely, R.S.; et al. Global hotspots of species richness are not congruent with endemism or threat. Nature 2005, 436, 1016–1019. [Google Scholar] [CrossRef]
- Parisod, C.; Christin, P.-A. Genome-wide association to fine-scale ecological heterogeneity within a continuous population of Biscutella laevigata (Brassicaceae). New Phytol. 2008, 178, 436–447. [Google Scholar] [CrossRef]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar] [CrossRef]
- Qin, A.; Ding, Y.; Jian, Z.; Ma, F.; Worth, J.R.P.; Pei, S.; Xu, G.; Guo, Q.; Shi, Z. Low genetic diversity and population differentiation in Thuja sutchuenensis Franch., an extremely endangered rediscovered conifer species in southwestern China. Glob. Ecol. Conserv. 2021, 25, e01430. [Google Scholar] [CrossRef]
- Ramírez-Barahona, S.; Eguiarte, L.E. The role of glacial cycles in promoting genetic diversity in the Neotropics: The case of cloud forests during the Last Glacial Maximum. Ecol. Evol. 2013, 3, 725–738. [Google Scholar] [CrossRef] [PubMed]
- Rull, V. Speciation timing and neotropical biodiversity: The Tertiary-Quaternary debate in the light of molecular phylogenetic evidence. Mol. Ecol. 2008, 17, 2722–2729. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, T. Molecular biogeography of Europe: Pleistocene cycles and postglacial trends. Front. Zool. 2007, 4, 11. [Google Scholar] [CrossRef]
- Schönswetter, P.; Stehlik, I.; Holderegger, R.; Tribsch, A. Molecular evidence for glacial refugia of mountain plants in the European Alps. Mol. Ecol. 2005, 14, 3547–3555. [Google Scholar] [CrossRef]
- Schwery, O.; Onstein, R.E.; Bouchenak-Khelladi, Y.; Xing, Y.; Carter, R.J.; Linder, H.P. As old as the mountains: The radiations of the Ericaceae. New Phytol. 2015, 207, 355–367. [Google Scholar] [CrossRef]
- Smith, S.A.; Oca, A.N.M.D.; Reeder, T.W.; Wiens, J.J. A phylogenetic perspective on elevational species richness patterns in middle American treefrogs: Why so few species in lowland tropical rainforests? Evolution 2007, 61, 1188–1207. [Google Scholar] [CrossRef]
- Struwe, L.; Albert, V.A.; Calió, F.M.; Frasier, C.; Lepis, K.B.; Mathews, K.G.; Grant, J.R. Evolutionary patterns in neotropical Helieae (Gentianaceae): Evidence from morphology, chloroplast and nuclear DNA sequences. TAXON 2009a, 58, 479–499. [Google Scholar] [CrossRef]
- Struwe, L.; Haag, S.; Heiberg, E.; Grant, J.R. Andean speciation and vicariance in neotropical Macrocarpaea (Gentianaceae-Helieae). Ann. Mo. Bot. Gard. 2009b, 96, 450–469. [Google Scholar] [CrossRef]
- Trénel, P.; Hansen, M.M.; Normand, S.; Borchsenius, F. Landscape genetics, historical isolation and cross-Andean gene flow in the wax palm, Ceroxylon echinulatum (Arecaceae). Mol. Ecol. 2008, 17, 3528–3540. [Google Scholar] [CrossRef]
- van der Hammen, T.; Hooghiemstra, H. Neogene and Quaternary history of vegetation, climate, and plant diversity in Amazonia. Quat. Sci. Rev. 2000, 19, 725–742. [Google Scholar] [CrossRef]
- Vekemans, X.; Beauwens, T.; Lemaire, M.; Roldán-Ruiz, I. Data from amplified fragment length polymorphism (AFLP) markers show indication of size homoplasy and of a relationship between degree of homoplasy and fragment size. Mol. Ecol. 2002, 11, 139–151. [Google Scholar] [CrossRef]
- Vekemans, X.; Hardy, O.J. New insights from fine-scale spatial genetic structure analyses in plant populations. Mol. Ecol. 2004, 13, 921–935. [Google Scholar] [CrossRef]
- Vieu, J.C.; Hughes, C.E.; Kissling, J.; Grant, J.R. Evolutionary diversification in the hyper-diverse montane forests of the tropical Andes: Radiation of Macrocarpaea (Gentianaceae) and the possible role of range expansion. Bot. J. Linn. Soc. 2022, 199, 53–75. [Google Scholar] [CrossRef]
- Vieu, J.C.; Koubínová, D.; Grant, J.R. The Evolution of Trait Disparity during the Radiation of the Plant Genus Macrocarpaea (Gentianaceae) in the Tropical Andes. Biology 2021, 10, 825. [Google Scholar] [CrossRef]
- Vos, P.; Hogers, R.; Bleeker, M.; Reijans, M.; van de Lee, T.; Hornes, M.; Frijters, A.; Pot, J.; Peleman, J.; Kuiper, M. AFLP: A new technique for DNA fingerprinting. Nucleic Acids Res. 1995, 23, 4407–4414. [Google Scholar] [CrossRef]
- Wolff, D. Nectar sugar composition and volumes of 47 species of Gentianales from a southern Ecuadorian montane forest. Ann. Bot. 2006, 97, 767–777. [Google Scholar] [CrossRef]
- Wollenberg, K.C.; Vieites, D.R.; Meijden, A.V.D.; Glaw, F.; Cannatella, D.C.; Vences, M. Patterns of endemism and species richness in Malagasy cophyline frogs support a key role of mountainous areas for speciation. Evolution 2008, 62, 1890–1907. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, L.; Liu, Y.-H.; Zhou, X.-L.; Zhang, L.-Q.; Wang, Y.-H.; Shen, S.-K. Genetic diversity, genetic structure, and demographic history of Cinnamomum chago, a plant species with extremely small populations in China. Glob. Ecol. Conserv. 2021, 31, e01808. [Google Scholar] [CrossRef]
- Zhivotovsky, L.A. Estimating population structure in diploids with multilocus dominant DNA markers. Mol. Ecol. 1999, 8, 907–913. [Google Scholar] [CrossRef] [PubMed]




| Population | Voucher | Country | Region | Cluster | Latitude | Longitude | Altitude | N | PLP | Hj | S.E. (Hj) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| M. claireae 1 | JRG4666 | E | ZC | A1 | −4.5422 | −79.1304 | 1744 | 19 | 21.7 | 0.090 | 0.009 |
| M. claireae 2 | JRG4667 | E | ZC | A1 | −4.5590 | −79.1371 | 1571 | 17 | 39.9 | 0.116 | 0.011 |
| M. cortinae 1 M. dies-viridis 1 | JRG5114–5116 JRG4693 | E E | S ZC | B1 B3 | 0.3671 −3.9009 | −77.4923 −78.5117 | 1562 1609 | 12 9 | 38.9 43.8 | 0.136 0.119 | 0.011 0.011 |
| M. dies-viridis 2 | JRG4679 | E | ZC | B3 | −3.9373 | −78.6245 | 1353 | 10 | 48.3 | 0.143 | 0.012 |
| M. dies-viridis 3 | JRG4679 | E | ZC | B3 | −3.9263 | −78.6235 | 1545 | 20 | 49.8 | 0.136 | 0.011 |
| M. dies-viridis 4 | JRG4693 | E | ZC | B3 | −3.9120 | −78.5040 | 1742 | 6 | 44.3 | 0.127 | 0.011 |
| M. illuminata 1 | JRG4687 | E | ZC | B1 | −3.9673 | −78.6863 | 912 | 10 | 54.7 | 0.157 | 0.012 |
| M. illuminata 2 | JRG4679 | E | ZC | B1 | −3.9378 | −78.7200 | 985 | 7 | 41.9 | 0.139 | 0.012 |
| M. sp. nov. | JRG4700 | E | ZC | B1 | −3.5363 | −78.5288 | 777 | 14 | 44.8 | 0.152 | 0.011 |
| M. lenae | JRG4675 | E | ZC | B2 | −4.0891 | −78.9653 | 1110 | 18 | 56.2 | 0.168 | 0.011 |
| M. pacifica 1 | JRG4704 | E | EO | B2 | −3.6509 | −79.7469 | 934 | 11 | 58.6 | 0.162 | 0.012 |
| M. pringleana 1 | JRG5118, -20, -21 | E | MS | B1 | −2.2073 | −78.1985 | 1305 | 5 | 37.4 | 0.128 | 0.012 |
| M. quizhpei 1 | JRG4688 | E | ZC | B2 | −4.1809 | −78.6441 | 863 | 13 | 44.8 | 0.162 | 0.013 |
| M. quizhpei 2 | JRG4689 | E | ZC | B2 | −4.2503 | −78.6613 | 933 | 18 | 52.2 | 0.180 | 0.013 |
| M. quizhpei 3 | JRG4688 | E | ZC | B2 | −4.2597 | −78.6481 | 1026 | 5 | 45.8 | 0.191 | 0.014 |
| M. quechua 1 | JV20 | P | SM | B1 | −6.4560 | −76.2914 | 675 | 7 | 39.9 | 0.122 | 0.011 |
| M. sodiroana 1 | JRG5103, -06 | E | P | B1 | 0.3033 | −78.8689 | 1453 | 8 | 43.3 | 0.125 | 0.011 |
| M. umbellata 1 | JRG5107 | E | C | B1 | 0.9156 | −78.2013 | 1497 | 2 | 36.9 | 0.207 | 0.015 |
| M. xerantifulva 1 | JV27 | P | J | A3 | −5.9771 | −79.0516 | 1867 | 4 | 3.9 | 0.032 | 0.005 |
| M. xerantifulva 2 | JV26 | P | J | A2 | −5.6830 | −78.8715 | 1887 | 2 | 34 | 0.116 | 0.011 |
| M. xerantifulva 3 | JV26 | P | J | A3 | −5.6777 | −78.8779 | 2039 | 5 | 8.9 | 0.061 | 0.008 |
| M. xerantifulva 5 | JV26 | P | J | A3 | −5.6840 | −78.9044 | 1758 | 8 | 36.9 | 0.079 | 0.009 |
| M. xerantifulva 6 | JV26 | P | J | A3 | −5.6824 | −78.9032 | 1827 | 17 | 35 | 0.112 | 0.012 |
| M. xerantifulva 7 | JV26 | P | J | A3 | −5.6754 | −78.9116 | 1858 | 6 | 36.9 | 0.099 | 0.010 |
| M. xerantifulva 8 | JV46bis | P | J | A3 | −5.6857 | −78.9328 | 1943 | 5 | 32.5 | 0.088 | 0.010 |
| M. xerantifulva 9 | JV46 | P | J | A4 | −5.7051 | −78.9443 | 2085 | 3 | 32 | 0.099 | 0.010 |
| M. xerantifulva 10 | JV46 | P | J | A3 | −5.7023 | −78.9335 | 1859 | 3 | 3.4 | 0.036 | 0.005 |
| M. xerantifulva 11 | JV44 | P | J | A3 | −5.5770 | −78.8976 | 1714 | 10 | 42.4 | 0.107 | 0.011 |
| M. xerantifulva 12 | JV44 | P | J | A3 | −5.5816 | −78.9428 | 1908 | 3 | 34.5 | 0.132 | 0.012 |
| M. xerantifulva 13 | JV44 | P | J | A3 | −5.5788 | −78.9494 | 1795 | 14 | 11.3 | 0.060 | 0.008 |
| M. xerantifulva 14 | JV44 | P | J | A3 | −5.5748 | −78.9710 | 1549 | 5 | 34.5 | 0.086 | 0.010 |
| M. xerantifulva 15 | JV44 | P | J | A3 | −5.5655 | −78.9730 | 1588 | 5 | 37.4 | 0.089 | 0.009 |
| M. xerantifulva 16 | JV28 | P | J | A2 | −5.3705 | −78.9104 | 1648 | 17 | 41.4 | 0.105 | 0.010 |
| M. xerantifulva 17 | JV28 | P | J | A3 | −5.3747 | −78.9378 | 1760 | 12 | 35.5 | 0.082 | 0.009 |
| M. xerantifulva 18 M. xerantifulva 19 | JV29 JRG4666bis | P E | SI ZC | A2 A2 | −5.1384 −4.8490 | −79.0337 −79.2464 | 1472 1581 | 13 2 | 41.9 32.5 | 0.121 0.073 | 0.010 0.009 |
| Source of Variation | Df | Variance Components | Percentage of Variation | F Statistics | p-Value |
|---|---|---|---|---|---|
| Among species | 10 | 6.25 | 33.06 | FCT 0.33 | <0.001 |
| Among populations/species | 26 | 2.28 | 12.06 | FSC 0.18 | <0.001 |
| Within populations | 308 | 10.38 | 54.88 | FST 0.45 | <0.001 |
| Total | 344 | 18.91 | |||
| Among clusters | 6 | 4.96 | 27.25 | FCT 0.27 | <0.001 |
| Among populations/clusters | 30 | 2.85 | 15.68 | FSC 0.22 | <0.001 |
| Within populations | 308 | 10.38 | 57.07 | FST 0.43 | <0.001 |
| Total | 344 | 18.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieu, J.C.; Koubínová, D.; Grant, J.R. Population Genetic Structure and Diversity of Cryptic Species of the Plant Genus Macrocarpaea (Gentianaceae) from the Tropical Andes. Plants 2023, 12, 1710. https://doi.org/10.3390/plants12081710
Vieu JC, Koubínová D, Grant JR. Population Genetic Structure and Diversity of Cryptic Species of the Plant Genus Macrocarpaea (Gentianaceae) from the Tropical Andes. Plants. 2023; 12(8):1710. https://doi.org/10.3390/plants12081710
Chicago/Turabian StyleVieu, Julien C., Darina Koubínová, and Jason R. Grant. 2023. "Population Genetic Structure and Diversity of Cryptic Species of the Plant Genus Macrocarpaea (Gentianaceae) from the Tropical Andes" Plants 12, no. 8: 1710. https://doi.org/10.3390/plants12081710





