Implementing Dirac Approach to Quantum Mechanics in a Hungarian Secondary School
Abstract
:1. Introduction
2. Research Questions
- RQ1
- What is the impact of the chosen approach on the students’ learning process, focusing on discussion of the fundamental concepts of QM?
- RQ2
- How did students understand the main aspects of QM?
- RQ3a.
- How can we identify the problematic aspects faced by students?
- RQ3b.
- What are the perspectives and difficulties that emerged, in particular on the quantum state?
- RQ4
- How do the learning outcomes confirm the previous studies regarding this approach to QM by implementing it in Hungary?
3. Research Instruments and Methods
4. Context and Sample
5. The Structure of the Path
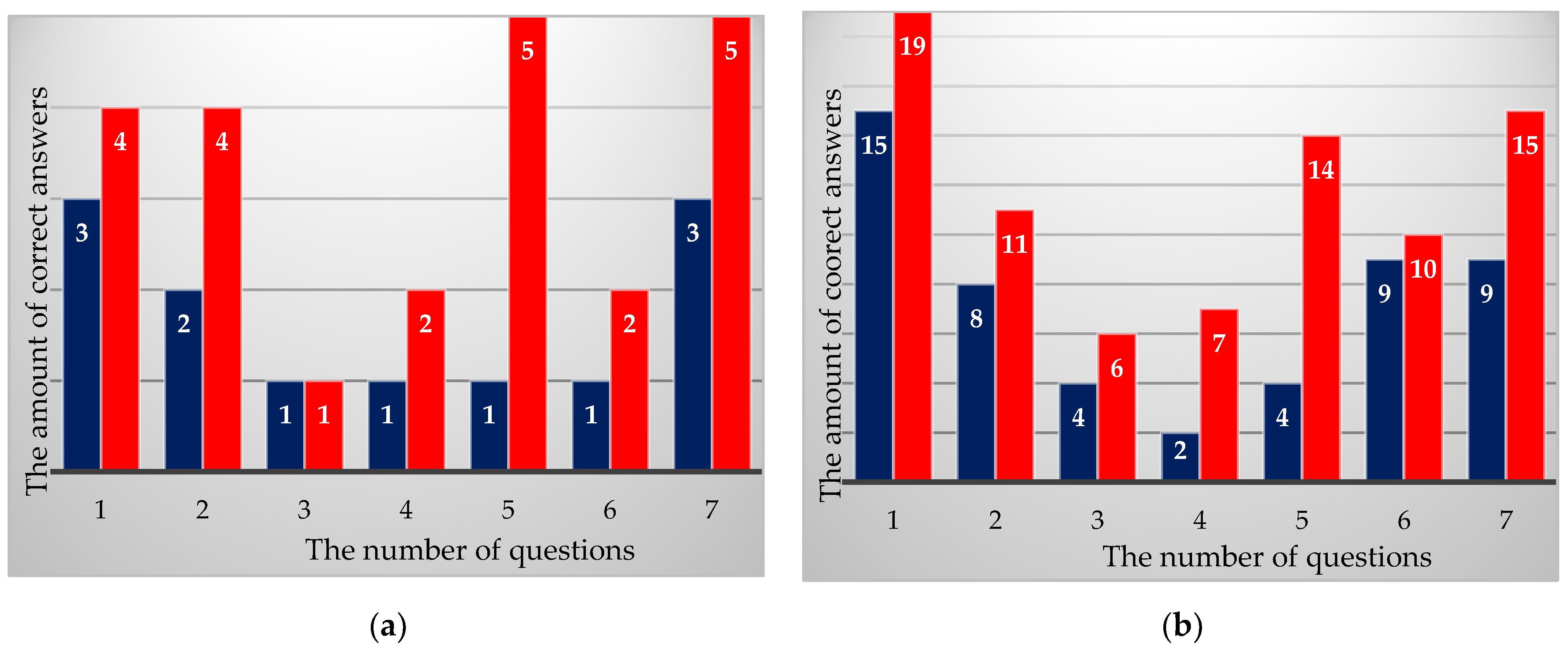
6. Data from Multiple Choice Items of Pre/Post-Test on the Essential Features of QM
7. Answers to Open-Ended Questions Q8–Q9
- In QM, state and properties are indeterminate (2/4—A1—“In quantum mechanics, there is no accurate position, there are only probabilities”; A3—“In quantum mechanics, we cannot define the state exactly”).
- Each system has some physical properties (2/4 B7—“Every material has physical properties (color, smell) and we know their form, too”; B1—“Physical state: every material has physical properties, and we are able to make predictions”
- The formal representation is linked to the possibility of calculating the probabilities of measurements outcomes (cat. C1),
- The measurements results are usually uncertain (cat. C3),
- We can only assign properties to a system after performing a measurement of the property (cat. C2).
8. Students’ General Opinion about the Curriculum
“Experiments in previous courses were more complicated. Anyway, they went so fast that I didn’t even understand them right away or I wasn’t interested in them, or I just didn’t understand. Here, instead, there was more time to learn, it didn’t happen so fast. Everything happened bit by bit, and everyone saw the same thing. It was good that we digested the experiments for hours”.
“Will there be a course with a similar theme next year? I think it would be great”.
“I liked this approach; it was unique. […] There’s always something new here, we always add something, we always approach things differently, not monotonously”.
“I’m interested in minerals and that’s how I remember them”. The knowledge of this student is limited, and yet he was able to keep in mind all the experiments during the course.
“I’ve never been a fan of physics experiments. Chemistry experiments have always been much more spectacular, but to be honest, I liked them now. When we were after the illustration of principles, and not after the show, that was good. By the way, the calcite crystal was pretty spectacular”.
- -
- Would you like to talk about these, outside classes?
- -
- Yes, and I suggest that we involve others, such as…, he is also trained in philosophy and …, I think they may also be interested in it.
9. Reflection in a Context of Implementation and Suggestions from Interviews
- To provide more examples for the state transition that are not assigned to vertical, horizontal, or 45° degrees directions. Before generalization, there were only these polarization states mentioned, and thus, by seeing the letter u, many students immediately associated it with the 45° state vector (“if v = vertical, h = horizontal then u must be polarized 45° direction”).
- The notation appears to be too general; there were no exercises with specific numbers. Giving specific numerical examples would be useful: “what is the probability of a photon in the state represented by passing through a vertical polaroid?”
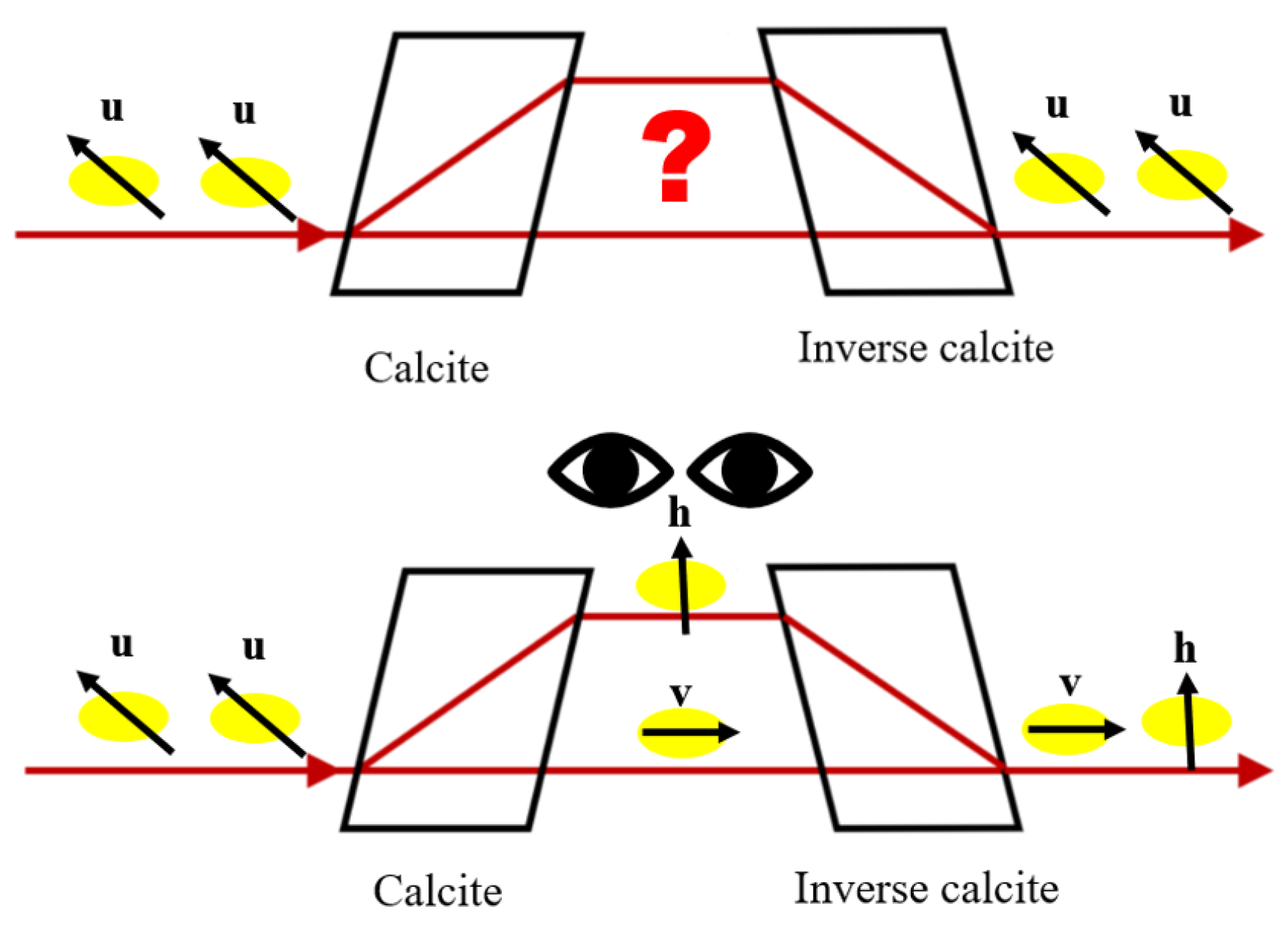
- Rethinking some previous tasks about trajectory would also be helpful after becoming acquainted with the superposition principle at the end of the curriculum. Earlier, students discovered that if we place another inverted calcite behind a birefringent calcite crystal, it unites the beams, and the polarization of the transmitted photons will be the same as that of the incident beam. However, if we theoretically make a measurement between the two calcites, the outcome will change, so we can help students distinguish the property from the state. The schematic diagram illustrating the problem is reproduced in Figure 2.
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| # | Cat. | Pre | Post |
| A4 | C1 | No answer | “There is some data in classical physics that describes the object. There is a vector in quantum mechanics from which we can calculate probabilities”. |
| B3 | C1 | No answer | “In classical physics, the physical state is what can be measured, and an accurate quantity can be assigned from data and measurements, but in quantum mechanics we can only work with probability”. |
| B4 | C1 | No answer | “In classical physics, the physical state of an arbitrary body can be described e.g., with a vector of motion. In quantum mechanics, this is a bit more complicated: although we can characterize the state of a photon, we can only give it according to a probability”. |
| B8 | C1 | No answer | “In classical physics, it characterizes the system at a given point in time, while in quantum mechanics it gives information about the polarization of photon”. |
| B9 | C1 | No answer | “Quantum: some vector, which transforms to another vector in a measurement”. |
| B6 | C2 | No answer | “The state is different in classical physics and quantum mechanics, namely, we never really get accurate results, we can just deduce what happens with a photon after it goes through a polarizer, but in classical physics our measurements to define an object’s position are accurate (e.g in motion)”. |
| B10 | C2 | No answer | “In classical physics a set of properties can be determined precisely, while in quantum mechanics it can only be observed at a studied moment”. |
| B11 | C2 | No answer | “Classical: some real state, Quantum: the existence of something given by measurements” |
| A3 | C3 | “In quantum mechanics we cannot define the state exactly” | “In classical physics, the state that we find by measurement is almost always the same. In quantum mechanics, however, there is always something else, very rarely the same value”. |
| B1 | C3 | “Physical state: every material has physical properties, and we are able to make predictions” | “In classical physics, measurements yield the same property over and over again. In contrast, in quantum mechanics measurements can provide different results”. |
| B12 | C3 | No answer | “In classical physics, the physical state of something is a constant property, whether it is during observation or measurement. However, in quantum mechanics, these two are different from each other, because we can get different results out of our observations and measurements (inversion of two calcite crystals, observation of light and examination yield different result)”. |
| A1 | C4 | “In quantum mechanics, there is no accurate position, there are only probabilities”. | “Classically, the place and position of a given object can be determined exactly, but not so in the quantum world”. |
| B5 | C4 | No answer | “Physical state is a measurable factor in classical physics, but in quantum mechanics we can only estimate it”. |
| A2 | C5 | No answer | “In classical physics, the physical state of an object can be described by its spatial position and velocity. In quantum mechanics, the physical state of a particle can be described by its spatial position and polarization property”. |
| B2 | C5 | No answer | “In classical physics, the physical state refers to a property, or fact, that is absolutely certain, and we can easily determine the physical state even with the naked eye. In quantum mechanics, the physical state can be determined with probability, e.g., polarization, because it is not possible to simply determine the physical state with absolute certainty”. |
| B7 | C5 | “Every material has physical properties (colour, smell) and we know their form, too” | “In classical physics, it is possible to determine the location of an object and what forces act on it. In quantum mechanics, the physical state of an object can be characterized by its polarization property”. |
References
- Stadermann, E.H.K.; van den Berg, E.; Goedhart, J.M. Analysis of secondary school quantum physics curricula of 15 different countries. Phys. Rev. Phys. Educ. Res. 2019, 15, 010130. [Google Scholar] [CrossRef]
- Krijtenburg-Lewerissa, K.; Pol, H.J.; Brinkman, A.; van Joolingen, W.R. Key topics for quantum mechanics at secondary schools: A Delphi study into expert opinions. Int. J. Sci. Educ. 2019, 41, 349–366. [Google Scholar] [CrossRef]
- Styer, D.F.; Balkin, M.S.; Becker, K.M.; Burns, M.R.; Dudley, C.E.; Forth, S.T.; Gaumer, J.G.; Kramer, M.A.; Oertel, D.O.; Park, L.H.; et al. Nine formulations of quantum mechanics. Am. J. Phys. 2002, 70, 288–297. [Google Scholar] [CrossRef]
- Born, M. Atomic Physics, 8th ed.; Blackie & Son: Glasgow, UK, 1969. [Google Scholar]
- Pospiech, G. Teaching the hearth of quantum theory. In Frontiers of Physics Education; Jurdana-Sepic, R., Labinac, V., Zuvic, M., Susac, A., Eds.; Zlatni: Rijeka, Croatia, 2008; p. 90. [Google Scholar]
- Ebison, M.G. Introducing the Uncertainty Principle. In Seminar on the Teaching of Physics in Schools 2, GIREP; Loria, A., Thomsen, P., Eds.; Gyldendal: Copenhagen, Denmark, 1975; p. 220. [Google Scholar]
- Haber-Schaim, U. On the Teaching of Quantum Physics in the Senior High School. In Seminar on the Teaching of Physics in Schools 2, GIREP; Loria, A., Thomsen, P., Eds.; Gyldendal: Copenhagen, Denmark, 1975; p. 273. [Google Scholar]
- Tóth, E. Fizika IV; Tankönyvkiadó: Budapest, Hungary, 1984; ISBN 963-17-7666-2. [Google Scholar]
- Fischler, H.; Lichtfeldt, M. Modern physics and students’ conceptions. Int. J. Sci. Educ. 1992, 14, 181–190. [Google Scholar] [CrossRef]
- Müller, R.; Wiesner, H. Teaching quantum mechanics on an introductory level. Am. J. Phys. 2002, 70, 200–209. [Google Scholar] [CrossRef]
- Michelini, M.; Ragazzon, R.; Santi, L.; Stefanel, A. Proposal for quantum physics in secondary school. Phys. Educ. 2000, 35, 406–410. [Google Scholar] [CrossRef]
- Michelini, M.; Stefanel, A. A path to build basic Quantum Mechanics ideas in the context of light polarization and learning outcomes of secondary students. J. Phys. Conf. Ser. 2021, 1929, 012052. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Grassi, R.; Michelini, M. A Fundamental Concept in Quantum Theory: The Superposition Principle. In Thinking Physics for Teaching; Bernardini, C., Tarsitani, C., Vicentini, M., Eds.; Springer: Boston, MA, USA, 1995; p. 329. [Google Scholar] [CrossRef]
- Michelini, M.; Ragazzon, R.; Santi, L.; Stefanel, A. Quantum Physics as a way of thinking: An educational proposal. In Physics Teacher Education beyond 2000, GIREP Book of Selected Papers; Pinto, R., Santiago, S., Eds.; Elsevier: Paris, France, 2001; pp. 479–482. [Google Scholar]
- Michelini, M. Approaching the theory of quantum mechanics: The first steps towards a coherent synthesized interpretation with a supporting formalism. In Frontiers of Physics Education; Jurdana-Sepic, R., Labinac, V., Zuvic-Butorac, M., Susac, A., Eds.; Zlatni: Rijeka, Croatia, 2008; pp. 93–101. [Google Scholar]
- Pospiech, G. Uncertainty and complementarity. Phys. Educ. 2000, 35, 393–399. [Google Scholar] [CrossRef]
- Bitzenbauer, P.; Meyn, J.-P. A new teaching concept on quantum physics in secondary schools. Phys. Educ. 2020, 55, 055031. [Google Scholar] [CrossRef]
- Bitzenbauer, P. Practitioners’ view on new teaching material for introducing quantum optics in secondary schools. Phys. Educ. 2021, 56, 055008. [Google Scholar] [CrossRef]
- Galvez, E.J. Quantum optics laboratories for teaching quantum physics. In Proceedings of the Fifteenth Conference on Education and Training in Optics and Photonics: ETOP 2019, Quebec, PQ, Canada, 2 July 2019; p. 111431A. [Google Scholar] [CrossRef]
- Scholz, R.; Wessnigk, S.; Weber, K. A classical to quantum transition via key experiments. Eur. J. Phys. 2020, 41, 055304. [Google Scholar] [CrossRef]
- Special Issues. Am. J. Phys. 2002, 70. [CrossRef]
- Special Issues on Quantum Physics. Phys. Educ. 2000, 35. [CrossRef]
- Pospiech, G.; Michelini, M.; Stefanel, A.; Santi, L. Central features of quantum theory in physics education. In Frontiers of Physics Education; Jurdana-Sepic, R., Labinac, V., Zuvic-Butorac, M., Susac, A., Eds.; Zlatni: Rijeka, Croatia, 2008; pp. 85–87. [Google Scholar]
- Quantum Technology Education Webpage, an European Open Portal. 2020. Available online: https://qtedu.eu/ (accessed on 28 August 2022).
- Michelini, M.; Stefanel, A. High school students face QM basic concepts. In New Trends in Science and Technology Education, Selected Papers; Menabue, L., Santoro, G., Eds.; CLUEB: Bologna, Italy, 2010; Volume 1, pp. 308–322. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Clarendon Press: Oxford, UK, 1958. [Google Scholar]
- McDermott, L.C. Millikan Lecture 1990: What we teach and what is learned—Closing the gap. Am. J. Phys. 1991, 59, 301–315. [Google Scholar] [CrossRef]
- McDermott, L.C.; Shaffer, P.S. Tutorials in Introductory Physics; Prentice Hall Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Cobal, M.; Corni, F.; Michelini, M.; Santi, L.; Stefanel, A. A resource environment to learn optical polarization. In Physics in New Fields, Proceedings of the GIREP International Conference Proceedings, Lund, Sweden, 5–9 August 2002; Available online: http://www.fisica.uniud.it/URDF/laurea/idifo1/materiali/g6/T-G6_MQUDMPTL02.pdf (accessed on 1 September 2022).
- Michelini, M.; Stefanel, A. Hands-on sensors for the exploration of light polarization. In Informal Learning and Public Understanding of Physics, Selected Papers in GIREP Book; Planinsic, G., Mohoric, A., Eds.; University of Ljubljana: Ljubljana, Slovenia, 2006; pp. 202–208. Available online: http://www.fisica.uniud.it/URDF/articoli/ftp/2006/2006-05.pdf (accessed on 1 September 2022).
- Michelini, M.; Santi, L.; Stefanel, A. Research based proposals to build modern physics way of thinking in secondary students. In Teaching Physics Innovatively (TPI-15), New Learning Environments and Methods in Physics Education; Király, A., Tél, T., Eds.; Eötvös Loránd University: Budapest, Hungary, 2015; pp. 331–349. [Google Scholar]
- Michelini, M.; Santi, L.; Stefanel, A. JQM per affrontare nella scuola secondaria i fondamenti di meccanica quantistica. In Proceedings of the On-Line Del XXX Convegno Didamatica, Udine, Italy, 19–21 April 2016; ISBN 9788898091447. Available online: https://core.ac.uk/download/pdf/154285679.pdf (accessed on 1 September 2022).
- Dégen, C.; Elblinger, F.; Simon, P. Fizika 11; Oktatáskutató és Fejlesztő Intézet: Budapest, Hungary, 2015; ISBN 978-963-19-7859-9. (In Hungarian) [Google Scholar]
- Zollmann, D. (Ed.) NARST 1999: Research on Teaching and Learning Quantum Mechanics; NARTS: Reston, VA, USA, 1999; Available online: https://web.phys.ksu.edu/papers/narst/QM_papers.pdf (accessed on 1 September 2022).
- Singh, C. Student understanding of quantum mechanics. Am. J. Phys. 2001, 69, 885–895. [Google Scholar] [CrossRef]
- Zhu, G.; Singh, C. Students’ difficulties with quantum measurement. In Proceedings of the 2011 Physics Education Research Conference, Omaha, Nebraska, 3–4 August 2016; Rebello, S., Engelhardt, P., Singh, C., Eds.; 2012; Volume 1413, pp. 387–390. [Google Scholar] [CrossRef]
- Styer, D.F. Common misconceptions regarding quantum mechanics. Am. J. Phys. 1996, 64, 31–34. [Google Scholar] [CrossRef]
- Michelini, M.; Stefanel, A. Learning paths of high school students in quantum mechanics. In Frontiers of Physics Education; Jurdana-Sepic, R., Labinac, V., Zuvic, M., Susac, A., Eds.; Zlatni: Rijeka, Croatia, 2008; pp. 337–343. Available online: https://www.researchgate.net/publication/228603591_LEARNING_PATHS_OF_HIGH_SCHOOL_STUDENTS_IN_QUANTUM_MECHANICS (accessed on 1 September 2022).
- Michelini, M.; Santi, L.; Stefanel, A. Worksheets for pupils involvement in learning quantum mechanics. In Frontiers of Physics Education; Jurdana-Sepic, R., Labinac, V., Zuvic, M., Susac, A., Eds.; Zlatni: Rijeka, Croatia, 2008; pp. 102–111. Available online: http://www.fisica.uniud.it/URDF/articoli/ftp/2008/2008-05.pdf (accessed on 1 September 2022).
- Stefanel, A. Physics Didactic Innovation Materials to Support Initial and In-Service Teacher Education. 2006. Available online: http://www.fisica.uniud.it/URDF/interreg/quanto/schede_stu/schede_stu_it.htm (accessed on 19 June 2022).
- Niedderer, H.; Bethge, T. Students’ Conceptions in Quantum Physics; University of Bremen: Bremen, Germany, 1995. Available online: https://www.researchgate.net/publication/239541643 (accessed on 1 September 2022).
- Baily, C.; Finkelstein, N.D. Teaching quantum interpretation: Revisiting the goals and practices of introductory quantum physics courses. Phys. Rev. Phys. Educ. Res. 2015, 11, 020124. [Google Scholar] [CrossRef] [Green Version]
- Denzin, N.; Lincoln, Y. Handbook of Qualitative Research; SAGE Publications: Los Angeles, CA, USA, 2011. [Google Scholar] [CrossRef]
- Erickson, F. Qualitative Research Methods for Science Education. In Second International Handbook of Science Education, Springer International Handbooks of Education; Fraser, B., Tobin, K., McRobbie, C., Eds.; Springer: Dordrecht, The Netherlands, 2012; Volume 24. [Google Scholar] [CrossRef]
- Lumbelli, L. Focusing on Text Comprehension as a Problem-Solving Task: A Fostering Project for Culturally Deprived Children. In Reading Comprehension Difficulties; Cornoldi, C., Oakhill, J.V., Eds.; Erlbaum: Mahwah, MJ, USA, 1996; pp. 301–330. ISBN 9780203053324. [Google Scholar]
- Steinar, K. Analyzing Interviews. In Doing Interviews; Steinar, K., Ed.; Sage Publications: Los Angeles, CA, USA, 2007. [Google Scholar] [CrossRef]
- Michelini, M.; Santi, L.; Stefanel, A. How students link quantum concept and formalism. In Proceedings of the12th International Conference APLIMAT 2013, Bratislava, Slovakia, 5–7 February 2013. [Google Scholar]
- Michelini, M.; Santi, L.; Stefanel, A. Building quantum formalism in upper secondary school students. Teaching and Learning Physics Today: Challenges? Benefits? In Proceedings of the International Conference GIREP-ICPE-MPTL 2010 Proceedings, Reims, France, 22–27 August 2010. [Google Scholar]
- Niedderer, H.; Bethge, T.; Cassens, H.; Petri, J. Teaching quantum atomic physics in college and research results about a learning pathway. In The Changing Role of Physics Departments in Modern Universities, AIP Conference Proceedings 339; Redish, E.F., Rigden, J.S., Eds.; American Institute of Physics: New York, NY, USA, 1997; pp. 659–668. [Google Scholar]
- Michelini, M.; Ragazzon, R.; Santi, L.; Stefanel, A. Quantum Physics in secondary school. Friulian J. Sci. Res. 2003, 3, 9–19. [Google Scholar]
| Worksheet Code | Topic | Number of Questions |
|---|---|---|
| FEN1 | Phenomenological exploration of polarization, | 10 |
| Con1 | Malus law and its probabilistic interpretation assuming ideal polarizers | 4 |
| Con2 | Epilogue on photon-polarizer interaction and probabilistic interpretation | 2 |
| Con3 | Mutually exclusive properties | 4 |
| Con4 | Formulating hypotheses on superposition | 2 |
| Con5 | Incompatible properties and distinction with mutually exclusive properties | 4 |
| Con6 | Non-epistemic uncertainty | 2 |
| Con7 | Quantum particles and trajectories | 6 |
| Form1 | From concepts to formalism: vector representation of quantum state | 10 |
| Hours | Activities | Contents |
|---|---|---|
| 1 | Pre-test (individual work) | (See Table 1 for tutorial.) |
| 2–3 | The students experimented with polarizers, and they explored the phenomenon of light polarization. They worked in groups (2–3 students) and used the worksheet for exploration, and thereafter, the argumentation and explanation happened with the whole class together. Questions were like: “What happen if we put a third polarizer between two orthogonal polarizers?” | The main goal is to distinguish the polarization property of light from intensity of light. Using tutorial FEN1. |
| 4 | Quantitative experiment on the Malus law (the whole class together): where is the intensity of transmitted light, coefficient means polarizers are not ideal, is the intensity of incident light and shows the relative position of polarizers. | Explore and discuss the Malus law. |
| 5–6 | Interpreting and practising the Malus law, students made quantitative tasks and explored the meaning of the different factors of Malus law (work groups of 2–3 students or the whole class). Light consists of photons, so the Malus law can be expressed in terms of the photon number, too (monochromatic light): where is the number of transmitted photons and that of incident photons. Typical question: “What information does Malus law: provide about the transmission of each photon?” | Ideal and real polarizers. From macro to micro level by the hypothesis. The probabilistic meaning of Malus law with single photon thought experiment. Using tutorials Con1–2. |
| 7–8 | Polarization properties of single photon. Every photon has a well-defined polarization property determined by a well-defined measurement. The property can be indicated by symbols (iconographic representation): * is for horizontal, Δ is for vertical and ♢ is for 45° polarized photons. Discovering that properties * and are mutually exclusive properties. Interpretative hypothesis for polarized photons and discussion of its meaning: the polarized photons are not a statistical mixture of * and (workgroup of 2–3 students and discussion with the whole class). Discovering incompatible properties (* and ) and understanding the uncertainty principle (whole class). | Polarization properties. Interpretive hypothesis:. Mutually exclusive properties. Incompatible properties. Uncertainty principle. Using tutorials Con3–6. |
| 9–10 | Phenomenology with birefringent crystals, and nonlocality (workgroup of 2–3 students or the whole class). The calcite crystal splits the light into two mutually exclusive polarized beams. There is a close relationship between polarization property and trajectory. Because of the probabilistic interpretation, we cannot assign trajectory to photons. | Face with birefringent crystals and exploring the nonlocality of photons. Using tutorial Con7. |
| 11 | The statistical interpretation of Malus law (the whole class in online teaching). Every photon has a probabilistic nature, so an ensemble of photons shows statistical feature. | Analysis of ideal simulated experiments of interaction of photons with polarizers, using the applet JQM 1 [31,32]. |
| 12–13 | Assign vectors to the polarizers. The polarization of photons is uniquely given by polarizers, so a vector can be assigned to the photons. Concept of quantum state as a vector. Polarization as a state transition. The superposition principle and generalization (individual work in digital work schedule): every state can be expressed as a linear combination of bases. So not only measurable states are possible states, but also their linear combinations too. | Quantum state (via polarization), superposition principle. Using tutorial Form1 in online version. |
| 14 | Post-Test (individual work) |
| Q1: Measuring a physical observable, which aspect among the following ones characterizes in a peculiar way quantum mechanics in respect of classic mechanics? | ||||
| Answer options | Pre(A) | Post(A) | Pre(B) | Post(B) |
| (A) Under some conditions, discrete values of the measured observable are obtained | 0 | 0 | 1 | 0 |
| (B) Results of measurements are predictable only in probabilistic terms | 2 | 2 | 10 | 13 |
| (C) In general, systems initially prepared in the same state evolve in a different way when subjected to a process of measure | 1 | 2 | 5 | 6 |
| (D) The interaction with the measurement apparatus produces a perturbation on the system | 1 | 1 | 2 | 0 |
| (E) The result of a measurement is affected by an unavoidable uncertainty | 1 | 0 | 1 | 0 |
| No answer | 0 | 0 | 0 | 0 |
| Q2: Consider the following probabilistic forecasts: (K) The heads outcome in launching a coin has ½ probability to be realized; (J) A photon with vertical polarization has ½ probability to pass through a polarizer at 45°. | ||||
| Answer options | Pre(A) | Post(A) | Pre(B) | Post(B) |
| (A) In the K case, we do not know initial conditions precisely enough, in the J case initial conditions are known, but the phenomenon itself has a probabilistic nature. | 2 | 4 | 8 | 11 |
| (B) In both cases, we do not know initial conditions precisely enough. | 3 | 1 | 1 | 0 |
| (C) In the K case, we do not know initial conditions precisely; in the J case, we do not know with enough precision how the interaction photon-polarizer happens. | 0 | 0 | 10 | 8 |
| No answer | 0 | 0 | 0 | 0 |
| Q3: Which of the following statements better outlines the meaning of uncertainty relations? | ||||
| Answer options | Pre(A) | Post(A) | Pre(B) | Post(B) |
| (A) There are properties of the same system, which cannot be simultaneously determined with arbitrary precision | 1 | 1 | 4 | 6 |
| (B) It is not possible to measure with arbitrary precision a physical observable | 1 | 1 | 3 | 5 |
| (C) It is not possible to make the uncertainty measurement arbitrarily small | 0 | 0 | 1 | 0 |
| (D) It is never possible, not even in principle, to predict measurements precisely | 0 | 0 | 0 | 1 |
| (E) It is not possible to measure with arbitrary precision position and momentum of a particle. | 3 | 3 | 11 | 7 |
| No answer | 0 | 0 | 0 | 0 |
| Q4: In classic mechanics, it is always possible to attribute a trajectory to a particle. What statement can be made as far as a quantum particle is concerned (choose only one option)? | ||||
| Answer options | Pre(A) | Post(A) | Pre(B) | Post(B) |
| (A) It is possible to attribute a trajectory, but it is not possible to determine with arbitrary precision all the information needed to determine it with arbitrary precision | 3 | 0 | 7 | 3 |
| (B) It is possible to attribute a trajectory, but it is not experimentally accessible | 1 | 1 | 5 | 5 |
| (C) It is possible to attribute a trajectory only when a position measurement is performed | 0 | 0 | 4 | 2 |
| (D) It is impossible to attribute a trajectory to a particle due to perturbations arising from measurements | 0 | 2 | 1 | 2 |
| (E) It is not possible, not even in principle, to associate a trajectory to a particle | 1 | 2 | 2 | 7 |
| No answer | 0 | 0 | 0 | 0 |
| Q5: Suppose that a beam of light polarized at 45° is split into two beams by a calcite crystal: a beam of light horizontally and vertically polarized. If somehow these two beams are recombined with an inverted calcite crystal, what kind of polarization will the resulting light beam have? | ||||
| Answer options | Pre(A) | Post(A) | Pre(B) | Post(B) |
| (A) The combined light beam consists of semi-horizontal and semi-vertically polarized photons. | 2 | 0 | 1 | 1 |
| (B) The combined light beam consists of 45° polarized photons. | 1 | 5 | 4 | 14 |
| (C) The combined light beam will not be polarized. | 0 | 0 | 5 | 4 |
| (D) Photons are polarized both vertically and horizontally. | 2 | 0 | 8 | 0 |
| No answer | 0 | 0 | 1 | 0 |
| Q6: Choose the correct statement for the relation between classical physics and quantum mechanics. | ||||
| Answer options | Pre(A) | Post(A) | Pre(B) | Post(B) |
| (A) Classical physics and quantum mechanics operate by very different laws, the two are incompatible. | 3 | 3 | 4 | 6 |
| (B) Quantum mechanics includes classical physics as a boundary. | 1 | 2 | 9 | 10 |
| (C) Classical physics can be applied in the quantum world, but not vice versa. | 1 | 0 | 5 | 2 |
| (D) The description of quantum mechanics and classical physics is equivalent. | 0 | 0 | 1 | 1 |
| No answer | 0 | 0 | 0 | 0 |
| Q7: A non-polarized light beam passes through two polarizers in succession. The first polarizer halves the intensity of the incoming light and then reduces the intensity of the resulting beam again by half the second polarizer. In the end, the brightness is reduced to ¼ of the original. Which statement is correct? | ||||
| Answer options | Pre(A) | Post(A) | Pre(B) | Post(B) |
| (A) Each polarizer halves the energy of each photon as it passes through. | 2 | 0 | 2 | 1 |
| (B) These polarizers are such that they absorb half of the photons at all positions. | 0 | 0 | 5 | 1 |
| (C) The position of the polarizers is such that exactly half of the photons pass through them. | 0 | 0 | 2 | 2 |
| (D) The position of the polarizers is such that each photon passes through them with ½ probability. | 3 | 5 | 9 | 15 |
| No answer | 0 | 0 | 1 | 0 |
| Code | Category Description |
|---|---|
| C1 | The state is identified with its formal representative entity: a vector (2/17); a probability (3/17). |
| A4—“There is some data in classical physics that describes the object. There is a vector in quantum mechanics from which we can calculate probabilities”. B3—“In classical physics, the physical state is what can be measured, and an accurate quantity can be assigned from data and measurements, but in quantum mechanics we can only work with probability”. B4—“In classical physics, the physical state of an arbitrary body can be described e.g., with a vector of motion. In quantum mechanics, this is a bit more complicated: although we can characterize the state of a photon, we can only give it according to a probability”. | |
| C2 | In classical mechanics (CM), the properties of a system before and after a measurement are the same, in QM the measurement allows us to attribute properties to the systems, i.e., only after carrying out a measurement or only at the time of the measurement can properties be attributed to the system (3/17). |
| B6—“The state is different in classical physics and quantum mechanics, namely, we never really get accurate results with the latter, we can just deduce what happens with a photon after it goes through a polarizer, but in classical physics our measurements to define an object’s position are accurate (e.g., in motion)”. B10—“In classical physics, a set of properties can be determined precisely, while in quantum mechanics it can only be observed at a studied moment”. B11—“Classical: some real state, Quantum: the existence of something given by measurements”. | |
| C3 | In CM if you repeat a measurement, you will get the same results, in QM you will get uncertain results (3/17). |
| A3—“In classical physics, the state that we find by measurement is almost always the same. In quantum mechanics, however, there is always something else, very rarely the same value”. B1—“In classical physics, measurements yield the same property over and over again. In contrast, in quantum mechanics measurements can provide different results” B12—“In classical physics, the physical state of something is a constant property, whether it is during observation or measurement. However, in quantum mechanics, these two are different from each other, because we can get different results out of our observations and measurements (inversion of two calcite crystals, observation of light and examination yield different result)”. | |
| C4 | State and property are determined in CM, and indeterminate in QM (2/17). |
| A1—“Classically, the place and position of a given object can be determined exactly, but not so in the quantum world”. B5—“Physical state is a measurable factor in classical physics, but in quantum mechanics we can only estimate it”. | |
| C5 | In CM, the state is identified by position and velocity, in QM by polarization (and position) (3/17). |
| A3—“In classical physics, the physical state of an object can be described by its spatial position and velocity. In quantum mechanics, the physical state of a particle can be described by its spatial position and polarization property”. B7- “In classical physics, it is possible to determine the location of an object and what forces act on it. In quantum mechanics, the physical state of an object can be characterized by its polarization property”. | |
| NA | No answer (1/17). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michelini, M.; Stefanel, A.; Tóth, K. Implementing Dirac Approach to Quantum Mechanics in a Hungarian Secondary School. Educ. Sci. 2022, 12, 606. https://doi.org/10.3390/educsci12090606
Michelini M, Stefanel A, Tóth K. Implementing Dirac Approach to Quantum Mechanics in a Hungarian Secondary School. Education Sciences. 2022; 12(9):606. https://doi.org/10.3390/educsci12090606
Chicago/Turabian StyleMichelini, Marisa, Alberto Stefanel, and Kristóf Tóth. 2022. "Implementing Dirac Approach to Quantum Mechanics in a Hungarian Secondary School" Education Sciences 12, no. 9: 606. https://doi.org/10.3390/educsci12090606





