A New Variational Iteration Method for a Class of Fractional Convection-Diffusion Equations in Large Domains
Abstract
:1. Introduction
2. Fractional calculus
3. Variational Iteration Method with an Auxiliary Parameter
4. Convergence Analysis
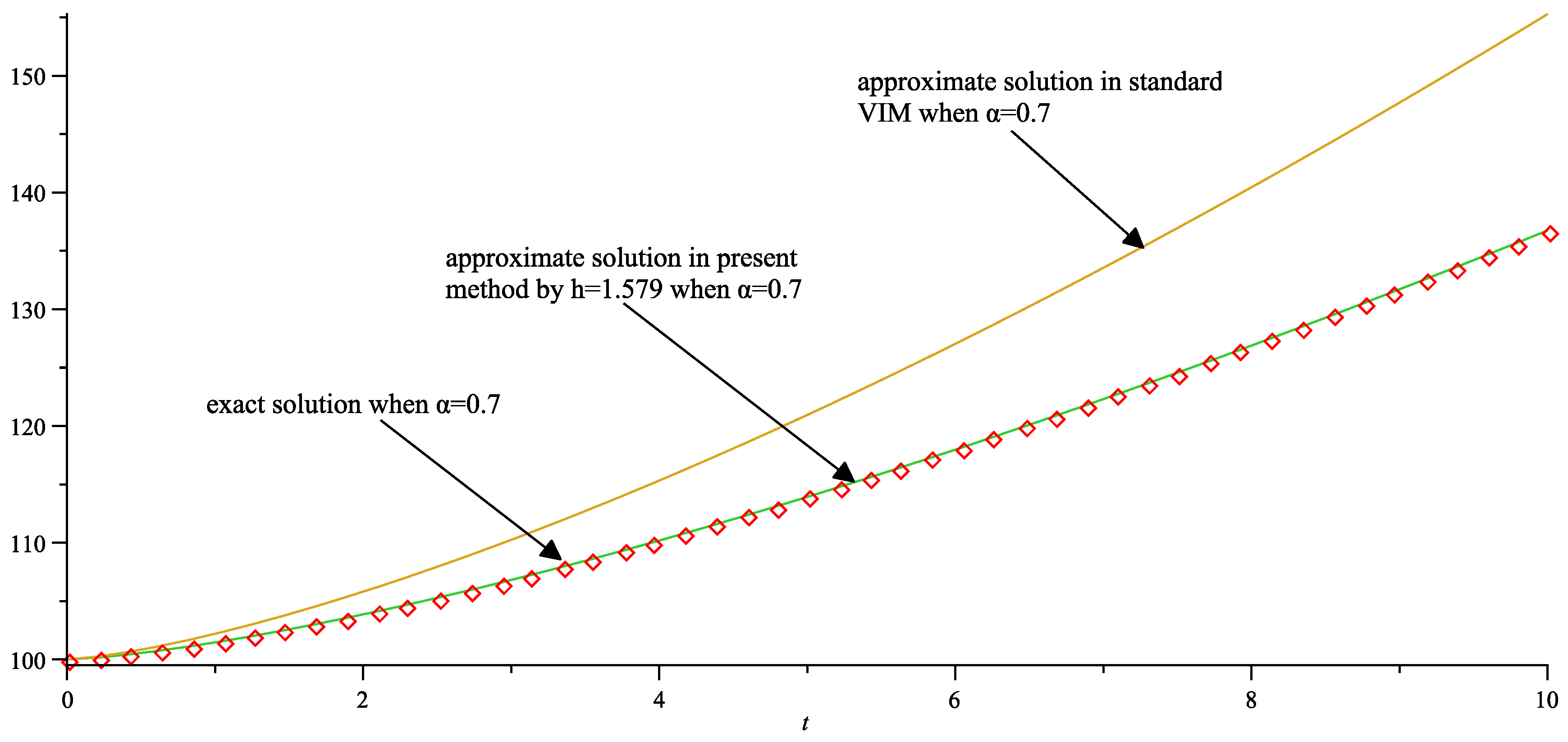
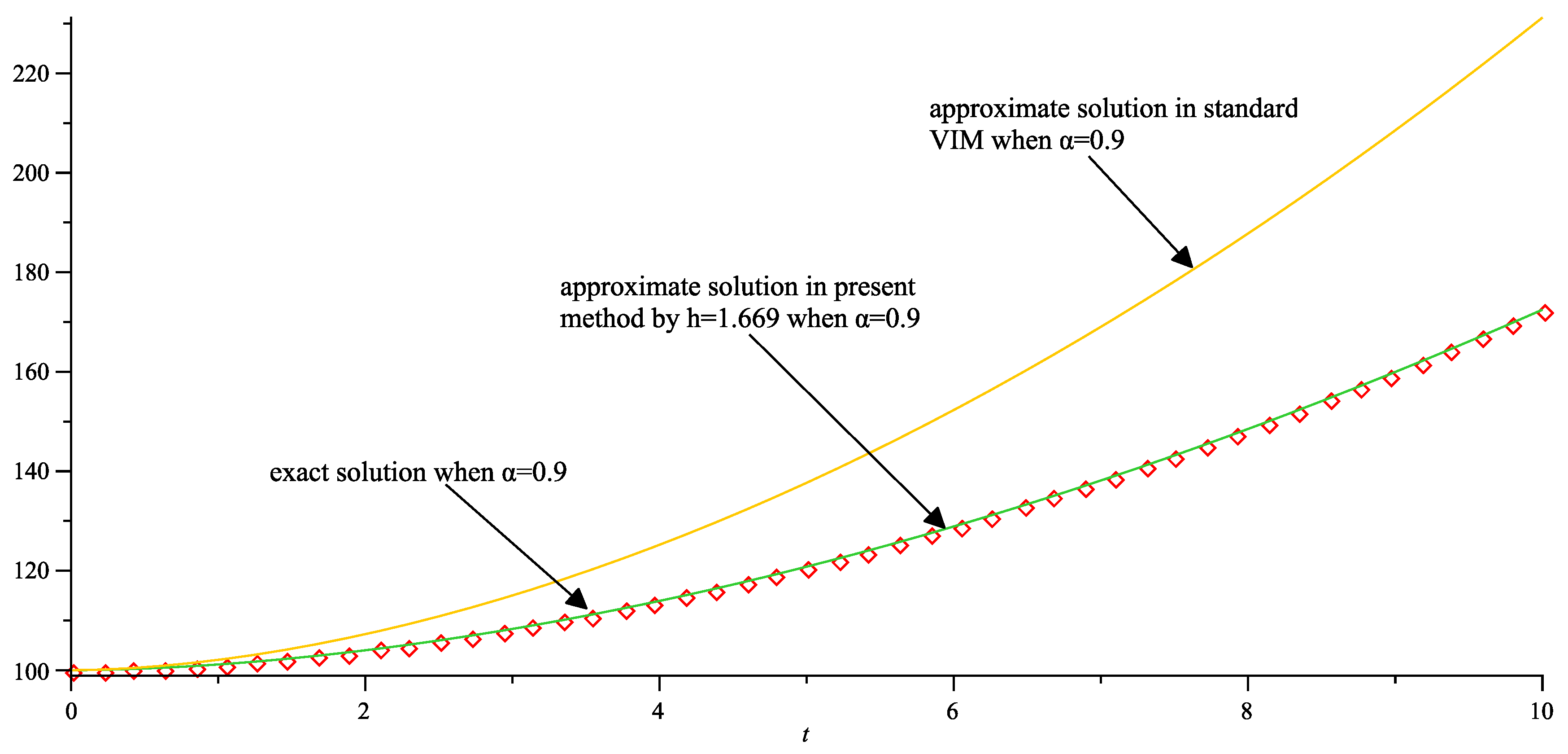
5. Numerical Examples
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; Volume 128. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998; Volume 198. [Google Scholar]
- Shawagfeh, N.T. Analytical approximate solutions for nonlinear fractional differential equations. Appl. Math. Comput. 2002, 131, 517–529. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Blow-up for solutions of some linear wave equations with mixed nonlinear boundary conditions. Appl. Math. Comput. 2001, 123, 133–140. [Google Scholar] [CrossRef]
- Jafari, H.; Seifi, S. Homotopy analysis method for solving linear and nonlinear fractional diffusion-wave equation. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2006–2012. [Google Scholar] [CrossRef]
- Wu, F.; Yang, X.J. Approximate solution of the non–linear diffusion equation of multiple orders. Therm. Sci. 2016, 20, 683–687. [Google Scholar] [CrossRef]
- Yan, S.P.; Zhong, W.P.; Yang, X.J. A novel series method for fractional diffusion equation within Caputo fractional derivative. Therm. Sci. 2016, 20, 695–699. [Google Scholar] [CrossRef]
- Gao, F.; Yang, X.J. Fractional Maxwell fluid with fractional derivative without singular kernel. Therm. Sci. 2016, 20, 871–877. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974; Volume 111. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Rossikhin, Y.A.; Shitikova, M.V. Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 1997, 50, 15–67. [Google Scholar] [CrossRef]
- Carpinteri, A.; Mainardi, F. (Eds.) Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin, Germany, 2014; Volume 378. [Google Scholar]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Huang, F.H.; Guo, B.L. General solutions to a class of time fractional partial differential equations. Appl. Math. Mech. 2010, 31, 815–826. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J.Z.; Wang, X.M.; Zhou, Y.H. Exact solutions of multi-term fractional diffusion-wave equations with Robin type boundary conditions. Appl. Math. Mech. 2014, 35, 49–62. [Google Scholar] [CrossRef]
- Momani, S.; Shawagfeh, N. Decomposition method for solving fractional Riccati differential equations. Appl. Math. Comput. 2006, 182, 1083–1092. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. Solving a multi-order fractional differential equation using Adomian decomposition. Appl. Math. Comput. 2007, 189, 541–548. [Google Scholar] [CrossRef]
- Wang, Q. Numerical solutions for fractional KdV-Burgers equation by Adomian decomposition method. Appl. Math. Comput. 2006, 182, 1048–1055. [Google Scholar] [CrossRef]
- Hashim, I.; Abdulaziz, O.; Momani, S. Homotopy analysis method for fractional IVPs. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 674–684. [Google Scholar] [CrossRef]
- Zurigat, M.; Momani, S.; Alawneh, A. Analytical approximate solutions of systems of fractional algebraic-differential equations by homotopy analysis method. Comput. Math. Appl. 2010, 59, 1227–1235. [Google Scholar] [CrossRef]
- Ye, C.; Luo, X.N.; Wen, L.P. High-order numerical methods of fractional-order Stokes’ first problem for heated generalized second grade fluid. Appl. Math. Mech. 2012, 33, 65–80. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59, 1326–1336. [Google Scholar] [CrossRef]
- Kumar, P.; Agrawal, O.P. An approximate method for numerical solution of fractional differential equations. Signal Process. 2006, 86, 2602–2610. [Google Scholar] [CrossRef]
- Yuste, S.B. Weighted average finite difference methods for fractional diffusion equations. J. Comput. Phys. 2006, 216, 264–274. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, X.; He, Y. Analysis of a local discontinuous Galerkin method for time-fractional advection-diffusion equations. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 634–648. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl. Math. Model. 2011, 35, 5662–5672. [Google Scholar] [CrossRef]
- Kazem, S. An integral operational matrix based on Jacobi polynomials for solving fractional-order differential equations. Appl. Math. Model. 2013, 37, 1126–1136. [Google Scholar] [CrossRef]
- Kazem, S.; Abbasbandy, S.; Kumar, S. Fractional-order Legendre functions for solving fractional-order differential equations. Appl. Math. Model. 2013, 37, 5498–5510. [Google Scholar] [CrossRef]
- Rad, J.A.; Kazem, S.; Shaban, M.; Parand, K.; Yildirim, A. Numerical solution of fractional differential equations with a Tau method based on Legendre and Bernstein polynomials. Math. Methods Appl. Sci. 2014, 37, 329–342. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method-a kind of non-linear analytical technique: some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Liu, H.; Xiao, A.; Su, L. Convergence of variational iteration method for second-order delay differential equations. J. Appl. Math. 2013, 2013, 634670. [Google Scholar] [CrossRef]
- Abbasbandy, S. A new application of He’s variational iteration method for quadratic Riccati differential equation by using Adomian’s polynomials. J. Comput. Appl. Math. 2007, 207, 59–63. [Google Scholar] [CrossRef]
- Salkuyeh, D.K.; Tavakoli, A. Interpolated variational iteration method for initial value problems. Appl. Math. Model. 2016, 40, 3979–3990. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M.M. On the convergence of variational iteration method for nonlinear coupled system of partial differential equations. Int. J. Comput. Math. 2010, 87, 1120–1130. [Google Scholar] [CrossRef]
- Rezazadeh, G.; Madinei, H.; Shabani, R. Study of parametric oscillation of an electrostatically actuated microbeam using variational iteration method. Appl. Math. Model. 2012, 36, 430–443. [Google Scholar] [CrossRef]
- Abassy, T.A.; El-Tawil, M.A.; El Zoheiry, H. Solving nonlinear partial differential equations using the modified variational iteration Padé technique. J. Comput. Appl. Math. 2007, 207, 73–91. [Google Scholar] [CrossRef]
- Geng, F.; Lin, Y.; Cui, M. A piecewise variational iteration method for Riccati differential equations. Comput. Math. Appl. 2009, 58, 2518–2522. [Google Scholar] [CrossRef]
- Ghorbani, A.; Saberi-Nadjafi, J. An effective modification of He’s variational iteration method. Nonlinear Anal. Real World Appl. 2009, 10, 2828–2833. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. The variational iteration method: an efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl. 2009, 58, 2199–2208. [Google Scholar] [CrossRef]
- Wu, G.C. Laplace transform overcoming principle drawbacks in application of the variational iteration method to fractional heat equations. Therm. Sci. 2012, 16, 1257–1261. [Google Scholar] [CrossRef]
- Hristov, J. An exercise with the He’s variation iteration method to a fractional Bernoulli equation arising in a transient conduction with a non-linear boundary heat flux. Int. Rev. Chem. Eng. 2012, 4, 489–497. [Google Scholar]
- El-Wakil, S.A.; Abdou, M.A. New applications of variational iteration method using Adomian polynomials. Nonlinear Dyn. 2008, 52, 41–49. [Google Scholar] [CrossRef]
- Yilmaz, E.; Inc, M. Numerical simulation of the squeezing flow between two infinite plates by means of the modified variational iteration method with an auxiliary parameter. Nonlinear Sci. Lett. A 2010, 1, 297–306. [Google Scholar]
- Hosseini, M.M.; Mohyud-Din, S.T.; Ghaneai, H.; Usman, M. Auxiliary parameter in the variational iteration method and its optimal determination. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 495–502. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An optimal variational iteration method. Applied Mathematics Letters 2011, 24, 762–765. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. A modified variational iteration method for strongly nonlinear problems. Nonlinear Sci. Lett. A 2010, 1, 183–192. [Google Scholar]
- Turkyilmazoglu, M. Convergent optimal variational iteration method and applications to heat and fluid flow problems. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 790–804. [Google Scholar] [CrossRef]
- Momani, S. An algorithm for solving the fractional convection-diffusion equation with nonlinear source term. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 1283–1290. [Google Scholar] [CrossRef]
- Merdan, M. Analytical approximate solutions of fractional convection-diffusion equation with modified Riemann-Liouville derivative by means of fractional variational iteration method. Iran. J. Sci. Technol. Sci. 2013, 37, 83–92. [Google Scholar]
- Abbasbandy, S.; Kazem, S.; Alhuthali, M.S.; Alsulami, H.H. Application of the operational matrix of fractional-order Legendre functions for solving the time-fractional convection-diffusion equation. Appl. Math. Comput. 2015, 266, 31–40. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus; Springer: Vienna, Austria, 1997; pp. 223–276. [Google Scholar]
- Liu, Y. Studies on boundary value problems of singular fractional differential equations with impulse effects. Rostock. Math. Kolloqu. 2015, 70, 3–108. [Google Scholar]
- Wang, K.; Liu, S. A new solution procedure for nonlinear fractional porous media equation based on a new fractional derivative. Nonlinear Sci. Lett. A Math. Phys. Mech. 2017, 135. [Google Scholar]
- Wang, K.L.; Liu, S.Y. He’s fractional derivative for non-linear fractional heat transfer equation. Therm. Sci. 2016, 20, 793–796. [Google Scholar] [CrossRef]
- Odibat, Z.M. A study on the convergence of variational iteration method. Math. Comput. Model. 2010, 51, 1181–1192. [Google Scholar] [CrossRef]
- Ghaneai, H.; Hosseini, M.M. Variational iteration method with an auxiliary parameter for solving wave-like and heat-like equations in large domains. Comput. Math. Appl. 2015, 69, 363–373. [Google Scholar] [CrossRef]
- Ghaneai, H.; Hosseini, M.M. Solving differential-algebraic equations through variational iteration method with an auxiliary parameter. Appl. Math. Model. 2015, 40, 3991–4001. [Google Scholar] [CrossRef]
- Ghaneai, H.; Hosseini, M.M.; Tauseef Mohyud-Din, S. Modified variational iteration method for solving a neutral functional-differential equation with proportional delays. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 1086–1095. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, Y.; Cui, Y.; Wang, Z.; Jin, D. Wavelet method for a class of fractional convection-diffusion equation with variable coefficients. J. Comput. Sci. 2010, 1, 146–149. [Google Scholar] [CrossRef]
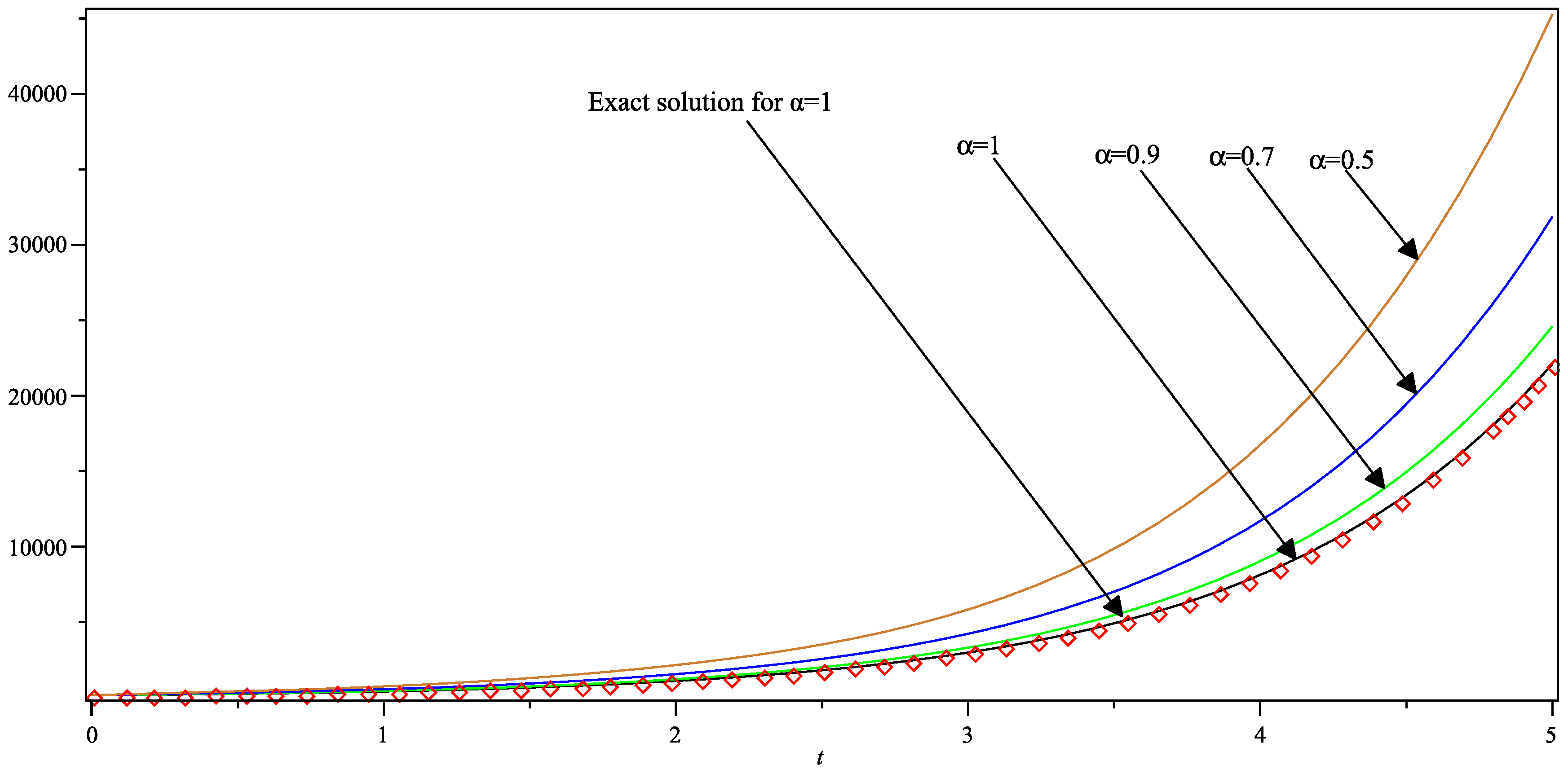
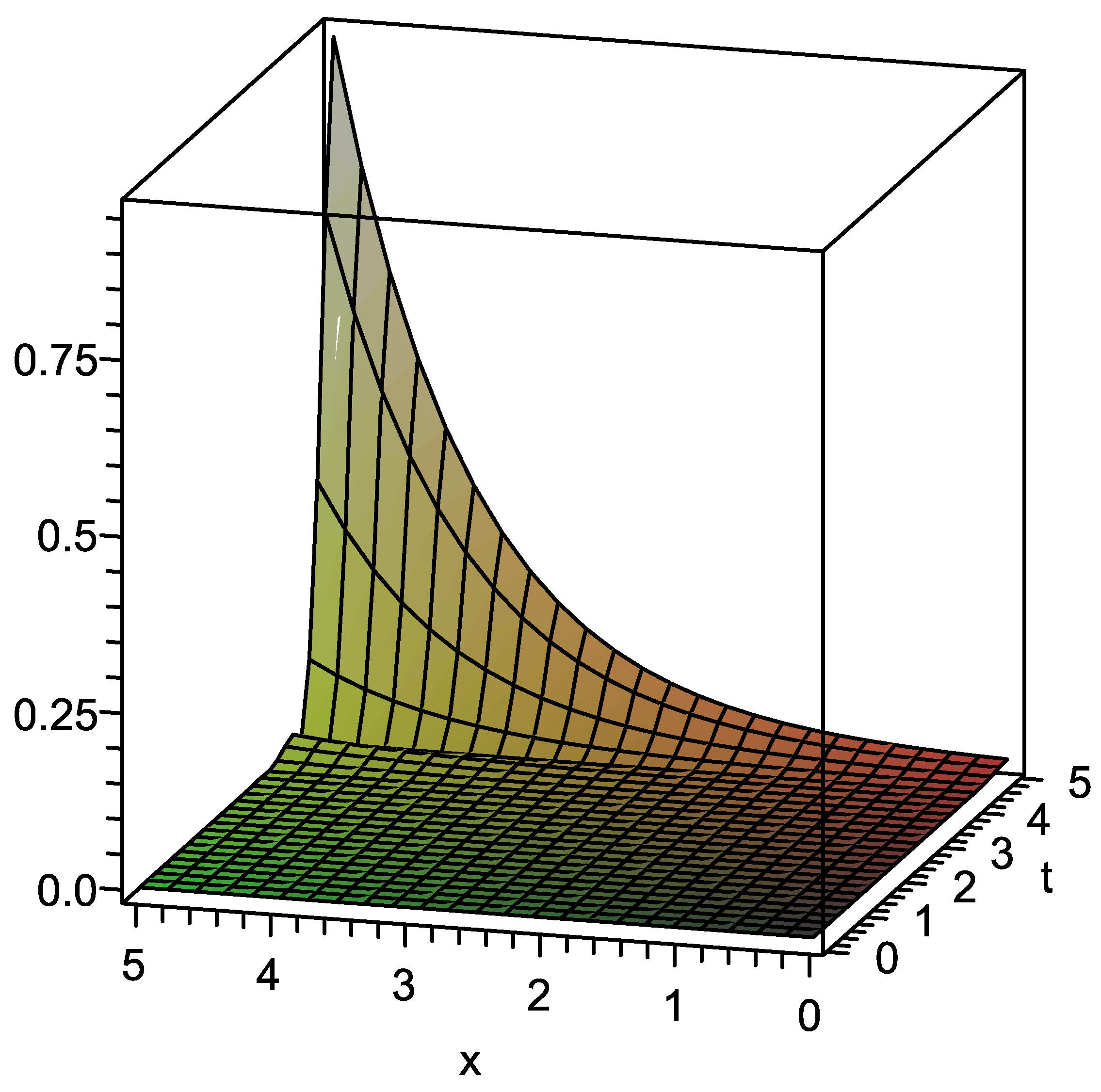
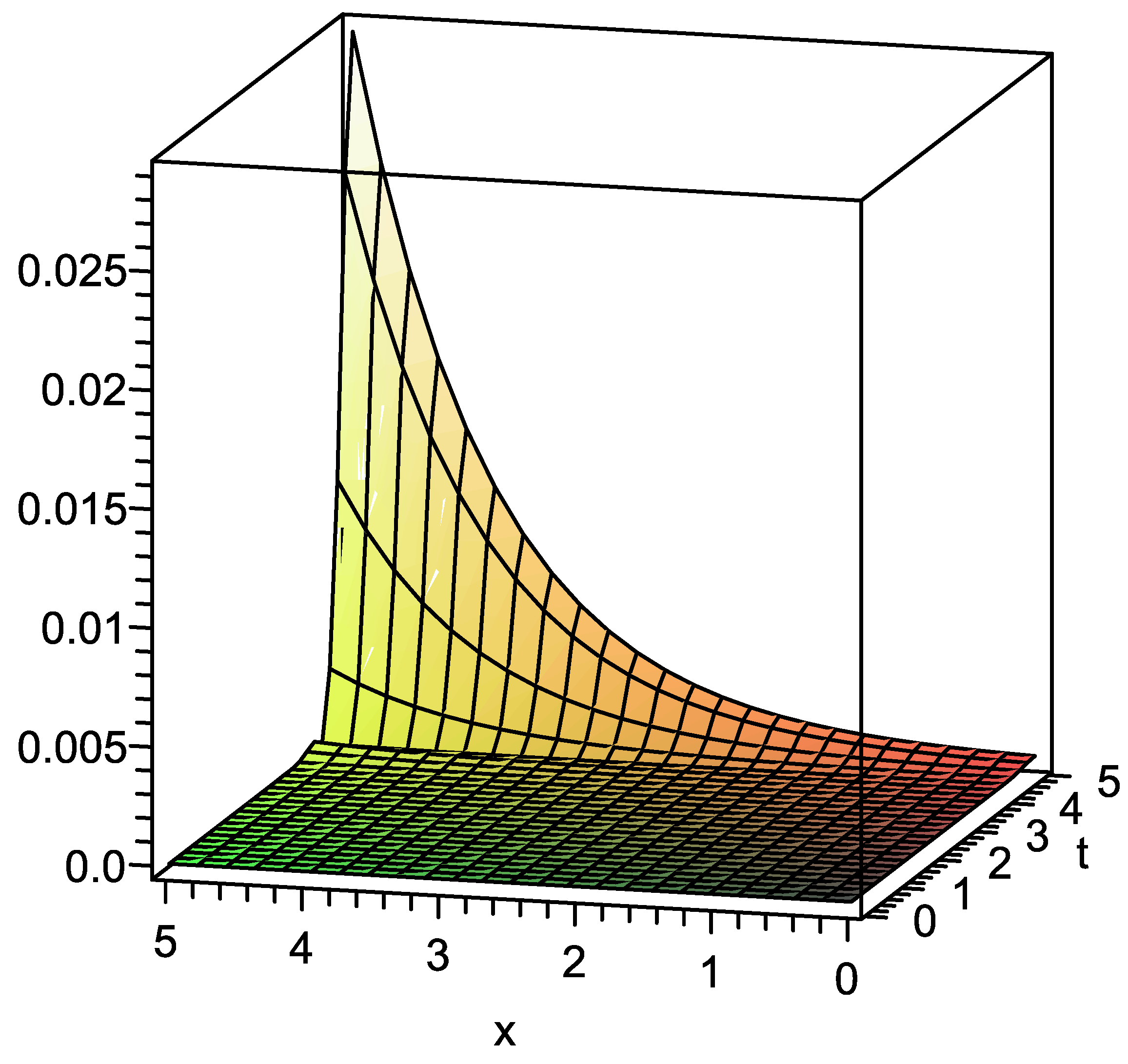
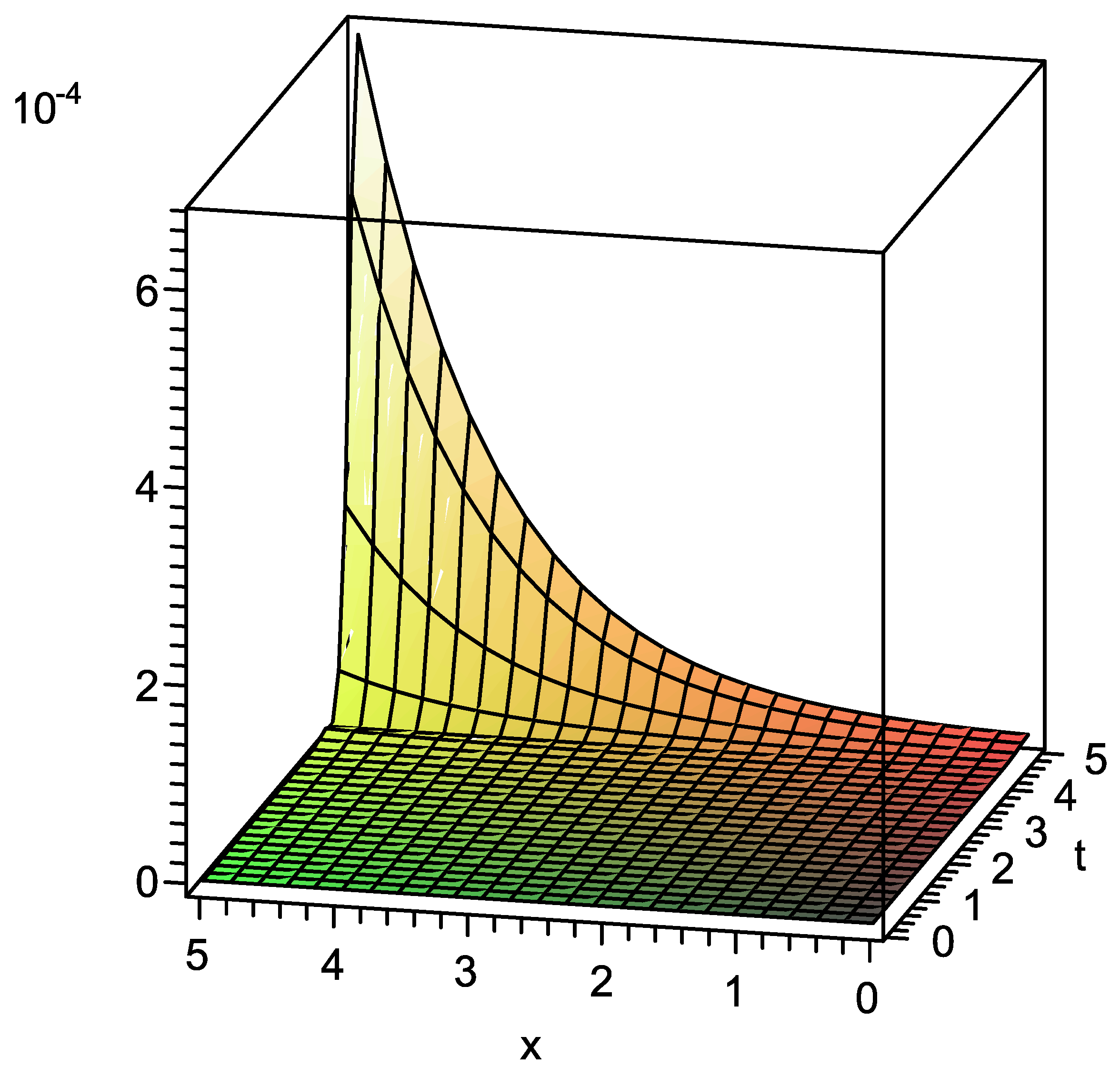

| x | t | Absolute Error in Present Method | Absolute Error in Standard VIM |
|---|---|---|---|
| 0.5 | 0.5 | ||
| 1 | 1 | ||
| 1.5 | 1.5 | ||
| 2 | 2 | ||
| 2.5 | 2.5 | ||
| 3 | 3 | ||
| 3.5 | 3.5 | ||
| 4 | 4 | ||
| 4.5 | 4.5 | ||
| 5 | 5 |
| x | t | Absolute Error in Present Method | Absolute Error in Standard VIM |
|---|---|---|---|
| 0.5 | 0.5 | ||
| 1 | 1 | ||
| 1.5 | 1.5 | ||
| 2 | 2 | ||
| 2.5 | 2.5 | ||
| 3 | 3 | ||
| 3.5 | 3.5 | ||
| 4 | 4 | ||
| 4.5 | 4.5 | ||
| 5 | 5 |
| x | t | Absolute Error in Present Method | Absolute Error in Standard VIM |
|---|---|---|---|
| 0.5 | 0.5 | ||
| 1 | 1 | ||
| 1.5 | 1.5 | ||
| 2 | 2 | ||
| 2.5 | 2.5 | ||
| 3 | 3 | ||
| 3.5 | 3.5 | ||
| 4 | 4 | ||
| 4.5 | 4.5 | ||
| 5 | 5 |
| Present | Standard | Present | Standard | Present | Standard | Present | Standard | |
|---|---|---|---|---|---|---|---|---|
| Method | VIM | Method | VIM | Method | VIM | Method | VIM | |
| N | ||||
|---|---|---|---|---|
| 14 | ||||
| 16 | ||||
| 18 | ||||
| 20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abolhasani, M.; Abbasbandy, S.; Allahviranloo, T. A New Variational Iteration Method for a Class of Fractional Convection-Diffusion Equations in Large Domains. Mathematics 2017, 5, 26. https://doi.org/10.3390/math5020026
Abolhasani M, Abbasbandy S, Allahviranloo T. A New Variational Iteration Method for a Class of Fractional Convection-Diffusion Equations in Large Domains. Mathematics. 2017; 5(2):26. https://doi.org/10.3390/math5020026
Chicago/Turabian StyleAbolhasani, Mohammad, Saeid Abbasbandy, and Tofigh Allahviranloo. 2017. "A New Variational Iteration Method for a Class of Fractional Convection-Diffusion Equations in Large Domains" Mathematics 5, no. 2: 26. https://doi.org/10.3390/math5020026








