On the Achievable Stabilization Delay Margin for Linear Plants with Time-Varying Delays

Abstract

The paper contributes to stabilization problems of linear systems subject to time-varying delays. Drawing upon small gain criteria and robust analysis techniques, upper and lower bounds on the largest allowable time-varying delay are developed by using bilinear transformation and rational approximates. The results achieved are not only computationally efficient but also conceptually appealing. Furthermore, analytical expressions of the upper and lower bounds are derived for specific situations that demonstrate the dependence of those bounds on the unstable poles and nonminumum phase zeros of systems.

1. Introduction

Stability of time-delay systems has been long and well-studied for recent decades; nevertheless, the stabilization of time-delay systems proves a problem fundamentally more difficult, for which a satisfactory answer is yet to be available. Classic stabilization techniques include the time-domain approaches, involving with the solvability of algebraic riccati equations (AREs) or the feasibility of linear matrix inequalities) (LMIs) [1,2], the Smith predictor [3], the finite spectrum assignment [4], and the like. On the other hand, a robust stabilization problem draws more and more attention nowadays, allowing us to consider various classes of perturbations, such as time-varying type, with the aid of robust tools. There are two major approaches for robust stabilization. One is the time-domain approach, concerning the quadratic Lyapunov functions [5,6,7,8,9]. The other is the frequency-domain approach, employing the $H_{\infty }$ optimization tools (see [5,10,11,12,13,14], and the references therein). The existing results, however, have been largely focused on the synthesis issues. On the other hand, the results for fundamental robustness analysis are few. Moreover, the analysis on stabilizability is generally investigated case by case, without generalized solution.

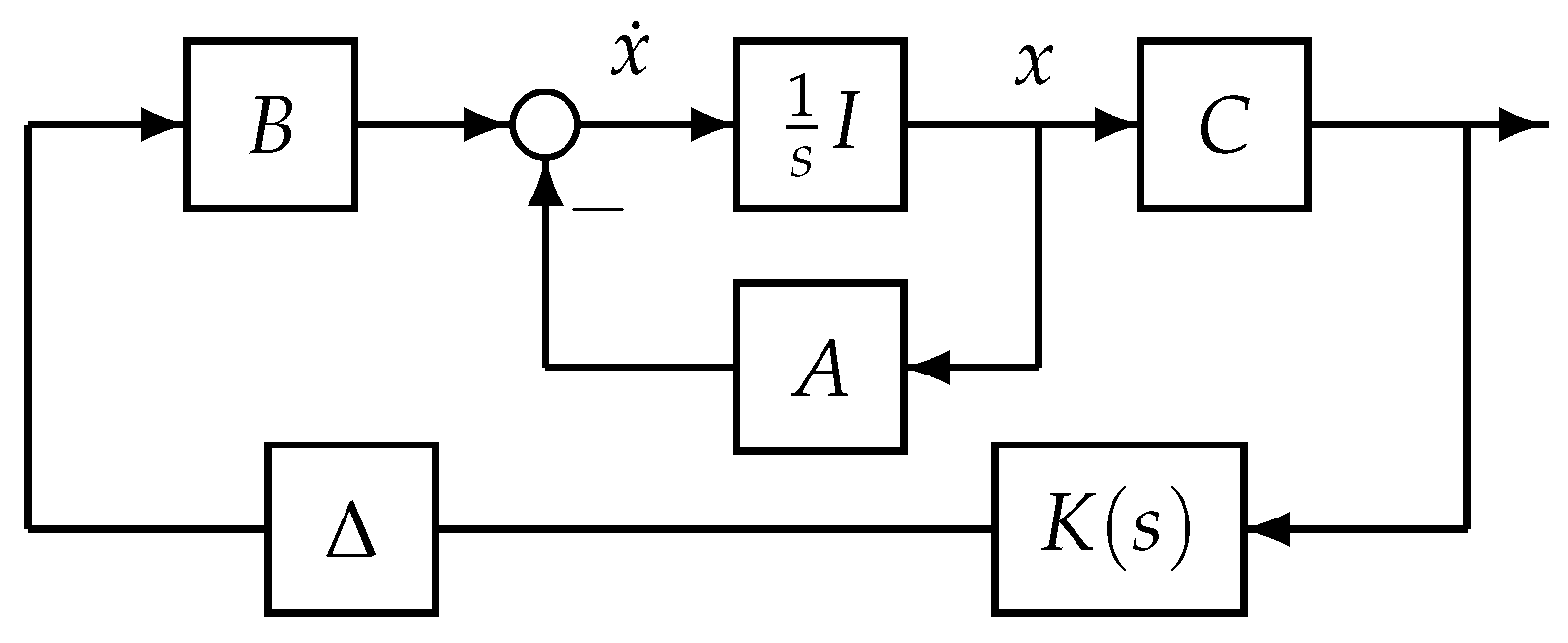
In this paper, we are concerned with linear systems with an input time-varying delay

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{x}=& Ax+Bu(t-\tau (t)),\hfill \\ \hfill y=& Cx.\hfill \end{array}\end{array}$$

(1)

Let the time-varying delay be specified as

$$\begin{array}{c}\hfill 0\le \tau (t)\le h,\end{array}$$

(2)

and

$$\begin{array}{c}\hfill 0\le |\dot{\tau }(t)|\le \delta <1.\end{array}$$

(3)

The purpose of this paper is to find a general method to determine the largest delay range such that there exists an LTI feedback controller $K(s)$ that can stabilize the system (1) through the output feedback

$$u(s)=K(s)y(s),$$

for all time-varying delays that satisfy Label (2). The feedback configuration is shown in Figure 1, where $\Delta$ represents the linear operator

$$\Delta u(t)=u(t-\tau (t)).$$

The problem on stabilization delay margin has been under investigation for some time. In [2] (p. 154), the delay margin was examined for the first-order system with a constant delay stabilized by static feedback, while in [15], the stabilization was achieved by using PID controllers for first-order systems. Furthermore, for single-input single-output (SISO) systems with constant delays, the upper bound was determined in [16,17] for general LTI systems with an arbitrary number of unstable poles. These bounds consequently provide a limit beyond which no single LTI output feedback controller may exist to robustly stabilize a delay plant family within the delay margin. On the other hand, lower bounds on the delay margin were developed by the authors in [18], which provide instead, an interval of the delay range ensuring that the delayed plant can be robustly stabilized for SISO systems with constant delays and the possibility that the lower bounds can be extended to LTI systems with time-varying delays.

In this paper, we seek to explore both the upper and lower bounds on the delay margin for LTI systems with time-varying delays and investigate the $H_{\infty }$ optimal controller synthesis problem in this paper. This development is nontrivial. It appears that, in all cases, our results not only are computationally attractive, but shed significant conceptual insights; furthermore, our developments generate analytical expressions for specific plants, such as systems with one unstable pole or one nonminimum phase zero, revealing how fundamentally unstable poles and nonminimum phase zeros may limit the range of delays over which a plant may or may not be stabilized. In addition, the $H_{\infty }$ optimal feedback controller can be obtained by solving the $H_{\infty }$ control problem. The results can be applied directly to SISO systems subject to time-varying delays and extended to multiple-input multiple-output (MIMO) systems with time-varying delays.

We end this section with a brief description on the notation. Let $\mathbb{R}$ be the space of real numbers, ${\mathbb{R}}^n$ the space of n-dimensional real vectors, and ${\mathbb{R}}_{+}^n$ the n-dimensional space of positive real numbers. Let ${\mathbb{C}}_{-}:=\{s:Re(s)<0\}$, ${\mathbb{C}}_{+}:=\{s:Re(s)>0\}$, and ${\overline{\mathbb{C}}}_{+}:=\{s:Re(s)\ge 0\}$ be the open left and the open right-half of the complex plane, and the closed right-half of the complex plane, respectively. $\overline{z}$ denotes the conjugate of a complex number z, and $x^H$ denotes the conjugate transpose of a complex vector x, while $A^H$ denotes the conjugate transpose of a complex matrix A. We denote the largest real eigenvalue of a matrix A by ${\sigma }_{\max }(A)$, and for a Hermitian matrix A, its largest eigenvalue is denoted by $\overline{\lambda }(A)$. $A\ge 0$ or $A>0$ means that A is nonnegative definite or positive definite. For any stable transfer function matrix $G(s)$, define its $H_{\infty }$ norm by

$${\parallel G(s)\parallel }_{\infty }=\underset{\omega }{sup}\overline{\sigma }(G(j\omega )),$$

where $\overline{\sigma }(·)$ denotes the largest singular value. For an n-tuple of scalars, vectors and matrices $\{f_1,\dots ,f_n\}$ with compatible dimensions, we denote $D_f=\mathrm{diag}\left(f_1,\dots ,f_n\right).$

2. Problem Formulation

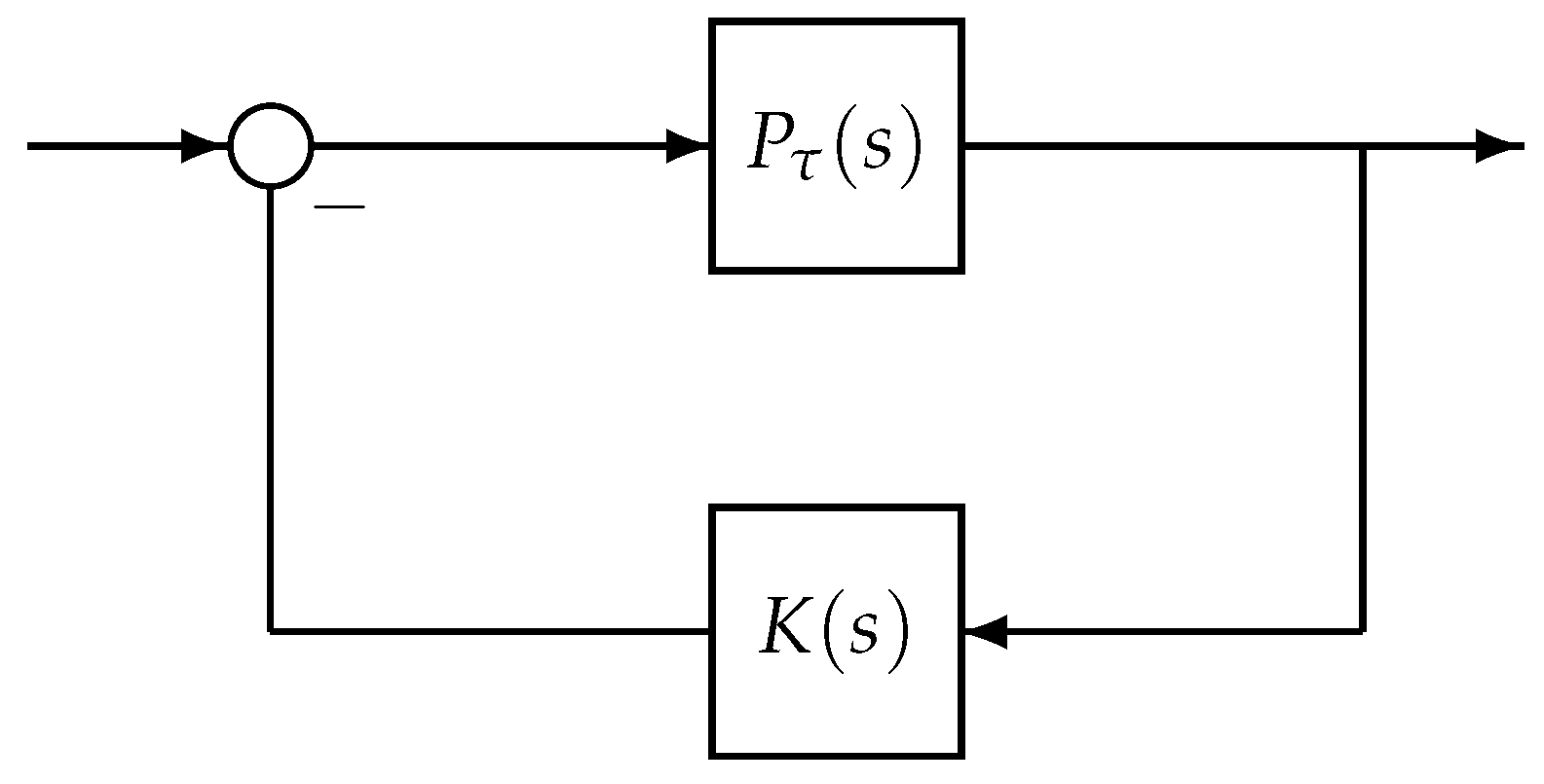
Before dealing with the robust stabilization analysis for LTI systems with time-varying delays, we focus on the stabilization delay margin problem under the constant delay situation firstly. Consider the feedback system depicted in Figure 2, where $P_{\tau }(s)$ denotes a family of plants with an unknown constant delay $\tau$, and $P_0(s)$ denotes the delay-free plant

$$\begin{array}{c}\hfill P_{\tau }(s)=e^{-\tau s}{P}_0(s),\tau \ge 0.\end{array}$$

(4)

Suppose that $P_0(s)$ can be robustly stabilized by some finite-dimensional LTI controller $K(s)$. Hence, the same controller $K(s)$ can thus stabilize $P_{\tau }(s)$ for sufficiently small $\tau >0$ by continuity. The delay margin problem concerns the fundamental limit on robust stabilization of systems with time delays, i.e., what is the largest delay such that there exists a certain LTI controller that can stabilize all the plants within that range? In other words, the delay margin problem seeks to determine the largest delay range within which $P_{\tau }(s)$ can be stabilized by a finite-dimensional LTI controller $K(s)$, or equivalently, the endpoint of delay range where the delay plan cannot be robustly stabilized by a single, fixed controller. Therefore, the problem amounts to computing

$$\begin{array}{c}\hfill {\tau }^{*}=sup\{r:K(s)\mathrm{stabilizes}{P}_{\tau }(s),\forall \tau \in [0,r)\},\end{array}$$

(5)

or, alternatively,

$$\begin{array}{cc}\hfill {\tau }^{*}& =inf\left\{r:\mathrm{There}\mathrm{exists}\mathrm{no}K(s)\mathrm{to}\mathrm{stabilize}{P}_{\tau }(s),\forall \tau \in [0,r)\right\}.\hfill \end{array}$$

(6)

For $K(s)$ to stabilize the delayed plant (4), it is both necessary and sufficient that

$$1+P_{\tau }(s)K(s)\ne 0,\forall s\in {\overline{\mathbb{C}}}_{+}.$$

Since $P_0(s)$ can be stabilized by $K(s)$, the above condition is equivalent to

$$\begin{array}{c}\hfill 1+T_0(s)\left(e^{-\tau s}-1\right)\ne 0,\forall s\in {\overline{\mathbb{C}}}_{+},\end{array}$$

where $T_0(s)=P_0(s)K(s){(1+P_0(s)K(s))}^{-1}$ is the system’s complementary sensitivity function. Thus, the delay margin problem is equivalent to find

$${\tau }^{*}=sup\left\{\nu :\underset{K(s)}{inf}\underset{s\in {\overline{\mathbb{C}}}_{+}}{inf}\left|1+T_0(s)\left(e^{-\tau s}-1\right)\right|>0,\forall \tau \in [0,\nu )\right\}.$$

Since the exact delay margin is difficult to achieve, an alternative way is to estimate the upper bound $\overline{\tau }$ and lower bound $\underline{\tau }$ of the delay margin. Evidently, $\underline{\tau }\le {\tau }^{\star }\le \overline{\tau }$. Based on a small gain theorem, there exists some stabilizing $K(s)$ for all $\tau \in [0,\underline{\tau }]$ if

$$\begin{array}{c}\hfill \underset{\tau \in [0,\underline{\tau }]}{sup}\underset{K(s)}{inf}{∥T_0(s)(e^{-\tau s}-1)∥}_{\infty }<1.\end{array}$$

(7)

Hence, a sufficient condition is obtained that provides a computing method on the lower bound of the delay margin. Similarly, there exists no controller $K(s)$ to stabilize $P_{\tau }(s)$ if for any $K(s)$ such that

$$1+T_0(j\omega )\left(e^{-j\omega \tau }-1\right)=0,\mathrm{for}\mathrm{some}\omega .$$

In other words, the upper bound of the delay margin can be calculated according to the following condition. The plant $P_{\tau }(s)$ can not be stabilized by any controller if $\tau >\overline{\tau }$ with

$$\begin{array}{cc}\hfill \overline{\tau }& =inf\left\{\tau >0:\underset{K(s)}{inf}\underset{\omega }{inf}\left|1+T_0(j\omega )\left(e^{-j\omega \tau }-1\right)\right|=0\right\},\hfill \end{array}$$

(8)

$$\begin{array}{c}=sup\left\{\tau >0:\underset{K(s)}{inf}\underset{\omega }{inf}\left|1+T_0(j\omega )\left(e^{-j\omega \tau }-1\right)\right|>0\right\}.\hfill \end{array}$$

(9)

3. Main Results

3.1. Upper Bounds on the Delay Margin

Consider the time-varying delay system (1). It is easy to see that the upper bound for the constant delay case is also an upper bound on h, i.e., $h\le \overline{\tau }$. Consequently, the main point is to compute $\overline{\tau }$ by conditions (8) and (9). However, it is still difficult compute $\overline{\tau }$ since the all-pass function $e^{-\tau s}$ is irrational. Thus, it is useful to use another all-pass and rational function to estimate $e^{-\tau s}$. In this paper, we use bilinear transformation to estimate the upper bound.

Define an all-pass function ${\displaystyle W_T(s)=\frac{1-Ts}{1+Ts}.}$ Note that ${\displaystyle \left|e^{-\tau s}\right|=\left|\frac{1-Ts}{1+Ts}\right|}$. Then, for any $(\omega ,\tau )$, let

$$\begin{array}{c}\hfill \omega \tau =2{tan}^{-1}\omega T.\end{array}$$

(10)

Since ${tan}^{-1}(\theta )<\theta ,$ we have

$$\begin{array}{c}\hfill \tau =\frac{2{tan}^{-1}\omega T}{\omega }\le \frac{2\omega T}{\omega }\le 2T.\end{array}$$

Define $f(s,T)=1+T_0(s)\left(W_T(s)-1\right).$ Then, the following conditions are satisfied

$$\begin{array}{c}\hfill f(s,0)=1,\end{array}$$

(11)

$$\begin{array}{c}\hfill f\left(p,\frac{1}{p}\right)=0,\end{array}$$

(12)

where p is the unstable pole of the delay-free plant $P_0(s)$. Note that condition (12) holds due to the interpolation $T_0(p)=1$. By continuity, we have

$$\begin{array}{c}\hfill f(p,T)<0,\forall T>\frac{1}{p}.\end{array}$$

(13)

Referring to condtion (9), it can be concluded that the nominal plant is stabilizable for all $T\le 1/p$. Hence, we are led to the following lemma.

Lemma 1.

Suppose that $P_0(s)$ has only one unstable pole $p\in {\mathbb{C}}_{+}$, and no nonminimum phase zero. Then, there exists no controller $K(s)$ that can stabilize the system (4) for all $\tau >\overline{\tau }$ with

$$\begin{array}{c}\hfill \overline{\tau }=\frac{2}{p}.\end{array}$$

(14)

Moreover, if $P_0(s)$ has multiple unstable poles $p_i\in {\mathbb{C}}_{+}$, $i=1,...,n$, and no mominimum phase zero. Then,

$$\begin{array}{c}\hfill \overline{\tau }=\underset{i}{min}\frac{2}{p_i}.\end{array}$$

(15)

Additionaly, suppose also that $P_0(s)$ has one unstable pole $p\in {\mathbb{C}}_{+}$, and one nominimum phase zero $z\in {\mathbb{C}}_{+}$. If $p<z$, then there exists no controller $K(s)$ that can stabilize the system (4) for all $\tau >\overline{\tau }$ with

$$\begin{array}{c}\hfill \overline{\tau }=min\left\{\frac{2}{p},\frac{2}{p}-\frac{2}{z}\right\}.\end{array}$$

(16)

Proof. 

By bilinear transformation, $W_T(s)$ is equal to $e^{-\tau s}$ as long as $\tau \le 2T$. Let $s=p$, condition (13) turns to be

$$\left|1+T_0(s)\left(\frac{1-Ts}{1+Ts}-1\right)\right|>0,\forall T>\frac{1}{p}.$$

Upon Label (9), the upper bound can be obtained as Label (14) $P_0(s)$ only has one unstable pole. The upper bound (15) can be derived in the similar manner. On the other hand, under the circumstance that $P_0(s)$ has one unstable pole and one nominimum phase zero, the bilinear transformation function is chosen to be

$${\widehat{W}}_T(s)=\frac{1-Ts}{1+Ts}\frac{z+s}{z-s},$$

by noting that $\left|W_T(s)\right|=\left|e^{-\tau s}\right|.$ For any $(\omega ,\tau )$, let

$$\begin{array}{c}\hfill \tau \omega =\left|-2{tan}^{-1}\left(\omega T\right)+2{tan}^{-1}\left(\frac{\omega }{z}\right)\right|,\end{array}$$

(17)

which gives rise to

$$\tau \le 2\left|T-\frac{1}{z}\right|.$$

Define $\widehat{f}(s,T)=1+T_0(s)({\widehat{W}}_T(s)-1).$ Analogously, the upper bound (16) can be easily obtained. ☐

In what follows, we shall extend our results on upper bounds of delay margin to LTI systems with time-varying delays. The following theorem is an easy consequence of Lemma 1. Evidently, if no controller may exist to robustly stabilize a plant with a constant delay beyond the range of delay margin, then no controller may achieve the same for plants subject to time-varying delays.

Theorem 1.

Let $p\in {\mathbb{C}}_{+}$ be a real unstable pole of $P_0(s)$. Then, there exists no controller $K(s)$ that can stabilize the system (1) subject to (2) if

$$\begin{array}{c}\hfill h>\frac{2}{p}.\end{array}$$

(18)

Moreover, if $P_0(s)$ has multiple unstable poles $p_i\in {\mathbb{C}}_{+}$, $i=1,...,n$, and no mominimum phase zero. Then, there exists no controller $K(s)$ that can stabilize system (1) subject to Label (2) if

$$\begin{array}{c}\hfill h>\underset{i}{min}\frac{2}{p_i}.\end{array}$$

(19)

Additionally, let $p\in {\mathbb{C}}_{+}$ be a real unstable pole of $P_0(s)$, and $z\in {\mathbb{C}}_{+}$ a real nonminimum phase zero $P_0(s)$. If $p<z$, then there exists no controller $K(s)$ that can stabilize the system (1) subject to Label (2) if

$$\begin{array}{c}\hfill h>min\left\{\frac{2}{p},\frac{2}{p}-\frac{2}{z}\right\}.\end{array}$$

(20)

Note that the upper bound of the delay margin only involves with the delay bound h, which implies the time-varying delay may vary arbitrarily fast, as long as it is bounded by some certain value.

3.2. Lower Bounds on the Delay Margin

In the following part, we work to find an LTI controller $K(s)$ such that the delay system (1) is stabilized by way of the output feedback $u(s)=K(s)y(s)$ within a region defined by ($h,\delta$).

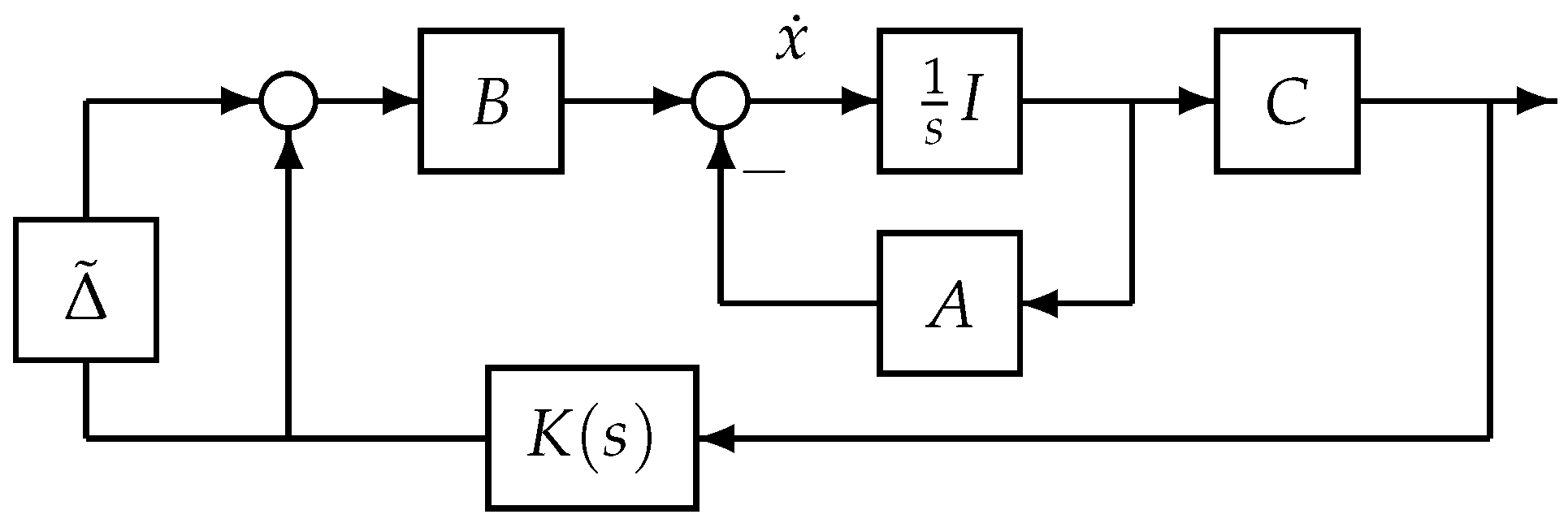
By model transformation, it is possible to employ the approximations of the time-varying operator

$$\tilde{\Delta }\left(x(t)\right)=\Delta \left(x(t)\right)-x(t),$$

i.e.,

$$\tilde{\Delta }=\Delta -I,$$

where I is the identity operator. Then, the original system (1) can be regarded as Figure 3. In view of the small gain theorem [19], system (1) subject to Labels (2) and (3) is stable if

$$\begin{array}{c}\hfill \underset{K(s)}{inf}{∥\widehat{\Delta }{T}_0(s)∥}_{2,2}<1,\end{array}$$

(21)

with $T_0(s)$ and $\widehat{\Delta }$ being the certain and uncertain part, respectively.

It is worth noting that the original system (1) with the controller $K(s)$ in Figure 1 is stable whenever the system depicted in Figure 3 is stable [1]. Let $P_0(s)=C{(sI-A)}^{-1}B$ be the transfer function of the delay-free plant. It is then useful to estimate the induced norm of the uncertainty $\tilde{\Delta }$. One such estimate can be obtained by employing the Littlewood’s Second Principle. An approximation in this spirit was developed in [20].

Lemma 2.

Let $\tau (t)$ be specified by Labels (2) and (3). Then, for any $\omega >0$,

$$\begin{array}{c}\hfill {∥\tilde{\Delta }{\left(\varphi (\omega )+ϵ\right)}^{-1}∥}_{2,2}\le 1,\end{array}$$

(22)

where

$$\begin{array}{c}\hfill \varphi (\omega )=\left\{\begin{array}{cc}\sqrt{\frac{8}{2-\delta }}sin\left(\omega h/2\right)\hfill & \left|\omega \right|\le \pi /h,\hfill \\ \sqrt{\frac{8}{2-\delta }}\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

(23)

Proof. 

Let $[{\omega }_i,{\omega }_{i+1}],i=1,...,n-1,$ be an arbitrary small subset of the interval $[{\omega }_m,{\omega }_M]$. Assume that a real-valued function $u(t)$ with $\mathrm{supp}\left(\left|\widehat{u}(j\omega )\right|\right)=\left[{\omega }_m,{\omega }_M\right]$ can be approximated well by some function $\underline{u}(t)$ with $\underline{u}(t)={\displaystyle \sum _i}\underline{u_i}(t)$. Thus, the Fourier transform of of $\underline{u_i}(t)$ should satisfy

$$\begin{array}{c}\hfill \widehat{\underline{u_i}}(j\omega )=\left\{\begin{array}{c}\frac{1}{\sqrt{2}}\left|\widehat{u}\left(j{\gamma }_i\right)\right|\omega \in \left[{\omega }_i,{\omega }_{i+1}\right]\cup \left[-{\omega }_{i+1},-{\omega }_i\right],\hfill \\ 0\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(24)

with ${\gamma }_i\in \left[{\omega }_i,{\omega }_{i+1}\right].$ It is evident that

$$\begin{array}{cc}\hfill {∥\tilde{\Delta }u(t)∥}_2& \le {∥\tilde{\Delta }\left(u(t)-\underline{u}(t)\right)∥}_2+{∥\tilde{\Delta }\underline{u}(t)∥}_2\hfill \\ \hfill & \le \mathbb{O}\left({∥u(t)-\underline{u}(t)∥}_2\right)+\sum _i{∥\tilde{\Delta }{\underline{u}}_i(t)∥}_2,\hfill \end{array}$$

(25)

which can be further extended to be

$$\begin{array}{c}\hfill {∥\tilde{\Delta }u\left(t\right)∥}_2\le \mathbb{O}\left({∥u(t)-\underline{u}(t)∥}_2\right)+\left(\underset{\omega \in \left[{\omega }_m,{\omega }_M\right]}{sup}\phi (\omega )\right)\sum _i{∥{\underline{u}}_i(t)∥}_2,\end{array}$$

(26)

by constructing a positive function $\phi (\omega )$ such that

$$\begin{array}{c}\hfill {∥\tilde{\Delta }{\underline{u}}_i\left(t\right)∥}_2\le \left(\underset{\omega \in \left[{\omega }_i,{\omega }_{i+1}\right]}{sup}\phi (\omega )\right){∥{\underline{u}}_i(t)∥}_2.\end{array}$$

(27)

We note that

$$\sum _i{∥{\underline{u}}_i(t)∥}_2={∥\sum _i{\underline{u}}_i(t)∥}_2={\parallel u(t)\parallel }_2+\mathbb{O}\left({∥u(t)-\underline{u}(t)∥}_2\right).$$

As such, Inequality (26) is equivalent to

$$\begin{array}{c}\hfill {∥\tilde{\Delta }u\left(t\right)∥}_2\le \mathbb{O}\left({∥u(t)-\underline{u}(t)∥}_2\right)+\left(\underset{\omega \in \left[{\omega }_m,{\omega }_M\right]}{sup}\phi (\omega )\right){∥u(t)∥}_2,\end{array}$$

(28)

where $\mathbb{O}\left({∥u(t)-\underline{u}(t)∥}_2\right)$ can be arbitrarily small.

Next, we concern the estimation of $\phi (\omega )$. Recalling Label (24), we can express ${\underline{u}}_i(t)$ by the following sink function

$$\begin{array}{c}\hfill {\underline{u}}_i(t)=\left|\widehat{u}\left(j{\gamma }_i\right)\right|\times \sqrt{{\omega }_{i+1}-{\omega }_i}\times \frac{sin\left({\omega }_{i+1}t\right)-sin\left({\omega }_{i}t\right)}{\sqrt{\pi \left({\omega }_{i+1}-{\omega }_i\right)}t},\end{array}$$

(29)

satisfying

$${∥{\underline{u}}_i(t)∥}_2=\left|\widehat{u}\left(j{\gamma }_i\right)\right|\sqrt{{\omega }_{i+1}-{\omega }_i}.$$

Define $g(t)=\frac{sin\left({\omega }_{i+1}t\right)-sin\left({\omega }_{i}t\right)}{\sqrt{\pi \left({\omega }_{i+1}-{\omega }_i\right)}t}$. Then, its Fourier transform satisfies

$$\begin{array}{c}\hfill \widehat{G}(j\omega )=\left\{\begin{array}{c}\frac{1}{\sqrt{2\left({\omega }_{i+1}-{\omega }_i\right)}}\omega \in \left[{\omega }_i,{\omega }_{i+1}\right]\cup \left[-{\omega }_{i+1},-{\omega }_i\right],\hfill \\ 0\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

Thus, $\phi (\omega )$ can be estimated by $\underset{i}{sup}{∥\tilde{\Delta }g(t)∥}_2$ with sufficient small $[{\omega }_i,{\omega }_{i+1}]$. Let $a=\left({\omega }_{i+1}+{\omega }_i\right)/2$ and $b=\left({\omega }_{i+1}-{\omega }_i\right)/2$. We can rewirte $g(t)$ as

$$\begin{array}{c}\hfill g(t)=\frac{\sqrt{2}cos(at)sin(bt)}{\sqrt{\pi b}t},\end{array}$$

(30)

with

$$\begin{array}{c}\hfill {\parallel g(t)\parallel }_2={∥\sqrt{\frac{2}{\pi b}}\frac{cos(at)sin(bt)}{t}∥}_2=1.\end{array}$$

(31)

Consequently,

$$\begin{array}{cc}\hfill \tilde{\Delta }g(t)& =g\left(t-\tau (t)\right)-g(t)\hfill \\ \hfill & =\sqrt{\frac{2}{\pi b}}\left(\frac{cos\left(a\left(t-\tau (t)\right)\right)sin\left(b\left(t-\tau (t)\right)\right)}{t-\tau (t)}-\frac{cos(at)sin(bt)}{t}\right).\hfill \end{array}$$

(32)

Define

$$\begin{array}{cc}\hfill g_1(t)& =\left(cos\left(a\left(t-\tau (t)\right)\right)-cos(at)\right)\times \frac{sin\left(b\left(t-\tau (t)/2\right)\right)}{t-\tau (t)/2},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill g_2(t)& =cos\left(a\left(t-\tau (t)\right)\right)\times \left(\frac{sin\left(b\left(t-\tau (t)\right)\right)}{t-\tau (t)}-\frac{sin\left(b\left(t-\tau (t)/2\right)\right)}{t-\tau (t)/2}\right),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill g_3(t)& =cos(at)\times \left(\frac{sin\left(b\left(t-\tau (t)/2\right)\right)}{t-\tau (t)/2}-\frac{sin\left(bt\right)}{t}\right).\hfill \end{array}$$

(35)

Thus, we can rewrite Equation (32) to be

$$\tilde{\Delta }g(t)=\sqrt{\frac{2}{\pi b}}\times \left(g_1(t)+g_2(t)+g_3(t)\right).$$

We then estimate the ${\mathcal{L}}_2$ norm of $g_1(t)$, $g_2(t)$ and $g_3(t)$ one by one. Since that $g_1(t)$ can be expressed as

$$g_1(t)=2sin\left(\frac{a\tau (t)}{2}\right)\times sin\left(at-\frac{a\tau (t)}{2}\right)\times \frac{sin\left(b\left(t-\tau (t)/2\right)\right)}{t-\tau (t)/2},$$

the ${\mathcal{L}}_2$ norm bound of $g_1(t)$ can be obtained as follows

$$\begin{array}{cc}\hfill {∥g_1(t)∥}_2& \le \underset{t}{sup}2\left|sin\left(\frac{a\tau (t)}{2}\right)\right|\times {∥sin\left(at-\frac{a\tau (t)}{2}\right)\times \frac{sin\left(b\left(t-\tau (t)/2\right)\right)}{t-\tau (t)/2}∥}_2\hfill \\ \hfill & \le \underset{t}{sup}2\left|sin\left(\frac{a\tau (t)}{2}\right)\right|\times {\left(1-\frac{\delta }{2}\right)}^{-1/2}\times {∥\frac{sin(at)sin(bt)}{t}∥}_2\hfill \\ \hfill & \le \sqrt{\frac{4\pi b}{2-\delta }}\times \underset{t}{sup}\left|sin\left(\frac{a\tau (t)}{2}\right)\right|,\hfill \end{array}$$

(36)

where the last inequality is derived in light of (31).

Concerning $[{\omega }_i,{\omega }_{i+1}]$ is arbitrarily small (i.e., b is arbitrary small) and $\underset{x\to 0}{lim}\frac{sin(x)}{x}=1,$ we are led to

$$\begin{array}{c}\hfill \parallel g_2{(t)\parallel }_2\le 2b\to 0,\end{array}$$

(37)

and

$$\begin{array}{c}\hfill \parallel g_3{(t)\parallel }_2\le 2b\to 0.\end{array}$$

(38)

As a result,

$${∥\tilde{\Delta }g(t)∥}_2\le \sqrt{\frac{2}{\pi b}}\times {∥g_1(t)∥}_2.$$

In other words, ${∥\tilde{\Delta }g(t)∥}_2$ is bounded by

$${∥\tilde{\Delta }g(t)∥}_2\le \sqrt{\frac{8}{2-\delta }}\times \underset{t}{sup}\left|sin\left(\frac{{\omega }_i\tau (t)}{2}\right)\right|.$$

The expression of $\phi (\omega )$ in Label (23) and Inequality (22) thus follow directly. ☐

Upon above, condition (21) is equivalent to

$$\begin{array}{c}\hfill \underset{\omega }{sup}\left|T_0(j\omega )\left(\varphi (\omega )+ϵ\right)\right|<1,\end{array}$$

(39)

for sufficiently small $ϵ$. Construct a parameter-dependent rational approximation

$$\begin{array}{c}\hfill w_h(s)=\frac{b_h(s)}{a_h(s)}=\frac{b_q{(hs)}^q+\cdots +b_1(hs)+b_0}{a_q{(hs)}^q+\cdots +a_1(hs)+a_0},\end{array}$$

(40)

such that

$$\begin{array}{c}\hfill |\varphi (\omega )+ϵ|\le \left|w_h(j\omega )+ϵ\right|,\forall \omega .\end{array}$$

(41)

Since $ϵ$ can be selected to be arbitrarily small, condition (39) is satisfied whenever

$$\begin{array}{c}\hfill \underset{K(s)}{inf}{∥T_0(s){\omega }_h(s)∥}_{\infty }<1.\end{array}$$

(42)

We require that $w_h(s)$ be stable and has no nonminimum phase zero, excluding the origin where $w_h(s)$ might have a zero, that is, $w_h(0)=0$. This latter condition may be imposed to ensure a close-fit of $|w_h(j\omega )|$ to $\left|\varphi (\omega )\right|$ at low frequencies. Without losing any generality, we let $a_i>0$ for $i=0,1,\dots ,q$, and $b_i>0$ for $i=1,\dots ,q$. The following are some specific approximants obtained in, e.g., [21,22,23]:

$$\begin{array}{c}{w}_{1h}(s)=\sqrt{\frac{2}{2-\delta }}hs,\hfill \end{array}$$

(43)

$$\begin{array}{c}{w}_{2h}(s)=\sqrt{\frac{2}{2-\delta }}\frac{hs}{1+hs/3.465},\hfill \end{array}$$

(44)

$$\begin{array}{c}{w}_{3h}(s)=\sqrt{\frac{2}{2-\delta }}\frac{1.216hs}{1+hs/2},\hfill \end{array}$$

(45)

$$\begin{array}{c}{w}_{4h}(s)=\sqrt{\frac{2}{2-\delta }}\frac{hs(2\times 0.{2152}^{2}hs+1)}{{(0.2152hs+1)}^2},\hfill \end{array}$$

(46)

$$\begin{array}{c}{w}_{5h}(s)=\sqrt{\frac{2}{2-\delta }}\frac{hs}{1+hs/2}\frac{0.1791{(hs)}^2+0.7093hs+1}{0.1791{(hs)}^2+0.5798hs+1},\hfill \end{array}$$

(47)

and

$$\begin{array}{c}\hfill w_{6h}(s)=\sqrt{\frac{2}{2-\delta }}\frac{hs}{1+hs/2}\frac{0.02952{(hs)}^4+0.210172{(hs)}^3+0.70763{(hs)}^2+1.3188hs+1}{0.02952{(hs)}^4+0.191784{(hs)}^3+0.64174{(hs)}^2+1.195282hs+1}.\end{array}$$

(48)

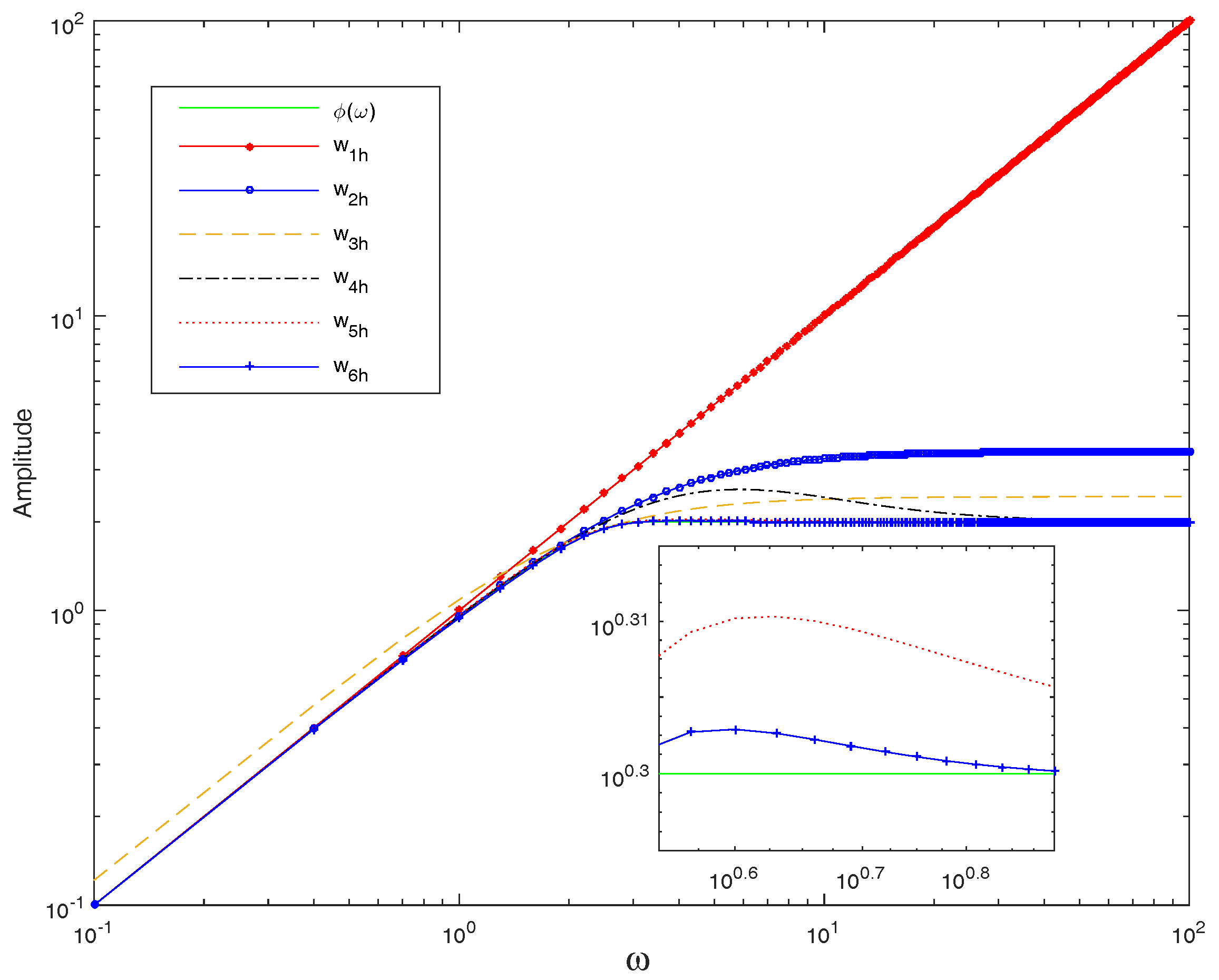
The frequency responses of these candidates are shown in Figure 4, from which we can conclude that $w_{ih}(s)$ approximates better one after one with the higher function order. By solving the $H_{\infty }$ optimization problem in Label (42), a lower bound h on the delay margin can be derived that will guarantee the existence of a stabilizing controller $K(s)$ for system (1) with all subject to Labels (2) and (3).

Since h corresponds to an optimal $H_{\infty }$ optimization problem, this robustly stabilizing controller can be synthesized accordingly. Indeed, to synthesize this robustly stabilizing controller $K(s)$, it suffices to solve the standard $H_{\infty }$ control problem in Label (42), which gives rise an optimal controller K(s) depending on h. In this vein, it is worth pointing out that a lower order ${\omega }_h(s)$, such as those given in Label (43)–(48), can be particularly desirable, since they potentially result in low-order controllers. We shall demonstrate this point explicitly in the numerical example.

The following lemma, adopted from [24,25], is concerned with the Nevanlinna–Pick tangential interpolation problem, providing an essential tool converting the $H_{\infty }$ computation into the analytical interpolation.

Lemma 3.

Let $z_i\in {\mathbb{C}}_{+},i=1,\cdots ,l$ and $p_j\in {\mathbb{C}}_{+},j=1,\cdots ,k$ denote distinct points with $z_i\ne p_j$ for any i and j. Consider a rational matrix function $G(s)$, satisfying

$$\begin{array}{cc}\hfill m_i^{H}G(z_i)=& n_i^H,i=1,\cdots ,l,\hfill \\ \hfill G(p_j)u_j=& v_j,j=1,\cdots ,k,\hfill \end{array}$$

for some vectors $m_i,n_i,i=1,\cdots ,l$ and $u_j,v_j,j=1,\cdots ,k$ with compatible dimensions. Then, $G(s)$ is stable and ${\parallel G(s)\parallel }_{\infty }\le 1$ if and only if

$$Q=\left[\begin{array}{cc}{Q}_1& Q_{12}^H\\ Q_{12}& Q_2\end{array}\right]\ge 0,$$

with

$${\displaystyle Q_1=\left[\frac{m_i^H{m}_j-n_i^H{n}_j}{z_i+{\overline{z}}_j}\right],Q_2=\left[\frac{u_i^H{u}_j-v_i^H{v}_j}{{\overline{p}}_i+p_j}\right],Q_{12}=\left[\frac{n_i^H{u}_j-m_i^H{v}_j}{z_i-p_j}\right].}$$

Theorem 2.

Let $p_i\in {\mathbb{C}}_{+},i=1,\cdots ,l$ and $z_i\in {\mathbb{C}}_{+},i=1,\cdots ,k$ be the unstable poles and nonminimum phase zeros of $P_0(s),$ respectively, with $z_i\ne p_j$ for any i and j. Suppose that $P_0(s)$ has neither zero nor pole on the imaginary axis, and can be stabilized by some $K(s)$. Then, system (1) subject to Labels (2) and 3) can be stabilized by some $K(s)$ with ($h,\delta$) is the solution of

$$\begin{array}{c}\hfill {\overline{\lambda }}^{\frac{1}{2}}\left(Q_p^{-\frac{1}{2}}{D}_w^{H}Z{D}_w{Q}_p^{-\frac{1}{2}}\right)=1,\end{array}$$

(49)

with $Z=Q_p+Q_{zp}^H{Q}_z^{-1}{Q}_{zp},Q_z=\left[{\displaystyle \frac{1}{z_i+{\overline{z}}_j}}\right].Q_p=\left[{\displaystyle \frac{1}{{\overline{p}}_i+p_j}}\right],$ $Q_{zp}=\left[{\displaystyle \frac{1}{z_i-p_j}}\right],$ and $D_w=\mathrm{diag}\left(w_h(p_1),\dots ,w_h(p_l)\right).$

Proof. 

The proof follows directly from Lemma 3, together with Label (42). ☐

To put it simply, analytical bounds can be obtained for some specific cases.

Corollary 1.

Consider the delay free plant $P_0(s)$ with one unstable pole $p\in {\mathbb{C}}_{+}$ and one nonminimum phase zero $z\in {\mathbb{C}}_{+}$. Let $P_0(s)$ be stabilized by some $K(s)$. Then, for $w_h(s)$ satisfying Label (41), system (1) subject to Labels (2) and (3) can be stabilized by some $K(s)$ with ($h,\delta$) is the solution of

$$w_h(p)=\left|\frac{z-p}{z+p}\right|.$$

In particular, if $w_h(s)=w_{ih}(s)$ given in Labels (43)–(46), $i=1,...,4$, for $\delta \in [0,1)$, we have:

(1) 

$\begin{array}{c}{h}_{(1)}=\left|\frac{z-p}{z+p}\right|\frac{\sqrt{1-\delta /2}}{p},\hfill \end{array}$

(2) 

$\begin{array}{c}{h}_{(2)}=\left|\frac{z-p}{z+p}\right|\frac{\sqrt{1-\delta /2}}{\left(1-\sqrt{1-\delta /2}/3.465\right)p},\hfill \end{array}$

(3) 

$\begin{array}{c}{h}_{(3)}=\left|\frac{z-p}{z+p}\right|\frac{\sqrt{1-\delta /2}}{\left(1.216-\sqrt{1-\delta /2}/2\right)p},\hfill \end{array}$

(4) 

$\begin{array}{c}{h}_{(4)}=\left|\frac{z-p}{z+p}\right|\frac{-0.0173\left(-625+269\sqrt{1-\delta /2}+\sqrt{390625-191528\sqrt{1-\delta /2}}\right)}{\left(\sqrt{1-\delta /2}-2\right)p}.\hfill \end{array}$

Moreover, consider the delay free plant $P_0(s)$ with one unstable pole $p\in {\mathbb{C}}_{+}$, and distinct nonminimum phase zeros $z_i\in {\mathbb{C}}_{+},i=1,...,k$. Let $P_0(s)$ be stabilized by some $K(s)$. Then, for $w_h(s)$ satisfying (41), system (1) subject to Labels (2) and (3) can be stabilized by some $K(s)$ with ($h,\delta$) is the solution of

$$w_h(p)=\prod _{i=1}^k\left|\frac{z_i-p}{{\overline{z}}_i+p}\right|.$$

In particular, if $w_h(s)=w_{ih}(s)$ given in Labels (43)–(46), $i=1,...,4$, for $\delta \in [0,1)$, we have:

(1) 

${\displaystyle h_{(1)}=\prod _{i=1}^k\left|\frac{z_i-p}{{\overline{z}}_i+p}\right|\frac{\sqrt{1-\delta /2}}{p},}$

(2) 

${\displaystyle h_{(2)}=\prod _{i=1}^k\left|\frac{z_i-p}{{\overline{z}}_i+p}\right|\frac{\sqrt{1-\delta /2}}{\left(1-\sqrt{1-\delta /2}/3.465\right)p},}$

(3) 

${\displaystyle h_{(3)}=\prod _{i=1}^k\left|\frac{z_i-p}{{\overline{z}}_i+p}\right|\frac{\sqrt{1-\delta /2}}{\left(1.216-\sqrt{1-\delta /2}/2\right)p},}$

(4) 

${\displaystyle h_{(4)}=\prod _{i=1}^k\left|\frac{z_i-p}{{\overline{z}}_i+p}\right|\frac{-0.0173\left(-625+269\sqrt{1-\delta /2}+\sqrt{390625-191528\sqrt{1-\delta /2}}\right)}{\left(\sqrt{1-\delta /2}-2\right)p}.}$

Note that, for $\delta =0$, h recovers essentially the delay margin obtained for LTI systems with a constant unknown delay [18].

4. Illustrative Example

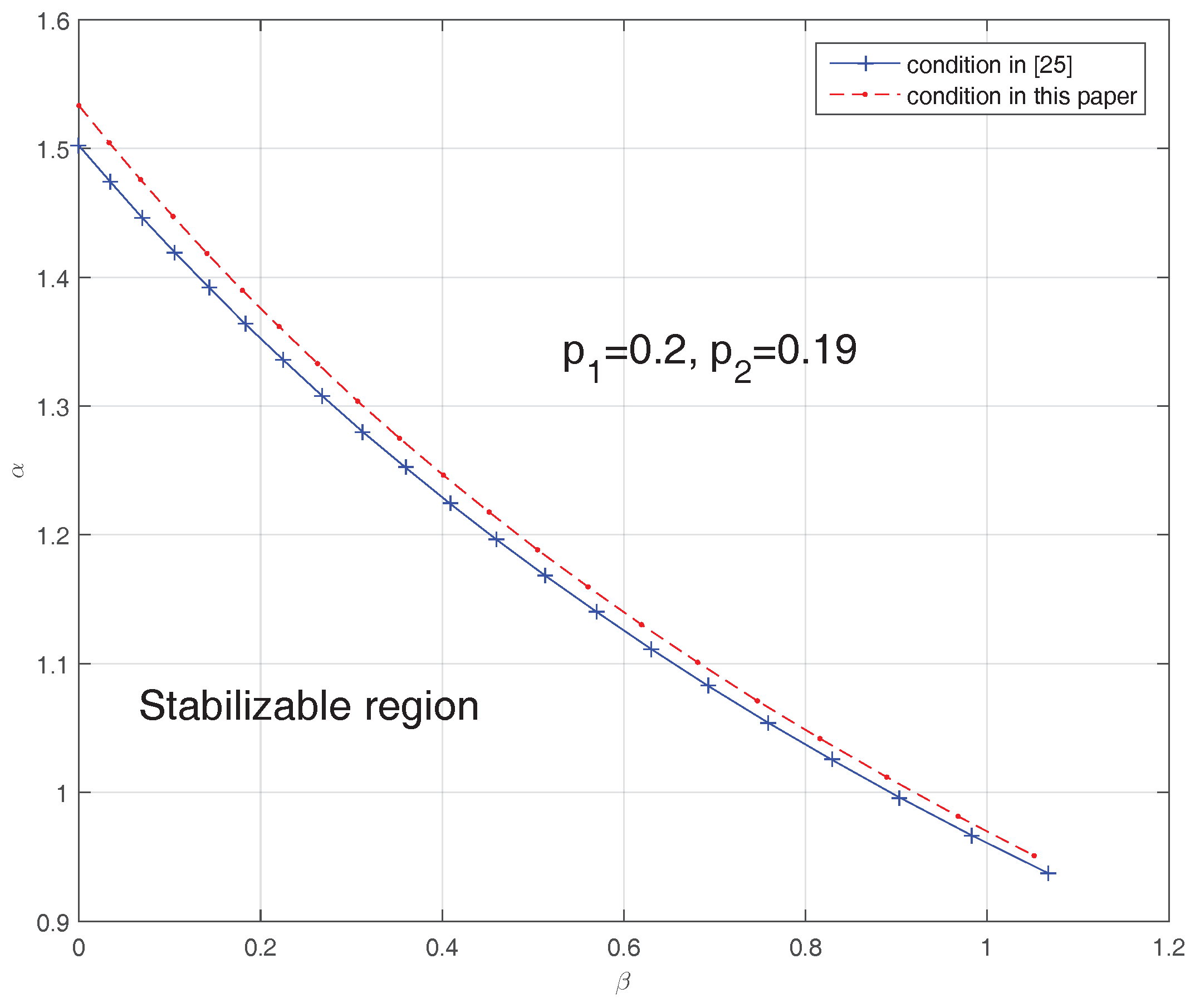
Example 1.

Consider the following system with a time-varying delay

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{x}(t)& =\left[\begin{array}{cc}0.39& -0.038\\ 1& 0\end{array}\right]x(t)+\left[\begin{array}{c}1\\ 0\end{array}\right]u(t-\tau (t)),\hfill \\ \hfill y(t)& =\left[\begin{array}{cc}0& 1\end{array}\right]x(t).\hfill \end{array}\end{array}$$

(50)

The transfer function of the delay-free plant is

$$P_0(s)=\frac{1}{(s-0.2)(s-0.19)},$$

with two unstable poles, $p_1=0.2$, and $p_2=0.19$. Suppose that the input $u(t)$ is a square wave signal, given by $u(t)=sgn\left(sin(t)\right)$, and the time-varying delay is

$$\begin{array}{c}\hfill \tau (t)=\alpha \left(1-sin\left(\beta t\right)\right).\end{array}$$

(51)

Then, the maximal delay range and variation rate are $h=2\alpha ,$ and $\delta =\alpha \beta .$ The upper bound of the delay margin can be computed to be $\overline{h}=2.5$ by Theorem 1, which means that there exists no controller $K(s)$ that can stabilize system (50) with time-varying delay (51) if $\alpha >2.5$. On the other hand, the lower bound can be calculated according to Theorem 2. Figure 5 shows that our stabilizable region in terms of of $(\beta ,\alpha )$ improves that in [23].

Let us then consider a specific delay function with $\beta =0.1$, ${\displaystyle \alpha =1.4}$; that is,

$$\tau (t)=1.4(1-sin(0.1t)).$$

Since $(0.1,1.4)$ lies in the stabilizability region, system (50) can be stabilized by some controller $K(s)$; indeed, the optimal $H_{\infty }$ controller can be found by solving the $H_{\infty }$ control problem in Label (42) with rational approximant in Label (48), as

$$\begin{array}{c}\hfill K(s)=\frac{1.492\times {10}^7(s+0.714)\left(s^2+0.865s+0.906\right)}{(s+69.15)(s+0.978)\left(s^2+1.041s+0.995\right)}\frac{(s-0.0695)\left(s^2+0.865s+0.906\right)}{(s+0.667)\left(s^2+937.2s+2.393\times {10}^5\right)}.\end{array}$$

(52)

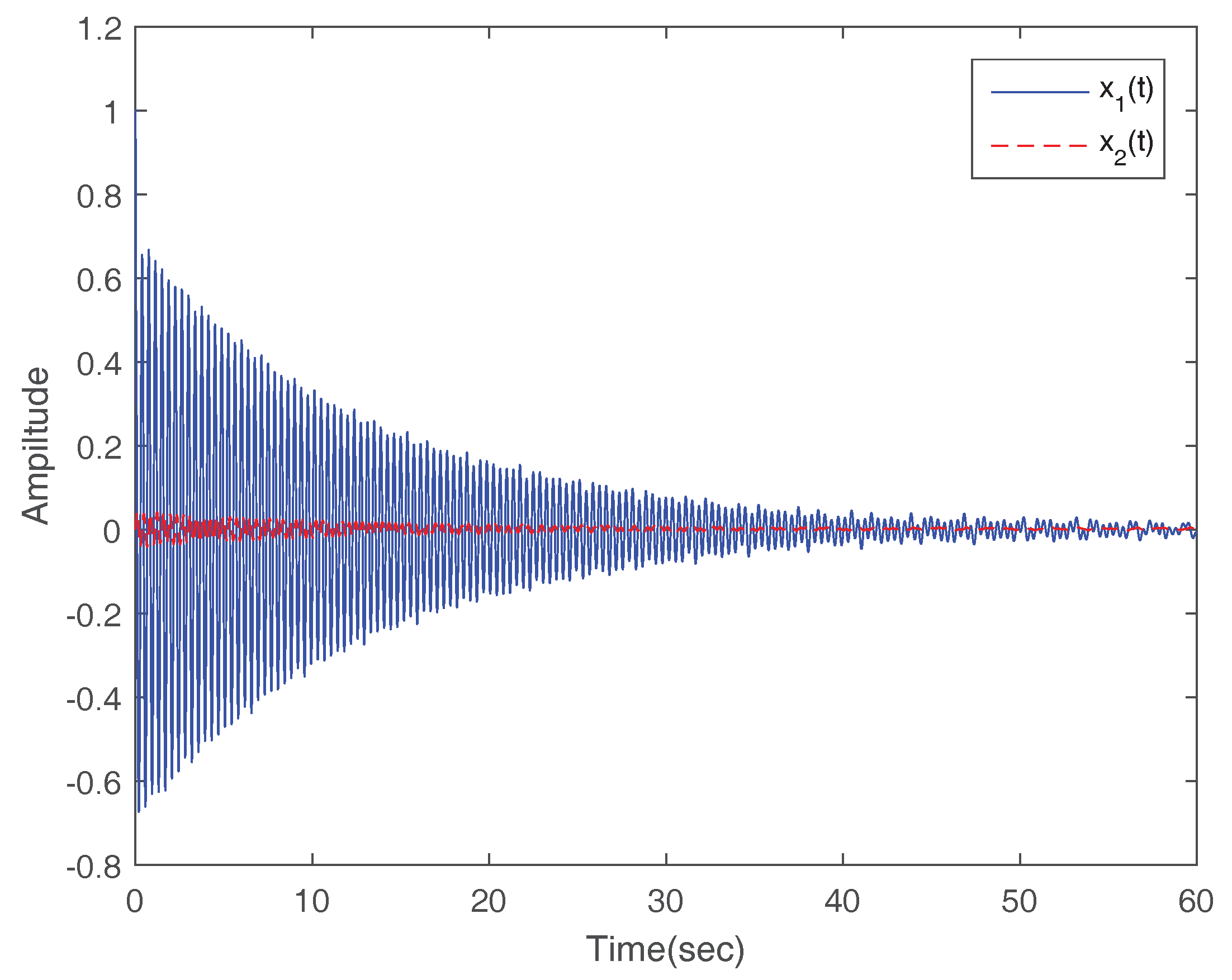
Figure 6 exhibits a stable state response, where the system is excited by the unit step input $u(t)$.

5. Conclusions

In this paper, we develop readily computational upper and lower bounds on the robust stabilization margin for LTI systems with time-varying delays. By employing a bilinear transformation, the upper bounds for systems with constant delays are extended to systems with time-varying delays, while the lower bounds are investigated by means of analytical interpolations and rational approximations. Moreover, our results yield analytical expressions for more specific plants, such as systems with unstable poles and nonminimum phase zeros, demonstrating the significant dependencies of the upper and lower stabilization bounds on those poles and zeros. Furthermore, the $H_{\infty }$ optimal stabilizing controller can be obtained directly from our stabilization conditions. These results are efficiently computable, less conservative and conceptually appealing, which can be applied directly to SISO systems, while the delay region can be estimated by solving an LMI problem for MIMO systems with time-varying delays.