Invariant Solutions for a Class of Perturbed Nonlinear Wave Equations
Abstract
:1. Introduction
2. Perturbed Nonlinear (1 + 1)-Dimension Wave Equation
Approximate Invariant Solution
3. Perturbed Nonlinear (2 + 1)-Dimension Wave Equation
3.1. Exact Symmetries
3.2. Approximate Symmetries
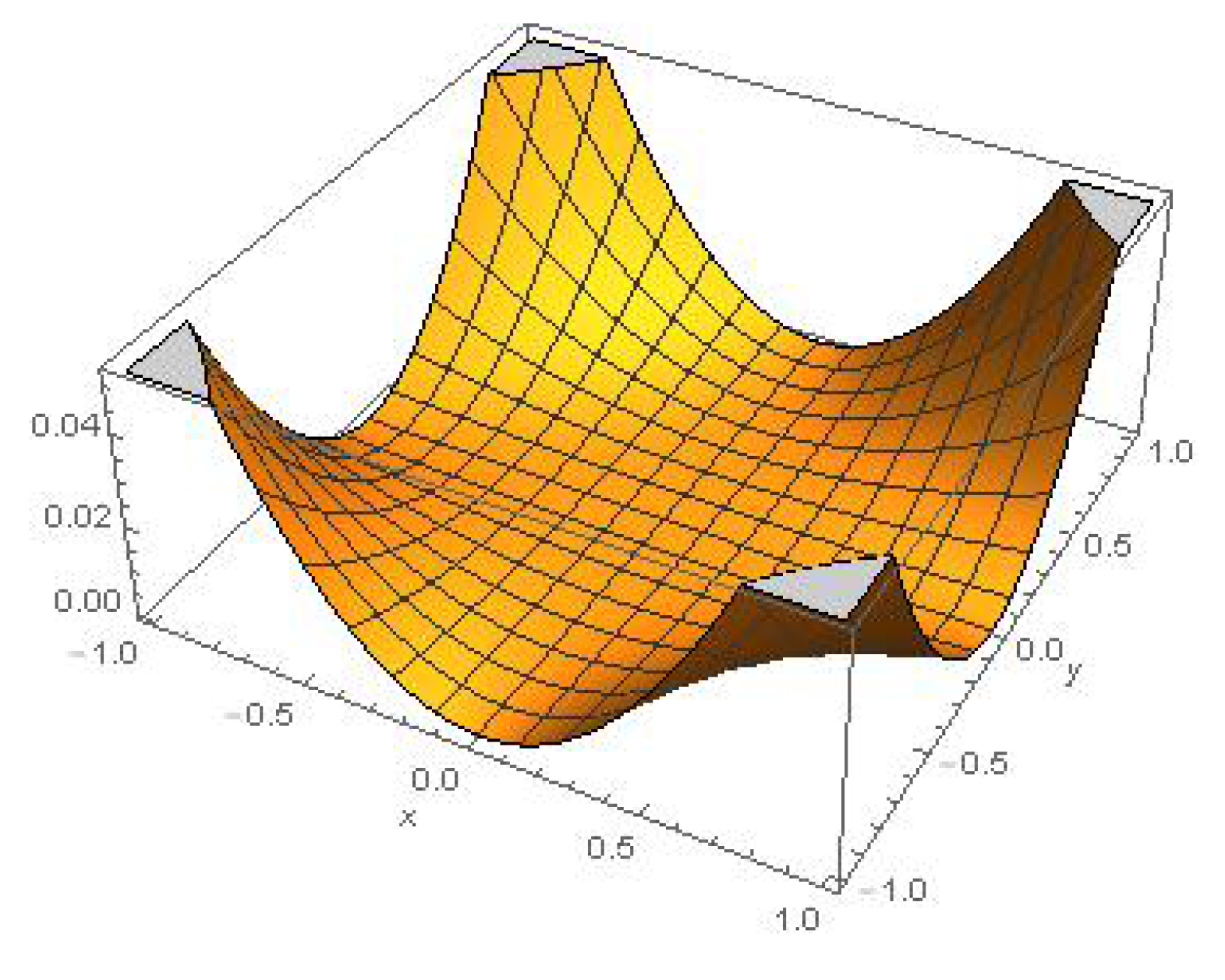
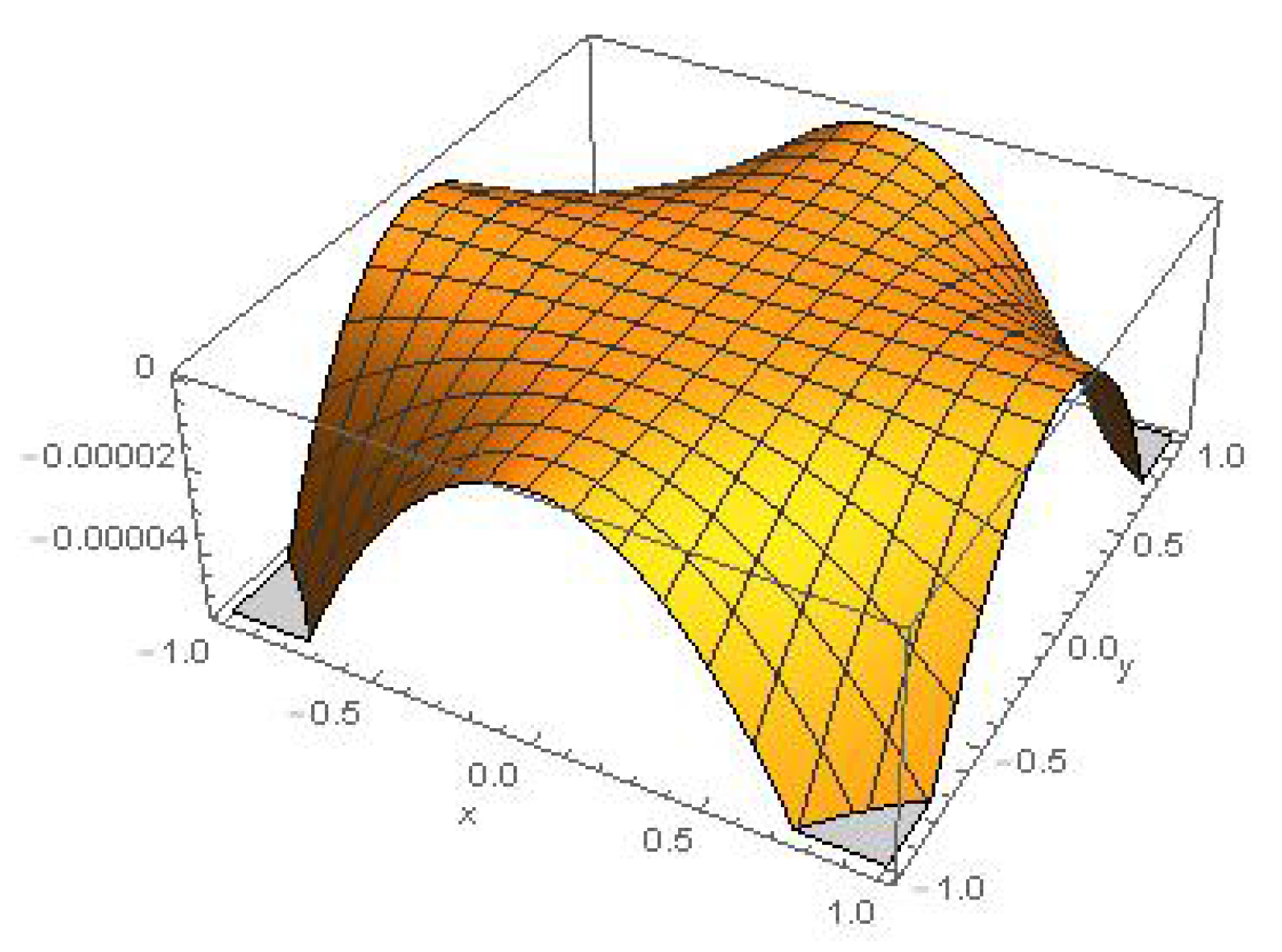
3.3. Approximate Invariant Solutions
4. Nonlinear Wave Equation with a Forcing Term
4.1. Approximate Symmetries by Method I
4.2. Approximate Symmetries by Method II
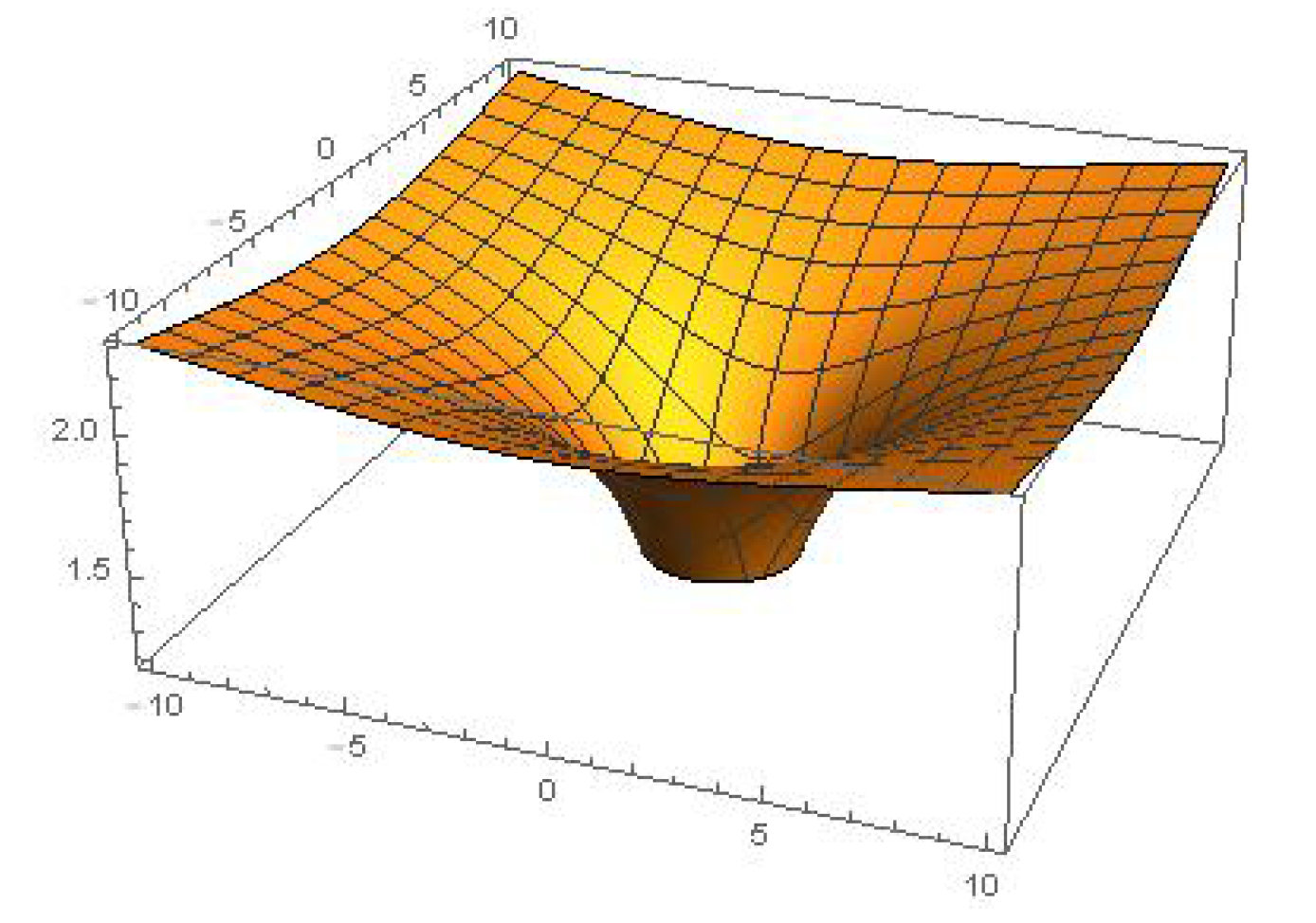
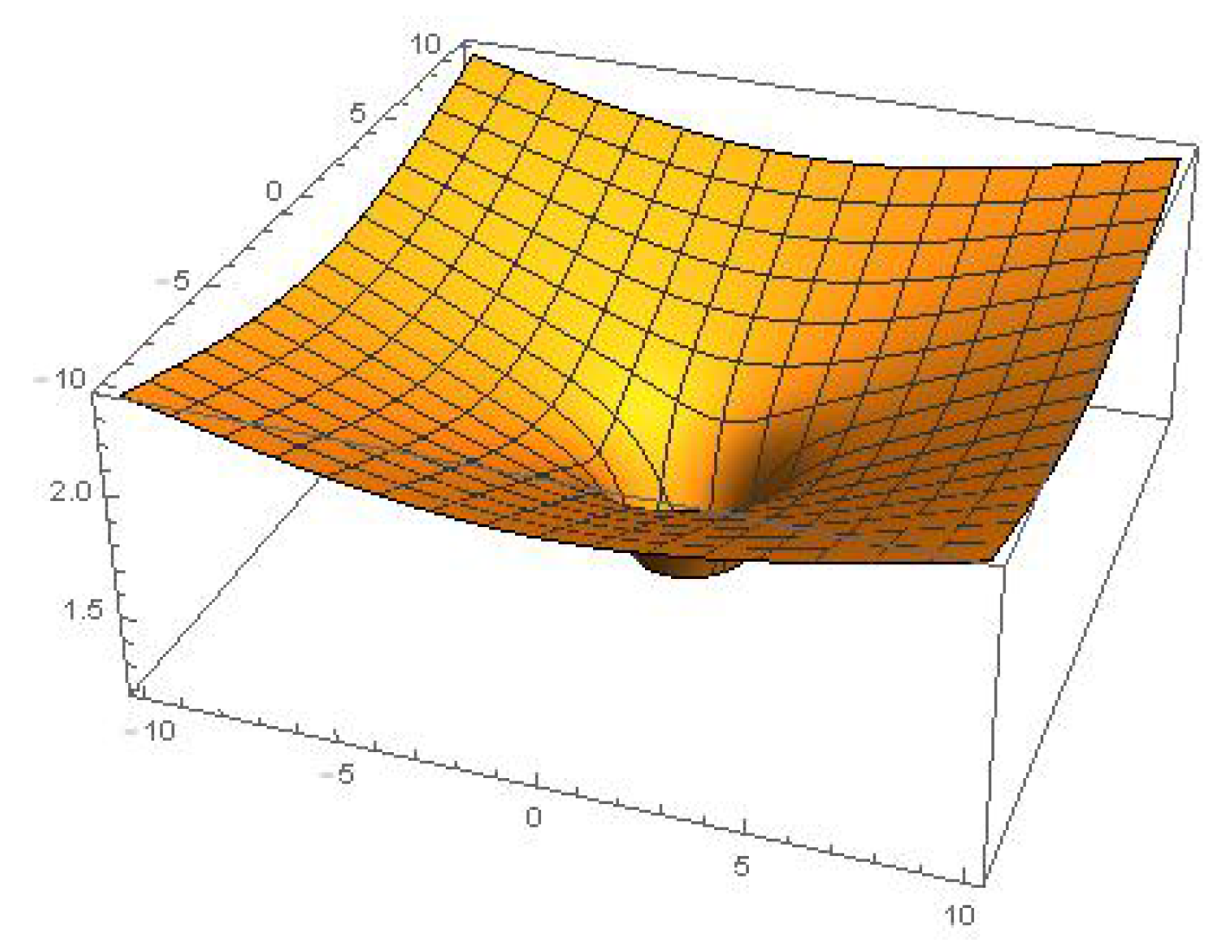
4.3. Approximate Invariant Solution
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baikov, V.A.; Gazizov, R.K.; Ibragimov, N. Approximate symmetries. Mat. Sb. 1988, 178, 435–450. [Google Scholar] [CrossRef]
- Fushchich, W.; Shtelen, W. On approximate symmetry and approximate solutions of the nonlinear wave equation with a small parameter. J. Phys. A Math. Gen. 1989, 22, L887. [Google Scholar] [CrossRef]
- Gazizov, R.K. Lie algebras of approximate symmetries. J. Nonlinear Math. Phys. 1996, 3, 96–101. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Kara, A.; Zaman, F.D. Invariant solutions of certain nonlinear evolution type equations with small parameters. Appl. Math. Comput. 2006, 182, 1075–1082. [Google Scholar] [CrossRef]
- Jefferson, G.; Carminati, J. Asp: Automated symbolic computation of approximate symmetries of differential equations. Comput. Phys. Commun. 2013, 184, 1045–1063. [Google Scholar] [CrossRef]
- Li, X.; Qian, S. Approximate symmetry reduction to the perturbed coupled kdv equations derived from two-layer fluids. Math. Sci. 2012, 6, 13. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Chen, Y.F.; Yong, X.L. Classification and approximate solutions to a class of perturbed nonlinear wave equations. Commun. Theor. Phys. 2009, 52, 769–772. [Google Scholar]
- Pakdemirli, M.; Yürüsoy, M.; Dolapci, I. Comparison of approximate symmetry methods for differential equations. Acta Appl. Math. 2004, 80, 243–271. [Google Scholar] [CrossRef]
- Valenti, A. Approximate symmetries for a model describing dissipative media. In Proceedings of the 10th International Conference in Modern Group Analysis, Larnaca, Cyprus, 24–31 October 2004; Volume 236, p. 243. [Google Scholar]
- Ma, W.X. A refined invariant subspace method and applications to evolution equations. Sci. China Math. 2012, 55, 1769–1778. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, B.; Chen, Y. Second-order approximate symmetry classification and optimal system of a class of perturbed nonlinear wave equations. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2709–2719. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Yong, X.-L.; Chen, Y.-F. A new method to obtain approximate symmetry of nonlinear evolution equation from perturbations. Chin. Phys. B 2009, 18, 2629–2633. [Google Scholar]
- Baikov, V.; Gazizov, R.; Ibragimov, N. Approximate transformation groups and deformations of symmetry lie algebras. In CRC Handbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1996; Volume 3. [Google Scholar]
- Grigotieve, Y.N.; Ibragimov, N.H.; Kovalev, V.F.; Meleshko, S.V. Symmetries of Integro-Differential Equations with Application in Mechanics and Plasma Physics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Bokhari, A.H.; Kara, A.; Karim, M.; Zaman, F.D. Invariance analysis and variational conservation laws for the wave equation on some manifolds. Int. J. Theor. Phys. 2009, 48, 1919–1928. [Google Scholar] [CrossRef]
- Ahmad, A.; Bokhari, A.H.; Kara, A.; Zaman, F.D. A complete symmetry classification and reduction of some classes of the nonlinear (1-2) wave equation. Quaest. Math. 2010, 33, 75–94. [Google Scholar] [CrossRef]
- Euler, M.; Euler, N.; Kohler, A. On the construction of approximate solutions for a multidimensional nonlinear heat equation. J. Phys. A Math. Gen. 1994, 27, 2083–2092. [Google Scholar] [CrossRef]
- Euler, N.; Euler, M. Symmetry properties of the approximations of multidimensional generalized van der pol equations. J. Nonlinear Math. Phys. 1994, 1, 41–59. [Google Scholar] [CrossRef]
- Ma, W.X.; Fuchssteiner, B. Integrable theory of the perturbation equations. Chaos Soliton Fractal 1996, 7, 1227–1250. [Google Scholar] [CrossRef]
- Ma, W.X. A bi-Hamiltonian formulation for triangular systems by perturbations. J. Math. Phys. 2002, 43, 1408–1421. [Google Scholar] [CrossRef]
- Ibragimov, N.H.; Kovalev, V.F. Approximate and Renormgroup Symmetries; Springer: Berlin, Germany, 2009. [Google Scholar]
- Murray, J.D. Asymptotic analysi. In Applied Mathematical Sciences; Springer: New York, NY, USA, 1984; Volume 1. [Google Scholar]
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, W.A.; Zaman, F.D.; Saleh, K. Invariant Solutions for a Class of Perturbed Nonlinear Wave Equations. Mathematics 2017, 5, 59. https://doi.org/10.3390/math5040059
Ahmed WA, Zaman FD, Saleh K. Invariant Solutions for a Class of Perturbed Nonlinear Wave Equations. Mathematics. 2017; 5(4):59. https://doi.org/10.3390/math5040059
Chicago/Turabian StyleAhmed, Waheed A., F. D. Zaman, and Khairul Saleh. 2017. "Invariant Solutions for a Class of Perturbed Nonlinear Wave Equations" Mathematics 5, no. 4: 59. https://doi.org/10.3390/math5040059




