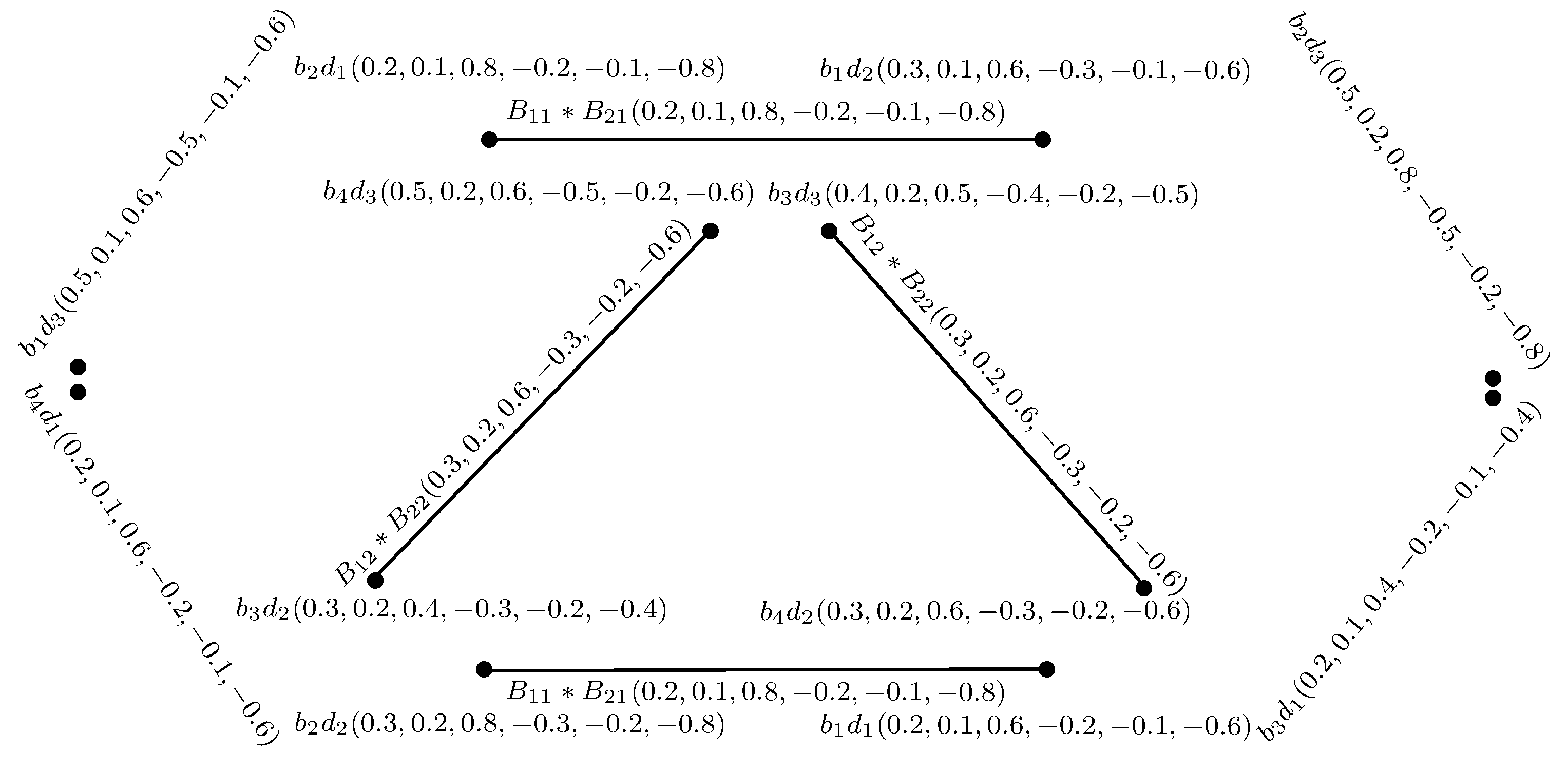Graph Structures in Bipolar Neutrosophic Environment

Abstract

A bipolar single-valued neutrosophic (BSVN) graph structure is a generalization of a bipolar fuzzy graph. In this research paper, we present certain concepts of BSVN graph structures. We describe some operations on BSVN graph structures and elaborate on these with examples. Moreover, we investigate some related properties of these operations.

1. Introduction

Fuzzy graphs are mathematical models for dealing with combinatorial problems in different domains, including operations research, optimization, computer science and engineering. In 1965, Zadeh [1] proposed fuzzy set theory to deal with uncertainty in abundant meticulous real-life phenomena. Fuzzy set theory is affluently applicable in real-time systems consisting of information with different levels of precision. Subsequently, Atanassov [2] introduced the idea of intuitionistic fuzzy sets in 1986. However, for many real-life phenomena, it is necessary to deal with the implicit counter property of a particular event. Zhang [3] initiated the concept of bipolar fuzzy sets in 1994. Evidently bipolar fuzzy sets and intuitionistic fuzzy sets seem to be similar, but they are completely different sets. Bipolar fuzzy sets have large number of applications in image processing and spatial reasoning. Bipolar fuzzy sets are more practical, advantageous and applicable in real-life phenomena. However, both bipolar fuzzy sets and intuitionistic fuzzy sets cope with incomplete information, because they do not consider indeterminate or inconsistent information that clearly appears in many systems of different fields, including belief systems and decision-support systems. Smarandache [4] introduced neutrosophic sets as a generalization of fuzzy sets and intuitionistic fuzzy sets. A neutrosophic set has three constituents: truth membership, indeterminacy membership and falsity membership, for which each membership value is a real standard or non-standard subset of the unit interval $[0^{-},1^{+}]$. In real-life problems, neutrosophic sets can be applied more appropriately by using the single-valued neutrosophic sets defined by Smarandache [4] and Wang et al. [5]. Deli et al. [6] considered bipolar neutrosophic sets as a generalization of bipolar fuzzy sets. They also studied some operations and applications in decision-making problems.

On the basis of Zadeh’s fuzzy relations [7], Kauffman defined fuzzy graphs [8]. In 1975, Rosenfeld [9] discussed a fuzzy analogue of different graph-theoretic ideas. Later on, Bhattacharya [10] gave some remarks on fuzzy graphs in 1987. Akram [11] first introduced the notion of bipolar fuzzy graphs. In 2011, Dinesh and Ramakrishnan [12] studied fuzzy graph structures and discussed their properties. In 2016, Akram and Akmal [13] proposed the concept of bipolar fuzzy graph structures. Certain concepts on graphs have been discussed in [14,15,16,17,18,19]. Ye [20,21,22] considered several applications of single-valued neutrosophic sets. Inthis research paper, we present certain concepts of bipolar single-valued neutrosophic graph structures (BSVNGSs). We introduce some operations on BSVNGSs and elaborate on these with examples. Moreover, we investigate some relevant and remarkable properties of these operators.

We have used standard definitions and terminologies in this paper. For other notations, terminologies and applications not mentioned in the paper, the readers are referred to [23,24,25,26,27,28,29].

2. Bipolar Single-Valued Neutrosophic Graph Structures

Definition 1.

[4] A neutrosophic set N on a non-empty set V is an object of the form

$$N=\{(v,T_N\left(v\right),I_N\left(v\right),F_N\left(v\right)):v\in V\}$$

where $T_N,I_N,F_N:V\to [0^{-},1^{+}]$ and there is no restriction on the sum of $T_N\left(v\right)$, $I_N\left(v\right)$ and $F_N\left(v\right)$ for all $v\in V$.

Definition 2.

[5] A single-valued neutrosophic set N on a non-empty set V is an object of the form

$$N=\{(v,T_N\left(v\right),I_N\left(v\right),F_N\left(v\right)):v\in V\}$$

where $T_N,I_N,F_N:V\to [0,1]$ and the sum of $T_N\left(v\right)$, $I_N\left(v\right)$ and $F_N\left(v\right)$ is confined between 0 and 3 for all $v\in V$.

Definition 3.

[23] A BSVN set on a non-empty set V is an object of the form

$$B=\{(v,T_B^P\left(v\right),I_B^P\left(v\right),F_B^P\left(v\right),T_B^N\left(v\right),I_B^N\left(v\right),F_B^N\left(v\right)):v\in V\}$$

where $T_B^P,I_B^P,F_B^P:V\to [0,1]$ and $T_B^N,I_B^N,F_B^N:V\to [-1,0]$. The positive values $T_B^P\left(v\right),I_B^P\left(v\right)$ and $F_B^P\left(v\right)$ denote the truth, indeterminacy and falsity membership values of an element $v\in V$, whereas negative values $T_B^N\left(v\right),I_B^N\left(v\right)$ and $F_B^N\left(v\right)$ indicate the implicit counter property of truth, indeterminacy and falsity membership values of an element $v\in V$.

Definition 4.

[23] A BSVN graph on a non-empty set V is a pair $G=(B,R)$, where B is a BSVN set on V and R is a BSVN relation in V such that

$$T_R^P(b,d)\le T_B^P\left(b\right)\wedge T_B^P\left(d\right),I_R^P(b,d)\le I_B^P\left(b\right)\wedge I_B^P\left(d\right),F_R^P(b,d)\le F_B^P\left(b\right)\vee F_B^P\left(d\right),$$

$$T_R^N(b,d)\ge T_B^N\left(b\right)\vee T_B^N\left(d\right),I_R^N(b,d)\ge I_B^N\left(b\right)\vee I_B^N\left(d\right),F_R^N(b,d)\ge F_B^N\left(b\right)\wedge F_B^N\left(d\right)$$

$forallb,d\in V.$

We now define the BSVNGS.

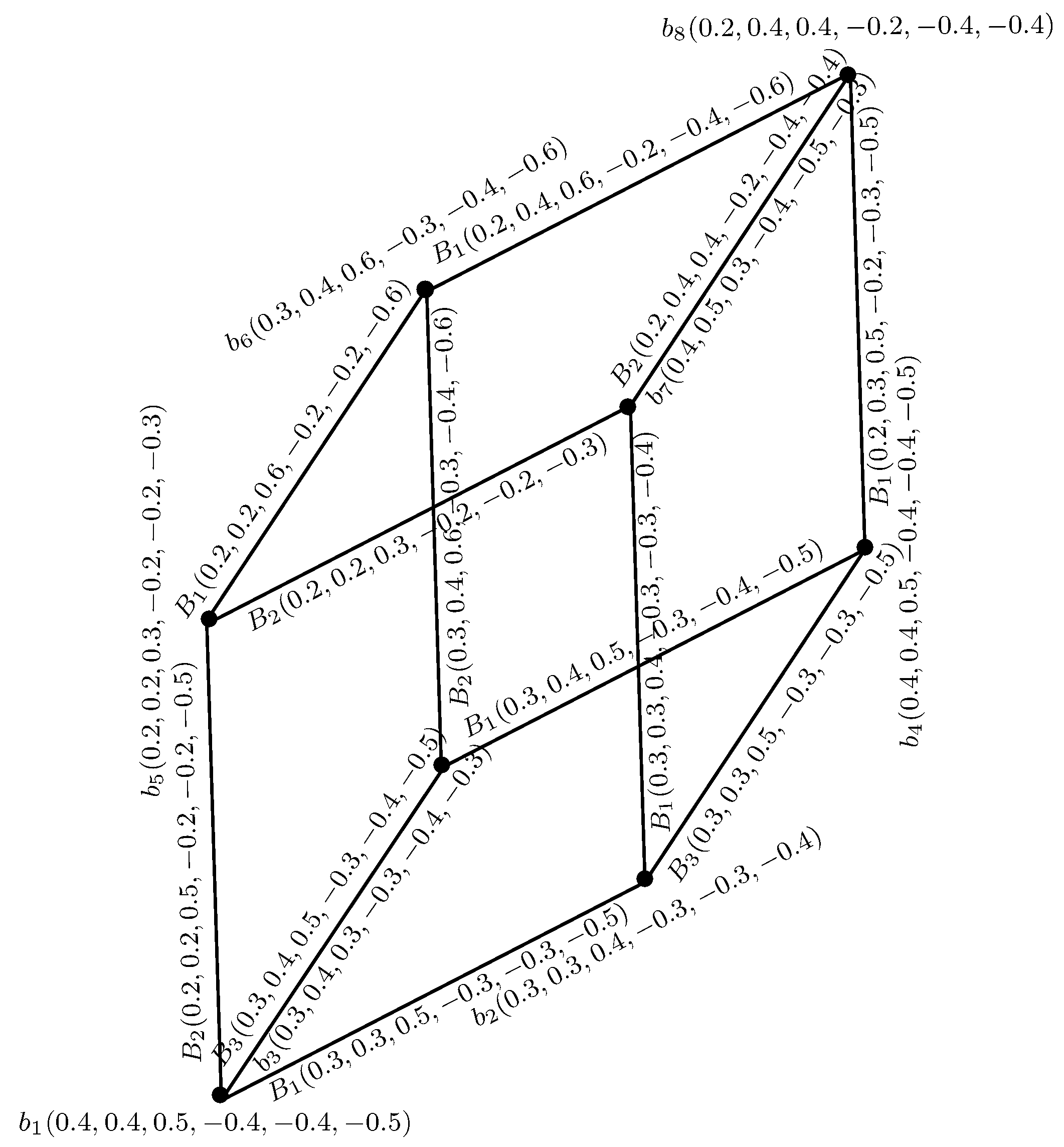
Definition 5.

[30] A BSVNGS of a graph structure ${\check{G}}_s$ = $(V,V_1,V_2,\dots ,V_m)$ is denoted by ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$, where $B=<b,T^P\left(b\right),I^P\left(b\right),F^P\left(b\right),T^N\left(b\right),I^N\left(b\right),F^N\left(b\right)>$ is a BSVN set on the set V and $B_k=<(b,d),T_k^P(b,d),I_k^P(b,d),F_k^P(b,d),T_k^N(b,d),I_k^N(b,d),F_k^N(b,d)>$ are the BSVN sets on $V_k$ such that

$$T_k^P(b,d)\le min\{T^P\left(b\right),T^P\left(d\right)\},I_k^P(b,d)\le min\{I^P\left(b\right),I^P\left(d\right)\},F_k^P(b,d)\le max\{F^P\left(b\right),F^P\left(d\right)\},$$

$$T_k^N(b,d)\ge max\{T^N\left(b\right),T^N\left(d\right)\},I_k^N(b,d)\ge max\{I^N\left(b\right),I^N\left(d\right)\},F_k^N(b,d)\ge min\{F^N\left(b\right),F^N\left(d\right)\}$$

for all $b,d\in V.$ Note that $0\le T_k^P(b,d)+I_k^P(b,d)+F_k^P(b,d)\le 3$, $-3\le T_k^N(b,d)+I_k^N(b,d)+F_k^N(b,d)\le 0$ for all $(b,d)\in V_k$, and $(b,d)$ represents an edge between two vertices b and d. In this paper we use $bd$ in place of $(b,d)$.

Example 1.

Consider a graph structure ${\check{G}}_s=(V,V_1,V_2,V_3)$ such that $V=\{b_1,b_2,b_3,b_4,b_5,b_6,b_7,b_8\}$, $V_1=\{b_1{b}_2,b_2{b}_7,b_4{b}_8,b_6{b}_8,b_5{b}_6,b_3{b}_4\}$, $V_2=\{b_1{b}_5,b_5{b}_7,b_3{b}_6,b_7{b}_8\}$, and $V_3=\{b_1{b}_3,b_2{b}_4\}$. Let B be a BSVN set on V given in

Table 1. Bipolar single-valued neutrosophic (BSVN) set B on vertex set V.

B	${\mathit{b}}_1$	${\mathit{b}}_2$	${\mathit{b}}_3$	${\mathit{b}}_4$	${\mathit{b}}_5$	${\mathit{b}}_6$	${\mathit{b}}_7$	${\mathit{b}}_8$
$T^P$	0.5	0.4	0.4	0.5	0.3	0.4	0.5	0.3
$I^P$	0.4	0.3	0.4	0.4	0.2	0.4	0.5	0.4
$F^P$	0.6	0.5	0.4	0.6	0.4	0.7	0.4	0.5
$T^N$	−0.5	−0.4	−0.4	−0.5	−0.3	−0.4	−0.5	−0.3
$I^N$	−0.4	−0.3	−0.4	−0.4	−0.2	−0.4	−0.5	−0.4
$F^N$	−0.6	−0.5	−0.4	−0.6	−0.4	−0.7	−0.4	−0.5

and $B_1$, $B_2$ and $B_3$ be BSVN sets on $V_1$, $V_2$ and $V_3$, respectively, given in

Table 2. BSVN sets $B_1$, $B_2$ and $B_3$.

${\mathit{B}}_1$	${\mathit{b}}_1{\mathit{b}}_2$	${\mathit{b}}_2{\mathit{b}}_7$	${\mathit{b}}_4{\mathit{b}}_8$	${\mathit{b}}_6{\mathit{b}}_8$	${\mathit{b}}_5{\mathit{b}}_6$	${\mathit{b}}_3{\mathit{b}}_4$	${\mathit{B}}_2$	${\mathit{b}}_1{\mathit{b}}_5$	${\mathit{b}}_5{\mathit{b}}_7$	${\mathit{b}}_3{\mathit{b}}_6$	${\mathit{b}}_7{\mathit{b}}_8$	${\mathit{B}}_3$	${\mathit{b}}_1{\mathit{b}}_3$	${\mathit{b}}_2{\mathit{b}}_4$
$T^P$	0.4	0.4	0.3	0.3	0.3	0.4	$T^P$	0.3	0.3	0.4	0.3	$T^P$	0.4	0.4
$I^P$	0.3	0.3	0.4	0.4	0.2	0.4	$I^P$	0.2	0.2	0.4	0.4	$I^P$	0.4	0.3
$F^P$	0.6	0.5	0.6	0.7	0.7	0.6	$F^P$	0.6	0.4	0.7	0.5	$F^P$	0.6	0.6
$T^N$	−0.4	−0.4	−0.3	−0.3	−0.3	−0.4	$T^N$	−0.3	−0.3	−0.4	−0.3	$T^N$	−0.4	−0.4
$I^N$	−0.3	−0.3	−0.4	−0.4	−0.2	−0.4	$I^N$	−0.2	−0.2	−0.4	−0.4	$I^N$	−0.4	−0.3
$F^N$	−0.6	−0.5	−0.6	−0.7	−0.7	−0.6	$F^N$	−0.6	−0.4	−0.7	−0.5	$F^N$	−0.6	−0.6

.

By direct calculations, it is easy to show that ${\check{G}}_{bn}$ = $(B,B_1,B_2,B_3)$ is a BSVNGS. This BSVNGS is shown in Figure 1. Generated with LaTeXDraw 2.0.8 on Saturday March 11 20:30:24 PKT 2017.

Definition 6.

A BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ is called a $B_k$-cycle if $(supp\left(B\right),supp\left(B_1\right)$,$supp\left(B_2\right),\dots ,supp\left(B_m\right))$ is a $B_k$-cycle.

Example 2.

Consider a BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ as shown in Figure 2.

${\check{G}}_{bn}$ is a $B_1$-cycle, as $(supp\left(B\right),supp\left(B_1\right),supp\left(B_2\right))$, is a $B_1$-cycle, that is, $b_2$-$b_3$-$b_4$-$b_5$-$b_2$.

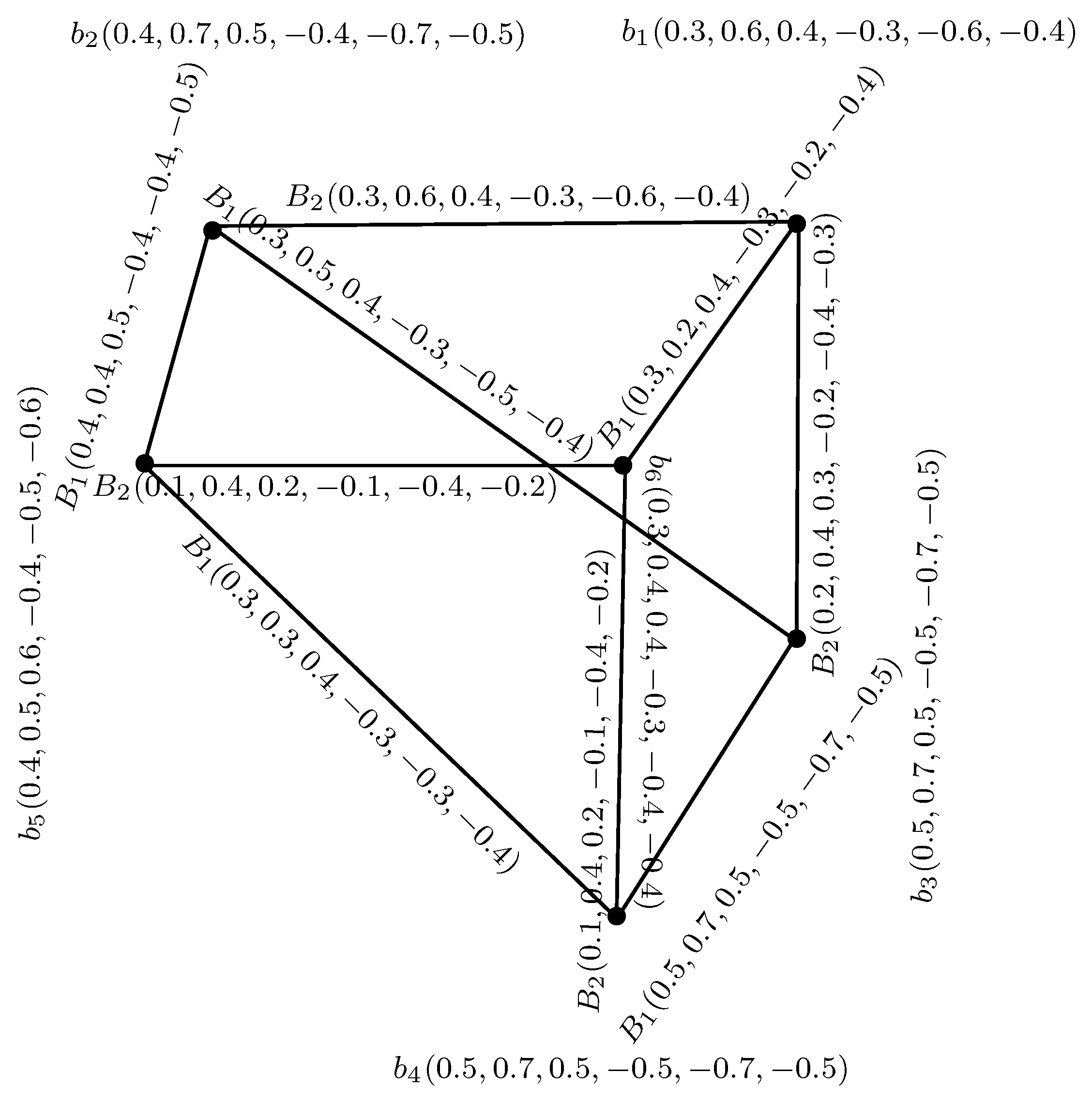
Definition 7.

A BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ is a BSVN fuzzy $B_k$-cycle (for any k) if ${\check{G}}_{bn}$ is a $B_k$-cycle and no unique $B_k$-edge $bd$ exists in ${\check{G}}_{bn}$, such that $T_{B_k}^P\left(bd\right)=min\{T_{B_k}^P\left(ef\right):ef\in B_k=supp\left(B_k\right)\}$, $I_{B_k}^P\left(bd\right)=min\{I_{B_k}^P\left(ef\right):ef\in B_k=supp\left(B_k\right)\}$, $F_{B_k}^P\left(bd\right)=max\{F_{B_k}^P\left(ef\right):ef\in B_k=supp\left(B_k\right)\}$, $T_{B_k}^N\left(bd\right)=max\{T_{B_k}^N\left(ef\right):ef\in B_k=supp\left(B_k\right)\}$, $I_{B_k}^N\left(bd\right)=max\{I_{B_k}^N\left(ef\right):ef\in B_k=supp\left(B_k\right)\}$ or $F_{B_k}^N\left(bd\right)=min\{F_{B_k}^N\left(ef\right):ef\in B_k=supp\left(B_k\right)\}.$

Example 3.

Consider a BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ as depicted in Figure 3.

$T_{B_2}^P\left(bd\right)=min\{T_{B_2}^P\left(ef\right):ef\in B_2=supp\left(B_2\right)\}$, $I_{B_2}^P\left(bd\right)=min\{I_{B_2}^P\left(ef\right):ef\in B_2=supp\left(B_2\right)\}$, $F_{B_2}^P\left(bd\right)=max\{F_{B_2}^P\left(ef\right):ef\in B_2=supp\left(B_2\right)\}$, $T_{B_2}^N\left(bd\right)=max\{T_{B_2}^N\left(ef\right):ef\in B_2=supp\left(B_2\right)\}$, $I_{B_2}^N\left(bd\right)=max\{I_{B_2}^N\left(ef\right):ef\in B_2=supp\left(B_2\right)\}$ or $F_{B_2}^N\left(bd\right)=min\{F_{B_2}^N\left(ef\right):ef\in B_2=supp\left(B_2\right)\}.$

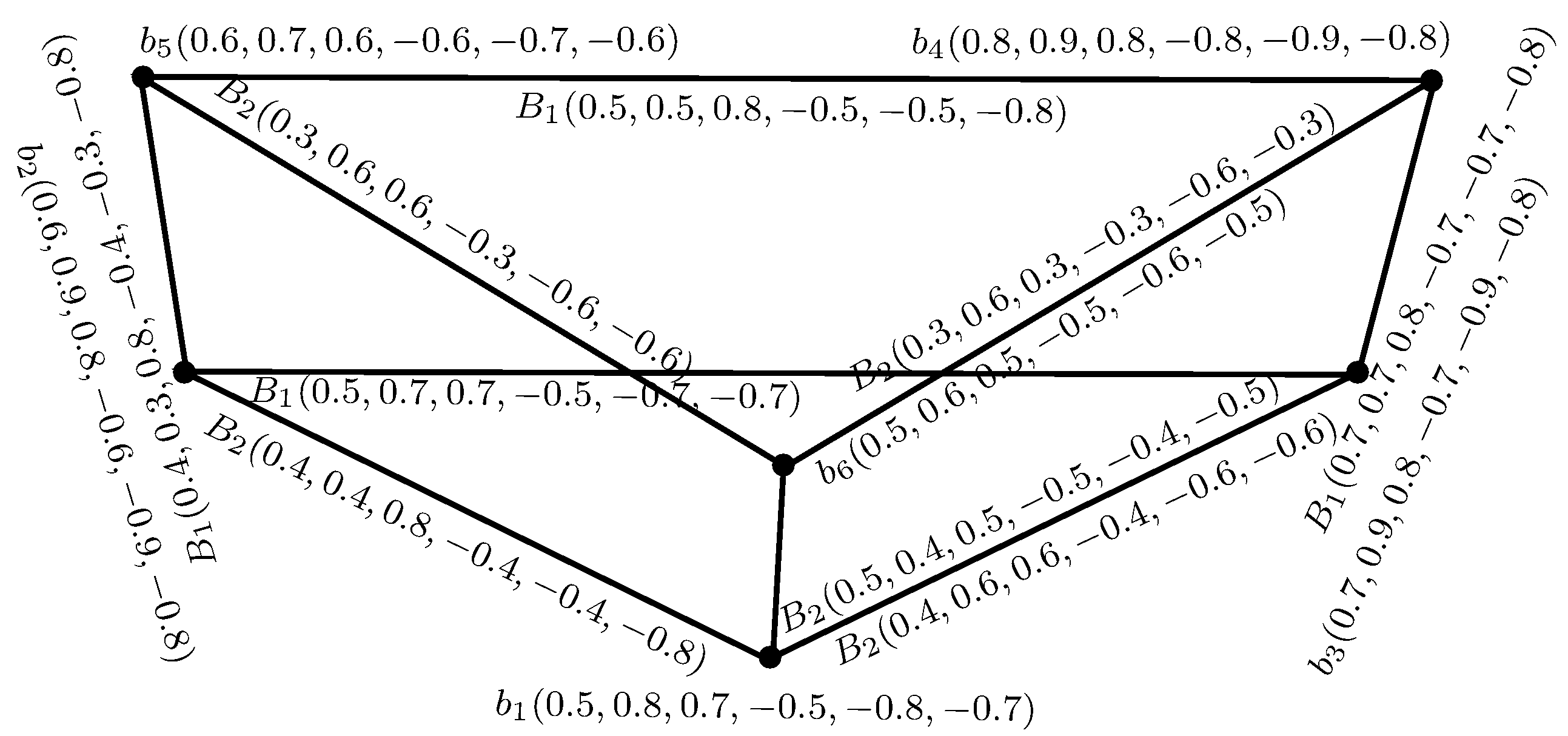
Definition 8.

A sequence of vertices (distinct) in a BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ is called a $B_k$-path, that is, $b_1,b_2,\dots ,b_m$, such that $b_{k-1}{b}_k$ is a BSVN $B_k$-edge, for all $k=2,\dots ,m$.

Example 4.

Consider a BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ as represented in Figure 4.

In this BSVNGS, the sequence of distinct vertices $b_1,b_4,b_3,b_2$ is a BSVN $B_2$-path.

Definition 9.

Let ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ be a BSVNGS. The positive truth strength $T^P.P_{B_k}$, positive falsity strength $F^P.P_{B_k}$, and positive indeterminacy strength $I^P.P_{B_k}$ of a $B_k$-path, $P_{B_k}$ = $b_1,b_2,\dots ,b_n$, are defined as

$$T^P.P_{B_k}=\underset{h=2}{\overset{n}{\bigwedge }}[T_{B_k}^P\left(b_{h-1}{b}_h\right)],I^P.P_{B_k}=\underset{h=2}{\overset{n}{\bigwedge }}[I_{B_k}^P\left(b_{h-1}{b}_h\right)],F^P.P_{B_k}=\underset{h=2}{\overset{n}{\bigvee }}[F_{B_k}^P\left(b_{h-1}{b}_h\right)]$$

Similarly, the negative truth strength $T^N.P_{B_k}$, negative falsity strength $F^N.P_{B_k}$, and negative indeterminacy strength $I^N.P_{B_k}$ of a $B_k$-path are defined as

$$T^N.P_{B_k}=\underset{h=2}{\overset{n}{\bigvee }}[T_{B_k}^N\left(b_{h-1}{b}_h\right)],I^N.P_{B_k}=\underset{h=2}{\overset{n}{\bigvee }}[I_{B_k}^N\left(b_{h-1}{b}_h\right)],F^N.P_{B_k}=\underset{h=2}{\overset{n}{\bigwedge }}[F_{B_k}^N\left(b_{h-1}{b}_h\right)]$$

Example 5.

Consider a BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2,B_3)$ as shown in Figure 5.

In this BSVNGS, there is a $B_1$-path, that is, $P_{B_1}$ = $b_5,b_6,b_8$,$b_4,b_3$. Thus, $T^N.P_{B_1}$= $-0.2$, $I^N.P_{B_1}$= $-0.2$, $F^N.P_{B_2}$= $-0.6$, $T^P.P_{B_1}$ = $0.2$, $I^P.P_{B_1}$ = $0.2$ and $F^P.P_{B_2}$ = $0.6$.

Definition 10.

Let ${\check{G}}_{bn}$ = $(B,B_1,B_2,\cdots ,B_m)$ be a BSVNGS. Then

• The $B_k$-positive strength of connectedness of truth between two nodes b and d is defined by $T_{B_k}^{P\infty }\left(bd\right)$ = ${\displaystyle \underset{l\ge 1}{\bigvee }}\{T_{B_k}^{Pl}\left(bd\right)\}$, such that $T_{B_k}^{Pl}\left(bd\right)$ = $(T_{B_k}^{Pl-1}\circ T_{B_k}^{P1})\left(bd\right)$ for $l\ge 2$ and $T_{B_k}^{P2}\left(bd\right)$ = $(T_{B_k}^{P1}\circ T_{B_k}^{P1})\left(bd\right)$ = ${\displaystyle \underset{y}{\bigvee }}(T_{B_k}^{P1}\left(by\right)\wedge T_{B_k}^{P1}\left(yd\right))$.
• The $B_k$-positive strength of connectedness of indeterminacy between two nodes b and d is defined by $I_{B_k}^{P\infty }\left(bd\right)$ = ${\displaystyle \underset{l\ge 1}{\bigvee }}\{I_{B_k}^{Pl}\left(bd\right)\}$, such that $I_{B_k}^{Pl}\left(bd\right)$ = $(I_{B_k}^{Pl-1}\circ I_{B_k}^{P1})\left(bd\right)$ for $l\ge 2$ and $I_{B_k}^{P2}\left(bd\right)$ = $(I_{B_k}^{P1}\circ I_{B_k}^{P1})\left(bd\right)$ = ${\displaystyle \underset{y}{\bigvee }}(I_{B_k}^{P1}\left(by\right)\wedge I_{B_k}^{P1}\left(yd\right))$.
• The $B_k$-positive strength of connectedness of falsity between two nodes b and d is defined by $F_{B_k}^{P\infty }\left(bd\right)$ = ${\displaystyle \underset{l\ge 1}{\bigwedge }}\{F_{B_k}^{Pl}\left(bd\right)\}$, such that $F_{B_k}^{Pl}\left(bd\right)$ = $(F_{B_k}^{Pl-1}\circ F_{B_k}^{P1})\left(bd\right)$ for $l\ge 2$ and $F_{B_k}^{P2}\left(bd\right)$ = $(F_{B_k}^{P1}\circ F_{B_k}^{P1})\left(bd\right)$ = ${\displaystyle \underset{y}{\bigwedge }}(F_{B_k}^{P1}\left(by\right)\vee F_{B_k}^{P1}\left(yd\right))$.
• The $B_k$-negative strength of connectedness of truth between two nodes b and d is defined by $T_{B_k}^{N\infty }\left(bd\right)$ = ${\displaystyle \underset{l\ge 1}{\bigwedge }}\{T_{B_k}^{Nl}\left(bd\right)\}$, such that $T_{B_k}^{Nl}\left(bd\right)$ = $(T_{B_k}^{Nl-1}\circ T_{B_k}^{N1})\left(bd\right)$ for $l\ge 2$ and $T_{B_k}^{N2}\left(bd\right)$ = $(T_{B_k}^{N1}\circ T_{B_k}^{N1})\left(bd\right)$ = ${\displaystyle \underset{y}{\bigwedge }}(T_{B_k}^{N1}\left(by\right)\vee T_{B_k}^{N1}\left(yd\right))$.
• The $B_k$-negative strength of connectedness of indeterminacy between two nodes b and d is defined by $I_{B_k}^{N\infty }\left(bd\right)$ = ${\displaystyle \underset{l\ge 1}{\bigwedge }}\{I_{B_k}^{Nl}\left(bd\right)\}$, such that $I_{B_k}^{Nl}\left(bd\right)$ = $(I_{B_k}^{Nl-1}\circ I_{B_k}^{N1})\left(bd\right)$ for $l\ge 2$ and $I_{B_k}^{N2}\left(bd\right)$ = $(I_{B_k}^{N1}\circ I_{B_k}^{N1})\left(bd\right)$ = ${\displaystyle \underset{y}{\bigwedge }}(I_{B_k}^{N1}\left(by\right)\vee I_{B_l}^{N1}\left(yd\right))$.
• The $B_k$-negative strength of connectedness of falsity between two nodes b and d is defined by $F_{B_k}^{N\infty }\left(bd\right)$ = ${\displaystyle \underset{l\ge 1}{\bigvee }}\{F_{B_k}^{Nl}\left(bd\right)\}$, such that $F_{B_k}^{Nl}\left(bd\right)$ = $(F_{B_k}^{Nl-1}\circ F_{B_k}^{N1})\left(bd\right)$ for $l\ge 2$ and $F_{B_k}^{N2}\left(bd\right)$ = $(F_{B_k}^{N1}\circ F_{B_k}^{N1})\left(bd\right)$ = ${\displaystyle \underset{y}{\bigvee }}(F_{B_k}^{N1}\left(by\right)\wedge F_{B_k}^{N1}\left(yd\right))$.

Definition 11.

Let ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ be a BSVNGS and “b” be a node in ${\check{G}}_{bn}$. Let $(B^{\prime },B_1^{\prime },B_2^{\prime },\dots ,B_m^{\prime })$ be a BSVN subgraph structure of ${\check{G}}_{bn}$ induced by $B\backslash \left\{b\right\}$ such that $\forall e\ne b,f\ne b$

$$T_{B^{\prime }}^P\left(b\right)=I_{B^{\prime }}^P\left(b\right)=F_{B^{\prime }}^P\left(b\right)=T_{B_k^{\prime }}^P\left(be\right)=I_{B_k^{\prime }}^P\left(be\right)=F_{B_k^{\prime }}^P\left(be\right)=0$$

$$T_{B^{\prime }}^N\left(b\right)=I_{B^{\prime }}^N\left(b\right)=F_{B^{\prime }}^N\left(b\right)=T_{B_k^{\prime }}^N\left(be\right)=I_{B_k^{\prime }}^N\left(be\right)=F_{B_k^{\prime }}^N\left(be\right)=0$$

$$T_{B^{\prime }}^P\left(e\right)=T_B^P\left(e\right),I_{B^{\prime }}^P\left(e\right)=I_B^P\left(e\right),F_{B^{\prime }}^P\left(e\right)=F_B^P\left(e\right),T_{B^{\prime }}^N\left(e\right)=T_B^N\left(e\right),I_{B^{\prime }}^N\left(e\right)=I_B^N\left(e\right),F_{B^{\prime }}^{N}e)=F_B^N\left(e\right)$$

$$T_{B_k^{\prime }}^P\left(ef\right)=T_{B_k}^P\left(ef\right),I_{B_k^{\prime }}^P\left(ef\right)=I_{B_k}^P\left(ef\right),F_{B_k^{\prime }}^P\left(ef\right)=F_{B_k}^P\left(ef\right),T_{B_k^{\prime }}^N\left(ef\right)=T_{B_k}^N\left(ef\right),I_{B_k^{\prime }}^N\left(ef\right)=I_{B_k}^N\left(ef\right)$$

$$F_{B_k^{\prime }}^N\left(ef\right)=F_{B_k}^N\left(ef\right),\forall edgesbe,ef\in {\check{G}}_{bn}$$

Then b is a BSVN fuzzy $B_k$ cut-vertex if $T_{B_k}^{P\infty }\left(ef\right)>T_{B_k^{\prime }}^{P\infty }\left(ef\right)$, $I_{B_k}^{P\infty }\left(ef\right)>I_{B_k^{\prime }}^{P\infty }\left(ef\right)$, $F_{B_k}^{P\infty }\left(ef\right)>F_{B_k^{\prime }}^{P\infty }\left(ef\right)$, $T_{B_k}^{N\infty }\left(ef\right)<T_{B_k^{\prime }}^{N\infty }\left(ef\right)$, $I_{B_k}^{N\infty }\left(ef\right)<I_{B_k^{\prime }}^{N\infty }\left(ef\right)$ and $F_{B_k}^{N\infty }\left(ef\right)<F_{B_k^{\prime }}^{N\infty }\left(ef\right)$, for some $e,f\in B\backslash \left\{b\right\}$. Note that vertex b is a BSVN fuzzy $B_k-T^P$ cut-vertex if $T_{B_k}^{P\infty }\left(ef\right)>T_{B_k^{\prime }}^{P\infty }\left(ef\right)$, it is a BSVN fuzzy $B_k-I^P$ cut-vertex if $I_{B_k}^{P\infty }\left(ef\right)>I_{B_k^{\prime }}^{P\infty }\left(ef\right)$, and it is a BSVN fuzzy $B_k-F^P$ cut-vertex if $F_{B_k}^{P\infty }\left(ef\right)>F_{B_k^{\prime }}^{P\infty }\left(ef\right)$. Moreover, vertex b is a BSVN fuzzy $B_k-T^N$ cut-vertex if $T_{B_k}^{N\infty }\left(ef\right)<T_{B_k^{\prime }}^{N\infty }\left(ef\right)$, it is a BSVN fuzzy $B_k-I^N$ cut-vertex if $I_{B_k}^{N\infty }\left(ef\right)<I_{B_k^{\prime }}^{N\infty }\left(ef\right)$ and it is a BSVN fuzzy $B_k-F^N$ cut-vertex if $F_{B_k}^{N\infty }\left(ef\right)<F_{B_k^{\prime }}^{N\infty }\left(ef\right)$.

Example 6.

Consider a BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ as depicted in Figure 6, and let ${\check{G}}_{bh}^{\prime }$ = $(B^{\prime },B_1^{\prime },B_2^{\prime })$ be a BSVN subgraph structure of the BSVNGS ${\check{G}}_{bn}$, which is obtained through deletion of vertex $b_2$.

The vertex $b_2$ is a BSVN fuzzy $B_1-I^P$ cut-vertex and a BSVN fuzzy $B_1-I^N$ cut-vertex, because $I_{B_1^{\prime }}^{P\infty }\left(b_2{b}_5\right)=0$, $I_{B_1}^{P\infty }\left(b_2{b}_5\right)=0.5$, $I_{B_1^{\prime }}^{P\infty }\left(b_4{b}_3\right)=0.7$, $I_{B_1}^{P\infty }\left(b_4{b}_3\right)=0.7$, $I_{B_1^{\prime }}^{P\infty }\left(b_3{b}_5\right)=0.3$, $I_{B_1}^{P\infty }\left(b_3{b}_5\right)=0.4$. $I_{B_1^{\prime }}^{N\infty }\left(b_2{b}_5\right)=0>-0.5=I_{B_1}^{N\infty }\left(b_2{b}_5\right)$, $I_{B_1^{\prime }}^{N\infty }\left(b_4{b}_3\right)=0.7=I_{B_1}^{N\infty }\left(b_4{b}_3\right)$ and $I_{B_1^{\prime }}^{N\infty }\left(b_3{b}_5\right)=-0.3>-0.4=I_{B_1}^{N\infty }\left(b_3{b}_5\right)$.

Definition 12.

Suppose ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ is a BSVNGS and $bd$ is a $B_k$-edge. Let $(B^{\prime },B_1^{\prime },B_2^{\prime },\dots ,B_m^{\prime })$ be a BSVN fuzzy spanning subgraph structure of ${\check{G}}_{bn}$, such that

$$T_{B_k^{\prime }}^P\left(bd\right)=0=I_{B_k^{\prime }}^P\left(bd\right)=F_{B_k^{\prime }}^P\left(bd\right),T_{B_k^{\prime }}^N\left(bd\right)=0=I_{B_k^{\prime }}^N\left(bd\right)=F_{B_k^{\prime }}^N\left(bd\right)$$

$$T_{B_k^{\prime }}^P\left(gh\right)=T_{B_k}^P\left(gh\right),I_{B_k^{\prime }}^P\left(gh\right)=I_{B_k}^P\left(gh\right)$$

$$F_{B_k^{\prime }}^P\left(bd\right)=F_{B_k}^P\left(bd\right),T_{B_k^{\prime }}^N\left(gh\right)=T_{B_k}^N\left(gh\right),I_{B_k^{\prime }}^N\left(gh\right)=I_{B_k}^N\left(gh\right),F_{B_k^{\prime }}^N\left(bd\right)=F_{B_k}^N\left(bd\right),\forall edgesgh\ne bd$$

Then $bd$ is a BSVN fuzzy $B_k$-bridge if $T_{B_k}^{P\infty }\left(ef\right)>T_{B_k^{\prime }}^{P\infty }\left(ef\right)$, $I_{B_k}^{P\infty }\left(ef\right)>I_{B_k^{\prime }}^{P\infty }\left(ef\right)$, $F_{B_k}^{P\infty }\left(ef\right)>F_{B_k^{\prime }}^{P\infty }\left(ef\right)$, $T_{B_k}^{N\infty }\left(ef\right)<T_{B_k^{\prime }}^{N\infty }\left(ef\right)$, $I_{B_k}^{N\infty }\left(ef\right)<I_{B_k^{\prime }}^{N\infty }\left(ef\right)$ and $F_{B_k}^{N\infty }\left(ef\right)<F_{B_k^{\prime }}^{N\infty }\left(ef\right)$, for some $e,f\in V$. Note that $bd$ is a BSVN fuzzy $B_k-T^P$ bridge if $T_{B_k}^{P\infty }\left(ef\right)>T_{B_k^{\prime }}^{{}^P\infty }\left(ef\right)$, it is a BSVN fuzzy $B_k-I^P$ bridge if $I_{B_k}^{P\infty }\left(ef\right)>I_{B_k^{\prime }}^{P\infty }\left(ef\right)$ and it is a BSVN fuzzy $B_k-F^P$ bridge if $F_{B_k}^{P\infty }\left(ef\right)>F_{B_k^{\prime }}^{P\infty }\left(ef\right)$. Moreover, $bd$ is a BSVN fuzzy $B_k-T^N$ bridge if $T_{B_k}^{N\infty }\left(ef\right)<T_{B_k^{\prime }}^{{}^N\infty }\left(ef\right)$, it is a BSVN fuzzy $B_k-I^N$ bridge if $I_{B_k}^{N\infty }\left(ef\right)<I_{B_k^{\prime }}^{N\infty }\left(ef\right)$ and it is a BSVN fuzzy $B_k-F^N$ bridge if $F_{B_k}^{N\infty }\left(ef\right)<F_{B_k^{\prime }}^{N\infty }\left(ef\right)$.

Example 7.

Consider a BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ as depicted in Figure 6 and ${\check{G}}_{bs}^{\prime }$ = $(B^{\prime },B_1^{\prime },B_2^{\prime })$, a BSVN spanning subgraph structure of the BSVNGS ${\check{G}}_{bn}$ obtained by deleting$B_1$-edge $\left(b_2{b}_5\right)$ and that is shown in Figure 7.

This edge $\left(b_2{b}_5\right)$ is a BSVN fuzzy $B_1$-bridge, as $T_{B_1^{\prime }}^{P\infty }\left(b_2{b}_5\right)$ = $0.3$, $T_{B_1}^{P\infty }\left(b_2{b}_5\right)$ = 0.4, $I_{B_1^{\prime }}^{P\infty }\left(b_2{b}_5\right)$= $0.3$, $I_{B_1}^{P\infty }\left(b_2{b}_5\right)$ = $0.4$, $F_{B_1^{\prime }}^{P\infty }\left(b_2{b}_5\right)$= $0.4$, $F_{B_1}^{P\infty }\left(b_2{b}_5\right)=0.5.$, $T_{B_1^{\prime }}^{N\infty }\left(b_2{b}_5\right)$ = $-0.3>-0.4$ = $T_{B_1}^{N\infty }\left(b_2{b}_5\right)$, $I_{B_1^{\prime }}^{N\infty }\left(b_2{b}_5\right)$= $-0.3>-0.4$= $I_{B_1}^{N\infty }\left(b_2{b}_5\right)$, and $F_{B_1^{\prime }}^{N\infty }\left(b_2{b}_5\right)$= $-0.4>-0.5$ = $F_{B_1}^{N\infty }\left(b_2{b}_5\right).$

Definition 13.

A BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ is a $B_k$-tree if $(supp\left(B\right),supp\left(B_1\right),supp\left(B_2\right),$$\dots ,supp\left(B_m\right))$ is a $B_k$-tree. Alternatively, ${\check{G}}_{bn}$ is a $B_k$-tree if ${\check{G}}_{bn}$ has a subgraph induced by $supp\left(B_k\right)$ that forms a tree.

Example 8.

Consider the BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ as depicted in Figure 8.

This BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ is a $B_2$-tree, as $(supp\left(B\right),supp\left(B_1\right),supp\left(B_2\right))$ is a $B_2$-tree.

Definition 14.

A BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2,\dots ,B_m)$ is a BSVN fuzzy $B_k$-tree if ${\check{G}}_{bn}$ has a BSVN fuzzy spanning subgraph structure ${\check{H}}_{bn}$ = $(B^{\prime },B_1^{\prime },B_2^{\prime },\dots ,B_m^{\prime })$ such that for all $B_k$-edges, $bd$ not in ${\check{H}}_{bn}$:

• ${\check{H}}_{bn}$ is a $B_k^{\prime }$-tree.
• $T_{B_k}^P\left(bd\right)<T_{B_k^{\prime }}^{P\infty }\left(bd\right)$, $I_{B_k}^P\left(bd\right)<I_{B_k^{\prime }}^{P\infty }\left(bd\right)$, $F_{B_k}^P\left(bd\right)<F_{B_k^{\prime }}^{P\infty }\left(bd\right)$, $T_{B_k}^N\left(bd\right)>T_{B_k^{\prime }}^{N\infty }\left(bd\right)$, $I_{B_k}^N\left(bd\right)>I_{B_k^{\prime }}^{N\infty }\left(bd\right)$, and $F_{B_k}^N\left(bd\right)>F_{B_k^{\prime }}^{N\infty }\left(bd\right)$.

In particular, ${\check{G}}_{bn}$ is a BSVN fuzzy $B_k-T^P$ tree if $T_{B_k}^P\left(bd\right)<T_{B_k^{\prime }}^{P\infty }\left(bd\right)$, it is a BSVN fuzzy $B_k-I^P$ tree if $I_{B_k}^P\left(bd\right)<I_{B_k^{\prime }}^{P\infty }\left(bd\right)$, and it is a BSVN fuzzy $B_k-F^P$ tree if $F_{B_k}^P\left(bd\right)>F_{B_k^{\prime }}^{P\infty }\left(bd\right)$. Moreover, ${\check{G}}_{bn}$ is a BSVN fuzzy $B_k-T^N$ tree if $T_{B_k}^N\left(bd\right)>T_{B_k^{\prime }}^{N\infty }\left(bd\right)$, it is a BSVN fuzzy $B_k-I^N$ tree if $I_{B_k}^N\left(bd\right)>I_{B_k^{\prime }}^{N\infty }\left(bd\right)$, and it is a BSVN fuzzy $B_k-F^N$ tree if $F_{B_k}^N\left(bd\right)<F_{B_k^{\prime }}^{N\infty }\left(bd\right)$.

Example 9.

Consider the BSVNGS ${\check{G}}_{bn}$ = $(B,B_1,B_2)$ as depicted in Figure 9.

It is $B_2$-tree, rather than a $B_1$-tree. However, it is a BSVN fuzzy $B_1$-tree, because it has a BSVN fuzzy spanning subgraph $(B^{\prime },B_1^{\prime },B_2^{\prime })$ as a $B_1^{\prime }$-tree, which is obtained through the deletion of the $B_1$-edge $b_2{b}_5$ from ${\check{G}}_{bn}$. Moreover, $T_{B_1^{\prime }}^{P\infty }\left(b_2{b}_5\right)=0.3$, $T_{B_1}^P\left(b_2{b}_5\right)=0.2$, $I_{B_1^{\prime }}^{P\infty }\left(b_2{b}_5\right)=0.3$, $I_{B_1}^P\left(b_2{b}_5\right)=0.1$, $F_{B_1^{\prime }}^{P\infty }\left(b_2{b}_5\right)=0.4$, $F_{B_1}\left(b_2{b}_5\right)=0.5.$ $T_{B_1^{\prime }}^{N\infty }\left(b_2{b}_5\right)=-0.3<-0.2=T_{B_1}^N\left(b_2{b}_5\right)$, $I_{B_1^{\prime }}^{N\infty }\left(b_2{b}_5\right)=-0.3<-0.1=I_{B_1}^N\left(b_2{b}_5\right)$ and $F_{B_1^{\prime }}^{N\infty }\left(b_2{b}_5\right)=-0.4>-0.5=F_{B_1}\left(b_2{b}_5\right).$

Now we define the operations on BSVNGSs.

Definition 15.

Let ${\check{G}}_{b1}$ = $(B_1,B_{11},B_{12},\dots ,B_{1m})$ and ${\check{G}}_{b2}$ = $(B_2,B_{21},B_{22},\dots ,B_{2m})$ be two BSVNGSs. The Cartesian product of ${\check{G}}_{b1}$ and ${\check{G}}_{b2}$, denoted by

$${\check{G}}_{b1}\times {\check{G}}_{b2}=(B_1\times B_2,B_{11}\times B_{21},B_{12}\times B_{22},\dots ,B_{1m}\times B_{2m})$$

is defined as

(i)

$\left\{\begin{array}{c}{T}_{(B_1\times B_2)}^P\left(bd\right)=(T_{B_1}^P\times T_{B_2}^P)\left(bd\right)=T_{B_1}^P\left(b\right)\wedge T_{B_2}^P\left(d\right)\hfill \\ I_{(B_1\times B_2)}^P\left(bd\right)=(I_{B_1}^P\times I_{B_2}^P)\left(bd\right)=I_{B_1}^P\left(b\right)\wedge I_{B_2}^P\left(d\right)\hfill \\ F_{(B_1\times B_2)}^P\left(bd\right)=(F_{B_1}^P\times F_{B_2}^P)\left(bd\right)=F_{B_1}^P\left(b\right)\vee F_{B_2}^P\left(d\right)\hfill \end{array}\right.$

(ii)

$\left\{\begin{array}{c}{T}_{(B_1\times B_2)}^N\left(bd\right)=(T_{B_1}^N\times T_{B_2}^N)\left(bd\right)=T_{B_1}^N\left(b\right)\vee T_{B_2}^N\left(d\right)\hfill \\ I_{(B_1\times B_2)}^N\left(bd\right)=(I_{B_1}^N\times I_{B_2}^N)\left(bd\right)=I_{B_1}^N\left(b\right)\vee I_{B_2}^N\left(d\right)\hfill \\ F_{(B_1\times B_2)}^N\left(bd\right)=(F_{B_1}^N\times F_{B_2}^N)\left(bd\right)=F_{B_1}^N\left(b\right)\wedge F_{B_2}^P\left(d\right)\hfill \end{array}\right.$

for all $\left(bd\right)\in V_1\times V_2$,

(iii)

$\left\{\begin{array}{c}{T}_{(B_{1k}\times B_{2k})}^P\left(b{d}_1\right)\left(b{d}_2\right)=(T_{B_{1k}}^P\times T_{B_{2k}}^P)\left(b{d}_1\right)\left(b{d}_2\right)=T_{B_1}^P\left(b\right)\wedge T_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ I_{(B_{1k}\times B_{2k})}^P\left(b{d}_1\right)\left(b{d}_2\right)=(I_{B_{1k}}^P\times I_{B_{2k}}^P)\left(b{d}_1\right)\left(b{d}_2\right)=I_{B_1}^P\left(b\right)\wedge I_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ F_{(B_{1k}\times B_{2k})}^P\left(b{d}_1\right)\left(b{d}_2\right)=(F_{B_{1k}}^P\times F_{B_{2k}}^P)\left(b{d}_1\right)\left(b{d}_2\right)=F_{B_1}^P\left(b\right)\vee F_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \end{array}\right.$

(iv)

$\left\{\begin{array}{c}{T}_{(B_{1k}\times B_{2k})}^N\left(b{d}_1\right)\left(b{d}_2\right)=(T_{B_{1k}}^N\times T_{B_{2k}}^N)\left(b{d}_1\right)\left(b{d}_2\right)=T_{B_1}^N\left(b\right)\vee T_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ I_{(B_{1k}\times B_{2k})}^N\left(b{d}_1\right)\left(b{d}_2\right)=(I_{B_{1k}}^N\times I_{B_{2k}}^N)\left(b{d}_1\right)\left(b{d}_2\right)=I_{B_1}^N\left(b\right)\vee I_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ F_{(B_{1k}\times B_{2k})}^N\left(b{d}_1\right)\left(b{d}_2\right)=(F_{B_{1k}}^N\times F_{B_{2k}}^N)\left(b{d}_1\right)\left(b{d}_2\right)=F_{B_1}^N\left(b\right)\wedge F_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \end{array}\right.$

for all $b\in V_1$, $\left(d_1{d}_2\right)\in V_{2k},and$

(v)

$\left\{\begin{array}{c}{T}_{(B_{1k}\times B_{2k})}^P\left(b_{1}d\right)\left(b_{2}d\right)=(T_{B_{1k}}^P\times T_{B_{2k}}^P)\left(b_{1}d\right)\left(b_{2}d\right)=T_{B_2}^P\left(d\right)\wedge T_{B_{1k}}^P\left(b_1{b}_2\right)\hfill \\ I_{(B_{1k}\times B_{2k})}^P\left(b_{1}d\right)\left(b_{2}d\right)=(I_{B_{1k}}^P\times I_{B_{2k}}^P)\left(b_{1}d\right)\left(b_{2}d\right)=I_{B_2}^P\left(d\right)\wedge I_{B_{2k}}^P\left(b_1{b}_2\right)\hfill \\ F_{(B_{1k}\times B_{2k})}^P\left(b_{1}d\right)\left(b_{2}d\right)=(F_{B_{1k}}^P\times F_{B_{2k}}^P)\left(b_{1}d\right)\left(b_{2}d\right)=F_{B_2}^P\left(d\right)\vee F_{B_{2k}}^P\left(b_1{b}_2\right)\hfill \end{array}\right.$

(vi)

$\left\{\begin{array}{c}{T}_{(B_{1k}\times B_{2k})}^N\left(b_{1}d\right)\left(b_{2}d\right)=(T_{B_{1k}}^N\times T_{B_{2k}}^N)\left(b_{1}d\right)\left(b_{2}d\right)=T_{B_2}^N\left(d\right)\vee T_{B_{1k}}^N\left(b_1{b}_2\right)\hfill \\ I_{(B_{1k}\times B_{2k})}^N\left(b_{1}d\right)\left(b_{2}d\right)=(I_{B_{1k}}^N\times I_{B_{2k}}^N)\left(b_{1}d\right)\left(b_{2}d\right)=I_{B_2}^N\left(d\right)\vee I_{B_{2k}}^N\left(b_1{b}_2\right)\hfill \\ F_{(B_{1k}\times B_{2k})}^N\left(b_{1}d\right)\left(b_{2}d\right)=(F_{B_{1k}}^N\times F_{B_{2k}}^N)\left(b_{1}d\right)\left(b_{2}d\right)=F_{B_2}^N\left(d\right)\wedge F_{B_{2k}}^N\left(b_1{b}_2\right)\hfill \end{array}\right.$

for all $d\in V_2$, $\left(b_1{b}_2\right)\in V_{1k}$.

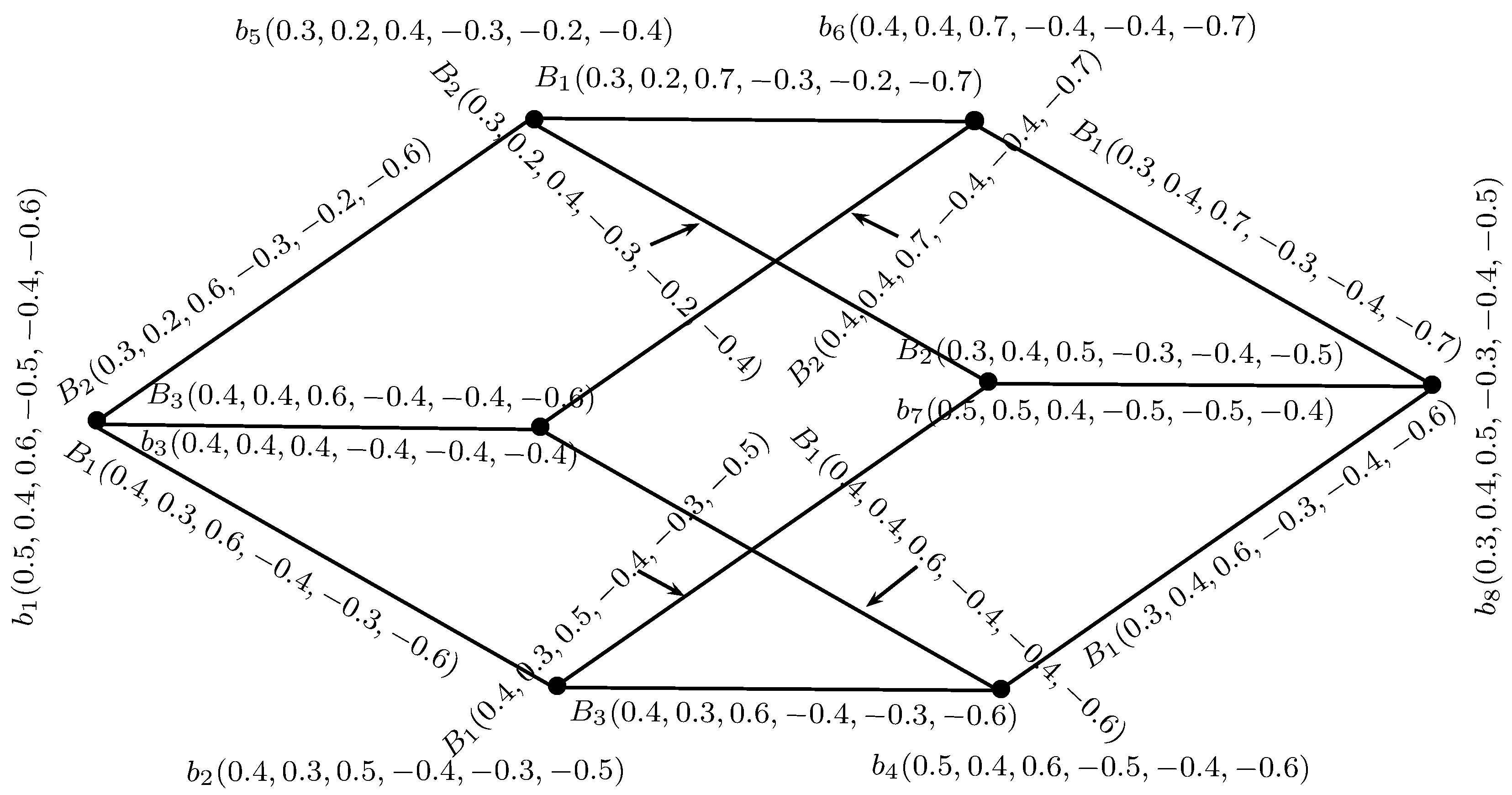
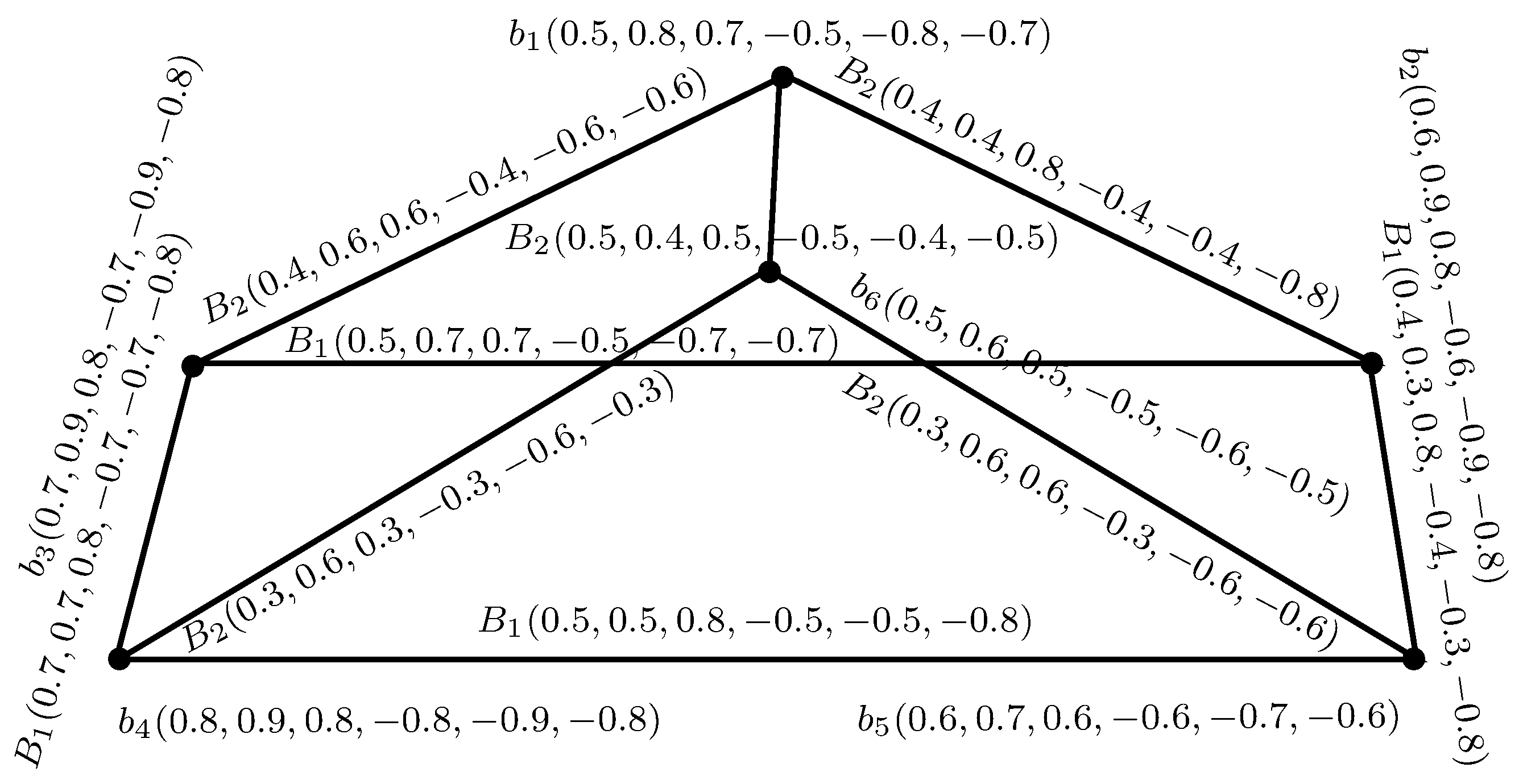
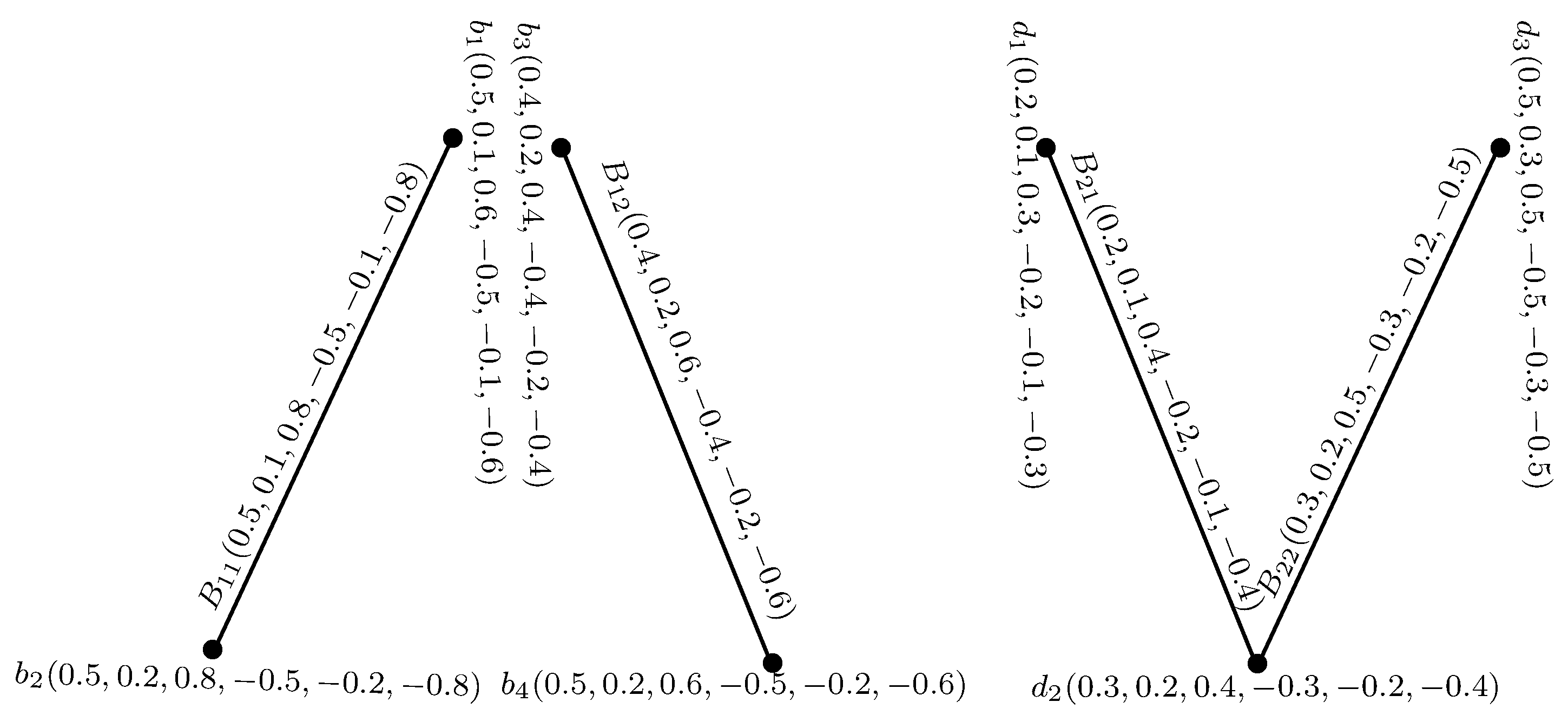
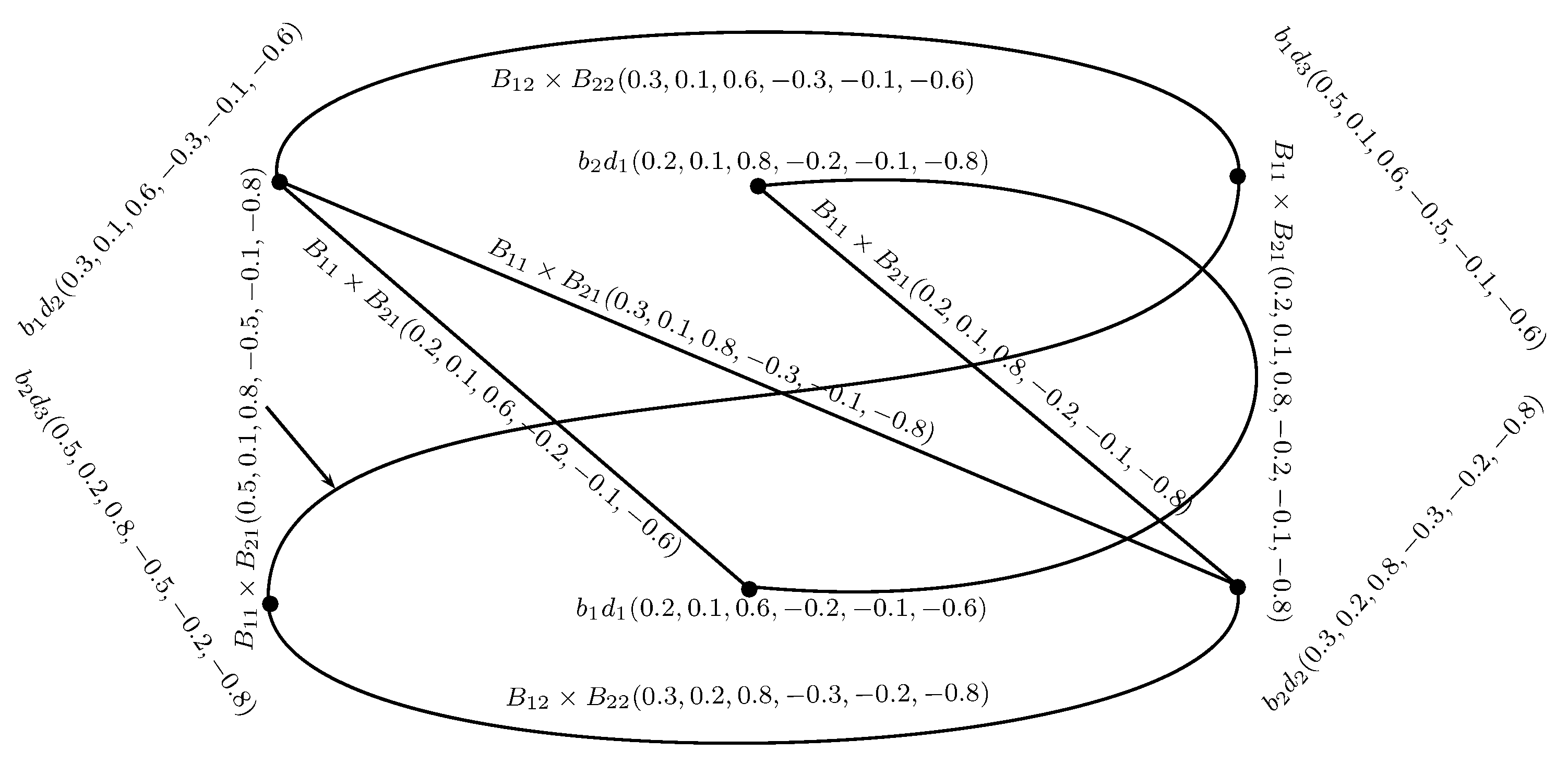
Example 10.

Consider ${\check{G}}_{b1}$ = $(B_1,B_{11},B_{12})$ and ${\check{G}}_{b2}$ = $(B_2,B_{21},B_{22})$ as BSVNGSs of GSs ${\check{G}}_{s1}$ = $(V_1,V_{11},V_{12})$ and ${\check{G}}_{s2}$ = $(V_2,V_{21},V_{22})$, respectively, as depicted in Figure 10, where $V_{11}=\left\{b_1{b}_2\right\}$, $V_{12}=\left\{b_3{b}_4\right\}$, $V_{21}=\left\{d_1{d}_2\right\}$, and $V_{22}=\left\{d_2{d}_3\right\}$.

The Cartesian product of ${\check{G}}_{b1}$ and ${\check{G}}_{b2}$, defined as ${\check{G}}_{b1}\times {\check{G}}_{b2}$ = $\{B_1\times B_2,B_{11}\times B_{21},B_{12}\times B_{22}\}$, is depicted in Figure 11 and Figure 12.

Theorem 1.

The Cartesian product ${\check{G}}_{b1}\times {\check{G}}_{b2}$ = $(B_1\times B_2,B_{11}\times B_{21},B_{12}\times B_{22},\dots ,B_{1m}\times B_{2m})$ of two BSVNSGSs of GSs $\check{G_{s1}}$ and $\check{G_{s2}}$ is a BSVNGS of $\check{G_{s1}}\times \check{G_{s2}}$.

Proof. 

Consider two cases:

Case 1.

For $b\in V_1$, $d_1{d}_2\in V_{2k}$,

$$\begin{array}{cc}\hfill T_{(B_{1k}\times B_{2k})}^P\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =T_{B_1}^P\left(b\right)\wedge T_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le T_{B_1}^P\left(b\right)\wedge [T_{B_2}^P\left(d_1\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =[T_{B_1}^P\left(b\right)\wedge T_{B_2}^P\left(d_1\right)]\wedge [T_{B_1}^P\left(b\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =T_{(B_1\times B_2)}^P\left(b{d}_1\right)\wedge T_{(B_1\times B_2)}^P\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill T_{(B_{1k}\times B_{2k})}^N\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =T_{B_1}^N\left(b\right)\vee T_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge T_{B_1}^N\left(b\right)\vee [T_{B_2}^N\left(d_1\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =[T_{B_1}^N\left(b\right)\vee T_{B_2}^N\left(d_1\right)]\vee [T_{B_1}^N\left(b\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =T_{(B_1\times B_2)}^N\left(b{d}_1\right)\vee T_{(B_1\times B_2)}^N\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\times B_{2k})}^P\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =I_{B_1}^P\left(b\right)\wedge I_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le I_{B_1}^P\left(b\right)\wedge [I_{B_2}^P\left(d_1\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =[I_{B_1}^P\left(b\right)\wedge I_{B_2}^P\left(d_1\right)]\wedge [I_{B_1}^P\left(b\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =I_{(B_1\times B_2)}^P\left(b{d}_1\right)\wedge I_{(B_1\times B_2)}^P\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\times B_{2k})}^N\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =I_{B_1}^N\left(b\right)\vee I_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge I_{B_1}^N\left(b\right)\vee [I_{B_2}^N\left(d_1\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =[I_{B_1}^N\left(b\right)\vee I_{B_2}^N\left(d_1\right)]\vee [I_{B_1}^N\left(b\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =I_{(B_1\times B_2)}^N\left(b{d}_1\right)\vee I_{(B_1\times B_2)}^N\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\times B_{2k})}^P\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =F_{B_1}^P\left(b\right)\vee F_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le F_{B_1}^P\left(b\right)\vee [F_{B_2}^P\left(d_1\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =[F_{B_1}^P\left(b\right)\vee F_{B_2}^P\left(d_1\right)]\vee [F_{B_1}^P\left(b\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =F_{(B_1\times B_2)}^P\left(b{d}_1\right)\vee F_{(B_1\times B_2)}^P\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\times B_{2k})}^N\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =F_{B_1}^N\left(b\right)\wedge F_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge F_{B_1}^N\left(b\right)\wedge [F_{B_2}^N\left(d_1\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =[F_{B_1}^N\left(b\right)\wedge F_{B_2}^N\left(d_1\right)]\wedge [F_{B_1}^N\left(b\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =F_{(B_1\times B_2)}^N\left(b{d}_1\right)\wedge F_{(B_1\times B_2)}^N\left(b{d}_2\right)\hfill \end{array}$$

for $b{d}_1,b{d}_2\in V_1\times V_2.$

Case 2.

For $b\in V_2$, $d_1{d}_2\in V_{1k}$,

$$\begin{array}{cc}\hfill T_{(B_{1k}\times B_{2k})}^P\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =T_{B_2}^P\left(b\right)\wedge T_{B_{1k}}^P\left(d_1{d}_2\right)\hfill \\ & \le T_{B_2}^P\left(b\right)\wedge [T_{B_1}^P\left(d_1\right)\wedge T_{B_1}^P\left(d_2\right)]\hfill \\ & =[T_{B_2}^P\left(b\right)\wedge T_{B_1}^P\left(d_1\right)]\wedge [T_{B_2}^P\left(b\right)\wedge T_{B_1}^P\left(d_2\right)]\hfill \\ & =T_{(B_1\times B_2)}^P\left(d_{1}b\right)\wedge T_{(B_1\times B_2)}^P\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill T_{(B_{1k}\times B_{2k})}^N\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =T_{B_2}^N\left(b\right)\vee T_{B_{1k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge T_{B_2}^N\left(b\right)\vee [T_{B_1}^N\left(d_1\right)\vee T_{B_1}^N\left(d_2\right)]\hfill \\ & =[T_{B_2}^N\left(b\right)\vee T_{B_1}^N\left(d_1\right)]\vee [T_{B_2}^N\left(b\right)\vee T_{B_1}^N\left(d_2\right)]\hfill \\ & =T_{(B_1\times B_2)}^N\left(d_{1}b\right)\vee T_{(B_1\times B_2)}^N\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\times B_{2k})}^P\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =I_{B_2}^P\left(b\right)\wedge I_{B_{1k}}^P\left(d_1{d}_2\right)\hfill \\ & \le I_{B_2}^P\left(b\right)\wedge [I_{B_1}^P\left(d_1\right)\wedge I_{B_1}^P\left(d_2\right)]\hfill \\ & =[I_{B_2}^P\left(b\right)\wedge I_{B_1}^P\left(d_1\right)]\wedge [I_{B_2}^P\left(b\right)\wedge I_{B_1}^P\left(d_2\right)]\hfill \\ & =I_{(B_1\times B_2)}^P\left(d_{1}b\right)\wedge I_{(B_1\times B_2)}^P\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\times B_{2k})}^N\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =I_{B_2}^N\left(b\right)\vee I_{B_{1k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge I_{B_2}^N\left(b\right)\vee [I_{B_1}^N\left(d_1\right)\vee I_{B_1}^N\left(d_2\right)]\hfill \\ & =[I_{B_2}^N\left(b\right)\vee I_{B_1}^N\left(d_1\right)]\vee [I_{B_2}^N\left(b\right)\vee I_{B_1}^N\left(d_2\right)]\hfill \\ & =I_{(B_1\times B_2)}^N\left(d_{1}b\right)\vee I_{(B_1\times B_2)}^N\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\times B_{2k})}^P\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =F_{B_2}^P\left(b\right)\vee F_{B_{1k}}^P\left(d_1{d}_2\right)\hfill \\ & \le F_{B_2}^P\left(b\right)\vee [F_{B_1}^P\left(d_1\right)\vee F_{B_1}^P\left(d_2\right)]\hfill \\ & =[F_{B_2}^P\left(b\right)\vee F_{B_1}^P\left(d_1\right)]\vee [F_{B_2}^P\left(b\right)\vee F_{B_1}^P\left(d_2\right)]\hfill \\ & =F_{(B_1\times B_2)}^P\left(d_{1}b\right)\vee F_{(B_1\times B_2)}^P\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\times B_{2k})}^N\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =F_{B_2}^N\left(b\right)\wedge F_{B_{1k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge F_{B_2}^N\left(b\right)\wedge [F_{B_1}^N\left(d_1\right)\wedge F_{B_1}^N\left(d_2\right)]\hfill \\ & =[F_{B_2}^N\left(b\right)\wedge F_{B_1}^N\left(d_1\right)]\wedge [F_{B_2}^N\left(b\right)\wedge F_{B_1}^N\left(d_2\right)]\hfill \\ & =F_{(B_1\times B_2)}^N\left(d_{1}b\right)\wedge F_{(B_1\times B_2)}^P\left(d_{2}b\right)\hfill \end{array}$$

for $d_{1}b,d_{2}b\in V_1\times V_2.$

Both cases hold for all $k\in \{1,2,\dots ,m\}$. This completes the proof.  ☐

Definition 16.

Let ${\check{G}}_{b1}$ = $(B_1,B_{11},B_{12},\dots ,B_{1m})$ and ${\check{G}}_{b2}$ = $(B_2,B_{21},B_{22},\dots ,B_{2m})$ be two BSVNGSs. The cross product of ${\check{G}}_{b1}$ and ${\check{G}}_{b2}$, denoted by

$${\check{G}}_{b1}\ast {\check{G}}_{b2}=(B_1\ast B_2,B_{11}\ast B_{21},B_{12}\ast B_{22},\dots ,B_{1m}\ast B_{2m})$$

is defined as

(i)

$\left\{\begin{array}{c}{T}_{(B_1\ast B_2)}^P\left(bd\right)=(T_{B_1}^P\ast T_{B_2}^P)\left(bd\right)=T_{B_1}^P\left(b\right)\wedge T_{B_2}^P\left(d\right)\hfill \\ I_{(B_1\ast B_2)}^P\left(bd\right)=(I_{B_1}^P\ast I_{B_2}^P)\left(bd\right)=I_{B_1}^P\left(b\right)\wedge I_{B_2}^P\left(d\right)\hfill \\ F_{(B_1\ast B_2)}^P\left(bd\right)=(F_{B_1}^P\ast F_{B_2}^P)\left(bd\right)=F_{B_1}^P\left(b\right)\vee F_{B_2}^P\left(d\right)\hfill \end{array}\right.$

(ii)

$\left\{\begin{array}{c}{T}_{(B_1\ast B_2)}^N\left(bd\right)=(T_{B_1}^N\ast T_{B_2}^N)\left(bd\right)=T_{B_1}^N\left(b\right)\vee T_{B_2}^N\left(d\right)\hfill \\ I_{(B_1\ast B_2)}^N\left(bd\right)=(I_{B_1}^N\ast I_{B_2}^N)\left(bd\right)=I_{B_1}^N\left(b\right)\vee I_{B_2}^N\left(d\right)\hfill \\ F_{(B_1\ast B_2)}^N\left(bd\right)=(F_{B_1}^N\ast F_{B_2}^N)\left(bd\right)=F_{B_1}^N\left(b\right)\wedge F_{B_2}^P\left(d\right)\hfill \end{array}\right.$

for all $\left(bd\right)\in V_1\times V_2$, and

(iii)

$\left\{\begin{array}{c}{T}_{(B_{1k}\ast B_{2k})}^P\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(T_{B_{1k}}^P\ast T_{B_{2k}}^P)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=T_{B_{1k}}^P\left(b_1{b}_2\right)\wedge T_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ I_{(B_{1k}\ast B_{2k})}^P\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(I_{B_{1k}}^P\ast I_{B_{2k}}^P)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=I_{B_{1k}}^P\left(b_1{b}_2\right)\wedge I_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ F_{(B_{1k}\ast B_{2k})}^P\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(F_{B_{1k}}^P\ast F_{B_{2k}}^P)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=F_{B_{1k}}^P\left(b_1{b}_2\right)\vee F_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \end{array}\right.$

(iv)

$\left\{\begin{array}{c}{T}_{(B_{1k}\ast B_{2k})}^N\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(T_{B_{1k}}^N\ast T_{B_{2k}}^N)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=T_{B_{1k}}^N\left(b_1{b}_2\right)\vee T_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ I_{(B_{1k}\ast B_{2k})}^N\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(I_{B_{1k}}^N\ast I_{B_{2k}}^N)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=I_{B_{1k}}^N\left(b_1{b}_2\right)\vee I_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ F_{(B_{1k}\ast B_{2k})}^N\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(F_{B_{1k}}^N\ast F_{B_{2k}}^N)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=F_{B_{1k}}^N\left(b_1{b}_2\right)\wedge F_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \end{array}\right.$

for all $\left(b_1{b}_2\right)\in V_{1k}$, $\left(d_1{d}_2\right)\in V_{2k}.$

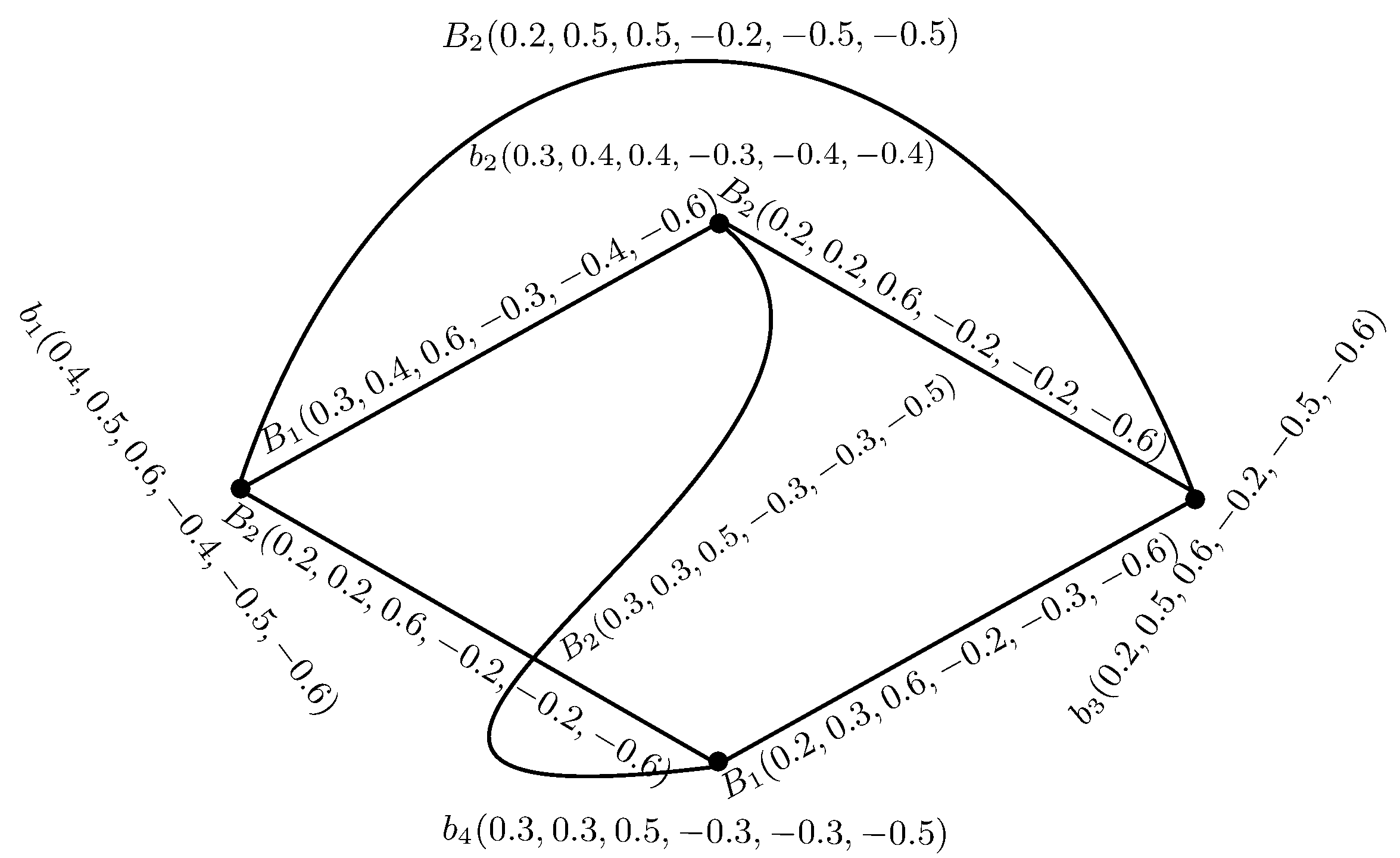
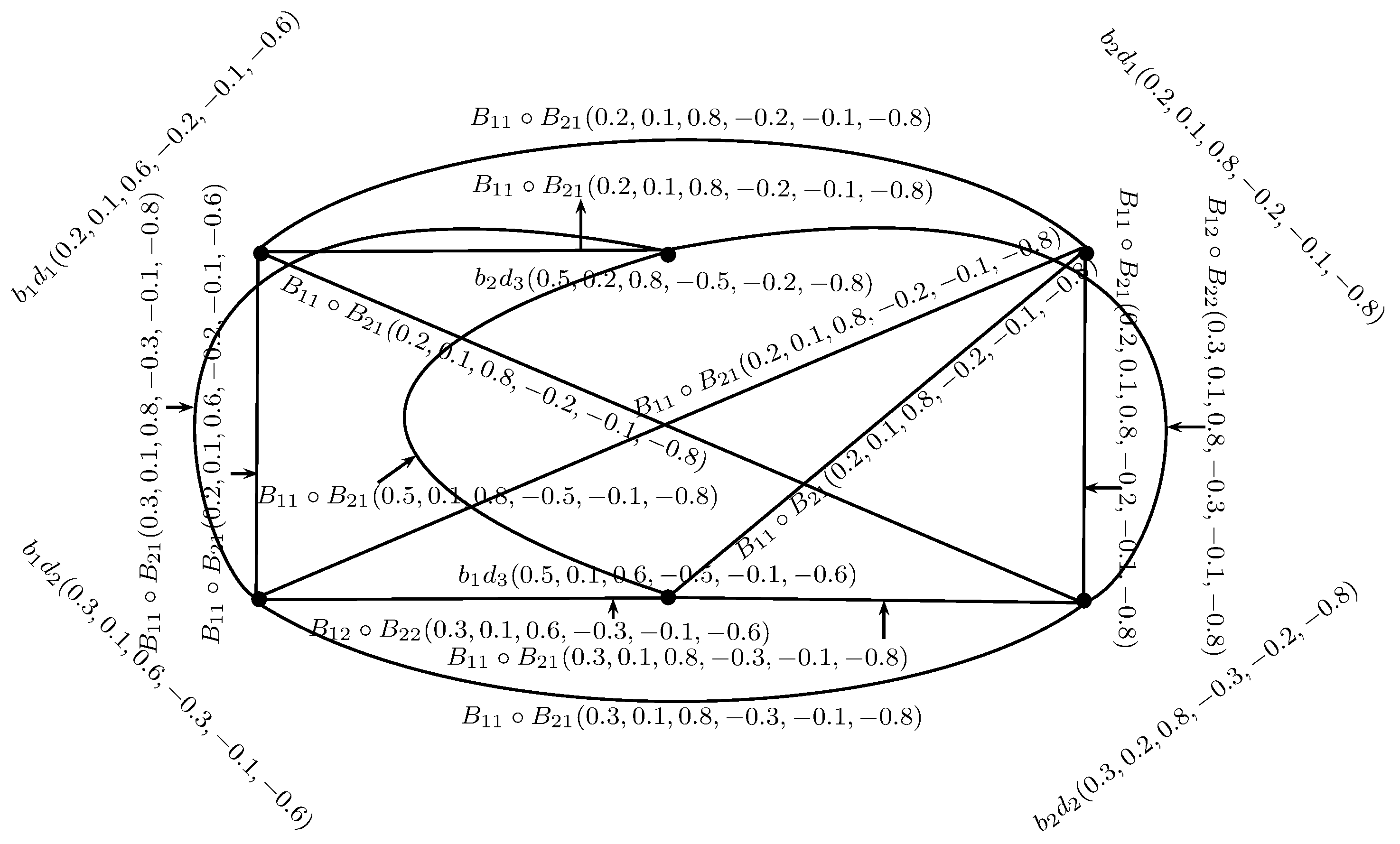
Example 11.

The cross product of BSVNGSs ${\check{G}}_{b1}$ and ${\check{G}}_{b2}$ shown in Figure 10 is defined as ${\check{G}}_{b1}\ast {\check{G}}_{b2}$ = $\{B_1\ast B_2,B_{11}\ast B_{21},B_{12}\ast B_{22}\}$ and is depicted in Figure 13.

Theorem 2.

The cross product ${\check{G}}_{b1}\ast {\check{G}}_{b2}$ = $(B_1\ast B_2,B_{11}\ast B_{21},B_{12}\ast B_{22},\dots ,B_{1m}\ast B_{2m})$ of two BSVNSGSs of GSs $\check{G_{s1}}$ and $\check{G_{s2}}$ is a BSVNGS of $\check{G_{s1}}\ast \check{G_{s2}}$.

Proof. 

For $b_1{b}_2\in V_{1k}$, $d_1{d}_2\in V_{2k}$,

$$\begin{array}{cc}\hfill T_{(B_{1k}\ast B_{2k})}^P\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =T_{B_{1k}}^P\left(b_1{b}_2\right)\wedge T_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le [T_{B_1}^P\left(b_1\right)\wedge T_{B_1}^P(b_2]\wedge [T_{B_2}^P\left(d_1\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =[T_{B_1}^P\left(b_1\right)\wedge T_{B_2}^P\left(d_1\right)]\wedge [T_{B_1}^P\left(b_2\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =T_{(B_1\ast B_2)}^P\left(b_1{d}_1\right)\wedge T_{(B_1\ast B_2)}^P\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill T_{(B_{1k}\ast B_{2k})}^N\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =T_{B_{1k}}^N\left(b_1{b}_2\right)\vee T_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge [T_{B_1}^N\left(b_1\right)\vee T_{B_1}^N(b_2]\vee [T_{B_2}^N\left(d_1\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =[T_{B_1}^N\left(b_1\right)\vee T_{B_2}^N\left(d_1\right)]\vee [T_{B_1}^N\left(b_2\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =T_{(B_1\ast B_2)}^N\left(b_1{d}_1\right)\vee T_{(B_1\ast B_2)}^N\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\ast B_{2k})}^P\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =I_{B_{1k}}^P\left(b_1{b}_2\right)\wedge I_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le [I_{B_1}^P\left(b_1\right)\wedge I_{B_1}^P(b_2]\wedge [I_{B_2}^P\left(d_1\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =[I_{B_1}^P\left(b_1\right)\wedge I_{B_2}^P\left(d_1\right)]\wedge [I_{B_1}^P\left(b_2\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =I_{(B_1\ast B_2)}^P\left(b_1{d}_1\right)\wedge I_{(B_1\ast B_2)}^P\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\ast B_{2k})}^N\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =I_{B_{1k}}^N\left(b_1{b}_2\right)\vee I_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge [I_{B_1}^N\left(b_1\right)\vee I_{B_1}^N(b_2]\vee [I_{B_2}^N\left(d_1\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =[I_{B_1}^N\left(b_1\right)\vee I_{B_2}^N\left(d_1\right)]\vee [I_{B_1}^N\left(b_2\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =I_{(B_1\ast B_2)}^N\left(b_1{d}_1\right)\vee I_{(B_1\ast B_2)}^N\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\ast B_{2k})}^P\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =F_{B_{1k}}^P\left(b_1{b}_2\right)\vee F_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le [F_{B_1}^P\left(b_1\right)\vee F_{B_1}^P(b_2]\vee [F_{B_2}^P\left(d_1\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =[F_{B_1}^P\left(b_1\right)\vee F_{B_2}^P\left(d_1\right)]\vee [F_{B_1}^P\left(b_2\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =F_{(B_1\ast B_2)}^P\left(b_1{d}_1\right)\vee F_{(B_1\ast B_2)}^P\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\ast B_{2k})}^N\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =F_{B_{1k}}^N\left(b_1{b}_2\right)\wedge F_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge [F_{B_1}^N\left(b_1\right)\wedge F_{B_1}^N(b_2]\wedge [F_{B_2}^N\left(d_1\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =[F_{B_1}^N\left(b_1\right)\wedge F_{B_2}^N\left(d_1\right)]\wedge [F_{B_1}^N\left(b_2\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =F_{(B_1\ast B_2)}^N\left(b_1{d}_1\right)\wedge F_{(B_1\ast B_2)}^N\left(b_2{d}_2\right)\hfill \end{array}$$

where $b_1{d}_1,b_2{d}_2\in V_1\ast V_2$ and $h\in \{1,2,\dots ,m\}$.  ☐

Definition 17.

Let ${\check{G}}_{b1}$ = $(B_1,B_{11},B_{12},\dots ,B_{1m})$ and ${\check{G}}_{b2}$ = $(B_2,B_{21},B_{22},\dots ,B_{2m})$ be two BSVNGSs. The composition of ${\check{G}}_{b1}$ and ${\check{G}}_{b2}$, denoted by

$${\check{G}}_{b1}\circ {\check{G}}_{b2}=(B_1\circ B_2,B_{11}\circ B_{21},B_{12}\circ B_{22},\dots ,B_{1m}\circ B_{2m})$$

is defined as

(i)

$\left\{\begin{array}{c}{T}_{(B_1\circ B_2)}^P\left(bd\right)=(T_{B_1}^P\circ T_{B_2}^P)\left(bd\right)=T_{B_1}^P\left(b\right)\wedge T_{B_2}^P\left(d\right)\hfill \\ I_{(B_1\circ B_2)}^P\left(bd\right)=(I_{B_1}^P\circ I_{B_2}^P)\left(bd\right)=I_{B_1}^P\left(b\right)\wedge I_{B_2}^P\left(d\right)\hfill \\ F_{(B_1\circ B_2)}^P\left(bd\right)=(F_{B_1}^P\circ F_{B_2}^P)\left(bd\right)=F_{B_1}^P\left(b\right)\vee F_{B_2}^P\left(d\right)\hfill \end{array}\right.$

(ii)

$\left\{\begin{array}{c}{T}_{(B_1\circ B_2)}^N\left(bd\right)=(T_{B_1}^N\circ T_{B_2}^N)\left(bd\right)=T_{B_1}^N\left(b\right)\vee T_{B_2}^N\left(d\right)\hfill \\ I_{(B_1\circ B_2)}^N\left(bd\right)=(I_{B_1}^N\circ I_{B_2}^N)\left(bd\right)=I_{B_1}^N\left(b\right)\vee I_{B_2}^N\left(d\right)\hfill \\ F_{(B_1\circ B_2)}^N\left(bd\right)=(F_{B_1}^N\circ F_{B_2}^N)\left(bd\right)=F_{B_1}^N\left(b\right)\wedge F_{B_2}^N\left(d\right)\hfill \end{array}\right.$

for all $\left(bd\right)\in V_1\times V_2$,

(iii)

$\left\{\begin{array}{c}{T}_{(B_{1k}\circ B_{2k})}^P\left(b{d}_1\right)\left(b{d}_2\right)=(T_{B_{1k}}^P\circ T_{B_{2k}}^P)\left(b{d}_1\right)\left(b{d}_2\right)=T_{B_1}^P\left(b\right)\wedge T_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ I_{(B_{1k}\circ B_{2k})}^P\left(b{d}_1\right)\left(b{d}_2\right)=(I_{B_{1k}}^P\circ I_{B_{2k}}^P)\left(b{d}_1\right)\left(b{d}_2\right)=I_{B_1}^P\left(b\right)\wedge I_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ F_{(B_{1k}\circ B_{2k})}^P\left(b{d}_1\right)\left(b{d}_2\right)=(F_{B_{1k}}^P\circ F_{B_{2k}}^P)\left(b{d}_1\right)\left(b{d}_2\right)=F_{B_1}^P\left(b\right)\vee F_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \end{array}\right.$

(iv)

$\left\{\begin{array}{c}{T}_{(B_{1k}\circ B_{2k})}^N\left(b{d}_1\right)\left(b{d}_2\right)=(T_{B_{1k}}^N\circ T_{B_{2k}}^N)\left(b{d}_1\right)\left(b{d}_2\right)=T_{B_1}^N\left(b\right)\vee T_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ I_{(B_{1k}\circ B_{2k})}^N\left(b{d}_1\right)\left(b{d}_2\right)=(I_{B_{1k}}^N\circ I_{B_{2k}}^N)\left(b{d}_1\right)\left(b{d}_2\right)=I_{B_1}^N\left(b\right)\vee I_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ F_{(B_{1k}\circ B_{2k})}^N\left(b{d}_1\right)\left(b{d}_2\right)=(F_{B_{1k}}^N\circ F_{B_{2k}}^N)\left(b{d}_1\right)\left(b{d}_2\right)=F_{B_1}^N\left(b\right)\wedge F_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \end{array}\right.$

for all $b\in V_1$, $\left(d_1{d}_2\right)\in V_{2k},$

(v)

$\left\{\begin{array}{c}{T}_{(B_{1k}\circ B_{2k})}^P\left(b_{1}d\right)\left(b_{2}d\right)=(T_{B_{1k}}^P\circ T_{B_{2k}}^P)\left(b_{1}d\right)\left(b_{2}d\right)=T_{B_2}^P\left(d\right)\wedge T_{B_{1k}}^P\left(b_1{b}_2\right)\hfill \\ I_{(B_{1k}\circ B_{2k})}^P\left(b_{1}d\right)\left(b_{2}d\right)=(I_{B_{1k}}^P\circ I_{B_{2k}}^P)\left(b_{1}d\right)\left(b_{2}d\right)=I_{B_2}^P\left(d\right)\wedge I_{B_{1k}}^P\left(b_1{b}_2\right)\hfill \\ F_{(B_{1k}\circ B_{2k})}^P\left(b_{1}d\right)\left(b_{2}d\right)=(F_{B_{1k}}^P\circ F_{B_{2k}}^P)\left(b_{1}d\right)\left(b_{2}d\right)=F_{B_2}^P\left(d\right)\vee F_{B_{1k}}^P\left(b_1{b}_2\right)\hfill \end{array}\right.$

(vi)

$\left\{\begin{array}{c}{T}_{(B_{1k}\circ B_{2k})}^N\left(b_{1}d\right)\left(b_{2}d\right)=(T_{B_{1k}}^N\circ T_{B_{2k}}^N)\left(b_{1}d\right)\left(b_{2}d\right)=T_{B_2}^N\left(d\right)\vee T_{B_{1k}}^N\left(b_1{b}_2\right)\hfill \\ I_{(B_{1k}\circ B_{2k})}^N\left(b_{1}d\right)\left(b_{2}d\right)=(I_{B_{1k}}^N\circ I_{B_{2k}}^N)\left(b_{1}d\right)\left(b_{2}d\right)=I_{B_2}^N\left(d\right)\vee I_{B_{1k}}^N\left(b_1{b}_2\right)\hfill \\ F_{(B_{1k}\circ B_{2k})}^N\left(b_{1}d\right)\left(b_{2}d\right)=(F_{B_{1k}}^N\circ F_{B_{2k}}^N)\left(b_{1}d\right)\left(b_{2}d\right)=F_{B_2}^N\left(d\right)\wedge F_{B_{1k}}^N\left(b_1{b}_2\right)\hfill \end{array}\right.$

for all $d\in V_2$, $\left(b_1{b}_2\right)\in V_{1k},$ and

(vii)

$\left\{\begin{array}{c}{T}_{(B_{1k}\circ B_{2k})}^P\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(T_{B_{1k}}^P\circ T_{B_{2k}}^P)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=T_{B_{1k}}^P\left(b_1{b}_2\right)\wedge T_{B_2}^P\left(d_1\right)\wedge T_{B_2}^P\left(d_2\right)\hfill \\ I_{(B_{1k}\circ B_{2k})}^P\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(I_{B_{1k}}^P\circ I_{B_{2k}}^P)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=I_{B_{1k}}^P\left(b_1{b}_2\right)\wedge I_{B_2}^P\left(d_1\right)\wedge I_{B_2}^P\left(d_2\right)\hfill \\ F_{(B_{1k}\circ B_{2k})}^P\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(F_{B_{1k}}^P\circ F_{B_{2k}}^P)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=F_{B_{1k}}^P\left(b_1{b}_2\right)\vee F_{B_2}^P\left(d_1\right)\vee F_{B_2}^P\left(d_2\right)\hfill \end{array}\right.$

(viii)

$\left\{\begin{array}{c}{T}_{(B_{1k}\circ B_{2k})}^N\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(T_{B_{1k}}^N\circ T_{B_{2k}}^N)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=T_{B_{1k}}^N\left(b_1{b}_2\right)\vee T_{B_2}^N\left(d_1\right)\vee T_{B_2}^N\left(d_2\right)\hfill \\ I_{(B_{1k}\circ B_{2k})}^N\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(I_{B_{1k}}^N\circ I_{B_{2k}}^N)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=I_{B_{1k}}^N\left(b_1{b}_2\right)\vee I_{B_2}^N\left(d_1\right)\vee I_{B_2}^N\left(d_2\right)\hfill \\ F_{(B_{1k}\circ B_{2k})}^N\left(b_1{d}_1\right)\left(b_2{d}_2\right)=(F_{B_{1k}}^N\circ F_{B_{2k}}^N)\left(b_1{d}_1\right)\left(b_2{d}_2\right)=F_{B_{1k}}^N\left(b_1{b}_2\right)\wedge F_{B_2}^N\left(d_1\right)\wedge F_{B_2}^N\left(d_2\right)\hfill \end{array}\right.$

for all $\left(b_1{b}_2\right)\in V_{1k}$, $\left(d_1{d}_2\right)\in V_{2k}$ such that $d_1\ne d_2$.

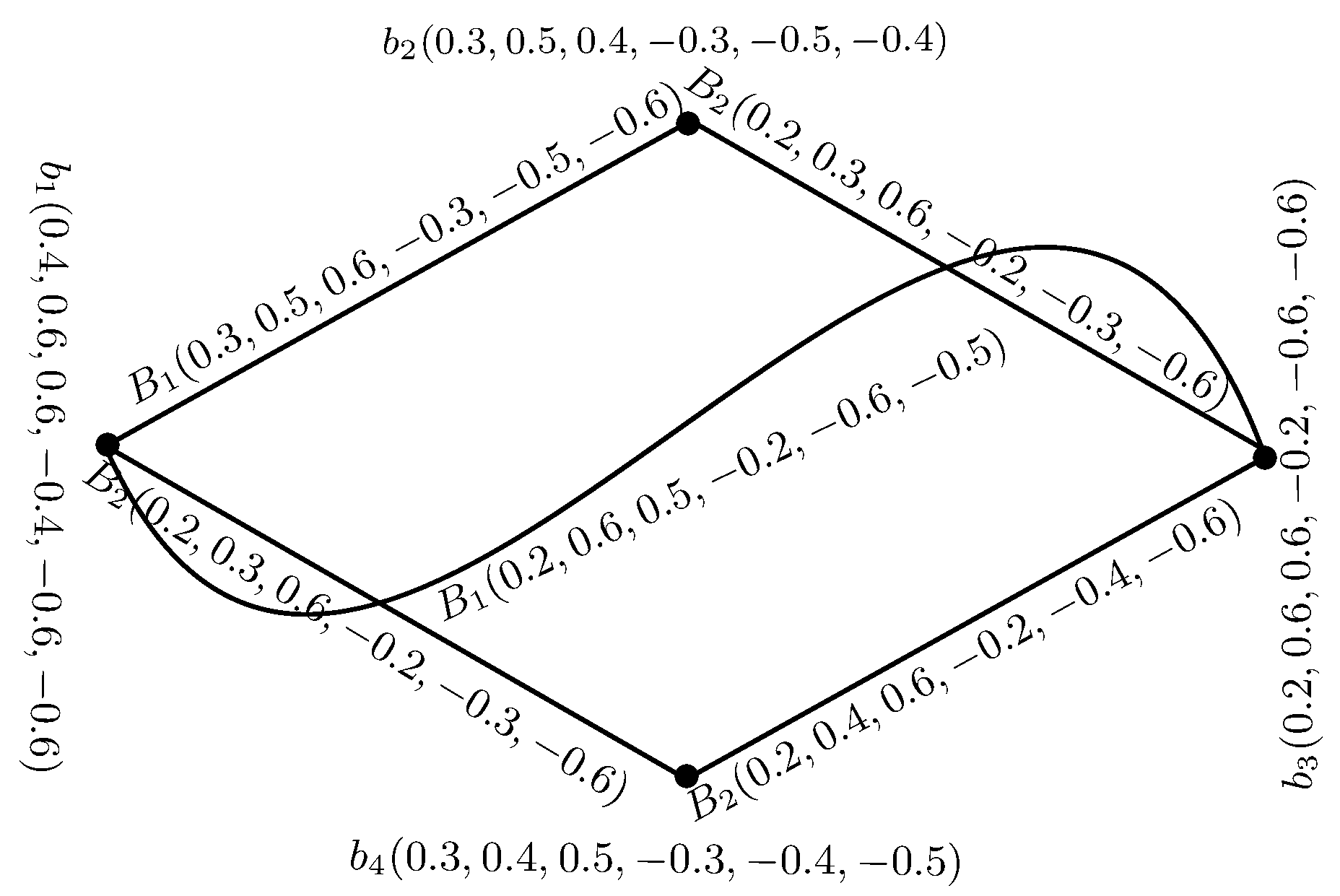
Example 12.

The composition of BSVNGSs ${\check{G}}_{b1}$ and ${\check{G}}_{b2}$ shown in Figure 10 is defined as ${\check{G}}_{b1}\circ {\check{G}}_{b2}$ = $\{B_1\circ B_2,B_{11}\circ B_{21},B_{12}\circ B_{22}\}$ and is depicted in Figure 14 and Figure 15.

Theorem 3.

The composition ${\check{G}}_{b1}\circ {\check{G}}_{b2}$ = $(B_1\circ B_2,B_{11}\circ B_{21},B_{12}\circ B_{22},\dots ,B_{1m}\circ B_{2m})$ of two BSVNGSs of GSs $\check{G_{s1}}$ and $\check{G_{s2}}$ is a BSVNGS of $\check{G_{s1}}\circ \check{G_{s2}}$.

Proof. 

Consider three cases:

Case 1.

For $b\in V_1$, $d_1{d}_2\in V_{2k}$,

$$\begin{array}{cc}\hfill T_{(B_{1k}\circ B_{2k})}^P\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =T_{B_1}^P\left(b\right)\wedge T_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le T_{B_1}^P\left(b\right)\wedge [T_{B_2}^P\left(d_1\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =[T_{B_1}^P\left(b\right)\wedge T_{B_2}^P\left(d_1\right)]\wedge [T_{B_1}^P\left(b\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =T_{(B_1\circ B_2)}^P\left(b{d}_1\right)\wedge T_{(B_1\circ B_2)}^P\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill T_{(B_{1k}\circ B_{2k})}^N\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =T_{B_1}^N\left(b\right)\vee T_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge T_{B_1}^N\left(b\right)\vee [T_{B_2}^N\left(d_1\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =[T_{B_1}^N\left(b\right)\vee T_{B_2}^N\left(d_1\right)]\vee [T_{B_1}^N\left(b\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =T_{(B_1\circ B_2)}^N\left(b{d}_1\right)\vee T_{(B_1\circ B_2)}^N\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\circ B_{2k})}^P\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =I_{B_1}^P\left(b\right)\wedge I_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le I_{B_1}^P\left(b\right)\wedge [I_{B_2}^P\left(d_1\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =[I_{B_1}^P\left(b\right)\wedge I_{B_2}^P\left(d_1\right)]\wedge [I_{B_1}^P\left(b\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =I_{(B_1\circ B_2)}^P\left(b{d}_1\right)\wedge I_{(B_1\circ B_2)}^P\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\circ B_{2k})}^N\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =I_{B_1}^N\left(b\right)\vee I_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge I_{B_1}^N\left(b\right)\vee [I_{B_2}^N\left(d_1\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =[I_{B_1}^N\left(b\right)\vee I_{B_2}^N\left(d_1\right)]\vee [I_{B_1}^N\left(b\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =I_{(B_1\circ B_2)}^N\left(b{d}_1\right)\vee I_{(B_1\circ B_2)}^N\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\circ B_{2k})}^P\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =F_{B_1}^P\left(b\right)\vee F_{B_{2k}}^P\left(d_1{d}_2\right)\hfill \\ & \le F_{B_1}^P\left(b\right)\vee [F_{B_2}^P\left(d_1\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =[F_{B_1}^P\left(b\right)\vee F_{B_2}^P\left(d_1\right)]\vee [F_{B_1}^P\left(b\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =F_{(B_1\circ B_2)}^P\left(b{d}_1\right)\vee F_{(B_1\circ B_2)}^P\left(b{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\circ B_{2k})}^N\left(\left(b{d}_1\right)\left(b{d}_2\right)\right)& =F_{B_1}^N\left(b\right)\wedge F_{B_{2k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge F_{B_1}^N\left(b\right)\wedge [F_{B_2}^N\left(d_1\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =[F_{B_1}^N\left(b\right)\wedge F_{B_2}^N\left(d_1\right)]\wedge [F_{B_1}^N\left(b\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =F_{(B_1\circ B_2)}^N\left(b{d}_1\right)\wedge F_{(B_1\circ B_2)}^N\left(b{d}_2\right)\hfill \end{array}$$

for $b{d}_1,b{d}_2\in V_1\circ V_2.$

Case 2.

For $b\in V_2$, $d_1{d}_2\in V_{1k}$,

$$\begin{array}{cc}\hfill T_{(B_{1k}\circ B_{2k})}^P\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =T_{B_2}^P\left(b\right)\wedge T_{B_{1k}}^P\left(d_1{d}_2\right)\hfill \\ & \le T_{B_2}^P\left(b\right)\wedge [T_{B_1}^P\left(d_1\right)\wedge T_{B_1}^P\left(d_2\right)]\hfill \\ & =[T_{B_2}^P\left(b\right)\wedge T_{B_1}^P\left(d_1\right)]\wedge [T_{B_2}^P\left(b\right)\wedge T_{B_1}^P\left(d_2\right)]\hfill \\ & =T_{(B_1\circ B_2)}^P\left(d_{1}b\right)\wedge T_{(B_1\circ B_2)}^P\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill T_{(B_{1k}\circ B_{2k})}^N\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =T_{B_2}^N\left(b\right)\vee T_{B_{1k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge T_{B_2}^N\left(b\right)\vee [T_{B_1}^N\left(d_1\right)\vee T_{B_1}^N\left(d_2\right)]\hfill \\ & =[T_{B_2}^N\left(b\right)\vee T_{B_1}^N\left(d_1\right)]\vee [T_{B_2}^N\left(b\right)\vee T_{B_1}^N\left(d_2\right)]\hfill \\ & =T_{(B_1\circ B_2)}^N\left(d_{1}b\right)\vee T_{(B_1\circ B_2)}^N\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\circ B_{2k})}^P\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =I_{B_2}^P\left(b\right)\wedge I_{B_{1k}}^P\left(d_1{d}_2\right)\hfill \\ & \le I_{B_2}^P\left(b\right)\wedge [I_{B_1}^P\left(d_1\right)\wedge I_{B_1}^P\left(d_2\right)]\hfill \\ & =[I_{B_2}^P\left(b\right)\wedge I_{B_1}^P\left(d_1\right)]\wedge [I_{B_2}^P\left(b\right)\wedge I_{B_1}^P\left(d_2\right)]\hfill \\ & =I_{(B_1\circ B_2)}^P\left(d_{1}b\right)\wedge I_{(B_1\circ B_2)}^P\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\circ B_{2k})}^N\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =I_{B_2}^N\left(b\right)\vee I_{B_{1k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge I_{B_2}^N\left(b\right)\vee [I_{B_1}^N\left(d_1\right)\vee I_{B_1}^N\left(d_2\right)]\hfill \\ & =[I_{B_2}^N\left(b\right)\vee I_{B_1}^N\left(d_1\right)]\vee [I_{B_2}^N\left(b\right)\vee I_{B_1}^N\left(d_2\right)]\hfill \\ & =I_{(B_1\circ B_2)}^N\left(d_{1}b\right)\vee I_{(B_1\circ B_2)}^N\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\circ B_{2k})}^P\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =F_{B_2}^P\left(b\right)\vee F_{B_{1k}}^P\left(d_1{d}_2\right)\hfill \\ & \le F_{B_2}^P\left(b\right)\vee [F_{B_1}^P\left(d_1\right)\vee F_{B_1}^P\left(d_2\right)]\hfill \\ & =[F_{B_2}^P\left(b\right)\vee F_{B_1}^P\left(d_1\right)]\vee [F_{B_2}^P\left(b\right)\vee F_{B_1}^P\left(d_2\right)]\hfill \\ & =F_{(B_1\circ B_2)}^P\left(d_{1}b\right)\vee F_{(B_1\circ B_2)}^P\left(d_{2}b\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\circ B_{2k})}^N\left(\left(d_{1}b\right)\left(d_{2}b\right)\right)& =F_{B_2}^N\left(b\right)\wedge F_{B_{1k}}^N\left(d_1{d}_2\right)\hfill \\ & \ge F_{B_2}^N\left(b\right)\wedge [F_{B_1}^N\left(d_1\right)\wedge F_{B_1}^N\left(d_2\right)]\hfill \\ & =[F_{B_2}^N\left(b\right)\wedge F_{B_1}^N\left(d_1\right)]\wedge [F_{B_2}^N\left(b\right)\wedge F_{B_1}^N\left(d_2\right)]\hfill \\ & =F_{(B_1\circ B_2)}^N\left(d_{1}b\right)\wedge F_{(B_1\circ B_2)}^N\left(d_{2}b\right)\hfill \end{array}$$

for $d_{1}b,d_{2}b\in V_1\circ V_2.$

Case 3.

For $\left(b_1{b}_2\right)\in V_{1k}$, $\left(d_1{d}_2\right)\in V_{2k}$ such that $d_1\ne d_2$,

$$\begin{array}{cc}\hfill T_{(B_{1k}\circ B_{2k})}^P\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =T_{B_{1k}}^P\left(b_1{b}_2\right)\wedge T_{B_2}^P\left(d_1\right)\wedge T_{B_2}^P\left(d_2\right)\hfill \\ & \le [T_{B_1}^P\left(b_1\right)\wedge T_{B_1}^P(b_2]\wedge [T_{B_2}^P\left(d_1\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =[T_{B_1}^P\left(b_1\right)\wedge T_{B_2}^P\left(d_1\right)]\wedge [T_{B_1}^P\left(b_2\right)\wedge T_{B_2}^P\left(d_2\right)]\hfill \\ & =T_{(B_1\circ B_2)}^P\left(b_1{d}_1\right)\wedge T_{(B_1\circ B_2)}^P\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill T_{(B_{1k}\circ B_{2k})}^N\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =T_{B_{1k}}^N\left(b_1{b}_2\right)\vee T_{B_2}^N\left(d_1\right)\vee T_{B_2}^N\left(d_2\right)\hfill \\ & \ge [T_{B_1}^N\left(b_1\right)\vee T_{B_1}^N(b_2]\vee [T_{B_2}^N\left(d_1\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =[T_{B_1}^N\left(b_1\right)\vee T_{B_2}^N\left(d_1\right)]\vee [T_{B_1}^N\left(b_2\right)\vee T_{B_2}^N\left(d_2\right)]\hfill \\ & =T_{(B_1\circ B_2)}^N\left(b_1{d}_1\right)\vee T_{(B_1\circ B_2)}^N\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\circ B_{2k})}^P\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =I_{B_{1k}}^P\left(b_1{b}_2\right)\wedge I_{B_2}^P\left(d_1\right)\wedge I_{B_2}^P\left(d_2\right)\hfill \\ & \le [I_{B_1}^P\left(b_1\right)\wedge I_{B_1}^P(b_2]\wedge [I_{B_2}^P\left(d_1\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =[I_{B_1}^P\left(b_1\right)\wedge I_{B_2}^P\left(d_1\right)]\wedge [I_{B_1}^P\left(b_2\right)\wedge I_{B_2}^P\left(d_2\right)]\hfill \\ & =I_{(B_1\circ B_2)}^P\left(b_1{d}_1\right)\wedge I_{(B_1\circ B_2)}^P\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{(B_{1k}\circ B_{2k})}^N\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =I_{B_{1k}}^N\left(b_1{b}_2\right)\vee I_{B_2}^N\left(d_1\right)\vee I_{B_2}^N\left(d_2\right)\hfill \\ & \ge [I_{B_1}^N\left(b_1\right)\vee I_{B_1}^N(b_2]\vee [I_{B_2}^N\left(d_1\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =[I_{B_1}^N\left(b_1\right)\vee I_{B_2}^N\left(d_1\right)]\vee [I_{B_1}^N\left(b_2\right)\vee I_{B_2}^N\left(d_2\right)]\hfill \\ & =I_{(B_1\circ B_2)}^N\left(b_1{d}_1\right)\vee I_{(B_1\circ B_2)}^N\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\circ B_{2k})}^P\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =F_{B_{1k}}^P\left(b_1{b}_2\right)\vee F_{B_2}^P\left(d_1\right)\vee F_{B_2}^P\left(d_2\right)\hfill \\ & \le [F_{B_1}^P\left(b_1\right)\vee F_{B_1}^P(b_2]\vee [F_{B_2}^P\left(d_1\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =[F_{B_1}^P\left(b_1\right)\vee F_{B_2}^P\left(d_1\right)]\vee [F_{B_1}^P\left(b_2\right)\vee F_{B_2}^P\left(d_2\right)]\hfill \\ & =F_{(B_1\circ B_2)}^P\left(b_1{d}_1\right)\vee F_{(B_1\circ B_2)}^P\left(b_2{d}_2\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill F_{(B_{1k}\circ B_{2k})}^N\left(\left(b_1{d}_1\right)\left(b_2{d}_2\right)\right)& =F_{B_{1k}}^N\left(b_1{b}_2\right)\wedge F_{B_2}^N\left(d_1\right)\wedge F_{B_2}^N\left(d_2\right)\hfill \\ & \ge [F_{B_1}^N\left(b_1\right)\wedge F_{B_1}^N(b_2]\wedge [F_{B_2}^N\left(d_1\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =[F_{B_1}^N\left(b_1\right)\wedge F_{B_2}^N\left(d_1\right)]\wedge [F_{B_1}^N\left(b_2\right)\wedge F_{B_2}^N\left(d_2\right)]\hfill \\ & =F_{(B_1\circ B_2)}^N\left(b_1{d}_1\right)\wedge F_{(B_1\circ B_2)}^N\left(b_2{d}_2\right)\hfill \end{array}$$

where $b_1{d}_1,b_2{d}_2\in V_1\circ V_2$.

All cases are satisfied for all $k\in \{1,2,\dots ,m\}$.  ☐

3. Conclusions

The notion of bipolar fuzzy graphs is applicable in several domains of engineering, expert systems, pattern recognition, signal processing, neural networks, medical diagnosis and decision-making. BSVNGSs show more flexibility, compatibility and precision for a system than single-valued neutrosophic graph structures. In this research paper, we introduced certain concepts of BSVNGSs and elaborated on them with suitable examples. Further, we defined some operations on BSVNGSs and investigated some relevant properties of these operations. We intend to generalize our research of fuzzification to (1) concepts of BSVN soft graph structures, (2) concepts of BSVN rough fuzzy graph structures, (3) concepts of BSVN fuzzy soft graph structures, and (4) concepts of BSVN rough fuzzy soft graph structures.