Cyber Insurance Premium Setting for Multi-Site Companies under Risk Correlation
Abstract
:1. Introduction
- Threat: the causes that create risks (e.g., theft of information, dangerous weather, fire);
- Vulnerability: existing weaknesses that can be exploited to cause security accidents;
- Impact: the amount of loss suffered.
- Risk transfer;
- Risk mitigation.
2. Literature Review
- Increased breach probability;
- Correlation coefficient;
- Regression;
- Joint probability distribution function;
- Multi-dimensional stochastic process;
- Copulas.
3. Multi-Site Companies, Cyber Risk Correlation, and Cyber Insurance
- Direct attack due to the attacker attempting to breach the site without exploiting information or vantage positions from another site;
- Indirect attack due to breaches that take place in another site.
- Is a twice differentiable function on ;
- Is an increasing function and concave on .
- is the gradient of the function u, ;
- is its hessian matrix with entries , ;
- denotes the standard scalar product between two vectors a and .
4. Premium Model with Risk Correlation for Multi-Site Companies
- is the gradient of the function u, ;
- is its hessian matrix with entries , ;
- denotes the standard scalar product between two vectors a and .
- .
- .
- .
5. Risk-Aversion Coefficient
- Risk-averse if they accept to pay a sum of money rather than accepting an uncertain outcome with the same expected loss;
- Risk-neutral if they are indifferent between the certain payment and the uncertain outcome with the same expected loss;
- Risk-seeking otherwise.
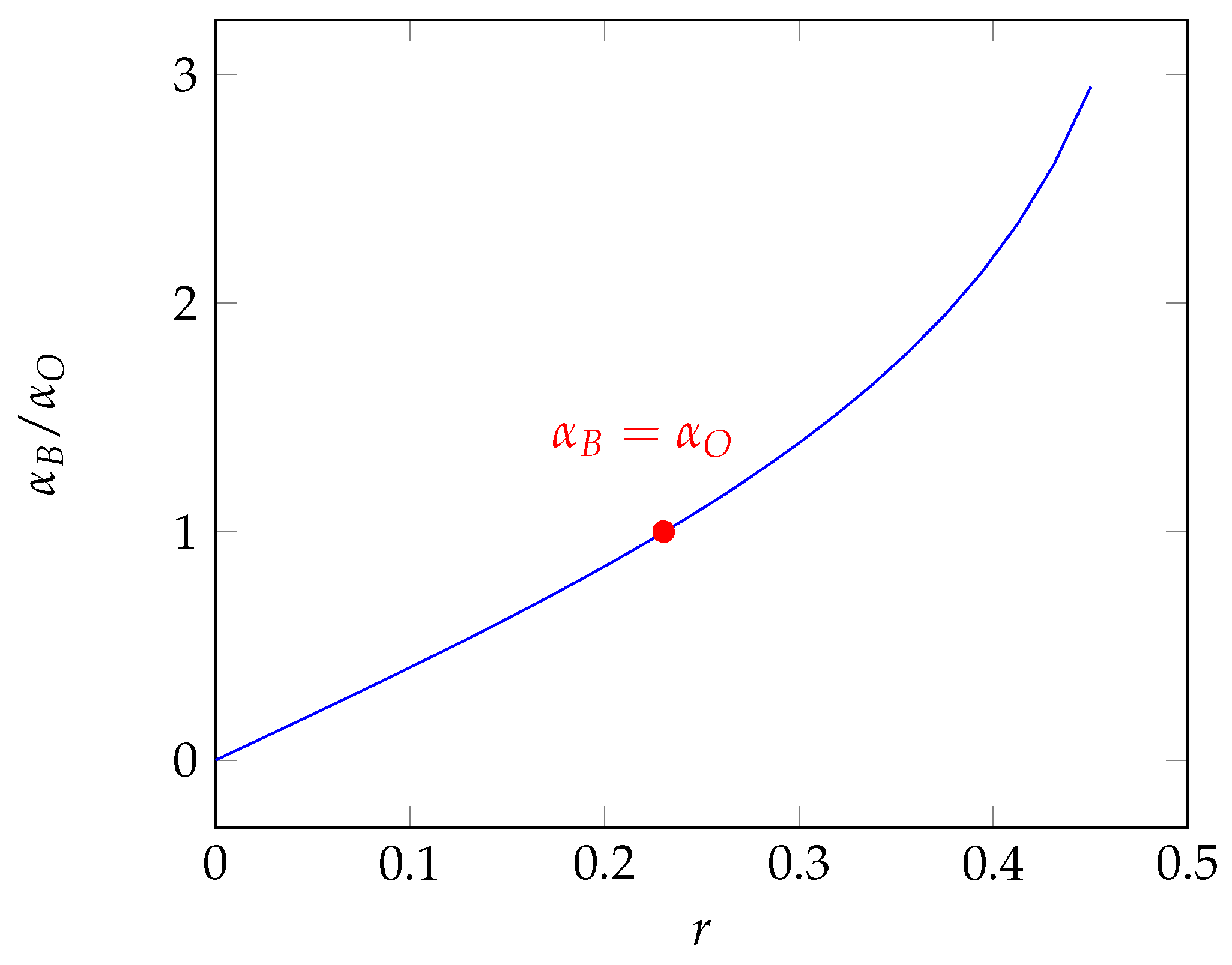
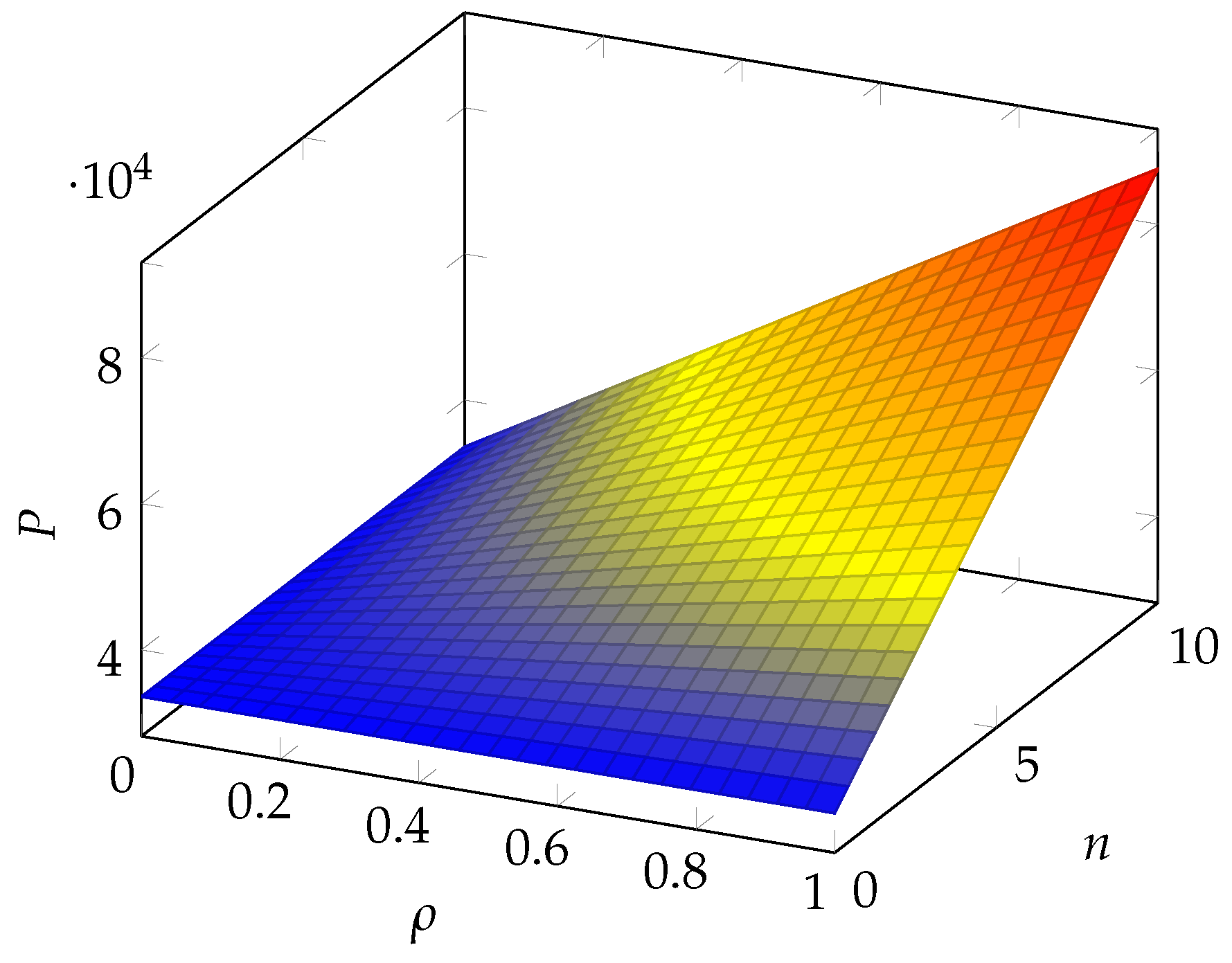
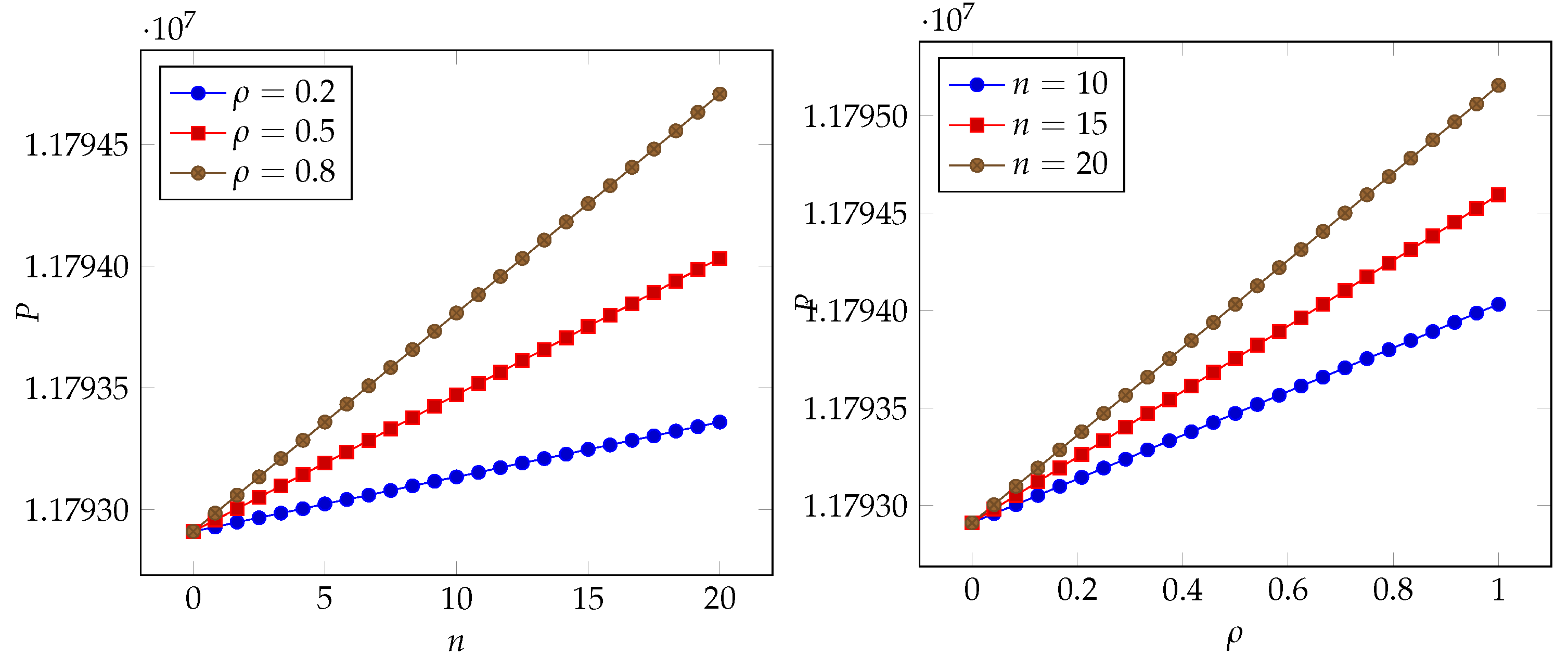
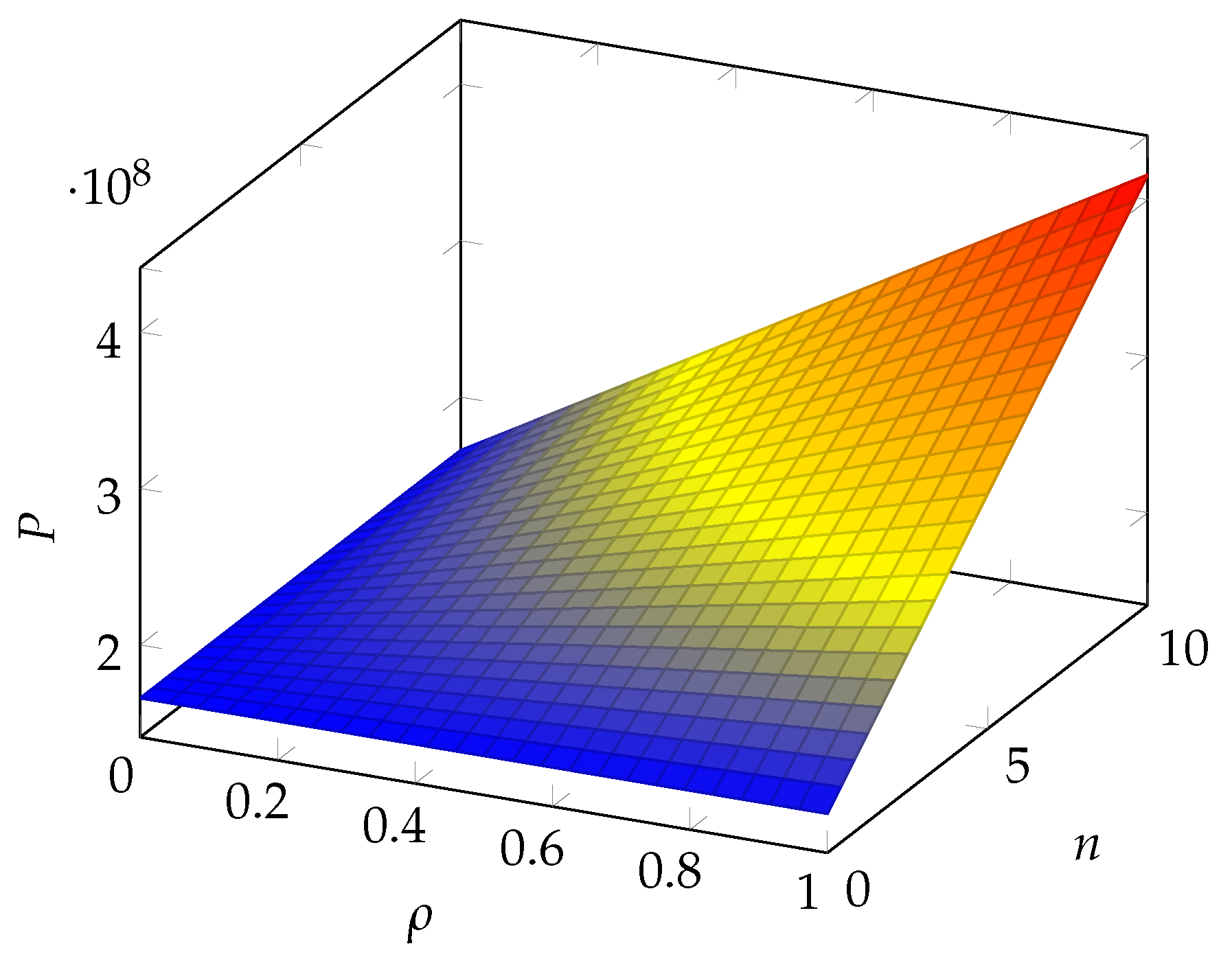
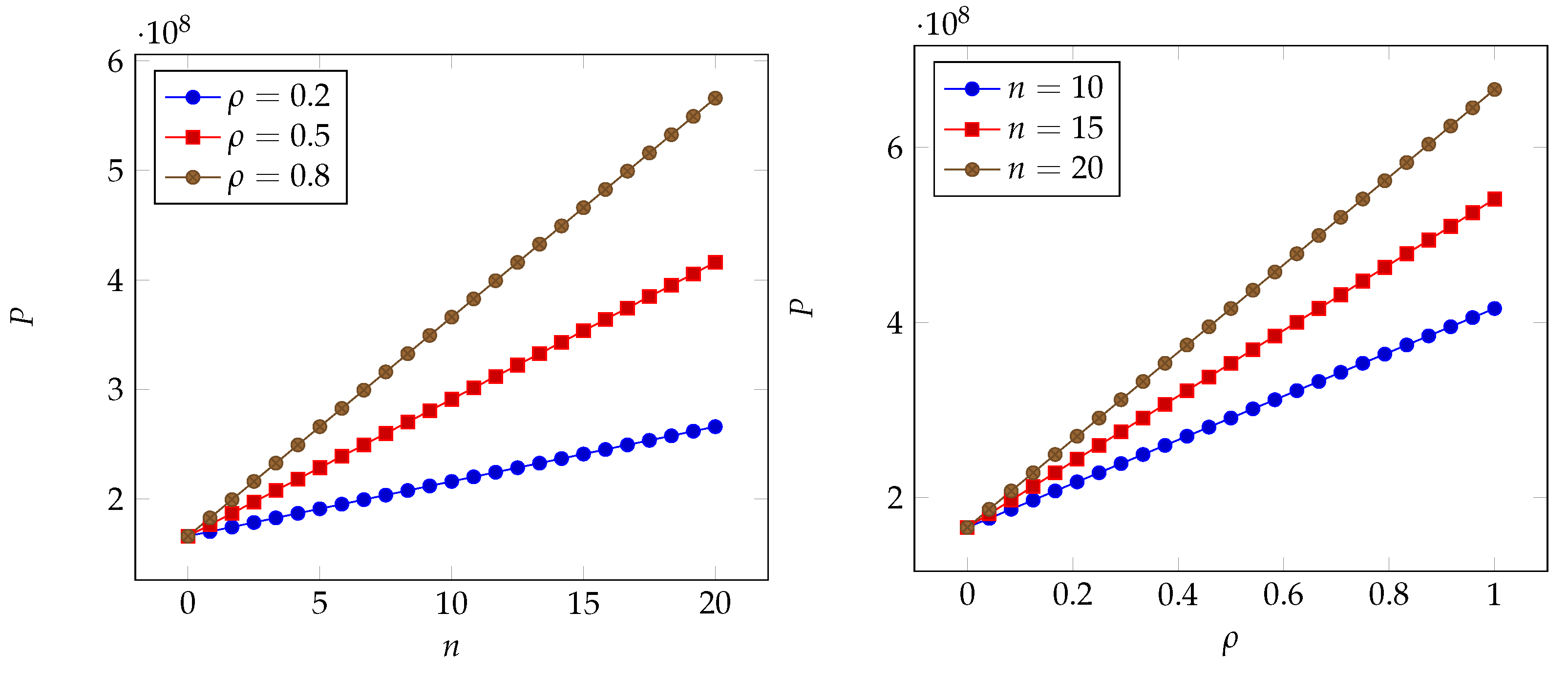
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albadarneh, Aalaa, Israa Albadarneh, and Abdallah Qusef. 2015. Risk management in agile software development: A comparative study. Paper presented at 2015 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Amman, Jordan, November 3–5; pp. 1–6. [Google Scholar]
- Antonio, Yeftanus, Sapto Wahyu Indratno, and Suhadi Wido Saputro. 2021. Pricing of cyber insurance premiums using a markov-based dynamic model with clustering structure. PLoS ONE 16: e0258867. [Google Scholar] [CrossRef]
- Armenia, Stefano, Marco Angelini, Fabio Nonino, Giulia Palombi, and Mario Francesco Schlitzer. 2021. A dynamic simulation approach to support the evaluation of cyber risks and security investments in smes. Decision Support Systems 147: 113580. [Google Scholar] [CrossRef]
- Aven, Terje. 2010. On how to define, understand and describe risk. Reliability Engineering & System Safety 95: 623–31. [Google Scholar]
- Aven, Terje, and Louis Anthony Cox Jr. 2016. National and global risk studies: How can the field of risk analysis contribute? Risk Analysis 36: 186–90. [Google Scholar] [CrossRef] [PubMed]
- Aven, Terje, and Roger Flage. 2020. Foundational challenges for advancing the field and discipline of risk analysis. Risk Analysis 40: 2128–36. [Google Scholar] [CrossRef]
- Babcock, Bruce A., E. Kwan Choi, and Eli Feinerman. 1993. Risk and probability premiums for cara utility functions. Journal of Agricultural and Resource Economics 18: 17–24. [Google Scholar]
- Bandyopadhyay, Tridib, Varghese Jacob, and Srinivasan Raghunathan. 2010. Information security in networked supply chains: Impact of network vulnerability and supply chain integration on incentives to invest. Information Technology and Management 11: 7–23. [Google Scholar] [CrossRef]
- Bandyopadhyay, Tridib, Vijay S. Mookerjee, and Ram C. Rao. 2009. Why it managers do not go for cyber-insurance products. Communications of the ACM 52: 68–73. [Google Scholar] [CrossRef]
- Böhme, Rainer, and Galina Schwartz. 2010. Modeling cyber-insurance: Towards a unifying framework. Paper presented at Workshop on the Economics of Information Security: WEIS, Cambridge, MA, USA, June 7–8. [Google Scholar]
- Böhme, Rainer, and Gaurav Kataria. 2006. Models and measures for correlation in cyber-insurance. Paper presented at Workshop on the Economics of Information Security: WEIS, Cambridge, UK, June 28–30; Volume 2, p. 3. [Google Scholar]
- Böhme, Rainer, Stefan Laube, and Markus Riek. 2019. A fundamental approach to cyber risk analysis. Variance 12: 161–85. [Google Scholar]
- Broner, Fernando, and Jaume Ventura. 2011. Globalization and risk sharing. The Review of Economic Studies 78: 49–82. [Google Scholar] [CrossRef]
- Brunello, Giorgio. 2002. Absolute risk aversion and the returns to education. Economics of Education Review 21: 635–40. [Google Scholar] [CrossRef]
- Bürger, Olga, Björn Häckel, Philip Karnebogen, and Jannick Töppel. 2019. Estimating the impact of it security incidents in digitized production environments. Decision Support Systems 127: 113144. [Google Scholar] [CrossRef]
- Covello, Vincent T., and Jeryl Mumpower. 1985. Risk analysis and risk management: An historical perspective. Risk Analysis 5: 103–20. [Google Scholar] [CrossRef]
- Da, Gaofeng, Maochao Xu, and Peng Zhao. 2021. Multivariate dependence among cyber risks based on l-hop propagation. Insurance: Mathematics and Economics 101: 525–46. [Google Scholar] [CrossRef]
- David, Mihaela. 2015. Auto insurance premium calculation using generalized linear models. Procedia Economics and Finance 20: 147–56. [Google Scholar] [CrossRef]
- Dhaene, Jan, Michel Denuit, Marc J. Goovaerts, Rob Kaas, and David Vyncke. 2002. The concept of comonotonicity in actuarial science and finance: Theory. Insurance: Mathematics and Economics 31: 3–33. [Google Scholar] [CrossRef]
- Dou, Wanchun, Wenda Tang, Xiaotong Wu, Lianyong Qi, Xiaolong Xu, Xuyun Zhang, and Chunhua Hu. 2020. An insurance theory based optimal cyber-insurance contract against moral hazard. Information Sciences 527: 576–89. [Google Scholar] [CrossRef]
- Edwards, Benjamin, Steven Hofmeyr, and Stephanie Forrest. 2016. Hype and heavy tails: A closer look at data breaches. Journal of Cybersecurity 2: 3–14. [Google Scholar] [CrossRef]
- Eeckhoudt, Louis, Christian Gollier, and Harris Schlesinger. 2011. Economic and Financial Decisions under Risk. Princeton: Princeton University Press. [Google Scholar]
- Eling, Martin. 2020. Cyber risk research in business and actuarial science. European Actuarial Journal 10: 303–33. [Google Scholar] [CrossRef]
- Erb, Claude B., Campbell R. Harvey, and Tadas E. Viskanta. 1996. Political risk, economic risk, and financial risk. Financial Analysts Journal 52: 29–46. [Google Scholar] [CrossRef]
- Fahrenwaldt, Matthias A., Stefan Weber, and Kerstin Weske. 2018. Pricing of cyber insurance contracts in a network model. ASTIN Bulletin: The Journal of the IAA 48: 1175–218. [Google Scholar] [CrossRef]
- Fielder, Andrew, Emmanouil Panaousis, Pasquale Malacaria, Chris Hankin, and Fabrizio Smeraldi. 2016. Decision support approaches for cyber security investment. Decision Support Systems 86: 13–23. [Google Scholar] [CrossRef]
- Florackis, Chris, Christodoulos Louca, Roni Michaely, and Michael Weber. 2023. Cybersecurity risk. The Review of Financial Studies 36: 351–407. [Google Scholar] [CrossRef]
- Frigo, Mark L., and Richard J. Anderson. 2011. What is strategic risk management? Strategic Finance 92: 21. [Google Scholar]
- Herath, Hemantha, and Tejaswini Herath. 2011. Copula-based actuarial model for pricing cyber-insurance policies. Insurance Markets and Companies: Analyses and Actuarial Computations 2: 7–20. [Google Scholar]
- Hillairet, Caroline, Olivier Lopez, Louise d’Oultremont, and Brieuc Spoorenberg. 2022. Cyber-contagion model with network structure applied to insurance. Insurance: Mathematics and Economics 107: 88–101. [Google Scholar] [CrossRef]
- Hillson, David, and Ruth Murray-Webster. 2017. Understanding and Managing Risk Attitude. London: Routledge. [Google Scholar]
- Hoang, Dinh Thai, Ping Wang, Dusit Niyato, and Ekram Hossain. 2017. Charging and discharging of plug-in electric vehicles (pevs) in vehicle-to-grid (v2g) systems: A cyber insurance-based model. IEEE Access 5: 732–54. [Google Scholar] [CrossRef]
- Johnson, Benjamin, Aron Laszka, and Jens Grossklags. 2014. How many down? toward understanding systematic risk in networks. Paper presented at 9th ACM Symposium on Information, Computer and Communications Security, Kyoto, Japan, June 4–6; pp. 495–500. [Google Scholar]
- Kaas, Rob, Marc Goovaerts, Jan Dhaene, and Michel Denuit. 2008. Modern Actuarial Risk Theory: Using R. Berlin/Heidelberg: Springer Science & Business Media, Volume 128. [Google Scholar]
- Kaplan, Stan. 1991. Risk assessment and risk management-basic concepts and. In Risk Management: Expanding Horizons in Nuclear Power and Other Industries. Boca Raton: CRC Press, p. 11. [Google Scholar]
- Kaplan, Stanley, and B. John Garrick. 1981. On the quantitative definition of risk. Risk Analysis 1: 11–27. [Google Scholar] [CrossRef]
- Khalili, Mohammad Mahdi, Mingyan Liu, and Sasha Romanosky. 2019. Embracing and controlling risk dependency in cyber-insurance policy underwriting. Journal of Cybersecurity 5: tyz010. [Google Scholar] [CrossRef]
- Khalili, Mohammad Mahdi, Parinaz Naghizadeh, and Mingyan Liu. 2018. Designing cyber insurance policies: The role of pre-screening and security interdependence. IEEE Transactions on Information Forensics and Security 13: 2226–39. [Google Scholar] [CrossRef]
- Kröger, Wolfgang. 2008. Critical infrastructures at risk: A need for a new conceptual approach and extended analytical tools. Reliability Engineering & System Safety 93: 1781–87. [Google Scholar]
- Kunreuther, Howard, and Geoffrey Heal. 2003. Interdependent security. Journal of Risk and Uncertainty 26: 231–49. [Google Scholar] [CrossRef]
- Laeven, Roger J. A., and Marc J. Goovaerts. 2008. Premium calculation and insurance pricing. Encyclopedia of Quantitative Risk Analysis and Assessment 3: 1302–14. [Google Scholar]
- Landsman, Zinoviy, and Michael Sherris. 2001. Risk measures and insurance premium principles. Insurance: Mathematics and Economics 29: 103–15. [Google Scholar] [CrossRef]
- Lau, Pikkin, Lingfeng Wang, Zhaoxi Liu, Wei Wei, and Chee-Wooi Ten. 2021. A coalitional cyber-insurance design considering power system reliability and cyber vulnerability. IEEE Transactions on Power Systems 36: 5512–24. [Google Scholar] [CrossRef]
- Lau, Pikkin, Wei Wei, Lingfeng Wang, Zhaoxi Liu, and Chee-Wooi Ten. 2020. A cybersecurity insurance model for power system reliability considering optimal defense resource allocation. IEEE Transactions on Smart Grid 11: 4403–14. [Google Scholar] [CrossRef]
- Lima Ramos, Pedro. 2017. Premium calculation in insurance activity. Journal of Statistics and Management Systems 20: 39–65. [Google Scholar] [CrossRef]
- Lin, Zhaoxin, Travis Sapp, Rahul Parsa, Jackie Rees Ulmer, and Chengxin Cao. 2018. Pricing cyber security insurance. Journal of Mathematical Finance 12: 46–70. [Google Scholar] [CrossRef]
- Liu, Zhaoxi, Wei Wei, Lingfeng Wang, Chee-Wooi Ten, and Yeonwoo Rho. 2020. An actuarial framework for power system reliability considering cybersecurity threats. IEEE Transactions on Power Systems 36: 851–64. [Google Scholar] [CrossRef]
- Lowrance, William W. 1976. Of Acceptable Risk: Science and the Determination of Safety. Los Altos: William Kaufmann Inc., p. 192. [Google Scholar] [CrossRef]
- Maglaras, Leandros A., Ki-Hyung Kim, Helge Janicke, Mohamed Amine Ferrag, Stylianos Rallis, Pavlina Fragkou, Athanasios Maglaras, and Tiago J Cruz. 2018. Cyber security of critical infrastructures. ICT Express 4: 42–45. [Google Scholar] [CrossRef]
- Marotta, Angelica, Fabio Martinelli, Stefano Nanni, Albina Orlando, and Artsiom Yautsiukhin. 2017. Cyber-insurance survey. Computer Science Review 24: 35–61. [Google Scholar] [CrossRef]
- Martinelli, Fabio, Albina Orlando, Ganbayar Uuganbayar, and Artsiom Yautsiukhin. 2018. Preventing the drop in security investments for non-competitive cyber-insurance market. In Risks and Security of Internet and Systems: Proceedings of the 12th International Conference, CRiSIS 2017, Dinard, France, 19–21 September 2017. Revised Selected Papers 12. Cham: Springer, pp. 159–174. [Google Scholar]
- Mastroeni, Loretta, Alessandro Mazzoccoli, and Maurizio Naldi. 2019. Service level agreement violations in cloud storage: Insurance and compensation sustainability. Future Internet 11: 142. [Google Scholar] [CrossRef]
- Mazzoccoli, Alessandro, and Maurizio Naldi. 2020a. The expected utility insurance premium principle with fourth-order statistics: Does it make a difference? Algorithms 13: 116. [Google Scholar] [CrossRef]
- Mazzoccoli, Alessandro, and Maurizio Naldi. 2020b. Robustness of optimal investment decisions in mixed insurance/investment cyber risk management. Risk Analysis 40: 550–64. [Google Scholar] [CrossRef]
- Mazzoccoli, Alessandro, and Maurizio Naldi. 2021. Optimal investment in cyber-security under cyber insurance for a multi-branch firm. Risks 9: 24. [Google Scholar]
- Mazzoccoli, Alessandro, and Maurizio Naldi. 2022. Optimizing cybersecurity investments over time. Algorithms 15: 211. [Google Scholar] [CrossRef]
- Nagurney, Anna, and Shivani Shukla. 2017. Multifirm models of cybersecurity investment competition vs. cooperation and network vulnerability. European Journal of Operational Research 260: 588–600. [Google Scholar] [CrossRef]
- Naldi, Maurizio, and Alessandro Mazzoccoli. 2018. Computation of the insurance premium for cloud services based on fourth-order statistics. International Journal of Simulation: Systems, Science and Technology 19: 1–6. [Google Scholar] [CrossRef]
- Olivieri, Annamaria, and Ermanno Pitacco. 2015. Introduction to Insurance Mathematics: Technical and Financial Features of Risk Transfers. Berlin/Heidelberg: Springer. [Google Scholar]
- Öğüt, Hulisi, Srinivasan Raghunathan, and Nirup Menon. 2011. Cyber security risk management: Public policy implications of correlated risk, imperfect ability to prove loss, and observability of self-protection. Risk Analysis: An International Journal 31: 497–512. [Google Scholar] [CrossRef] [PubMed]
- Paté-Cornell, M-Elisabeth, Marshall Kuypers, Matthew Smith, and Philip Keller. 2018. Cyber risk management for critical infrastructure: A risk analysis model and three case studies. Risk Analysis 38: 226–41. [Google Scholar] [CrossRef] [PubMed]
- Peng, Chen, Maochao Xu, Shouhuai Xu, and Taizhong Hu. 2018. Modeling multivariate cybersecurity risks. Journal of Applied Statistics 45: 2718–40. [Google Scholar] [CrossRef]
- Peterson, Kevin E. 2020. What is risk management? In The Professional Protection Officer. Amsterdam: Elsevier, pp. 367–72. [Google Scholar]
- Power, Michael. 2005. The invention of operational risk. Review of International Political Economy 12: 577–99. [Google Scholar] [CrossRef]
- Refsdal, Atle, Bjørnar Solhaug, and Ketil Stølen. 2015. Cyber-risk management. In Cyber-Risk Management. Berlin/Heidelberg: Springer, pp. 33–47. [Google Scholar]
- Straub, Erwin, and Swiss Association of Actuaries (Zürich). 1988. Non-Life Insurance Mathematics. Number 517/S91n. Berlin/Heidelberg: Springer. [Google Scholar]
- Su, Karen C., Chung-Bow Lee, Shu-Hui Lin, I-Chien Liu, and Hong-Chi Chen. 2021. Pricing cyber risk: The copula-based approach. In Advances in Pacific Basin Business, Economics and Finance. Bingley: Emerald Publishing Limited. [Google Scholar]
- Weber, Elke U. 2010. Risk attitude and preference. Wiley Interdisciplinary Reviews: Cognitive Science 1: 79–88. [Google Scholar] [CrossRef]
- Wheatley, Spencer, Thomas Maillart, and Didier Sornette. 2016. The extreme risk of personal data breaches and the erosion of privacy. The European Physical Journal B 89: 1–12. [Google Scholar] [CrossRef]
- Xie, Danyang. 2000. Power risk aversion utility functions. Annals of Economics and Finance 1: 265–82. [Google Scholar]
- Xu, Lu, Yanhui Li, and Jing Fu. 2019. Cybersecurity investment allocation for a multi-branch firm: Modeling and optimization. Mathematics 7: 587. [Google Scholar] [CrossRef]
- Yang, Zhiyuan, Yun Liu, Meghan Campbell, Chee-Wooi Ten, Yeonwoo Rho, Lingfeng Wang, and Wei Wei. 2020. Premium calculation for insurance businesses based on cyber risks in ip-based power substations. IEEE Access 8: 78890–900. [Google Scholar] [CrossRef]
- Young, Derek, Juan Lopez Jr., Mason Rice, Benjamin Ramsey, and Robert McTasney. 2016. A framework for incorporating insurance in critical infrastructure cyber risk strategies. International Journal of Critical Infrastructure Protection 14: 43–57. [Google Scholar] [CrossRef]
- Zhang, Yunfan, Lingfeng Wang, Zhaoxi Liu, and Wei Wei. 2020. A cyber-insurance scheme for water distribution systems considering malicious cyberattacks. IEEE Transactions on Information Forensics and Security 16: 1855–67. [Google Scholar] [CrossRef]
- Zio, Enrico. 2007. An Introduction to the Basics of Reliability and Risk Analysis. Singapore: World Scientific, Volume 13. [Google Scholar]





| Parameter | Meaning |
|---|---|
| u | Utility function |
| w | Firm asset |
| X | Monetary loss variable |
| P | Insurance premium |
| Risk aversion coefficient | |
| r | Risk premium |
| Correlation coefficient |
| Scenarios | Frequency | Avg Loss (USD) |
|---|---|---|
| Edwards et al. (2016) | 0.008 | 2.82 |
| Mastroeni et al. (2019) | 0.036 | 8.6 |
| Lin et al. (2018) | 0.032 | 1.2 |
| Wheatley et al. (2016) | 0.38 | 1.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mastroeni, L.; Mazzoccoli, A.; Naldi, M. Cyber Insurance Premium Setting for Multi-Site Companies under Risk Correlation. Risks 2023, 11, 167. https://doi.org/10.3390/risks11100167
Mastroeni L, Mazzoccoli A, Naldi M. Cyber Insurance Premium Setting for Multi-Site Companies under Risk Correlation. Risks. 2023; 11(10):167. https://doi.org/10.3390/risks11100167
Chicago/Turabian StyleMastroeni, Loretta, Alessandro Mazzoccoli, and Maurizio Naldi. 2023. "Cyber Insurance Premium Setting for Multi-Site Companies under Risk Correlation" Risks 11, no. 10: 167. https://doi.org/10.3390/risks11100167






