Interactive Graph Layout of a Million Nodes
Abstract
:1. Introduction
2. Related Work
2.1. Large Graph Layout
2.2. Force-Directed Algorithms
2.3. Graph Layout on the GPU
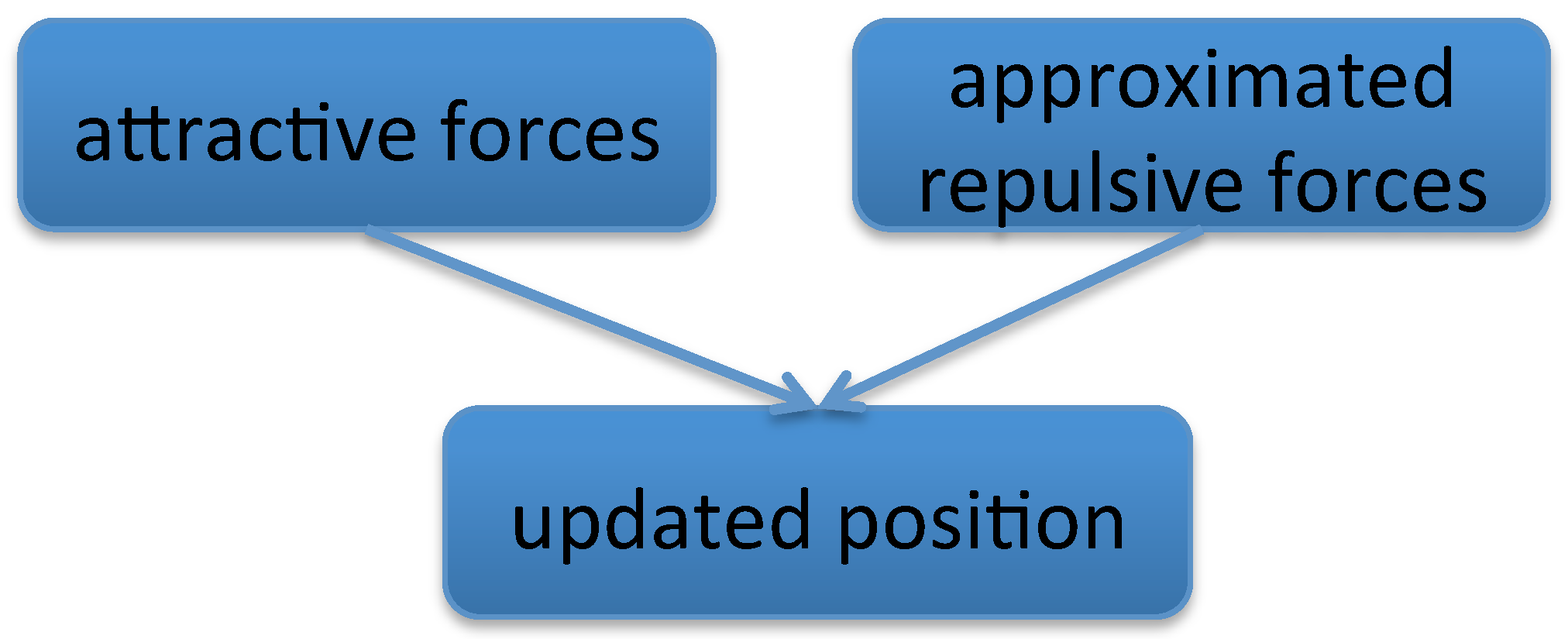
3. Algorithm Outline
3.1. Approximation of The Repulsive Force
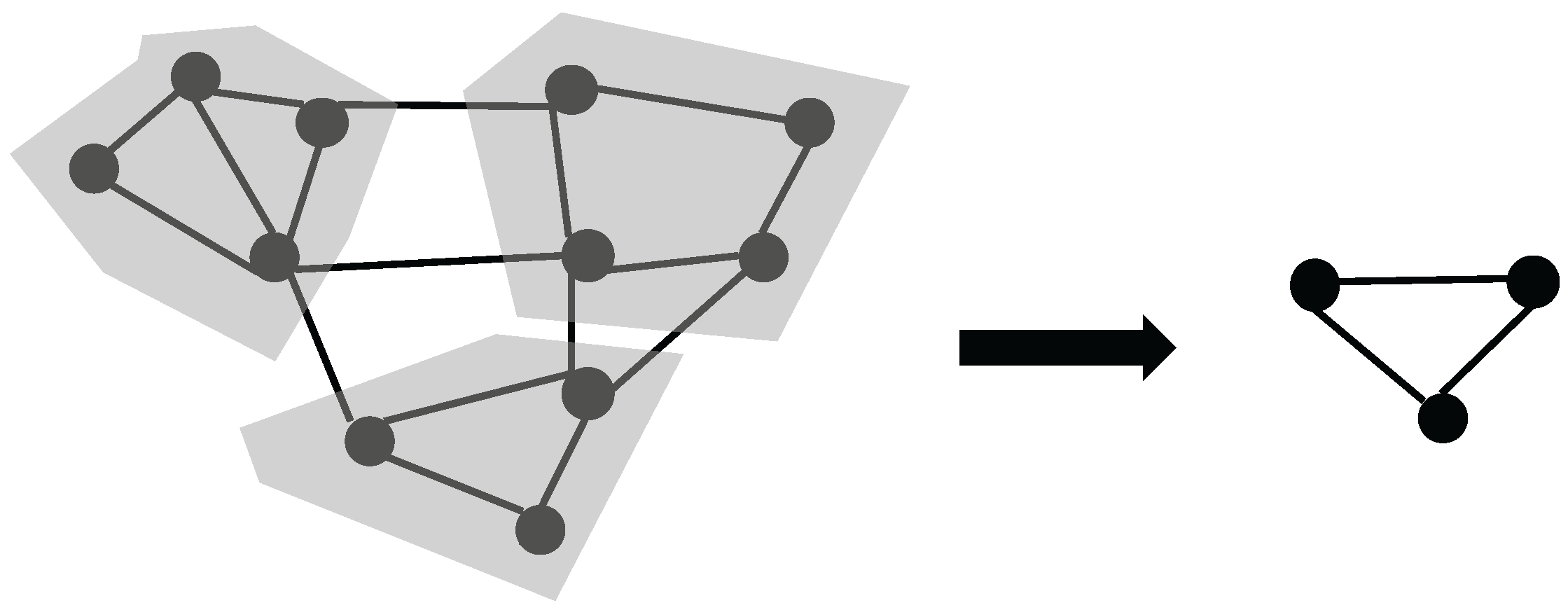
3.2. Multi-Level Approach
- Coarsening: We use the solar merger [37] to generate a sequence of graphs , , …, , where the maximum number of nodes in the coarsest is 50. Note that this hierarchical structure is strictly preprocessed, and does not need to be updated over time.
- Placement: To initialize the layout for the next level graph, we keep the sun node’s position and assign its child nodes along a circle around it.
- Layout: We use our approximated force-directed layout algorithm to update graph layout of each level. We parallelize our algorithm to achieve real-time interactions for graphs with millions of nodes.
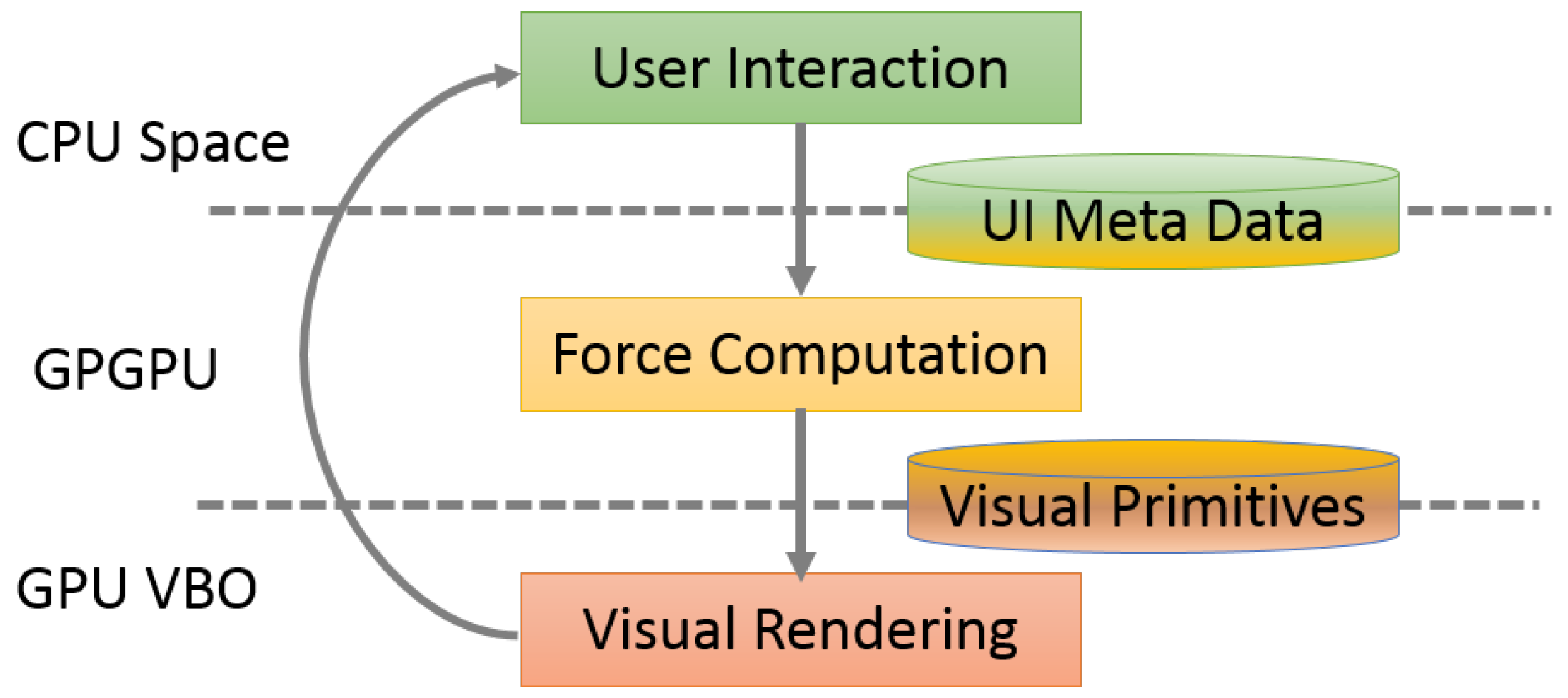
4. GPU Implementation
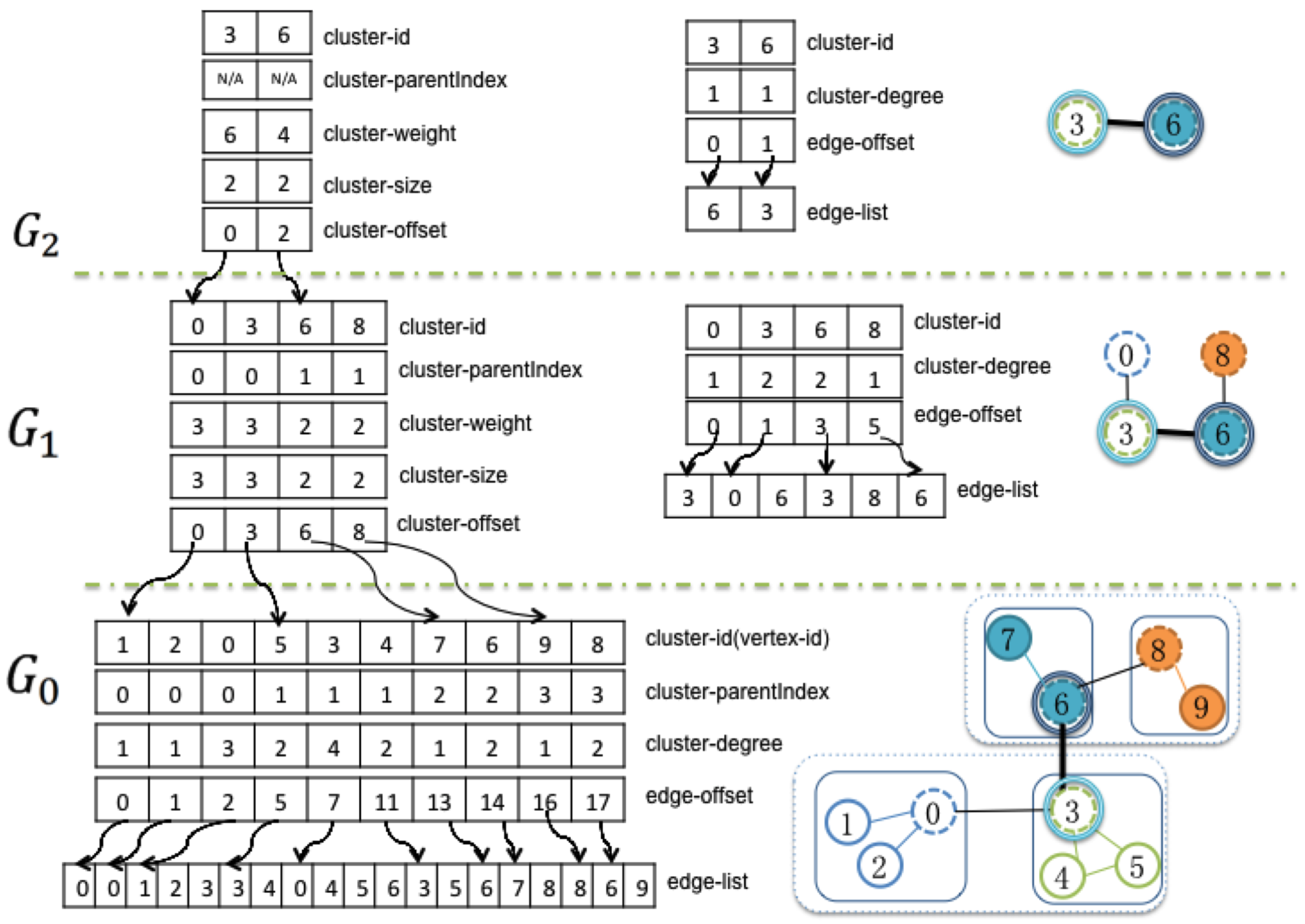
4.1. Data Storage
- cluster-id stores the nodes of the current level graph, which are the sun nodes from the lower level graph.
- cluster-parentIndex provides the indexes of the sun nodes for the next level graph.
- cluster-weight is the number of nodes in the finest level graph that are descendent members of current cluster.
- cluster-size is the number of nodes collapsed into this node from its next lower level graph.
- cluster-offset is the actual index of the nodes in the sub-graph.
- cluster-degree is the number of edges that other clusters connect to the current cluster.
- edge-offset stores the beginning index of the adjacency edge list.
- edge-list is the adjacency edge list of the current level graph.
4.2. GPU Kernels
| Algorithm 1: Attractive Force Kernel |
 |
4.3. Workload Imbalance
5. Results and Discussion
| Algorithm 2: Approximated Repulsive Forces |
 |
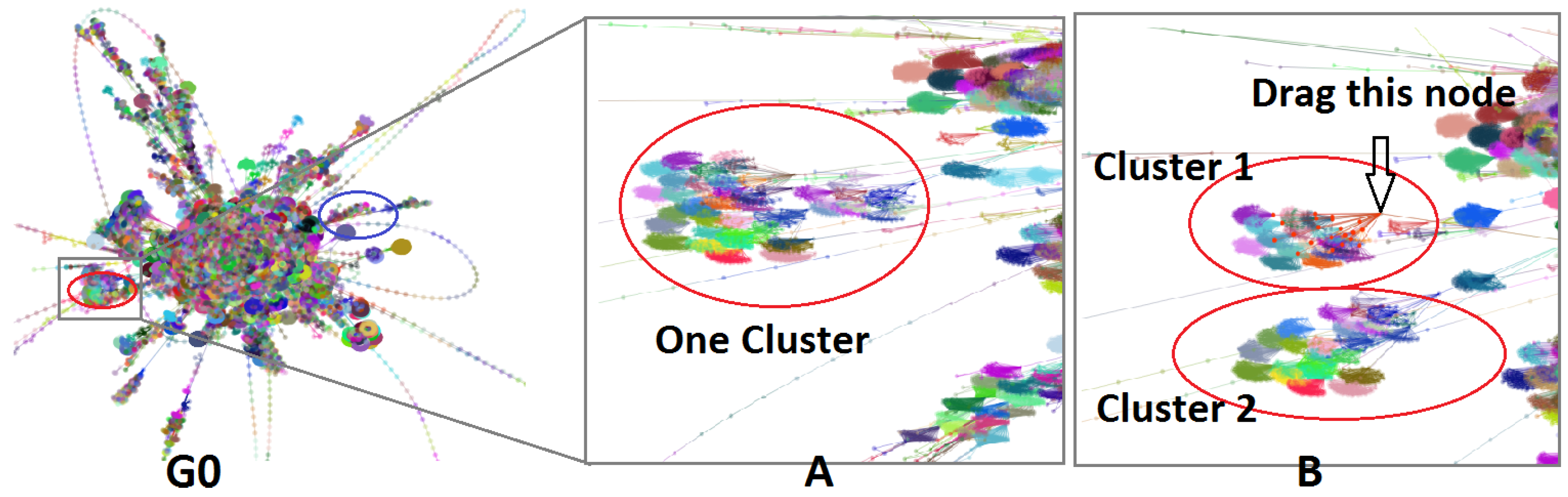
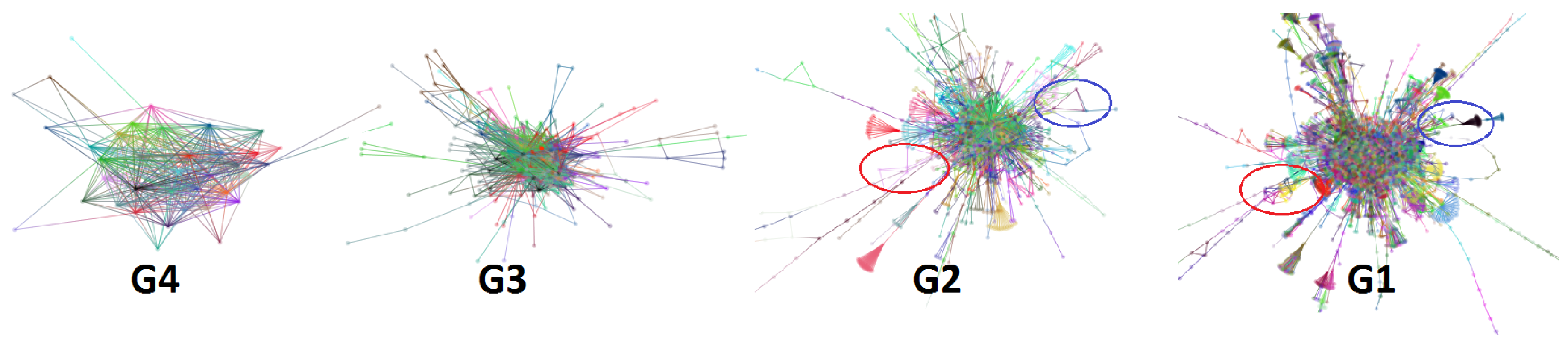
5.1. Visual Assessment
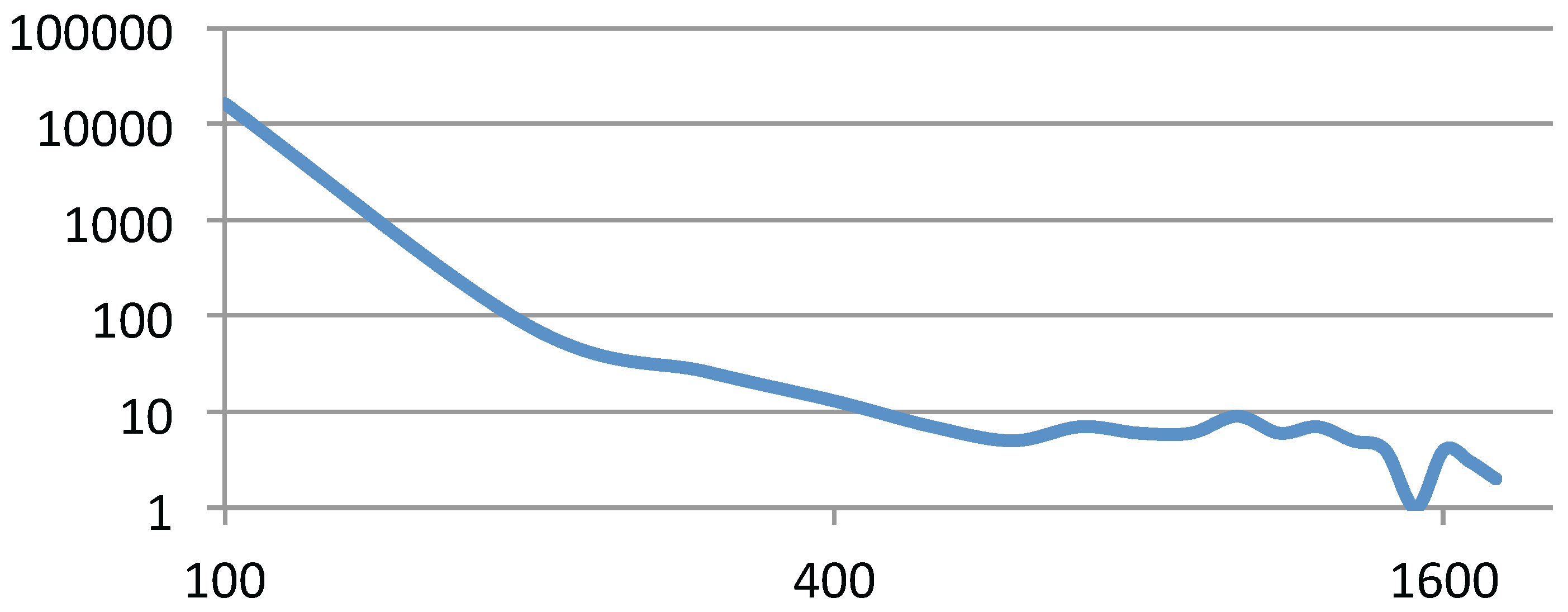
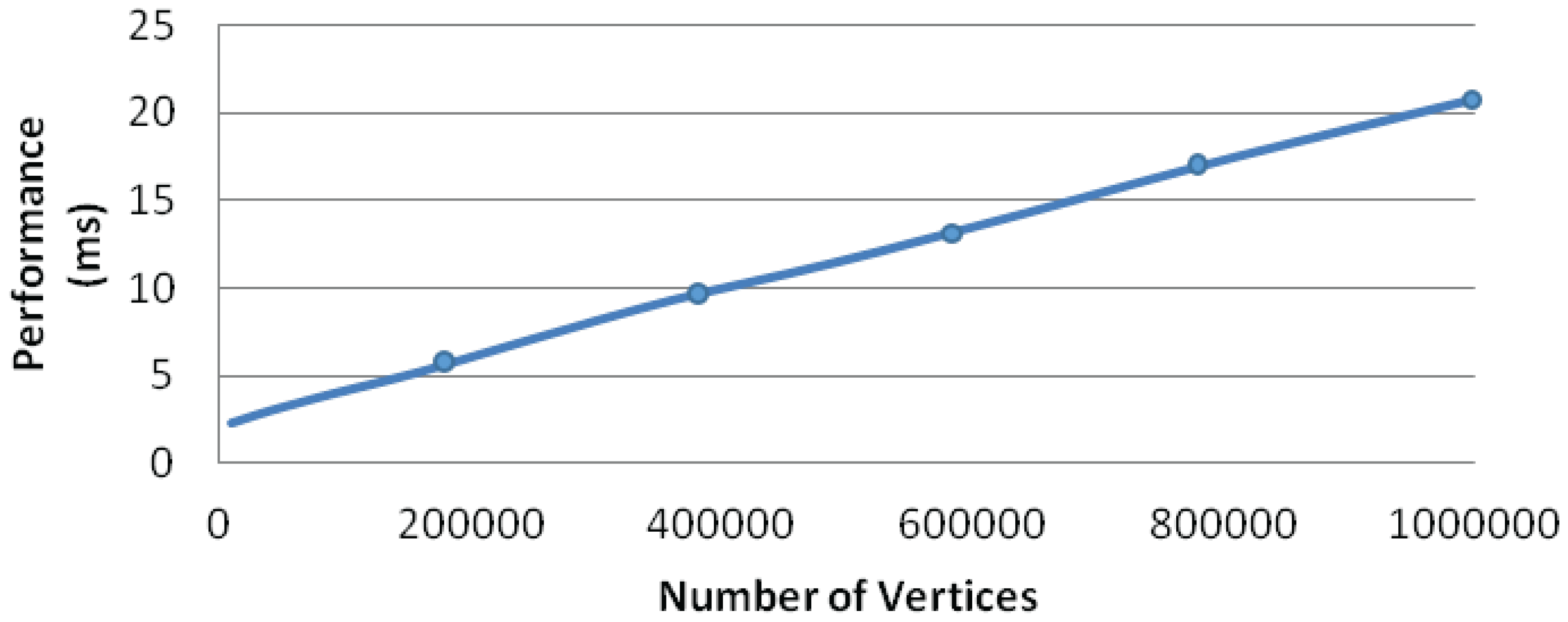
5.2. Performance Analysis
5.3. Discussion
6. Usage Scenarios
6.1. Visual Exploration of Web Networks
6.2. Visual Exploration of Co-Authorship Networks
7. Lessons Learned
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heer, J.; Boyd, D. Vizster: Visualizing online social networks. In Proceedings of the IEEE Symposium on Information Visualization, Minneapolis, MN, USA, 23–25 October 2005; pp. 32–39.
- Henry, N.; Fekete, J.D.; McGuffin, M.J. NodeTrix: A hybrid visualization of social networks. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1302–1309. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sun, M.; Yao, D.D.; North, C. Visualizing Traffic Causality for Analyzing Network Anomalies. In Proceedings of the ACM International Workshop on Security and Privacy Analytics, San Antonio, TX, USA, 2–4 March 2015; pp. 37–42.
- Sun, M.; Mi, P.; North, C.; Ramakrishnan, N. BiSet: Semantic Edge Bundling with Biclusters for Sensemaking. IEEE Trans. Vis. Comput. Graph. 2016, 22, 310–319. [Google Scholar] [CrossRef] [PubMed]
- Fiaux, F.; Sun, M.; Bradel, L.; North, C.; Ramakrishnan, N. Bixplorer: Visual analytics with biclusters. J. Comput. 2013, 8, 90–94. [Google Scholar] [CrossRef]
- Sun, M.; Bradel, L.; North, C.L.; Ramakrishnan, N. The role of interactive biclusters in sensemaking. In Proceedings of the ACM Conference on Human Factors in Computing Systems, Toronto, ON, Canada, 26 April–1 May 2014; pp. 1559–1562.
- Kaufmann, M.; Wagner, D. Drawing Graphs: Methods and Models; Springer: London, UK, 2001. [Google Scholar]
- Battista, G.D.; Eades, P.; Tamassia, R.; Tollis, I.G. Graph Drawing: Algorithms for the Visualization of Graphs; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Hachul, S.; Jünger, M. An Experimental Comparison of Fast Algorithms for Drawing General Large Graphs; Springer: Berlin/Heidelberg, Germany, 2006; pp. 235–250. [Google Scholar]
- Shneiderman, B.; Aris, A. Network visualization by semantic substrates. IEEE Trans. Vis. Comput. Graph. 2006, 12, 733–740. [Google Scholar] [CrossRef] [PubMed]
- Endert, A.; Fiaux, P.; North, C. Semantic interaction for visual text analytics. In Proceedings of the ACM Conference on Human Factors in Computing Systems, Austin, TX, USA, 5–10 May 2012; pp. 473–482.
- Fruchterman, T.M.; Reingold, E.M. Graph drawing by force-directed placement. Softw. Pract. Exp. 1991, 21, 1129–1164. [Google Scholar] [CrossRef]
- Greengard, L.; Rokhlin, V. A fast algorithm for particle simulations. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
- Godiyal, A.; Hoberock, J.; Garland, M.; Hart, J.C. Rapid Multipole Graph Drawing on the GPU; Springer: Berlin/Heidelberg, Germany, 2009; pp. 90–101. [Google Scholar]
- Burtscher, M.; Pingali, K. An Efficient CUDA Implementation of the Tree-Based Barnes Hut N-Body Algorithm, GPU Computing Gems Emerald Edition ed; Morgan Kaufmann: Burlington, MA, USA, 2011; pp. 13–75. [Google Scholar]
- Frishman, Y.; Tal, A. Multi-level graph layout on the GPU. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1310–1319. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y. Algorithms for visualizing large networks. Comb. Sci. Comput. 2011, 5, 180–186. [Google Scholar]
- Davidson, R.; Harel, D. Drawing graphs nicely using simulated annealing. ACM Trans. Graph. 1996, 15, 301–331. [Google Scholar] [CrossRef]
- Eades, P. A heuristics for graph drawing. Congr. Numer. 1984, 42, 146–160. [Google Scholar]
- Kamada, T.; Kawai, S. An algorithm for drawing general undirected graphs. Inf. Process. Lett. 1989, 31, 7–15. [Google Scholar] [CrossRef]
- Harel, D.; Koren, Y. Graph Drawing by High-Dimensional Embedding; Springer: Irvine, CA, USA, 2002; pp. 207–219. [Google Scholar]
- Koren, Y.; Carmel, L.; Harel, D. ACE: A fast multiscale eigenvectors computation for drawing huge graphs. In Proceedings of the IEEE Symposium on Information Visualization, Boston, MA, USA, 28–29 October 2002; pp. 137–144.
- Muelder, C.; Ma, K.L. A treemap based method for rapid layout of large graphs. In Proceedings of the PacificVIS, Kyoto, Japan, 5–7 March 2008; pp. 231–238.
- Wong, P.C.; Foote, H.; Mackey, P.; Chin, G.; Huang, Z.; Thomas, J. A space-filling visualization technique for multivariate small-world graphs. IEEE Trans. Vis. Comput. Graph. 2012, 18, 797–809. [Google Scholar] [CrossRef] [PubMed]
- Khoury, M.; Hu, Y.; Krishnan, S.; Scheidegger, C. Drawing Large Graphs by Low Rank Stress Majorization. Comput. Graph. Forum 2012, 31, 975–984. [Google Scholar] [CrossRef]
- Kobourov, S.G. Spring embedders and force directed graph drawing algorithm. arXiv, 2012; arXiv:1201.3011. [Google Scholar]
- Barnes, J.; Hut, P. A hierarchical O (N log N) force-calculation algorithm. Nature 1986, 324, 446–449. [Google Scholar] [CrossRef]
- Quigley, A.; Eades, P. FADE: Graph Drawing, Clustering, and Visual Abstraction; Springer: Berlin/Heidelberg, Germany, 2011; pp. 197–210. [Google Scholar]
- Yunis, E.; Yokota, R.; Ahmadia, A. Scalable force directed graph layout algorithms using fast multipole methods. In Proceedings of the 2012 11th International Symposium on Parallel and Distributed Computing, Munich, Germany, 25–29 June 2012; pp. 180–187.
- Gajer, P.; Kobourov, S.G. GRIP: Graph Drawing with Intelligent Placement; Springer: Berlin/Heidelberg, Germany, 2002; pp. 222–228. [Google Scholar]
- Walshaw, C. A Multilevel Algorithm for Force-Directed Graph Drawing; Springer: Berlin/Heidelberg, Germany, 2001; pp. 171–182. [Google Scholar]
- Bartel, G.; Gutwenger, C.; Klein, K. An Experimental Evaluation of Multilevel Layout Methods; Springer: Berlin/Heidelberg, Germany, 2011; pp. 80–91. [Google Scholar]
- Mi, P.; Sun, M.; Masiane, M.; Cao, Y.; North, C. AVIST: A GPU-Centric Design for Visual Exploration of Large Multidimensional Datasets. Informatics 2016, 3, 18. [Google Scholar] [CrossRef]
- Auber, D.; Chriricota, Y. Improved efficiency of spring embedders: Taking advantage of GPU programming. In Proceedings of the Visualization, Imaging, and Image Processing, Palma de Mallorca, Spain, 29–31 August 2007; pp. 169–175.
- Jezowicz, T.; Kudelka, M.; Platos, J.; Snasel, V. Visualization of large graphs using GPU computing. In Proceedings of the Intelligent Networking and Collaborative Systems, Xi’an, China, 9–11 September 2013; pp. 662–667.
- Tikhonova, A.; Ma, K.L. A scalable parallel force-directed graph layout algorithm. In Proceedings of the 8th Eurographics Conference on Parallel Graphics and Visualization, Crete, Greece, 14–15 April 2008; pp. 25–32.
- Hachul, S.; Jünger, M. Drawing Large Graphs with a Potential-Field-Based Multilevel Algorithm, Graph Drawing; Springer: Berlin/Heidelberg, Germany, 2005; pp. 285–295. [Google Scholar]
- Chen, L.; Villa, O.; Krishnamoorthy, S.; Gao, G. Dynamic load balancing on single-and multi-GPU systems. In Proceedings of the Parallel & Distributed Processing, Atlanta, GA, USA, 19–23 April 2010; pp. 1–12.
- Hong, S.; Kim, S.K.; Oguntebi, T.; Olukotun, K. Accelerating CUDA Graph Algorithms at Maximum Warp. ACM SIGPLAN Not. 2011, 46, 267–276. [Google Scholar] [CrossRef]
- Chimani, M.; Gutwenger, C.; Jünger, M.; Klau, G.W.; Klein, K.; Mutzel, P. The open graph drawing framework (OGDF). In Handbook of Graph Drawing and Visualization; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011; pp. 543–569. [Google Scholar]
- Endert, A.; Hossain, M.S.; Ramakrishnan, N.; North, C.; Fiaux, P.; Andrews, C. The human is the loop: New directions for visual analytics. J. Intell. Inf. Syst. 2014, 43, 411–435. [Google Scholar] [CrossRef]
- Liu, Z.; Heer, J. The effects of interactive latency on exploratory visual analysis. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2122–2131. [Google Scholar] [CrossRef] [PubMed]
- Chalmers, M. A linear iteration time layout algorithm for visualizing high-dimensional data. In Proceedings of the 7th Conference on Visualization, San Francisco, CA, USA, 28–29 October 1996; pp. 127–131.
- Aila, T.; Laine, S. Understanding the Efficiency of Ray Traversal on GPUs. In Proceedings of the Conference on High Performance Graphics, New Orleans, LA, USA, 1–3 August 2009; pp. 145–149.
- Merrill, D.; Garland, M.; Grimshaw, A. High-Performance and Scalable GPU Graph Traversal. ACM Trans. Parallel Comput. 2009, 1, 1–30. [Google Scholar] [CrossRef]
- Ingram, S.; Munzner, T.; Olano, M. Glimmer: Multilevel MDS on the GPU. IEEE Trans. Vis. Comput. Graph. 2009, 15, 249–261. [Google Scholar] [CrossRef] [PubMed]
- The Computer Science Bibliography Website. Available online: http://dblp.uni-trier.de/ (accessed on 30 November 2016).
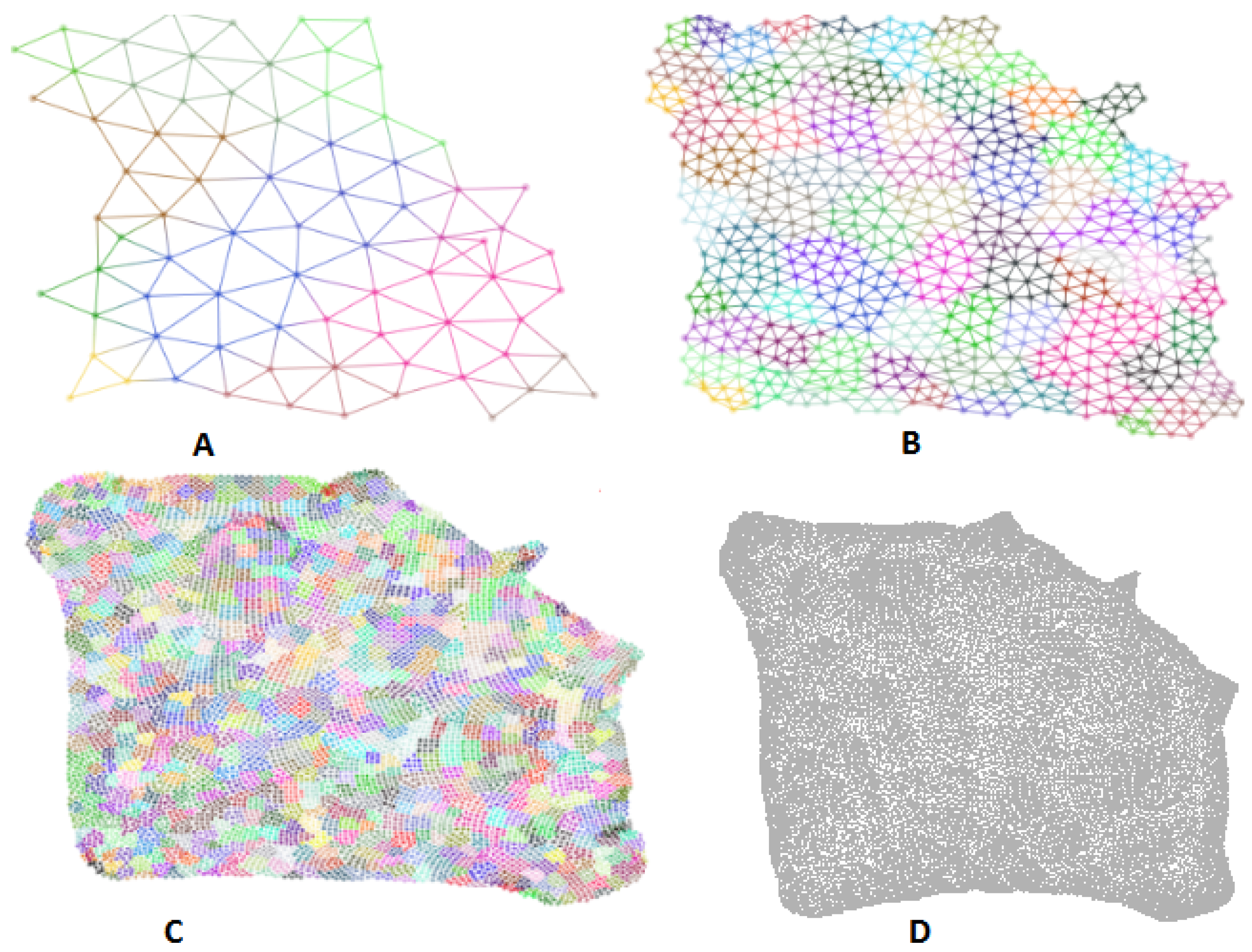

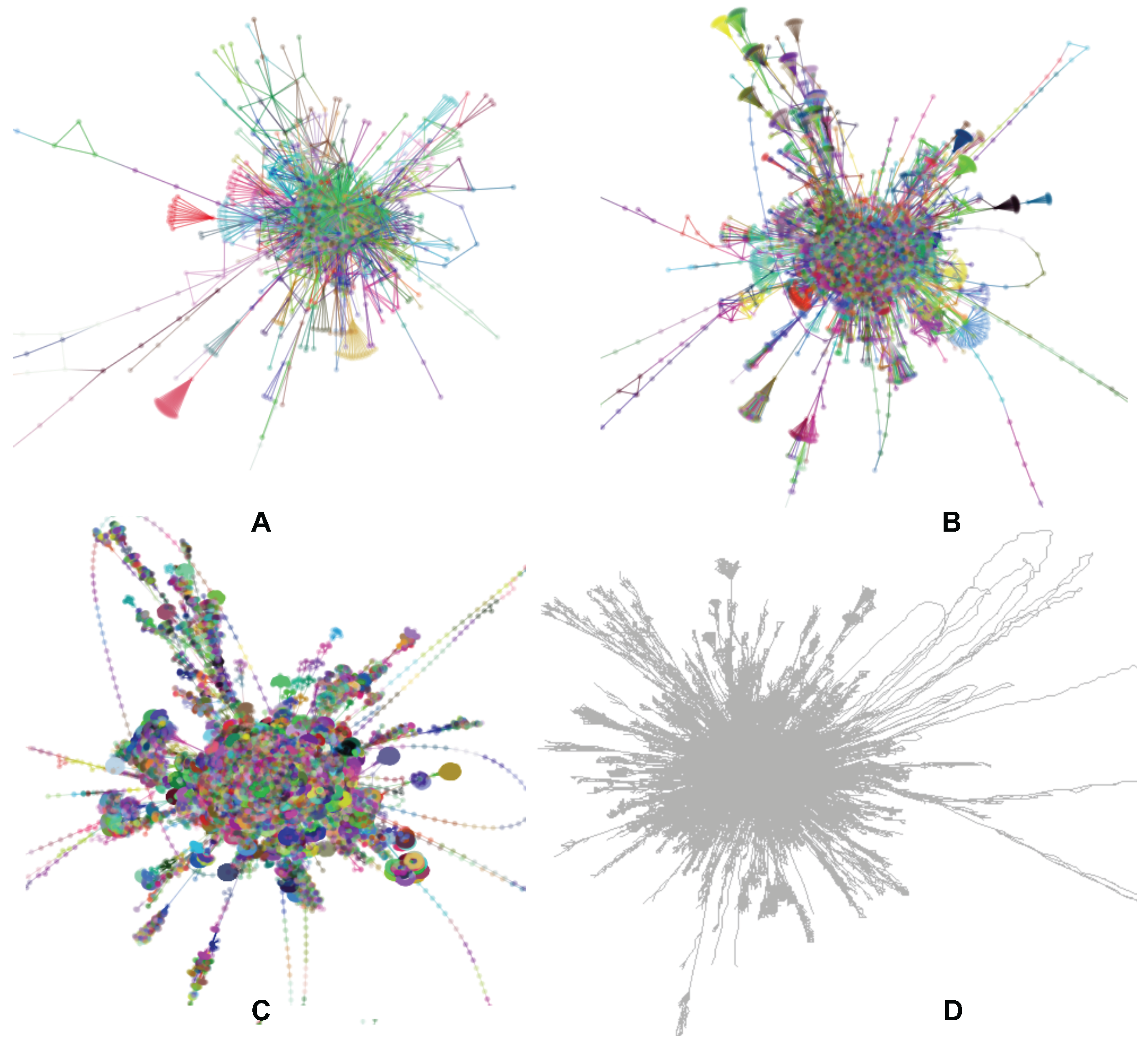

| Graph | Number of Vertices | Number of Edges |
|---|---|---|
| crack | 10,240 | 30,380 |
| finan512 | 74,752 | 261,120 |
| web-Stanford | 255,265 | 1,941,926 |
| grid-mesh | 1,000,000 | 1,998,000 |
| roadNet-TX | 1,379,917 | 3,843,320 |
| Performance | Crack | Finan512 | Web-Stanford | Grid-Mesh | RoadNet-TX |
|---|---|---|---|---|---|
| on CPU | 63.900 | 630.000 | 2581.399 | 7814.100 | 11,484.799 |
| Our approximated force calculation on CPU | 6.799 | 83.738 | 337.049 | 476.548 | 473.564 |
| GPU Kernel Attractive-Force | 0.315 | 0.660 | 38.177 | 1.287 | 1.767 |
| GPU Kernel Approximated Repulsive-Force | 2.099 | 3.887 | 28.184 | 14.484 | 17.819 |
| GPU Kernel Updated-Position | 0.007 | 0.008 | 0.015 | 0.013 | 0.011 |
| GPU Others | 0.302 | 0.383 | 0.728 | 1.296 | 1.727 |
| GPU Total | 2.732 | 4.938 | 67.104 | 17.080 | 21.324 |
| Rendering (graph nodes) | 0.809 | 1.288 | 2.252 | 4.958 | 9.727 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, P.; Sun, M.; Masiane, M.; Cao, Y.; North, C. Interactive Graph Layout of a Million Nodes. Informatics 2016, 3, 23. https://doi.org/10.3390/informatics3040023
Mi P, Sun M, Masiane M, Cao Y, North C. Interactive Graph Layout of a Million Nodes. Informatics. 2016; 3(4):23. https://doi.org/10.3390/informatics3040023
Chicago/Turabian StyleMi, Peng, Maoyuan Sun, Moeti Masiane, Yong Cao, and Chris North. 2016. "Interactive Graph Layout of a Million Nodes" Informatics 3, no. 4: 23. https://doi.org/10.3390/informatics3040023
APA StyleMi, P., Sun, M., Masiane, M., Cao, Y., & North, C. (2016). Interactive Graph Layout of a Million Nodes. Informatics, 3(4), 23. https://doi.org/10.3390/informatics3040023





